On the Involution Generators of the Mapping Class Group of a Punctured Surface
Abstract.
Let denote the mapping class group of a connected orientable surface of genus with punctures. For every even integer and , we prove that can be generated by three involutions. If the number of punctures is odd and , we show that for can be generated by four involutions. Moreover, we show that for an even integer and , can be generated by four involutions.
1. Introduction
Let denote a connected orientable surface of genus- with -punctures, when we write . The mapping class group of is the group of isotopy classes of orientation-preserving homeomorphisms of preserving the set of punctures.
Here is a brief history of generating sets for : Dehn [4] showed that can be generated by Dehn twists. About a quarter century later, Lickorish [15] gave a generating set consisting of Dehn twists. Later, Humphries [8] reduced the number of Dehn twist generators to . He also proved that the number is minimal for . Johnson [10] proved that the same set of Dehn twists also generates . In the presence of multiple punctures, Gervais [7] proved that can be generated by Dehn twists for .
If it is not required that the generators are Dehn twists, then it is possible to obtain smaller generating sets for : For and , Lu [17, Theorem ] proved that can be generated by three elements.For and or , a minimal (since the group is not abelian) generating set of two elements, a product of two Dehn twists and a product of Dehn twists, was first given by Wajnryb [25]. Korkmaz [12, Theorem ] improved this result by showing that one of these two generators can be taken as a Dehn twist. He also showed that this group is generated by two elements of finite order [12, Theorem ]. For , Kassabov obtained a generating set of involution elements where the number of generators depends on and the parity of (see [11, Theorem 1]). Later, Monden [20] removed the parity condition on for and . For and , Monden [21] also gave a generating set for consisting of three elements. Recently, he [22] gave a minimal generating set for containing two elements for .
Note that any infinite group generated by two involutions must be isomorphic to the infinite dihedral group whose subgroups are either cyclic or dihedral. Since contains nonabelian free groups, it cannot be generated by two involutions. In this paper, we obtain the following result (cf. [11, Remark 5]):
Theorem A.
For every even integer and , can be generated by three involutions. Moreover, for every even integer and for or , can be generated by four involutions.
At the end of the paper, we also show that Theorem A also holds for the cases or . For surfaces with odd number of punctures, we have the following result:
Theorem B.
For every odd integer and , is generated by four involutions. Moreover, for every odd integer and for or , can be generated by five involutions.
The paper is organized as follows: In Section 2, we quickly provide the necessary background on mapping class groups. The proofs of Theorem A and Theorem B are given in Section 3.
Acknowledgements. This work was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK)[grant number 120F118].
2. Background and Results on Mapping Class Groups
Let denote a connected orientable surface of genus with punctures specified by the set of distinguished points. If is zero then we omit it from the notation and write . The mapping class group of the surface is defined to be the group of the isotopy classes of orientation preserving self-diffeomorphisms of which fix the set . The mapping class group of the surface is defined to be the group of isotopy classes of all orientation preserving self-diffeomorphisms of which fix the set . Let denote the subgroup of consisting of elements which fix the set pointwise. It is obviuos that we have the following exact sequence:
where denotes the symmetric group on the set and the last projection is given by the restriction of the isotopy class of a diffeomorphism to its action on the punctures.
Let be an embedded arc that joins two punctures and and does not intersect on .
Let denote a closed regular neighbourhood of , which is a disk with two punctures.
There exists a diffeomorphism , which interchanges the punctures such that is equal to the right handed Dehn twist about and is the identity on the complement of the interior of . Such a diffeomorphism is said to be the (right handed) half twist about . It can be extended to a diffeomorphism of . Throughout the paper we do not distinguish a
diffeomorphism from its isotopy class. For the composition of two diffeomorphisms, we
use the functional notation; if and are two diffeomorphisms, then
the composition means that is applied first and then .
For a simple closed
curve on , following [1, 13], we denote the right-handed
Dehn twist about by the corresponding capital letter .
Let us also remind the following basic facts of Dehn twists that we use frequently throughout the paper: Let and be
simple closed curves on and .
-
•
If and are disjoint, then (Commutativity).
-
•
If , then (Conjugation).
Let us finish this section by noting that we denote the conjugation relation by for any .
3. Involution generators for
Let us start this section by recalling the following set of generators given by Korkmaz [13, Theorem ].
Theorem 3.1.
If , then the mapping class group can be generated by the four elements , , , .
Let us also recall the following well known result from algebra.
Lemma 3.2.
Let and be groups. Suppose that the following short exact sequence holds,
Then the subgroup contains and has a surjection to if and only if .
In our case where and , we have the following short exact sequence:
Therefore, we obtain the following useful result which follows immediately from Lemma 3.2. Let be a subgroup of . If the subgroup contains and has a surjection to then .
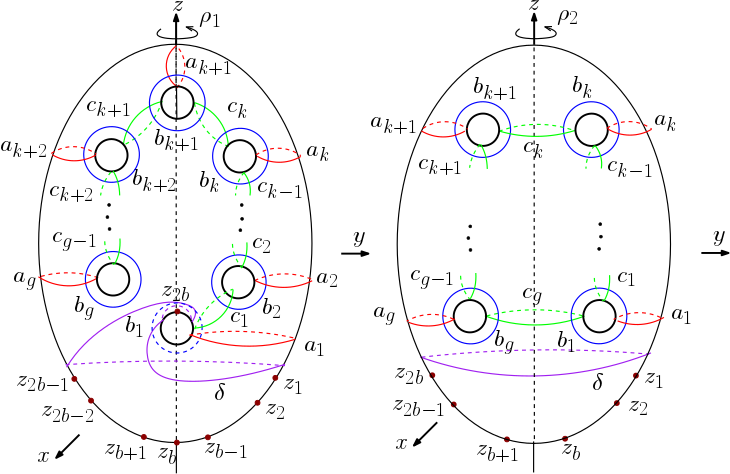
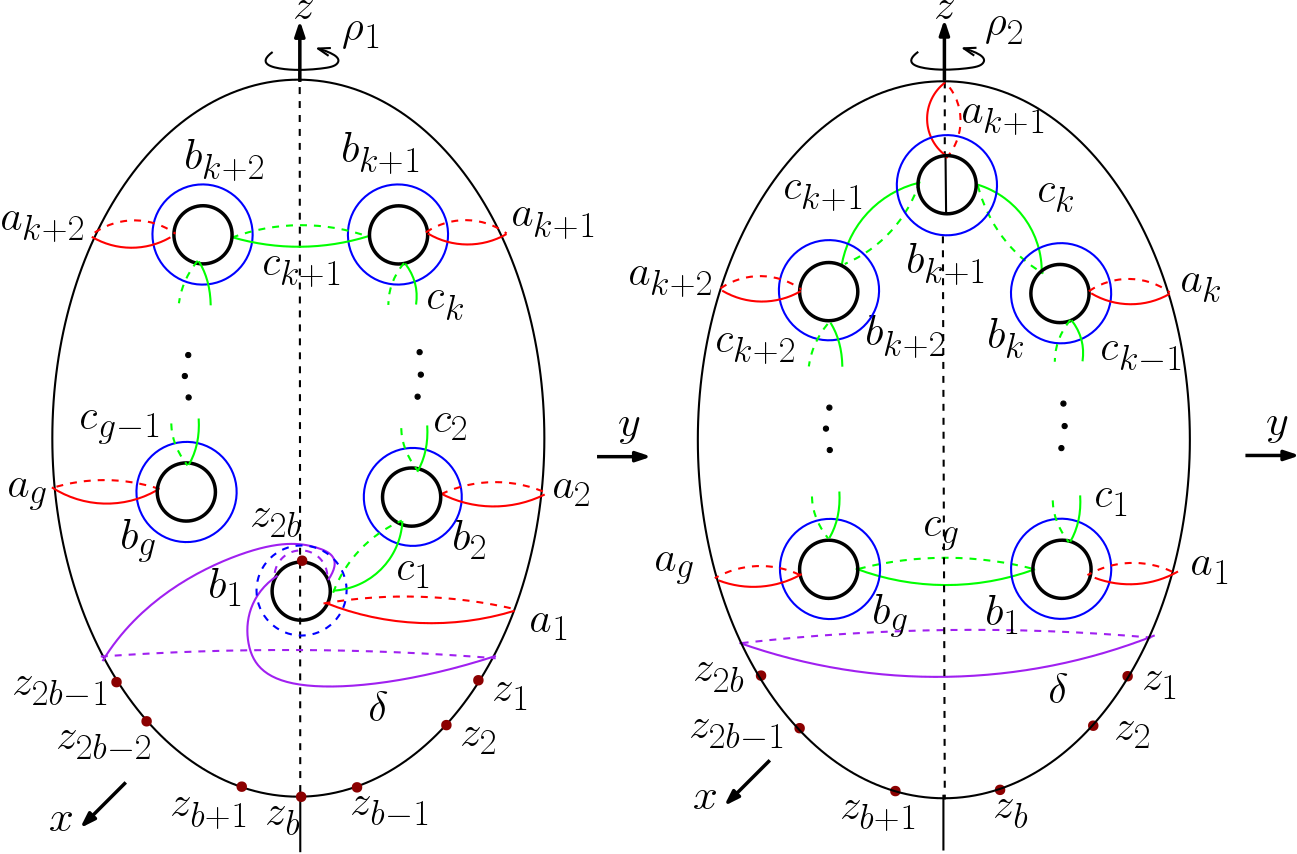
Throughout the paper, we consider the embeddings of into in such a way that it is invariant under the rotations and . Here, and are the rotations by about the -axis (see Figures 1 and 2). Note that contains the element which satisfies the following:
-
(i)
, for and ,
-
(ii)
for ,
-
(iii)
and for .
We want to note here that, in the following lemmata, where we present generating sets for surfaces with even number of punctures, we mainly follow the proof of [13, Theorem ]. We use them in the proof of Theorem A and then for surfaces with odd number of punctures we explain how our arguments are modified.
Lemma 3.3.
For every even integer and every even integer , the subgroup of generated by the elements
contains the Dehn twists , and for .
Proof.
Consider the models of depicted in Figure 1. Let and let be the subgroup of generated by the elements , and . One can see that the elements and are contained in the subgroup . Let be the element obtained by the conjugation of by . Since
and
Let be the element , that is
Since we use repeatedly similar calculations in the remaining parts of the paper, let us provide some details here. It can be shown that the diffeomorphism maps the curves to the curves , respectively. Also it follows from the factorizations of half twists and commute and we get
The subgroup contains the following elements:
From these, we obtain the element , which is contained in . By conjugating this element with powers of , we conclude that
The subgroup also contains the element . After conjugating with and considering the inverse, we have . This in turn implies that for , the elements
We also have the following elements in :
Hence, we can conclude that . Again conjugating with implies that
Furthermore, we can see that contains the following elements:
From these, we obtain . By the action of , we can conclude that
This completes the proof by Theorem 3.1 since the subgroup contains the elements
If is odd and is even, we have the following result:
Lemma 3.4.
For every odd integer and even integer , the subgroup of generated by the elements
contains the Dehn twists , and for .
Proof.
Consider the models for as shown in Figure 2. Let denote the subgroup of generated by the elements , and , where . The elements and belong to the subgroup . Let denote the conjugation of by ,
It is easy to verify that the element
is contained in . Let
Thus we get the element
which is contained in . This implies that . By conjugating with powers of , we see that
for all . In particular, the element . Hence, the subgroup contains the following element:
Then, we see that the elements
are contained in , which implies that the subgroup contains the element . By the action of we see that
for all . Moreover, we get
From these, we have so that
for , by the action of . The remaining part of the proof can be completed as in the proof of Lemma 3.3.
In the following four lemmata, we give generating sets for smaller genera.
Lemma 3.5.
For and every even integer , the group generated by the elements
contains the Dehn twists , and for .
Proof.
Consider the models for as shown in Figure 1. Let be the subgroup of generated by the elements , , and where and . Hence the elements , and are contained in the subgroup .
The subgroup contains the following elements:
Hence we get the element . By the action of , for all ,
Moreover, we have
This implies that and and so
for all , by conjugating these elements with powers of . The proof can be completed as in the proof of Lemma 3.3.
Lemma 3.6.
For and every even integer , the group generated by the elements
contains the Dehn twists , and for .
Proof.
Consider the models for as shown in Figure 2. Let denote the subgroup of generated by the elements , , and where and . Thus the elements , and are in the subgroup .
One can obtain the following elements:
which are contained in . Thus we get that and . By conjugating these elements with powers of , we see that
which also implies that for all and . Finally, it can be verified that
so that the group contains the element
Hence for all by the action of . The rest of the proof is similar to that of Lemma 3.3.
Lemma 3.7.
For and every even integer , the group generated by the elements
contains the Dehn twists , and for .
Proof.
Let us consider the models for as shown in Figure 1 and let be the subgroup of generated by the elements , , and where and . Thus it is clear that the elements , and belong to the subgroup . We have the element
Thus the subgroup contains the elements and . By conjugating these elements with powers of , we get
for all . One can also obtain that the subgroup contains the following elements:
Thus we obtain that . By the action of , for all . The remaining part of the proof is very similar to that of Lemma 3.3.
Lemma 3.8.
For and every even , the group generated by the elements
contains the Dehn twists , and for .
Proof.
Consider the models for as shown in Figure 2. Let be the subgroup of generated by the elements , , and where and . Thus the elements , and are contained in the subgroup . We get the elements
From these, the subgroup contains the elements and , which implies that . Hence
for all and , by the action of . We also have the following element
which is contained in . This implies that
for by the action of . One can complete the proof as in the proof of Lemma 3.3.
Remark 3.9.
Now, in the remainder of the paper let be the subgroup of generated by the elements given explicitly in lemmata 3.3–3.8 with the conditions mentioned in these lemmata. The proof of the following lemma is similar to that of [2, Lemma ], nevertheless we give a proof for the sake of completeness of the paper.
Lemma 3.10.
The group is contained in the group .
Proof.
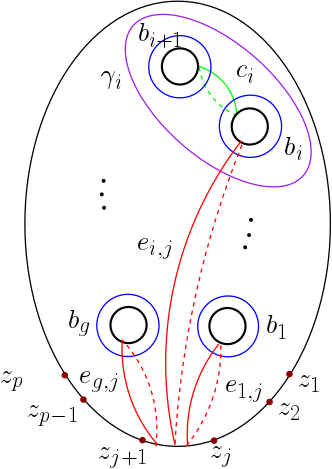
It follows from the subgroup contains the elements , and for all and by lemmata 3.3–3.8 that it is sufficient to prove that contains the Dehn twists for some fixed (). Let us first note that contains and . Consider the models for as shown in Figures 1 and 2. By the fact that the diffeomorphism maps to , we get
The diffeomorphism which maps each to for (see Figure 3). By the proof of [2, Lemma ], the group contains the element . Thus we have
Likewise, the diffeomorphism sends to . Then we obtain
It follows from
that
Continuing in this way, we conclude that the elements belong to , which completes the proof.
Proof of Theorem A.
If and : In this case, consider the surface as in Figure 1. Since
we get
Also, since , it is easy to see that is an involution. Therefore, the generators of the subgroup given in Lemma 3.3 are involutions.
If and : In this case, consider the surface as in Figure 2. It follows from
that we have
Also, by the fact that , it is easy to see that the element is an involution. We conclude that the generators of the subgroup given in Lemma 3.4 are involutions.
If or and : It follows from
-
•
, and if ,
-
•
, and if ,
-
•
, and if
-
•
, and if and
-
•
if or
that the following elements:
-
•
and if ,
-
•
and if ,
-
•
and if and
-
•
and if
Next, we show that the subgroup is equal to the mapping class group . By Lemma 3.10, the group is contained in the group . Hence, by Lemma 3.2, we need to prove that is mapped surjectively onto . The element has the image .
As proven above, the Dehn twists , and belong to the subgroup . Thus, it can be easily observed that the factorization of half twists are contained in subgroup . Therefore, the group also contains the following element:
which has the image . This completes the proof since the elements and of generate the whole group if is even [9, Theorem B].
When the number of punctures is odd, we introduce an additional involution (depicted in Figure 4) to our generating set. The main reason behind adding an extra involution is for generating the symmetric group . We want to point out that aside from generating , all of our proofs in the case of even number of punctures work for odd number of punctures. For and , we distribute punctures as in Figures and in [2] (see also Remark 3.9).
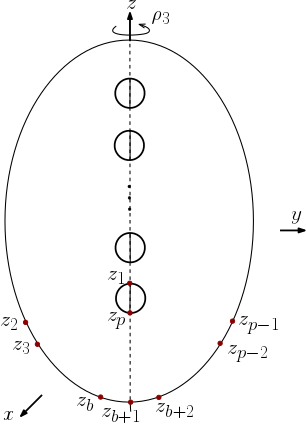
Proof of Theorem B.
For the first part of the proof we show that
-
(i)
For every even integer and every odd integer , the subgroup of generated by the elements
-
(ii)
For every odd integer and odd integer , the subgroup of generated by the elements
Note that, it is enough to prove that the subgroup generated by the elements above mapped surjectively onto . For this, consider the images of the elements , and
This finishes the proof for the first part,since these elements generate , see [20, Lemma 6]. For the second part of the theorem, note that adding to the corresponding generating set given in Theorem A, finishes the proof.
As a last observation, one can prove that Theorem A also holds for the cases or . In theses cases, the generating set of can be chosen as
It can be easily proven that the group contains by the similar arguments in the proofs of lemmata 3.3–3.8. The element has the image . Hence, this element generates for . If , we distribute the punctures as in [11, Figure ]. Then the element has the image , which generate together with the element . Therefore, the group is mapped surjectively onto for . One can conclude that the group is equal to .
References
- [1] T. Altunöz, M. Pamuk and O. Yildiz: Generating the twist subgroup by involutions, to appear in the Journal of Topology and Analysis.
- [2] T. Altunöz, M. Pamuk and O. Yildiz: Generating the extended mapping class group by three involutions, to appear in Osaka J. Math.
- [3] D. R. J. Chillingworth: A finite set of generators for the homeotopy group of a non-orientable surface, Proc. Cambridge Philos. Soc. 65, (2) (1969), 409–430.
- [4] M. Dehn: The group of mapping classes, In: Papers on Group Theory and Topology. Springer-Verlag, 1987. Translated from the German by J. Stillwell (Die Gruppe der Abbildungsklassen, Acta Math 69, (1938), 135–206).
- [5] X. Du: The extended mapping class group can be generated by two torsions, Journal of Knot Theory and Its Ramifications 26, (11), (2017).
- [6] B. Farb and D. Margalit: A primer on mapping class groups, Princeton University Press. 49 (2011).
- [7] S. Gervais: A finite presentation of the mapping class group of a punctured surface, Topology. 40, (4) (2001), 703–725.
- [8] S. Humphries: Generators for the mapping class group, In: Topology of LowDimensional Manifolds, Proc. Second Sussex Conf., Chelwood Gate, (1977), Lecture Notes in Math. 722, (2) (1979), Springer-Verlag, 44–47.
- [9] I. M. Isaacs,and Thilo Zieschang, Generating symmetric groups, Amer. Math. Monthly 102, (8) (1995), 734–739.
- [10] D. Johnson, The structure of the Torelli group. I. A finite set of generators for , Ann. of Math. (2), 118, (3) (1983), 423–442.
- [11] M. Kassabov: Generating mapping class groups by involutions, ArXiv math.GT/0311455, v1 25Nov2003.
- [12] M. Korkmaz: Generating the surface mapping class group by two elements, Trans. Amer. Math. Soc. 367, (8) (2005), 3299–3310.
- [13] M. Korkmaz: Mapping class group is generated by three involutions, Math. Res. Lett. 27, (4) (2020), 1095-1108.
- [14] W. B. R. Lickorish: Homeomorphisms of non-orientable two manifolds, Proc. Cambridge Philos. Soc. 59, (2) (1963), 307–317.
- [15] W. B. R. Lickorish: A finite set of generators for the homeotopy group of a -manifold, Proc. Cambridge Philos. Soc. 60, (4) (1964), 769–778.
- [16] W. B. R. Lickorish: On the homeomorphisms of a non-orientable surface, Proc. Cambridge Philos. Soc. 61, (1) (1965), 61–64.
- [17] N. Lu: On the mapping class groups of the closed orientable surfaces, Topology Proc. 13 (1988), 293–-324.
- [18] F. Luo: Torsion elements in the mapping class group of a surface, ArXiv math.GT/0004048, v1 8Apr2000.
- [19] J. D. McCarthy, A. Papadopoulos: Involutions in surface mapping class groups, Enseign. Math. 33, (2) (1987), 275–290.
- [20] N. Monden: Generating the mapping class group of a punctured surface by involutions, Tokyo J. Math. 34, (2) (2011), 303–312.
- [21] N. Monden: The mapping class group of a punctured surface is generated by three elements, Hiroshima Math. J. 41, (1) (2011), 1–9.
- [22] N. Monden: On minimal generating sets for the mapping class group of a punctured surface, ArXiv math.GT/2103.01525, v1 2Mar2021.
- [23] J. Powell: Two theorems on the mapping class group of a surface, Proc. Amer. Math. Soc. 68, (3) (1978), 347–350.
- [24] M. Stukow: The extended mapping class group is generated by symmetries, C. R. Math. Acad. Sci. Paris 338, (5) (2004), 403–406. 117, (1) (2006), 1-9.
- [25] B. Wajnryb: Mapping class group of a surface is generated by two elements, Topology 35, (2) (1996), 377–383.