On the geography of -folds via asymptotic behavior of invariants
Abstract.
Roughly speaking, the problem of geography asks for the existence of varieties of general type after we fix some invariants. In dimension , where we fix the genus, the geography question is trivial, but already in dimension it becomes a hard problem in general. In higher dimensions, this problem is essentially wide open. In this paper, we focus on geography in dimension . We generalize the techniques that compare the geography of surfaces with the geography of arrangements of curves via asymptotic constructions. This involves resolutions of singularities and a certain asymptotic behavior of the associated Dedekind sums and continued fractions. We discuss the general situation with emphasis on dimension , analyzing the singularities and various resolutions that show up, and proving results about the asymptotic behavior of the invariants we fix.
Keywords: Complex algebraic geometry, Geography of threefolds, Chern numbers.
MSC2020: 14A99, 14C17, 14J30, 14J40.
1. Introduction
We work with normal projective varieties over the complex numbers . As usual, when , , or we say that is a curve, a surface, or a -fold respectively. The main purpose of this paper is to study the geography problem for -folds of general type. Following the philosophy of Hirzebruch and Sommese [Hir83][Som84] studying the slopes of Chern numbers for minimal surfaces of general type, in [Hun89] the author proposed the study of slopes
for non-singular minimal -folds of general type. This, allows us to work by charts, in this case, in the charts or .
Since minimal models may admit singularities in higher dimensions, we want to extend our problem, but we do not directly have the notion of Chern numbers. If is a non-singular -fold, then we have Chern numbers
From the birational geometry of -folds, the triple is invariant between minimal models of the same birational class [Mat10, 12.1.2] [Kol91, Th.3.2.2]. Then we are extending naturally to the singular case by taking slopes . There are several inequalities for minimal -folds, most of them for Gorenstein minimal -folds, since we have well-behaved dualities on the cohomology groups. For example, in this case . The most important for us are the Miyaoka-Yau inequality ([Miy87] [GKPT19]), and the classical general type inequalities where the last one is just for the Gorestein case. The search for Noether’s type inequalities is an active research area, see [CH06] [Hu18] [CCJ20].
Previous results in this research line are the following. In [Hun89], the author studied slopes of non-singular -folds with ample canonical class in the chart . In [CL01] is proved that the Chern slopes of non-singular -folds with ample canonical bundle define a bounded region by finding inequalities for the coordinate . For a more general result, let be the number of partitions of . In [DS22], it is proved that Chern slopes of non-singular -folds with ample canonical bundle define a bounded region in the chart . See [TN23, p.14-18] to see an updated map in the chart for non-singular -folds with ample canonical class. The problem is that we do not know if those regions are optimal as we have for surfaces, i.e., the slopes are dense in the interval .
1.1. Results of this work
When working with slopes, it turns out that we can apply the tool of -th root coverings to investigate their behavior. The main reason is that, as grows to infinity, the slopes erase the effects of the degree of the cover. This allows us to control the slopes from the base of the cover, and this is the main technique to get density results for surfaces
Consider the following data. Let be a non-singular -fold, and let be distinct prime divisors in . Assume that is a simple normal crossing divisor (SNC). Let be a positive integer, and let be a collection of integers coprime to . Assume that there exists a line bundle on such that
| (1) |
Then, there exists an -th root cover branched along , where is a -fold (Section 2.2). These are the -th root covers developed by Esnault and Viehweg (Cf. [EV92]). For curves, the prime divisors are distinct points on . Since points are isolated, we have as a non-singular curve. By the Riemann-Hurwitz formula, we have
Here is the first logarithmic Chern number of the pair (see Section 2.1). Hence, if we fix the points and we consider partitions with a prime number, then we asymptotically have .
Question 1.1.
Does this asymptotic phenomenon happen in higher dimensions?
In Section 3, we prove that this phenomenon occurs in any dimension for logarithmic morphisms of degree with branch locus as a disjoint collection of non-singular distinct prime divisors . As an application, for -root cover we have as a non-singular projective variety, thus in Corollary 3.2 we get.
Theorem A.
Assume we have -th root covers branched at . If is non-singular, then for each partition , the Chern numbers satisfy,
as for prime numbers.
∎
However, this theorem is restrictive for us in terms of geography. It is not easy to get the necessary hypothesis to construct a minimal -fold of general type. On the other hand, we do not drop the possibility of having applications in other contexts. Also, this is a cornerstone of our research and opens the following discussion.
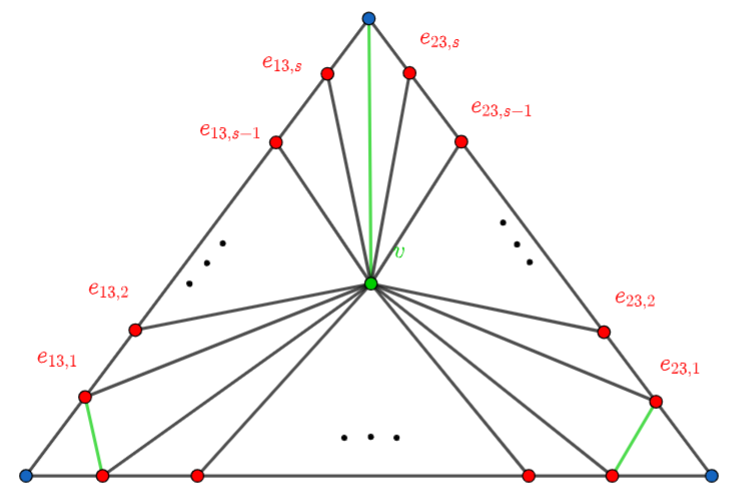
For , if the branch divisor has singularities, then have rational singularities [Vie77]. In order to have well-behaved invariants, we can choose a (partial) resolution of singularities. For , the asymptoticity of Chern numbers was proved in [Urz09] for random -th root covers. Let us explain briefly what random means (see Section 2.5 for more details). First, in dimension two, each singularity of is a cyclic surface singularity of type for some . Thus, we use the Hirzebruch-Jung algorithm (see Section 2.4.1) to resolve these singularities in a minimal way. For us, there are two important quantities, (1) the length of the resolution, i.e., the number of steps of the algorithm, and (2) the Dedekind sums,
where is the saw-tooth function (see Section 2.4.2). We get a resolution of singularities . However, the Chern numbers and depend on the lengths and the Dedekind sums coming from all cyclic singularities resolved. To guarantee asymptoticity, we have to consider asymptotic arrangements. Indeed, for each prime number , there exists a set (Section 2.5) such that for each , the lengths and Dedekind sums are bounded by for a constant . Thus we say that is an asymptotic arrangement if satisfies :
-
•
For prime numbers , there exists multiplicities such that the singularity over of is of type with .
-
•
For each there are line bundles such that
The main set-up is when there exists such that for each component of . Observe that the condition (1) is satisfied as
thus we can construct -th root covers. In [Urz09] was proved that for a random partition , the probability of being an asymptotic arrangement tends to as grows. In this way, for we take random asymptotic partitions, and we get a family of random surfaces with
Now we can discard the SNC property for the branch divisor for those one having only normal crossings. We consider a resolution such that the reduced divisor defined by is SNC. If such a divisor turns out to be an asymptotic arrangement, then we have the asymptotic result for Chern numbers as above. For this see [TN23, p. 57]), and see [Urz16] to connect this result with minimal models. A direct application is a relation between Chern slopes of simply connected surfaces of general type and Chern slopes of arrangements of lines [EFU22]. In this way, in higher dimensions, we have several issues with achieving an analog asymptotic result. For example, the singularities of are not cyclic, and the choice of a right (partial) resolution of with good behavior as grows is a challenging problem.
Question 1.2.
Is there an analog of the asymptotic results in dimension two for dimension three?
For instance, if this question has a positive answer, then we would be able to study the geography of -folds using arrangements of planes in . The first result in this direction is in Section 4.1, where we find that the Chern number is asymptotic and independent of the chosen resolution.
Theorem B.
Let be any non-singular projective -fold, and let be an asymptotic arrangement. For prime numbers there are projective non-singular -folds covers of degree such that
as
∎
However, the canonical volume and the topological characteristic depend on the chosen resolution. In this way, the first issue is that the singularities of are of order (multiplicity) , too big. This means that to connect with a non-singular model, at a bad choice of resolution we could have big exceptional data with respect to , and so we would lose the asymptotic property. In Section 4.2, we introduce a prototype of first step, i.e., by toric methods we construct a local cyclic resolution In this way, we get singularities of multiplicity lower than , and of cyclic quotient type. We are interested in cyclic quotient singularities since they are -terminal and have a well-known algorithm to resolve them: the Fujiki-Oka continuous fraction (Cf. [Ash19]). In Section 4.3 we globalize this local cyclic resolution, and we get a cyclic resolution having the desired asymptotic property. The following is a summary of Theorem 4.2 (using Corollary 2.16), Theorem 4.18, and Theorem 4.24.
Theorem C.
Let be any non-singular -fold, and let be an asymptotic arrangement. For prime numbers there are -folds with at most cyclic quotient singularities of order lower than such that
where are the Chern classes of the arrangement.
∎
It is important to note that the above is an embedded -resolution in the language of [ABMMOG12], introduced as an efficient resolution without useless data. In Section 5.1, as a by-product of the computations to get C, we construct minimal non-singular -folds of general type using as a base -folds with hyperplane sections. This allows us to prove.
Corollary 1.3.
For and prime numbers there are minimal non-singular -folds of general type over with slopes
as . In particular, as the degree of grows, the slopes have limit point .
∎
In Section 5.2, we see our resolution in terms of pairs . As a corollary, we prove that for asymptotic arrangements of hyperplane sections on a minimal -fold of general type, the resolution preserves the bigness of the -canonical divisor .
Corollary 1.4.
Let be a minimal non-singular projective -fold of general type, and let be a collection of hyperplane sections in general position. Then, for prime numbers there are finite morphisms of degree such that:
-
(1)
is of -general type, i.e., is big and nef,
-
(2)
,
-
(3)
has cyclic singularities (-terminal) of order lower than , and
-
(4)
the slopes of are arbitrarily near to .
We point out that our cyclic resolution preserves the positivity of the canonical volume, i.e., we start with and we get . So in future work, if we are able to control the MMP of the chosen resolution, then we will have the asymptotic results with nef, so for , the varieties will be minimal of general type. For us, the goal is that the asymptotic behavior of the slopes of coincides with the slopes of its minimal models. For this, we need a good terminalization of the cyclic singularities obtained. In Section 6 we discuss what means the word good.
Acknowledgments: I am grateful to my Ph.D. thesis advisor Giancarlo Urzúa for his time, guidance, and support throughout this work. The results in this paper are part of my Ph.D. thesis at the Pontificia Universidad Católica de Chile. I would also like to thank Jungkai Alfred Chen for his hospitality during my stay at the National Center for Theoretical Sciences in Taiwan. Special thanks to Pedro Montero and Maximiliano Leyton, for many comments and suggestions to improve this work. I was funded by the Agencia Nacional de Investigación y Desarrollo (ANID) through the Beca Doctorado Nacional 2019.
2. Preliminaries
2.1. Logarithmic properties
For a non-singular projective variety of dimension , let be its Chow ring, where are the Chow groups of -cycles. We denote its Chern classes by , i.e. the Chern classes of its tangent bundle [Har77, Appendix A]. We have that , where is the canonical class. We define the Chern numbers of as the degree of the top-intersection of its Chern classes
In the following, if the context is understood, we abuse notation using the symbol for Chern numbers or more simply the notation .
We have , and since we work over , it is well-known that , the topological Euler characteristic. These numbers are codified into the Todd class of by the following formal sum
As a consequence of the Hirzebruch-Riemann-Roch Theorem, we have the Noether’s identities, i.e., the analytic Euler characteristic are equal to the -th summand of . For example,
Definition 2.1.
A simple normal crossing (SNC) divisor is a reduced effective divisor with distinct non-singular components satisfying the following condition: for each there are local coordinates on such that the equation defining on is , with .
From [Iit77] we introduce the following sheaf on .
Definition 2.2.
For a SNC divisor , the sheaf of -differentials along , denoted by , is the -submodule of described as follows. Let be a point.
-
(i)
If , then .
-
(ii)
If , we choose local coordinates on with defining on . Then, is generated as -module by
If is a divisor on , whose associated reduced divisor is a SNC divisor, then for simplicity we set
In the rest of this section, we assume as a divisor with a SNC divisor.
Definition 2.3.
The -Chern classes of a pair are defined as
The -Chern numbers of a pair are defined as the degree of top-dimensional intersections
Lemma 2.4.
We have a natural exact sequence
which is known as the residual exact sequence.
Proof.
See [EV92, Proposition 2.3]. ∎
From the residual exact sequence, we can compute the Chern polynomial through the identity
| (2) |
Let , and let be any partition of positive integers. By convention, for the case we assume the existence of a unique partition, i.e., . We introduce the following notation,
Examples of this notation are,
and in general,
| (3) |
Corollary 2.5.
We have the identity,
Proof.
Using identity (2), and the previous identity (3) we can compute as the degree element of the expression
∎
Corollary 2.6.
Assume is non-singular, i.e., its non-singular components are pairwise disjoint. Then for each we have where
for each .
Proof.
Since is non-singular, then for all . Thus, from the identity (2) , we get
Using the Cauchy product formula for polynomials we have
and from this, the formula follows. ∎
Corollary 2.7.
Consider a non-singular -fold , and on . We have
Thus, the logarithmic Chern numbers for -folds are,
Proof.
Using identity (2) for , and looking for the degree terms we obtain . The other formulas are direct computations using the above lemmas. ∎
Example 2.8.
For a non-singular curve, set where are points. So for the unique -Chern number we have
Let be a non-singular surface, and with non-singular curves. Then
Where is the number of nodes of . See [Urz09, Prop. 3.1]. As in the case of nodes for surfaces, let us denote the number of triple points of by . Then we can rewrite
Example 2.9.
Let be a non-singular projective -fold. Let hyperplane sections defining an SNC arrangement. We have
Thus as grows, we have
Logarithmic Chern classes are well-behaved under logarithmic morphisms.
Definition 2.10.
Let be a non-singular projective variety and an effective divisor with as SNC divisor. A surjective morphism between non-singular projective varieties is called a -morphism, if is a SNC divisor.
Lemma 2.11.
For any -morphism , we have an injection
Moreover, if is finite and ramified at , then we have isomorphism outside the singularities of .
Proof.
See [Vie82, Lemma 1.6]. ∎
2.2. -th root covers
In this section, we follow [EV92, Sec. 3]. Consider the following building data where
-
(1)
is a non-singular projective variety of dimension ,
-
(2)
is an effective divisor on , with a SNC divisor,
-
(3)
is a prime number, and
-
(4)
a line bundle on such that .
With this building data, we construct
and the normalization will be called the -th root covering associated to the building data . Since the morphisms are finite of degree prime, both and are projective and irreducible. The morphism is branched at , and has its singularities over the intersection of components of . Thus, is non-singular if for all . On the other hand, if , then the intersection is defined by a local equation
where are local parameters for on . Thus the singularity of over is locally analytically isomorphic to the normalization of
Definition 2.12.
A partial resolution of singularities of is a projective, surjective, birational morphism with a projective normal variety having at most rational singularities. This last means that for any resolution of singularities we have for . As usual, we omit the word partial if is non-singular.
Since the degree of is a prime number, we have , where . Thus, for any partial resolution we must have a ramification formula
where is a divisor supported in the exceptional divisors of over .
Theorem 2.13.
For the -th root covering we have
-
(1)
The morphism is flat.
-
(2)
The variety has rational singularities.
-
(3)
We have the following decomposition on eigenspaces
Indeed, . Therefore is an affine morphism.
-
(4)
For any partial resolution of singularities , the composition satisfies the following -numerical equivalence
where is a divisor supported on the exceptional divisor of .
Proof.
For (1), (2), and (3) see [EV92, Ch. 3]. For (4), we use the fact that . In this way, there are non-singular open sets avoiding the singularities of . From Lemma 2.11, we get where is the strict transform of . In terms of divisors,
from where the result holds locally. After extending globally the exceptional term appears. ∎
The following corollary will be useful in Section 5. First recall that on a variety a curve is -negative, -positive or -trivial if its intersection with the canonical divisor is negative, positive, or zero.
Corollary 2.14.
The -divisor is an effective -divisor. Thus, if is nef, then the -negative curves of are contained in the support of .
Proof.
The first assertion is a direct consequence of 4.5. Now assume that is nef, and let be a curve in . If is not contained in the support of , then
since is nef (projection formula), and effectiveness of . Thus, if is negative must lie in the support of .
∎
Lemma 2.15.
Let be a normal variety and a proper, surjective, birational morphism. Assume that has rational singularities. Then and for all if and only if has rational singularities.
Proof.
See [Vie77, Lemma 1].∎
Corollary 2.16.
For any partial resolution of singularities , we have , i.e., the analytic Euler characteristic of is independent of the chosen partial resolution.
Proof.
Let be a resolution of singularities. Since has rational singularities, by Lemma 2.15, we must have , and for all . Thus, . Then, we assume that is just a resolution of singularities, so
Since is an affine morphism, also we have for all . Thus, we have . ∎
Finally, we give a state about the connectedness of a partial resolution.
Proposition 2.17.
Any partial resolution is irreducible.
Proof.
Since is normal we reduce the proof to show that is connected [Sta18, Tag. 0347]. From Corollary 2.16 we know that
If is not connected, then , so there exists a such that . We have,
So, we choose curves on such that . Thus, we get a system of equations where and . Since is prime, , and since , we get a contradiction. ∎
2.3. Toric picture
In this section, for toric varieties we mainly follow the notation of [CLS11].
Let be a prime number and integers. Choose a , and let be integers such that modulo . In particular, . As usual set and with canonical basis , and with . Consider the semigroup
Since
we have that the saturation [CLS11, p. 27] of is where
is the simplicial -cone defined by those elements. It is the dual cone of
Observe that and . Let the fundamental parallelepiped of , i.e., the points of with coordinates in respect its generators. Direct computations show that every element of can written as
| (4) |
Proposition 2.18.
The toric variety associated with the semigroup is
Moreover, its normalization correspond with .
Proof.
For simplicity, we will prove the result in the case . Since we will prove the first. Take the surjective morphism of semigroups such that
It induces a surjective morphism of coordinate rings , and by [CLS11] in Proposition 1.1.9 it is known that
If we set , the condition gives equations
We can assume with , then , and the equations reduces to
So is generated by elements of the form
and the result follows. ∎
Corollary 2.19.
The normalization of the affine varieties and are isomorphic.
Proof.
Observe that the cones defining both varieties are the same, equal to .
∎
Remark 2.20.
We point out the following. Assume that and . Thus , and we have a toric description of the normalization of the varieties embedded in for any .
Remark 2.21.
It is known that the cone defines a toric variety isomorphic to the -dimensional quotient cyclic singularity of type
We have , where is defined by
with (Cf. [Ash15]). In this way, quotient cyclic singularities are geometrically dual to the singularities of -th root covers. We will denote a cyclic singularity of this type by . In dimension , it occurs the accident that singularities of -th root covers are also cyclic quotient singularities.
2.4. Hirzebruch-Jung algorithm and Dedekind sums
2.4.1. Planar cones and Hirzebruch-Jung algorithm
Set and . A planar cone in is a cone of dimension , i.e., it is generated by two rays defined by primitive generators ( will have sense soon). Assume that . It is known that if , then there exists some such that generate , i.e., . If , with , then
On the other hand, since , we have . If we set , we say that is of type in direction to , or type in the opposite direction, where is the inverse modulo of .
Assume that are coprime, then consider the Hirzebruch-Jung algorithm of division for , i.e., a pair of sequences
which are related by
where are integers satisfying . Usually we denote . These sequences define the Hirzebruch-Jung continuous fraction as
Remark 2.22.
Observe that sequence is the sequence for , i.e., if the pair is the resolution of then .
Lemma 2.23.
For each , we have the following relations
-
(1)
-
(2)
-
(3)
∎
The non-singular resolution of the planar cone is a refinement by adding the rays defined recursively by
See Figure 1. Each cone is non-singular, since
From Remark 2.22 observe that we have a dual non-singular resolution given by the sequence
from where we have .
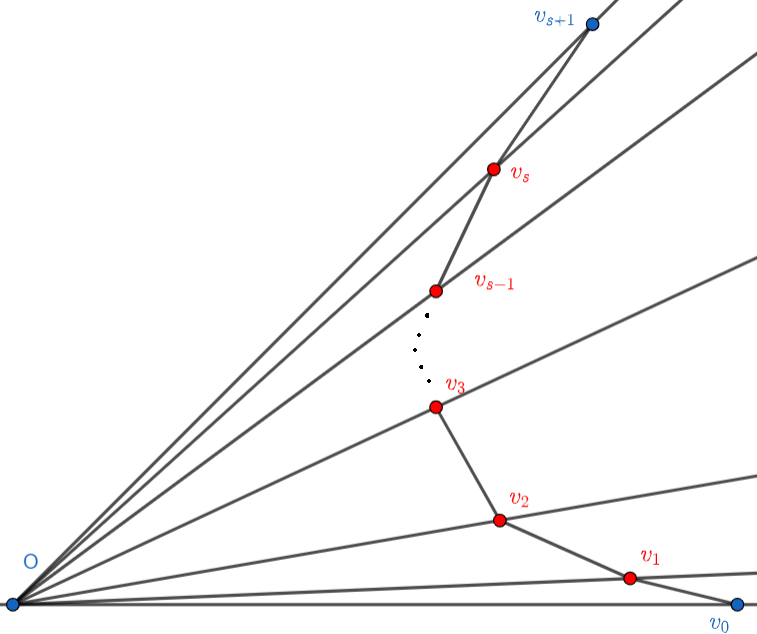
Let us change the -base of such that and . So, we have . We have,
where the are such that and on for any . Thus, in terms of toric varieties, , where is the cyclic quotient surface singularity of type (Remark 2.21). Thus, the constructed resolution is a blow-up , where and
For details see [CLS11, 11.3.6]. In particular, . We can give a explicit description of noting that the projection is given by the surjection .
2.4.2. Dedekind sums
Consider the sawtooth function is defined as
Observe that is an odd periodic function of period . For prime and define the Dedekind sum of dimension by
By periodicity, we can reduce to , then
where is the residue modulo of . Since is an odd function, we always have
i.e., for any odd dimension . Therefore, the non-trivial Dedekind sums are those of even dimension. We can rewrite this sum as
Lemma 2.24.
We have the following relations,
Proof.
We have an identity
for each integer. Then, we use repeatedly this identity in the following expressions. The first formula follows from,
and using that
we get the other two.
∎
A well-known result due to Barkan [Bar77] (see Holzapfel [Hol88]) is the following formula relating the length of the continued fraction and Dedekind sums,
Theorem 2.25.
Let be a prime number, and be an integer such that . Let . Then
∎
Remark 2.26.
In [Zag73] was studied the trigonometric version of the Dedekind sum treated here.
2.5. Asymptotic resolution in dimension 2
Let be a non-singular projective surface, and let be an effective divisor with SNC reduced divisor. Assume the necessary hypothesis to construct the normal -th root cover along (Section 2.2). We have to choose a resolution of singularities , and the Chern numbers of will depend on this resolution. The singularities of over each point of are analytically isomorphic to the normalization of
where modulo . This singularity is a cyclic quotient singularity of type , and the singular point can be resolved by some weighted blow-ups. The exceptional data will be a chain of non-singular rational curves with and , where the are the integers that define the negative regular continued fraction
usually called Hirzebruch-Jung continued fraction. See Section 2.4.1 for explicit computations. The number is called the length of the resolution and we denoted it by . In this way, we resolve all singularities of obtaining a morphism , with composition .
In dimension , for the chosen resolution Dedekind sums and lengths appear in the following formulas [Urz09],
Then, we can recover a formula for by Noether’s identity. In [Gir03] and [Gir06], Girstmair proved that the lengths and the values of Dedekind sums have a particular asymptotical behavior.
Theorem 2.27 (Girstmair).
For there exists a set such that for any we have . Moreover .
∎
Remark 2.28.
Observe that from the Barkan-Holzapfel relation (Theorem 2.25), and combining it with the results of Girstmair, we have an asymptotic behavior for the coefficients of the Hirzebruch-Jung continued fraction in the following sense: For a prime number , and integers with , we have
Definition 2.29.
A collection of prime divisors on a non-singular -fold is an asymptotic arrangement if is SNC, and for prime numbers :
-
(1)
There are multiplicities , such that for any with , we have , the unique integer such that modulo .
-
(2)
There are line bundles such that .
Example 2.30.
Inside the proof of [Urz09, Th. 6.1], it was proved that for any large prime number there exist a partition
with such that modulo . We call it an asymptotic partition of . Indeed, the probability of a partition of to be asymptotic tends to as grows to infinity. Thus, any collection of hyperplanes on defining a SNC divisor, is itself an asymptotic arrangement with
where is a general hyperplane section on .
3. Asymptoticity for a non-singular branch locus
3.1. Logarithmic asymptoticity
Let be the extended Chow ring of a fixed non-singular variety . For each assume the existence of finite -morphisms between non-singular varieties of the same dimension with (Definition 2.10). We have a morphism of extended Chow rings for each . Since is flat, we have that [Har77, III.9.6], then the same applies for the extended ring.
Theorem 3.1.
For assume the existence of finite -morphisms ramified at a non-singular divisor whose reduced form is a SNC divisor. Let be the components of , and the reduced preimage of each . Assume . Then, we have,
Proof.
The proof of the theorem is based on proving the following,
| (5) |
for all . Then, for any partition , we have
where the sum runs over each a permutation of . The result follows directly since the combinatorial quantities obtained do not depend on . We proceed by induction on the dimension . The trivial case for is assuming by convention Since is non-singular, by Lemma 2.11 we have . Thus, by Corollary 2.6 we get
Since , we have,
Assuming the induction hypothesis (5) for we get,
where the last step is by a telescopic argument using . ∎
The main situation to apply Theorem 3.1 is the case of -th root covers. In this case, take a non-singular SNC divisor on , and we restrict our attention to prime numbers . For each , assume the existence of and such that (Section 2.2). Construct the non-singular covers along each . Then and we get.
Corollary 3.2.
Under the above hypothesis, the -th root covers satisfy,
as for prime numbers .
∎
For our purposes in geography, this result has a disadvantage, the difficulty in finding good pairs whose covers are minimal of general type. For example, from Theorem 2.13 would be enough big and nef, and ample with many components. However, at least the condition big seems difficult to assure since most of varieties with arbitrary collections of disjoint divisors appear to be a fiber space. In [BPS16] was proved the following: Assume that has a collection of disjoint divisors , if , then there exists a surjective morphism from to a curve such that every is contained in a fiber. Thus, generically any variety of having collections of disjoint divisors is a fiber space over some variety .
Remark 3.3.
We can extend Corollary 3.2 to Abelian covers, i.e., to the case a sequence of Abelian groups of order with each a prime number with . See [Par91] or [Gao11]. In this case, the Abelian covers depend on a data with a SNC divisor for . Then the SNC divisor to take is . The ramification numbers for each component of are given by , where is the multiplicity of in . From here, we leave to the reader the analog asymptotic result. However, we can ask: How can this argument be extended to any Galois cover?
By the above discussion, in the rest of this paper, we will study the above results for the case of -folds when has its components with non-empty intersections. Thus will have singularities.
4. Asymptoticity of invariants
4.1. Asymptoticity of for -folds
Consider a data as in Section 2.2, with a non-singular projective -fold. Let be any resolution of singularities of the branched -th root cover along the effective divisor whose reduced form is SNC. We have,
Proposition 4.1.
We have,
where
Proof.
By Corollary 2.16, and Hirzebruch-Riemann-Roch theorem for -folds we can compute
where is a quantity depending only on and . We have the following identities: , and
The above is not difficult to deduce from the formulas in Lemma 2.24. To illustrate, we compute as follows. The first step, we compute explicitly:
From here it is not too difficult to note that we have , the quantities previously mentioned.
∎
Theorem 4.2.
If is an asymptotic arrangement, then
as for prime numbers .
Proof.
First observe the following limits
From formulas in Corollary 2.7, we get the identity
Since the collection of divisors is an asymptotic arrangement, we use Theorem 2.27 to get for prime numbers . Thus, in this case we have
for prime numbers .∎
Remark 4.3.
Observe that the formula for can be extended to higher dimensions. In the same way of Lemma 2.24, we can find formulas for depending only on the combinatorial aspects of and higher dimensional Dedekind sums. Thus, for asymptoticity of in any dimension, we need asymptoticity of Dedekind sums, i.e., the higher dimensional analogs of Girstmair’s results (Theorem 2.27). For dimension this is an open problem.
4.2. Toric local resolutions
In this section, we study the -fold singularity given by the normalization of , with a prime number and . The aim is to achieve good local resolutions of singularities in asymptotic terms with respect to . Since this singularity is toric, it can be resolved by subdivisions of its associated cone obtaining a refinement fan. To assure asymptotic properties, we have to pay attention to the combinatorial aspects of the refinement. Let be integers such that and modulo . By Section 2.3, this -fold singularity is a toric variety defined by the cone , where , and are the primitive ray generators. A transversal section of this cone is sketched in Figure 2.
The fan defined by the cone has 2-dimensional faces (walls) given by for . By Section 2.4.1, each wall can be resolved by Hirzebruch-Jung sequences in direction to with initial data
where and are the inverse modulo of and . Thus, there are integers , such that
Then, the walls can be resolved by subdividing them in a sequence of steps by rays with generators defined recursively as
If we fix , we denote by the exceptional divisors in direction to . We have the relation . In Figure 3 are illustrated the border generators.
In order to choose a good asymptotic local resolution of , imitating the -dimensional case, we can ask for a minimal local resolution, i.e., with nef canonical bundles. However, minimal varieties in higher dimensions may have terminal singularities, minimal singular models are not necessarily unique, and there are no efficient algorithms in the toric case. In this last, at least there exists a kind of optimal method. Minimal resolutions can be obtained by the canonical resolution of which is obtained by the canonical refinement of the cone [CLS11, Prop. 11.4.15]. However, the canonical refinement appears not to have a regular pattern for any . For example, if , and are free, the canonical and minimal resolutions look very simple but release a lot of exceptional data. See Figure 4. The resolution to the case takes the same form, just rotate the figure. And completely different from the above is the case . See Figure 5. Thus, we do not consider these cases in the following, i.e., , or . For more details see [TN23].

To have a systematic way to construct resolutions, we choose the following way: We construct a cyclic resolution, i.e., a refinement of composed by -cones defining cyclic singularities. The advantage is that cyclic singularities have a well-known algorithm to resolve them [Fuj74]. Also, as we will see in the examples, we can construct some minimal resolutions. So, in future work, we expect that, under suitable conditions, these resolutions have good asymptotical behavior with respect to .
4.2.1. Cyclic resolution.
Step 1: We refine by a star subdivision along obtaining a fan as illustrate Figure 6.

Step 2: Now we refine each wall by doing toric blow-ups following the Hirzebruch-Jung algorithm. So we obtain a refinement and denote by the toric variety associated. This refinement gives us a birational projective morphism [CLS11, 11.1.6]. This refinement is sketched in Figure 7.

Denote each -cone of by
The -cones of are given in two types. The exterior walls , and the inner walls . For any permutation with , using determinants and properties of Section 2.4.1, we have
Lemma 4.4.
Each cone is a cyclic singularity of type
where is the residue modulo .
Proof.
Since is non-singular, then is semi-unimodular respect to . By [Ash15, Prop. 1.2.3] if there is positive integer such that
then define the type of the cyclic singularity. Since , we can solve the equations modulo and the result follows.
∎
Denote by the composition with the natural projection to . Denote by the divisor in defined by the coordinate . Each ray on generated by or defines a toric divisor on given by
where denotes the orbit closure of a cone [CLS11, p. 121]. At the same time we fix notation for by . we can compute
| (6) |
where
It is satisfied the relation which gives
Proposition 4.5.
The -divisor
is an effective -divisor.
Proof.
The local pullback equals
Thus, equals to
i.e., an effective -divisor. ∎
Each inner wall defines a closed curve on given by
The refinement is simplicial with cones of multiplicity one, and the canonical divisor is a -Cartier divisor. For any pair , , let be the another coordinate. The following relation among lattices generators,
describe the intersection theory on [Ful93, Ch. V]. We have,
| (7) |
Lemma 4.6.
We have
Proof.
The divisor is Cartier for any , then from the pullback identities above we have
where the last is by projection formula.∎
As a consequence, we can compute,
From the last one, we get
Example 4.7.
Case : For , we have . Thus, these coordinates define an interior lattice point , and it minimizes . We have
i.e., is non-singular. On the other hand,
for all and . Thus, is nef.
Example 4.8.
Case : In this case, again defines the minimizer interior lattice point . In this case, we have and as non-singular cones. On the other hand, each is cyclic singularity of order . Thus, they define canonical and terminal singularities. The first ones achieve a terminal resolution with one blow-up. Moreover,
so there are with canonical divisor nef. In the worst case, i.e., for , we can do toric flips a to get a nef toric variety given whose fan is sketched in Figure 8.
Example 4.9.
If we drag the lattice point to one of the generators of the cone , we get a degenerated fan as in Figure 9. In this case, the singularities are of order , and as an advantage, we do not have a divisor .
As we see, having gives us good singularities to work. Indeed, if the are small enough, the singularities are also good in asymptotic terms. The following arithmetic lemma will be useful in Section 4.3.
Lemma 4.10.
There exists such that , so has multiplicity zero at . Moreover, for we can choose such that the slopes .
Proof.
By (4) we have . So , implies that are solutions of the Diophantine equation
Moreover, for any of those solutions with , we have . A degenerate case is , equivalently , thus the solution to the equation is the diagonal. Thus, we can choose , and the result follows for this case. Now, we assume that , otherwise we do . The integer points in the square solving the equation distribute in along the lines for . Thus, over each the integer solutions over the line are defined by those integers in the interval
For each , we have
where is the residue of modulo . So, . Let us choose and . In particular . So, as we have . By construction, we have . Let the residue of modulo , then . Since , the result follows choosing and as . ∎
4.3. Global resolution
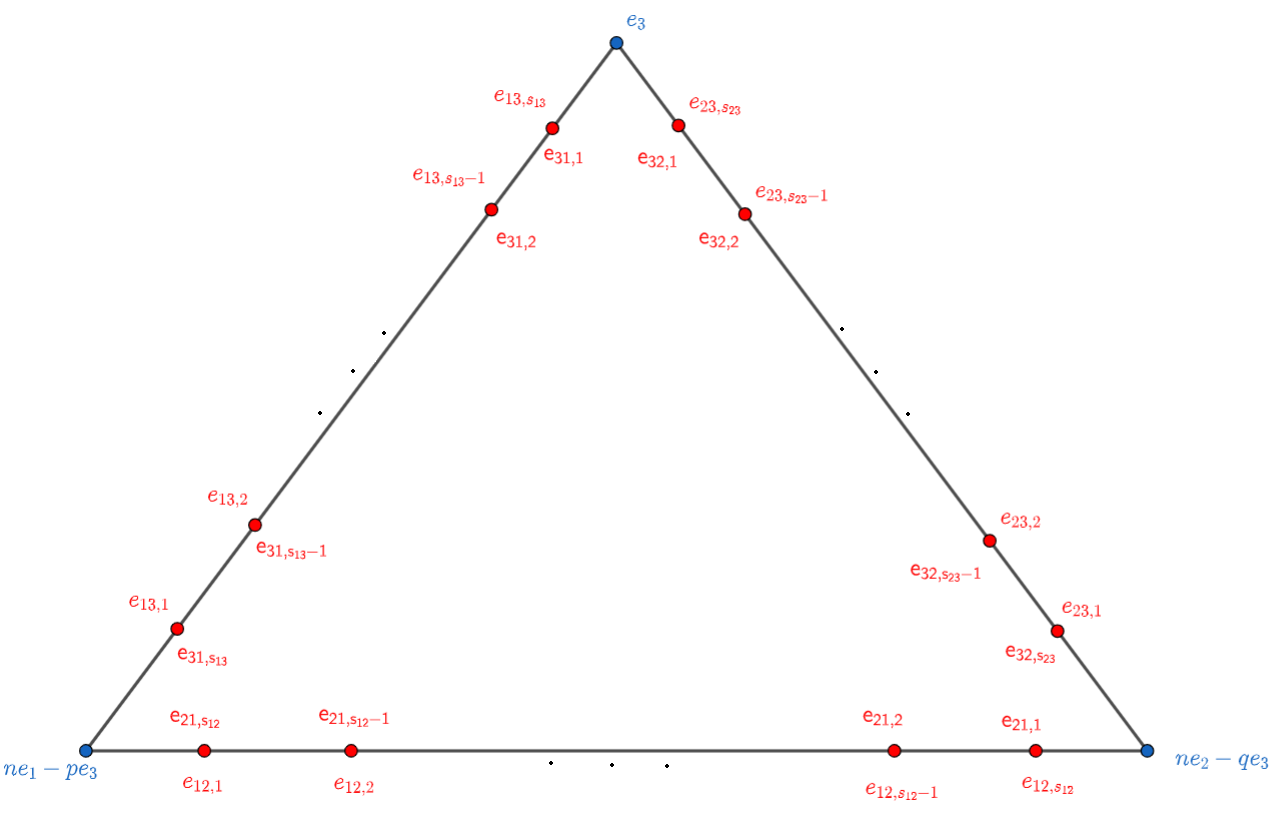
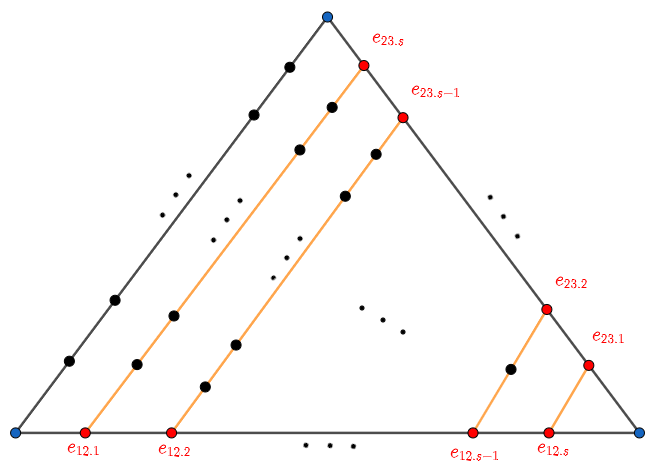
Let be an asymptotic arrangement on . Thus, for prime numbers we have multiplicities depending on , with its respective . We have -th root covers branched at each . Let us fix a , so we drop the subscript of the morphisms, i.e., we are fixing a .
For , the singularities of over curves in are locally analytically isomorphic to where is the surface cyclic quotient singularity of type . For a triple , the singularity of over a point in is locally analytically isomorphic to the normalization of where is a cone with walls of types as we see in Section 4.2. We will get the cyclic resolution via weighted blow-ups in two steps.
Step 1: Since singularities over are isolated, for each , we do a weighted blow-up at a convenient interior lattice point . So, this refinement locally gives a projective morphism which is a blow-up over an isolated point [CLS11, 11.1.6]. In this case, we get a projective birational morphism . We have exceptional divisors whose components are over the points of and they are isomorphic to weighted fake projective planes [Buc08]. For future computations, we fix the notation of and independent of the order of the triple . For example, .
Step 2: Since the centers of the above blow-ups are points, the singularity type over intersections was not affected. For curves in , locally by SNC property, we can assume that they are supported on a local equation for local coordinates . Then over such curves, the singularities on are locally analytically isomorphic to , thus we use the Hirzebruch-Jung algorithm which is a weighted blow-up to resolve . The Hirzebruch-Jung resolution can be realized by a single blow-up where is a maximal ideal determined explicitly in coordinates as we see at the end of Section 2.4.1 (also see [KM92, 10.5]). In terms of local resolutions, we need to follow an order compatible with the resolution, i.e., if we locally blow-up a curve in then this operation must be reflected on the other local toric pictures following the centers to blowing-up. See Figure 10. Thus, this construction extends and we have resolved the curves . Consequently, we get a projective morphism denoted by , and denote by the composition. Since was constructed by a sequence of weighted blow-ups with cyclic singularities, then, is an embedded -resolution of [ABMMOG12, 2.1]. As we see in 2.17, the varieties are irreducible. We summarize this in the following.
Proposition 4.11 (and Definition).
There exists a cyclic partial resolution , i.e. a projective, surjective, birational morphism such that is irreducible and, it has at most isolated cyclic quotient singularities of order lower than .
∎

In the rest, we will abuse notation using and for both, set-theoretic intersections and , and for intersections of cycles and . Over each , we get exceptional divisors , , where and whose components are over those of . From the local computations of the section above, we have
| (8) |
where is a divisor whose components are the exceptional divisors over points in .
Explicitly, for any triple of positive integers numbers , let the position of if we order the triple. For example , or . Thus, if is the exceptional divisor over a point , then
| (9) |
In terms of intersection theory, we have
From Theorem 2.13 we have
| (10) |
Now we describe how the intersection theory on behaves under pullbacks of divisors of . In what follows, we set and .
Proposition 4.12.
Let any divisors on , then as -cycle, for any ,
Proof.
We use the projection formula repeatedly. The first one is given by the fact that has codimension . Now for a we have supported in codimension , thus
Finally, for any we have
The recursive relations with give
From Lemma 2.23 we have the determinant , thus
In particular, we have
and the result follows. ∎
Corollary 4.13.
For any divisor on we have
Proof.
Since vanishes at top-dimensional intersections, and for , we have
where the last identity is by telescoping sum argument. ∎
Corollary 4.14.
If is a curve on contained in and disjoint to any exceptional divisor , then
Proof.
4.4. Asymptoticity of .
For simplicity, let us denote . Let us introduce the following notation
where satisfy
Lemma 4.15.
We have
Proof.
Using equations from (7), observe that depends on slopes of weights of the lattice points . Using (9), we get the result.
∎
We need this to compute the intersection of with the external walls of the local toric resolution. Recursively we denote,
Thus, we can write
| (11) |
Using the -numerical equivalence of in 2.13, we compute
Proposition 4.16.
We have
Where and analogous for .
Proof.
Using the recursion given by the , and formulas for and of (11), we have
The determinant , implies second relation for , and
The recurrence for with a telescopic sum argument give the result.
∎
Proposition 4.17.
We have,
Proof.
We will compute using the numerical equivalence of (10). Squaring we get
We have explicitly
In the rest, we will denote
Using Corollary 4.13 for , we get
Just rest to compute
From Corollary 4.13, we have
So, we have explicitly
∎
Theorem 4.18.
If is an asymptotic arrangement, then
for prime numbers .
Proof.
The first term of the sum contains , which is asymptotic respect to by previous discussion (Section 2.5). Thus, we just have to prove asymptoticity for
| (12) |
Proceeding as above, it is not difficult to show the following identity,
So, the asymptoticity of (12) depends only on the asymptoticity of
| (13) |
By 4.16, equals to
where , and analogous for . Observe that these terms are bounded by for some constant . On the other hand, the terms and asymptotically depend only on the slopes of coordinates of the chosen lattice points on each intersection . By Lemma 4.10, we can choose lattice points with slopes asymptotically bounded by as grows, with having for all . So, we have
Thus, as grows, all the terms in vanish except . ∎
4.5. Asymptoticity of .
The topological characteristic can be computed from the topology of and the exceptional divisors . The divisors where is the corresponding exceptional divisor over a . Thus, . In the toric picture (Section 4.2) of over , let the ray generator defining .
Lemma 4.19.
We have .
Proof.
It is well-known that is the toric variety associated to the star-fan , i.e., the induced fan by the lattice quotient . In this case, the -cones of are the induced by each . Since is the sum of its top-dimensional cones [CLS11, Thm. 12.3.9], we have the result.
∎
The components of divisors are determined locally as exterior divisors of the toric picture of . They intersect at the rational curves . Locally each component of is isomorphic to over , where is a weighted projective line. This follows for the star-fan construction.
Lemma 4.20.
If is the decomposition in componenets, then we compute
Proof.
We have . Since is a fibration over with fiber . Since the topological characteristics of weighted and non-weighted projective spaces are the same, we have that . ∎
Lemma 4.21.
If is a complex algebraic variety, and is a subvariety such that is smooth, then .
Proof.
See [Ful93, p. 141].∎
Remark 4.22.
The above lemma implies the exclusion-inclusion principle, i.e., for subvarieties we have .
Proposition 4.23.
We have,
Proof.
Denote by the ramification divisor of . This is a morphism which is an isomorphism outside we have
On the other hand, , where is the exceptional data of . Topologically is given by
By the exclusion-inclusion observe that
So, we get
On the other hand, the components of are curves over isomorphic to their respective components. Also, each component of is a rational curve over its corresponding point in . Thus, we have identities,
Using repeatedly the exclusion-inclusion principle we we compute
∎
Theorem 4.24.
If is an asymptotic arrangement, then
for prime numbers .
Proof.
As a corollary of the previous identity for , and by the previous discussion in Section 2.5, the lengths are asymptotically zero as grows. Thus, as grows. ∎
5. Applications to the geography of 3-folds
5.1. The case of hyperplanes.
Consider of degree . In this case, we have explicitly
for a generic hyperplane section . Take 3 hyperplane sections in general position, and asymptotic partitions . Along consider the respective -th root cover . Its singularities are over points in . As we see in Example 4.7, these singularities admit a locally nef non-singular resolution. Unfortunately, in this resolution the lattice point does not satisfy the condition of Lemma 4.10, i.e., the volume will not be completely asymptotic to the logarithmic Chern number . However, since the chosen satisfy . So, following the methods of Theorem 4.18 to compute , we get
Now we compute
since
In particular for prime numbers ,
On the other hand, from Section 4.1 we have
where
Since, the partition is asymptotic, for we have
For , the topological characteristic behaves as
Following the proof of Theorem 5.2, we get nef for . As a consequence of the above computations, we have.
Theorem 5.1.
For and there are minimal non-singular -folds of general type having degree over with slopes
In particular, as the degree of grows, the slopes have limit point .
∎
5.2. Hyperplane sections arrangements.
The above partial resolution can be seen as a resolution of pairs
where is the inverse direct image of . The reduced divisor of is an SNC divisor. Indeed, in terms of -resolutions [KM92, p. 5], we can see that our partial resolution has good behavior in logarithmic terms, i.e., they preserves the -structure of the variety -th root cover . The following result illustrates these ideas.
Theorem 5.2.
Let be a minimal non-singular projective -fold, and let , be a collection of hyperplane sections in general position. Then, for prime numbers there are -morphisms of degree such that:
-
(1)
is of -general type, i.e., is big and nef,
-
(2)
has cyclic quotient singularities, and so -terminal of order lower than , and
-
(3)
the slopes of are arbitrarily near to .
Proof.
We take , where are hyperplane sections on and an asymptotic partition. Recall that for any . Take the asymptotic cyclic resolution constructed in Theorem 4.18. Again for simplicity let us denote . From, the explicit description given in 4.5, we have
First observe that for any curve outside the exceptional data of , we have , by projection formula and since is ample. For every closed curve of of the local toric picture (Section 4.2) of the resolution, we have . For the remainder curves, we just need to concern about the positivity of its intersection with . Since is a nef divisor, by Corollary 2.14 we must have any -negative curve contained in the support of . Thus, the rest of rational curves in are of the following types:
-
(1)
Curves defined by the closure of a wall for
-
(2)
A curve contained in but not in for .
-
(3)
A curve contained in .
If is of type (1), from 4.12 we have,
for any . If is of type (2), then must be a fiber of the ruled surface ,i.e., is in the class of . But, by (6) we have . Finally, if is of type (3), we assume that it does not intersect interior divisors . If does it, then by the toric local description must be of the form for some . Again by projection formula, we have . Then, is a nef divisor, and moreover .Thus, by [Laz04, Th. 2.2.16.], the divisor is big. Now, from Theorem 4.18 we know that for
where is a generic hyperplane section on . Thus, if we choose depending on with as grows, then the numbers goes to zero respect with . Then, we have . Moreover, from Example 2.9 we have arbitrarily near to . ∎
6. Discussion
In this section, we will briefly discuss some possible future paths in order to extend this work.
6.1. Asymptoticity through minimal models
One of the main horizons of this research is to achieve the asymptoticity of invariants through minimal models. This means that the invariants of , with respect to , could be asymptotically equal to the respective invariants of its minimal model. Thus, we will be in a very nice position to do geography, i.e., the study of arrangements of hypersurfaces is identified through the slopes of Chern numbers with a "region" of minimal projective varieties. As we see in Theorem 5.2 and Theorem 5.1, if the basis pair has minimal of general type and composed by ample divisors, then our constructions preserve important features in terms of minimal models. However, this in general is not something easy to work on. For the future of this work, aspects are important.
-
(1)
Asymptotic study of (partial) desingularization of cyclic quotient singularities of dimension .
-
(2)
Hirzebruch-Riemann-Roch for singular varieties with terminal and - terminal singularities with their asymptotic analogs. In particular, this requires to establish what invariants will be the correct version of the Chern numbers. As we did in the case of dimension .
-
(3)
The behavior of the invariants after applying the MMP to our constructed varieties.
In the next section, we discuss (1). If we achieve our goal we will be, able to construct good partial resolutions , i.e., the Chern numbers, with respect to , are asymptotically equal to the logarithmic Chern numbers of the basis . We expect that we can improve the singularities to the terminal ones, so we will be able to run the MMP, i.e. we want to construct a terminal good partial resolution. For (2), we have results of [Rei87] and [BS05] which are a kind of starting point for future work. These contain versions of the Hirzebruch-Riemann-Roch theorem for varieties with canonical and cyclic quotient singularities. For (3), we think that the answer could be hidden in all the massive previous work done around the minimal model program [BCHM10], [KM92]. We expect, that the involved invariants do not suffer dramatic changes after flipping or contractions operations as occur in the case of surfaces. Then, asymptotically with respect to , the invariants remain unchanged. We state the above discussion as conjecture.
Conjecture 6.1.
Let be a terminal good partial resolution of singularities of the -th root cover construction. Assume that is nef, and let a minimal model of . Then, for any partition we have
for prime numbers .
6.2. What about the length of resolution of -fold c.q.s
Cyclic quotient singularities of dimension can be desingularized using a generalization of the Hirzebruch-Jung algorithm, which is the Fujiki-Oka algorithm. See [Ash19] for a modern treatment. After the local cyclic toric resolution of Section 4.2, instinctively we want to desingularize each one with the Fujiki-Oka process. However, since we want asymptoticy of invariants in our resolutions, we ask for the topological length and the intersection number behavior of such an algorithm. For the first, we mean the amount of new topological data, i.e., how the Betti numbers grow for the chosen resolutions. For last, we mean how the new curves and divisors on the exceptional data affect the volume . As we discussed in Section 2.5, the algorithm in dimension has both aspects behaving as for a suitable class of integer numbers.
Let us assume that we choose a partial resolution for the local cyclic resolution, so the amount of new topological data will behave approximately as
where is a length number depending on each cyclic singularities given in Lemma 4.4. Thus, asymptotically respect with , we require that for . In particular, Fujiki-Oka algorithm for a cyclic quotient singularity of type contains the processes for those of dimension two and . Thus, in the best case, we will have . To assure asymptoticity in Theorem 4.18 we must have , thus after resolve we lose the asymptoticity on the topological side. On the other hand, if we admit all small as we see in Theorem 5.1, then after resolve we lose the asymptoticity of the volume. These observations lead us to the following problem: the existence of a well-behaved algorithmic terminal resolution for cyclic quotient singularities, i.e., having only terminal singularities.
The terminalization of a toric singularity is a well-known process [CLS11, Sec. 11.4]. Indeed, assume that our toric singularity has associated cone . First, we have to compute the convex hull of . This will give us a refinement of , which is a canonical resolution, i.e. having at most canonical singularities with ample canonical bundle. Finally, each canonical toric singularity defined by a cone can be terminalizated by blowing-up each lattice point on the plane generated by the primitive generators of the cone. However, we do not know the growing behavior of this algorithm. In fact, it is known that the best convex-hull algorithm behaves as when the number of lattice points is [Gre90]. This not seems like a good algorithm to choose.
Question 6.2.
How can we construct a terminal algorithm for cyclic quotient singularities with the desired asymptotic properties? Is it possible?
As we see in Figure 4 and Figure 5, to achieve a well-behaved resolution it is probable that we will have to impose different conditions on the integer and . In Theorem 5.2 we see that there are -folds with cyclic quotient singularities accumulating in the well-known point of the map . We are curious if after applying the process proposed in Section 6.1, the minimal -folds expected will preserve the accumulating point or they move out. Finally, the principal motivation for all this work is the connection between arrangements of hypersurfaces and the geography of invariants of minimal varieties. For us will be interesting to explore the geography through arbitrary arrangements of planes on .
Question 6.3.
What is the region covered by minimal models of -th root cover along arrangements of planes in ?
References
- [ABMMOG12] E. Artal-Bartolo, J. Martín-Morales, and J. Ortigas-Galindo. Intersection theory on abelian-quotient V-surfaces and -resolutions. Eleventh international conference Zaragoza-Pau on applied mathematics and statistics, Jaca, Spain, September 15–17, 2010., pages 13–23, 2012.
- [Ash15] T. Ashikaga. Toric modifications of cyclic orbifolds and an extended Zagier reciprocity for Dedekind sums. Tôhoku Math. J. (2), 67(3):323–347, 2015.
- [Ash19] T. Ashikaga. Multidimensional continued fractions for cyclic quotient singularities and Dedekind sums. Kyoto J. Math., 59(4):993–1039, 2019.
- [Bar77] P. Barkan. Sur les sommes de Dedekind et les fractions continues finies. C. R. Acad. Sci. Paris Sér. A-B, 284(16):A923–A926, 1977.
- [BCHM10] C. Birkar, P. Cascini, C. Hacon, and J. McKernan. Existence of minimal models for varieties of log general type. J. Am. Math. Soc., 23(2):405–468, 2010.
- [BPS16] F. Bogomolov, A. Pirutka, and A. Silberstein. Families of disjoint divisors on varieties. Eur. J. Math., 2(4):917–928, 2016.
- [BS05] A. Buckley and B. Szendrői. Orbifold Riemann-Roch for threefolds with an application to Calabi-Yau geometry. J. Algebr. Geom., 14(4):601–622, 2005.
- [Buc08] Weronika Buczynska. Fake weighted projective spaces. arXiv: math.AG.0805.1211, 2008.
- [CCJ20] J. Chen, M. Chen, and C. Jiang. The Noether inequality for algebraic threefold (Appendix by Kollar, J.). Math. Ann. 202, Springer-Verlag, 2020.
- [CH06] M. Chen and C. Hacon. On the geography of Gorenstein minimal 3-folds of general type. Asian J. Math., 10(4):757–763, 2006.
- [CL01] M. Chang and A. Lopez. A linear bound on the Euler number of threefolds of Calabi-Yau and of general type. Manuscr. Math., 105(1):47–67, 2001.
- [CLS11] T. Cox, J. Little, and H. Schenck. Toric Varieties, volume 124. AMS, Graduate Studies in Mathematics, 2011.
- [DS22] R. Du and H. Sun. Inequalities of Chern classes on nonsingular projective -folds with ample canonical or anti-canonical line bundles. J. Differ. Geom., 122(3):377–398, 2022.
- [EFU22] S. Eterović, F. Figueroa, and G. Urzúa. On the geography of line arrangements. Adv. Geom., 22(2):269–276, 2022.
- [EV92] H. Esnault and E. Viehweg. Lectures on Vanishing Theorems, volume OWS 20. Birkhause Basel, 1992.
- [Fuj74] A. Fujiki. On resolutions of cyclic quotient singularities. Publ. Res. Inst. Math. Sci., 10:293–328, 1974.
- [Ful93] W. Fulton. Introduction to toric varieties, volume 131. Princeton University Press, 1993.
- [Gao11] Y. Gao. A note on finite abelian covers. Sci. China, Math., 54(7):1333–1342, 2011.
- [Gir03] K. Girstmair. Zones of large and small values for Dedekind sums. Acta Arith., 109(3):299–308, 2003.
- [Gir06] K. Girstmair. Continued fractions and Dedekind sums: three-term relations and distribution. J. Number Theory, 119(1):66–85, 2006.
- [GKPT19] D. Greb, S. Kebekus, T. Peternell, and B. Taji. The Miyaoka-Yau inequality and uniformisation of canonical models. Ann. Sci. Éc. Norm. Supér. (4), 52(6):1487–1535, 2019.
- [Gre90] J. Greenfield. A proof for a quickhull algorithm. Electrical Engineering and Computer Science - Technical Reports. 65., 1990.
- [Har77] R. Hartshorne. Algebraic geometry, volume GTM 52. Springer, 1977.
- [Hir83] F. Hirzebruch. Arrangement of lines and algebraic surfaces. Progress in Math. Vol.II, 36:113–240, 1983.
- [Hol88] R.-P. Holzapfel. Chern number relations for locally abelian Galois coverings of algebraic surfaces. Math. Nachr., 138:263–292, 1988.
- [Hu18] Y. Hu. Inequality for Gorenstein minimal 3-folds of general type. Commun. Anal. Geom., 26(2):347–359, 2018.
- [Hun89] B. Hunt. Complex manifolds geography in dimension 2 and 3. J. Differential Geometry, 30:51–153, 1989.
- [Iit77] S. Iitaka. On logarithmic Kodaira dimension of algebraic varieties. Complex An.and Alg. Geom., pages 175–190, 1977.
- [Iit78] S. Iitaka. Geometry on complements of lines in . Tokyo J. Math., 1:1–19, 1978.
- [KM92] J. Kollár and S. Mori. Classification of three-dimensional flips. J. Am. Math. Soc., 5(3):533–703, 1992.
- [Kol91] J. Kollár. Flips, flops, minimal models, etc. Surveys in differential geometry. Vol. I, pages 113–199, 1991.
- [Laz04] R. Lazarsfeld. Positivity in algebraic geometry. I. Classical setting: line bundles and linear series, volume 48 of Ergeb. Math. Grenzgeb., 3. Folge. Berlin: Springer, 2004.
- [Mat10] K. Matsuki. Introduction to the Mori program. Universitext. Springer-Verlag, New York, 2010.
- [Miy87] Y. Miyaoka. The pseudo-effectivity of for varieties with numerically effective canonical classes. Adv. Stud. Pure Math., 10:449––476, 1987.
- [Par91] R. Pardini. Abelian covers of algebraic varieties. J. Reine Angew. Math., 417:191–213, 1991.
- [Rei87] M. Reid. Young person’s guide to canonical singularities. Algebraic geometry, Proc. Summer Res. Inst., Brunswick/Maine 1985, part 1, Proc. Symp. Pure Math. 46, 345-414 (1987)., 1987.
- [Som84] A. Sommese. On the density of ratios of chern numbers of algebraic surfaces. Math. Ann., 268:207–221, 1984.
- [Sta18] The Stacks Project Authors. Stacks Project. https://stacks.math.columbia.edu, 2018.
- [TN23] Y. Torres-Nova. On geography of -folds via asymptotic behavior of its invariants. Ph.D. Thesis, Pontificia Universidad Católica de Chile, https://repositorio.uc.cl/handle/11534/74443, 2023.
- [Urz09] G. Urzúa. Algebraic surfaces and arrangements of curves. Journal of Algebraic Geometry, 19:169 – 189, 2009.
- [Urz16] G. Urzúa. Chern slopes of surfaces of general type in positive characteristic. Duke Math. J., 166:975–1004, 2016.
- [Vie77] E. Viehweg. Rational singularities of higher dimensional schemes. Proc. Am. Math. Soc., 63:6–8, 1977.
- [Vie82] E. Viehweg. Vanishing theorems. J. Reine Angew. Math., 335:1–8, 1982.
- [Zag73] D. Zagier. Higher dimensional Dedekind sums. Math. Ann., 202:149–172, 1973.