On the first three minimum Mostar indices of tree-like phenylenes
Abstract
Let be a simple connected graph with its vertex set and edge set . The Mostar index was defined as , where (resp., ) is the number of vertices whose distance to vertex (resp., ) is smaller than the distance to vertex (resp., ). In this study, we determine the first three minimum Mostar indices of tree-like phenylenes and characterize all the tree-like phenylenes attaining these values. At last, we give some numerical examples and discussion.
Keywords: Mostar index; Tree-like phenylene; Extremal value.
2020 Mathematics Subject Classification: 05C09, 05C92.
1 Introduction
Chemical indices are a class of numerical invariants that are closely related to the structure of a chemical graph. Chemical indices can be used to predicte the structural and physic-chemical properties of a chemical molecular. They are mainly used for the quantitative characterisation of chemical structures and thus contribute to the study of QSAR, QSTR and QSPR relationships of chemical structures. In recent years, chemical indices have been found a wide range of applications in chemical science, medical science, complex networks, toxicology, etc. The combination of quantum chemistry and chemical graph theory has also become a promising area in the study of QSAR and QSPR.
Our convention in this paper follows [4] for notations that we omit here. Phenylenes are a class of chemical compounds in which the carbon atoms form 6-membered cycles and 4-membered cycles. Each 4-membered cycle(=square) is adjacent to two disjoint 6-membered cycles(=hexagons), and no two hexagons are adjacent [25]. If there is a hexagon of phenylene adjacent to three squares, we call it the tree-type phenylene (the definition of tree-type phenylene is similar to tree-type hexagonal system, see [7]). Related structures include extended sp-carbon nets and heterocyclic analogs. These molecules have great theoretical and potential practical significance in finding new molecules with (super) conductive properties [28].
Nowadays, phenylene is still a hot topic in many experimental and theoretical studies. Some topological properties of phenylenes has been established such as (total -electron) energy [11], HOMO LUMO separation [13], cyclic conjugation [15], Kekulé structure count[12], Wiener index [10], PI index [6, 14], Detour index [21] and Kirchhoff index [23, 31].
Let be the set of tree-like phenylenes with hexagons and squares. And . Suppose , and is a hexagon of . Then is called an -hexagon, if it has exactly adjacent squares in . A -hexagon is called a terminal hexagon of . A -hexagon is called turn-hexagon of if its two -vertices (the vertices of degree ) are adjacent in . A -hexagon is called a full-hexagon of . Let be the set of phenylenes with full-hexagons. Each graph in (or denoted by ) is called a phenylene chain. A phenylene chain is called a linear phenylene chain (denoted by ) if it contains no turn-hexagons. Let be the set of phenylene chains with turn-hexagons.
A segment of a phenylene chain is a maximal linear sub-chain. Denote by a non-terminal segment of a phenylene chain . We call a non-zigzag segment (resp., a zigzag segment) if it’s two neighboring segments lie on the same sides (resp., on different sides) of the line through centers of all hexagons and squares on .
Denote by the phenylene chain with hexagons and exactly segments of lengths , respectively, where and are the terminal segments, all are zagzig segments, , and . Particularly, is the graph including two vertex-disjoint linear phenylene chains and as subgraphs, where , and . is the graph including three vertex-disjoint linear phenylene chains , and as subgraphs, where , the second segment is a zigzag segment and .
Denote by the graph including three vertex-disjoint linear phenylene chains , and as subgraphs, where , and .
Došlić et al.[9] introduced Mostar index [9] of a graph , which is defined as
Došlić et al. determined extremal values of Mostar index among trees and unicyclic graphs, then gave a cut method for computing the Mostar index of benzenoid systems.
Similarly, the edge Mostar index [20] is defined as
where (resp.,) is the number of edges whose distance to vertex (resp., ) is smaller than the distance to vertex (resp., ). We can refer to [1, 2, 3, 7, 8, 9, 16, 17, 18, 19, 20, 22, 26, 27, 29, 30] for more details about (edge) Mostar index.
Mostar indices can be used to measure the peripherality of chemical graphs, so in addition to chemical applications, Mostar indices have a wide range of applications in complex networks. It can be used to describe structural properties of the network. Mostar indices can also be used to extend quantum estimates and expand reactivity based on electronic descriptors. In this study, our aim is to solve the extremal problem of tree-like phenylenes with respect to Mostar indices. Using the methods of [7], we determine the first three minimum values of the Mostar index of tree-like phenylenes with a fixed number of hexagons and characterize all the tree-like phenylenes attaining these values.
2 Preliminaries
An orthogonal cut is a line segment that starts from the middle of a peripheral edge of a phenylene, goes orthogonal to this edge and ends at the first next peripheral edge that it intersects. Let . Denote by the set of edges that parallel with in , and . Let be the set of all disjoint parallel classes in . Note that is an edge cut, denote by the connected components of contain . Denote by the number of hexagons in . Note that, for any , and .
Bearing in mind that is the graph including three vertex-disjoint linear phenyene chains , and as subgraphs, where , and . By the definition of , we can calculate the value of .
Lemma 2.1
Given a phenylene with three branches and hexagons, then
If , then .
If , then for even ; for odd .
Proof. By using the cut method to , we have
If , then
If , and is even, then
If , and is odd, similarly, we have .
This completes the proof.
3 The minimal tree-like phenylenes
Let and , are two terminal hexagons of . Denote by the six clockwise successive vertices in for , where for . Let for and (let ).
Suppose that and be two adjacent -vertices (vertices with degree 2) in for . Let be the phenylene obtained from by connecting with , and with , respectively.
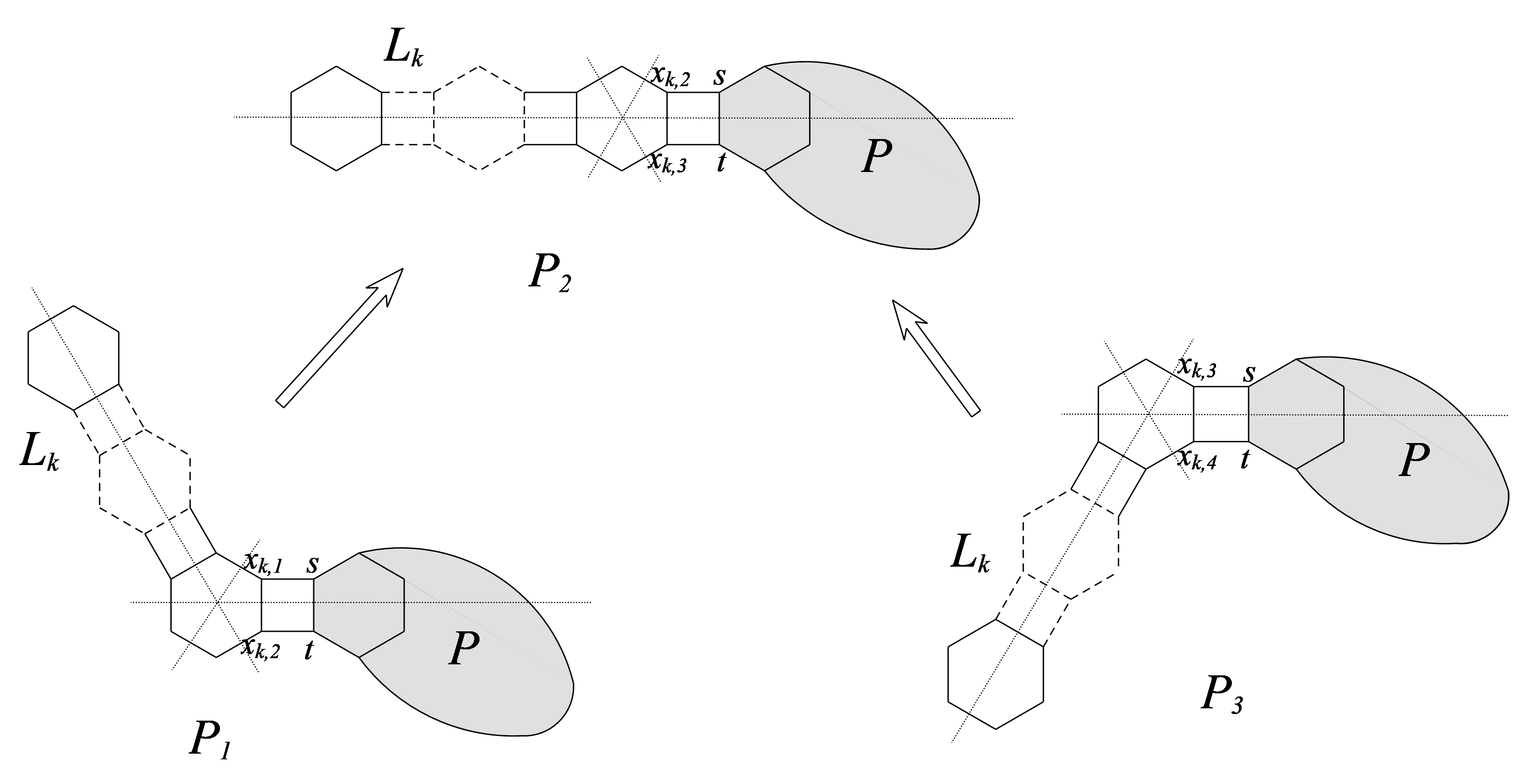
For , we denote (or ) the number of vertices in lying closer to vertex than to vertex . Some symbols involved in the proof are described in Section 2.
Proof. Let denote the set of edges that are parallel to edge in . Assume that . Denote . Denote (), we have ().
Note that , then
;
;
.
Bearing in mind that and .
If , then , with equality iff .
If , then .
.
This completes the proof.
By Lemma 3.1, we have
Corollary 3.2
Let with being two adjacent -vertices of its turn hexagon. Denote by a phenylene chain with hexagons, and are two adjacent -vertices of its one terminal hexagon. Then .
Let , where , . are vertices in Figure 2, and , . Then we have
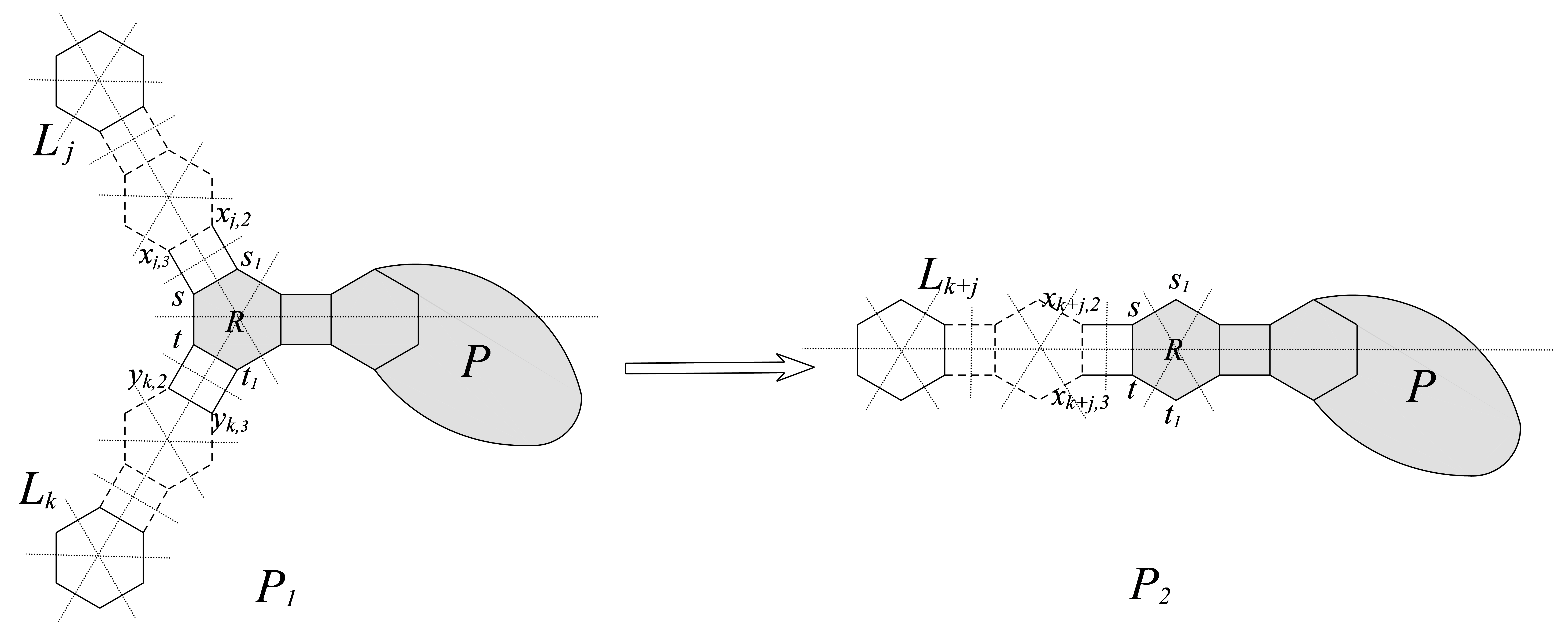
Lemma 3.3
Let and , see Figure 2, then .
Proof. Denote (). Let (), then .
Since , then
Note that , and .
Case 1. .
Subcase 1.1. .
.
Subcase 1.2. .
If is even, then , and
If is odd, then , and
Case 2. .
Note that and .
Subcase 2.1. .
.
Subcase 2.2. .
If is even, then , and
If is odd, then , and
Thus, . This completes the proof.
By Lemma 3.1, we can directly obtain the smallest Mostar index among .
Lemma 3.4
[5] Let , then , with equality iff .
By Corollary 3.2, Lemma 3.3 and Lemma 3.4, we can obtain the smallest Mostar index among . The proof of Theorem 3.5 follows from the same arguments as the proof of Theorem 1.3 of [7], thus we omit the proof.
Theorem 3.5
Let , then , with equality iff .
4 The second minimal tree-like phenylenes
Bearing in mind that is the graph including two vertex-disjoint linear phenylene chains and as subgraphs, where , and . is the graph including three vertex-disjoint linear phenylene chains , and as subgraphs, where , the second segment is a zigzag segment and . In the following, we give some useful results for our proofs of main theorem.
Using the cut method to and , and comparing the change of Mostar index among and , we also have
Lemma 4.1
[5] Let , , be the phenylene chain with hexagons, then .
By Lemma 3.1, Lemma 4.1 and Lemma 3.4, we can also obtain the second minimum Mostar index among phenylene chains .
Lemma 4.3
Given a phenylene with three branches and hexagons. Then for , and for .
Proof. Note that . Then, by Lemma 2.1, we have
Case 1.
Subcase 1.1. If is even, then , and we have
whenever , or , or , whereas .
Subcase 1.2. If is odd, then , and we have
whenever , or .
Case 2.
.
The proof is completed
By Lemma 3.3, Theorem 3.5, Lemma 4.2 and Lemma 4.3, we obtain the second minimum Mostar index of tree-like phenylenes .
Theorem 4.4
Let , and , then
If , with equality iff or .
If , , with equality iff .
5 The third minimal tree-like phenylenes
Bearing in mind is the phenylene chian with hexagons and exactly segments of lengths , respectively, where and are the terminal segments, all are zagzig segments, , and . In the following, we give the following Lemma 5.1 and Lemma 5.2, which are important for our proofs of main theorem 5.3. At first, we give the third minimum Mostar index among phenylene chains.
Lemma 5.2
Given a phenylene with three branches and hexagons. Then
If , then .
If , then .
If , then .
Proof. Note that . Then by Lemma 2.1, we have
Case 1.
Subcase 1.1. If is even, then , and we have
whenever , or , or , or , whereas , , .
Subcase 1.2. If is odd, then , and we have
whenever , or , or , whereas , .
Case 2.
whenever , whereas with .
Thus, we have If , then ; If , then ; If , then .
The proof is completed
Comparing the Mostar indices of with , with . By Lemma 2.1, we have , and . By Lemma 3.3, Theorem 3.5, Theorem 4.4, Lemma 5.1 and Lemma 5.2, we obtain the third minimum Mostar index of tree-like phenylenes .
Theorem 5.3
Let , and . Then , with equality iff .
6 More about (edge) Mostar indices
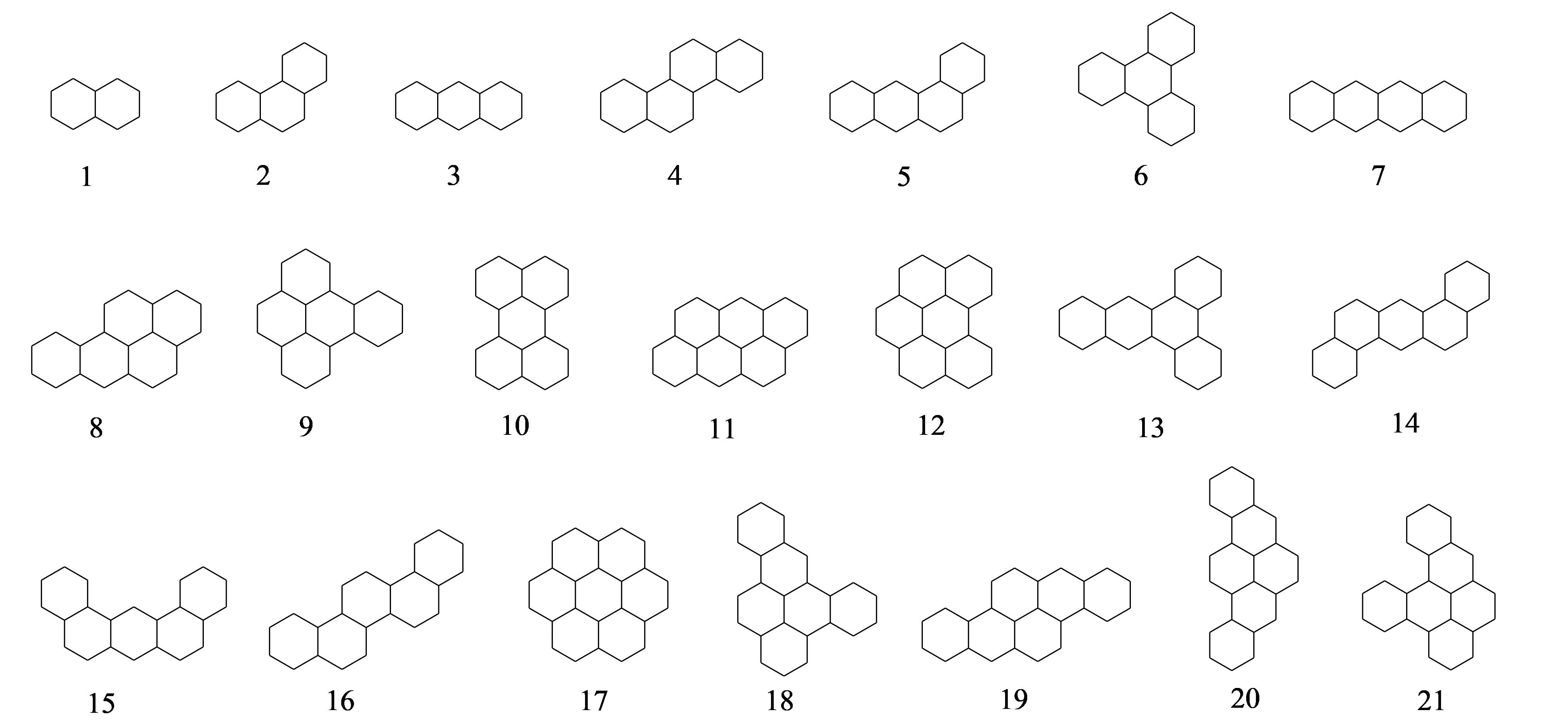
In this section, we investegate the correlation between boiling points (BP) of benzenoid hydrocarbons and edge Mostar indices. The 21 benzenoid hydrocarbons were shown in Figure 5. The experimental values of boiling points of benzenoid hydrocarbons of Table 1 were taken from [24]. The experimental values of Mostar indices of benzenoid hydrocarbons of Table 1 were taken from [8]. With the data of Figure 1, scatter plots between BP and edge Mostar indices were shown in Figures 6. We obtain that the correlation coefficient () between boiling points and edge Mostar indices is about 0.9647, and
From [8], we know that the correction coefficient (R) between boiling ponits of benzenoid hydrocarbons and Wiener index is 0.9642, Mostar index is 0.9573, the first status connectivity index is 0.9677, the second status connectivity index is 0.9165, the first eccentric connectivity index is 0.9315, the second eccentric connectivity index is 0.8263. We compare the correction coefficient of edge Mostar index with other distance-based indices, we find the edge Mostar index is also a good predictor. The boiling points and edge Mostar indices are highly correlated since the correction coefficient (R) between boiling ponits of benzenoid hydrocarbons and edge Mostar index is 0.9647. It is worth noting that the regression model for the boilding point and edge Mostar index only applies to benzenoid hydrocarbons. We do not know whether it applies to phenylenes, which needs further study.
| No. | No. | ||||||
|---|---|---|---|---|---|---|---|
7 Concluding Remarks
Among the research of quantum chemistry, computational chemistry and mathematical chemistry, the research of chemical indices is currently one of the more popular areas, as these chemical indices have proven to have a wide range of applications in QSAR, QSPR relationships for new drug discovery, molecular design, hazard estimation of compounds, numerical coding of chemical structures, database search, prediction of bioactivity, prediction of physicochemical properties of molecular materials.
In this study, we determine the first three minimum values of the Mostar index of tree-like phenylenes with a fixed number of hexagons and characterize all the tree-like phenylenes attaining these values. Quite unexpectedly, the minimum and second minimum tree-like phenylenes are all in the phenylene chains, but the third minimum tree-like phenylenes are not in the phenylene chains. The results could be of some interest to researchers working in chemical applications of graph theory.
References
- [1] M. Arockiaraj, J. Clement, N. Tratnik. Mostar indices of carbon nanostructures and circumscribed donut benzenoid systems, Int. J. Quantum. Chem. 119 (2019) #e26043.
- [2] M. Arockiaraj, J. Clement, N. Tratnik, S. Mushtaq, K. Balasubramanian. Weighted Mostar indices as measures of molecular peripheral shapes with applications to graphene, graphyne and graphdiyne nanoribbons, SAR QSAR Environ. Res. 31 (2020) 187–208.
- [3] K. Balasubramanian, Topological peripheral shapes and distance-based characterization of fullerenes C20-C720 : existence of isoperipheral fullerenes, Polycyclic Aromat. Compd. doi: 10.1080/10406638.2020.1802303.
- [4] F. R. K. Chung, Spectral Graph theory, American Mathematical Society, Providence, RI, USA, 1997.
- [5] H. Chen, H. Liu, Q. Xiao, J. Zhang, Extremal phenylene chains with respect to the Mostar index, Discrete Math., Algor. Applicat. doi:10.1142/S1793830921500750.
- [6] H. Deng, S. Chen, J. Zhang, The PI index of phenylenes, J. Math. Chem. 41 (2007) 63–69.
- [7] K. Deng, S. Li, Extremal catacondensed benzenoids with respect to the Mostar index, J. Math. Chem. 58 (2020) 1437–1465.
- [8] K. Deng, S. Li, On the extremal values for the Mostar index of trees with given degree sequence, Appl. Math. Comput. 390 (2021) #125598.
- [9] T. Došlić, I. Marthinjak, R. Škrekovski, S. Tipurić Spužević, I. Zubac, Mostar index, J. Math. Chem. 56 (2018) 2995–3013.
- [10] B. Furtula, I. Gutman, T. Zeljko, A. Vesel, I. Pesek, Wiener-type topological indices of phenylenes, Indian. J. Chem. A. 41 (2002) 1767–1772.
- [11] I. Gutman, B. Furtula, The total -electron energy saga, Croat. Chem. Acta. 90 (2017) 359–368.
- [12] I. Gutman, B. Furtula, A Kekulé structure basis for phenylenes, J. Mol. Struct.: THEOCHEM, 770 (2006) 67–71.
- [13] I. Gutman, P. Petković, P. V. Khadikar, Bounds for the total -electron energy of phenylenes, Rev. Roum. Chim. 41 (1996) 637–643.
- [14] I. Gutman, A. R. Ashrafi, On the PI index of phenylenes and their hexagonal squeezes, MATCH Commun. Math. Comput. Chem. 60 (2008) 135–142.
- [15] I. Gutman, Ž. Tomović, Cyclic conjugation in terminally bent and branched phenylenes, Indian. J. Chem. A. 40 (2001) 678–681.
- [16] F. Gao, K. Xu, T. Došlić, On the difference of Mostar index and irregularity of graphs, Bull. Malays. Math. Sci. Soc. 44 (2021) 905–926.
- [17] S. Huang, S. Li, M. Zhang, On the extremal Mostar indices of hexagonal chains, MATCH Commun. Math. Comput. Chem. 84 (2020) 249–271.
- [18] F. Hayat, B. Zhou, On Mostar index of trees with parameters, Filomat, 33 (2019) 6453–6458.
- [19] F. Hayat, B. Zhou, On cacti with large Mostar index, Filomat, 33 (2019) 4865–4873.
- [20] M. Imran, S. Akhter, Z. Iqbal, Edge Mostar index of chemical structures and nanostructures using graph operations, Int. J. Quantum Chem. 120 (2020) #e26259.
- [21] H. Liu, X. Fang, Extremal phenylene chains with respect to detour indices, J. Appl. Math. Comput. 67 (2021) 301–316.
- [22] H. Liu, L. Song, Q. Xiao, Z. Tang, On edge Mostar index of graphs, Iranian J. Math. Chem. 11 (2020) 95–106.
- [23] J. B. Liu, Q. Zheng, Z. Q. Cai, S. Hayat, On the Laplacians and normalized Laplacians for graph transformation with respect to the dicyclobutadieno derivative of [n] Phenylenes, Polycyclic Aromat. Compd. doi:10.1080/10406638.2020.1781209.
- [24] Milano Chemometrics & QSAR Research Group, Molecular Descriptors: the free online resource, Milano Chemometrics and QSAR Research Group, http://www .moleculardescriptors.eu/dataset/dataset.htm. Accessed Dec 2017.
- [25] L. Pavlovic, I. Gutman, Wiener numbers of phenylenes: an exact result, J. Chem. Inf. Comput. Sci 37 (1997) 355–358.
- [26] A. Tepeh, Extremal bicyclic graphs with respect to Mostar index, Appl. Math. Comput. 355 (2019) 319–324.
- [27] N. Tratnik, Computing the Mostar index in networks with applications to molecular graphs, Iranian J. Math. Chem. 12 (2021) 1–18.
- [28] K. P. C. Vollhardt, The phenylenes, Pure Appl. Chem. 65 (1993) 153–156.
- [29] Q. Xiao, M. Zeng, Z. Tang, H. Deng, H. Hua, Hexagonal chains with the first three minimal Mostar indices, MATCH Commun. Math. Comput. Chem. 85 (2021) 47–61.
- [30] Q. Xiao, M. Zeng, Z. Tang, H. Hua, H. Deng, The hexagonal chains with the first three maximal Mostar indices, Discrete Appl. Math. 288 (2021) 180-191.
- [31] Z. Zhu, J. B. Liu, The normalized Laplacian, degree-Kirchhoff index and the spanning tree numbers of generalized phenylenes, Discrete Appl. Math. 254 (2019) 256-267.