On the distribution of the time-integral of the geometric Brownian motion

In order to put these results into context, we summarize briefly the known short maturity asymptotics of the continuous time average of the geometric Brownian motion $a_{T}:=\frac{1}{T}\int_{0}^{T}e^{2(W_{s}+\mu s)}ds$. Dufresne [5] proved convergence in law of this quantity to a normal distribution, see Theorem 2.1 in [5]

This can be formulated equivalently as a log-normal limiting distribution in the same $T\to 0$ limit, see Theorem 2.2 in [5]. The log-normal approximation for the time-integral of the gBM is widely used in financial practice, see [5] for a literature review. When applied to the pricing of Asian options, this is known as the Lévy approximation [17].

The log-normal approximation is also used for the conditional distribution of $A_{t}^{(\mu)}$ at given terminal value of the gBM, as discussed for example in [22, 23]. This conditional distribution appears in conditional Monte Carlo simulations of stochastic volatility models [33], see [2] for an overview and recent results.

The result (7) can be immediately extended to the joint distribution of $(a_{T},z_{T})$ with $z_{T}=e^{W_{T}+\mu T}$. We state it without proof which can be given along the lines of the proof of Theorem 2.1 in [5].

The covariance matrix $\hat{\Sigma}$ is computed as (with $W_{sT}=\sqrt{T}B_{s}$ and $0\leq s\leq 1$)

In other words, as $T\to 0$, the joint distribution of $(a_{T},z_{T})$ approaches a bivariate normal distribution with correlation $\rho_{az}=\frac{\sqrt{3}}{2}$. In analogy with Theorem 2.2 in [5], this result can be formulated equivalently as a bivariate log-normal limiting distribution.

Another asymptotic result in the $T\to 0$ limit is the large deviations property of the time-average $a_{T}$. Using large deviations theory methods it was showed in [26] that, for a wide class of diffusions which includes the geometric Brownian motion, the time average of the diffusion satisfies a large deviations property in the small time limit, see Theorem 2 in [26]. For the particular case of a gBM this result reads, in our notations

with $J_{\rm BS}(a)$ a rate function given in closed form in Proposition 12 of [26]. For convenience the result is reproduced below in Eq. (22). In contrast to the fluctuations result of (7) which holds in a region of width $a-1\sim\sqrt{T}$ around the central value $a=1$, the large deviations result (13) holds for $a-1\sim O(1)$.

The explicit asymptotic result (4) for the small time asymptotics of the joint distribution of $(A_{t}^{(\mu)},W_{t})$ satisfies all these limiting results and improves on them by including all contributions up to terms of $O(t)$. It is instructive to see explicitly the connection to the asymptotic results presented above.

The exponential factor in (6) reproduces the large deviations result (13) by identifying $J(a)=\frac{1}{4}J_{\rm BS}(a)$. The emergence of the log-normal limit implied by Proposition  1.1 can be also seen explicitly by expanding the exponent in (4) around $a=v=1$ using the results of Propositions 2 and 3 in [28]. Keeping the leading order terms in the expansion of $F(\rho)=\frac{\pi^{2}}{2}-1-\log\rho+\log^{2}\rho+O(\log^{3}\rho)$ in powers of $\log\rho$ gives the quadratic approximation

The joint distribution (4) is thus approximated in a neighborhood of $(v,a)=(1,1)$ as

where the $(\cdots)$ in the exponent are the error terms in (14) and we defined

Up to the factor $C_{\rm LN}(a,v)$ and the error terms in the exponent, the expression (1.2) coincides with a log-normal bivariate distribution in variables $(a,v)$. Recall the bivariate normal distribution of two random variables $N(X,Y;\sigma_{X},\sigma_{Y},\rho)$ with volatility and correlation parameters $\sigma_{X},\sigma_{Y},\rho$

The density (1.2) corresponds to parameters

These parameters correspond precisely to the covariance matrix $\hat{\Sigma}$ appearing in the fluctuations result of Proposition 1.1.

Improving on the log-normal approximation (1.2) requires adding higher order terms in the coefficient $C_{\rm LN}(a,v)$ and in the exponent. All these corrections are expressed in terms of $F(\rho),G(\rho)$ which can be evaluated by expansion around $\rho=1$. In this paper we present series expansions of $F(\rho),G(\rho)$ in powers of $\log\rho$ that can be used for such evaluation, and we study in detail their properties. We determine their convergence radii and coefficient asymptotics in Proposition 4.2. We note that alternative series expansions which improve on the log-normal approximation have been considered in the literature (in the context of the expansion of the density of $A_{t}^{(\mu)}$), based on Gram-Charlier series [6].

Although closed form results are available for the functions $F(\rho),G(\rho)$, they are inefficient for practical use because of the need to solve one non-linear equation for each evaluation. The series expansions for $F(\rho),G(\rho)$ allow much faster and reliable numerical evaluation, inside their convergence domain. In Section 5 we construct efficient numerical approximations for $F(\rho),G(\rho)$, based on the series expansions derived here within the convergence domain, which are easy to use in numerical applications. This gives a numerical approximation for the joint distribution of the time integral of the gBM and its terminal value, which appears in many problems of mathematical finance, such as the simulation of the SABR model [3] and option pricing in the Hull-White model [15]. As an application we discuss the numerical pricing of Asian options in the Black-Scholes model, and demonstrate good agreement with standard benchmark cases used in the literature.

Let us now restrict $f$ to a small neighborhood of the origin. Then the range of $f$ is in a small neighborhood of $1$. Clearly, $f$ is not locally invertible as $f$ is an even function, that is $f(\xi)=f(-\xi)$, and thus is not injective. A natural way to make the function at least locally invertible is to define

In light of (26), we have $g(z)=f(\sqrt{z})=\sinh(\sqrt{z})/\sqrt{z}$. Here, and in the sequel, unless stated otherwise, the notation $\sqrt{z}$ will only be used in the argument of even functions so as both values of $\sqrt{z}$ give the same result. Recall the following simple fact: if $g^{\prime}(z)\neq 0$, then there is a small neighborhood $D$ of $z$ so that $g:D\to g(D)$ is biholomorphic (see for example Theorem 3.4.1 in [30]). Since $g^{\prime}(0)\neq 0$, $g$ is locally invertible at zero. We also note that $g$ is an entire function as its Taylor series converges everywhere. We will show next that $g:\mathbb{C}\mapsto\mathbb{C}$ is surjective. One says that an entire function $f$ has finite order $\rho$ if constants $A,B$ can be found such that $|f(z)|\leq Ae^{B|z|^{\rho}}$ for all $z\in\mathbb{C}$. See for example Chapter 5 in [31] and Section 1.3 in [16] for a detailed discussion of entire functions of finite order.

The order of the entire function $g(z)=\sum_{n=0}^{\infty}a_{n}z^{n}$ can be expressed in terms of the coefficients of its Taylor expansion as, see Theorem 2 in Sec. 1.3 of [16]

Using the expansion (27) it follows that the function $g$ has order $\rho=\frac{1}{2}$. Any entire function with order $<1$ is surjective, see Section 5.1 of [16]. Since in our case $\rho=1/2$, $g:\mathbb{C}\mapsto\mathbb{C}$ is surjective.

We study next the critical points of $f$ and $g$ which are given by the zeros of $f^{\prime}$ and $g^{\prime}$, respectively. To identify the zeros of $g^{\prime}$, let us write $0=\eta_{0}<\eta_{1}<\eta_{2}<...$ for the non-negative solutions of the equation $\tan\eta=\eta$ (and note that all real solutions are given by $\eta_{k},k\in\mathbb{Z}$ with $\eta_{-k}=-\eta_{k}$). We also write

(see Table 1 for the numerical values for $k=1,...,5$). Now we have

We note that $\omega_{k}\in\mathbb{R}$ for all $k\geq 1$. Furthermore, $\omega_{1}\approx-0.217234$, and $|\omega_{k}|<|\omega_{1}|$ for all $k\geq 2$.

Let $B_{\rho}(A)$ be the open $\rho$-neighborhood of the set $A\subset\mathbb{C}$ and $B_{\rho}(w)=B_{\rho}(\{\omega\})$. Now we are ready to state the analyticity of the local inverse of $g$ on the region that is most important for our applications.

Theorem 3.1 tells us that the inverse $h(\omega)$ can be defined with $h(1)=0$. Furthermore, $h$ is analytic and the Taylor expansion

has a radius of convergence of at least $1-\omega_{1}$. We note that the inverse $g^{-1}$ can be defined in the sense of a sheaf (also known as global analytic function, or Riemann surface). In this general sense, $g^{-1}$ has a second order algebraic branch point at $\omega_{1}=g(z_{1})$ by Lemma 3.2. Thus the function $h$ cannot be analytically extended to $\omega_{1}$ and so the power series (29) has radius of convergence exactly $1-\omega_{1}$. We will be mostly interested in this expansion (see Section 3.4). However, for completeness we first discuss how to visualize the sheaf $g^{-1}$.

First, observe that $h$ can be analytically extended to $\mathbb{C}\setminus\Gamma_{1}$, where $\Gamma_{1}$ is any curve starting at $\omega_{1}$ and tending to $\infty$ (for example $\Gamma_{1}=\omega_{1}+i\mathbb{R}_{\geq 0}$; however as we will see later, sometimes other choices are more convenient). Indeed, replacing $D$ by

in the last step of the proof of Theorem 3.1 and noting that this domain is simply connected, analyticity of $h$ follows (of course the expansion (29) is not valid on the larger domain). The function $h$ can be identified with a chart of the Riemann structure of the sheaf $g^{-1}$ (in this identification, its domain is sometimes referred to as Riemann sheet).

Next, we can define another analytic function $h_{2}$ on $\mathbb{C}\setminus(\Gamma_{1}\cup\Gamma_{2})$, where $\Gamma_{2}=\omega_{2}+i\mathbb{R}_{\geq 0}$. Since the function $z\mapsto g(z)-\omega_{1}$ has a zero of order $2$ at $z_{1}$, we can extend $h$ analytically from

to

Let the resulting function be denoted by $\tilde{h}$. Clearly, $\tilde{h}$ takes values in a small neighborhood of $z_{1}$ and since there is a branch point at $\omega_{1}$, $\tilde{h}(\omega)\neq h(\omega)$ for $\omega=\omega_{1}+t$ with $t\in\mathbb{R}_{+}$, $t<\varepsilon$. Now observe that $g((z_{2},{z_{1}}])=[\omega_{1},\omega_{2})$. Since the branch point is of order $2$, we conclude that $\tilde{h}(\omega_{1}+t)$ for $t$ as above has to be real, and slightly bigger than $z_{1}$. Thus we can extend $\tilde{h}$ analytically to $B_{\delta}(g(I_{2}))$ where $I_{2}=[z_{2}+\varepsilon_{-},z_{1}-\varepsilon_{+}]$ and $g(I_{2})=[\omega_{1}+\varepsilon/2,\omega_{2}-\varepsilon/2]$. Now restrict $\tilde{h}$ to

and denote this restriced function by $h_{2}$. Then $h_{2}$ can be extended analytically to $\mathbb{C}\setminus(\Gamma_{1}\cup\Gamma_{2})$ by the monodromy theorem as in the proof of Theorem 3.1.

Furthermore, we can ”glue together” the domains of $h_{1}$ and $h_{2}$ along $\Gamma$ since $\lim_{x\rightarrow\omega_{1}\pm}h_{1}(x+yi)=\lim_{x\rightarrow\omega_{1}\mp}h_{2}(x+yi)$ and the gluing is analytic (see the analyticity of $\tilde{h}$ and the fact that the branch point is algebraic of order $2$). Since $g$ preserves the real line and all branch points are of second order, this construction can be continued inductively, i.e. we can define the Riemann sheet $k\geq 2$ by $h_{k}$ and glue together with the sheets $k\pm 1$ along $\Gamma_{k\pm 1}$. This gives a complete elementary description of the sheaf $g^{-1}$.

For better visualization of the sheaf constructed in the previous section, we include some figures. We start with listing the numerical values of the first few critical points $\eta_{k}$, $\eta_{k}^{2}$, $\omega_{k}$ and $|i\pi+\log|\omega_{k}||$ (the latter will be needed later) in Table 1.

Given $\omega$, there may be infinitely many $z$’s so that $g(z)=\omega$. A plot of some of these $z$’s for $\omega\in(\omega_{1},1)$ are shown in Fig. 3.1 (note that both $\omega$ and $z$ are real). The first branch corresponds to $z\in(z_{1},\infty)$ when $\omega>\omega_{1}$. On this branch $h_{1}(1)=0$. We call this Riemann sheet the principal branch. The second branch corresponds to $z\in(z_{2},z_{1})$, where $\omega\in(\omega_{2},\omega_{1})$, and the $k$-th branch corresponds to $z\in(z_{k},z_{k-1})$, where $\omega$ is in between $\omega_{k-1}$ and $\omega_{k}$.

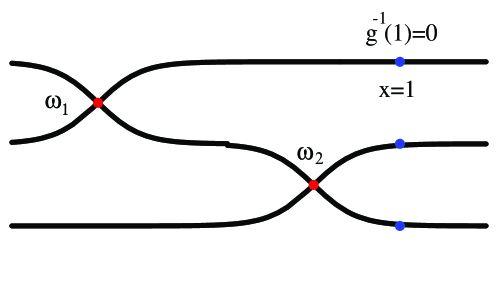
Figure 3.2 is a schematic representation of the first three Riemann sheets. This figure illustrates the apparently counterintuitive result that, although the branch point at $\omega_{2}=0.1284$ is closer to $\omega=1$ than the branch point at $\omega_{1}=-0.2172$, it is the latter which determines the radius of convergence of the series expansion around $\omega=1$, rather than the former. The explanation for this fact is that the branch point at $\omega_{2}$ is not “visible” on the main Riemann sheet, and thus the branch point at $\omega_{1}$ is the dominant singularity around $\omega=1$.

Next, we study the coefficients $c_{n}$ of the Taylor expansion (29). The first few coefficients are easily computed by the Lagrange inversion theorem using (27) and Theorem 3.1. In particular, we obtain

Writing $e^{y}=\omega$ we can also expand $h$ as a series in $y=\log\omega$ (here, $\log\omega$ means the principal value of the logarithm). In applications to Asian options pricing [26], the parameter $\omega$ is related to the option strike. In practice, it is usual to expand implied volatilities in log-strike, which corresponds to expanding in $y=\log\omega$. See for example [11].

Comparing the first few derivatives with (30), the expansion (30) becomes

Explicitly computing high order terms of these expansions is difficult (cf. [24], pages 411-413). However, we can study the asymptotic properties of the sequences $c_{n}$ and $d_{n}$.