On the Convergence of Monte Carlo UCB for Random-Length Episodic MDPs
Abstract
In reinforcement learning, Monte Carlo algorithms update the Q function by averaging the episodic returns. In the Monte Carlo UCB (MC-UCB) algorithm, the action taken in each state is the action that maximizes the Q function plus a UCB exploration term, which biases the choice of actions to those that have been chosen less frequently. Although there has been significant work on establishing regret bounds for MC-UCB, most of that work has been focused on finite-horizon versions of the problem, for which each episode terminates after a constant number of steps. For such finite-horizon problems, the optimal policy depends both on the current state and the time within the episode. However, for many natural episodic problems, such as games like Go and Chess and robotic tasks, the episode is of random length and the optimal policy is stationary. For such environments, it is an open question whether the Q-function in MC-UCB will converge to the optimal Q function; we conjecture that, unlike Q-learning, it does not converge for all MDPs. We nevertheless show that for a large class of MDPs, which includes stochastic MDPs such as blackjack and deterministic MDPs such as Go, the Q-function in MC-UCB converges almost surely to the optimal Q function. An immediate corollary of this result is that it also converges almost surely for all finite-horizon MDPs. We also provide numerical experiments, providing further insights into MC-UCB.
1 Introduction
One of the most fundamental results in tabular reinforcement learning is that the Q-function estimator for Q-learning converges almost surely to the optimal Q-function, without any restriction on the environment. This classic result was originally proved for infinite-horizon discounted MDPs, for which the the optimal policy is both stationary and deterministic (Tsitsiklis 1994; Jaakkola, Jordan, and Singh 1994). Q-learning is based on dynamic programming and uses back-ups to update the estimates of the optimal action-value function.
Besides Q-learning, another major class of reinforcement learning algorithms is Monte Carlo (MC) algorithms (Sutton and Barto 1998), which are often employed for episodic MDPs. With MC algorithms, an optimal policy is sought by repeatedly running episodes and recording the episodic returns. After each episode, the estimate for the optimal Q function is updated using the episodic return. Then a new episode is generated using the most recent estimate of the Q-function. In contrast with Q-learning, pure MC algorithms do not employ backups.
For many natural episodic problems, such as games like Go and Chess and robotic tasks, the episode ends when a terminal state is reached. The episode therefore is of random length. For episodic environments with random length episodes, the natural optimization criterion is to maximize the (expected) total return until the episode ends. For this class of problems, it is well known in the MDP literature that there is an optimal policy that is both stationary (does not depend on the time index) and deterministic.
As with Q-learning, it is important to understand the convergence properties of Monte Carlo algorithms with random-length episodes. We note that MC algorithms are often used in practice. For example, training AlphaZero (Silver et al. 2018) employs Monte Carlo in both the inner loop (where Monte Carlo Tree Search (MCTS) is used) and in the outer loop, where a two-player MC episode is run until game termination, at which time estimates for the Q functions are updated. As it turns out, unlike Q-learning, MC algorithms are not guaranteed to converge. Indeed, counterexamples exist for non-convergence for an important class of MC algorithms (Bertsekas and Tsitsiklis 1996; Wang et al. 2022).
In this paper, we consider an important class of MC algorithms, namely, MC algorithms that use Upper-Confidence Bound (UCB) exploration at each state. As discussed in the related work, such algorithms have been studied extensively for the fixed horizon optimization criterion, for which the optimal policy is non-stationary. Here we explore MC-UCB algorithms for random-length episodes, which is often the more natural setup in practice. For such environments, although the optimal policy is stationary, we conjecture that MC-UCB does not always converge.
The main contribution of this paper is to establish almost sure convergence for MC-UCB for a very large and important class of environments, specifically, for environments whose states are never revisited when employing an optimal policy. (States may be revisited when employing a non-optimal policy). This class of MDPs includes stochastic MDPs such as blackjack and many gridworld environments with randomness (for example, due to wind). It also includes all deterministic environments and all episodic environments with a monotonically changing value in the state. The proof is based on induction and a probabilistic argument invoking the strong law of large numbers.
A second contribution of this paper is an extensive numerical study of MC-UCB. These results show that in two classic episodic environments, MC-UCB can achieve competitive performance and converge in both the policy and the value-function, when compared to an ideal but less practical exploration scheme where each episode is initialized with a random state-action pair.
2 Preliminaries
RL typically aims to find the optimal policy for a Markov Decision Process (MDP). A finite MDP can be represented by a tuple , where is the finite state space; is the finite action space; is the reward function from to the reals; and is the dynamics function where for any and , gives a probability distribution over the state space . We denote for the policy. In general a policy may depend on the current state, the current time and the entire past history. Denote and for the state and action at time under policy , respectively.
We assume that the state space has a terminal state denoted by . When the MDP enters state , the MDP terminates. Let denote the time when the MDP enters . is a random variable, and can be infinite if the MDP doesn’t reach the terminal state. The expected total reward when starting in state is
| (1) |
Similarly we define the action-value function as
| (2) |
Further denote
Let denote a policy that maximizes (1). We say that the MDP is episodic if under any optimal policy , for all . Note that in this definition of an episodic MDP, episodes are of random-length. Maximizing (1) for an episodic MDP is sometimes referred to as the stochastic shortest path problem (for example, see (Bertsekas and Tsitsiklis 1991)). For the stochastic shortest path problem, there exists an optimal policy that is both stationary and deterministic, that is, a policy of the form .
Another popular optimization criterion is the finite-horizon criterion, where in (1) is replaced with a fixed deterministic value . In this case rewards accumulate to time whether the MDP terminates or not. For finite horizon problems, optimal policies are typically not stationary; however, it can be shown that there exists an optimal policy that depends on the current state and the current time (Bertsekas and Tsitsiklis 1991).
An MDP is said to be Optimal Policy Feed-Forward (OPFF) if under any optimal policy a state is never revisited (Wang et al. 2022). Note that this definition allows for MDPs for which states are revisited under non-optimal policies. Many important MDPs are OPFF, including Blackjack (a stochastic environment), the environments examined at the end of this paper, and all deterministic environments.
2.1 Monte Carlo with Upper Confidence Bound Framework
In Monte Carlo reinforcement learning, an optimal policy is sought by repeatedly running episodes and recording the episodic returns. After each episode, the estimate for the optimal Q function, denoted here as , is updated using the episodic return. Then a new episode is generated using the most recent estimate of the Q-function .
There are many possible variations of Monte Carlo RL algorithms. Two broad classes are MC with Exploring Starts (MCES) and MC using Upper Confidence Bounds (MC-UCB). In MCES, the policy used to select actions when in state is simply , that is, the action that maximizes the current estimates of the Q function. In MCES, exploration is performed by starting the episodes in randomly chosen pairs. One of the major drawbacks of MCES is that it assumes that during training we have the ability to choose the starting state and action for an episode. This is not a feasible option for many real-world environments. MC-UCB does not have this drawback; for example, during training, each episode may start in a given fixed state. In MC-UCB, exploration is performed by adding an exploration term to , then taking the of the sum to select an action. It is very similar to how UCB is done with multi-armed bandits, but in the MDP case, the Q estimate and the exploration term depend on the state.
In this paper we focus on the convergence properties of MC-UCB for MDPs with random-length episodes where rewards accrue until the episode enters the terminal state, as is typically the case in real applications. Algorithm 1 provides a basic form of the MC-UCB algorithm.
In the algorithm, after every episode, the optimal action-value function for a particular state-action pair is estimated by averaging all the sampled returns seen for that pair. When running an episode, when in state , we select the action that maximizes the sum of and the Upper Confidence Bound exploration term , where is a constant controlling the exploration rate, is the total number of visits for a state , and is the total number of visits for a state-action pair . We emphasize that the above framework is for environments where states are never re-visited. We will later modify the algorithm for OPFF environments where cycles are possible.
Because the policy for generating episodes changes after each episode, we cannot directly apply the Strong Law of Large Numbers (SLLN) to prove almost sure convergence; indeed the returns collected for a given state-action pair are neither independently distributed nor identically distributed.
3 Related Work
In contrast with Monte Carlo methods, Q-learning is based on dynamic programming and uses back-ups to update the estimates of the optimal action-value function. For infinite-horizon discounted MDPs, Q-learning can be shown to converge with probability one to the optimal action-value function under general conditions, by putting Q-learning into the stochastic approximations framework (Tsitsiklis 1994; Jaakkola, Jordan, and Singh 1994). Moreover, for the stochastic shortest path problem (random-length episodes), it has been shown that the sequence of Q-learning iterates is bounded, implying the convergence of the action-value function (Yu and Bertsekas 2013). While the MC-UCB algorithm also aims to solve the stochastic shortest path problem, the proofs of convergence for Q-learning cannot be easily adapted for Monte Carlo algorithms. The MCES algorithm is related to the MC-UCB algorithm since both MCES and MC-UCB average Monte Carlo episodic returns to estimate the action-value function. However, the two algorithms employ very different exploration strategies. While MCES randomly chooses state-action pairs at the beginning of each episode, MC-UCB explores by adding UCB exploration to the current action-value estimate. In the general RL setting, the convergence of MCES is not guaranteed, since there exists a counterexample where MCES indeed does not converge to the optimal action-value function (Bertsekas and Tsitsiklis 1996; Wang et al. 2022). We conjecture that the MC-UCB algorithm also does not converge in general.
However, if the MCES algorithm is modified so that the Q-value estimates are updated at the same rate for all state-action pairs, and the discount factor is strictly less than one, then the convergence will be guaranteed. (Tsitsiklis 2002). Furthermore, by assuming that all policies are proper, it is shown via the stochastic approximations methodology that MCES also converges for undiscounted cases (discounted factor equal to one) (Chen 2018; Liu 2020). Recently, a new but simple approach (Wang et al. 2022) to this problem relaxes the assumption of a uniform update rate for all state-action pairs, providing almost sure convergence under the OPFF assumption, that is, a state is never re-visited within an episode under an optimal policy. In this paper we pursue this same strategy for the MC-UCB algorithm. However, we emphasize here that our proof is significantly more challenging than the proof in Wang et al. (2022) due to the nature MC-UCB algorithm.
There has been significant work on regret bounds for the finite-horizon MDP problems(Agarwal, Jiang, and Kakade 2019; Chang et al. 2005; Azar, Osband, and Munos 2017). When the horizon is finite, then the optimal policy is non-stationary. Furthermore, many problems of practical interest do not have a fixed-length horizon. We also note regret bounds typically only imply convergence in expectation, not almost sure convergence. Although regret bounds are important, we argue that it is first important to understand the convergence properties of the MC-UCB algorithm since convergence is not guaranteed as it is in finite-horizon problems.
We also note that the MC-UCB framework shares some similarities with the Monte Carlo Tree Search (MCTS) algorithms. According to Vodopivec, Samothrakis, and Šter (2017), the UCT algorithm (Kocsis and Szepesvári 2006), one of the fundamental MCTS algorithms, can be viewed as an offline on-policy every-visit MC control algorithm that uses the UCB1 (a variant of UCB, discussed in appendix A) as the policy. The MCTS algorithms can also be considered as finite-horizon since they truncate the complete game trajectories at a fixed length.
4 Almost Sure Convergence for OPFF MDPs
In this section, we return to the MC-UCB framework described in Section 2 and derive the almost sure convergence of both the action-value function and state-value function under the OPFF assumption.
Before we present the almost sure convergence proof for the OPFF setting, we note that OPFF environments allow the learning agent to revisit previous states for sub-optimal policies; therefore, the agent may get into an infinite loop where the terminal state is never reached. To address this issue, we set a time limit depending on the number of states in the MDP, as shown in Algorithm 2. If the length of an episode exceeds this limit, we terminate the algorithm (line 3). Additionally, there are some special corner cases where taking sub-optimal actions never yields a complete episode, such as actions leading to a self-loop. Although such actions do not prevent the convergence of the estimated state-value functions and the policy, they cause the Q estimates not to converge. In order to address this issue, we add lines 5 and 6 to the algorithm. Since the action-value function for optimal actions will be almost surely greater than that for sub-optimal actions, as we will show in the proof, we can generate a complete episode in those corner cases.
Note that one can modify MC-UCB to make all Q estimates converge even faster. For example, similar to the model-based method (Azar, Osband, and Munos 2017), one can estimate transition probabilities and V estimates, and then update Q estimates by the Bellman equation. In this case, our analytical methodology still applies. However, in order to follow the standard MC-UCB framework and to simplify the analysis in this paper, we use the approach mentioned above to deal with the theoretical convergence of all Q values. Finally, we use the first-visit mechanism (line 12) to calculate the average returns, since the every-visit mechanism may cause a slower convergence for tasks with cycles (Singh and Sutton 1996; Sutton and Barto 1998).
Let be the estimated state-value function of state by averaging total returns , where is the -th return collected in state ; be the estimated action-value function, where is the -th return collected in state by choosing action ; be the number of selections of action in the state out of total visits of that state. Let be finite reward random variables following an unknown law with an unknown but finite mean . We now present the main result:
Theorem 1 (Almost sure convergence of MC-UCB for OPFF MDPs).
Suppose the MDP is OPFF. Then converges to , for all ; converges to , for all and .
Proof.
Since the MDP is OPFF, its graph induced by an optimal policy is a directed acyclic graph (DAG). So we can reorder the states so that by taking the optimal action from state , we only transition to a state in the set , for any . Here, is a terminal state.
The proof is then done by backward induction. For , the result is trivially true. Suppose the statement is true for all states . We now show it is true for the state as well. For simplicity, we use to denote the state for any .
Note that we have the following decomposition:
Let be an optimal action for state . We first show that the estimate converges to the optimal Q value almost surely for the optimal action . We have:
where is the next state from state in the -th iteration that contains the pair; and .
Due to the UCB exploration, will be visited infinitely often, which implies . Hence, by SLLN, we have and . Moreover, by the inductive hypothesis, the V values for any states in the set will converge almost surely. Therefore, given that is the average return starting in the state , it eventually converges to almost surely, since the UCB exploration will visit the transition infinitely often.
In this way, we have
| (3) |
Since taking non-optimal action may lead to states visited before, where the inductive hypothesis does not apply, we cannot follow the same procedure to prove the almost sure convergence of for any . Instead, we can first prove converges almost surely by showing for any .
Let denote the set of all deterministic policies. For any , we can rewrite:
where, when following a policy , denotes the number of visits of the pair , out of total visits of the state ; denotes the -th return collected in state by choosing action . By SLLN , for any such that , we have:
where is the action-value function for policy . The above result further implies that :
| (4) |
Moreover, we observe that for any , there exists some such that:
Let be the underlying sample space. Then, the set has probability measure 1 for any suboptimal actions (by the inequality (4)); and the set has probability measure 1 for the optimal action (by the convergence result (3)). Letting , we have .
Now, we fix . By the definition of limit superior, for any , there exists such that for , we have:
Hence, for any , we have:
Now, we are ready to show for any . Following a standard upper bound in Multi-armed Bandit literature (for example, see inequality 8.4 of section 8.1 of Lattimore and Szepesvári (2020)), we have for any :
where is defined to be the estimated action-value function of the pair by using the first samples stored in the array; if , we will just set .
For the first term on the right side of the above inequality, we have for :
On the other hand, choose such that . Then, there exists such that for any , , we can also bound the second term:
From the above two inequalities, it is easy to see: for any , for any . Since , we have for any .
Together with the assumption that the Q values are finite, the almost sure convergence of the V values for the state follows:
| (5) |
Therefore, we can conclude that for any .
Lastly, it remains to establish the almost sure convergence of the Q values for any sub-optimal action . We have:
If there is no potential for a loop after the transition , the analysis for the almost sure convergence is the same as that for the Q value of the optimal action. However, for those transitions leading to an infinite loop (e.g., a self-loop), the episode cannot reach the terminal state. Note that the convergence result (3) and the inequality (4) implies that . Thanks to the line 5 and 6 in Algorithm 2, if a loop is detected in the state , then the remaining episode will almost surely be the same episode generated by . In this case, a complete episode starting in the state after choosing the suboptimal action can occur. It follows for any and for all . ∎
Note that the convergence result for the estimated Q-value to the optimal action-value function (3) together with the inequality (4) imply that the induced policy converges almost surely to an optimal policy (which is stationary and deterministic).
We also emphasize that the theorem implies almost sure convergence for all MDPs for the (fixed) finite-horizon criterion (in which case the optimal policy is non-stationary). Given a finite-horizon period = {0, 1, …, h}, the policy , Q values , and V values are now time-dependent for . In this case, one can consider the time as part of the state, making the state space . Since the time step always increases within an episode, the algorithm never revisits previous states. Therefore, all finite-horizon MDPs are OPFF, and Theorem 1 applies.
5 Numerical Experiments
We now present additional numerical experiments comparing MC-UCB and MCES. We emphasize that this numerical study aims to bring a better understanding of our theoretical results. Note that, MCES uses a more ideal, but less practical exploration scheme: for each episode, the initial state-action pair has to be randomly sampled from the state-action space. While MC-UCB does not require this condition and can be applied to more practical tasks. To be more consistent with prior works, we follow Wang et al. (2022) and focus on two classic OPFF environments: Blackjack and Cliff-Walking.
5.1 Blackjack
We first experiment on the classic card game Blackjack (discussed in detail in Sutton and Barto (1998)). Blackjack is an episodic task. For each episode, the player starts with 2 random cards with 2 possible actions each step: Hit or Stick. Choosing Hit gives the player another random card; Choosing Stick means the player will not draw more cards. The player’s goal is to obtain a set of cards whose point sum is as large as possible without going bust (more than 21 points). A dealer will draw cards following a fixed, predetermined policy, and will reveal one card to the player at the beginning of the episode. The player wins if they have a higher sum than the dealer without going bust, and receive a reward of 1. A draw yields a reward of 0 and losing yields -1.





We compare the performance, policy correctness, and absolute update difference. The performance is simply the average return of the learned policy. The policy correctness is the total number of states where the learned policy matches the optimal policy computed by the value iteration algorithm (Sutton and Barto 1998). The absolute update difference is the absolute differences between the action-value functions before and after an update, which can measure the convergence rate of the action-value function.
The second and the third plots in Figure 1 show that MC-UCB indeed converges and learns a good policy in Blackjack (Note Blackjack has 220 states in total), and converges faster than MCES in terms of the action-value function, even though MCES has a more ideal exploration scheme (requires that each episode starts with a random state-action pair). In this case, the faster convergence rate of MC-UCB might be due to the fact that the initial state distribution of Blackjack has a good coverage of the state space, allowing the MC-UCB agent to also initialize from a large number of states, making the action-value function converges efficiently.
5.2 Cliff-Walking

We now study the stochastic Cliff-Walking environment. The goal here is to successfully walk from a fixed starting point (bottom-left) to a terminal state (bottom-right) as soon as possible, without falling over the cliff. The state space contains each position in this 2-D grid, and the agent can move in 4 directions. The agent receives a reward of -0.01 for each step it takes, receives -1 for falling over the cliff at the bottom row, and receives 0 for reaching the goal. Additionally, we add stochasticity to this environment: when moving to the right, a wind with probability can blow the agent upwards or downwards with equal probability. The wind only applies when moving to the right in order to ensure the OPFF condition (Wang et al. 2022).
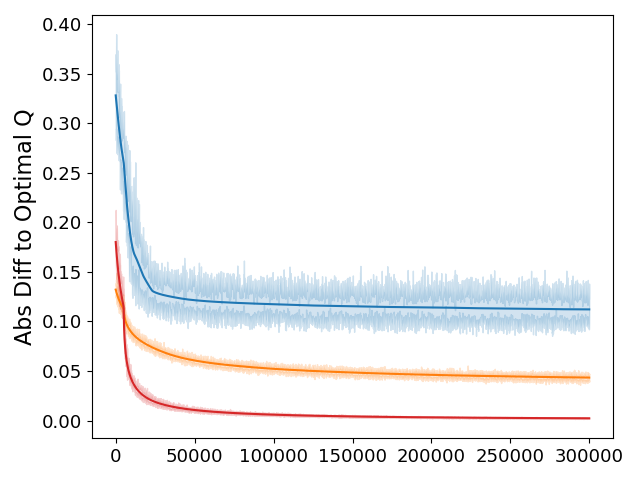
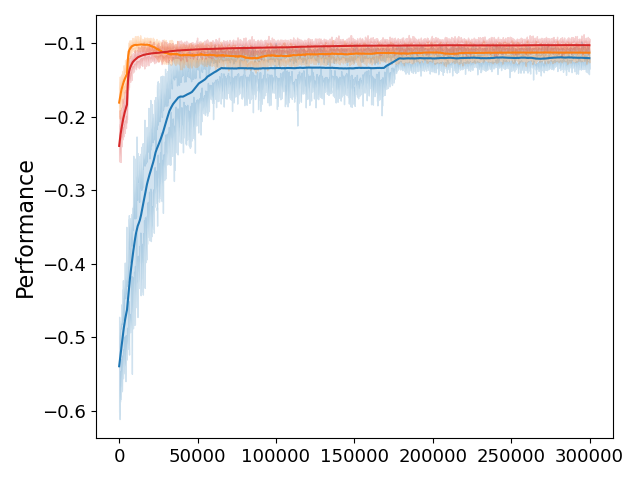
In this environment, we compare MCES, MC-UCB with a fixed initialization (FI_MC-UCB), and MC-UCB with a uniform initialization (UI_MC-UCB). Note that MC-UCB can be applied to tasks with all possible initial state distributions while MCES must rely on random initial state-action pairs from the entire state-action space. We expect MCES to work better in certain cases, but this does not affect the significance of MC-UCB because it can be applied to more practical settings. We compare the absolute difference between optimal Q values and estimated Q values; the average algorithm performance, and the absolute difference between optimal V values and estimated V values.
In Figure 2, each curve is averaged over a number of different world size and wind probability settings (additional details in appendix C). The first plot shows that when compared to MCES, MC-UCB has a slower convergence of the action-value function. Here, we point out that it is due to the slowly growing UCB exploration terms in the later learning phase that some Q values for suboptimal actions are updated infrequently though infinitely often (compared to MCES, MC-UCB take these suboptimal actions less often). If we run the algorithm for a longer time, the Q values will drop. Then, the performance plot indicates that for all three algorithms, the (induced) policy converges fast, which matches our theoretical findings that show the policy will first converge, and then the value-function (3, 4). Lastly, although Q values of the MC-UCB have not all converged yet, its convergent V value figure indeed demonstrates the convergence of the ratio to 0 as (5) shown in the proof. Compared with MCES, the relatively primitive MC-UCB (especially, the UI_MC-UCB variant) shows competitive performance and long-term V value convergence rate in small-size grid settings. We also note that in practice, MC-UCB can be further modified to improve the convergence rate.
6 Conclusion
We conclude this paper by outlining some possible directions for future research. We have established the almost sure convergence for the MC-UCB algorithm for OPFF environments. Earlier in Bertsekas and Tsitsiklis (1996) and Wang et al. (2022), it was shown that for some non-OPFF environments, the MCES algorithm does not converge. We conjecture that this is also the case for MC-UCB. Finding a counterexample remains an open question.
As a first step for understanding the properties of MC-UCB with random episode lengths, it is important to understand under what conditions it does and does not converge. As a second step, it would be of interest to establish tight regret bounds for MC-UCB with random episode lengths with the OPFF assumption.
It would also be interesting to extend the theory presented here to the MDP game context. For example, it would be of interest to study convergence in the context of 2-person 0-sum games for OPFF MDPs. This would allow us to move the theory in this paper a step closer toward a general convergence theory for AlphaZero (Silver et al. 2018).
References
- Agarwal, Jiang, and Kakade (2019) Agarwal, A.; Jiang, N.; and Kakade, S. M. 2019. Reinforcement learning: Theory and algorithms. CS Dept., UW Seattle, Seattle, WA, USA, Tech. Rep.
- Auer, Cesa-Bianchi, and Fischer (2002) Auer, P.; Cesa-Bianchi, N.; and Fischer, P. 2002. Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2): 235–256.
- Azar, Osband, and Munos (2017) Azar, M. G.; Osband, I.; and Munos, R. 2017. Minimax Regret Bounds for Reinforcement Learning. In Precup, D.; and Teh, Y. W., eds., Proceedings of the 34th International Conference on Machine Learning, volume 70 of Proceedings of Machine Learning Research, 263–272. PMLR.
- Bertsekas and Tsitsiklis (1991) Bertsekas, D. P.; and Tsitsiklis, J. N. 1991. An analysis of stochastic shortest path problems. Mathematics of Operations Research, 16(3): 580–595.
- Bertsekas and Tsitsiklis (1996) Bertsekas, D. P.; and Tsitsiklis, J. N. 1996. Neuro-dynamic programming, volume 5. Athena Scientific Belmont, MA.
- Bubeck et al. (2012) Bubeck, S.; Cesa-Bianchi, N.; Bubeck, S.; and Cesa-Bianchi, N. O. 2012. Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems. Foundations and Trends R in Machine Learning, 5: 1–122.
- Chang et al. (2005) Chang, H. S.; Fu, M. C.; Hu, J.; and Marcus, S. I. 2005. An adaptive sampling algorithm for solving Markov decision processes. Operations Research, 53: 126–139.
- Chen (2018) Chen, Y. 2018. On the convergence of optimistic policy iteration for stochastic shortest path problem. arXiv preprint arXiv:1808.08763.
- Cowan and Katehakis (2015) Cowan, W.; and Katehakis, M. N. 2015. Asymptotic Behavior of Minimal-Exploration Allocation Policies: Almost Sure, Arbitrarily Slow Growing Regret.
- Jaakkola, Jordan, and Singh (1994) Jaakkola, T.; Jordan, M. I.; and Singh, S. P. 1994. Convergence of stochastic iterative dynamic programming algorithms. In Advances in neural information processing systems, 703–710.
- Kocsis and Szepesvári (2006) Kocsis, L.; and Szepesvári, C. 2006. Bandit Based Monte-Carlo Planning. In Fürnkranz, J.; Scheffer, T.; and Spiliopoulou, M., eds., Machine Learning: ECML 2006, 282–293. Berlin, Heidelberg: Springer Berlin Heidelberg. ISBN 978-3-540-46056-5.
- Lattimore and Szepesvári (2020) Lattimore, T.; and Szepesvári, C. 2020. Bandit Algorithms. Cambridge University Press.
- Liu (2020) Liu, J. 2020. On the Convergence of Reinforcement Learning with Monte Carlo Exploring Starts. arXiv preprint arXiv:2007.10916.
- Silver et al. (2018) Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. 2018. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science, 362(6419): 1140–1144.
- Singh and Sutton (1996) Singh, S. P.; and Sutton, R. S. 1996. Reinforcement Learning with Replacing Eligibility Traces. Mach. Learn., 22(1–3): 123–158.
- Sutton and Barto (1998) Sutton, R. S.; and Barto, A. G. 1998. Introduction to reinforcement learning, volume 2. MIT press Cambridge.
- Tsitsiklis (1994) Tsitsiklis, J. N. 1994. Asynchronous stochastic approximation and Q-learning. Machine learning, 16(3): 185–202.
- Tsitsiklis (2002) Tsitsiklis, J. N. 2002. On the convergence of optimistic policy iteration. Journal of Machine Learning Research, 3(Jul): 59–72.
- Vodopivec, Samothrakis, and Šter (2017) Vodopivec, T.; Samothrakis, S.; and Šter, B. 2017. On Monte Carlo Tree Search and Reinforcement Learning. J. Artif. Int. Res., 60(1): 881–936.
- Wang et al. (2022) Wang, C.; Yuan, S.; Shao, K.; and Ross, K. W. 2022. On the Convergence of the Monte Carlo Exploring Starts Algorithm for Reinforcement Learning. In International Conference on Learning Representations.
- Yu and Bertsekas (2013) Yu, H.; and Bertsekas, D. P. 2013. On boundedness of Q-learning iterates for stochastic shortest path problems. Mathematics of Operations Research, 38(2): 209–227.
Appendix A Almost Sure Convergence for Multi-Armed Bandits
Since the UCB algorithm was first introduced in the Multi-Armed Bandit (MAB) literature, we discuss some background related to our work in this section. The MAB problem has been widely studied in the past decades (Lattimore and Szepesvári 2020). In each round out of a total of plays, an agent pulls one arm and receives the reward which is a random variable. We assume that successive plays of arm output rewards which are independent and identically distributed following an unknown law with an unknown bounded mean value . Also, we assume rewards from different arms are independent but may not be identically distributed.
One classic strategy to solve the exploration-exploitation dilemma in the MAB problem is called the UCB1 algorithm (Auer, Cesa-Bianchi, and Fischer 2002). The agent maintains a one-sided upper confidence interval for the estimated mean reward for each arm , where is how many times the arm is pulled during the rounds of play. By the algorithmic design of UCB1, the choice of arm for the -th round , where is a constant controlling the rate of exploration; and the second term will be if .
Much of the study of the MAB problem aims to develop efficient exploration-exploitation strategies in order to achieve low finite-horizon expected regret bound (Bubeck et al. 2012). However, instead of being satisfied with only the expected behavior of bandit algorithms, the convergence of pseudo-regret has also been studied. Cowan and Katehakis (2015) shows that the pseudo-regret converges to 0 for two families of policies involving slow-growing functions. In particular, the authors mention that the convergence result of the g-ISM index policy proposed in section 3.2 of Cowan and Katehakis (2015) can be extended to the UCB1 policy without providing a complete proof. We provide a direct, self-contained proof of almost sure convergence for the MAB problem using the UCB1 policy in Appendix B.
Lemma 1 (Almost Sure Convergence for the MAB with UCB1).
In the -arm Bandit setting employing UCB1 exploration, let be the rewards collected at each time of pulling one arm among . Then, w.p.1.
We emphasize that the MAB problem is not enough to model the two-node OPFF MDPs, since the latter one may contain an action leading to the self-cycle. Also, the analysis of the MAB problem is largely simplified, as the Q estimates for suboptimal actions can be guaranteed to converge to their optimal ones solely by the SLLN, which thus leads to the logarithmic bound for the first component of in the line (7) below.
Appendix B Proof of Lemma 1
Proof.
We can decompose:
where is the optimal arm that yields the reward with the highest mean reward .
Let be the underlying sample space. By the design of the UCB1 algorithm, each arm will be pulled infinitely often if we conduct infinite rounds of play. In other words, as for any arm . By the Strong Law of Large Number for random variables , the estimated mean converges to the true mean , for any arm . That is, the set has probability measure 1. Moreover, let and we have . Then, what remains to show is , for any .
For any , according to the inequality 8.4 of Section 8.1 in (Lattimore and Szepesvári 2020), given any and a positive and increasing function , we can bound:
| (6) | ||||
| (7) | ||||
| (8) |
where is defined to be the estimated mean reward of arm by using the first samples; if , we will just set .
Let for any . On the one hand, for any , given satisfying , there exists such that for any , . Thus, we can further bound the first term:
where the last equation is guaranteed if the function is chosen such that as .
On the other hand, for any , given satisfying , there exists such that for any , , we can also bound the second term:
Now, from the above three inequalities, it is easy to see: for any , , as , for any . Since , , for any . And therefore, we finally have: w.p.1.. ∎
Appendix C Additional Figures and Discussions for Numerical Experiments
We introduce additional details about the experimental results of the Cliff-Walking environment. Figure 2 is the average result of all experiments shown in Figures 4, 5, and 6, where we test the three algorithms on grid world sizes of and with wind probabilities 0, 0.3, 0.5, and 0.7. The time limit is set to be 50 in the grid and is increased to 70 in the grid ( should be chosen to be longer than the longest possible loop-free path in any tested grid world). If one wants to run experiments on a larger grid world, it will be important to increase the time limit so in the early stage of learning, trajectories generated by suboptimal policies are more likely to reach the terminal state. In the figures, each curve is averaged over five random seeds. The solid lines are the mean value and the shaded areas represent the variance.
Figure 4 shows convergence rate comparison for the three MC algorithm variants. Results show that when using a fixed initial state, the convergence speed will become lower in a larger grid world. Figure 5 shows that the performance of MC-UCB with uniform initialization can match or outperform MCES. And performance drops when using a fixed initialization. Figure 6 shows that in terms of the value function, MC-UCB with uniform initialization can converge relatively quickly similar to MCES. When using fixed initialization, MC-UCB works similarly compared to the other two in a smaller grid world, and observes a drop in performance in the larger grid world.