On the algorithm to perform Monte Carlo simulations in cells with constant volume and variable shape

Let us assume that, in addition to volume, the partition function in the canonical, or NVT for short, ensemble $Q(N,T,V;\tau)=\int_{V;\tau}\rm{exp}[{-\beta U(\Gamma)}]\mathrm{d}\Gamma$ explicitly depends on some geometrical parameter $\tau$, for instance the aspect ratio of the box sides. Here, $\beta$ is the inverse temperature, $V$ is the volume, $U(\Gamma)$ is the potential energy and $\Gamma$ is the abbreviation for the point in the configuration space. The integration is carried out over volume $V$ with the set parameter $\tau$. The full partition function then should be constructed as a weighted sum (or integral) over all possible realizations of the additional degree of freedom [12]. In the most general case, one finds:

where $f(\tau)$ is the weighting function of the extended ensemble defined by both volume and the shape of the box and $P(\tau)$ is the probability distribution function of $\tau$, characteristic of the NVT ensemble with variable shape. In principle, one is free to choose $f(\tau)$ arbitrarily, provided that it satisfies certain conditions typically imposed on distribution functions, such as positive definiteness or integrability. Here, we will select $f(\tau)$ on the condition that the extended ensemble with fixed volume satisfies distribution of $\tau$ specific for the constant pressure, or NPT, ensemble. In this way, modelling in the two ensembles, constant-volume and constant-pressure, will be consistent, hence minimizing finite size effects.

The distribution function in the constant-pressure ensemble reads:

where $\mathcal{P}$ is the pressure. Let us focus now on 2D space and obtain formulas for this simpler case first. The relevant volume is $V=L_{x}L_{y}\sin\alpha$, where $L_{x}$ and $L_{y}$ are the lengths of the simulation box and $\sin\alpha$ is the sine of the angle between them. In NPT simulations, volume is sampled randomly from a uniform distribution. This can be achieved either by uniformly sampling one of the variables involved in volume, $L_{x}$, $L_{y}$ or $\sin\alpha$, or by non-uniformly sampling some combination of these variables which leads to a uniformly distributed volume [2]. Let us assume that the first scenario takes place, as it is more general and can be applied to both liquids and crystals, and each concerned variable is sampled uniformly, one at a time and in random order. The joint distribution function measured in such simulations for variables $L_{x}$, $L_{y}$ and $\sin\alpha$ will be given by the following expression:

which can also be obtained by integrating distribution function (2.2) over all configurations $\Gamma$. The dependence on $\tau$ in the partition function arises because the integration over $\Gamma$ is carried out for the box with specific dimensions $L_{x}$ and $L_{y}$, which in addition to the volume $V=L_{x}L_{y}$ also define other geometrical parameters including $\tau=L_{x}/L_{y}$.

As an illustration, consider a schematic distribution ${P(L}_{x},L_{y})$ shown in figure 2, specific for rectangular boxes with $\sin\alpha=1$. Among all possible configurations, those that correspond to volume $V$ satisfy the constraint $V=L_{x}L_{y}$, creating a one-dimensional sub-ensemble characterized by a single degree of freedom. If $L_{x}$ is chosen as the independent degree of freedom, configurations with given $V$ and $L_{x}$ will appear in simulations with probability ${P(L}_{x},{V}/{L_{x}})$. Any other geometric parameter of the system will also be characterized by a unique distribution function. This includes the aspect ratio $\tau=L_{x}/L_{y}$, for which the distribution function $P_{V}(\tau)$ represents the relative frequency of seeing conformations with different $\tau$. This function is directly accessible in simulations.

Our goal is to evaluate $P_{V}(\tau)$ and then try to reproduce it in simulations at a constant volume. Using ${P(L}_{x},L_{y},\sin\alpha)$ as the starting point, $P_{V}(\tau)$ can be evaluated as $P_{V}(\tau)=\left\langle\delta\left(\tau-{L_{x}}/{L_{y}}\right)\right\rangle_{V}$, where the brackets $\langle\cdots\rangle_{V}$ indicate a statistical average over sub-ensemble with fixed $V$. The constant-volume constraint can be imposed through another delta function, leading to the following expression in terms of the unbiased distribution function:

This integral can be evaluated in two steps. First, a change of variables $y=L_{x}L_{y}\sin\alpha$ helps to eliminate the integration over $L_{y}$ while keeping the other variable constant. The result is:

The second integration can be carried out by making a change of variables $y=L_{x}^{2}\sin{\alpha/V}$, which after dropping the terms that are independent of $\tau$ yields:

Let us now require that $P_{V}(\tau)=P(\tau)$, i.e., the distribution functions in the NPT and NVT ensembles are equal. It is easy to see then from equation (2.1) that $\int{Q(N,T,V;\tau)f(\tau)\mathrm{d}\tau}=\int{P(\tau)\mathrm{d}\tau}=\int{P_{V}(\tau)\mathrm{d}\tau}=\int{Q(N,T,V;\tau)({1}/{\tau})\mathrm{d}\tau}$, indicating that $f(\tau)=1/\tau$. In other words, we arrive at the conclusion that new aspect ratios in constant-volume simulations should be drawn from the $1/\tau$ distribution in order to reproduce the result of the NPT simulations. Furthermore, it is seen from equation (2.6) that free energy $\beta F(\tau)=-\log{\left[Q(N,T,V;\tau)\right]}$ associated with the degree of freedom $\tau$ can be computed as $\beta F(\tau)=-\log{\left[\tau P_{V}(\tau)\right]}$. Therefore, the aspect ratio $\tau$ is not suitable for the computation of free energy differences directly from the distribution function. In other words, $\displaystyle\beta\Delta F=\beta\left[F\left(\tau_{1}\right)-F\left(\tau_{2}\right)\right]\neq\log{\left[{P_{V}\left(\tau_{2}\right)}/{P_{V}\left(\tau_{1}\right)}\right]}$, where $\tau_{1}$ and $\tau_{2}$ are some values defining two macroscopic states. It is easy to show, however, that $P_{V}(z)=\tau(z)P_{V}(\tau(z))$ is the distribution function for a new variable $z=\log(\tau)$. Thus, in terms of this variable $\beta F\left[\tau(z)\right]={\beta F(z)=-\log}{\left[\ \tau(z)P_{V}(\tau(z))\right]=-\log[P_{V}(z)]}$, making $z$ the proper order parameter associated with the geometry parameter $\tau$. In the Appendix we show that $1/\tau$ sampling law also applies in the three-dimensional space.

Given that the sampling law is known, how does one conduct a constant-volume simulation with the variable shape? Let us first point out the following auxiliary results. The lengths of the box can be expressed in terms of $\tau$ and volume when the cell angle is considered constant: $L_{x}=\sqrt{{V\tau}/{\sin\alpha}}$ and $L_{y}=\sqrt{{V}/{(\tau\sin\alpha)}}$. Given that the volume is fixed, one can find the appropriate distributions for the lengths using the standard identity: $P_{eq}(x)\mathrm{d}x=P_{eq}(y)\mathrm{d}y$, where $y(x)$ is some function of $x$ and $P_{eq}(x)$ is the distribution function of this variable. It can be shown that they are given by the same expression as for $\tau$: $f\left(L_{\nu}\right)\sim 1/L_{\nu}$, where $\nu=x,\ y.$ In other words, the sampling distributions of the size in $x$ and $y$ directions obey the same law. This result is of fundamental importance. The invariance with respect to the swap of $x$ and $y$ coordinates is central to simulations of condensed matter (with the exception of cases where external fields are imposed that break the symmetry). Any algorithm that violates this condition should be considered flawed. For instance, uniform sampling of $\tau$ assumes that $f(\tau)\sim\mathrm{const}$, and so one can find that $f\left(L_{x}\right)\sim L_{x}$ while $f\left(L_{y}\right)\sim{1/L}_{y}^{3}$. Both distributions are incorrect and will lead to a bias in the sampled ensemble. Another point that should be made regarding the $1/\tau$ law concerns its interpretation. Since small $\tau$’s correspond to narrow boxes while large ones — to wide boxes, the decline of the distribution function with $\tau$ may seem to indicate that the balance between the two types of boxes is broken. This impression, however, is misleading and the number of generated narrow and wide boxes is actually the same. The number of the former can be estimated as $f(\tau){\Delta L}/{L_{y}}$, where $\Delta L$ is some small range in which $L_{x}$ is allowed to vary. If, instead, one varies $L_{y}$, the same number of boxes should be $f(\tau)({L_{x}\mathrm{\Delta}L}/{L^{2}_{y}})$. Now, let us swap $x$ and $y$ coordinates in the last expression and obtain $f\left({1}/{\tau}\right)({L_{y}\Delta L}/{L^{2}_{x}})$. This operation is expected not to affect the number of boxes, so one should find that $f(\tau){\Delta L}/{L_{y}}=f\left({1}/{\tau}\right)({L_{y}\Delta L}/{L^{2}_{x}})$. After some rearrangement, it follows that the condition for the balance between narrow and wide boxes is $f(\tau)\tau=f\left({1}/{\tau}\right){1}/{\tau}$. It is easy to see that the derived $1/\tau$ formula satisfies this condition, proving that the symmetry between different shapes is preserved.

Up to this point we implicitly assumed that $\tau$ can be changed by changing either $L_{x}$ or $L_{y}$. It is easy to see, however, that when the volume of the box $V=L_{x}L_{y}\sin\alpha$ is kept fixed ${\tau=L}_{x}^{2}\sin{\alpha/V}$. Thus, it is possible to change the aspect ratio also by changing the cell angle $\alpha$. It is clear that the distribution law should not depend on how $\tau$ is changed. We conclude, therefore, that the $1/\tau$ function should also apply for the angle moves. It is also clear from the expression of the volume that the term $\sin\alpha$ can be treated on the same footing as that of $L_{y}$. Thus, one can bypass the derivation and immediately conclude that the sampling probability $P(\sin\alpha)\sim{1}/{\sin\alpha}$. The pertinent order parameter for the cell angle is $z=\log(\sin\alpha)$. Accordingly, free energy associated with $\alpha$ can be computed as $\displaystyle\beta F(\alpha)=-\log\left[P_{V}(\alpha)({\sin\alpha}/{\cos\alpha})\right]$.

It is convenient to combine the two types of moves, one in which $L_{x}$ and $L_{y}$ change simultaneously and one in which $\sin\alpha$ changes together with either $L_{x}$ or $L_{y}$, in one algorithm that consists of two steps:

1. 1.

   A new value for $L_{x}^{\prime}$ is generated from ${1/L}_{x}$ distribution.

2. 2.

   A decision is made randomly with equal probability about which step is to take next: a) new $L_{y}^{\prime}={V}/({L_{x}^{\prime}\sin\alpha})$, or b) new $\sin\alpha^{\prime}={V}/({L_{x}^{\prime}L_{y}})$. The coordinates of the particles are appropriately scaled by $L_{x}^{\prime}/L_{x}$ and $L_{y}^{\prime}/L_{y}$ in the $x$ and $y$ directions in trial moves. Changes of the cell angle $\alpha$ do not affect the coordinates.

Generating $1/\tau$ distributions can be achieved in a variety of ways. Probably, the easiest is the Metropolis importance sampling [9]. It consists in using a uniformly distributed random variable to generate a trial $\tau^{\prime}$ that is then accepted with probability $1/\tau^{\prime}$.

We test the designed algorithm for the system of hard-core ellipses. Ellipses have long and short half-axes $\frac{1}{2}\sigma_{a}$ and $\frac{1}{2}\sigma_{b}$, respectively. Aspect ratio is defined as $\kappa={\sigma_{a}}/{\sigma_{b}}>1$. It is a key parameter determining the general behavior of the system. The geometrical details are explained in figure 3 (a).

There are $N$ particles in the system. For the sake of generality we use a skew reference frame. Each particle is characterized by three degrees of freedom: two coordinates $x_{i},\ y_{i}$ and one rotation angle $\phi_{i},\ i=1,N$, see figure 3 (b) for illustration. In addition to the skew coordinates, one can also assign Cartesian coordinates $x^{\prime},\ y^{\prime}$ to each particle; the two are related as follows:

The volume elements of the two coordinates systems are related through the Jacobian of transformation $\mathrm{d}V=\mathrm{d}x^{\prime}\mathrm{d}y^{\prime}=\frac{\partial(x^{\prime},y^{\prime})}{\partial(x,y)}\mathrm{d}x\mathrm{d}y=\sin\alpha\mathrm{d}x\mathrm{d}y$. The particles are placed in a box with sides $L_{x}$ and $L_{y}$ and an angle $\alpha$ between them under periodic boundary conditions, as shown in figure 3 (b)–(c). The skew simulation boxes are designed to accommodate lattices of all possible types. The minimum image convention is applied to compute the interaction energy. As illustrated in figure 3 (c), certain particle $i$ interacts with the closest periodic image of particle $j$. The distance between the two particles is computed as $r_{ij}=\sqrt{x_{ij}^{2}+y_{ij}^{2}+2x_{ij}y_{ij}\cos\alpha}$, where $x_{ij}=x_{i}-x_{j}$ and $y_{ij}=y_{i}-y_{j}$. The usual rule for computing the shortest distance is used: if $x_{ij}>L_{x}/2$, then it is replaced by $x_{ij}-L_{x}$. Similarly, if $x_{ij}<-L_{x}/2$, then it is replaced by $x_{ij}+L_{x}$. The same transformations are applied to the coordinate $y$. The Cartesian coordinates of the vector $\mathrm{d}\vec{r}^{\prime}$ connecting two particles are $\mathrm{d}x^{\prime}=x_{ij}+y_{ij}\cos\alpha$ and $\mathrm{d}y^{\prime}=y_{ij}\sin\alpha$. Together with the rotation angles $\phi_{i}$ and $\phi_{j}$, they are used to determine whether two ellipses overlap [13]. The density of the system is reported in reduced units $\rho=({N}/{V})\ ({1}/{\rho_{\max}})$ where $\rho_{\max}=({2}/{\sqrt{3}})[{1}/({\sigma_{a}\sigma_{b}})]$ is the density of the maximally compact lattice configuration.

To measure free energy difference between prospective lattice structures, we use the properly defined order parameters. As discussed in the section 2, one such parameter is $\log(\tau)$, where $\tau=L_{x}/L_{y}$. The ratio of the side lengths is measured directly in simulations and then binned to compute the associated distribution.

Another order parameter that will be utilized is $\alpha$. The rational why the cell angle can be employed as an order parameter is as follows. The system of ellipses can exist either as a fluid or a solid lattice phase, depending on the density [14]. At $\kappa\lesssim 1.5$ [15, 16], ellipses in the solid phase are not aligned with one another, making the so-called plastic lattice [13]. At larger aspect ratios, the particles are aligned similarly to nematic fluids. An example of the simulation cell in which ellipses are aligned is shown in figure 4 (a). The depicted close-packed conformation can be generated from the minimal motif that contains 4 ellipses. It is shown in panel (b) and also highlighted in the right-hand lower corner of the cell. This motif can be obtained from a close-packed configuration of disks by a sequence of unique steps. Let us assume that the diameter of the disks is $\sigma$ and the angle that the left side of the initial box makes with the vertical axis is $\piup/6$, see figure 4 (e). Let us rotate the box counterclockwise by an angle $\gamma$, as shown in figure 4 (d). After that let us stretch the box by the amount $\kappa>1$ in the vertical direction. As a result, disks are transformed into ellipses. The length of the long axis of the ellipses becomes $\kappa\sigma$, as shown in figure 4 (c). Simultaneously, stretching changes the angle that the lower side of the box makes with the horizontal axis, as figure 4 (c) illustrates. While initially it was $\gamma$, now the angle becomes

The angle between the left-hand side and the vertical axis also changes. Immediately following the rotation, it is $\piup/6-\gamma$ but after stretching it becomes

As can be seen from figure 4, physically distinct configurations are generated when $\gamma$ changes between 0 and $\piup/6$. All other values lead to redundant configurations. To characterize the state of each ellipse in a specific lattice state, one can use, for instance, the angle that the long axis makes with the horizontal axis, $\phi$. As can be seen from figure 4 (b) $\phi={\piup}/{2}-\beta$. The geometry of the box, on the other hand, can be uniquely specified by its angle $\alpha$ (given that the aspect ratio $\kappa$ is fixed). Both angles, $\phi$ and $\alpha$, are functions of $\gamma$, so there is only one independent variable that fully defines the close-packed structure. All other parameters can be expressed as functions of the chosen variable via relations (3.2) and (3.3). For instance, the rotation angle $\phi$ can be cast as a function of $\alpha$:

where $\kappa$ is the aspect ratio. For the purpose of illustration, figure 4 (e) shows this function for $\kappa=2$, $F_{2}(\alpha)$.

It can be shown that $\alpha$ varies in the range $\{\alpha_{\rm{min}}=\cos^{-1}[\sqrt{{3}/({3+\kappa^{2}})}],\ \alpha_{\rm{max}}={\piup}/{2}-\cos^{-1}[\sqrt{{3\kappa^{2}\ }/({3+\kappa^{2}})}]\}$, while the corresponding limits of the rotation angle $\phi$ are $\{\phi_{\rm{min}}={\piup}/{2}-\cos^{-1}[\sqrt{{3\ }/({3+\kappa^{2}})}],\ \phi_{\rm{max}}={\piup}/{2}\}$. As $\alpha$ changes, the structure of the lattice changes with it, creating the manifold of an infinite number of lattices differing from one another by the rotation angle $\phi$. This is in contrast to the system of disks, which makes a single hexagonal lattice at high densities. As will become clear below, the lattice types corresponding to the extreme points have a special meaning. At $\alpha=\alpha_{\rm{min}}$, see figure 4 (a), the lattice can be viewed as being assembled from vertical lines of ellipses that make contact with one another through the pole at the short side of the particle. The ellipses are aligned along the line connecting their centers. Consequently, the corresponding lattice type is termed longitudinal (L). The lattice observed at $\alpha=\alpha_{\rm{max}}$ can be assembled from horizontal lines of ellipses which contact each other through the pole at their long side. The orientation of particles is perpendicular to the line connecting their centers, so the corresponding lattice type is called transverse (T). In simulations, the longitudinal lattice can be transformed into the transverse lattice and vice versa by varying the angle $\alpha$. If $\alpha$ is treated as a variable, the transition will happen spontaneously. The system in this case will sample various types of lattices in the course of a single simulation, thereby enabling the computation of their statistical weight. A major difficulty associated with this approach is convergence. To collect sufficient statistics for the distribution function $P(\alpha)$, the system should visit different lattice types a large number of times, which may be difficult if the free energy difference between the concerned lattices is large. To improve the convergence, in this study we employ the method of umbrella sampling [17]. The range $[\alpha_{\rm{min}},\alpha_{\rm{max}}]$ is broken equidistantly into a number of bins, or windows, each assigned a distinct value of $\alpha$. Harmonic potential is applied to bias sampling in simulations to the vicinity of each window. The unbiased distribution $P(\alpha)$ is reconstructed by collecting information on $\alpha$ sampled in all windows. The order parameter relevant for the cell angle is $\log(\sin\alpha)$.

We also compute free energy differences by the method of Einstein crystal (EC) [18, 19]. The key idea of this method is to obtain free energy of the lattice states of interest relative to a common reference state. The free energy of the reference state then drops when the free energy difference is taken. The reference state is modelled by the harmonic Hamiltonian $U_{\rm H}$. Free energy with respect to this model is computed by thermodynamic integration with the help of a coupling constant $\lambda$. How this scheme works in skew coordinates is described in detail in the Appendix. The main formula we use to compute the free energy difference between lattice states characterized by different $\alpha$’s is:

Here, $\langle\Delta U\rangle_{\lambda}$ is the average of the potential energy difference $\Delta U=U_{\rm{HS}}-U_{\rm H}$ computed in simulations driven by the “hybrid” Hamiltonian $U(\lambda)=U_{\rm H}+\lambda\Delta U$. The actual potential energy of the hard-ellipse system is $U_{\rm{HS}}$ and the simulations are performed at a fixed volume $V$ and cell angle $\alpha$ in the reference frame associated with the center of mass. As $\lambda$ is varied between 0 and 1, the Hamiltonian $U(\lambda)$ is transformed from $U_{\rm H}$ to $U_{\rm{HS}}$. As the harmonic potential gradually becomes weaker, the integral in equation (3.5) reports on the spatial extent by which the system is allowed to deviate from the initial configuration, thus providing a measure of the configurational freedom.

The reference Hamiltonian

contains a set of coordinates $x_{i}^{0},y_{i}^{0},~{}i=1,N$ with respect to which the free energy is evaluated. As a reference we chose a lattice configuration $x_{i}^{0}=(j-0.5)L^{E}_{x}/n,j=1,n$ and $y_{i}^{0}=(k-0.5)L^{E}_{y}/n,\ k=1,n$; ${i=\sum_{j^{\prime}=1}^{j}\sum_{k^{\prime}=1}^{k}}1$, $n\times n=N$. Here, $L^{E}_{x}$ and $L^{E}_{y}$ are the dimensions of the simulation cell in $x$ and $y$ direction, $\phi_{i}^{0}$ are initial angles and $\gamma_{T}$ and $\gamma_{R}$ are adjustable spring constants. It is easy to show that ${N}/{\rho}=\tau{L^{E}_{y}}^{2}\sin\alpha$, where $\tau={L^{E}_{x}}/{L^{E}_{y}}$ is the ratio of the $x$ and $y$ dimensions. Thus, $L^{E}_{y}$ is uniquely defined by $N$, $\rho$, $\alpha$ and $\tau$. Parameter $\tau$ was extracted from constant-volume simulations as the average over all sampled cell side ratios. The integral in equation (3.5) was evaluated by numerical quadrature. In order to reduce the variation seen in $\langle\Delta U\rangle_{\lambda}$, a non-uniform transformation $\zeta(\lambda)$ was applied before integration. A total of 33 grid points, $\zeta_{i},i=1,33$, were generated non-uniformly between $\zeta(0)$ and $\zeta(1)$. The points were chosen so as to maintain a constant level of the numerical integration error, which, after optimization, we judge to be negligible. The statistical error was estimated by performing 5 independent measurements for each state point from which standard deviation was extracted.

The performed MCVS simulations consist of two types of moves. The first type is the regular MC steps in which particles are randomly displaced and rotated. The maximum magnitude of these steps are adjusted to achieve greater than 30% acceptance. The second type of moves are changes of geometry. They are attempted randomly with 10% overall probability. Box lengths and box angle are updated as described in the previous section. Parameters of these moves are adjusted to achieve greater than 50% acceptance rate. Changes of box lengths are accompanied with the appropriate scaling of particle coordinates. The algorithm of Vieillard-Baron [13] is used to determine if two ellipses overlap.

To perform the umbrella sampling simulations, the range [$\alpha_{\rm{min}}$,$\ \alpha_{\rm{max}}$] was divided equidistantly into 50 windows,$\ \alpha_{i}=\alpha_{\rm{min}}+\Delta(i-1),\ \ \Delta=({\alpha_{\rm{max}}-\alpha_{\rm{min}}})/{49},\ i=1,50$. Simulations were performed in each window with an additional harmonic potential $U_{h}=\frac{1}{2}\epsilon\left(\alpha-\alpha_{i}\right)^{2}$ applied. The strength of the potential $\epsilon$ was set such that the adequate overlap of the histograms at the neighboring windows was achieved. The unbiased distribution $P_{V}(\alpha)$ was obtained at the end of the simulations by the multiple-histogram reweighting method [20, 21].

The first test was performed for a system with $\kappa=1.2$. We used rectangular boxes and set the density at $\rho=0.83$ which is high enough to trigger the transition into the crystalline state yet low enough to preclude aligning of the ellipses. Under these conditions, the system makes the so-called plastic lattice in which particles occupy lattice sites but are capable of rotating by all 180 degrees. A time trace of $\tau$ observed in simulations of this system is shown in figure 5 (a). The aspect ratio varies in the range $[1.0,1.3]$ around an average of ~1.15. At all times, the system occupies a lattice configuration with the distance between neighboring sites $1.17\sigma_{b}$ while the ellipses are capable of adopting any angle $0<\phi<\piup$. A cartoon representation of this structure and its pair distribution function computed for the centers of the ellipses are shown in figure 5 (f) and figure 5 (e), respectively. The lack of alignment between particles is immediately apparent.

We find that the alignment (or rotational degrees of freedom more generally) plays a critical role in determining the structure of the lattice. When it is introduced manually by constraint $\phi_{i}=\phi,\ i=1,N$ where $\phi$ is the common angle of all particles which is allowed to change, the lattice splits into two sub-lattices with a distinct structure. One sub-lattice displays contacts between neighboring ellipses going through the pole at the long side and can be recognized as the transverse lattice. A cartoon representation of this lattice is shown in figure 5 (h). The second sub-lattice is the longitudinal lattice, exhibiting closest contacts between the neighboring ellipses going through their short side, as illustrated in figure 5 (g). All other lattice configurations correspond to free energy maxima and are not directly observable. It is not clear if this is a genuine property of the system or an artifact resulting from the use of rectangular box geometry, suppressing all structures other than the mentioned two. For the demonstration purposes, we considered a small system consisting of $N=16$ particles making $4\times 4$ lattice, so as to enable spontaneous T-L transitions. The time trace of $\tau$ obtained in simulations of this system is shown in figure 5 (b). It is seen that $\tau$ changes in a discontinuous manner among four different values, indicating that the geometry of the box is specific to the lattice type that it contains and suggesting that the aspect ratio can be used as a structural parameter to distinguish between T and L states. Pair distribution functions $g(r)$ obtained for each lattice type, shown in figures 5 (c), (d), demonstrate that the two lattices have a noticeably different structure. The most obvious differences concern the first coordination shell. Compared to the model with full particle rotations, $g(r)$ in the T and L states is split into two sub-maxima. The position of the first sub-maximum in T conformations is at $1.01\sigma_{b}$ while in L conformations it is at $1.1\sigma_{b}$, demonstrating that the particles in the transverse arrangement are capable of approaching each other at shorter distances. This is understandable, given how ellipses are stacked in the two structures, see figure 5 (g) and (h). The second sub-maximum appears at $1.2\sigma_{b}$ in both states. The second and third coordinate shells also show significant differences between T and L conformations.

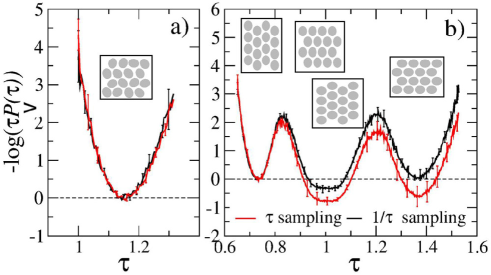
So how well does the proposed algorithm reproduce the statistics of the different conformational states? Figure 6 shows the free energy profile $\beta F(\tau)=-\log[\tau P_{V}(\tau)]$ obtained for the system where all particles are free to rotate — panel a), and for the rotationally-constrained system — panel b). As can be expected from figure 5, a single minimum is seen for the unconstrained system and four minima are present for the constrained one. The specific aspect ratios of the minima are $\tau=0.7$, $0.95$, $1.05$ and $1.4$. The two extreme values, $0.7$ and $1.4\approx 1/0.7$, correspond to the longitudinal state. The two minima in the middle are characteristic of the transverse state; they appear to merge in the graph because of being closely spaced. Conformations with $\tau=0.95$ and $1.05$, and those with $\tau=0.7$ and $1.4$, are related by a 90-degree rotation of the reference frame (note that no such transformation ever takes place in the simulations). Corresponding to the same state, they should exhibit the same free energy. It is a crucial test for the algorithm to reproduce this behavior. It is seen from figure 6 (b) that $\beta F(0.95)=\beta F(1.05)$ and $\beta F(0.7)=\beta F(1.4)$ within the error bars, so the proposed $1/\tau$ algorithm successfully passes the test. By contrast, the $\tau$-sampling algorithm predicts that $\beta F(0.95)=\beta F(1.05)$ but $\beta F(1.4)<\beta F(0.7)$ and the difference is statistically significant. The greater population of $\tau=1.4$ state can be explained by the greater statistical weight assigned to conformations with larger $\tau$ by an algorithm in which the sampling probability is flat compared to the case when it declines with $\tau$. Furthermore, even though the $\tau$-sampling method generates the same free energy for $\tau=0.95$ and $1.05$, the value it predicts is twice as large as that of the proper algorithm. Again, the difference is statistically meaningful, which leads us to the conclusion that this method is not capable of reproducing accurately the inter-state statistics for the constrained model under the considered conditions.

By contrast, figure 6 (a) shows that both sampling algorithms lead to the same results, within error bars, for the unconstrained system. It follows, therefore, that the performance of geometry sampling algorithms strongly depends on the system under study, more specifically on the range in which the geometry parameter is varied. If the range is narrow, as in figure 6 (a), the use of the proper algorithm does not make much difference. The average $\tau$ and the shape of the distribution function are generally well reproduced. The algorithm matters, however, when $\tau$ changes in a wide range, as shown in figure 6 (b). Improper sampling leads to significant distortions in $P_{V}(\tau)$ that may ultimately affect the free energy estimates.

When $\kappa$ is increased beyond ~1.5, the ellipses in the crystalline state become aligned [15, 16]. What is the statistical weight of lattice types with different ellipse orientations? To find that out, we considered the system with $\kappa=4$. The cell angle $\alpha$ for this system varies in the range [0.41, 1.43], which is much wider than the range [0.96, 1.12] appropriate for $\kappa=1.2$. This improves the chances of observing a quantitative difference between the results of using different sampling methods. We considered the cells with 6 rows and 6 columns of ellipses because smaller systems failed to produce stable lattices. Since spontaneous transitions among different lattice types were not observed for the considered system, we had to employ umbrella sampling method to compute the distribution function of the structural order parameter $\alpha$. The details are provided in the section 3. The density of the system was set at $\rho=0.95$ which is much higher than the density of the fluid-solid transition.

Free energy profile $\beta F(\alpha)=-\log\left[P_{V}(\alpha)\frac{\sin\alpha}{\cos\alpha}\right]$ obtained in simulations using the proposed sampling algorithm is shown in figure 7 by black line. It has two minima with the lowest free energy corresponding to the transverse and longitudinal states. This agrees with our results for the constrained model of $\kappa=1.2$, suggesting that the presence of two identified stable states is not an artifact of the used cell geometry. The free energy of the longitudinal state is $\beta\Delta F=3.5\pm 0.5$ higher than that of the transverse state. The corresponding figure obtained by the $\tau$-sampling method is $\beta\Delta F=2.2\pm 0.4$. It is seen that this method assigns additional statistical weight to the longitudinal state with smaller $\alpha$. This is in line with our observation from the previous section where we saw states with larger $\tau$ experiencing more frequent sampling. Indeed, since $\sin\alpha={V}/{\tau L_{y}^{2}}$, more sampling for large $\tau$ means more sampling for small $\sin\alpha$ and, by extension, small $\alpha$.

Free energy difference between the L and T states was also evaluated by the EC method. The geometry of the cell was determined in simulations using $1/\tau$ sampling. For the longitudinal structure we used $\alpha=\phi^{0}=\alpha_{\rm{min}}=0.43$ and $\tau=0.558$. For the transverse state, the corresponding numbers were $\alpha=\alpha_{\rm{max}}=1.43$, $\tau=0.288$ and $\phi^{0}=\piup/2$. The initial ellipse orientations $\phi^{0}$ were generated by $F_{4}(\alpha)$ for both structures. Upon combining the results of 5 independent measurements, the free energy difference was evaluated as $\beta\Delta F=3.2\pm 0.2$. This number is in excellent numerical agreement with the prediction made in the $1/\tau$ sampling simulations, $3.5\pm 0.5$, providing an essential validation for this method. By contrast, the $\tau$-sampling algorithm generates an incorrect free energy, $2.2\pm 0.4$, and the error is statistically significant. Based on these observations, we conclude that the use of the proper sampling algorithm is essential for the studied system.

The free energy of the transverse state appears to be lower than that of the longitudinal state. This could be a genuine physical effect stemming from conformational preferences of different lattice configurations. Alternatively, the difference could be a by-product of the small size of the simulation cell. Simulations designed to extract free energy difference as a function of $N$ could help to resolve this ambiguity. Linear segments in $\beta\Delta F(N)$ at large $N$ would indicate genuine free energy difference between the two lattice states. Any other dependence would signal finite-size artifacts. Which of these two scenarios takes place needs to be answered in careful finite-size scaling studies.

It is possible to conduct constant-volume simulations with the changing shape in the three-dimensional space. Let us assume that the geometry of the box is defined by six variables, three lengths $L_{x},L_{y}$ and $L_{z}$, and three angles $\alpha,\beta$ and $\gamma$, as shown in figure A.1. Let us further assume for now that the box is rectangular, $\alpha=\beta=\gamma=\piup/2$. The analogue of the constant-pressure distribution (2.3) in 3D will be a function of the lengths of the box:

Aspect ratios can be computed for all three sides of the box lying in $xy$, $xz$ and $zy$ planes. We will try to change only one $\tau$ at a time. The corresponding distribution function, for instance for $\tau=L_{x}/L_{y}$, can be computed as follows:

By making the substitution $y=L_{x}L_{y}L_{z}$ one can eliminate the integral over $L_{z}$ obtaining:

After the second substitution $y=L_{x}{/L}_{y}$ and elimination of $L_{x}$, one arrives at:

This result does not depend on the integration order. Therefore, we find that the sampling law in three-dimensional space is the same as in the two-dimensional space.

Since there is no difference with respect to the dimensionality, it is convenient to use the algorithms developed for 2D and apply them to 3D boxes. In particular, the idea of sampling one side of the box and then updating alternatively either another side or the angle between the sides can be reused. The volume of the box with variable angles is

In MC sampling, one should take alternatively pairs of a side and a second side or a side and an angle until all such combinations are exhausted. If the length $L_{x}$ is updated to $L^{\prime}_{x}$ then companion steps should be updating $L_{y}$ or $\cos\alpha$. The second possible combination is ($L_{x}$, $L_{z})$ or $(L_{x},\ \cos\beta)$. The third and final combination is ($L_{y}$, $L_{z})$ or $(L_{y},\ \cos\gamma)$. Specific formulas for how to update the lengths and angles can be obtained from the condition that the volume of the cell remains constant. If for instance $L_{x}$ is sampled and a trial value is $L^{\prime}_{x}$, then the trial value for the length in the $y$-direction should be $L^{\prime}_{y}=V/L^{\prime}_{x}$ and the trial angle in the $xy$ plane

Similar formulas can be obtained for $(L_{x},\ L_{z},\ \cos\beta)$ and $(L_{y},\ L_{z},\cos\gamma)$ combinations by permutations.