On Some Geometric Behavior of Value Iteration on the Orthant: Switching System Perspective
Abstract
In this paper, the primary goal is to offer additional insights into the value iteration through the lens of switching system models in the control community. These models establish a connection between value iteration and switching system theory and reveal additional geometric behaviors of value iteration in solving discounted Markov decision problems. Specifically, the main contributions of this paper are twofold: 1) We provide a switching system model of value iteration and, based on it, offer a different proof for the contraction property of the value iteration. 2) Furthermore, from the additional insights, new geometric behaviors of value iteration are proven when the initial iterate lies in a special region. We anticipate that the proposed perspectives might have the potential to be a useful tool, applicable in various settings. Therefore, further development of these methods could be a valuable avenue for future research.
I Introduction
Dynamic programming [1, 2] is a general and effective methodology for finding an optimal solution for Markov decision problems [3]. Value iteration is a popular class of dynamic programming algorithms, and its exponential convergence is a fundamental and well-established [1, 2] result through the contraction mapping property of the Bellman operator.
In this paper, we offer some additional insights on the value iteration based on switching system models [4, 5, 6, 7, 8, 9, 10, 11] in the control community. These models provide new geometric behaviors of value iteration to solve Markov decision problems [3]. In particular, the main contributions of this paper are twofold: 1) We present a switching system model of value iteration and, based on it, provide a different proof for the contraction property of value iteration. 2) Furthermore, from the new perspectives and frameworks, we study additional geometric behaviors of value iteration when the initial iterate lies in a special region. More specifically, the detailed contributions are summarized as follows:
-
1.
A switching system model of value iteration is introduced along with its special properties. Based on it, we offer a different proof for the following contraction property of the value iteration:
(1) where is the th iterate of the value iteration, is the optimal Q-function, and is the so-called discount factor in the underlying Markov decision problem. Although this result is fundamental and classical, the proof technique utilized in this paper is distinct from the classical approaches, offering additional insights.
-
2.
Furthermore, from the additional insights provided in the first part, we prove new geometric behaviors of value iteration when the initial iterate lies in a special region. Specifically, when the initial iterate is within the set (shifted orthant), the iterates of the value iteration remain in the set, displaying different behaviors than the cases with a general initial iterate. When , one can establish the new contraction property
(2) where is the weighted Euclidean norm, is any real number such that , and is a positive definite matrix dependent on . This result corresponds to a contraction mapping property of the Bellman operator in terms of the weighted Euclidean norm, which cannot be derived from the classical approaches. Geometrically, the sublevel sets corresponding to the infinity norm are squares, while the sublevel sets corresponding to the weighted Euclidean norm are ellipsoids.
A more notable result is that when , the iterates satisfy the linear inequality
(3) where is any real number such that , and is a positive vector dependent on . Geometrically, this implies that the component along the direction of in diminishes exponentially.
The analysis presented in this paper employs insights and tools from switching systems [4, 5, 6, 7, 8, 9, 10, 11], positive switching systems [12, 13, 14, 15], nonlinear systems [16], and linear systems [17]. We emphasize that our goal in this paper is to offer additional insights and analysis templates for value iteration via its connections to switching systems, rather than improving existing convergence rates. We anticipate that the proposed switching system perspectives may have the potential to be a useful tool, applicable in various settings, and stimulate the synergy between dynamic system theory and dynamic programming. Thus, further development of these methods could be a valuable avenue for future research. Finally, some ideas in this paper have been inspired by [11, 18], which develop switching system models of Q-learning [19]. However, most technical results and derivation processes are nontrivial and entirely different from those in [11, 18]. Another related work is [20], which provides a linear programming-based analysis of value iteration and also employs positive switching system models for their analysis. However, the previous work merely proposed a numerical linear programming-based analysis to verify convergence properties and did not obtain the explicit relations given in (1), (2) ,(3). Therefore, our analysis offers significantly different results than those in [20].
II Preliminaries
II-A Notations
The adopted notation is as follows: : set of real numbers; : -dimensional Euclidean space; : set of all real matrices; : transpose of matrix ; (, , and , respectively): symmetric positive definite (negative definite, positive semi-definite, and negative semi-definite, respectively) matrix ; : identity matrix with appropriate dimensions; : cardinality of a finite set ; : Kronecker’s product of matrices and ; : the vector with ones in all elements; : maximum eigenvalue; : minimum eigenvalue.
II-B Markov decision problem
We consider the infinite-horizon discounted Markov decision problem (MDP) [3], where the agent sequentially takes actions to maximize cumulative discounted rewards. In a Markov decision process with the state-space and action-space , the decision maker selects an action with the current state . The state then transitions to a state with probability , and the transition incurs a reward , where is a reward function. For convenience, we consider a deterministic reward function and simply write . A deterministic policy, , maps a state to an action . The objective of the Markov decision problem (MDP) is to find an optimal (deterministic) policy, , such that the cumulative discounted rewards over infinite time horizons are maximized, i.e.,
where is the discount factor, is the set of all admissible deterministic policies, is a state-action trajectory generated by the Markov chain under policy , and represents an expectation conditioned on the policy . The Q-function under policy is defined as
for all , and the optimal Q-function is defined as for all . Once is known, then an optimal policy can be retrieved by . Throughout, we make the following standard assumption.
Assumption 1
The reward function is unit bounded as follows:
The unit bound imposed on is just for simplicity of analysis. Under 1, Q-function is bounded as follows.
Lemma 1
We have .
Proof:
The proof is straightforward from the definition of Q-function as follows: . ∎
II-C Switching system
Let us consider the switched linear system (SLS) [4, 5, 6, 7, 8, 9, 10, 11],
| (4) |
Where is the state, is called the mode, is called the switching signal, and are called the subsystem matrices. The switching signal can be either arbitrary or controlled by the user under a certain switching policy. Specifically, a state-feedback switching policy is denoted by . The analysis and control synthesis of SLSs have been actively studied during the last decades [4, 5, 6, 7, 8, 9, 10, 11]. A more general class of systems is the switched affine system (SAS)
where is the additional input vector, which also switches according to . Due to the additional input , its stabilization becomes much more challenging. Lastly, when all elements of the subsystem matrices, , are nonnegative, then SLS is called positive SLS [12, 13, 14, 15].
II-D Definitions
Throughout the paper, we will use the following compact notations:
where , , and is an enumerate of with an appropriate order compatible with other definitions. Note that , and . In this notation, Q-function is encoded as a single vector , which enumerates for all and with an appropriate order. In particular, the single value can be written as where and are -th basis vector (all components are except for the -th component which is ) and -th basis vector, respectively. Therefore, in the above definitions, all entries are ordered compatible with this vector .
For any stochastic policy, , where is the set of all probability distributions over , we define the corresponding action transition matrix as
| (5) |
where . Then, it is well-known that is the transition probability matrix of the state-action pair under policy . If we consider a deterministic policy, , the stochastic policy can be replaced with the corresponding one-hot encoding vector where , and the corresponding action transition matrix is identical to (5) with replaced with . For any given , denote the greedy policy with respect to as . We will use the following shorthand frequently:
II-E Q-value iteration (Q-VI)
In this paper, we consider the so-called Q-value iteration (Q-VI) [1] given in Algorithm 1, where is called Bellman operator. It is well-known that the iterates of Q-VI converge exponentially to in terms of the infinity norm [1, Lemma 2.5].
Lemma 2
We have the bounds for Q-VI iterates .
The proof is given in [1, Lemma 2.5], which is based on the contraction property of Bellman operator. Note that [1, Lemma 2.5] deals with the value iteration for value function instead of Q-function addressed in our work. However, it is equivalent to Q-VI. Next, a direct consequence of Lemma 2 is the convergence of Q-VI
| (6) |
In what follows, an equivalent switching system model that captures the behavior of Q-VI is introduced, and based on it, we provide a different proof of Lemma 2.
III Switching system model
In this section, we study a discrete-time switching system model of Q-VI and establish its finite-time convergence based on the stability analysis of the switching system. Using the notation introduced in Section II-D, the update in Algorithm 1 can be rewritten as
| (7) |
Recall the definitions and . Invoking the optimal Bellman equation , (7) can be further rewritten by
| (8) |
which is a SAS (switched affine system). In particular, for any , define
Hence, Q-VI can be concisely represented as the SAS
| (9) |
where and switch among matrices from and vectors from according to the changes of . Therefore, the convergence of Q-VI is now reduced to analyzing the stability of the above SAS. Th main obstacle in proving the stability arises from the presence of the affine term. Without it, we can easily establish the exponential stability of the corresponding deterministic switching system, under arbitrary switching policy. Specifically, we have the following result.
Proposition 1
For arbitrary , the linear switching system , is exponentially stable such that and .
The above result follows immediately from the key fact that , which we formally state in the lemma below.
Lemma 3
For any , , where the matrix norm and is the element of in -th row and -th column.
Proof:
Note , which completes the proof. ∎
However, because of the additional affine term in the original switching system (9), it is not obvious how to directly derive its finite-time convergence. To circumvent the difficulty with the affine term, we will resort to two simpler upper and lower bounds, which are given below.
Proposition 2 (Upper and lower bounds)
For all , we have
Proof:
For the lower bound, we have
where the third line is due to . For the upper bound, one gets
where we used the fact that in the first inequality. This completes the proof. ∎
The lower bound is in the form of an LTI system. Specifically, the lower bound corresponds to a special LTI system form known as a positive linear system [21], where all the elements of the system matrix are nonnegative. In our analysis, this property will be utilized to derive new behaviors of Q-VI. Similarly, the system matrix in the upper bound switches according to the changes in . Therefore, it can be proven that the upper bound is in the form of positive SLSs [12, 13, 14, 15], where all the elements of the system matrix for each mode are nonnegative.
III-A Finite-time error bound of Q-VI
In this subsection, we provide a proof for the contraction property outlined in Lemma 2. Although this result represents one of the most basic and fundamental outcomes in classical dynamic programming, we offer an alternative proof in this paper. This proof, grounded in the switching system model discussed in earlier sections, is provided below.
Since from Proposition 2, it follows that . If , then , where and are the -th and -th standard basis vectors, respectively. If , then . Therefore, one gets
which completes the proof.
IV Convergence of Q-VI on the orthant
In the previous section, we revisited the convergence of Q-VI from the perspective of switching system viewpoints. In this section, we study additional geometric behaviors of Q-VI, again using the switching system perspective. Let us suppose that holds. Please note that such an initial value can be found by setting
because
holds according to Lemma 1. Then, using the bound provided in Proposition 2, it can be proved that . This is equivalent to saying . In other words, if the initial iterate falls within the shifted orthant, , then future iterates will also stay within the same set, i.e., .
Proposition 3
Suppose that holds. Then, .
Proof:
For an induction argument, suppose for any . Then, by Proposition 2, it follows that because is a nonnegative matrix. Therefore, , and the proof is completed by induction. ∎
From the results above, it can be observed that the behavior of is fully dictated by the lower bound, which is a linear function of . Therefore, the fundamental theory of linear systems can be applied to analyze the behavior of Q-VI. To facilitate this, the subsequent result reviews the Lyapunov theory for discrete-time linear systems.
Proposition 4
For any such that , there exists the corresponding positive definite such that
and
The proof of Proposition 4 is provided in the Appendix. Note that Proposition 4 can be applied to general LTI systems. However, because the lower bound takes the form of positive linear systems, it can be demonstrated that the Lyapunov matrix also possesses the additional special property outlined below.
Proposition 5
is a nonnegative matrix.
Proof:
The proof is easily done from the construction in (12). ∎
From the perspectives provided above, we can derive a bound on in terms of the weighted Euclidean norm . This is an alternative to the infinity norm , which cannot be derived from classical contraction mapping arguments.
Theorem 1
For any ,
holds
Proof:
We have
where the first inequality follows from the fact that is a nonnegative matrix and from Proposition 2, and the equality is due to the Lyapunov theorem in Proposition 4. Taking the squared root on both sides yields the desired conclusion. ∎
The result in Theorem 1 provides
for an arbitrarily small , which implies
and
This relationship reveals different geometric convergence behaviors: the sublevel sets associated with the infinity norm are squares, whereas those corresponding to the weighted Euclidean norm are ellipsoids.
Furthermore, our new approach enables us to derive a bound on a linear function of . Specifically, for positive LTI systems, one common Lyapunov function is a linear Lyapunov function of the form for a positive vector . We proceed by providing an explicit form of such a vector .
Proposition 6
For any such that and for any positive vector , define
Then, it holds true that
and
| (10) |
The proof is given in Appendix. Proposition 6 proves that plays the role of a linear Lyapunov function for the positive LTI system. From Proposition 6, one can prove another convergence result of Q-VI.
Theorem 2
Proof:
Multiplying both sides of (10) in Proposition 6 by from the right leads to
where the first equality comes from (10), the first inequality is due to in Proposition 2, , and the second inequality follows from in Proposition 3. This completes the proof. ∎
Suppose that , where represents the component of in the direction of , and represents the components of orthogonal to . Then, according to (11), the component of in the direction of diminishes exponentially. From the construction of in Proposition 6, it can be seen that there could be infinitely many such vectors , depending on the positive vector . Therefore, becomes trapped in the intersections of the nonpositive orthant and infinitely many half planes. An illustration of a single half plane is provided in Figure 1.
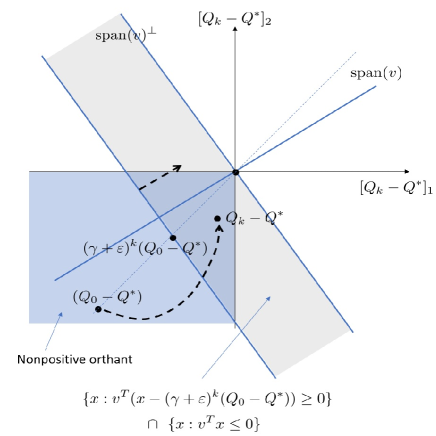
V Conclusion
In this paper, we have presented additional insights on value iteration, approached through the lens of switching system models in the control community. This offers a connection between value iteration and switching system theory and reveals additional geometric behaviors of value iteration. Specifically, we introduced a switching system model of value iteration and, based on it, provided a novel proof for the contraction property of the value iteration. Moreover, our insights led to the proof of new geometric behaviors of value iteration when the initial iterate resides in a particular set (the shifted orthant). We believe that the perspectives proposed here could serve as useful tools applicable in various settings. As such, further development of these methods may present a valuable future direction.
References
- [1] D. P. Bertsekas and J. N. Tsitsiklis, Neuro-dynamic programming. Athena Scientific Belmont, MA, 1996.
- [2] D. P. Bertsekas, “Dynamic programming and optimal control 4th edition, volume ii,” Athena Scientific, 2015.
- [3] M. L. Puterman, Markov decision processes: Discrete stochastic dynamic programming. John Wiley & Sons, 2014.
- [4] D. Liberzon, Switching in systems and control. Springer Science & Business Media, 2003.
- [5] D. Lee and J. Hu, “Periodic stabilization of discrete-time switched linear systems,” IEEE Transactions on Automatic Control, vol. 62, no. 7, pp. 3382–3394, 2017.
- [6] ——, “Stabilizability of discrete-time controlled switched linear systems,” IEEE Transactions on Automatic Control, vol. 63, no. 10, pp. 3516–3522, 2018.
- [7] J. C. Geromel and P. Colaneri, “Stability and stabilization of discrete time switched systems,” Int. J. Control, vol. 79, no. 7, pp. 719–728, 2006.
- [8] T. Hu, L. Ma, and Z. Lin, “Stabilization of switched systems via composite quadratic functions,” IEEE Trans. Autom. Control, vol. 53, no. 11, pp. 2571–2585, 2008.
- [9] H. Lin and P. J. Antsaklis, “Stability and stabilizability of switched linear systems: a survey of recent results,” IEEE Transactions on Automatic control, vol. 54, no. 2, pp. 308–322, 2009.
- [10] W. Zhang, A. Abate, J. Hu, and M. P. Vitus, “Exponential stabilization of discrete-time switched linear systems,” Automatica, vol. 45, no. 11, pp. 2526–2536, 2009.
- [11] D. Lee and N. He, “A unified switching system perspective and convergence analysis of q-learning algorithms,” in 34th Conference on Neural Information Processing Systems, NeurIPS 2020, 2020.
- [12] F. Blanchini, P. Colaneri, and M. E. Valcher, “Co-positive lyapunov functions for the stabilization of positive switched systems,” IEEE Transactions on Automatic Control, vol. 57, no. 12, pp. 3038–3050, 2012.
- [13] E. Fornasini and M. E. Valcher, “Linear copositive lyapunov functions for continuous-time positive switched systems,” IEEE Transactions on Automatic Control, vol. 55, no. 8, pp. 1933–1937, 2010.
- [14] J. Zhang, Z. Han, and J. Huang, “Stabilization of discrete-time positive switched systems,” Circuits, Systems, and Signal Processing, vol. 32, pp. 1129–1145, 2013.
- [15] E. Fornasini and M. E. Valcher, “Stability and stabilizability criteria for discrete-time positive switched systems,” IEEE Transactions on Automatic Control, vol. 57, no. 5, pp. 1208–1221, 2011.
- [16] H. K. Khalil, “Nonlinear systems,” Upper Saddle River, 2002.
- [17] C.-T. Chen, Linear System Theory and Design. Oxford University Press, Inc., 1995.
- [18] D. Lee, J. Hu, and N. He, “A discrete-time switching system analysis of q-learning,” arXiv preprint arXiv:2102.08583, 2021.
- [19] R. S. Sutton and A. G. Barto, Reinforcement learning: An introduction. MIT Press, 1998.
- [20] X. Guo and B. Hu, “Convex programs and lyapunov functions for reinforcement learning: A unified perspective on the analysis of value-based methods,” in 2022 American Control Conference (ACC), 2022, pp. 3317–3322.
- [21] B. Roszak and E. J. Davison, “Necessary and sufficient conditions for stabilizability of positive lti systems,” Systems & Control Letters, vol. 58, no. 7, pp. 474–481, 2009.
VI Appendix
VI-A Proof of Proposition 4
Proof:
For simplicity, denote . Consider matrix such that
| (12) |
Noting that
we have , resulting in the desired conclusion. Next, it remains to prove the existence of by proving its boundedness. Taking the norm on leads to
Finally, we prove the bounds on the maximum and minimum eigenvalues. From the definition (12), , and hence . On the other hand, one gets
where and denote the cardinality of the sets and , respectively. The proof is completed. ∎
VI-B Proof of Proposition 6
Proof:
We have
Moreover,
and
∎