On signed graphs whose spectral radius does not exceed
Abstract
The Hoffman program with respect to any real or complex square matrix associated to a graph stems from Hoffman’s pioneering work on the limit points for the spectral radius of adjacency matrices of graphs does not exceed . A signed graph is a pair where is a simple graph and is the sign function. In this paper, we study the Hoffman program of signed graphs. Here, all signed graphs whose spectral radius does not exceed will be identified.
AMS classification: 05C50
Keywords: Signed graphs; Spectral radius; Hoffman program.
1 Introduction
All graphs considered here are simple, undirected and finite. For a graph let denote the adjacency matrix of the eigenvalues of are all real and the spectral radius of is equal to the largest eigenvalue of .
The Hoffman program is the identification of connected graphs whose spectral radius does not exceed some special limit points established by Hoffman [8]. The smallest limit point for the spectral radius of is 2, that is, identifies all connected graphs whose spectral radius does not exceed 2. This problem has already been completely solved by Smith [13]. They are known as Smith graphs. After that, the problem jumps to the next significant limit point, which is where is the golden mean. In [5], Cvetkovi, Doob and Gutman determined the structures of graphs with spectral radius between 2 and . Their description was completed by Brouwer and Neumaier [2]. In 2020, Jiang and Polyanskii [9] studied the forbidden subgraphs characterization for (where denotes the family of connected graphs of spectral radius ) with applications to estimate the maximum cardinality of equiangular lines in the -dimensional Euclidean space For more on the results between Hoffman program and equiangular lines, see [9, 11, 13].

A signed graph is a pair where is a simple graph with vertices and edges, called the underlying graph, and is the sign function. An edge is called positive (negative) if (resp. ) and denoted by (resp. ). An unsigned graph (or a graph) is a signed graph without negative edges. Given a signed graph , its adjacency matrix is defined by where if and otherwise. The eigenvalues, denoted by of are defined as the eigenvalues of ; they are all real since is a real symmetric matrix. The spectral radius of is defined by
The theory of limit points for the spectral radius of graph sequences studied by Hoffman is still valid in the context of signed graphs. Some interesting results on the Hoffman program of signed graphs can be found in [1, 14, 7, 10]. In [10], Jiang and Polyanskii studied the forbidden subgraphs characterization for families of signed graphs with eigenvalues bounded from below with applications to determine the maximum cardinality of a spherical two-distance set with two fixed angles in high dimensions. The smallest limit point for the spectral radius of is also 2, see [14, Propostion 6.1]. Those signed graphs have been identified by McKee and Smyth [12]. Therefore, the natural next step is the next limit point: that is, identifies all connected signed graphs whose spectral radius does not exceed . In this paper, we study the Hoffman program of signed graphs and all signed graphs whose spectral radius does not exceed will be identified.
In this paper, positive edges are depicted as bold lines and negative edges are depicted as dashed lines. The rest of the paper is organized as follows. Our contribution is reported in Section In Section , we give some preliminaries lemmas and theorems. In Section , we will prove the Theorem 2.4.
2 Main results
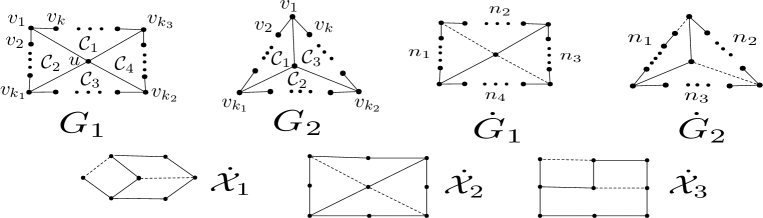
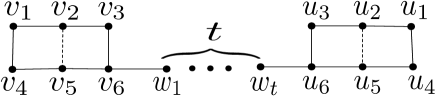
Let be the graph with vertices consisting of three paths with and edges, respectively, where these paths have one end vertex in common, and let be the graph with vertices consisting of a path with edges and two extra edges affixed at and See Fig. 2.
For any fixed the symbol (resp. ) denotes the set of the connected (resp. signed) graphs whose spectral radius does not exceed

Theorem 2.2.
[12] Signed graphs in are the induced subgraphs of or

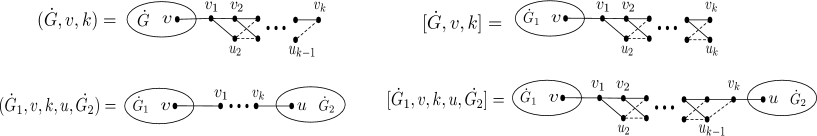
Definition 2.3.
Let be a connected signed graph, and let be a vertex in
Denote the signed graph obtained from by appending a at
Denote the signed graph obtained from by appending a at
Let be two connected disjoint signed graphs, and let be vertices in respectively.
Define to be the signed graph obtained from and by joining them with a path of vertices connecting and
Define to be the signed graph obtained from and by joining them with a connecting and
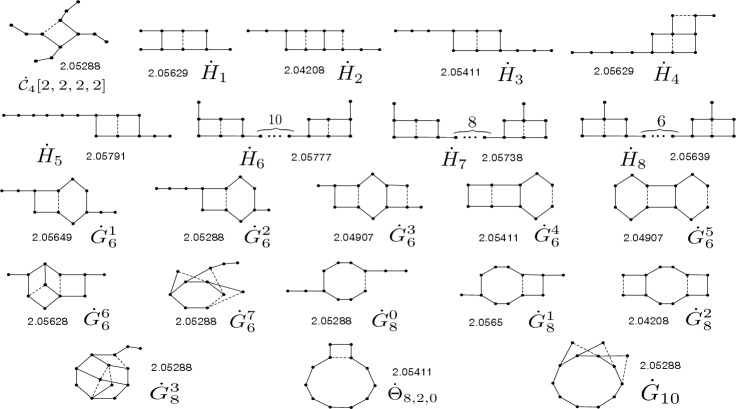
The main results of this paper are presented as following.
Theorem 2.4.
Signed graphs in are the induced subgraphs (up to switching isomorphic) of
is even, and is even and and
, where and ,
, , , , , , , where for .
Remark 2.5.
3 Preliminaries
The sign of a cycle of is , whose sign is (resp. ) is called positive (resp. negative) and denoted by (resp. ). A signed graph is called balanced if all its cycles are positive; otherwise it is called unbalanced. If there is a vertex subset , such that is obtained by reversing the sign of every edge with one end in and the other in , then we say that and are switching equivalent and write . If is isomorphic to a signed graph switching equivalent to , we say is switching isomorphic to , denoted by . Switching isomorphic signed graphs share the same spectrum. More basic results on the signed graphs, see [15].
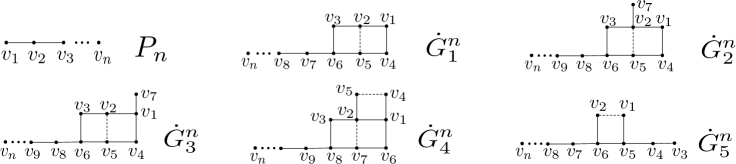
As usual, is the degree of a vertex and . Let be the set of neighbours of a vertex in a set and be the cardinality of . For denotes the induced subgraph of respect to the The signed graph (resp. ) is obtained by a balanced cycle (resp. an unbalanced cycle ) with one pendent edge. The signed graph () is obtained by an unbalanced cycle with one pendent edge at vertex (in ) and one pendent edge at vertex (in ).
A signed graph is called maximal with respect to some property if it is not a proper induced subgraph of some other signed graph satisfying In this context, we call a signed graph is maximal if it is not a proper induced subgraph of some other signed graphs whose spectral radius does not exceed .
Given a signed graph and , a subset of and a vertex not in the signed graph is obtained by inserting the edges (the sign of edge is any) between and all vertices of We call that is a good vertex if .
The first lemma is interlacing theorem.
Lemma 3.1.
[3] Let be a symmetric matrix of order with eigenvalues and a principal submatrix of of order with eigenvalues Then the eigenvalues of interlace the eigenvalues of that is, for
Define to be the set of the connected unbalanced signed graphs with spectral radius Note that the balanced signed graph and unsigned graph share the same spectrum, thus the main goal of this paper is to determine all signed graphs of the set Some properties of the signed graph of the set are listed as following.
Lemma 3.2.
Let . Then
Proof.
Note that then Since then ∎
We designate that a signed graph is an induced subgraph of by writing . If is not an induced subgraph of , then we say that is -free.
Lemma 3.3.
Let . Then is -free.
Proof.
Suppose on the contrary that By the table of the spectra of signed graphs with at most six vertices [4], we find that there is no signed graph of order Next we consider Then must contain an induced subgraph with order and By [4, page 19–40], we have Since is 4-regular, then which contradicts to Lemma 3.2. Hence, is -free. ∎
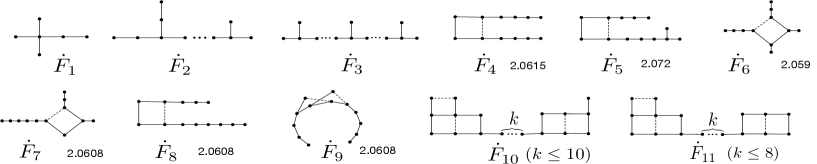
We say that is forbidden if Evidently, if is forbidden, then is -free.
Lemma 3.4.
All (unsigned) graphs expect the graphs in the set the signed graph and the signed graphs of Fig. 8 are forbidden.
Proof.
It is easily to see that all (unsigned) graphs expect the graphs in the set the signed graph (since ) and the signed graphs of Fig. 8 have spectral radius So all of them are forbidden by interlacing. ∎
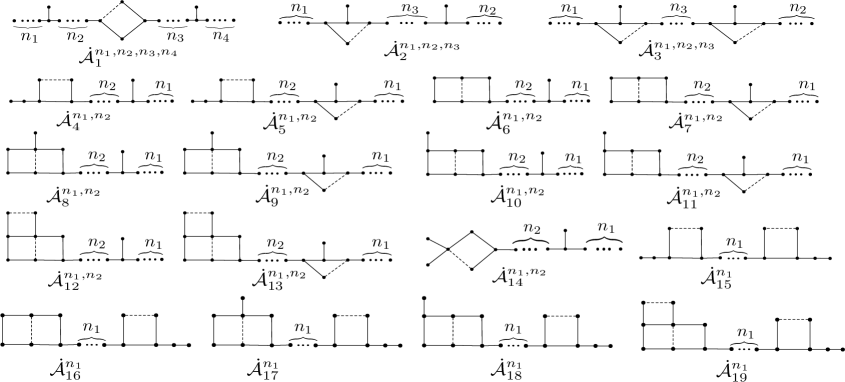
The next lemma plays an important role in this paper. The proof is presented in Appendix A.
Lemma 3.5.
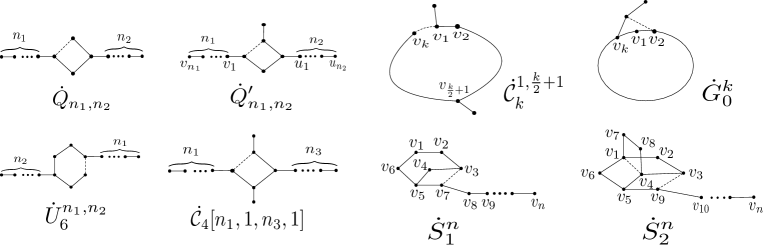
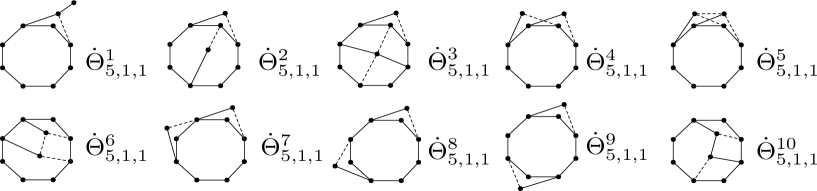
Let , be the signed graphs depicted in Fig. 9. Then
if , then is an induced subgraph of or ,
if , then is an induced subgraph of , where or
if , then is an induced subgraph of or
if , then is an induced subgraph of or ,
if , then is an induced subgraph of or ,
if , then is an induced subgraph of or
if , then is an induced subgraph of or
if , then is an induced subgraph of or
if , then is an induced subgraph of or
if , then is an induced subgraph of or
if , then is an induced subgraph of or
if , then or .
if , then is an induced subgraph of , where
where for and .
Remark 3.6.
Now we pay attention to the uncyclic and bicyclic signed graphs of the set .
Proof.
Let and let and be the new neighbor of By forbidding and , then the cycle is unbalanced and is even. In addition, by forbidding , if then for all
Case 1. Then for , otherwise and let , then and , which is a contradiction. Because of symmetry, we have for If , let then induces the and , which is a contradiction. So Therefore, .
Case 2. or 12. Then , otherwise and let then induces the and , which is a contradiction. So all vertices of are within distance 1 of the cycle By directed calculations, it is not hard to get that , .
Case 3. or If all vertices of are within distance 1 of the cycle a directed calculation leads that or Otherwise, we assume that and let be the new neighbor of If by forbidding and , then and for respectively. So . If then (by forbidding ). If or let (resp. ) be the new neighbor of (resp. ), by forbidding , , and we have , and . Then See Fig. 10. Next we consider that then See Fig. 6. Since is -free, then each vertex of expect the vertices of has degree at most 2. Hence,
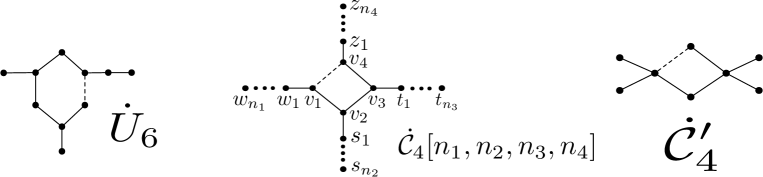
Case 4. Then . Let If then (by forbidding ) and at most one vertex of has degree 3 (by forbidding ). So, if (where ) or if . See Figs. 9 and 10. Next suppose that for If there is one vertex expect having degree greater than 2, without loss of generality, assume that ( By forbidding , and , then and at most one vertex of has degree 3. If then (if ), (if ) and (if ), which is a contradiction. So Furthermore, if then (by forbidding ). Therefore, (if ), (if ) or (if ). If all vertices expect have degree at most 2, then is If for , then by forbidding and . So . Otherwise, or If then If and by forbidding and , we have where ∎
It is known that there are three types of bicyclic graphs in term of their base graph as described next. A bicyclic graph is said to be a bicyclic base graph if contains no pendent vertices.
The type is the union of three internally disjoint paths , and which have the same two distinct end vertices, where
The type consists of two vertex disjoint cycles and joined by a path having only its end vertices in common with the cycles, where and
The type is the union of two cycles and with precisely one vertex in common, where and
Lemma 3.8.
Let be a bicyclic signed base graph. Then is switching equivalent to one of the , , or See Fig. 11.
Proof.
For types and , by forbidding , , and then and . So or For type by forbidding and , then (if , then and are odd) or ( and are even).
Case 1. . If and , then , which contradicts to Lemma 3.4. Therefore, or .
Case 2. . If (resp. ), then (resp. ), which contradicts to Lemma 3.4. Therefore, and
Hence, , , or ∎
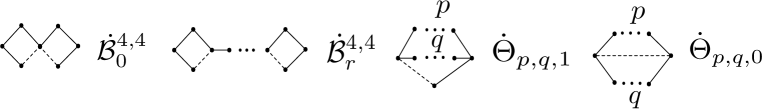
Let be a signed graph with and be a cycle in If each vertex outside of is adjacent to at most one vertex of , then or (by Lemma 3.8). So . Therefore, if then there is a vertex outside of adjacent to at least two vertices of Then we have
Lemma 3.9.
Proof.
If then is bicyclic. By Lemma 3.8, then or . Next assume that then the underlying graph of is or See Fig. 12. By forbidding and then the cycles in and are even and unbalanced. If and , or and , then at least one of the cycles and is balanced, which is a contradiction. So, either and , or and Then or If , then (by forbidding and ). If , then for and at most one of and is equal to 3 (by forbidding , and ). Hence, for or 3. See Fig. 12. ∎
In the final of this section, we give an algorithm for searching the signed graph with spectral radius
Algorithm 1:
Input: The adjacency matrix of a signed graph with order and a positive integer number
Output: The set of the matrices
Step 1. For constructing a vector set . (Restrict that by Lemma 3.2).
(1.1) Traverse each vector of and construct a matrix
(1.2) ,
(1.3) Traverse each matrix and add to the set if the sum of each row of the matrix is less than or equal to 4 (by Lemma 3.2) and
Step 2. For each matrix of constructing a vector set . (Restrict that by Lemma 3.2).
(2.1) Traverse each vector of and construct a matrix
(2.2) ,
(2.3) Traverse each matrix and add to the set if the sum of each row of the matrix is less than or equal to 4 (by Lemma 3.2) and
Step k. For each matrix of constructing a vector set . (Restrict that by Lemma 3.2).
Traverse each vector of and construct a matrix
,
Traverse each matrix and add to the set if the sum of each row of the matrix is less than or equal to 4 (by Lemma 3.2) and
Output the
The whole algorithm is over.
Corollary 3.10.
Applying algorithm 1 to each signed graph of Theorem 2.4 , we can check that all of them are maximal.
4 Signed graph whose spectral radius does not exceed
In this section, we identify all signed graphs whose spectral radius does not exceed . By Lemma 3.7, we assume that We break into four subsections.
4.1 where is odd or
Firstly we consider that where is odd or .
Lemma 4.1.
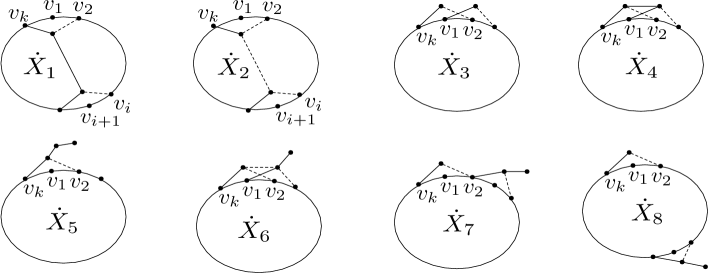
Let be one of the signed graphs where is odd or , see Fig. 13. Then if and only if and .
Proof.
If and , then Note that (), or , ( and is even), ( is odd), and for By Lemma 3.4, then for expect the signed graph where . ∎
Proof.
By Lemma 3.9, then or . By Corollary 3.10, we know that is maximal. Then we consider that . Let be the induced subgraph of such that and . Clearly, . We use the vertex label of Fig. 1 and let . Let be a good vertex in .
Claim 1. If for one , then and .
Proof.
By Lemmas 3.4 and 3.9, then and for one (mod ). It is not hard to get that and (otherwise and ). Since is not an induced subgraph of then one of the followings happens:
for one then or
for one , then
for one , then
By Lemma 4.1, then if and only if and . ∎
Claim 2. If for all , then . Moreover, .
Proof.
If , then or Applying algorithm 1 to , we obtain that .
Remark 4.3.
By Lemma 4.2, we next state that the signed graph is bipartite.
4.2
Secondly we consider that is -free where and . By Lemma 3.9, then or is an induced subgraph of Let be the induced subgraph of such that , or and
Lemma 4.4.
Let be a -free bipartite signed graph with . If , then for See Fig. 5.
Proof.
Applying algorithm 1 to , we obtain that or We next suppose that or
If , then . So, or Then By Fig. 1, if then is ; if then for (see Fig. 14); if or then is switching isomorphic to one of the signed graphs of Fig. 15. Moreover, if then contains one () as an induced subgraph. Now applying algorithm 1 to where is or one of the signed graphs of Fig. 15, we get that there is no signed graph with order and and applying algorithm 1 to for , we get that . If , or , we can similarly get that ∎
4.3
Thirdly we consider that is -free where and . By Lemma 3.9, then or . Let be the induced subgraph of such that or and .
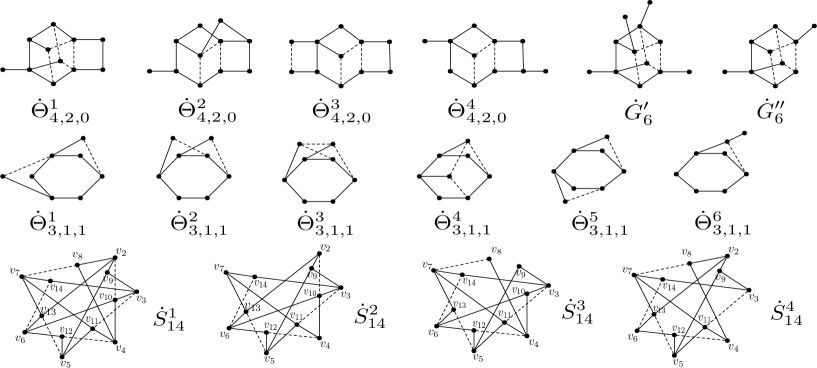
Proof.
If then or . Since is -free by Fig. 1, then for See Fig. 16. Applying algorithm 1 to where for , we get that or for .

If , then or . So, By Fig. 1, if then is if , then for ; if or 13, then for . See Fig. 16. Moreover, if then contains one () as an induced subgraph. Now applying algorithm 1 to and for , then there is no signed graph with order and and applying algorithm 1 to for , we can get all signed graphs (where ) of order which are the induced subgraphs of or . Notice that . See Figs. 5 and 6. If then . Set Since is the unique signed graph of order 12 such that and , then for each and all By forbidding , then for all . Hence, and is maximal.
If , then or From above discussions, we can suppose that is -free. By Fig. 1, then , or . See Figs. 16 and 6. Similarly, applying algorithm 1 to , then all signed graphs of order can be found, which are the induced subgraphs of () or See Figs. 17 and 6. If then or ().
Case 1. Set Since and are the only four signed graphs of order such that and , then for each and all By forbidding , then for all . Hence, and is maximal.
Case 2. for or . We will prove that Set If there is a vertex () adjacent to some vertices of then and . By case 1, then . Otherwise, for each and all . By forbidding , then for all . Hence, and The proofs of the cases or are similar. ∎
4.4 is -free where or
In last subsection we shall consider that is -free where or , i.e., For convenience, let be the induced subgraph of such that . Since may not be unique, we choose one that the order of is maximal.
4.4.1

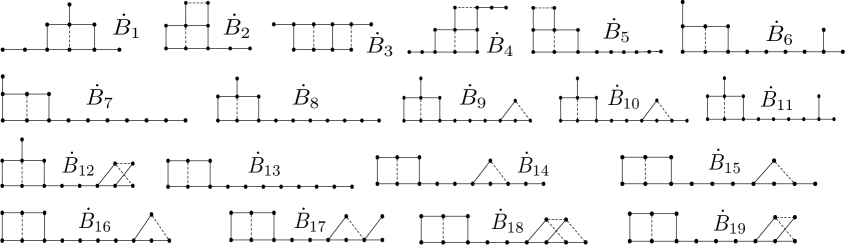
First of all, we focus on that the order of is less than or equal to
Lemma 4.6.
Proof.
Remark 4.7.
By algorithm 1, we can check that the signed graphs and are maximal -free (where or ) signed graphs.
, , for and for .
If then is -free. Furthermore, let be the vertex subset of with order , then is disconnected or switching equivalent to for one
Secondly, we consider that . By Lemma 4.6, then ( or ) is an induced subgraph of where and See Fig. 6. Without loss of generality, assume that the choice of is largest. Let
| (4.1) |
Lemma 4.8.
Let and be two vertices in or . Then or Furthermore, if and where and then .
Proof.
Suppose on the contrary that and Then and where and If , then induces a cycle , which is a contradiction. If then contains a or is not switching equivalent to for which is a contradiction. So or Furthermore, if and where and and if , then contains a or is not switching equivalent to for which is a contradiction. So . ∎
Then we let
| (4.2) |
where each vertex in is adjacent to no vertex of each vertex in is adjacent to some vertices of and each vertex in is adjacent to some vertices of
Set for , then we have
Lemma 4.9.
If is nonempty, then and there is a vertex in such that for . See Fig. 9.
If for , then ; if for , then
Proof.
(1) Let be a vertex in Then there is a shortest path () from to a vertex . If we can find a connected induced subgraph of with order and is not switching equivalent to for which contradicts to Remark 4.7 (3). Then Since is -free, then and . Therefore, for If then there is another vertex in and a vertex in such that . And now we can check that or which contradicts to Lemma 3.4. Hence,
(2) Choose vertices (say vertex set ) from such that is connected. By Remark 4.7 (3), then for one It is not hard to see that if for , then ; if for , then ∎
The next lemma deals with the case that . See Fig. 20. Note that By Lemma 3.5 (6), we have Then we let
where each vertex in is adjacent to no vertices of each vertex in is adjacent to some vertices of , each vertex in is adjacent to some vertices of and each vertex in is adjacent to some vertices of By Lemma 4.8, then , , and there is no edge between three parts , and If let Lemma 4.9 (1) implies that there is a path (where ) from the vertex to the vertex . Then which contradicts to Lemma 3.4. So
Lemma 4.10.
Proof.
By Lemma 4.9 (2), then , where , if or (by forbidding and ) and otherwise (by Lemma 3.5 (6) and (8)).
Let , then (by forbidding ). Up to switching equivalence, let and for where and . Since is -free (), then if , if and if . So, ().
If then for . If then (), where By Lemma 3.5 (6), (8) and (10), then if if if if Hence, is the induced subgraph of , or . ∎
Next we assume that is -free.
Lemma 4.11.
Let be a -free bipartite signed graph of order . If , then is the induced subgraph of , or , where and , , and
Proof.
Recall that ( or ) is an induced subgraph of Here, we only consider that The proofs of the cases for are similar. We use the vertex partitions of Eqs. (4.1) and (4.2). By Lemma 4.9 (2), then Since is -free, then each vertex in is adjacent to at most two vertices of Then let where each vertex in ( or 2) is adjacent to vertices of Furthermore, set () where for , and ( where and for Since is -free (), we have
is or . If is , then (by forbidding ),
if , if and if .
Then , or and .
Case 1. is empty. If or is empty, then we are done. If and are not empty, according to (A1), we break into two subcases:
Subcase 1.1. . Then , and (otherwise or , which contradicts to Lemma 3.4).
Subsubcase 1.1.1. By , then By forbidding then So, .
Subsubcase 1.1.2. By , then If or 2, then . If , by forbidding (where ), then . So, .
Subsubcase 1.1.3. Then and If then and (by forbidding ). By , then If by forbidding and , then . By Lemma 3.5 (2), then if and if . So, .
Subcase 1.2. . Then and Since is -free, then If then , which has been done in subsubcase 1.1.3. If then By Lemma 3.5 (4), then . So, .
Case 2. is nonempty. Then as is -free. Similarly, by (A2) and forbidding , then which has been done in subsubcase 1.1.3.
This completes the proof. ∎
4.4.2 is -free
Lastly it remains that is -free. First we suppose that Notice that if then for all Without loss of generality, we assume that , where is maximal. Up to switching isomorphic, let where and (). Let be a good vertex in If or 4, applying algorithm 1 to , then there is no signed graph with order and Next we let
Before giving the main result of this subsubsection, we need some preliminary lemmas.
Lemma 4.12.
and .
Proof.
Since is -free, then If , then and (switching at if necessary). Since is -free , then , for all and if . So and , which is a contradiction. Hence, Similarly, we have ∎
Then we let
where each vertex in is adjacent to no vertex of , each vertex in is adjacent to exactly one vertex of and no vertex of , each vertex in is adjacent to exactly one vertex of and no vertex of , each vertex in is adjacent to exactly one vertex of and exactly one vertex of .
Lemma 4.13.
If then
, and for or
, and for .
Proof.
Let and Since is -free then or If then and (switching at if necessary). By forbidding , then . If (resp. ), then (resp. ), which is a contradiction. So If , since is -free, then , , and for If then By Lemma 3.5 (2), then which is a contradiction. So If because of symmetry, then , , and for . ∎
Lemma 4.14.
is empty.
Proof.
For a contradiction, assume that . Then there is a shortest path () from to where or . Since is maximal, then and . By forbidding , then and or and or and By forbidding and , if then or and if then and . Therefore, is a tree or unicyclic, which has been done in Theorem 2.1 and Lemma 3.7. Hence, is empty. ∎
Lemma 4.15.
If , then
if , then and for
if , then and for
if then and one of the following holds: and and
Proof.
By forbidding , then . Since is not an induced subgraph of then By forbidding and then and . If then By Lemma 3.5 (2), then which is a contradiction. Hence,
The proof is similar to ().
By forbidding , then . By forbidding , it is impossible that and for . So, or If then . Otherwise, If then . Otherwise, ∎
Now we are going to give the main result of this subsubsection. Set where for each , and where for each If for one and one by forbidding , and we have and So, (see Lemma 3.7). Otherwise, for all and all Then there is a switching isomorphic of such that and for all that is, becomes empty and
Lemma 4.16.
Let be a -free bipartite signed graph with . Then is an induced subgraph of or , where , and
Proof.
Since is -free then , where (by forbidding ). By Lemma 4.13, we break into three cases.
Case 1.
Subcase 1.1. Then Since is maximal, then . Recall that is maximal. By Lemma 4.15, then we have
Subsubcase 1.1.1. or Then .
Subsubcase 1.1.2. If or then (), where (by Lemma 3.5 (2)). If or then , where (by forbidding ). If or then ( and ), where (by Lemma 3.5 (1)).
Subcase 1.2. Then Similar to subcase 1.1, then or , where ( and ).
Subcase 1.3. Then and Without loss of generality, we may assume that Since is maximal, then . By Lemma 4.15, then . So, By forbidding (where ), then . If or , then or , respectively, which contradicts to Lemma 3.4. So, and
Subcase 1.4. Then where and By subcases 1.1 and 1.3, then or , where ( and ).
Subcase 1.5. Similar to subcase 1.3, then
Case 2. By forbidding and , then
Subcase 2.1. . By Lemma 4.13, then
Subcase 2.2. By subcases 1.1 and 2.1, then or where ( and ).
Subcase 2.3. By subcases 1.3 and 2.1, then or .
Case 3. Then and By forbidding and , then is empty. If then . If then (by Lemma 4.13). So .
This completes the proof. ∎
Remark 4.17.
Finally, it remains the case that is an induced subgraph of or but not an induced subgraph of . Since then or is an induced subgraph of More importantly, or is also an induced subgraph of From Fig. 1, it is not too hard to get that there is no such signed graph .
Proof of Theorem 2.4. Summarizing with all results of Theorems 2.1 and 2.2, Lemmas 3.5, 3.7, 4.2, 4.4, 4.5, 4.6, 4.10, 4.11, 4.16 and 4.21, we complete the proof of Theorem 2.4. ∎
Acknowledgments
This project is supported by the National Natural Science Foundation of China (No.119
71164, 12001185, 12100557) and the Zhejiang Provincial Natural Science Foundation of China (LQ21A010004).
References
- [1] F. Belardo, S. Cioab, J. Koolen, J. F. Wang, Open problems in the spectral theory of signed graphs, Art Discrete Appl. Math. 1 (2018) P2.10.
- [2] A. E. Brouwer, A. Neumaier, The graphs with spectral radius between 2 and , Linear Algebra Appl. 114/115 (1989) 273–276.
- [3] A. E. Brouwer, W. H. Haemers, Spectra of graphs, Springer, 2011.
- [4] F. C. Bussemaker, P. J. Cameron, J. J. Seidel, S. V. Tsaranov, Tables of signed graphs, Eut Report 91-WSK-01, Eindhoven, 1991.
- [5] D. Cvetkovi M. Doob, I. Gutman, On graphs whose spectral radius does not exceed , Ars Combinat. 14 (1982) 225–239.
- [6] M. K. Gill, B. D. Acharya, A recurrence formula for computing the characteristic polynomial of a sigraph, J. Comb. Inf. Syst. Sci. 5 (1980) 68–72.
- [7] G. Greaves, J. Koolen, A. Munemasa, Y. Sano, T. Taniguchi, Edge-signed graphs with smallest eigenvalue greater than , J. Combin. Theory Ser. B 110 (2015) 90–111.
- [8] A. J. Hoffman, On limit points of spectral radii of non-negative symmetric integral matrices, in: Y. Alavi, et al. (Eds.), Lecture Notes Math, vol. 303, Springer-Verlag, Berlin, 1972, pp. 165–172.
- [9] Z. L. Jiang, A. Polyanskii, Forbidden subgraphs of bounded spectral radius with applications to equiangular lines, Israel J. Math. 236 (2020) 393–421.
- [10] Z. L. Jiang, A. Polyanskii, Forbidden induced subgraphs of graphs and signed graphs with eigenvalues bounded from below, arXiv: 2111.10366v1.
- [11] P. W. H. Lemmens, J. J. Seidel, Equiangular lines, J. Algebra 24 (1973) 494–512.
- [12] J. McKee, C. Smyth, Integer symmetric matrices having all their eigenvalues in the interval J. Algebra 317 (2007) 260–290.
- [13] J. H. Smith, Some properties of the spectrum of a graph, Combinatorial Structures and their Applications, Gordon and Breach, New York, 1970, pp. 403–406.
- [14] J. F. Wang, J. Wang, M. Brunetti, The hoffman program of graphs: old and new, arXiv: 2012.13079v1.
- [15] T. Zaslavsky, Signed graphs, Discrete Appl. Math. 4 (1982) 47–74.
Appendix A
Gill and Acharya [6] obtained the following recurrence formula for the characteristic polynomial of a signed graph.
Lemma 4.18.
[6] Let be a signed graph and be its arbitrary vertex. Then
where denotes the set of signed cycles passing through and denotes the signed graph obtained from by deleting .
Denote and the characteristic polynomials of and respectively. Then
for all Moreover, the recursion gives
| (4.3) |
Then
| (4.4) |
Let be the signed graph depicted in Fig. 1 with the adjacency matrix and let be a partition of the vertex set. Then
It is known that the spectrum of is (see [12, Theorem 1]). Then
Lemma 4.19.
If is an eigenvalue of then is an eigenvalue of
Proof.
Let be the eigenvector corresponding to the eigenvalue of If then
This gives that is an eigenvalue of and which contradicts to hypothesis. So Since then Hence, is an eigenvalue of ∎
Corollary 4.20.
Proof.
Note that and By Lemma 3.1, then is an eigenvalue of (resp. , ) with multiplicity at least (resp. , ).
() It is known that the spectrum of is By Lemma 4.19, then is an eigenvalue of with multiplicity . Therefore,
The proofs of () and () are similar since the spectrum of is and the spectrum of is . ∎
By Lemma 4.18 and Eqs. (4.3)(4.6), we can obtain the characteristic polynomials of all signed graphs of Theorem 2.4 and . More importantly, by computations (using Wolfram Mathematica 12), we get that . See Tables 1 and 2. (In Table 1, and ). Then we have
Lemma 4.21.
Let be one of the signed graphs of Theorem 2.4 and with vertices. Then
Proof.
Let be one of the signed graphs of Theorem 2.4 and , then we can get that is bipartite and contains an induced subgraph with order and . (For example, if is let then .) Then by interlacing theorem. Since (by Tables 1 and 2), then ∎
Finally we are going to give the proof of Lemma 3.5.
Proof of Lemma 3.5. Let be a signed graph in Lemma 3.5. We can check that is bipartite and contains an induced subgraph with order and . Then by interlacing theorem. So if , then Now we just need to prove that Obviously, if is an induced subgraph of the signed graphs of Theorem 2.4 , then by Lemma 4.21.
(1) If , by forbidding (where ), then Similarily, if then Therefore, if and then if and then if and or and then where
If and , then .
If and , and if and , then (where by Table 3 (3)); otherwise, , where , and .
Next we consider that
Case 1.
Subcase 1.1. If by computations, we have and Then and
Subcase 1.2. By forbidding (where ), then By Table 3 (1), we have . Then and
Case 2. Then . Furthermore, by forbidding (where ), then
Subcase 2.1. Then . Note that , then
Subcase 2.2. If by computations, we have . Then . So where .
Subcase 2.3. By forbidding (where ), then If , then (by Table 3 (2)) and . If , then where .
Case 3. By forbidding the graph we obtain that if and , or and then otherwise, .
Subcase 3.1. and . Then By computations, we have and .
Subcase 3.2. and . Then By computations, we have and So .
Subcase 3.3. and . Then By computations, we have and So .
Subcase 3.4. and . Then . By computations, we have and .
Subcase 3.5. and . Let Then
where . If then and as and If then and as So, where We complete the proof of
() Let where By forbidding (where ), we have
Case 1. By computations, we have and Then . So (if ) or where (if ).
Case 2.
Subcase 2.1. By computations, we have and Then . So (if ) or where (if ).
Subcase 2.2. By computations, we have and Then So where .
Case 3.
Subcase 3.1. By computations, we have and Then So (if ) or where (if ).
Subcase 3.2. By computations, if then Then . So where .
Case 4.
Subcase 4.1. By forbidding (where ), we have Since and (by Table 3 (4) and (5)), then . So (if ) or where (if ).
Subcase 4.2. By forbidding (where ), we have Since and (by Table 3 (6) and (7)), then . So where .
Subcase 4.3. If and by forbidding (where ), we have By computations, we have , and Then So (if ) or where (if ). Otherwise, either and or and By forbidding (where ), we have If , then Therefore, .
If , then , where Since
then . If then and . If then for So, .
Hence, (if ) or where (if ). We complete the proof of
The proofs of are similar, and all values () are presented in Table 3, where
(12) If by forbidding (where ), then . So (if ) or (if ), where
(13) By computations, we have and for and and for Therefore, is an induced subgraph of () is an induced subgraph of () is an induced subgraph of ∎
| is even) | |