On signed graphs whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$

Dijian Wang^a, Wenkuan Dong^a, Yaoping Hou^b, Deqiong Li^c
^aSchool of Science, Zhejiang University of Science and Technology,
Hangzhou, Zhejiang, 310023, P. R. China
^bCollege of Mathematics and Statistics, Hunan Normal University,
Changsha, Hunan, 410081, P. R. China
^cSchool of Mathematics and Statistics, Hunan University of Technology and Business,
Changsha, Hunan, 410205, P. R. China
Corresponding author: [email protected]

Abstract

The Hoffman program with respect to any real or complex square matrix $M$ associated to a graph $G$ stems from Hoffman’s pioneering work on the limit points for the spectral radius of adjacency matrices of graphs does not exceed $\sqrt{2+\sqrt{5}}$ . A signed graph $\dot{G}=(G,\sigma)$ is a pair $(G,\sigma),$ where $G=(V(G),E(G))$ is a simple graph and $\sigma:E(G)\rightarrow\{+1,-1\}$ is the sign function. In this paper, we study the Hoffman program of signed graphs. Here, all signed graphs whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$ will be identified.

AMS classification: 05C50

Keywords: Signed graphs; Spectral radius; Hoffman program.

1 Introduction

All graphs considered here are simple, undirected and finite. For a graph $G=(V(G),E(G)),$ let $A(G)$ denote the adjacency matrix of $G,$ the eigenvalues of $A(G)$ are all real and the spectral radius of $G$ is equal to the largest eigenvalue of $A(G)$ .

The Hoffman program is the identification of connected graphs whose spectral radius does not exceed some special limit points established by Hoffman [8]. The smallest limit point for the spectral radius of $G$ is 2, that is, identifies all connected graphs whose spectral radius does not exceed 2. This problem has already been completely solved by Smith [13]. They are known as Smith graphs. After that, the problem jumps to the next significant limit point, which is $\lambda^{\ast}:=\sqrt{2+\sqrt{5}}=\tau^{\frac{1}{2}}+\tau^{-\frac{1}{2}}$ $(\approx 2.05817),$ where $\tau$ is the golden mean. In [5], Cvetkovi $\acute{c}$ , Doob and Gutman determined the structures of graphs with spectral radius between 2 and $\sqrt{2+\sqrt{5}}$ . Their description was completed by Brouwer and Neumaier [2]. In 2020, Jiang and Polyanskii [9] studied the forbidden subgraphs characterization for $\mathcal{G}^{\lambda}$ (where $\mathcal{G}^{\lambda}$ denotes the family of connected graphs of spectral radius $\leq\lambda$ ) with applications to estimate the maximum cardinality of equiangular lines in the $n$ -dimensional Euclidean space $\mathbb{R}^{n}.$ For more on the results between Hoffman program and equiangular lines, see [9, 11, 13].

Refer to caption — Figure 1: The signed graphs $\dot{S}_{14},\dot{S}_{16}$ and $\dot{T}_{2k}$ .

A signed graph $\dot{G}=(G,\sigma)$ is a pair $(G,\sigma),$ where $G$ is a simple graph with $n$ vertices and $m$ edges, called the underlying graph, and $\sigma:E(G)\rightarrow\{+1,-1\}$ is the sign function. An edge $v_{i}v_{j}$ is called positive (negative) if $\sigma(v_{i}v_{j})=+1$ (resp. $\sigma(v_{i}v_{j})=-1$ ) and denoted by $v_{i}\mathop{\sim}\limits^{+}v_{j}$ (resp. $v_{i}\mathop{\sim}\limits^{-}v_{j}$ ). An unsigned graph (or a graph) is a signed graph without negative edges. Given a signed graph $\dot{G}$ , its adjacency matrix is defined by $A(\dot{G})=(\sigma_{ij}),$ where $\sigma_{ij}=\sigma(v_{i}v_{j})$ if $v_{i}\sim v_{j},$ and $\sigma_{ij}=0$ otherwise. The eigenvalues, denoted by $\lambda_{1}(\dot{G})\geq\dots\geq\lambda_{n}(\dot{G}),$ of $A(\dot{G})$ are defined as the eigenvalues of $\dot{G}$ ; they are all real since $A(\dot{G})$ is a real symmetric matrix. The spectral radius of $\dot{G}$ is defined by $\rho(\dot{G})=max\{|\lambda_{i}(\dot{G})|:1\leq i\leq n\}=max\{\lambda_{1}(\dot{G}),-\lambda_{n}(\dot{G})\}.$

The theory of limit points for the spectral radius of graph sequences studied by Hoffman is still valid in the context of signed graphs. Some interesting results on the Hoffman program of signed graphs can be found in [1, 14, 7, 10]. In [10], Jiang and Polyanskii studied the forbidden subgraphs characterization for families of signed graphs with eigenvalues bounded from below with applications to determine the maximum cardinality of a spherical two-distance set with two fixed angles in high dimensions. The smallest limit point for the spectral radius of $\dot{G}$ is also 2, see [14, Propostion 6.1]. Those signed graphs have been identified by McKee and Smyth [12]. Therefore, the natural next step is the next limit point: $\lambda^{\ast}=\sqrt{2+\sqrt{5}},$ that is, identifies all connected signed graphs whose spectral radius does not exceed $\lambda^{\ast}$ . In this paper, we study the Hoffman program of signed graphs and all signed graphs whose spectral radius does not exceed $\lambda^{\ast}$ will be identified.

In this paper, positive edges are depicted as bold lines and negative edges are depicted as dashed lines. The rest of the paper is organized as follows. Our contribution is reported in Section $2.$ In Section $3$ , we give some preliminaries lemmas and theorems. In Section $4$ , we will prove the Theorem 2.4.

2 Main results

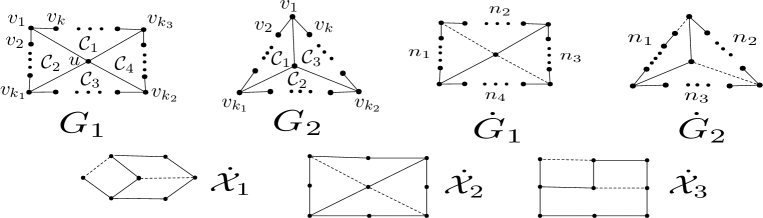
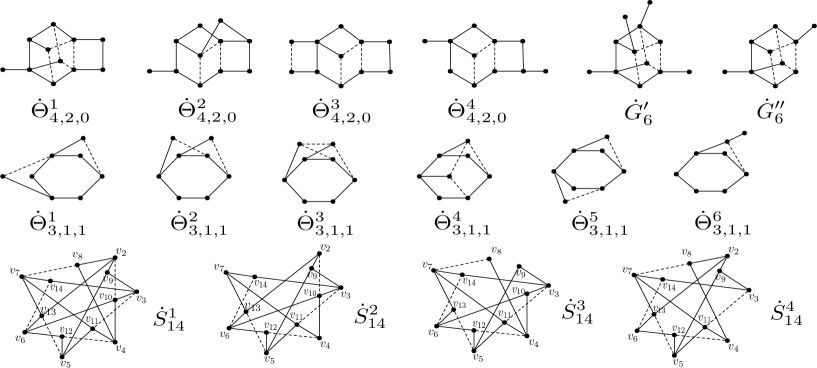
Let $T_{a,b,c}$ be the graph with $a+b+c+1$ vertices consisting of three paths with $a,b,$ and $c$ edges, respectively, where these paths have one end vertex in common, and let $Q_{a,b,c}$ be the graph with $a+b+c+3$ vertices consisting of a path with $a+b+c$ edges and two extra edges affixed at $v_{0}$ and $w_{0}.$ See Fig. 2.

For any fixed $\rho>0,$ the symbol $\mathcal{G}^{\rho}$ (resp. $\mathcal{G}_{S}^{\rho}$ ) denotes the set of the connected (resp. signed) graphs whose spectral radius does not exceed $\rho.$

Theorem 2.1.

[13, 2, 5] Let the graphs $T_{a,b,c}$ and $Q_{a,b,c}$ be depicted in Fig. 2. Then

$(i)$ $\mathcal{G}^{2}=\{C_{n},K_{1,4},T_{2,2,2},T_{1,3,3},P_{n},T_{1,1,n-1},T_{1,2,2},T_{1,2,3},T_{1,2,4},Q_{1,n-5,1}\}.$

$(ii)$ $\mathcal{G}^{\lambda^{\ast}}=\mathcal{G}^{2}\cup\{T_{a,b,c}|a=1,b=2,c>5;or~{}a=1,b>2,c>3;or~{}a=b=2,c>2;or~{}a=2,b=c=3\}\cup\{Q_{a,b,c}|(a,b,c)\in\mathcal{S};or~{}c\geq a>0,b\geq b^{\ast}(a,c),(a,c)\neq(1,1)\}$ where

\mathcal{S}=\{(1,1,2),(2,4,2),(2,5,3),(3,7,3),(3,8,4)\}

and

b^{\ast}(a,c)=\begin{cases}a+c+2&\text{for $a>2$};\\ c+3&\text{for $a=2$};\\ c&\text{for $a=1$}.\end{cases}

Theorem 2.2.

[12] Signed graphs in $\mathcal{G}_{S}^{2}$ are the induced subgraphs of $\dot{S}_{14},$ $\dot{S}_{16}$ or $\dot{T}_{2k}.$

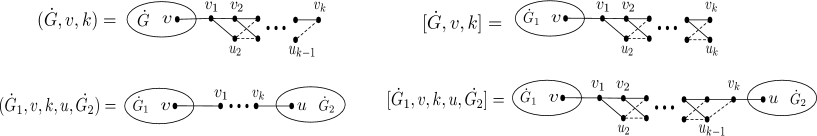
Definition 2.3.

$(1)$ Let $\dot{G}$ be a connected signed graph, and let $v$ be a vertex in $\dot{G}.$

$\bullet$ Denote $(\dot{G},v,k)$ the signed graph obtained from $\dot{G}$ by appending a $\dot{T}_{2k}^{\prime\prime\prime}$ at $v.$

$\bullet$ Denote $[\dot{G},v,k]$ the signed graph obtained from $\dot{G}$ by appending a $\dot{T}_{2k}^{\prime\prime}$ at $v.$

$(2)$ Let $\dot{G}_{1},$ $\dot{G}_{2}$ be two connected disjoint signed graphs, and let $v,$ $u$ be vertices in $\dot{G}_{1},$ $\dot{G}_{2}$ respectively.

$\bullet$ Define $(\dot{G}_{1},v,k,u,\dot{G}_{2})$ to be the signed graph obtained from $\dot{G}_{1}$ and $\dot{G}_{2}$ by joining them with a path of $k$ vertices connecting $v$ and $u.$

$\bullet$ Define $[\dot{G}_{1},v,k,u,\dot{G}_{2}]$ to be the signed graph obtained from $\dot{G}_{1}$ and $\dot{G}_{2}$ by joining them with a $\dot{T}_{2k}^{\prime\prime\prime}$ connecting $v$ and $u.$

The above mentioned signed graphs are depicted in Figs. 3 and 4.

The main results of this paper are presented as following.

Theorem 2.4.

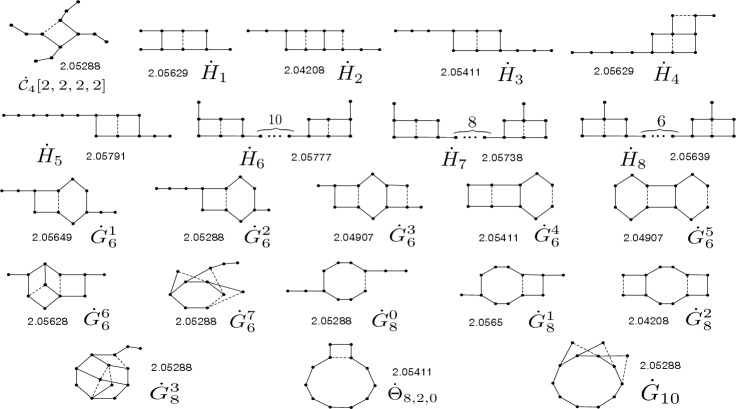
Signed graphs in $\mathcal{G}_{S}^{\lambda^{\ast}}$ are the induced subgraphs (up to switching isomorphic) of

$(i)$ $\dot{S}_{14},\dot{S}_{16},\dot{T}_{2k},$

$(ii)$ $\dot{\mathcal{C}}_{4}[2,2,2,2],\dot{H}_{1}-\dot{H}_{8},\dot{G}_{6}^{1}-\dot{G}_{6}^{7},\dot{G}_{8}^{0}-\dot{G}_{8}^{3},\dot{\Theta}_{8,2,0},\dot{G}_{10},$

$(iii)$ $\dot{\mathcal{C}}_{k}^{1,\frac{k}{2}+1}$ $(k$ is even $)$ , $\dot{G}_{0}^{k}$ $(k\geq 12$ and $k$ is even $),$ $\dot{U}^{n_{1},n_{2}}_{6}$ $(n_{1}\geq 1$ and $n_{2}\geq 1),$ $\dot{\mathcal{C}}_{4}[n_{1},1,n_{3},1]$ $(n_{1}\geq 1$ and $n_{3}\geq 1),$ $\dot{S}_{1}^{n}$ $(n\geq 8),$ $\dot{S}_{2}^{n}$ $(n\geq 10),$

$(iv)$ $[\dot{G},v,s,u,\dot{H}]$ $(s\geq 3)$ , where $(\dot{G},v),$ $(\dot{H},u)\in\{(\dot{G}_{4}^{12},v_{12}),$ $(\dot{G}_{2}^{9},v_{9}),(T_{a,1,a-1},v_{a-1}),$ $(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}}),(\dot{G}_{5}^{10},v_{10}),(P_{4},v_{2})\},$ $a\geq 3$ and $n_{1}\geq 1$ ,

$(v)$ $(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{2},P_{4}),$ $(\dot{Q}^{\prime}_{a_{4},a_{4}},v_{a_{4}},2,v_{2},P_{4}),$ $(\dot{Q}^{\prime}_{b,b},v_{b},2,v_{a_{3}-1},T_{a_{3},1,a_{3}-1})$ $(b\geq a_{3}-1)$ , $(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{a_{3}-1},T_{a_{3},1,a_{3}-1})$ , $(\dot{Q}_{a_{1},a_{1}}^{\prime},v_{a_{1}},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{Q}_{a_{3},a_{3}}^{\prime},v_{a_{3}},2,v_{a_{2}},\dot{Q}_{a_{2},a_{2}}^{\prime}),$ $(\dot{G}_{5}^{10},v_{10},2,$ $v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{5}^{10},v_{10},2,v_{a_{4}},\dot{Q}^{\prime}_{a_{4},a_{4}})$ , $(\dot{G}_{2}^{9},v_{9},2,v_{2},P_{4}),$ $(\dot{G}_{2}^{9},v_{9},2,v_{2},T_{3,1,2}),$ $(\dot{G}_{2}^{9},v_{9},2,v_{3},T_{4,1,3})$ , $(\dot{G}_{2}^{9},v_{9},$ $2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{2}^{9},v_{9},2,v_{a_{2}},\dot{Q}^{\prime}_{a_{2},a_{2}}),$ $(\dot{G}_{3}^{11},v_{11},2,v_{2},T_{3,1,2}),$ $(\dot{G}_{3}^{11},v_{11},2,v_{3},T_{4,1,3})$ , $(\dot{G}_{3}^{11},$ $v_{11},2,v_{a_{2}},\dot{Q}^{\prime}_{a_{2},a_{2}})$ , $(\dot{G}_{4}^{12},v_{12},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{4}^{12},v_{12},2,v_{a_{4}},\dot{Q}^{\prime}_{a_{4},a_{4}})$ , where $a_{i}\geq i$ for $i=1,2,3,4$ .

The above mentioned signed graphs are depicted in Figs. 2, 5, 6 and 7.

Remark 2.5.

$(1)$ In Appendix A, we will prove that each signed graph of Theorem 2.4 $(iii)$ and $(iv)$ has spectral radius $\rho(\dot{G})<\lambda^{\ast}$ . See Lemma 4.21.

$(2)$ Each signed graph of Theorem 2.4 $(v)$ belongs to Lemma 3.5.

3 Preliminaries

The sign of a cycle $\dot{C}$ of $\dot{G}$ is $\sigma(\dot{C})=\prod_{e\in\dot{C}}\sigma(e)$ , whose sign is $+1$ (resp. $-1$ ) is called positive (resp. negative) and denoted by $\dot{C}_{n}^{+}$ (resp. $\dot{C}_{n}^{-}$ ). A signed graph $\dot{G}$ is called balanced if all its cycles are positive; otherwise it is called unbalanced. If there is a vertex subset $S\subseteq V(\dot{G})$ , such that $\dot{G}^{S}$ is obtained by reversing the sign of every edge with one end in $S$ and the other in $V(\dot{G})\setminus S$ , then we say that $\dot{G}$ and $\dot{G}^{S}$ are switching equivalent and write $\dot{G}\sim\dot{G}^{S}$ . If $\dot{G}$ is isomorphic to a signed graph switching equivalent to $\dot{G_{1}}$ , we say $\dot{G}$ is switching isomorphic to $\dot{G_{1}}$ , denoted by $\dot{G}\simeq\dot{G_{1}}$ . Switching isomorphic signed graphs share the same spectrum. More basic results on the signed graphs, see [15].

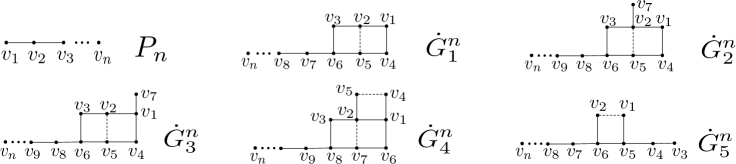
As usual, $d_{u}$ is the degree of a vertex $u$ and $\Delta(\dot{G})=max_{u\in V(\dot{G})}d_{u}$ . Let $N_{X}(u)$ be the set of neighbours of a vertex $u$ in a set $X$ and $d_{X}(u)$ be the cardinality of $N_{X}(u)$ . For $U\subset V(\dot{G}),$ $\dot{G}[U]$ denotes the induced subgraph of $\dot{G}$ respect to the $U.$ The signed graph $\dot{C}_{k}^{1}$ (resp. $\dot{\mathcal{C}}_{k}^{1}$ ) is obtained by a balanced cycle $\dot{C}_{k}^{+}$ (resp. an unbalanced cycle $\dot{C}_{k}^{-}$ ) with one pendent edge. The signed graph $\dot{\mathcal{C}}_{k}^{i,j}$ ( $i\neq j$ ) is obtained by an unbalanced cycle $\dot{C}_{k}^{-}$ with one pendent edge at vertex $v_{i}$ (in $\dot{C}_{k}^{-}$ ) and one pendent edge at vertex $v_{j}$ (in $\dot{C}_{k}^{-}$ ).

A signed graph is called maximal with respect to some property $\mathcal{P}$ if it is not a proper induced subgraph of some other signed graph satisfying $\mathcal{P}.$ In this context, we call a signed graph is maximal if it is not a proper induced subgraph of some other signed graphs whose spectral radius does not exceed $\lambda^{\ast}$ .

Given a signed graph $\dot{H}$ and $\rho(\dot{H})\leq 2$ , a subset $U$ of $V(\dot{H}),$ and a vertex $w$ not in $V(\dot{H}),$ the signed graph $\dot{H}_{U}(w)$ is obtained by inserting the edges (the sign of edge is any) between $w$ and all vertices of $U.$ We call that $w$ is a good vertex if $2<\rho(\dot{H}_{U}(w))\leq\lambda^{\ast}$ .

The first lemma is interlacing theorem.

Lemma 3.1.

[3] Let $A$ be a symmetric matrix of order $n$ with eigenvalues $\lambda_{1}\geq\lambda_{2}\geq\dots\geq\lambda_{n}$ and $B$ a principal submatrix of $A$ of order $m$ with eigenvalues $\mu_{1}\geq\mu_{2}\geq\dots\geq\mu_{m}.$ Then the eigenvalues of $B$ interlace the eigenvalues of $A,$ that is, $\lambda_{i}\geq\mu_{i}\geq\lambda_{n-m+i}$ for $i=1,\dots,m.$

Define $\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ to be the set of the connected unbalanced signed graphs with spectral radius $2<\rho(\dot{G})\leq\lambda^{\ast}.$ Note that the balanced signed graph and unsigned graph share the same spectrum, thus the main goal of this paper is to determine all signed graphs of the set $\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}.$ Some properties of the signed graph $\dot{G}$ of the set $\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ are listed as following.

Lemma 3.2.

Let $\dot{G}\in\mathcal{G}_{S}^{\lambda^{\ast}}$ . Then $\Delta(\dot{G})\leq 4.$

Proof.

Note that $\rho(\dot{G})^{2}=max\{\lambda_{i}(A(\dot{G})^{2})|i=1,\dots,n\},$ then $\rho(\dot{G})^{2}\geq max\{(A(\dot{G})^{2})_{ii}|i=1,\dots,n\}=\Delta(\dot{G}).$ Since $\Delta(\dot{G})\leq\rho(\dot{G})^{2}\leq(\lambda^{\ast})^{2}<5,$ then $\Delta(\dot{G})\leq 4.$ ∎

We designate that a signed graph $\dot{H}$ is an induced subgraph of $\dot{G}$ by writing $\dot{H}\subset\dot{G}$ . If $\dot{H}$ is not an induced subgraph of $\dot{G}$ , then we say that $\dot{G}$ is $\dot{H}$ -free.

Lemma 3.3.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ . Then $\dot{G}$ is $\dot{C}_{3}$ -free.

Proof.

Suppose on the contrary that $\dot{C}_{3}\subset\dot{G}.$ By the table of the spectra of signed graphs with at most six vertices [4], we find that there is no signed graph $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ of order $n\leq 6.$ Next we consider $n\geq 7.$ Then $\dot{G}$ must contain an induced subgraph $\dot{G}_{1}$ with order $|V(\dot{G}_{1})|=6$ and $\rho(\dot{G}_{1})\leq\lambda^{\ast}.$ By [4, page 19–40], we have $\dot{G}_{1}\sim\dot{T}_{6}.$ Since $\dot{T}_{6}$ is 4-regular, then $\Delta(\dot{G})\geq 5,$ which contradicts to Lemma 3.2. Hence, $\dot{G}$ is $\dot{C}_{3}$ -free. ∎

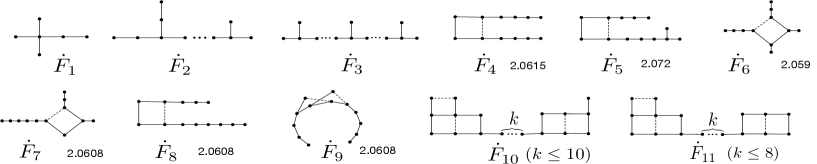
We say that $\dot{H}$ is forbidden if $\rho(\dot{H})>\lambda^{\ast}.$ Evidently, if $\dot{H}$ is forbidden, then $\dot{G}$ is $\dot{H}$ -free.

Lemma 3.4.

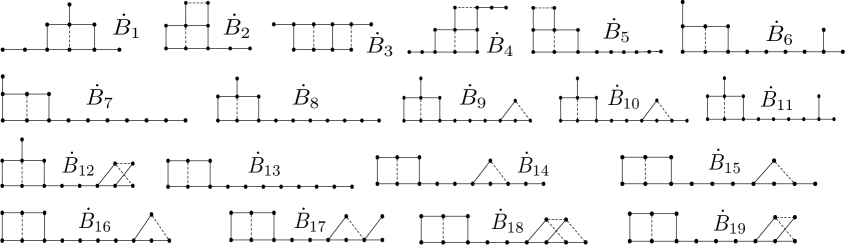
All (unsigned) graphs expect the graphs in the set $\mathcal{G}^{\lambda^{\ast}},$ the signed graph $\dot{\mathcal{C}}_{2\ell+1}^{1}$ and the signed graphs $\dot{F}_{i}$ $(i=1,\dots,11)$ of Fig. 8 are forbidden.

Proof.

It is easily to see that all (unsigned) graphs expect the graphs in the set $\mathcal{G}^{\lambda^{\ast}},$ the signed graph $\dot{\mathcal{C}}_{2\ell+1}^{1}$ (since $\rho(\dot{\mathcal{C}}_{2\ell+1}^{1})=\rho(\dot{C}_{2\ell+1}^{1})$ ) and the signed graphs $\dot{F}_{1}-\dot{F}_{11}$ of Fig. 8 have spectral radius $\rho(\dot{G})>\lambda^{\ast}.$ So all of them are forbidden by interlacing. ∎

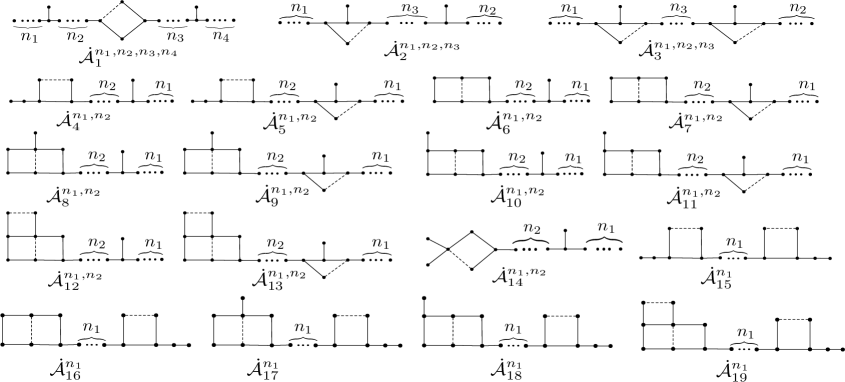
The next lemma plays an important role in this paper. The proof is presented in Appendix A.

Lemma 3.5.

Let $\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}},$ $\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}},$ $\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{3}}$ $(n_{1}\geq n_{2})$ , $\dot{\mathcal{A}}_{i}^{n_{1},n_{2}}$ $(i=4,\dots,14),$ $\dot{\mathcal{A}}_{i}^{n_{1}}$ $(i=15,\dots,19)$ be the signed graphs depicted in Fig. 9. Then

$(1)$ if $\rho(\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}}$ is an induced subgraph of $[P_{4},v_{2},s,v_{2},P_{4}],$ $[T_{a_{3},1,a_{3}-1},v_{a_{3}-1},s_{3},v_{2},P_{4}]$ or $[T_{a_{3},1,a_{3}-1},v_{a_{3}-1},s,v_{b_{3}-1},T_{b_{3},1,b_{3}-1}]$ ,

$(2)$ if $\rho(\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}}$ is an induced subgraph of $(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{2},P_{4}),$ $(\dot{Q}^{\prime}_{a_{4},a_{4}},v_{a_{4}},2,v_{2},P_{4}),$ $(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{a_{3}-1},T_{a_{3},1,a_{3}-1})$ , $(\dot{Q}^{\prime}_{a,a},v_{a},2,v_{a_{3}-1},T_{a_{3},1,a_{3}-1})$ $($ where $a\geq a_{3}-1),$ $[\dot{Q}^{\prime}_{a_{1},a_{1}},v_{a_{1}},s,v_{2},P_{4}]$ or $[\dot{Q}^{\prime}_{a_{1},a_{1}},v_{a_{1}},s,v_{a_{3}-1},T_{a_{3},1,a_{3}-1}],$

$(3)$ if $\rho(\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{3}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{3}}$ is an induced subgraph of $(\dot{Q}_{a_{1},a_{1}}^{\prime},v_{a_{1}},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{Q}_{a_{3},a_{3}}^{\prime},v_{a_{3}},2,v_{a_{2}},\dot{Q}_{a_{2},a_{2}}^{\prime})$ or $[\dot{Q}_{a_{1},a_{1}}^{\prime},v_{a_{1}},s,v_{b_{1}},\dot{Q}_{b_{1},b_{1}}^{\prime}],$

$(4)$ if $\rho(\dot{\mathcal{A}}_{4}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{4}^{n_{1},n_{2}}$ is an induced subgraph of $[\dot{G}_{5}^{10},v_{10},s,v_{2},P_{4}]$ or $[\dot{G}_{5}^{10},v_{10},s,v_{a_{3}-1},T_{a_{3},1,a_{3}-1}]$ ,

$(5)$ if $\rho(\dot{\mathcal{A}}_{5}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{5}^{n_{1},n_{2}}$ is an induced subgraph of $(\dot{G}_{5}^{10},v_{10},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{5}^{10},v_{10},2,v_{a_{4}},\dot{Q}^{\prime}_{a_{4},a_{4}})$ or $[\dot{G}_{5}^{10},v_{10},s,v_{a_{1}},\dot{Q}^{\prime}_{a_{1},a_{1}}]$ ,

$(6)$ if $\rho(\dot{\mathcal{A}}_{i}^{n_{1},n_{2}})\leq\lambda^{\ast}$ $(i=6,8)$ , then $\dot{\mathcal{A}}_{i}^{n_{1},n_{2}}$ is an induced subgraph of $(\dot{G}_{2}^{9},v_{9},2,v_{2},P_{4}),$ $[\dot{G}_{2}^{9},v_{9},s,v_{2},P_{4}],$ $(\dot{G}_{2}^{9},v_{9},2,v_{2},T_{3,1,2}),$ $(\dot{G}_{2}^{9},v_{9},2,v_{3},T_{4,1,3})$ or $[\dot{G}_{2}^{9},v_{9},s,v_{a_{3}-1},T_{a_{3},1,a_{3}-1}],$

$(7)$ if $\rho(\dot{\mathcal{A}}_{i}^{n_{1},n_{2}})\leq\lambda^{\ast}$ $(i=7,9)$ , then $\dot{\mathcal{A}}_{i}^{n_{1},n_{2}}$ is an induced subgraph of $(\dot{G}_{2}^{9},v_{9},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{2}^{9},v_{9},2,v_{a_{2}},\dot{Q}^{\prime}_{a_{2},a_{2}})$ or $[\dot{G}_{2}^{9},v_{9},s,v_{a_{1}},\dot{Q}^{\prime}_{a_{1},a_{1}}],$

$(8)$ if $\rho(\dot{\mathcal{A}}_{10}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{10}^{n_{1},n_{2}}$ is an induced subgraph of $[\dot{G}_{3}^{11},v_{11},s,v_{2},P_{4}],$ $(\dot{G}_{3}^{11},v_{11},$ $2,v_{2},T_{3,1,2}),$ $(\dot{G}_{3}^{11},v_{11},2,v_{3},T_{4,1,3})$ or $[\dot{G}_{3}^{11},v_{11},s,v_{a_{3}-1},T_{a_{3},1,a_{3}-1}],$

$(9)$ if $\rho(\dot{\mathcal{A}}_{11}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{11}^{n_{1},n_{2}}$ is an induced subgraph of $(\dot{G}_{3}^{11},v_{11},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{3}^{11},v_{11},2,v_{a_{2}},\dot{Q}^{\prime}_{a_{2},a_{2}})$ or $[\dot{G}_{3}^{11},v_{11},s,v_{a_{1}},\dot{Q}^{\prime}_{a_{1},a_{1}}],$

$(10)$ if $\rho(\dot{\mathcal{A}}_{12}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{12}^{n_{1},n_{2}}$ is an induced subgraph of $[\dot{G}_{4}^{12},v_{12},s,v_{2},P_{4}]$ or $[\dot{G}_{4}^{12},v_{12},s,v_{a_{3}-1},T_{a_{3},1,a_{3}-1}],$

$(11)$ if $\rho(\dot{\mathcal{A}}_{13}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{13}^{n_{1},n_{2}}$ is an induced subgraph of $(\dot{G}_{4}^{12},v_{12},2,v_{1},\dot{Q}^{\prime}_{1,0}),$ $(\dot{G}_{4}^{12},v_{12},2,v_{a_{4}},\dot{Q}^{\prime}_{a_{4},a_{4}})$ or $[\dot{G}_{4}^{12},v_{12},s,v_{a_{1}},\dot{Q}^{\prime}_{a_{1},a_{1}}],$

$(12)$ if $\rho(\dot{\mathcal{A}}_{14}^{n_{1},n_{2}})\leq\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{14}^{n_{1},n_{2}}\subset[P_{4},v_{2},s]$ or $\dot{\mathcal{A}}_{14}^{n_{1},n_{2}}\subset[T_{a_{3},1,a_{3}-1},v_{a_{3}-1},s]$ .

$(13)$ if $\rho(\dot{\mathcal{A}}_{i}^{n_{1}})\leq\lambda^{\ast}$ $(i=15,16,17,18,19)$ , then $\dot{\mathcal{A}}_{i}^{n_{1}}$ is an induced subgraph of $[\dot{G},v,s,u,\dot{H}]$ , where $(\dot{G},v),$ $(\dot{H},u)\in\{(\dot{G}_{4}^{12},v_{12}),$ $(\dot{G}_{2}^{9},v_{9}),(\dot{G}_{5}^{10},v_{10})\},$

where $b_{1}\geq 1,$ $b_{3}\geq 1,$ $a_{i}\geq i$ for $i=1,2,3,4$ and $s\geq 3$ .

Remark 3.6.

Each signed graph in Lemma 3.5 is one of the signed graphs of Theorem 2.4 $(v)$ or an induced subgraph of the signed graphs of Theorem 2.4 $(iv).$

Now we pay attention to the uncyclic and bicyclic signed graphs of the set $\mathcal{G}_{S}^{\lambda^{\ast}}$ .

Lemma 3.7.

Let $\dot{G}=(G,\sigma)\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ $(G\neq C_{n})$ be a uncyclic signed graph with a $k$ -cycle. Then $\dot{G}$ $\subset\dot{\mathcal{C}}_{k}^{1,\frac{k}{2}+1},\dot{\mathcal{C}}_{10}^{1,5},\dot{\mathcal{C}}_{8}^{1,4},\dot{G}_{8}^{0},\dot{U}_{6},\dot{U}_{6}^{n_{1},n_{2}},\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}},\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}},\dot{\mathcal{A}}_{4}^{n_{1},n_{2}},\dot{\mathcal{A}}_{14}^{n_{1},n_{2}},\dot{\mathcal{C}}_{4}[2,2,2,2]$ , $\dot{\mathcal{C}}_{4}[4,2,1,0]$ , $\dot{\mathcal{C}}_{4}[2,3,1,0]$ , $\dot{\mathcal{C}}_{4}[5,3,0,0]$ , $\dot{\mathcal{C}}_{4}[n_{1},1,n_{3},1]$ . See Figs. 5, 6, 9 and 10.

Proof.

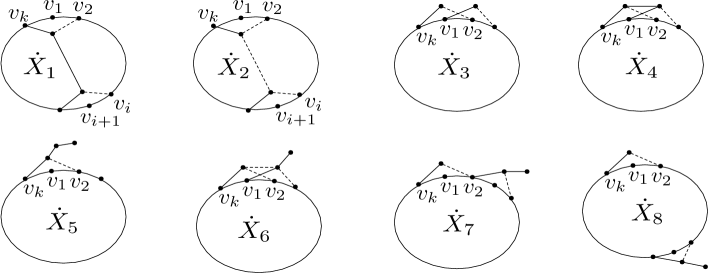
Let $V(\dot{C}_{k})=\{v_{1},v_{2},\dots,v_{k}\}$ and let $d_{v_{1}}\geq 3$ and $u_{1}$ be the new neighbor of $v_{1}.$ By forbidding $\dot{C}_{\ell}^{1}$ and $\dot{\mathcal{C}}_{2\ell+1}^{1}$ , then the cycle $\dot{C}_{k}$ is unbalanced and $k$ is even. In addition, by forbidding $\dot{F}_{1}$ , if $k\geq 6,$ then $d_{v_{i}}\leq 3$ for all $i=1,\dots,k.$

Case 1. $k\geq 14.$ Then $d_{v_{i}}=2$ for $i=2,3,\dots,\frac{k}{2}$ , otherwise $d_{v_{i}}\geq 3$ and let $u_{i}\sim v_{i}$ , then $Q_{2,i-1,\frac{k}{2}-3}\subset\dot{G}-v_{i+3}$ and $\rho(\dot{G})\geq\rho(Q_{2,i-1,\frac{k}{2}-3})>\lambda^{\ast}$ , which is a contradiction. Because of symmetry, we have $d_{v_{j}}=2$ for $j=\frac{k}{2}+2,\dots,k.$ If $d_{u_{1}}\geq 2$ , let $u_{2}\mathop{\sim}\limits^{+}u_{1},$ then $\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{k},v_{k-1},v_{k-2},u_{1},u_{2}\}$ induces the $T_{2,3,4}$ and $\rho(\dot{G})\geq\rho(T_{2,3,4})>\lambda^{\ast}$ , which is a contradiction. So $d_{u_{1}}=1.$ Therefore, $\dot{G}\subset\dot{\mathcal{C}}_{k}^{1,\frac{k}{2}+1}$ .

Case 2. $k=10$ or 12. Then $d_{u_{1}}=1$ , otherwise $d_{u_{1}}\geq 2$ and let $u_{2}\mathop{\sim}\limits^{+}u_{1},$ then $\{v_{1},v_{2},v_{3},v_{4},v_{5},$ $v_{k},v_{k-1},v_{k-2},u_{1},u_{2}\}$ induces the $T_{2,3,4}$ and $\rho(\dot{G})\geq\rho(T_{2,3,4})>\lambda^{\ast}$ , which is a contradiction. So all vertices of $V(\dot{G})\setminus V(\dot{C}_{k})$ are within distance 1 of the cycle $\dot{C}_{k}.$ By directed calculations, it is not hard to get that $\dot{G}\sim\dot{\mathcal{C}}_{10}^{1,5}$ , $\dot{\mathcal{C}}_{10}^{1,6},\dot{\mathcal{C}}_{12}^{1,7}$ .

Case 3. $k=8$ or $6.$ If all vertices of $V(\dot{G})\setminus V(\dot{C}_{k})$ are within distance 1 of the cycle $\dot{C}_{k},$ a directed calculation leads that $\dot{G}\subset\dot{\mathcal{C}}_{6}^{1,4},\dot{\mathcal{C}}_{8}^{1,4},\dot{\mathcal{C}}_{8}^{1,5}$ or $\dot{U}_{6}.$ Otherwise, we assume that $d_{u_{1}}\geq 2$ and let $u_{2}$ be the new neighbor of $u_{1}.$ If $k=8,$ by forbidding $T_{3,3,3}$ and $\dot{F}_{2}$ , then $d_{u_{2}}=1$ and $d_{u_{1}}=d_{v_{i}}=2$ for $i=2,3,4,6,7,8,$ respectively. So $\dot{G}\subset\dot{G}_{8}^{0}$ . If $k=6,$ then $d_{v_{2}}=d_{v_{6}}=2$ (by forbidding $\dot{F}_{2}$ ). If $d_{v_{3}}=3$ or $d_{v_{5}}=3,$ let $u_{3}$ (resp. $u_{5}$ ) be the new neighbor of $v_{3}$ (resp. $v_{5}$ ), by forbidding $\dot{F}_{2}$ , $Q_{1,2,3},$ $Q_{2,2,2}$ , $\dot{F}_{1}$ and $Q_{1,1,4},$ we have $d_{u_{1}}=2$ , $d_{u_{2}}=d_{u_{3}}=d_{u_{5}}=1$ and $d_{v_{4}}=2$ . Then $\dot{G}\subset\dot{U}_{6}.$ See Fig. 10. Next we consider that $d_{v_{3}}=d_{v_{5}}=2,$ then $\dot{U}_{6}^{n_{1},n_{2}}\subset\dot{G}.$ See Fig. 6. Since $\dot{G}$ is $\dot{F}_{2}$ -free, then each vertex of $\dot{U}_{6}^{n_{1},n_{2}}$ expect the vertices of $V(\dot{C}_{6})$ has degree at most 2. Hence, $\dot{G}\sim\dot{U}_{6}^{n_{1},n_{2}}.$

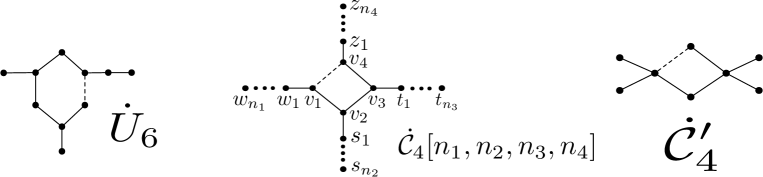
Case 4. $k=4.$ Then $\dot{\mathcal{C}}_{4}[n_{1},n_{2},n_{3},n_{4}]\subset\dot{G}$ . Let $n_{4}=min\{n_{1},n_{2},n_{3},n_{4}\}.$ If $d_{v_{1}}=4,$ then $n_{1}=1,$ $d_{v_{2}}=d_{v_{4}}=2$ (by forbidding $\dot{F}_{1}$ ) and at most one vertex of $\{t_{1},\dots,t_{n_{3}}\}$ has degree 3 (by forbidding $\dot{F}_{3}$ ). So, $\dot{G}\sim\dot{\mathcal{C}}_{4}^{\prime}$ if $d_{v_{3}}=4$ (where $\rho(\dot{\mathcal{C}}_{4}^{\prime})=2$ ) or $\dot{G}\subset\dot{\mathcal{A}}_{14}^{n_{1},n_{2}}$ if $d_{v_{3}}\leq 3$ . See Figs. 9 and 10. Next suppose that $d_{v_{i}}\leq 3$ for $i=1,2,3,4.$ If there is one vertex expect $v_{1},v_{2},v_{3},v_{4}$ having degree greater than 2, without loss of generality, assume that $d_{w_{i}}\geq 3$ ( $1\leq i\leq n_{1}-1).$ By forbidding $\dot{F}_{1}$ , $\dot{F}_{2}$ and $\dot{F}_{3}$ , then $d_{w_{i}}=3$ and at most one vertex of $V(\dot{G})\setminus\{v_{1},v_{3},w_{1},\dots,w_{n_{1}}\}$ has degree 3. If $n_{2}\geq 3,$ then $\rho_{1}(\dot{G})\geq\lambda_{1}(\dot{F}_{8})>\lambda^{\ast}$ (if $n_{1}\geq 6$ ), $\rho_{1}(\dot{G})\geq\lambda_{1}(\dot{F}_{5})>\lambda^{\ast}$ (if $n_{1}=5$ ) and $\rho_{1}(\dot{G})\geq\lambda_{1}(Q_{1,3,4})>\lambda^{\ast}$ (if $2\leq n_{1}\leq 4$ ), which is a contradiction. So $n_{2}\leq 2.$ Furthermore, if $n_{2}=2,$ then $n_{3}=0$ (by forbidding $\dot{F}_{2}$ ). Therefore, $\dot{G}\subset\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}}$ (if $n_{2}=0$ ), $\dot{G}\subset\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}}$ (if $n_{2}=1$ ) or $\dot{G}\subset\dot{\mathcal{A}}_{4}^{n_{1},n_{2}}$ (if $n_{2}=2$ ). If all vertices expect $v_{1},v_{2},v_{3},v_{4}$ have degree at most 2, then $\dot{G}$ is $\dot{\mathcal{C}}_{4}[n_{1},n_{2},n_{3},n_{4}].$ If $n_{i}\geq 2$ for $i=1,2,3$ , then $n_{1}=n_{2}=n_{3}=2$ by forbidding $T_{3,3,3}$ and $T_{2,3,4}$ . So $\dot{G}\subset\dot{\mathcal{C}}_{4}[2,2,2,2]$ . Otherwise, $n_{2}\leq 1$ or $n_{3}\leq 1.$ If $n_{2}\leq 1,$ then $\dot{G}\subset\dot{\mathcal{C}}_{4}[n_{1},1,n_{3},1].$ If $n_{3}\leq 1$ and $n_{2}\geq 2,$ by forbidding $\dot{F}_{4},$ $\dot{F}_{6},$ $\dot{F}_{7},$ $\dot{F}_{8}$ and $T_{2,3,4}$ , we have $\dot{G}\subset\dot{\mathcal{C}}_{4}[n_{1},n_{2},n_{3},n_{4}],$ where $(n_{1},n_{2},n_{3},n_{4})\in\{(2,2,2,2),(4,2,1,0),(2,3,1,0),(5,3,0,0),(n_{1},2,0,0)\}.$ ∎

It is known that there are three types of bicyclic graphs in term of their base graph as described next. A bicyclic graph is said to be a bicyclic base graph if contains no pendent vertices.

The type $\theta_{p,q,r}$ is the union of three internally disjoint paths $P_{p+2},$ $P_{q+2}$ , and $P_{r+2}$ which have the same two distinct end vertices, where $p\geq q\geq r\geq 0.$

The type $B_{r}^{a,b}$ consists of two vertex disjoint cycles $C_{a}$ and $C_{b}$ joined by a path $P_{r}$ having only its end vertices in common with the cycles, where $a\geq 3,$ $b\geq 3$ and $r\geq 2.$

The type $B^{a,b}_{0}$ is the union of two cycles $C_{a}$ and $C_{b}$ with precisely one vertex in common, where $a\geq 3$ and $b\geq 3.$

Lemma 3.8.

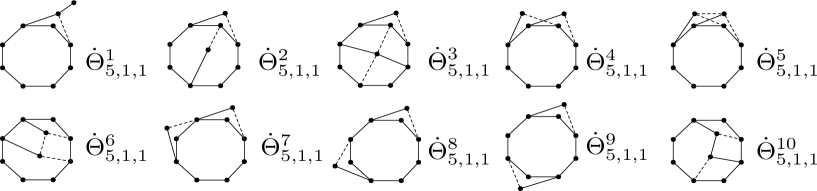
Let $\dot{G}\in\mathcal{G}_{S}^{\lambda^{\ast}}$ be a bicyclic signed base graph. Then $\dot{G}$ is switching equivalent to one of the $\dot{\mathcal{B}}_{0}^{4,4},$ $\dot{\mathcal{B}}^{4,4}_{r},$ $\dot{\Theta}_{3,3,1}$ , $\dot{\Theta}_{p,1,1}$ , $\dot{\Theta}_{2,2,0},$ $\dot{\Theta}_{4,2,0},$ $\dot{\Theta}_{6,2,0}$ or $\dot{\Theta}_{8,2,0}.$ See Fig. 11.

Proof.

For types $B_{0}^{a,b}$ and $B^{a,b}_{r}$ , by forbidding $\dot{C}_{\ell}^{1}$ , $\dot{\mathcal{C}}_{2\ell+1}^{1}$ , $\dot{F}_{1}$ and $\dot{F}_{2},$ then $\sigma(\dot{C}_{a})=\sigma(\dot{C}_{b})=-1$ and $a=b=4$ . So $\dot{G}\sim\dot{\mathcal{B}}_{0}^{4,4}$ or $\dot{G}\sim\dot{\mathcal{B}}^{4,4}_{r}.$ For type $\theta_{p,q,r},$ by forbidding $\dot{C}_{\ell}^{1}$ and $\dot{\mathcal{C}}_{2\ell+1}^{1}$ , then $\dot{G}\sim\dot{\Theta}_{p,q,1}$ (if $q>1$ , then $p$ and $q$ are odd) or $\dot{G}\sim\dot{\Theta}_{p,q,0}$ ( $p$ and $q$ are even).

Case 1. $\dot{G}\sim\dot{\Theta}_{p,q,1}$ . If $q\geq 3$ and $p\geq 5$ , then $Q_{2,2,2}\subset\dot{G}$ , which contradicts to Lemma 3.4. Therefore, $p=q=3$ or $q=1$ .

Case 2. $\dot{G}\sim\dot{\Theta}_{p,q,0}$ . If $q\geq 4$ (resp. $p\geq 10$ ), then $Q_{2,1,2}\subset\dot{G}$ (resp. $\dot{F}_{4}\subset\dot{G}$ ), which contradicts to Lemma 3.4. Therefore, $q=2$ and $p\in\{2,4,6,8\}.$

Hence, $\dot{G}\sim\dot{\Theta}_{3,3,1}$ , $\dot{\Theta}_{p,1,1}$ , $\dot{\Theta}_{2,2,0},$ $\dot{\Theta}_{4,2,0},$ $\dot{\Theta}_{6,2,0}$ or $\dot{\Theta}_{8,2,0}.$ ∎

Let $\dot{G}\in\mathcal{G}_{S}^{\lambda^{\ast}}$ be a signed graph with $m\geq n+1$ and $\dot{C}_{k}$ be a cycle in $\dot{G}.$ If each vertex outside of $\dot{C}_{k}$ is adjacent to at most one vertex of $\dot{C}_{k}$ , then $\dot{C}_{k}\subset$ $\dot{\mathcal{B}}_{r}^{4,4}$ or $\dot{C}_{k}\subset\dot{\mathcal{B}}^{4,4}_{0}$ (by Lemma 3.8). So $k=4$ . Therefore, if $k\geq 5,$ then there is a vertex outside of $\dot{C}_{k}$ adjacent to at least two vertices of $\dot{C}_{k}.$ Then we have

Lemma 3.9.

Let $\dot{G}=(G,\sigma)$ be a signed graph obtained by a cycle $\dot{C}_{k}$ and a vertex $u$ not in $\dot{C}_{k}$ such that $u$ is adjacent to at least two vertices of $\dot{C}_{k}$ . If $\rho(\dot{G})\leq\lambda^{\ast},$ then $\dot{G}$ is switching equivalent to one of the $\dot{\Theta}_{3,3,1},\dot{\Theta}_{k-3,1,1},\dot{\mathcal{X}}_{1}$ , $\dot{\mathcal{X}}_{2}$ or $\dot{\mathcal{X}}_{3}.$ See Figs. 11 and 12.

Proof.

If $d_{\dot{C}_{k}}(u)=2,$ then $\dot{G}$ is bicyclic. By Lemma 3.8, then $\dot{G}\sim\dot{\Theta}_{3,3,1}$ or $\dot{G}\sim\dot{\Theta}_{k-3,1,1}$ . Next assume that $3\leq d_{\dot{C}_{k}}(u)\leq 4,$ then the underlying graph $G$ of $\dot{G}$ is $G_{1}$ or $G_{2}.$ See Fig. 12. By forbidding $\dot{C}_{\ell}^{1}$ and $\dot{\mathcal{C}}_{2\ell+1}^{1},$ then the cycles $\mathcal{C}_{1},\mathcal{C}_{2},\mathcal{C}_{3},\mathcal{C}_{4}$ in $G_{1}$ and $G_{2}$ are even and unbalanced. If $\sigma(\dot{C}_{k})=+1$ and $d_{\dot{C}_{k}}(u)=3$ , or $\sigma(\dot{C}_{k})=-1$ and $d_{\dot{C}_{k}}(u)=4$ , then at least one of the cycles $\mathcal{C}_{1},\mathcal{C}_{2},\mathcal{C}_{3}$ and $\mathcal{C}_{4}$ is balanced, which is a contradiction. So, either $\sigma(\dot{C}_{k})=+1$ and $d_{\dot{C}_{k}}(u)=4$ , or $\sigma(\dot{C}_{k})=-1$ and $d_{\dot{C}_{k}}(u)=3.$ Then $\dot{G}\sim\dot{G}_{1}$ or $\dot{G}\sim\dot{G}_{2}.$ If $\dot{G}\sim\dot{G}_{1}$ , then $n_{1}=n_{2}=n_{3}=n_{4}=1$ (by forbidding $\dot{\mathcal{C}}_{2\ell+1}^{1}$ and $\dot{F}_{1}$ ). If $\dot{G}\sim\dot{G}_{2}$ , then $n_{i}\in\{1,3\}$ for $i=1,2,3$ and at most one of $n_{1},n_{2}$ and $n_{3}$ is equal to 3 (by forbidding $\dot{\mathcal{C}}_{2\ell+1}^{1}$ , $Q_{2,2,2}$ and $\dot{F}_{2}$ ). Hence, $\dot{G}\sim\dot{\mathcal{X}}_{i}$ for $i=1,2$ or 3. See Fig. 12. ∎

In the final of this section, we give an algorithm for searching the signed graph $\dot{G}$ with spectral radius $2<\rho(\dot{G})\leq\lambda^{\ast}.$

Algorithm 1:

Input: The adjacency matrix $A_{0}=A(\dot{G})=(a_{ij})_{n\times n}$ of a signed graph with order $n,$ and a positive integer number $k.$

Output: The set of the matrices $\mathcal{S}_{k}=\{A_{k}=A(\dot{G}_{k})=(a_{ij})_{(n+k)\times(n+k)}\mid 2<\rho(\dot{G}_{k})\leq\lambda^{\ast}\}.$

Step 1. For $A_{0},$ constructing a vector set $R_{1}=\{\textbf{r}_{1}=(r_{1},r_{2},\dots,r_{n})\mid r_{j}\in\{-1,0,1\},j=1,\dots,n\}$ . (Restrict that $\sum_{i=1}^{n}|r_{i}|\leq 4$ by Lemma 3.2).

(1.1) Traverse each vector $\textbf{r}_{1}$ of $R_{1}$ and construct a matrix $A_{1}=\begin{pmatrix}A_{0}&\textbf{r}_{1}^{T}\\ \textbf{r}_{1}&0\end{pmatrix},$

(1.2) $a_{1}$ $\leftarrow$ $max\{|\lambda_{i}(A_{1})|\mid i=1,n\}$ ,

(1.3) Traverse each matrix $A_{1},$ and add $A_{1}$ to the set $\mathcal{S}_{1}$ if the sum of each row of the matrix $|A_{1}|$ is less than or equal to 4 (by Lemma 3.2) and $a_{1}\leq\lambda^{\ast},$

Step 2. For each matrix $A_{1}$ of $\mathcal{S}_{1},$ constructing a vector set $R_{2}=\{\textbf{r}_{2}=(r_{1},r_{2},\dots,r_{n+1})\mid r_{j}\in\{-1,0,1\},j=1,\dots,n+1\}$ . (Restrict that $\sum_{i=1}^{n+1}|r_{i}|\leq 4$ by Lemma 3.2).

(2.1) Traverse each vector $\textbf{r}_{2}$ of $R_{2}$ and construct a matrix $A_{2}=\begin{pmatrix}A_{1}&\textbf{r}_{2}^{T}\\ \textbf{r}_{2}&0\end{pmatrix},$

(2.2) $a_{2}$ $\leftarrow$ $max\{|\lambda_{i}(A_{2})|\mid i=1,n\}$ ,

(2.3) Traverse each matrix $A_{2},$ and add $A_{2}$ to the set $\mathcal{S}_{2}$ if the sum of each row of the matrix $|A_{2}|$ is less than or equal to 4 (by Lemma 3.2) and $a_{2}\leq\lambda^{\ast},$

$\dots\dots$

Step k. For each matrix $A_{k-1}$ of $\mathcal{S}_{k-1},$ constructing a vector set $R_{k}=\{\textbf{r}_{k}=(r_{1},r_{2},\dots,$ $r_{n+k-1})\mid r_{j}\in\{-1,0,1\},j=1,\dots,n+k-1\}$ . (Restrict that $\sum_{i=1}^{n+k-1}|r_{i}|\leq 4$ by Lemma 3.2).

$(k.1)$ Traverse each vector $\textbf{r}_{k}$ of $R_{k}$ and construct a matrix $A_{k}=\begin{pmatrix}A_{k-1}&\textbf{r}_{k}^{T}\\ \textbf{r}_{k}&0\end{pmatrix},$

$(k.2)$ $a_{k}$ $\leftarrow$ $max\{|\lambda_{i}(A_{k})|\mid i=1,n\}$ ,

$(k.3)$ Traverse each matrix $A_{k},$ and add $A_{k}$ to the set $\mathcal{S}_{k}$ if the sum of each row of the matrix $|A_{k}|$ is less than or equal to 4 (by Lemma 3.2) and $2<a_{k}\leq\lambda^{\ast},$

$(k.4)$ Output the $\mathcal{S}_{k}.$

The whole algorithm is over.

Corollary 3.10.

Applying algorithm 1 to each signed graph of Theorem 2.4 $(ii)$ , we can check that all of them are maximal.

4 Signed graph whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$

In this section, we identify all signed graphs whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$ . By Lemma 3.7, we assume that $m\geq n+1.$ We break into four subsections.

4.1 $\dot{C}_{k}\subset\dot{G}$ where $k$ is odd or $k\geq 10$

Firstly we consider that $\dot{C}_{k}\subset\dot{G}$ where $k$ is odd or $k\geq 10$ .

Lemma 4.1.

Let $\dot{G}$ be one of the signed graphs $\dot{X}_{1},\dots,\dot{X}_{8}$ where $k$ is odd or $k\geq 10$ , see Fig. 13. Then $\rho(\dot{G})\leq\lambda^{\ast}$ if and only if $\dot{G}\sim\dot{X}_{3}$ and $k=10$ .

Proof.

If $\dot{G}\sim\dot{X}_{3}$ and $k=10$ , then $\dot{G}\subset\dot{G}_{10}.$ Note that $\dot{C}_{\ell}^{1}\subset\dot{X}_{1}$ ( $4\leq\ell<k$ ), $Q_{2,2,2}\subset\dot{X}_{2}$ or $\dot{\mathcal{C}}_{2\ell+1}^{1}\subset\dot{X}_{2}$ , $\dot{F_{9}}\subset\dot{X}_{3}$ ( $k\geq 12$ and $k$ is even), $\dot{\mathcal{C}}_{k}^{1}\subset\dot{X}_{3}$ ( $k$ is odd), $\dot{C}_{4}^{1}\subset\dot{X}_{4},$ $T_{2,3,4}\subset\dot{X}_{5}$ and $\dot{C}_{k}^{1}\subset\dot{X}_{j}$ for $j=6,7,8.$ By Lemma 3.4, then $\rho(\dot{X}_{i})>\lambda^{\ast}$ for $i=1,\dots,8$ expect the signed graph $\dot{X}_{3}$ where $k=10$ . ∎

Lemma 4.2.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a signed graph with $m\geq n+1$ . If $\dot{C}_{k}\subset\dot{G}$ where $k$ is odd or $k\geq 10$ , then $\dot{G}\subset\dot{\Theta}_{8,2,0},\dot{G}_{10}$ or $\dot{G}_{0}^{k}$ $(k\geq 12$ and $k$ is even $).$ See Figs. 5 and 6.

Proof.

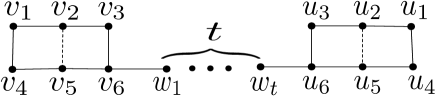
By Lemma 3.9, then $\dot{\Theta}_{8,2,0}\subset\dot{G}$ or $\dot{\Theta}_{k-3,1,1}\subset\dot{G}$ . By Corollary 3.10, we know that $\dot{\Theta}_{8,2,0}$ is maximal. Then we consider that $\dot{\Theta}_{k-3,1,1}\subset\dot{G}$ . Let $\dot{H}$ be the induced subgraph of $\dot{G}$ such that $\dot{\Theta}_{k-3,1,1}\subset\dot{H}$ and $\rho(\dot{H})\leq 2$ . Clearly, $\dot{H}\subset\dot{T}_{2k}$ . We use the vertex label of Fig. 1 and let $V(\dot{\Theta}_{k-3,1,1})=\{v_{1},\dots,v_{k},u_{1}\}$ . Let $w$ be a good vertex in $V(\dot{G})\setminus V(\dot{H})$ .

Claim 1. If $w\sim v_{i}$ for one $i$ , then $k=10$ and $\dot{H}_{U}(w)\sim\dot{X}_{3}$ .

Proof.

By Lemmas 3.4 and 3.9, then $w\mathop{\sim}\limits^{+}v_{i-1}$ and $w\mathop{\sim}\limits^{-}v_{i+1}$ for one $i$ (mod $k$ ). It is not hard to get that $i\neq 1$ and $u_{i}\not\in V(\dot{H})$ (otherwise $\dot{C}_{4}^{1}\subset\dot{G}$ and $\rho(\dot{G})\geq\rho(\dot{C}_{4}^{1})>\lambda^{\ast}$ ). Since $\dot{H}_{U}(w)$ is not an induced subgraph of $\dot{T}_{2k},$ then one of the followings happens:

$\bullet$ $w\sim u_{j}$ for one $j\neq i\pm 1,$ then $\dot{X}_{1}\subset\dot{G}$ or $\dot{X}_{2}\subset\dot{G};$

$\bullet$ $w\not\sim u_{j}$ for one $j\in\{i\pm 1\}$ , then $\dot{X}_{3}\subset\dot{G};$

$\bullet$ $w\mathop{\sim}\limits^{+}u_{j}$ for one $j\in\{i\pm 1\}$ , then $\dot{X}_{4}\subset\dot{G}.$

By Lemma 4.1, then $\rho(\dot{H}_{U}(w))\leq\lambda^{\ast}$ if and only if $k=10$ and $\dot{H}_{U}(w)\sim\dot{X}_{3}$ . ∎

Claim 2. If $w\not\sim v_{i}$ for all $i=1,\dots,k$ , then $w\sim u_{1}$ . Moreover, $\dot{H}_{U}(w)\sim\dot{G}_{0}^{k}$ .

Proof.

If $w\not\sim u_{1},$ then there is a path from the vertex $w$ to the vertex $u_{i}$ of $\dot{H}.$ And now $\dot{X}_{i}\subset\dot{G}$ for one $i\in\{5,6,7,8\}$ and $\rho(\dot{G})>\lambda^{\ast}$ (by Lemma 4.1), which is a contradiction. So $w\sim u_{1}.$ If $u_{i}\in V(\dot{H})$ for $i\neq 1,$ we also get that $\dot{X}_{i}\subset\dot{G}$ for one $i\in\{5,6,7,8\}$ , which is a contradiction. Hence, $\dot{H}_{U}(w)\sim\dot{G}_{0}^{k}$ . See Fig. 6. ∎

If $k=10$ , then $\dot{H}_{U}(w)\sim\dot{X}_{3}$ or $\dot{H}_{U}(w)\sim\dot{G}_{0}^{10}.$ Applying algorithm 1 to $A(\dot{H}_{U}(w))$ , we obtain that $\dot{G}\subset\dot{G}_{10}$ .

If $k$ is odd, or $k$ is even and $k\geq 12$ , then $\dot{H}_{U}(w)\sim\dot{G}_{0}^{k}$ . If $k$ is odd, then $\dot{\mathcal{C}}_{k}^{1}\subset\dot{G},$ which contradicts to Lemma 3.4. If $k$ is even and $k\geq 12$ , then $\dot{G}_{0}^{k}$ is maximal, otherwise there is another vertex $w^{\prime}$ in $V(\dot{G})\setminus V(\dot{H})$ , then $w^{\prime}\sim u_{1}$ (by Claims 1 and 2) and $\dot{F}_{1}\subset\dot{G}$ , which contradicts to Lemma 3.4. Hence, $\dot{G}\sim\dot{G}_{0}^{k}$ . ∎

Remark 4.3.

By Lemma 4.2, we next state that the signed graph $\dot{G}$ is bipartite.

4.2 $\dot{C}_{8}\subset\dot{G}$

Secondly we consider that $\dot{G}$ is $\dot{C}_{k}$ -free where $k\geq 10$ and $\dot{C}_{8}\subset\dot{G}$ . By Lemma 3.9, then $\dot{\Theta}_{5,1,1},\dot{\Theta}_{6,2,0},\dot{\Theta}_{3,3,1},\dot{\mathcal{X}}_{2}$ or $\dot{\mathcal{X}}_{3}$ is an induced subgraph of $\dot{G}.$ Let $\dot{H}$ be the induced subgraph of $\dot{G}$ such that $\dot{\Theta}_{5,1,1}\subset\dot{H}$ , $\dot{\Theta}_{3,3,1}\subset\dot{H},$ $\dot{\mathcal{X}}_{2}\subset\dot{H}$ or $\dot{\mathcal{X}}_{3}\subset\dot{H}$ and $\rho(\dot{H})=2.$

Lemma 4.4.

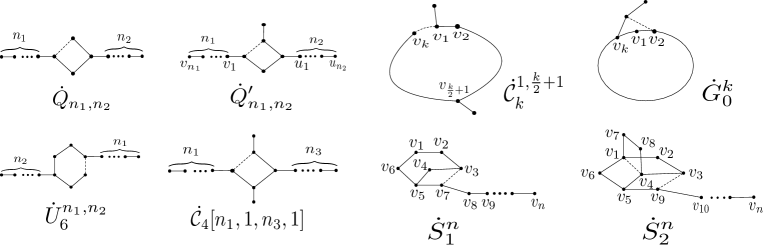
Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a $\dot{C}_{k}$ -free $(k\geq 10)$ bipartite signed graph with $m\geq n+1$ . If $\dot{C}_{8}\subset\dot{G}$ , then $\dot{G}\subset\dot{G}_{8}^{i}$ for $i=1,2,3.$ See Fig. 5.

Proof.

Applying algorithm 1 to $A(\dot{\Theta}_{6,2,0})$ , we obtain that $\dot{G}\subset\dot{G}_{8}^{1}$ or $\dot{G}\subset\dot{G}_{8}^{2}.$ We next suppose that $\dot{\Theta}_{5,1,1}\subset\dot{G},\dot{\Theta}_{3,3,1}\subset\dot{G},\dot{\mathcal{X}}_{2}\subset\dot{G}$ or $\dot{\mathcal{X}}_{3}\subset\dot{G}.$

If $\dot{\Theta}_{5,1,1}\subset\dot{G}$ , then $\dot{\Theta}_{5,1,1}\subset\dot{H}$ . So, $\dot{H}\subset\dot{S}_{16}$ or $\dot{H}\subset\dot{T}_{16}.$ Then $9\leq|V(\dot{H})|\leq 15.$ By Fig. 1, if $|V(\dot{H})|=9,$ then $\dot{H}$ is $\dot{\Theta}_{5,1,1}$ ; if $|V(\dot{H})|=10,$ then $\dot{H}\sim\dot{\Theta}_{5,1,1}^{i}$ for $i=1,\dots,10$ (see Fig. 14); if $|V(\dot{H})|=14$ or $15,$ then $\dot{H}$ is switching isomorphic to one of the signed graphs of Fig. 15. Moreover, if $11\leq|V(\dot{H})|\leq 13,$ then $\dot{H}$ contains one $\dot{\Theta}_{5,1,1}^{i}$ ( $i=1,\dots,10$ ) as an induced subgraph. Now applying algorithm 1 to $A(\dot{H})$ where $\dot{H}$ is $\dot{\Theta}_{5,1,1}$ or one of the signed graphs of Fig. 15, we get that there is no signed graph $\dot{G}$ with order $|V(\dot{H})|+1$ and $2<\rho(\dot{G})\leq\lambda^{\ast},$ and applying algorithm 1 to $A(\dot{\Theta}_{5,1,1}^{i})$ for $i=1,\dots,10$ , we get that $\dot{G}\subset\dot{G}_{8}^{3}$ . If $\dot{\Theta}_{3,3,1}\subset\dot{G}$ , $\dot{\mathcal{X}}_{2}\subset\dot{G}$ or $\dot{\mathcal{X}}_{3}\subset\dot{G}$ , we can similarly get that $\dot{G}\subset\dot{G}_{8}^{3}.$ ∎

4.3 $\dot{C}_{6}\subset\dot{G}$

Thirdly we consider that $\dot{G}$ is $\dot{C}_{k}$ -free where $k\geq 8$ and $\dot{C}_{6}\subset\dot{G}$ . By Lemma 3.9, then $\dot{\Theta}_{4,2,0}\subset\dot{G},\dot{\Theta}_{3,1,1}\subset\dot{G}$ or $\dot{\mathcal{X}}_{1}\subset\dot{G}$ . Let $\dot{H}$ be the induced subgraph of $\dot{G}$ such that $\dot{\Theta}_{4,2,0}\subset\dot{H},$ $\dot{\Theta}_{3,1,1}\subset\dot{H}$ or $\dot{\mathcal{X}}_{1}\subset\dot{H}$ and $\rho(\dot{H})\leq 2$ .

Lemma 4.5.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a $\dot{C}_{k}$ -free $(k\geq 8)$ bipartite signed graph with $m\geq n+1$ . If $\dot{C}_{6}\subset\dot{G}$ , then $\dot{G}\subset\dot{G}_{6}^{1},\dot{G}_{6}^{2},\dot{G}_{6}^{3},\dot{G}_{6}^{4},\dot{G}_{6}^{5},\dot{G}_{6}^{6},\dot{G}_{6}^{7},\dot{G}_{8}^{3},\dot{S}_{1}^{n}$ or $\dot{S}_{2}^{n}.$ See Figs. 5 and 6.

Proof.

If $\dot{\Theta}_{4,2,0}\subset\dot{H},$ then $\dot{H}\subset\dot{S}_{14}$ or $\dot{H}\subset\dot{S}_{16}$ . Since $\dot{G}$ is $\dot{C}_{k}$ -free $(k\geq 8),$ by Fig. 1, then $\dot{H}\subset\dot{\Theta}_{4,2,0}^{i}$ for $i=1,2,3,4.$ See Fig. 16. Applying algorithm 1 to $A(\dot{H})$ where $\dot{H}\subset\dot{\Theta}_{4,2,0}^{i}$ for $i=1,2,3,4$ , we get that $\dot{G}\subset\dot{G}^{3}_{8}$ or $\dot{G}\subset\dot{G}^{i}_{6}$ for $i=1,2,3,4,5,6$ .

If $\dot{\Theta}_{3,1,1}\subset\dot{H}$ , then $\dot{H}\subset\dot{S}_{14}$ or $\dot{H}\subset\dot{T}_{12}$ . So, $7\leq|V(\dot{H})|\leq 13.$ By Fig. 1, if $n=7,$ then $\dot{H}$ is $\dot{\Theta}_{3,1,1};$ if $|V(\dot{H})|=8$ , then $\dot{H}\sim\dot{\Theta}_{3,1,1}^{i}$ for $i=1,\dots,6$ ; if $|V(\dot{H})|=12$ or 13, then $\dot{H}\sim\dot{S}_{14}^{i}$ for $i=1,2,3,4$ . See Fig. 16. Moreover, if $9\leq|V(\dot{H})|\leq 11,$ then $\dot{H}$ contains one $\dot{\Theta}_{3,1,1}^{i}$ ( $i=1,\dots,6$ ) as an induced subgraph. Now applying algorithm 1 to $A(\dot{\Theta}_{3,1,1})$ and $A(\dot{S}_{14}^{i})$ for $i=1,2,3,4$ , then there is no signed graph $\dot{G}$ with order $|V(\dot{H})|+1$ and $2<\rho(\dot{G})\leq\lambda^{\ast},$ and applying algorithm 1 to $A(\dot{\Theta}_{3,1,1}^{i})$ for $i=1,\dots,6$ , we can get all signed graphs $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ (where $\dot{\Theta}_{3,1,1}^{i}\subset\dot{G}$ ) of order $n\leq 12,$ which are the induced subgraphs of $\dot{G}_{6}^{7}$ or $\dot{S}_{1}^{12}$ . Notice that $|V(\dot{G}_{6}^{7})|=11$ . See Figs. 5 and 6. If $n\geq 13,$ then $\dot{S}_{1}^{12}\subset\dot{G}$ . Set $V(\dot{G})\setminus V(\dot{S}_{1}^{12})=\{v_{13},\dots,v_{n}\}.$ Since $\dot{S}_{1}^{12}$ is the unique signed graph of order 12 such that $\dot{\Theta}_{3,1,1}\subset\dot{G}$ and $2<\rho(\dot{G})\leq\lambda^{\ast}$ , then $v_{j}\not\sim v_{i}$ for each $j\geq 13$ and all $i\leq 11.$ By forbidding $\dot{F}_{2}$ , then $d_{v_{i}}\leq 2$ for all $i\geq 12$ . Hence, $\dot{G}\sim\dot{S}_{1}^{n}$ and $\dot{S}_{1}^{n}$ is maximal.

If $\dot{\mathcal{X}}_{1}\subset\dot{H}$ , then $\dot{H}\subset\dot{S}_{14}$ or $\dot{H}\subset\dot{S}_{16}.$ From above discussions, we can suppose that $\dot{H}$ is $\{\dot{\Theta}_{4,2,0},\dot{\Theta}_{3,1,1}\}$ -free. By Fig. 1, then $\dot{H}\subset\dot{G}_{6}^{\prime}$ , $\dot{H}\subset\dot{G}_{6}^{\prime\prime}$ or $\dot{H}\subset\dot{S}_{2}^{11}$ . See Figs. 16 and 6. Similarly, applying algorithm 1 to $A(\dot{H})$ , then all signed graphs $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ of order $n\leq 14$ can be found, which are the induced subgraphs of $\dot{H}^{14}_{i}$ ( $i=1,2,3$ ) or $\dot{S}_{2}^{14}.$ See Figs. 17 and 6. If $n\geq 15,$ then $\dot{S}_{2}^{14}\subset\dot{G}$ or $\dot{H}^{14}_{i}\subset\dot{G}$ ( $i=1,2,3$ ).

Case 1. $\dot{S}_{2}^{14}\subset\dot{G}.$ Set $V(\dot{G})\setminus V(\dot{S}_{2}^{14})=\{v_{15},\dots,v_{n}\}.$ Since $\dot{H}^{14}_{1},\dot{H}^{14}_{2},\dot{H}^{14}_{3}$ and $\dot{S}_{2}^{14}$ are the only four signed graphs of order $n=14$ such that $\dot{\mathcal{X}}_{1}\subset\dot{G}$ and $2<\rho(\dot{G})\leq\lambda^{\ast}$ , then $v_{j}\not\sim v_{i}$ for each $j\geq 15$ and all $i\leq 9.$ By forbidding $\dot{F}_{2}$ , then $d_{v_{i}}\leq 2$ for all $i\geq 10$ . Hence, $\dot{G}\sim\dot{S}_{2}^{n}$ and $\dot{S}_{2}^{n}$ is maximal.

Case 2. $\dot{H}^{14}_{i}\subset\dot{G}$ for $i=1,2$ or $3$ . We will prove that $\dot{G}\subset\dot{S}_{2}^{n}.$ Set $V(\dot{G})\setminus V(\dot{H}^{14}_{3})=\{v_{15},\dots,v_{n}\}.$ If there is a vertex $v_{j}$ ( $j\geq 15$ ) adjacent to some vertices of $\{v_{1},\dots,v_{13}\},$ then $\dot{G}[\{v_{1},\dots,v_{13},v_{j}\}]\simeq\dot{S}_{2}^{14}$ and $\dot{S}_{2}^{14}\subset\dot{G}$ . By case 1, then $\dot{G}\subset\dot{S}_{2}^{n}$ . Otherwise, $v_{j}\not\sim v_{i}$ for each $j\geq 15$ and all $i\leq 13$ . By forbidding $\dot{F}_{2}$ , then $d_{v_{i}}\leq 2$ for all $i\geq 9$ . Hence, $\dot{G}\subset\dot{H}_{3}^{n}$ and $\dot{G}\subset\dot{S}_{2}^{n}.$ The proofs of the cases $\dot{H}^{14}_{1}\subset\dot{G}$ or $\dot{H}^{14}_{2}\subset\dot{G}$ are similar. ∎

4.4 $\dot{G}$ is $\dot{C}_{k}$ -free where $k=3$ or $k\geq 5$

In last subsection we shall consider that $\dot{G}$ is $\dot{C}_{k}$ -free where $k=3$ or $k\geq 5$ , i.e., $k\neq 4.$ For convenience, let $\dot{H}$ be the induced subgraph of $\dot{G}$ such that $\rho(\dot{H})\leq 2$ . Since $\dot{H}$ may not be unique, we choose one that the order of $\dot{H}$ is maximal.

4.4.1 $\dot{\Theta}_{2,2,0}\subset\dot{G}$

First of all, we focus on that the order of $\dot{G}$ is less than or equal to $14.$

Lemma 4.6.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a $\dot{C}_{k}$ -free (where $k=3$ or $k\geq 5$ ) bipartite signed graph of order $n\leq 14$ . If $\dot{\Theta}_{2,2,0}\subset\dot{G}$ , then $\dot{G}$ is the induced subgraph of $\dot{H}_{1},\dots,\dot{H}_{5},\dot{B}_{1},\dots,\dot{B}_{19}$ $($ up to switching equivalence $)$ . See Figs. 5 and 19.

Proof.

If $\dot{\Theta}_{2,2,0}\subset\dot{G}$ , then $\dot{\Theta}_{2,2,0}\subset\dot{H}$ . Obviously, $\dot{H}\subset\dot{S}_{14}$ or $\dot{H}\subset\dot{S}_{16}.$ By Fig. 1, then $\dot{H}\subset\dot{\mathcal{A}}_{i}$ for $i=1,\dots,10$ and $|V(\dot{H})|\leq 10.$ See Fig. 18. Applying algorithm 1 to $A(\dot{H}),$ then all signed graphs $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ of order $n\leq 14$ can be found, which are the induced subgraphs of $\dot{H}_{1},\dots,\dot{H}_{5},\dot{B}_{1},\dots,\dot{B}_{19}$ (up to switching equivalence). ∎

Remark 4.7.

$(1)$ By algorithm 1, we can check that the signed graphs $\dot{B}_{1},\dot{B}_{2},\dot{B}_{3}$ and $\dot{B}_{4}$ are maximal $\dot{C}_{k}$ -free (where $k=3$ or $k\geq 5$ ) signed graphs.

$(2)$ $\dot{B}_{1}\subset\dot{G}_{8}^{3},$ $\dot{B}_{2}\subset\dot{G}_{8}^{3}$ , $\dot{B}_{3}\subset\dot{G}_{6}^{6},$ $\dot{B}_{4}\subset\dot{G}_{10}$ , $\dot{B}_{i}\subset[\dot{G}^{12}_{4},v_{12},s]$ for $i=5,\dots,8$ and $\dot{B}_{i}\subset[\dot{G}_{2}^{9},v_{9},s]$ for $i=9,\dots,19$ .

$(3)$ If $n\geq 15,$ then $\dot{G}$ is $\{\dot{H}_{1},\dots,\dot{H}_{5},\dot{B}_{1},\dots,\dot{B}_{4}\}$ -free. Furthermore, let $V^{\prime}$ be the vertex subset of $V(\dot{G})\setminus V(\dot{\Theta}_{2,2,0})$ with order $8$ , then $\dot{G}[V(\dot{\Theta}_{2,2,0})\cup V^{\prime}]$ is disconnected or switching equivalent to $\dot{B}_{i}$ for one $i=5,\dots,19.$

Secondly, we consider that $n\geq 15$ . By Lemma 4.6, then $\dot{G}_{i}^{m_{i}}$ ( $i=1,2,3$ or $4$ ) is an induced subgraph of $\dot{G},$ where $m_{1}\geq 9,$ $m_{2}\geq 10,$ $m_{3}\geq 12$ and $m_{4}\geq 14.$ See Fig. 6. Without loss of generality, assume that the choice of $m_{i}$ is largest. Let

\begin{split}&V(\dot{G}_{1}^{m_{1}})=V_{1}\cup V_{2},~{}\text{where}~{}V_{1}=\{v_{1},\dots,v_{8}\}~{}\text{and}~{}V_{2}=\{v_{9},\dots,v_{m_{1}}\},\\ &V(\dot{G}_{2}^{m_{2}})=V_{1}\cup V_{2},~{}\text{where}~{}V_{1}=\{v_{1},\dots,v_{9}\}~{}\text{and}~{}V_{2}=\{v_{10},\dots,v_{m_{2}}\},\\ &V(\dot{G}_{3}^{m_{3}})=V_{1}\cup V_{2},~{}\text{where}~{}V_{1}=\{v_{1},\dots,v_{11}\}~{}\text{and}~{}V_{2}=\{v_{12},\dots,v_{m_{3}}\},\\ &V(\dot{G}_{4}^{m_{4}})=V_{1}\cup V_{2},~{}\text{where}~{}V_{1}=\{v_{1},\dots,v_{12}\}~{}\text{and}~{}V_{2}=\{v_{13},\dots,v_{m_{4}}\}.\end{split}

(4.1)

Lemma 4.8.

Let $x_{1}$ and $x_{2}$ be two vertices in $V(\dot{G})\setminus V(\dot{G}_{i}^{m_{i}})$ $(i=1,2,3$ or $4)$ . Then $d_{V_{1}}(x_{1})=0$ or $d_{V_{2}}(x_{1})=0.$ Furthermore, if $x_{1}\sim v_{i}$ and $x_{2}\sim v_{j}$ where $v_{i}\in V_{1}$ and $v_{j}\in V_{2},$ then $x_{1}\not\sim x_{2}$ .

Proof.

Suppose on the contrary that $d_{V_{1}}(x_{1})\geq 1$ and $d_{V_{2}}(x_{1})\geq 1.$ Then $x_{1}\sim v_{i}$ and $x_{1}\sim v_{j}$ where $v_{i}\in V_{1}$ and $v_{j}\in V_{2}.$ If $j\geq 15$ , then $\{v_{i},v_{i+1},\dots,v_{j},x_{1}\}$ induces a cycle $\dot{C}_{\ell}$ $(\ell\geq 5)$ , which is a contradiction. If $j\leq 14,$ then $\dot{G}$ contains a $\dot{C}_{\ell}$ $(\ell\geq 5)$ or $\dot{G}[\{v_{1},\dots,v_{13},x_{1}\}]$ is not switching equivalent to $\dot{B}_{i}$ for $i=5,\dots,19,$ which is a contradiction. So $d_{V_{1}}(x_{1})=0$ or $d_{V_{2}}(x_{1})=0.$ Furthermore, if $x_{1}\sim v_{i}$ and $x_{2}\sim v_{j}$ where $v_{i}\in V_{1}$ and $v_{j}\in V_{2},$ and if $x_{1}\sim x_{2}$ , then $\dot{G}[\{v_{1},\dots,v_{12},x_{1},x_{2}\}]$ contains a $\dot{C}_{\ell}$ $(\ell\geq 5)$ or is not switching equivalent to $\dot{B}_{i}$ for $i=5,\dots,19,$ which is a contradiction. So $x_{1}\not\sim x_{2}$ . ∎

Then we let

\begin{split}V(\dot{G})\setminus V(\dot{G}_{i}^{m_{i}})=U_{0}\cup U_{1}\cup U_{2},~{}\text{where $i=1,2,3$ or 4,}\end{split}

(4.2)

where each vertex in $U_{0}$ is adjacent to no vertex of $V(\dot{G}_{i}^{m_{i}}),$ each vertex in $U_{1}$ is adjacent to some vertices of $V_{1}$ and each vertex in $U_{2}$ is adjacent to some vertices of $V_{2}.$

Set $|U_{i}|=a_{i}$ for $i=0,1,2$ , then we have

Lemma 4.9.

$(1)$ If $U_{0}$ is nonempty, then $a_{0}=1$ and there is a vertex $w_{2}$ in $U_{2}$ such that $\dot{G}[V(\dot{G}_{i}^{m_{i}})\cup\{w_{2}\}\cup U_{0}]\sim\dot{\mathcal{A}}_{2i+5}^{n_{1},n_{2}}$ for $i=1,2,3,4$ . See Fig. 9.

$(2)$ If $\dot{G}_{i}^{m_{i}}\subset\dot{G}$ for $i=1,2$ , then $\dot{G}[V_{1}\cup U_{1}]\subset\dot{G}_{4}^{10}$ ; if $\dot{G}_{i}^{m_{i}}\subset\dot{G}$ for $i=3,4$ , then $\dot{G}[V_{1}\cup U_{1}]\subset\dot{G}_{4}^{12}.$

Proof.

(1) Let $w_{1}$ be a vertex in $U_{0}.$ Then there is a shortest path $P_{w_{1}v_{j}}=w_{1}\dots w_{\ell}v_{j}$ ( $\ell\geq 2$ ) from $w_{1}$ to a vertex $v_{j}\in V(\dot{G}_{i}^{m_{i}})$ . If $v_{j}\in V_{1},$ we can find a connected induced subgraph $\dot{G}^{\prime}$ of $\dot{G}$ with order $|V(\dot{G}^{\prime})|=14$ and is not switching equivalent to $\dot{B}_{i}$ for $i=5,\dots,19,$ which contradicts to Remark 4.7 (3). Then $v_{j}\in V_{2}.$ Since $\dot{G}$ is $\{\dot{F_{1}},\dot{F}_{2},\dot{G}_{i}^{m_{i}+1}\}$ -free, then $\ell=2$ and $d_{V_{2}}(w_{\ell})=2$ . Therefore, $\dot{G}[V(\dot{G}_{i}^{m_{i}})\cup\{w_{1},w_{2}\}]\sim\dot{\mathcal{A}}_{2i+5}^{n_{1},n_{2}}$ for $i=1,2,3,4.$ If $a_{0}\geq 2,$ then there is another vertex $w_{1}^{\prime}\neq w_{1}$ in $U_{0}$ and a vertex $w_{2}^{\prime}$ in $U_{2}$ such that $\dot{G}[V(\dot{G}_{i}^{m_{i}})\cup\{w_{1}^{\prime},w_{2}^{\prime}\}]\sim\dot{\mathcal{A}}_{2i+5}^{n_{1},n_{2}}$ . And now we can check that $\dot{F}_{1}\subset\dot{G},$ $\dot{F_{2}}\subset\dot{G}$ or $\dot{F}_{3}\subset\dot{G},$ which contradicts to Lemma 3.4. Hence, $a_{0}=1.$

(2) Choose $14-(|V_{1}|+a_{1})$ vertices (say vertex set $V_{1}^{\prime}$ ) from $V_{2}\cup U_{0}\cup U_{2}$ such that $\dot{G}[V_{1}\cup V_{1}^{\prime}]$ is connected. By Remark 4.7 (3), then $\dot{G}[V_{1}\cup V_{1}^{\prime}\cup U_{1}]\sim\dot{B}_{i}$ for one $i=5,\dots,19.$ It is not hard to see that if $\dot{G}_{i}^{m_{i}}\subset\dot{G}$ for $i=1,2$ , then $\dot{G}[V_{1}\cup U_{1}]\subset\dot{G}_{4}^{10}$ ; if $\dot{G}_{i}^{m_{i}}\subset\dot{G}$ for $i=3,4$ , then $\dot{G}[V_{1}\cup U_{1}]\subset\dot{G}_{4}^{12}.$ ∎

The next lemma deals with the case that $\dot{\varTheta}_{2,2,0}^{t}\subset\dot{G}$ . See Fig. 20. Note that $\dot{\mathcal{A}}_{6}^{3,t}\sim\dot{\varTheta}_{2,2,0}^{t}-u_{2}.$ By Lemma 3.5 (6), we have $t\geq 6.$ Then we let

V(\dot{G})\setminus V(\dot{\varTheta}_{2,2,0}^{t})=X_{0}\cup X_{1}\cup X_{2}\cup X_{3},

where each vertex in $X_{0}$ is adjacent to no vertices of $V(\dot{\varTheta}_{2,2,0}^{t}),$ each vertex in $X_{1}$ is adjacent to some vertices of $\{v_{1},\dots,v_{6},w_{1},w_{2}\}$ , each vertex in $X_{2}$ is adjacent to some vertices of $\{u_{1},\dots,u_{6},w_{t-1},w_{t}\}$ and each vertex in $X_{3}$ is adjacent to some vertices of $\{w_{3},\dots,w_{t-2}\}.$ By Lemma 4.8, then $X_{1}\cap X_{2}=\emptyset$ , $X_{1}\cap X_{3}=\emptyset$ , $X_{2}\cap X_{3}=\emptyset$ and there is no edge between three parts $X_{1}$ , $X_{2}$ and $X_{3}.$ If $X_{0}\neq\emptyset,$ let $u_{0}\in X_{0},$ Lemma 4.9 (1) implies that there is a path $P_{u_{0}z_{i}}=u_{0}u_{1}w_{i}$ (where $u_{1}\in X_{3}$ ) from the vertex $u_{0}$ to the vertex $w_{i}$ . Then $\dot{F}_{3}\subset\dot{G},$ which contradicts to Lemma 3.4. So $X_{0}=\emptyset.$

Lemma 4.10.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a $\dot{C}_{k}$ -free $(k\neq 4)$ bipartite signed graph of order $n\geq 15$ . If $\dot{\varTheta}_{2,2,0}^{t}\subset\dot{G}$ , then $\dot{G}$ is the induced subgraph of $\dot{H}_{6}$ , $\dot{H}_{7}$ , $\dot{H}_{8}$ , $[\dot{G}_{2}^{9},v_{9},s,v_{9},\dot{G}_{2}^{9}]$ , $[\dot{G}_{4}^{12},v_{12},s,v_{9},\dot{G}_{2}^{9}]$ or $[\dot{G}_{4}^{12},v_{12},s,v_{12},\dot{G}_{4}^{12}].$ See Figs. 5 and 7.

Proof.

By Lemma 4.9 (2), then $\dot{G}[V(\dot{\varTheta}_{2,2,0}^{t})\cup X_{1}\cup X_{2}]\sim(\dot{G}_{i}^{m_{i}},v_{m_{i}},s_{1},v_{m_{j}},\dot{G}_{j}^{m_{j}})$ , where $(\dot{G}_{i}^{m_{i}},v_{m_{i}}),$ $(\dot{G}_{j}^{m_{j}},v_{m_{j}})\in\{(\dot{G}_{1}^{8},v_{8}),(\dot{G}_{2}^{9},v_{9}),(\dot{G}_{3}^{11},v_{11}),$ $(\dot{G}_{4}^{12},v_{12})\}$ , $s_{1}\geq 3$ if $i=4$ or $j=4$ (by forbidding $\dot{F}_{10}$ and $\dot{F}_{11}$ ) and $s_{1}\geq 2$ otherwise (by Lemma 3.5 (6) and (8)).

Let $X_{3}=\{x_{i_{1}},\dots,x_{i_{\ell}}\}$ , then $d_{\dot{\varTheta}_{2,2,0}^{t}}(x_{i_{j}})=2$ (by forbidding $\dot{F}_{3}$ ). Up to switching equivalence, let $x_{j}\mathop{\sim}\limits^{+}w_{j}$ and $x_{j}\mathop{\sim}\limits^{-}w_{j+2}$ for $j=i_{1},\dots,i_{\ell},$ where $j\geq 3$ and $j+2\leq t-2$ . Since $\dot{G}$ is $\{\dot{F}_{3},\dot{C}_{k},\dot{C}^{1}_{4}\}$ -free ( $k\neq 4$ ), then $i_{j_{1}}\neq i_{j_{2}}$ if $j_{1}\neq j_{2}$ , $x_{i_{j_{1}}}\mathop{\sim}\limits^{-}x_{i_{j_{2}}}$ if $|i_{j_{1}}-i_{j_{2}}|=1$ and $x_{i_{j_{1}}}\not\sim x_{i_{j_{2}}}$ if $|i_{j_{1}}-i_{j_{2}}|\geq 2$ . So, $\dot{G}[V(\dot{\varTheta}_{2,2,0}^{t})\cup X_{3}]\subset[\dot{G}_{1}^{8},v_{8},s_{2},v_{8},\dot{G}_{1}^{8}]$ ( $s_{2}\geq 3$ ).

If $s_{1}=2,$ then $\dot{G}\subset\dot{H}_{i}$ for $i=6,7,8$ . If $s_{1}\geq 3,$ then $\dot{G}\subset[\dot{G}_{i}^{m_{i}},v_{m_{i}},s,v_{m_{j}},\dot{G}_{j}^{m_{j}}]$ ( $s\geq 3$ ), where $i,j\in\{1,2,3,4\}.$ By Lemma 3.5 (6), (8) and (10), then $m_{i},m_{j}\geq 8$ if $i,j=1;$ $m_{i},m_{j}\geq 9$ if $i,j=2;$ $m_{i},m_{j}\geq 11$ if $i,j=3;$ $m_{i},m_{j}\geq 12$ if $i,j=4.$ Hence, $\dot{G}$ is the induced subgraph of $[\dot{G}_{2}^{9},v_{9},s,v_{9},\dot{G}_{2}^{9}]$ , $[\dot{G}_{4}^{12},v_{12},s,v_{9},\dot{G}_{2}^{9}]$ or $[\dot{G}_{4}^{12},v_{12},s,v_{12},\dot{G}_{4}^{12}]$ . ∎

Next we assume that $\dot{G}$ is $\dot{\varTheta}_{2,2,0}^{t}$ -free.

Lemma 4.11.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a $\{\dot{C}_{k},\dot{\varTheta}_{2,2,0}^{t}\}$ -free $(k\neq 4)$ bipartite signed graph of order $n\geq 15$ . If $\dot{\Theta}_{2,2,0}\subset\dot{G}$ , then $\dot{G}$ is the induced subgraph of $\dot{\mathcal{A}}_{i}^{n_{1},n_{2}}$ $(i=8,9,10,11,12,13)$ , $\dot{\mathcal{A}}_{i}^{n_{1}}$ $(i=16,17,18,19)$ or $[\dot{G},v,s,u,\dot{H}]$ , where $(\dot{G},v)\in\{(\dot{G}_{4}^{12},v_{12}),$ $(\dot{G}_{2}^{9},v_{9})\}$ and $(\dot{H},u)\in\{(T_{a,1,a-1},v_{a-1}),$ $(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}}),(\dot{G}_{5}^{10},v_{10}),(P_{4},v_{2})\}$ , $s\geq 3$ , $a\geq 3$ and $n_{1}\geq 1.$

Proof.

Recall that $\dot{G}_{i}^{m_{i}}$ ( $i=1,2,3$ or $4$ ) is an induced subgraph of $\dot{G}.$ Here, we only consider that $\dot{G}_{4}^{m_{4}}\subset\dot{G}.$ The proofs of the cases $\dot{G}_{i}^{m_{i}}\subset\dot{G}$ for $i=1,2,3$ are similar. We use the vertex partitions of Eqs. (4.1) and (4.2). By Lemma 4.9 (2), then $U_{1}=\emptyset.$ Since $\dot{G}$ is $\dot{\varTheta}_{2,2,0}^{t}$ -free, then each vertex in $U_{2}$ is adjacent to at most two vertices of $V_{2}.$ Then let $U_{2}=U_{21}\cup U_{22},$ where each vertex in $U_{2i}$ ( $i=1$ or 2) is adjacent to $i$ vertices of $V_{2}.$ Furthermore, set $U_{21}=\{u_{j_{1}},\dots,u_{j_{p}}\}$ ( $13\leq{j_{1}}\leq\dots\leq{j_{p}}\leq m_{4}-1$ ) where $u_{j}\mathop{\sim}\limits^{+}v_{j}$ for $j=j_{1},\dots,j_{p}$ , and $U_{22}=\{u^{\prime}_{i_{1}},\dots,u^{\prime}_{i_{q}}\}$ ( $13\leq{i_{1}}\leq\dots\leq{i_{q}}\leq m_{4}-2)$ where $u^{\prime}_{i}\mathop{\sim}\limits^{+}v_{i}$ and $u^{\prime}_{i}\mathop{\sim}\limits^{-}v_{i+2}$ for $i=i_{1},\dots,i_{q}.$ Since $\dot{G}$ is $\{\dot{\varTheta}_{2,2,0}^{t},\dot{F}_{3},\dot{C}_{k},\dot{C}_{4}^{1},\dot{G}_{4}^{m_{4}+1}\}$ -free ( $k\neq 4$ ), we have

$(\textbf{A1})$ $\dot{G}[U_{21}]$ is $K_{1}$ or $K_{2}^{-}$ . If $\dot{G}[U_{21}]$ is $K_{2}^{-}$ , then $1\leq m_{4}-j_{2}\leq 2$ (by forbidding $\dot{F}_{8}$ ),

$(\textbf{A2})$ $i_{j_{1}}\neq i_{j_{2}}$ if $j_{1}\neq j_{2}$ , $u^{\prime}_{i_{j_{1}}}\mathop{\sim}\limits^{-}u^{\prime}_{i_{j_{2}}}$ if $|i_{j_{1}}-i_{j_{2}}|=1$ and $u^{\prime}_{i_{j_{1}}}\not\sim u^{\prime}_{i_{j_{2}}}$ if $|i_{j_{1}}-i_{j_{2}}|\geq 2$ .

Then $\dot{G}[V(\dot{G}_{4}^{m_{4}})\cup U_{21}]\sim\dot{\mathcal{A}}_{12}^{n_{1},n_{2}}$ , $\dot{\mathcal{A}}_{13}^{0,n_{2}}$ or $\dot{\mathcal{A}}_{19}^{n_{1}}$ and $\dot{G}[V(\dot{G}_{4}^{m_{4}})\cup U_{22}]\subset[\dot{G}_{4}^{12},v_{12},s]$ .

Case 1. $U_{0}$ is empty. If $U_{21}$ or $U_{22}$ is empty, then we are done. If $U_{21}$ and $U_{22}$ are not empty, according to (A1), we break into two subcases:

Subcase 1.1. $\dot{G}[U_{21}]=K_{1}$ . Then $U_{21}=\{u_{j_{1}}\}$ , $i_{q}\leq j_{1}-1$ and $i_{q}\neq j_{1}-2$ (otherwise $\dot{F_{1}}\subset\dot{G}$ or $\dot{F_{3}}\subset\dot{G}$ , which contradicts to Lemma 3.4).

Subsubcase 1.1.1. $i_{q}=j_{1}-3.$ By $(\textbf{A2})$ , then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s_{1},v_{2},P_{\ell}].$ By forbidding $Q_{1,1,3},$ then $\ell\leq 4.$ So, $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{2},P_{4}]$ .

Subsubcase 1.1.2. $i_{q}\leq j_{1}-4.$ By $(\textbf{A2})$ , then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s_{1},v_{c},T_{c,1,a}].$ If $a=1$ or 2, then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{2},P_{4}]$ . If $a\geq 3$ , by forbidding $Q_{1,c+1,a}$ (where $c\leq a-2$ ), then $c\geq a-1$ . So, $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{a-1},T_{a-1,1,a}]$ .

Subsubcase 1.1.3. $i_{q}=j_{1}-1.$ Then $u^{\prime}_{i_{q}}\mathop{\sim}\limits^{+}v_{j_{1}-1}$ and $u^{\prime}_{i_{q}}\mathop{\sim}\limits^{-}v_{j_{1}+1}.$ If $u^{\prime}_{i_{q}}\sim u_{j_{1}},$ then $u^{\prime}_{i_{q}}\mathop{\sim}\limits^{-}u_{j_{1}}$ and $j_{1}=m_{4}-1$ (by forbidding $\dot{C}_{4}^{1}$ ). By $(\textbf{A2})$ , then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s].$ If $u^{\prime}_{i_{q}}\not\sim u_{j_{1}},$ by forbidding $\dot{C}_{4}^{1}$ and $\dot{F}_{1}$ , then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s_{1},v_{n_{2}},\dot{Q}^{\prime}_{n_{1},n_{2}}]$ . By Lemma 3.5 (2), then $n_{2}\geq 1$ if $n_{1}=0$ and $n_{2}\geq n_{1}$ if $n_{1}\geq 1$ . So, $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{n_{1}},\dot{Q}^{\prime}_{n_{1},n_{1}}]$ $(n_{1}\geq 1)$ .

Subcase 1.2. $\dot{G}[U_{21}]=K_{2}^{-}$ . Then $U_{21}=\{u_{j_{1}},u_{j_{2}}\},$ $j_{2}=j_{1}+1$ and $u_{j_{1}}\mathop{\sim}\limits^{-}u_{j_{2}}.$ Since $\dot{G}$ is $\{\dot{\varTheta}_{2,2,0}^{t},\dot{F}_{1}\}$ -free, then $i_{q}\leq j_{1}-3.$ If $j_{2}=m_{4}-1,$ then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{n_{2}},\dot{Q}^{\prime}_{0,n_{2}}]$ , which has been done in subsubcase 1.1.3. If $j_{2}=m_{4}-2,$ then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{n_{1}},\dot{G}_{5}^{n_{1}}].$ By Lemma 3.5 (4), then $n_{1}\geq 10$ . So, $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{10},\dot{G}_{5}^{10}]$ $(s\geq 3)$ .

Case 2. $U_{0}$ is nonempty. Then $|U_{21}|=0$ as $\dot{G}$ is $\{\dot{F}_{1},\dot{F}_{3}\}$ -free. Similarly, by (A2) and forbidding $\dot{\varTheta}_{2,2,0}^{t},\dot{F}_{1},\dot{C}_{4}^{1}$ , then $\dot{G}\subset[\dot{G}_{4}^{12},v_{12},s,v_{n_{2}},\dot{Q}^{\prime}_{n_{1},n_{2}}],$ which has been done in subsubcase 1.1.3.

This completes the proof. ∎

4.4.2 $\dot{G}$ is $\dot{\Theta}_{2,2,0}$ -free

Lastly it remains that $\dot{G}$ is $\dot{\Theta}_{2,2,0}$ -free. First we suppose that $\dot{H}\subset\dot{T}_{2k}.$ Notice that if $\dot{H}\subset\dot{T}_{2k}^{\prime},$ then $\dot{H}\subset\dot{T}_{2n}^{\prime}$ for all $n\geq k.$ Without loss of generality, we assume that $\dot{H}\subset\dot{T}_{2t}^{\prime}$ , where $t$ is maximal. Up to switching isomorphic, let $V(\dot{H})=V_{1}\cup U_{1}$ where $V_{1}=\{v_{1},v_{2},\dots,v_{t}\}$ and $U_{1}=\{u_{k_{1}},\dots,u_{k_{\ell}}\}$ ( $1\leq k_{1}<\dots<k_{\ell}\leq t$ ). Let $w$ be a good vertex in $V(\dot{G})\setminus V(\dot{H}).$ If $t=3$ or 4, applying algorithm 1 to $A(\dot{H})$ , then there is no signed graph $\dot{G}$ with order $|V(\dot{H})|+1$ and $2<\rho(\dot{G})\leq\lambda^{\ast}.$ Next we let $t\geq 5.$

Before giving the main result of this subsubsection, we need some preliminary lemmas.

Lemma 4.12.

$d_{V_{1}}(w)\leq 1$ and $d_{U_{1}}(w)\leq 1$ .

Proof.

Since $\dot{G}$ is $\{\dot{\Theta}_{2,2,0},\dot{C}_{4}^{1}\}$ -free, then $d_{V_{1}}(w)\leq 2.$ If $d_{V_{1}}(w)=2$ , then $w\mathop{\sim}\limits^{+}v_{i-1}$ and $w\mathop{\sim}\limits^{-}v_{i+1}$ (switching at $w$ if necessary). Since $\dot{G}$ is $\{\dot{C}_{4}^{1},\dot{\Theta}_{2,2,0},\dot{C_{k}}\}$ -free $(k\neq 4)$ , then $u_{i}\not\in U_{1}$ , $w\not\sim u_{j}$ for all $j\neq i\pm 1$ and $w\mathop{\sim}\limits^{-}u_{i\pm 1}$ if $u_{i\pm 1}\in U_{1}$ . So $\dot{H}_{U}(w)\simeq\dot{G}[V(\dot{H})\cup\{u_{i}\}]$ and $\dot{H}_{U}(w)\subset\dot{T}_{2t}^{\prime}$ , which is a contradiction. Hence, $d_{V_{1}}(w)\leq 1.$ Similarly, we have $d_{U_{1}}(w)\leq 1.$ ∎

Then we let

V(\dot{G})\setminus V(\dot{H})=V_{0}\cup V_{1}^{\prime}\cup U_{1}^{\prime}\cup Y,

where each vertex in $V_{0}$ is adjacent to no vertex of $V_{1}\cup U_{1}$ , each vertex in $V_{1}^{\prime}$ is adjacent to exactly one vertex of $V_{1}$ and no vertex of $U_{1}$ , each vertex in $U_{1}^{\prime}$ is adjacent to exactly one vertex of $U_{1}$ and no vertex of $V_{1}$ , each vertex in $Y$ is adjacent to exactly one vertex of $V_{1}$ and exactly one vertex of $U_{1}$ .

Lemma 4.13.

If $w\in Y,$ then

$(i)$ $w\mathop{\sim}\limits^{+}v_{t-2}$ , $w\mathop{\sim}\limits^{-}u_{t}$ and $u_{i}\not\in U_{1}$ for $i=t-1,t-2,t-3,t-4,$ or

$(ii)$ $w\mathop{\sim}\limits^{+}v_{3}$ , $w\mathop{\sim}\limits^{+}u_{1}$ and $u_{i}\not\in U_{1}$ for $i=2,3,4,5$ .

Proof.

Let $w\sim v_{i}$ and $w\sim u_{j}.$ Since $\dot{G}$ is $\dot{C}_{k}$ -free $(k\neq 4),$ then $j=i$ or $j=i\pm 2.$ If $i=j,$ then $w\mathop{\sim}\limits^{+}v_{i}$ and $w\mathop{\sim}\limits^{-}u_{i}$ (switching at $w$ if necessary). By forbidding $\dot{C}_{4}^{1}$ , then $i=t-1$ . If $u_{t}\not\in U_{1}$ (resp. $u_{t}\in U_{1}$ ), then $\dot{H}_{U}(w)\subset\dot{T}_{2t}^{\prime}$ (resp. $\dot{G}[\{v_{t-1},v_{t},u_{t-1},u_{t},w\}]\sim\theta_{1,1,1}$ ), which is a contradiction. So $j=i\pm 2.$ If $j=i+2$ , since $\dot{G}$ is $\{\dot{C}_{4}^{1},\dot{\Theta}_{2,2,0},\dot{F}_{1}\}$ -free, then $t=i+2$ , $w\mathop{\sim}\limits^{+}v_{t-2}$ , $w\mathop{\sim}\limits^{-}u_{t}$ and $u_{i}\not\in U_{1}$ for $i=t-1,t-2,t-3.$ If $u_{t-4}\in U_{1},$ then $\dot{G}[v_{t},v_{t-1},v_{t-2},v_{t-3},v_{t-4},u_{t},u_{t-4},w]\sim\dot{\mathcal{A}}_{2}^{0,1,0}.$ By Lemma 3.5 (2), then $\rho(\dot{G})\geq\rho(\dot{\mathcal{A}}_{2}^{0,1,0})>\lambda^{\ast},$ which is a contradiction. So $u_{t-4}\not\in U_{1}.$ If $j=i-2,$ because of symmetry, then $i=3$ , $w\mathop{\sim}\limits^{+}v_{3}$ , $w\mathop{\sim}\limits^{+}u_{1}$ and $u_{i}\not\in U_{1}$ for $i=2,3,4,5$ . ∎

Lemma 4.14.

$V_{0}$ is empty.

Proof.

For a contradiction, assume that $w\in V_{0}$ . Then there is a shortest path $P_{wx_{i+1}}=ww_{1}\dots w_{\ell}x_{i+1}$ ( $\ell\geq 1$ ) from $w$ to $x_{i+1}\in V(\dot{H})$ where $x=v$ or $u$ . Since $t$ is maximal, then $\ell+1\leq i$ and $\ell+1\leq t-(i+1)$ . By forbidding $T_{2,3,4}$ , then $\ell=1,$ $i=2$ and $t\geq 5;$ or $\ell=1,$ $i=t-3$ and $t\geq 5;$ or $\ell=1,$ $i=3$ and $t=7.$ By forbidding $\dot{F}_{1}$ and $\dot{F_{2}}$ , if $x=v,$ then $V_{0}=\{w\},$ $U_{1}=\emptyset$ or $U_{1}=\{u_{i+1}\},$ $V_{1}^{\prime}=\{w_{1}\},$ $Y=\emptyset$ and $|U_{1}^{\prime}|\leq 1;$ if $x=u,$ then $V_{0}=\{w\},$ $U_{1}=\{u_{i+1}\},$ $U_{1}^{\prime}=\{w_{1}\},$ $Y=\emptyset$ and $|V_{1}^{\prime}|\leq 1$ . Therefore, $\dot{G}$ is a tree or unicyclic, which has been done in Theorem 2.1 and Lemma 3.7. Hence, $V_{0}$ is empty. ∎

Lemma 4.15.

If $w\in V_{1}^{\prime}$ , then

$(i)$ if $w\sim v_{2}$ , then $u_{2}\in U_{1}$ and $u_{i}\not\in U_{1}$ for $i=1,3,4,5,$

$(ii)$ if $w\sim v_{t-1}$ , then $u_{t-1}\in U_{1}$ and $u_{i}\not\in U_{1}$ for $i=t,t-2,t-3,t-4,$

$(ii)$ if $w\sim v_{i}$ $(3\leq i\leq t-2),$ then $u_{i\pm 1}\not\in U_{1}$ and one of the following holds: $(1)$ $k_{1}=i$ and $k_{2}\geq i+2;$ $(2)$ $k_{1}\geq i+2;$ $(3)$ $k_{\ell}=i$ and $k_{\ell-1}\leq i-2;$ $(4)$ $k_{\ell}\leq i-2.$

Proof.

$(i)$ By forbidding $\dot{F}_{1}$ , then $u_{1}\not\in U_{1}$ . Since $\dot{H}_{U}(w)$ is not an induced subgraph of $\dot{T}^{\prime}_{2t},$ then $u_{2}\in U_{1}.$ By forbidding $\dot{F}_{1}$ and $\dot{C}_{4}^{1},$ then $u_{4}\not\in U_{1}$ and $u_{3}\not\in U_{1}$ . If $u_{5}\in U_{1},$ then $\dot{G}[v_{1},v_{2},v_{3},v_{4},v_{5},u_{2},u_{5},w]\sim\dot{\mathcal{A}}_{2}^{0,1,0}.$ By Lemma 3.5 (2), then $\rho(\dot{G})\geq\rho(\dot{\mathcal{A}}_{2}^{0,1,0})>\lambda^{\ast},$ which is a contradiction. Hence, $u_{5}\not\in U_{1}.$

$(ii)$ The proof is similar to ( $i$ ).

$(iii)$ By forbidding $\dot{F}_{1}$ , then $u_{i\pm 1}\not\in U_{1}$ . By forbidding $\dot{F}_{3}$ , it is impossible that $k_{j_{1}}\leq i-2$ and $k_{j_{2}}\geq i+2$ for $1\leq j_{1}<j_{2}\leq\ell$ . So, $k_{1}\geq i$ or $k_{\ell}\leq i.$ If $k_{1}=i,$ then $k_{2}\geq i+2$ . Otherwise, $k_{1}\geq i+2.$ If $k_{\ell}=i,$ then $k_{\ell-1}\leq i-2$ . Otherwise, $k_{\ell}\leq i-2.$ ∎

Now we are going to give the main result of this subsubsection. Set $V_{1}^{\prime}=\{v^{\prime}_{i_{1}},\dots,v^{\prime}_{i_{p}}\}$ where $v^{\prime}_{i}\mathop{\sim}\limits^{+}v_{i}$ for each $i=i_{1},\dots,i_{p}$ , and $U_{1}^{\prime}=\{u^{\prime}_{j_{1}},\dots,u^{\prime}_{j_{q}}\}$ where $u^{\prime}_{j}\mathop{\sim}\limits^{+}u_{j}$ for each $j=j_{1},\dots,j_{q}.$ If $i_{s_{1}}=j_{s_{2}}$ for one $1\leq s_{1}\leq p$ and one $1\leq s_{2}\leq q,$ by forbidding $\dot{F}_{1}$ , $\dot{F}_{2}$ and $\dot{C}_{4}^{1},$ we have $|U_{1}|=|V_{1}^{\prime}|=|U_{1}^{\prime}|=1$ and $|Y|=0.$ So, $\dot{G}\sim\dot{\mathcal{C}}_{4}[n_{1},1,t-n_{1},1]$ (see Lemma 3.7). Otherwise, $i_{s_{1}}\neq j_{s_{2}}$ for all $s_{1}=1,\dots,p$ and all $s_{2}=1,\dots,q.$ Then there is a switching isomorphic of $\dot{G}$ such that $u^{\prime}_{j}\not\sim u_{j}$ and $u^{\prime}_{j}\mathop{\sim}\limits^{+}v_{j}$ for all $j=j_{1},\dots,j_{q},$ that is, $U_{1}^{\prime}$ becomes empty and $V_{1}^{\prime}=\{v^{\prime}_{i_{1}},\dots,v^{\prime}_{i_{p}},u^{\prime}_{j_{1}},\dots,u^{\prime}_{j_{q}}\}.$

Lemma 4.16.

Let $\dot{G}\in\overline{\mathcal{G}}_{S}^{\lambda^{\ast}}$ be a $\{\dot{C}_{k},\dot{\Theta}_{2,2,0}\}$ -free $(k\neq 4)$ bipartite signed graph with $m\geq n+1$ . Then $\dot{G}$ is an induced subgraph of $\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{3}},$ $\dot{\mathcal{A}}_{5}^{n_{1},n_{2}}$ or $[\dot{G},v,s,u,\dot{H}]$ , where $(\dot{G},v),(\dot{H},u)\in\{(P_{4},v_{2}),(T_{a,1,a-1},v_{a-1}),$ $(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}}),(\dot{G}_{5}^{10},v_{10})\}$ , $s\geq 3,$ $a\geq 3$ and $n_{1}\geq 1.$

Proof.

Since $\dot{G}$ is $\{\dot{\Theta}_{2,2,0},\dot{C}_{k}\}$ -free $(k\neq 4),$ then $\dot{G}[V_{1}^{\prime}]=t_{1}K_{2}^{-}\cup t_{2}K_{1}$ , where $t_{1}+t_{2}\leq 2$ (by forbidding $\dot{F}_{3}$ ). By Lemma 4.13, we break into three cases.

Case 1. $|Y|=0.$

Subcase 1.1. $\dot{G}[V_{1}^{\prime}]=K_{1}.$ Then $V_{1}^{\prime}=\{v^{\prime}_{i_{1}}\}.$ Since $t$ is maximal, then $2\leq i_{1}\leq t-1$ . Recall that $|V(\dot{H})|$ is maximal. By Lemma 4.15, then we have

Subsubcase 1.1.1. $i_{1}=2$ or $i_{1}=t-1.$ Then $\dot{G}\subset[\dot{Q}^{\prime}_{1,0},v_{1},s]\subset[\dot{Q}^{\prime}_{1,1},v_{1},s]$ .

Subsubcase 1.1.2. $3\leq i_{1}\leq t-2.$ If $k_{1}=i_{1}$ or $k_{\ell}=i_{1},$ then $\dot{G}\subset[\dot{Q}^{\prime}_{n_{1},n_{2}},v_{n_{2}},s]$ ( $n_{1}\geq 1$ ), where $n_{2}=n_{1}$ (by Lemma 3.5 (2)). If $k_{1}=i_{1}+2$ or $k_{\ell}=i_{1}-2,$ then $\dot{G}\subset[P_{\ell},v_{2},s]$ , where $\ell=4$ (by forbidding $Q_{1,1,3}$ ). If $k_{1}\geq i_{1}+3$ or $k_{\ell}\leq i_{1}-3,$ then $\dot{G}\subset[T_{a,1,b},v_{b},s]$ ( $a\geq 3$ and $b\geq 1$ ), where $b=a-1$ (by Lemma 3.5 (1)).

Subcase 1.2. $\dot{G}[V_{1}^{\prime}]=2K_{1}.$ Then $V_{1}^{\prime}=\{v^{\prime}_{i_{1}},v^{\prime}_{i_{2}}\}.$ Similar to subcase 1.1, then $\dot{G}\subset\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{3}}$ or $\dot{G}\subset[\dot{G},v,s,u,\dot{H}]$ , where $(\dot{G},v),(\dot{H},u)\in\{(T_{a,1,a-1},v_{a-1}),(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}}),$ $(P_{4},v_{2})\}$ ( $a\geq 3$ and $n_{1}\geq 1$ ).

Subcase 1.3. $\dot{G}[V_{1}^{\prime}]=K_{2}^{-}.$ Then $V_{1}^{\prime}=\{v^{\prime}_{i_{1}},v^{\prime}_{i_{2}}\},$ $i_{2}=i_{1}+1$ and $v^{\prime}_{i_{1}}\mathop{\sim}\limits^{-}v^{\prime}_{i_{2}}.$ Without loss of generality, we may assume that $i_{1}\leq\lfloor\frac{t}{2}\rfloor.$ Since $|V(\dot{H})|$ is maximal, then $i_{2}\geq 4$ . By Lemma 4.15, then $k_{1}\geq i_{2}+2$ . So, $Q_{i_{2}-1,k_{1}-i_{2}-1,1}\subset\dot{G}.$ By forbidding $Q_{i_{2}-1,b,1}$ (where $b\leq i_{2}-2$ ), then $k_{1}\geq 2i_{2}$ . If $i_{2}=5$ or $i_{2}\geq 6$ , then $\dot{F}_{8}\subset\dot{G}$ or $\dot{F}_{4}\subset\dot{G}$ , respectively, which contradicts to Lemma 3.4. So, $i_{2}=4$ and $\dot{G}\subset[G_{5}^{10},v_{10},s].$

Subcase 1.4. $\dot{G}[V_{1}^{\prime}]=K_{2}^{-}\cup K_{1}.$ Then $V_{1}^{\prime}=\{v^{\prime}_{i_{1}},v^{\prime}_{i_{2}},v^{\prime}_{i_{3}}\},$ where $i_{2}=i_{1}+1$ and $v^{\prime}_{i_{1}}\mathop{\sim}\limits^{-}v^{\prime}_{i_{2}}.$ By subcases 1.1 and 1.3, then $\dot{G}\subset\dot{\mathcal{A}}_{5}^{n_{1},n_{2}}$ or $\dot{G}\subset[G_{5}^{10},v_{10},s,v,\dot{G}]$ , where $(\dot{G},v)\in\{(P_{4},v_{2}),$ $(T_{a,1,a-1},v_{a-1}),(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}})\}$ ( $a\geq 3$ and $n_{1}\geq 1$ ).

Subcase 1.5. $\dot{G}[V_{1}^{\prime}]=2K_{2}^{-}.$ Similar to subcase 1.3, then $\dot{G}\subset[G_{5}^{10},v_{10},s,v_{10},G_{5}^{10}].$

Case 2. $|Y|=1.$ By forbidding $\dot{F}_{1}$ and $\dot{F}_{3}$ , then $t_{1}+t_{2}\leq 1.$

Subcase 2.1. $|V_{1}^{\prime}|=0$ . By Lemma 4.13, then $\dot{G}\subset[\dot{Q}^{\prime}_{1,0},v_{1},s]\subset[\dot{Q}^{\prime}_{1,1},v_{1},s].$

Subcase 2.2. $\dot{G}[V_{1}^{\prime}]=K_{1}.$ By subcases 1.1 and 2.1, then $\dot{G}\subset\dot{\mathcal{A}}_{3}^{0,n_{2},n_{3}}$ or $\dot{G}\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v,\dot{G}],$ where $(\dot{G},v)\in\{(T_{a,1,a-1},v_{a-1}),(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}}),(P_{4},v_{2})\}$ ( $a\geq 3$ and $n_{1}\geq 1$ ).

Subcase 2.3. $\dot{G}[V_{1}^{\prime}]=K_{2}^{-}.$ By subcases 1.3 and 2.1, then $\dot{G}\subset\dot{\mathcal{A}}_{5}^{0,n_{2}}$ or $\dot{G}\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v_{10},\dot{G}_{5}^{10}]$ .

Case 3. $|Y|=2.$ Then $k_{1}=1$ and $k_{\ell}=t.$ By forbidding $\dot{F}_{1}$ and $\dot{F}_{3}$ , then $V_{1}^{\prime}$ is empty. If $|U_{1}|=2,$ then $\dot{G}\sim\dot{\mathcal{A}}_{3}^{0,0,n_{3}}$ . If $|U_{1}|\geq 3,$ then $6\leq k_{2}<\dots<k_{\ell-1}\leq t-5$ (by Lemma 4.13). So $\dot{G}\subset[\dot{Q}^{\prime}_{1,0},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,0}]\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ .

This completes the proof. ∎

Remark 4.17.

Finally, it remains the case that $\dot{H}$ is an induced subgraph of $\dot{S}_{14}$ or $\dot{S}_{16}$ but not an induced subgraph of $\dot{T}_{2k}$ . Since $m\geq n+1,$ then $\dot{\mathcal{B}}_{r}^{4,4},$ $\dot{\mathcal{B}}^{4,4}_{0}$ or $\dot{\Theta}_{1,1,1}$ is an induced subgraph of $\dot{G}.$ More importantly, $\dot{\mathcal{B}}_{r}^{4,4},$ $\dot{\mathcal{B}}^{4,4}_{0}$ or $\dot{\Theta}_{1,1,1}$ is also an induced subgraph of $\dot{H}.$ From Fig. 1, it is not too hard to get that there is no such signed graph $\dot{H}$ .

Proof of Theorem 2.4. Summarizing with all results of Theorems 2.1 and 2.2, Lemmas 3.5, 3.7, 4.2, 4.4, 4.5, 4.6, 4.10, 4.11, 4.16 and 4.21, we complete the proof of Theorem 2.4. ∎

Acknowledgments

This project is supported by the National Natural Science Foundation of China (No.119
71164, 12001185, 12100557) and the Zhejiang Provincial Natural Science Foundation of China (LQ21A010004).

References

[1] F. Belardo, S. Cioab $\breve{a}$ , J. Koolen, J. F. Wang, Open problems in the spectral theory of signed graphs, Art Discrete Appl. Math. 1 (2018) $\#$ P2.10.
[2] A. E. Brouwer, A. Neumaier, The graphs with spectral radius between 2 and $\sqrt{2+\sqrt{5}}$ , Linear Algebra Appl. 114/115 (1989) 273–276.
[3] A. E. Brouwer, W. H. Haemers, Spectra of graphs, Springer, 2011.
[4] F. C. Bussemaker, P. J. Cameron, J. J. Seidel, S. V. Tsaranov, Tables of signed graphs, Eut Report 91-WSK-01, Eindhoven, 1991.
[5] D. Cvetkovi $\acute{c},$ M. Doob, I. Gutman, On graphs whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$ , Ars Combinat. 14 (1982) 225–239.
[6] M. K. Gill, B. D. Acharya, A recurrence formula for computing the characteristic polynomial of a sigraph, J. Comb. Inf. Syst. Sci. 5 (1980) 68–72.
[7] G. Greaves, J. Koolen, A. Munemasa, Y. Sano, T. Taniguchi, Edge-signed graphs with smallest eigenvalue greater than $-2$ , J. Combin. Theory Ser. B 110 (2015) 90–111.
[8] A. J. Hoffman, On limit points of spectral radii of non-negative symmetric integral matrices, in: Y. Alavi, et al. (Eds.), Lecture Notes Math, vol. 303, Springer-Verlag, Berlin, 1972, pp. 165–172.
[9] Z. L. Jiang, A. Polyanskii, Forbidden subgraphs of bounded spectral radius with applications to equiangular lines, Israel J. Math. 236 (2020) 393–421.
[10] Z. L. Jiang, A. Polyanskii, Forbidden induced subgraphs of graphs and signed graphs with eigenvalues bounded from below, arXiv: 2111.10366v1.
[11] P. W. H. Lemmens, J. J. Seidel, Equiangular lines, J. Algebra 24 (1973) 494–512.
[12] J. McKee, C. Smyth, Integer symmetric matrices having all their eigenvalues in the interval $[-2,2],$ J. Algebra 317 (2007) 260–290.
[13] J. H. Smith, Some properties of the spectrum of a graph, Combinatorial Structures and their Applications, Gordon and Breach, New York, 1970, pp. 403–406.
[14] J. F. Wang, J. Wang, M. Brunetti, The hoffman program of graphs: old and new, arXiv: 2012.13079v1.
[15] T. Zaslavsky, Signed graphs, Discrete Appl. Math. 4 (1982) 47–74.

Appendix A

Gill and Acharya [6] obtained the following recurrence formula for the characteristic polynomial of a signed graph.

Lemma 4.18.

[6] Let $\dot{G}$ be a signed graph and $v$ be its arbitrary vertex. Then

\phi_{\dot{G}}(x)=x\phi_{\dot{G}-v}(x)-\sum_{vu\in E(\dot{G})}\phi_{\dot{G}-v-u}(x)-2\sum_{\dot{C}\in\dot{C}(v)}\sigma(\dot{C})\phi_{\dot{G}-\dot{C}}(x),

where $\dot{C}(v)$ denotes the set of signed cycles passing through $v,$ and $\dot{G}-\dot{C}$ denotes the signed graph obtained from $\dot{G}$ by deleting $\dot{C}$ .

Denote $p_{n}$ and $q_{n}$ the characteristic polynomials of $P_{n}$ and $C_{n},$ respectively. Then

p_{0}(x)=1,~{}p_{1}(x)=x,~{}p_{n}(x)=xp_{n-1}(x)-p_{n-2}(x),~{}q_{n+1}(x)=p_{n+1}(x)-p_{n-1}(x)-2,

for all $n\geq 2.$ Moreover, the recursion gives

p_{n}(x)=\frac{\theta^{2n+2}-1}{\theta^{n+2}-\theta^{n}},~{}~{}q_{n}(x)=\theta^{n}+\theta^{-n}-2,~{}~{}\text{where}~{}~{}\theta=\theta(x):=\frac{x+\sqrt{x^{2}-4}}{2}.

(4.3)

Then

\begin{split}&\phi_{T_{a,1,b}}(x)=xp_{a+b+1}-p_{a}p_{b},\\ &\phi_{Q_{a,b,c}}(x)=x^{2}p_{a+b+c+1}-xp_{a+b}p_{c}-xp_{a}p_{b+c}+p_{a}p_{b-1}p_{c}.\end{split}

(4.4)

Let $\dot{T}_{2k}$ be the signed graph depicted in Fig. 1 with the adjacency matrix $A_{\sigma},$ and let $V(\dot{T}_{2k})=V_{1}\cup V_{2}$ be a partition of the vertex set. Then

A_{\sigma}=\begin{bmatrix}A_{1}&B\\ B^{T}&A_{2}\end{bmatrix},~{}~{}\text{where $A_{i}$ ($i=1,2$) is the adjacency matrix of $\dot{T}_{2k}[V_{i}].$ }

It is known that the spectrum of $\dot{T}_{2k}$ is $\{2^{k},-2^{k}\}$ (see [12, Theorem 1]). Then

({A_{\sigma}})^{2}=\begin{bmatrix}(A_{1})^{2}+BB^{T}&A_{1}B+BA_{2}\\ B^{T}A_{1}+A_{2}B^{T}&B^{T}B+({A_{2}})^{2}\\ \end{bmatrix}=4I_{2k}~{}~{}\text{and}~{}~{}B^{T}A_{1}+A_{2}B^{T}=\textbf{0}.

Lemma 4.19.

If $\mu\neq\pm 2$ is an eigenvalue of $\dot{T}_{2k}[V_{1}],$ then $-\mu$ is an eigenvalue of $\dot{T}_{2k}[V_{2}].$

Proof.

Let $\beta$ be the eigenvector corresponding to the eigenvalue $\mu\neq\pm 2$ of $\dot{T}_{2k}[V_{1}].$ If $B^{T}\beta=\textbf{0},$ then

A_{\sigma}\begin{bmatrix}\beta\\ \textbf{0}\\ \end{bmatrix}=\begin{bmatrix}A_{1}&B\\ B^{T}&A_{2}\\ \end{bmatrix}\begin{bmatrix}\beta\\ \textbf{0}\\ \end{bmatrix}=\begin{bmatrix}A_{1}\beta\\ B^{T}\beta\\ \end{bmatrix}=\begin{bmatrix}A_{1}\beta\\ \textbf{0}\\ \end{bmatrix}=\mu\begin{bmatrix}\beta\\ \textbf{0}\\ \end{bmatrix}.

This gives that $\mu$ is an eigenvalue of $A_{\sigma}$ and $\mu=\pm 2,$ which contradicts to hypothesis. So $B^{T}\beta\neq\textbf{0}.$ Since $B^{T}A_{1}+A_{2}B^{T}=\textbf{0},$ then $A_{2}B^{T}\beta=-B^{T}A_{1}\beta=-B^{T}\mu\beta=-\mu B^{T}\beta.$ Hence, $-\mu$ is an eigenvalue of $\dot{T}_{2k}[V_{2}].$ ∎

Corollary 4.20.

$(i)$ $\phi_{\dot{T}_{2s}^{\prime}}(x)=x^{2}(x\pm 2)^{s-1},$ $(ii)$ $\phi_{\dot{T}_{2s}^{\prime\prime}}(x)=x(x\pm\sqrt{2})(x\pm 2)^{s-2},$ $(iii)$ $\phi_{\dot{T}_{2s}^{\prime\prime\prime}}(x)=(x\pm\sqrt{2})^{2}(x\pm 2)^{s-3}.$

Proof.

Note that $V(\dot{T}_{2(s+1)})=V(\dot{T}_{2s}^{\prime})\cup V(2K_{1}),$ $V(\dot{T}_{2(s+1)})=V(\dot{T}_{2s}^{\prime\prime})\cup V(P_{3},\sigma)$ and $V(\dot{T}_{2(s+1)})=V(\dot{T}_{2s}^{\prime\prime\prime})\cup V(\dot{C}_{4}^{-}).$ By Lemma 3.1, then $\pm 2$ is an eigenvalue of $\dot{T}_{2s}^{\prime}$ (resp. $\dot{T}_{2s}^{\prime\prime}$ , $\dot{T}_{2s}^{\prime\prime\prime}$ ) with multiplicity at least $s-1$ (resp. $s-2$ , $s-3$ ).

( $i$ ) It is known that the spectrum of $2K_{1}$ is $\{0^{2}\}.$ By Lemma 4.19, then $0$ is an eigenvalue of $\dot{T}_{2s}^{\prime}$ with multiplicity $2$ . Therefore, $\phi_{\dot{T}_{2s}^{\prime}}(x)=x^{2}(x\pm 2)^{s-1}.$

The proofs of ( $ii$ ) and ( $iii$ ) are similar since the spectrum of $(P_{3},\sigma)$ is $\{\pm\sqrt{2},0\}$ and the spectrum of $\dot{C}_{4}^{-}$ is $\{\pm\sqrt{2}^{2}\}$ . ∎

Let the pair $(\dot{G},v)$ be defined in Theorem 2.4 ( $iv$ ) and $(v)$ , then

\begin{split}\phi_{[\dot{G},v,s]}(x)&=x\phi_{\dot{T}_{2s}^{\prime\prime}}(x)\phi_{\dot{G}-v}(x)-\phi_{\dot{T}_{2(s-1)}^{\prime}}(x)\phi_{\dot{G}-v}(x)-\phi_{\dot{T}_{2s}^{\prime\prime}}(x)\sum_{uv\in E(\dot{G})}\phi_{\dot{G}-v-u}(x)\\ &=x^{2}(x\pm\sqrt{2})(x\pm 2)^{s-2}\phi_{\dot{G}-v}(x)-x^{2}(x\pm 2)^{s-2}\phi_{\dot{G}-v}(x)\\ &~{}~{}~{}-x(x\pm\sqrt{2})(x\pm 2)^{s-2}\sum_{uv\in E(\dot{G})}\phi_{\dot{G}-v-u}(x)~{}~{}\text{(by Corollary \ref{lemma4.2})}\\ &=(x\pm 2)^{s-2}(x^{2}(x\pm\sqrt{2})\phi_{\dot{G}-v}(x)-x^{2}\phi_{\dot{G}-v}(x)-x(x\pm\sqrt{2})\sum_{uv\in E(\dot{G})}\phi_{\dot{G}-v-u}(x))\\ &=(x\pm 2)^{s-2}\phi_{[\dot{G},v,2]}(x),\end{split}

(4.5)

and $\phi_{[\dot{G},v,s]}(\lambda^{\ast})=(\sqrt{5}-2)^{s-2}\phi_{[\dot{G},v,2]}(\lambda^{\ast}).$ Similarly, we have

\begin{split}&\phi_{(\dot{G},v,s)}(\lambda^{\ast})=(\sqrt{5}-2)^{s-3}\phi_{(\dot{G},v,3)}(\lambda^{\ast}),\\ &\phi_{[\dot{G},v,s,u,\dot{H}]}(\lambda^{\ast})=(\sqrt{5}-2)^{s-3}\phi_{[\dot{G},v,3,u,\dot{H}]}(\lambda^{\ast}).\\ \end{split}

(4.6)

By Lemma 4.18 and Eqs. (4.3) $-$ (4.6), we can obtain the characteristic polynomials of all signed graphs $\dot{G}$ of Theorem 2.4 $(iii)$ and $(iv)$ . More importantly, by computations (using Wolfram Mathematica 12), we get that $\phi_{\dot{G}}(\lambda^{\ast})>0$ . See Tables 1 and 2. (In Table 1, $a_{1}=2\sqrt{\sqrt{5}-1}$ and $a_{2}=\sqrt{\sqrt{5}-2}$ ). Then we have

Lemma 4.21.

Let $\dot{G}$ be one of the signed graphs of Theorem 2.4 $(iii)$ and $(iv)$ with $n$ vertices. Then $\rho(\dot{G})<\lambda^{\ast}.$

Proof.

Let $\dot{G}$ be one of the signed graphs of Theorem 2.4 $(iii)$ and $(iv)$ , then we can get that $\dot{G}$ is bipartite and $\dot{G}$ contains an induced subgraph $\dot{G}_{1}$ with order $|V(\dot{G}_{1})|=n-1$ and $\lambda_{1}(\dot{G}_{1})<\lambda^{\ast}$ . (For example, if $\dot{G}$ is $[\dot{G}_{4}^{12},v_{12},s,v_{12},\dot{G}_{4}^{12}],$ let $\dot{G}_{1}=\dot{G}-v_{12},$ then $\lambda_{1}(\dot{G}_{1})=\lambda_{1}(\dot{G}_{4}^{12},v_{12},s)=\lambda_{1}(\dot{G}_{4}^{12},v_{12},3)<\lambda^{\ast}$ .) Then $\lambda_{2}(\dot{G})\leq\lambda_{1}(\dot{G}_{1})<\lambda^{\ast}$ by interlacing theorem. Since $\phi_{\dot{G}}(\lambda^{\ast})>0$ (by Tables 1 and 2), then $\rho(\dot{G})=\lambda_{1}(\dot{G})<\lambda^{\ast}.$ ∎

Finally we are going to give the proof of Lemma 3.5.

Proof of Lemma 3.5. Let $\dot{G}$ be a signed graph in Lemma 3.5. We can check that $\dot{G}$ is bipartite and $\dot{G}$ contains an induced subgraph $\dot{G}_{1}$ with order $|V(\dot{G}_{1})|=n-1$ and $\lambda_{1}(\dot{G}_{1})<\lambda^{\ast}$ . Then $\lambda_{2}(\dot{G})\leq\lambda_{1}(\dot{G}_{1})<\lambda^{\ast}$ by interlacing theorem. So if $\phi_{\dot{G}}(\lambda^{\ast})>0$ , then $\rho(\dot{G})<\lambda^{\ast}.$ Now we just need to prove that $\phi_{\dot{G}}(\lambda^{\ast})>0.$ Obviously, if $\dot{G}$ is an induced subgraph of the signed graphs of Theorem 2.4 $(iv)$ , then $\rho(\dot{G})<\lambda^{\ast}$ by Lemma 4.21.

(1) If $n_{1}\geq 3$ , by forbidding $Q_{n_{1},n_{2}+1,1}$ (where $n_{2}\leq n_{1}-2$ ), then $n_{2}\geq n_{1}-1.$ Similarily, if $n_{4}\geq 3,$ then $n_{3}\geq n_{4}-1.$ Therefore, if $n_{1}\leq 2$ and $n_{4}\leq 2,$ then $\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}}\subset[P_{4},v_{2},s,v_{2},P_{4}];$ if $n_{1}\geq 3$ and $n_{4}\geq 3,$ then $\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}}\subset[T_{a_{3},1,a_{3}-1},v_{a_{3}-1},s,v_{b_{3}-1},T_{b_{3},1,b_{3}-1}];$ if $n_{1}\leq 2$ and $n_{4}\geq 3,$ or $n_{1}\geq 3$ and $n_{4}\leq 2,$ then $\dot{\mathcal{A}}_{1}^{n_{1},n_{2},n_{3},n_{4}}\subset[T_{a_{3},1,a_{3}-1},v_{a_{3}-1},s,v_{2},P_{4}],$ where $s,a_{3},b_{3}\geq 3.$

(2) By Lemma 4.18 and Eq. (4.4), then

\begin{split}\phi_{\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}}}(x)=&x^{3}p_{n_{1}+n_{2}+n_{3}+4}-x^{2}(p_{n_{1}+n_{3}+3}p_{n_{2}}+p_{n_{1}+1}p_{n_{2}+n_{3}+2}-2p_{n_{1}}p_{n_{2}+n_{3}+1})\\ &+x(p_{n_{1}+1}p_{n_{3}+1}p_{n_{2}}-p_{n_{1}}p_{n_{2}+n_{3}+4}-p_{n_{1}+3}p_{n_{2}+n_{3}+1}-2p_{n_{1}}p_{n_{2}}p_{n_{3}})\\ &+p_{n_{1}}p_{n_{2}}p_{n_{3}+3}+p_{n_{1}+3}p_{n_{2}}p_{n_{3}}.\end{split}

(4.7)

If $n_{3}\geq n_{1}+n_{2}+2$ and $n_{2}\leq 2$ , then $\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}}\subset[\dot{Q}^{\prime}_{a_{1},a_{1}},v_{a_{1}},s,v_{2},P_{4}]$ $(a_{1}\geq 1)$ .

If $n_{3}\geq n_{1}+n_{2}+2$ and $n_{2}\geq 3$ , and if $n_{1}=0$ and $n_{3}=n_{2}+2$ , then $\dot{\mathcal{A}}_{2}^{0,n_{2},n_{2}+2}\sim(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{a_{3}-1},T_{a_{3},1,a_{3}-1})$ (where $\rho(\dot{\mathcal{A}}_{2}^{0,n_{2},n_{2}+2})<\lambda^{\ast}$ by Table 3 (3)); otherwise, $\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}}\subset[\dot{Q}^{\prime}_{a_{1},a_{1}},v_{a_{1}},s,v_{a_{3}-1},T_{a_{3},1,a_{3}-1}]$ , where $a_{1}\geq 1$ , $a_{3}\geq 3$ and $s\geq 3$ .

Next we consider that $n_{3}\leq n_{1}+n_{2}+1.$

Case 1. $n_{2}=1.$

Subcase 1.1. $n_{1}\leq 1.$ If $n_{3}=0,$ by computations, we have $\phi_{\dot{\mathcal{A}}_{2}^{0,1,0}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{2}^{1,1,0}}(\lambda^{\ast})<0.$ Then $n_{3}\geq 1$ and $\dot{\mathcal{A}}_{2}^{n_{1},1,n_{3}}\subset[\dot{Q}^{\prime}_{1,1},v_{1},s].$

Subcase 1.2. $n_{1}\geq 2.$ By forbidding $Q_{n_{1}+1,n_{3}+2,1}$ (where $n_{3}\leq n_{1}-2$ ), then $n_{3}\geq n_{1}-1.$ By Table 3 (1), we have $\phi_{\dot{\mathcal{A}}_{2}^{n_{1},1,n_{1}-1}}(\lambda^{\ast})<0$ . Then $n_{3}\geq n_{1}$ and $\dot{\mathcal{A}}_{2}^{n_{1},1,n_{3}}\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s].$

Case 2. $n_{2}=2.$ Then $n_{3}\leq n_{1}+3$ . Furthermore, by forbidding $Q_{2,n_{3}+1,2}$ (where $n_{3}\leq 2$ ), then $n_{3}\geq 3.$

Subcase 2.1. $n_{1}=0.$ Then $n_{3}=3$ . Note that $\rho(\dot{\mathcal{A}}_{2}^{0,2,3})=2.057<\lambda^{\ast}$ , then $\dot{\mathcal{A}}_{2}^{0,2,3}\sim(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{2},P_{4}).$

Subcase 2.2. $1\leq n_{1}\leq 3.$ If $n_{3}\leq n_{1}+2,$ by computations, we have $\phi_{\dot{\mathcal{A}}_{2}^{n_{1},2,n_{3}}}(\lambda^{\ast})<0$ . Then $n_{3}\geq n_{1}+3$ . So $\dot{\mathcal{A}}_{2}^{n_{1},2,n_{3}}\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s,v_{2},P_{4}]$ where $s\geq 3$ .

Subcase 2.3. $n_{1}\geq 4.$ By forbidding $Q_{n_{1}+1,n_{3}+2,2}$ (where $n_{3}\leq n_{1}+1$ ), then $n_{3}\geq n_{1}+2.$ If $n_{3}=n_{1}+2$ , then $\phi_{\dot{\mathcal{A}}_{2}^{n_{1},2,n_{1}+2}}(\lambda^{\ast})>0$ (by Table 3 (2)) and $\dot{\mathcal{A}}_{2}^{n_{1},2,n_{1}+2}\sim(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},2,v_{2},P_{4})$ . If $n_{3}\geq n_{1}+3$ , then $\dot{\mathcal{A}}_{2}^{n_{1},2,n_{3}}\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s,v_{2},P_{4}]$ where $s\geq 3$ .

Case 3. $n_{2}\geq 3.$ By forbidding the graph $Q_{a,b,c}\not\in\mathcal{G}^{\lambda^{\ast}},$ we obtain that if $n_{2}=3$ and $1\leq n_{1}\leq 3$ , or $n_{2}=4$ and $n_{1}=2,$ then $n_{3}\geq n_{1}+n_{2};$ otherwise, $n_{3}\geq n_{1}+n_{2}+1$ .

Subcase 3.1. $n_{2}=3$ and $n_{1}=1$ . Then $4\leq n_{3}\leq 5.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{2}^{1,3,4}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{2}^{1,3,5}}(\lambda^{\ast})<0$ .

Subcase 3.2. $n_{2}=3$ and $n_{1}=2$ . Then $5\leq n_{3}\leq 6.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{2}^{2,3,5}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{2}^{2,3,6}}(\lambda^{\ast})>0.$ So $\dot{\mathcal{A}}_{2}^{2,3,6}\sim(\dot{Q}^{\prime}_{2,2},v_{2},2,v_{2},T_{3,1,2})$ .

Subcase 3.3. $n_{2}=3$ and $n_{1}=3$ . Then $6\leq n_{3}\leq 7.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{2}^{3,3,6}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{2}^{3,3,7}}(\lambda^{\ast})>0.$ So $\dot{\mathcal{A}}_{2}^{3,3,7}\sim(\dot{Q}^{\prime}_{3,3},v_{3},2,v_{2},T_{3,1,2})$ .

Subcase 3.4. $n_{2}=4$ and $n_{1}=2$ . Then $6\leq n_{3}\leq 7$ . By computations, we have $\phi_{\dot{\mathcal{A}}_{2}^{2,4,6}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{2}^{2,4,7}}(\lambda^{\ast})<0$ .

Subcase 3.5. $n_{2}\geq 3$ and $n_{3}=n_{1}+n_{2}+1$ . Let $n_{1}=n_{2}+k.$ Then

\phi_{\dot{\mathcal{A}}_{2}^{n_{2}+k,n_{2},2n_{2}+k+1}}(\lambda^{\ast})=2^{n_{2}}(\sqrt{5}+1)^{-k-2n_{2}}f(k,n_{2}),

where $f(k,n_{2})=2^{k}(\sqrt{5}+1)^{n_{2}+1}((\frac{\sqrt{5}+3}{\sqrt{5}+1})(\frac{\sqrt{5}+1}{2})^{k}+2(\frac{2}{\sqrt{5}+1})^{n_{2}+1}-1)$ . If $k\leq-2,$ then $f(k,n_{2})<0$ and $\phi_{\dot{\mathcal{A}}_{2}^{n_{2}+k,n_{2},2n_{2}+k+1}}(\lambda^{\ast})<0$ as $(\frac{\sqrt{5}+3}{\sqrt{5}+1})(\frac{\sqrt{5}+1}{2})^{k}\leq(\frac{\sqrt{5}+3}{\sqrt{5}+1})(\frac{\sqrt{5}+1}{2})^{-2}\approx 0.618$ and $2(\frac{2}{\sqrt{5}+1})^{n_{2}+1}\leq 2(\frac{2}{\sqrt{5}+1})^{4}\approx 0.2918.$ If $k\geq-1,$ then $f(k,n_{2})>0$ and $\phi_{\dot{\mathcal{A}}_{2}^{n_{2}+k,n_{2},2n_{2}+k+1}}(\lambda^{\ast})>0$ as $(\frac{\sqrt{5}+3}{\sqrt{5}+1})(\frac{\sqrt{5}+1}{2})^{k}\geq(\frac{\sqrt{5}+3}{\sqrt{5}+1})(\frac{\sqrt{5}+1}{2})^{-1}=1.$ So, $\dot{\mathcal{A}}_{2}^{n_{1},n_{2},n_{3}}\subset(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},2,v_{n_{2}-1},T_{n_{2},1,n_{2}-1}),$ where $n_{1}\geq n_{2}-1.$ We complete the proof of $(2).$

( $3$ ) Let $n_{1}=n_{2}+k$ where $k\geq 0.$ By forbidding $Q_{2,b,2}$ (where $b\leq 3$ ), we have $n_{3}\geq 3.$

Case 1. $n_{1}=n_{2}=0.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{3}^{0,0,3}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{0,0,4}}(\lambda^{\ast})>0.$ Then $n_{3}\geq 4$ . So $\dot{\mathcal{A}}_{3}^{0,0,4}\sim(\dot{Q}^{\prime}_{1,0},v_{1},2,v_{1},\dot{Q}^{\prime}_{1,0})\subset(\dot{Q}^{\prime}_{1,1},v_{1},2,v_{1},\dot{Q}^{\prime}_{1,0})$ (if $n_{3}=4$ ) or $\dot{\mathcal{A}}_{3}^{0,0,n_{3}}\subset[\dot{Q}^{\prime}_{1,0},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,0}]\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ where $s\geq 3$ (if $n_{3}\geq 5$ ).

Case 2. $n_{1}=1.$

Subcase 2.1. $n_{2}=0.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{3}^{1,0,3}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{1,0,4}}(\lambda^{\ast})>0.$ Then $n_{3}\geq 4$ . So $\dot{\mathcal{A}}_{3}^{1,0,4}\sim(\dot{Q}^{\prime}_{1,1},v_{1},2,v_{1},\dot{Q}^{\prime}_{1,0})$ (if $n_{3}=4$ ) or $\dot{\mathcal{A}}_{3}^{1,0,n_{3}}\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,0}]\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ where $s\geq 3$ (if $n_{3}\geq 5$ ).

Subcase 2.2. $n_{2}=1.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{3}^{1,1,3}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{1,1,4}}(\lambda^{\ast})<0.$ Then $n_{3}\geq 5.$ So $\dot{\mathcal{A}}_{3}^{1,1,n_{3}}\subset[\dot{Q}^{\prime}_{1,1},v_{1},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ where $s\geq 3$ .

Case 3. $n_{1}=2.$

Subcase 3.1. $n_{2}=0.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{3}^{2,0,3}}(\lambda^{\ast})<0,$ $\phi_{\dot{\mathcal{A}}_{3}^{2,0,4}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{2,0,5}}(\lambda^{\ast})>0.$ Then $n_{3}\geq 5.$ So $\dot{\mathcal{A}}_{3}^{2,0,5}\sim(\dot{Q}^{\prime}_{2,2},v_{2},2,v_{1},\dot{Q}^{\prime}_{1,0})$ (if $n_{3}=5$ ) or $\dot{\mathcal{A}}_{3}^{2,0,n_{3}}\subset[\dot{Q}^{\prime}_{2,2},v_{2},s,v_{1},\dot{Q}^{\prime}_{1,0}]\subset[\dot{Q}^{\prime}_{2,2},v_{2},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ where $s\geq 3$ (if $n_{3}\geq 6$ ).

Subcase 3.2. $1\leq n_{2}\leq 2.$ By computations, if $n_{3}\leq n_{1}+n_{2}+2,$ then $\phi_{\dot{\mathcal{A}}_{3}^{2,n_{2},n_{3}}}(\lambda^{\ast})<0.$ Then $n_{3}\geq n_{1}+n_{2}+3$ . So $\dot{\mathcal{A}}_{3}^{2,n_{2},n_{3}}\subset[\dot{Q}^{\prime}_{2,2},v_{2},s,v_{n_{2}},\dot{Q}^{\prime}_{n_{2},n_{2}}]$ where $s\geq 3$ .

Case 4. $n_{1}\geq 3.$

Subcase 4.1. $n_{2}=0.$ By forbidding $Q_{n_{1}+1,n_{3}+2,2}$ (where $n_{3}\leq n_{1}+1$ ), we have $n_{3}\geq n_{1}+2.$ Since $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},0,n_{1}+2}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},0,n_{1}+3}}(\lambda^{\ast})>0$ (by Table 3 (4) and (5)), then $n_{3}\geq n_{1}+3$ . So $\dot{\mathcal{A}}_{3}^{n_{1},0,n_{1}+3}\sim(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},2,v_{1},\dot{Q}^{\prime}_{1,0})$ (if $n_{3}=n_{1}+3$ ) or $\dot{\mathcal{A}}_{3}^{n_{1},0,n_{3}}\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s,v_{1},\dot{Q}^{\prime}_{1,0}]\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ where $s\geq 3$ (if $n_{3}\geq n_{1}+4$ ).

Subcase 4.2. $n_{2}=1.$ By forbidding $Q_{n_{1}+1,n_{3}+3,2}$ (where $n_{3}\leq n_{1}+2$ ), we have $n_{3}\geq n_{1}+3.$ Since $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},1,n_{1}+3}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},1,n_{1}+4}}(\lambda^{\ast})>0$ (by Table 3 (6) and (7)), then $n_{3}\geq n_{1}+4$ . So $\dot{\mathcal{A}}_{3}^{n_{1},1,n_{3}}\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s,v_{1},\dot{Q}^{\prime}_{1,1}]$ where $s\geq 3$ .

Subcase 4.3. $n_{2}\geq 2.$ If $n_{1}=3$ and $n_{2}=2,$ by forbidding $Q_{4,n_{3}+3,3}$ (where $n_{3}\leq 4$ ), we have $n_{3}\geq 5.$ By computations, we have $\phi_{\dot{\mathcal{A}}_{3}^{3,2,5}}(\lambda^{\ast})<0$ , $\phi_{\dot{\mathcal{A}}_{3}^{3,2,6}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{3}^{3,2,7}}(\lambda^{\ast})>0.$ Then $n_{3}\geq 7.$ So $\dot{\mathcal{A}}_{3}^{3,2,7}\sim(\dot{Q}^{\prime}_{3,3},v_{3},2,v_{2},\dot{Q}^{\prime}_{2,2})$ (if $n_{3}=7$ ) or $\dot{\mathcal{A}}_{3}^{3,2,n_{3}}\subset[\dot{Q}^{\prime}_{3,3},v_{3},s,v_{2},\dot{Q}^{\prime}_{2,2}]$ where $s\geq 3$ (if $n_{3}\geq 8$ ). Otherwise, either $n_{1}\geq 4$ and $n_{2}=2,$ or $n_{1}\geq 3$ and $n_{2}\geq 3.$ By forbidding $Q_{n_{1}+1,n_{3}+3,n_{2}+1}$ (where $n_{3}\leq n_{1}+n_{2}$ ), we have $n_{3}\geq n_{1}+n_{2}+1.$ If $n_{3}=n_{1}+n_{2}+1$ , then $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{1}+n_{2}+1}}(\lambda^{\ast})=-2\sqrt{2}(\sqrt{5}+1)^{-n_{1}-n_{2}-\frac{1}{2}}((\sqrt{5}+1)^{n_{1}}2^{n_{2}}+2^{n_{1}}(\sqrt{5}+1)^{n_{2}}+(3-\sqrt{5})2^{n_{1}+n_{2}})<0.$ Therefore, $n_{3}\geq n_{1}+n_{2}+2$ .

If $n_{3}=n_{1}+n_{2}+2$ , then $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{1}+n_{2}+2}}(\lambda^{\ast})=(\sqrt{5}+1)^{-k-2n_{2}-1}f(n_{2},k)$ , where $f(n_{2},k)=(\sqrt{5}+1)^{k+2n_{2}+1}+(\sqrt{5}-3)2^{2n_{2}+k+2}-2^{n_{2}+2}(\sqrt{5}+1)^{n_{2}}((\sqrt{5}+1)^{k}+2^{k}).$ Since

\begin{split}f(n_{2},k)&>(\sqrt{5}+1)^{k+2n_{2}+1}-(\sqrt{5}+1)^{n_{2}}2^{k+n_{2}+2}-2^{n_{2}+2}(\sqrt{5}+1)^{k+n_{2}}-2^{k+2n_{2}+2}\\ &>(\sqrt{5}+1)^{n_{2}}((\sqrt{5}+1)^{k+n_{2}+1}-((\sqrt{5}+1)^{k}+2^{k+1})2^{n_{2}+2})=(\sqrt{5}+1)^{n_{2}}g(n_{2},k),\end{split}

then $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{1}+n_{2}+2}}(\lambda^{\ast})>(\sqrt{5}+1)^{-k-n_{2}-1}g(n_{2},k)$ . If $k=0,$ then $n_{1}=n_{2}\geq 3$ and $g(n_{2},0)=(\sqrt{5}+1)^{n_{2}+1}-3\cdot 2^{n_{2}+2}>0$ . If $k\geq 1,$ then $g(n_{2},k)>(\sqrt{5}+1)^{k}((\sqrt{5}+1)^{n_{2}+1}-2^{n_{2}+3})>0$ for $n_{2}\geq 2.$ So, $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{1}+n_{2}+2}}(\lambda^{\ast})>0$ .

Hence, $\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{1}+n_{2}+2}\sim(\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},2,v_{n_{2}},\dot{Q}^{\prime}_{n_{2},n_{2}})$ (if $n_{3}=n_{1}+n_{2}+2$ ) or $\dot{\mathcal{A}}_{3}^{n_{1},n_{2},n_{3}}\subset[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},s,v_{n_{2}},\dot{Q}^{\prime}_{n_{2},n_{2}}]$ where $s\geq 3$ (if $n_{3}\geq n_{1}+n_{2}+3$ ). We complete the proof of $(3).$

The proofs of $(4)-(11)$ are similar, and all values $\phi_{\dot{\mathcal{A}}_{i}^{n_{1},n_{2}}}(\lambda^{\ast})$ ( $i=4,\dots,13$ ) are presented in Table 3, where $a_{3}=\sqrt{\sqrt{5}-1},a_{4}=\sqrt{17\sqrt{5}+22},a_{5}=\sqrt{73\sqrt{5}+151},$ $a_{6}=\sqrt{17\sqrt{5}-22},$ $a_{7}=\sqrt{5\sqrt{5}-11},a_{8}=\sqrt{73\sqrt{5}-151},a_{9}=\sqrt{5\sqrt{5}-11},a_{10}=\sqrt{185\sqrt{5}-409},$ $a_{11}=\frac{2}{\sqrt{13\sqrt{5}+29}},a_{12}=\frac{31}{\sqrt{337\sqrt{5}+751}}.$

(12) If $n_{1}\geq 3,$ by forbidding $Q_{1,n_{2}+1,n_{1}}$ (where $n_{2}\leq n_{1}-2$ ), then $n_{2}\geq n_{1}-1$ . So $\dot{\mathcal{A}}_{14}^{n_{1},n_{2}}\subset[P_{4},v_{2},s]$ (if $n_{1}\leq 2$ ) or $\dot{\mathcal{A}}_{14}^{n_{1},n_{2}}\subset[T_{n_{1},1,n_{1}-1},v_{n_{1}-1},s]$ (if $n_{1}\geq 3$ ), where $s\geq 3.$

(13) By computations, we have $\phi_{\dot{\mathcal{A}}_{16}^{n_{1}}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{17}^{n_{1}}}(\lambda^{\ast})<0$ for $n_{1}\leq 8$ and $\phi_{\dot{\mathcal{A}}_{15}^{n_{1}}}(\lambda^{\ast})<0,$ $\phi_{\dot{\mathcal{A}}_{18}^{n_{1}}}(\lambda^{\ast})<0$ and $\phi_{\dot{\mathcal{A}}_{19}^{n_{1}}}(\lambda^{\ast})<0$ for $n_{1}\leq 10.$ Therefore, $\dot{\mathcal{A}}_{15}^{n_{1}}$ is an induced subgraph of $[\dot{G}_{5}^{10},v_{10},s,v_{10},\dot{G}_{5}^{10}],$ $\dot{\mathcal{A}}_{i}^{n_{1}}$ ( $i=16,17$ ) is an induced subgraph of $[\dot{G}_{2}^{9},v_{9},s,v_{10},\dot{G}_{5}^{10}],$ $\dot{\mathcal{A}}_{i}^{n_{1}}$ ( $i=18,19$ ) is an induced subgraph of $[\dot{G}_{4}^{12},v_{12},s,v_{10},\dot{G}_{5}^{10}].$ ∎

Table 1:

\phi_{\dot{G}}(x)

and

\phi_{\dot{G}}(\lambda^{\ast})

where

\dot{G}

belongs to Theorem 2.4 (

iii

) and

(iv)

	$\phi_{\dot{Q}_{n_{1},n_{2}}}(x)=xp_{n_{1}+n_{2}+3}-p_{n_{1}+2}p_{n_{2}}-p_{n_{1}}p_{n_{2}+2}+2p_{n_{1}}p_{n_{2}}$
	$\phi_{\dot{Q}^{\prime}_{n_{1},n_{2}}}(x)=x\phi_{\dot{Q}_{n_{1},n_{2}}}(x)-p_{n_{1}+n_{2}+3}$
	$\phi_{\dot{\mathcal{C}}_{k}^{1,\frac{k}{2}+1}}(x)=x(x(p_{k}-p_{k-2}+2)-p_{k-1})-\phi_{T_{\frac{k}{2}-1,1,\frac{k}{2}-1}}(x)$
	$\phi_{\dot{\mathcal{C}}_{k}^{1,\frac{k}{2}+1}}(\lambda^{\ast})=(\sqrt{5}+3)2^{\frac{k}{2}}(\sqrt{5}+1)^{1-\frac{k}{2}}>0$
	$\phi_{\dot{C}_{4}[n_{1},1,n_{3},1]}(x)=x\phi_{\dot{Q}^{\prime}_{n_{1},n_{3}}}(x)-\phi_{T_{n_{1}+1,1,n_{3}+1}}(x)$
	$\phi_{\dot{C}_{4}[n_{1},1,n_{3},1]}(\lambda^{\ast})=2^{\frac{1}{2}(n_{1}+n_{3}+2)}(\sqrt{5}+1)^{-\frac{n_{1}}{2}-\frac{n_{3}}{2}+1}>0$
	$\phi_{\dot{U}_{6}^{n_{1},n_{2}}}(x)=x\phi_{T_{n_{2},1,n_{1}+3}}(x)-p_{n_{1}+n_{2}+4}-\phi_{T_{n_{2},1,2}}(x)p_{n_{1}}+2p_{n_{1}}p_{n_{2}}$
	$\phi_{\dot{U}_{6}^{n_{1},n_{2}}}(\lambda^{\ast})=2^{\frac{1}{2}(n_{1}+n_{2}+2)}(\sqrt{5}+1)^{-\frac{n_{1}}{2}-\frac{n_{2}}{2}+1}>0$
	$\phi_{\dot{G}_{0}^{k}}(x)=x^{2}q_{k}-(q_{k}+2xp_{k-1})+2x^{2}+2xp_{k-3}$
	$\phi_{\dot{G}_{0}^{k}}(\lambda^{\ast})=2(1-(\frac{2}{\sqrt{5}+1})^{\frac{k}{2}})>0$ $(k$ is even)
	$\phi_{\dot{S}_{1}^{n}}(x)=xp_{n-8}\phi_{\dot{S}_{1}^{7}}(x)-q_{6}p_{n-8}-p_{n-9}\phi_{\dot{S}_{1}^{7}}(x)$
	$\phi_{\dot{S}_{1}^{n}}(\lambda^{\ast})=(5\sqrt{5}+11)^{\frac{1}{2}}2^{\frac{n}{2}+2}(\sqrt{5}+1)^{\frac{1}{2}(-n-1)}>0$
	$\phi_{\dot{S}_{2}^{n}}(x)=xp_{n-11}\phi_{\dot{S}_{2}^{10}}(x)-p_{n-11}\phi_{\dot{S}_{2}^{9}}(x)-p_{n-12}\phi_{\dot{S}_{2}^{10}}(x)$
	$\phi_{\dot{S}_{2}^{n}}(\lambda^{\ast})=2^{\frac{n}{2}+2}(\sqrt{5}+1)^{-\frac{n}{2}}>0$
	$\phi_{[\dot{G}_{4}^{12},v_{12},3,v_{n_{1}},\dot{Q}_{n_{1},n_{1}}^{\prime}]}(\lambda^{\ast})=\frac{(3194\sqrt{5}-7142)(\sqrt{5}+1)^{n_{1}}+(1292\sqrt{5}-2889)2^{n_{1}+3}}{(\sqrt{5}+1)^{n_{1}+1}(\sqrt{5}-2)^{5/2}}>0$
	$\phi_{[\dot{G}_{2}^{9},v_{9},3,v_{n_{1}},\dot{Q}_{n_{1},n_{1}}^{\prime}]}(\lambda^{\ast})=\frac{4((9-4\sqrt{5})(\sqrt{5}+1)^{n_{1}}+(29-13\sqrt{5})2^{n_{1}})}{(\sqrt{5}+1)^{n_{1}+1}}>0$
	$\phi_{[\dot{G}_{5}^{10},v_{10},3,v_{n_{1}},\dot{Q}_{n_{1},n_{1}}^{\prime}]}(\lambda^{\ast})=\frac{2(\sqrt{5}+1)^{n_{1}+1}-2^{n_{1}+3}}{(305\sqrt{5}+682)^{1/2}(\sqrt{5}+1)^{n_{1}+1}}>0$
	$\phi_{[\dot{Q}^{\prime}_{n_{1},n_{1}},v_{n_{1}},3,v_{n_{2}},\dot{Q}_{n_{2},n_{2}}^{\prime}]}(\lambda^{\ast})=\frac{8((\sqrt{5}+1)^{n_{1}+n_{2}+\frac{1}{2}}-a_{1}((\sqrt{5}+1)^{n_{1}}2^{n_{2}}+2^{n_{1}}(\sqrt{5}+1)^{n_{2}})+a_{2}2^{n_{1}+n_{2}+\frac{5}{2}})}{(\sqrt{5}+1)^{n_{1}+n_{2}+\frac{7}{2}}}$
	$\phi_{[T_{a,1,a-1},v_{a},3,v_{n_{1}},\dot{Q}_{n_{1},n_{1}}^{\prime}]}(\lambda^{\ast})=2^{a+2}((\sqrt{5}+1)^{n_{1}}-(\sqrt{5}-1)2^{n_{1}})(\sqrt{5}+1)^{-a-n_{1}-1}$
	$\phi_{[P_{4},v_{2},3,v_{n_{1}},\dot{Q}_{n_{1},n_{1}}^{\prime}]}(\lambda^{\ast})=\frac{(2(3-\sqrt{5})(\sqrt{5}+1)^{n_{1}}-(\sqrt{5}-2)2^{n_{1}+3})}{(\sqrt{5}+1)^{n_{1}+1}}>0$
	$\phi_{[\dot{G}_{4}^{12},v_{12},3,v_{a-1},T_{a,1,a-1}]}(\lambda^{\ast})\approx 0.0669(\frac{2}{\sqrt{5}+1})^{a}>0$
	$\phi_{[\dot{G}_{2}^{9},v_{9},3,v_{a-1},T_{a,1,a-1}]}(\lambda^{\ast})=(5\sqrt{5}-11)2^{n_{1}+1}(\sqrt{5}+1)^{-a}>0$
	$\phi_{[\dot{G}_{5}^{10},v_{10},3,v_{a-1},T_{a,1,a-1}]}(\lambda^{\ast})\approx 0.28(\frac{2}{\sqrt{5}+1})^{a}>0$
	$\phi_{[T_{b,1,b-1},v_{b-1},3,v_{a-1},T_{a,1,a-1}]}(\lambda^{\ast})=2^{a+b+1}(\sqrt{5}+1)^{-a-b+1}>0$
	$\phi_{[P_{4},v_{2},3,v_{a-1},T_{a,1,a-1}]}(\lambda^{\ast})=2^{a+3}(\sqrt{5}+1)^{-a-1}>0$

Table 2:

\phi_{\dot{G}}(\lambda^{\ast})

where

\dot{G}

belongs to Theorem 2.4

(iv)

$\phi_{[\dot{G}_{4}^{12},v_{12},3,v_{12},\dot{G}_{4}^{12}]}(\lambda^{\ast})\approx 0.0007$	$\phi_{[\dot{G}_{2}^{9},v_{9},3,v_{9},\dot{G}_{2}^{9}]}(\lambda^{\ast})\approx 0.02$	$\phi_{[\dot{G}_{5}^{10},v_{10},3,v_{2},P_{4}]}(\lambda^{\ast})\approx 0.03$
$\phi_{[\dot{G}_{4}^{12},v_{12},3,v_{9},\dot{G}_{2}^{9}]}(\lambda^{\ast})\approx 0.004$	$\phi_{[\dot{G}_{2}^{9},v_{9},3,v_{10},\dot{G}_{5}^{10}]}(\lambda^{\ast})\approx 0.015$	$\phi_{[P_{4},v_{2},3,v_{2},P_{4}]}(\lambda^{\ast})\approx 0.05$
$\phi_{[\dot{G}_{4}^{12},v_{12},3,v_{10},\dot{G}_{5}^{10}]}(\lambda^{\ast})\approx 0.003$	$\phi_{[\dot{G}_{2}^{9},v_{9},3,v_{2},P_{4}]}(\lambda^{\ast})\approx 0.033$
$\phi_{[\dot{G}_{4}^{12},v_{12},3,v_{2},P_{4}]}(\lambda^{\ast})\approx 0.006$	$\phi_{[\dot{G}_{5}^{10},v_{10},3,v_{10},\dot{G}_{5}^{10}]}(\lambda^{\ast})\approx 0.01$

Table 3:

\phi_{\dot{G}}(\lambda^{\ast})

where

\dot{G}

belongs to Lemma 3.5

	$(1)$ $\phi_{\dot{\mathcal{A}}_{2}^{n_{1},1,n_{1}-1}}(\lambda^{\ast})=-(\sqrt{5}-1)^{\frac{1}{2}}2^{n_{1}+\frac{1}{2}}\left(\sqrt{5}+1\right)^{-n_{1}}<0$
	$(2)$ $\phi_{\dot{\mathcal{A}}_{2}^{n_{1},2,n_{1}+2}}(\lambda^{\ast})=2\sqrt{2}(\sqrt{5}+1)^{-n_{1}-\frac{3}{2}}((\sqrt{5}+1)^{n_{1}}-\sqrt{5}\cdot 2^{n_{1}+1})>0$ $(n_{1}\geq 4)$
	$(3)$ $\phi_{\dot{\mathcal{A}}_{2}^{0,n_{2},n_{2}+2}}(\lambda^{\ast})=\frac{(\sqrt{5}-1)^{\frac{1}{2}}2^{n_{2}+\frac{3}{2}}}{(\sqrt{5}+1)^{n_{2}}}+3(\sqrt{5}+2)^{\frac{1}{2}}-(2(\sqrt{5}+1))^{\frac{1}{2}}>0$
	$(4)$ $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},0,n_{1}+2}}(\lambda^{\ast})=-(2\sqrt{5}+3)2^{n_{1}+5}(\sqrt{5}+1)^{-n_{1}-4}-\sqrt{5}+2<0$ $(n_{1}\geq 3)$
	$(5)$ $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},0,n_{1}+3}}(\lambda^{\ast})=(\sqrt{5}+1)^{-n_{1}-\frac{3}{2}}(2\sqrt{10}(\sqrt{5}+1)^{n_{1}}+(\sqrt{5}-4)2^{n_{1}+\frac{5}{2}})>0$
	$(6)$ $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},1,n_{1}+3}}(\lambda^{\ast})=(5\sqrt{5}-13)(\frac{2}{\sqrt{5}+1})^{n_{1}}+\sqrt{5}-2<0$
	$(7)$ $\phi_{\dot{\mathcal{A}}_{3}^{n_{1},1,n_{1}+4}}(\lambda^{\ast})=(\sqrt{5}-7)(\frac{1}{2}(\sqrt{5}+1))^{-n_{1}-\frac{5}{2}}+3\sqrt{\sqrt{5}-2}>0$
	$(8)$ $\phi_{\dot{\mathcal{A}}_{4}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{a_{3}\cdot 2^{n_{1}}(\sqrt{5}+1)^{n_{2}}+a_{4}\cdot 2^{n_{1}+n_{2}+\frac{3}{2}}-a_{5}(\sqrt{5}+1)^{n_{1}}2^{n_{2}}}{2^{\frac{1}{2}(n_{1}+n_{2}+2)}(\sqrt{5}+1)^{\frac{1}{2}(n_{1}+n_{2}-1)}}$
	$(9)$ $\phi_{\dot{\mathcal{A}}_{5}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{((4\sqrt{5}+7)(\sqrt{5}+1)^{n_{1}}+(5\sqrt{5}+1)2^{n_{1}})2^{n_{2}+8}-2^{n_{1}+8}(\sqrt{5}+1)^{n_{2}}}{(\sqrt{5}-3)(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2}+7)}}$
	$(10)$ $\phi_{\dot{\mathcal{A}}_{6}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{(\sqrt{5}-1)2^{n_{1}+1}(\sqrt{5}+1)^{n_{2}}+3((\sqrt{5}-1)2^{n_{1}}-(\sqrt{5}+1)^{n_{1}})2^{n_{2}+2}}{(\sqrt{5}-1)(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2})}}$
	$(11)$ $\phi_{\dot{\mathcal{A}}_{7}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{(\sqrt{5}-1)2^{n_{1}+4}(\sqrt{5}+1)^{n_{2}}+3((\sqrt{5}-3)2^{n_{1}}-(\sqrt{5}+1)^{n_{1}})2^{n_{2}+5}}{(\sqrt{5}-1)(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2}+3)}}$
	$(12)$ $\phi_{\dot{\mathcal{A}}_{8}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{3(\sqrt{5}+1)^{n_{1}+1}2^{n_{2}+5}-2^{n_{1}+6}(\sqrt{5}+1)^{n_{2}}-3\cdot 2^{n_{1}+n_{2}+7}}{(\sqrt{5}-3)(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2}+5)}}$
	$(13)$ $\phi_{\dot{\mathcal{A}}_{9}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{a_{3}\cdot 2^{n_{1}}(\sqrt{5}+1)^{n_{2}}-3((\sqrt{5}+1)^{n_{1}+\frac{1}{2}}+(\sqrt{\sqrt{5}-2})2^{n_{1}+\frac{3}{2}})2^{n_{2}}}{2^{\frac{n_{1}}{2}+\frac{n_{2}}{2}-1}(\sqrt{5}+1)^{\frac{1}{2}(n_{1}+n_{2}+3)}}$
	$(14)$ $\phi_{\dot{\mathcal{A}}_{10}^{n_{1},n_{2}}}(\lambda^{\ast})=-\frac{a_{6}(\sqrt{5}+1)^{n_{1}}(-2^{n_{2}+1})+a_{7}\cdot 2^{n_{1}+\frac{1}{2}}(\sqrt{5}+1)^{n_{2}}+a_{8}\cdot 2^{n_{1}+n_{2}+\frac{3}{2}}}{(\sqrt{5}-3)(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2})}}$
	$(15)$ $\phi_{\dot{\mathcal{A}}_{11}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{a_{6}(\sqrt{5}+1)^{n_{1}}2^{n_{2}+4}-a_{9}\cdot 2^{n_{1}+\frac{7}{2}}(\sqrt{5}+1)^{n_{2}}+a_{10}\cdot 2^{n_{1}+n_{2}+\frac{9}{2}}}{(\sqrt{5}-3)(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2}+3)}}$
	$(16)$ $\phi_{\dot{\mathcal{A}}_{12}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{(\sqrt{5}-2)((4\sqrt{5}+7)(\sqrt{5}+1)^{n_{1}}(-2^{n_{2}})+2^{n_{1}}(\sqrt{5}+1)^{n_{2}}+(3\sqrt{5}+13)2^{n_{1}+n_{2}})}{(2(\sqrt{5}+1))^{\frac{1}{2}(n_{1}+n_{2})}}$
	$(17)$ $\phi_{\dot{\mathcal{A}}_{13}^{n_{1},n_{2}}}(\lambda^{\ast})=\frac{a_{11}\cdot 2(2^{n_{1}}(\sqrt{5}+1)^{n_{2}}-(4\sqrt{5}+7)(\sqrt{5}+1)^{n_{1}}2^{n_{2}})-a_{12}\cdot 2^{n_{1}+n_{2}+2}}{2^{\frac{1}{2}(n_{1}+n_{2}-1)}(\sqrt{5}+1)^{\frac{1}{2}(n_{1}+n_{2}+2)}}$

On signed graphs whose spectral radius does not exceed 2+5\sqrt{2+\sqrt{5}}

Abstract

1 Introduction

2 Main results

Theorem 2.1.

Theorem 2.2.

Definition 2.3.

Theorem 2.4.

Remark 2.5.

3 Preliminaries

Lemma 3.1.

Lemma 3.2.

Proof.

Lemma 3.3.

Proof.

Lemma 3.4.

Proof.

Lemma 3.5.

Remark 3.6.

Lemma 3.7.

Proof.

Lemma 3.8.

Proof.

Lemma 3.9.

Proof.

Corollary 3.10.

4 Signed graph whose spectral radius does not exceed 2+5\sqrt{2+\sqrt{5}}

4.1 C˙k⊂G˙\dot{C}_{k}\subset\dot{G} where kk is odd or k≥10k\geq 10

Lemma 4.1.

Proof.

Lemma 4.2.

Proof.

Proof.

Proof.

Remark 4.3.

4.2 C˙8⊂G˙\dot{C}_{8}\subset\dot{G}

Lemma 4.4.

Proof.

4.3 C˙6⊂G˙\dot{C}_{6}\subset\dot{G}

Lemma 4.5.

Proof.

4.4 G˙\dot{G} is C˙k\dot{C}_{k}-free where k=3k=3 or k≥5k\geq 5

4.4.1 Θ˙2,2,0⊂G˙\dot{\Theta}_{2,2,0}\subset\dot{G}

Lemma 4.6.

Proof.

Remark 4.7.

Lemma 4.8.

Proof.

Lemma 4.9.

Proof.

Lemma 4.10.

Proof.

Lemma 4.11.

Proof.

4.4.2 G˙\dot{G} is Θ˙2,2,0\dot{\Theta}_{2,2,0}-free

Lemma 4.12.

Proof.

Lemma 4.13.

Proof.

Lemma 4.14.

Proof.

Lemma 4.15.

Proof.

Lemma 4.16.

Proof.

Remark 4.17.

References

Appendix A

Lemma 4.18.

Lemma 4.19.

Proof.

Corollary 4.20.

Proof.

Lemma 4.21.

Proof.

On signed graphs whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$

4 Signed graph whose spectral radius does not exceed $\sqrt{2+\sqrt{5}}$

4.1 $\dot{C}_{k}\subset\dot{G}$ where $k$ is odd or $k\geq 10$

4.2 $\dot{C}_{8}\subset\dot{G}$

4.3 $\dot{C}_{6}\subset\dot{G}$

4.4 $\dot{G}$ is $\dot{C}_{k}$ -free where $k=3$ or $k\geq 5$

4.4.1 $\dot{\Theta}_{2,2,0}\subset\dot{G}$

4.4.2 $\dot{G}$ is $\dot{\Theta}_{2,2,0}$ -free