On -matrix formulation of -characters
Abstract
We introduce an -matrix formulation of -characters and corresponding Frenkel-Reshetikhin deformed -algebras. The -matrix featuring in the construction is of Ding-Iohara-Miki (DIM) algebra, while the type of the -character is determined by the network of Fock representations corresponding to a web of 5-branes geometrically engineering a quiver gauge theory. Our formulation gives a unified description of -characters of type and their elliptic uplifts.
1 Introduction
Quantum deformation is one of the central themes of modern ‘‘physical mathematics’’. In particular, quantum deformations of Lie algebras [1, 2] were discovered in connection with lattice integrable models in statistical physics (see e.g. the classic book [3]), but soon found applications in many other areas such as knot theory [4], supersymmetric gauge theories [5], [6], and conformal field theory (CFT) [7]–[9].
To capture the intricacies of the representation theory of quantum affine Lie algebras Knight [10] and Frenkel-Reshetikhin [11] have introduced the notion of -characters which can be thought of as generalizations of conventional characters with more parameters. The principal ingredient in the construction of -character is the -matrix of . The -characters are partial traces of the -matrix taken in finite-dimensional representations, so that algebraic properties of the -matrix imply identities for the -characters.
It also turned out that there is a second quantum deformation of -characters involving parameter , called -characters, natural from both geometric [12] and algebraic [11] points of view. The deformation turns the parameters in the character into non-commutative operators so that the characters themselves generate a nontrivial algebra — the -deformed -algebra, .
It would be desirable to have an -matrix construction of -characters similar to that of -characters. Some attempts along these lines have been made in [13], but that paper dealt exclusively with a specific (and complicated) case of . In the current paper we propose a more general -matrix formalism for -characters, which to our knowledge has not been suggested previously.
There are some parallels between our formalism and that for -characters: we also use an -matrix as a central tool. However, the details differ a lot. Firstly, we use one and the same ‘‘master’’ -matrix to obtain all the -characters for the root systems . The -matrix is that of the Ding-Iohara-Miki (DIM) [14] or quantum toroidal algebra . In this sense both the root system and the representation featuring in the -character are free parameters that can be varied in our approach without changing the underlying algebraic structure.
The second important difference between our formalism and [11] is that we don’t take a trace of our -matrix, but instead a (partial) matrix element thereof. The states in the matrix element are what encodes the representation featuring in the -character.
The technical framework that we employ to derive the expressions for -characters is refined topological string. This allows us to interpret various algebraic expressions as refined amplitudes on certain toric Calabi-Yau (CY) three-folds. In fact the toric diagram of the three-fold can be viewed as a lattice statistical model [15] with crossings corresponding to DIM -matrices [16].
Let us note that ours is not the first attempt to obtain -characters in the refined topological string framework. In [17] (see also [18]) -characters were identified with specific generators of the algebra inserted between combinations of refined topological vertices. However, the generators were not viewed as coming from an -matrix. In [19] -characters were engineered by certain linear combinations of Lagrangian brane insertions, but no algebraic interpretation was given. In contrast, in the present paper we provide an explicit algorithm to draw a toric diagram whose refined partition function produces a given -character.
In the remaining part of the introduction we recall briefly the -matrix construction of -characters of quantum affine Lie algebras [11] (sec. 1.1), and then introduce the general idea of our approach to -characters and their connection with Type IIB 5-branes and refined topological strings (sec. 1.2). In this way we demonstrate both the similarities as well as differences between the two approaches before delving into full technical description.
The rest of the paper is organized as follows. In sec. 2 we introduce the DIM -matrix which can be interpreted as a spectator brane insertion. In sec. 3 we show how the -matrix formulas give rise to the coproduct of the generating current of the DIM algebra and match it with some previous works on the relation between DIM algebra and -characters. In sec. 4 we show how -characters are obtained from the -matrix insertion using Wick’s theorem. We apply our formalism to fundamental type -characters in sec. 5 and to higher representations of in sec. 6. In sec. 7 we consider the uplift of the formalism to elliptic -characters. We present our conclusions in sec. 8.
1.1 -characters and quantum affine algebras
-characters are partial traces of an -matrix. Let us be more precise. We consider finite-dimensional representations of quantum affine algebra . They have trivial central charges. The universal -matrix has the schematic form [20]
| (1) |
where the parts will be irrelevant for us. The ‘‘diagonal’’ part has the form222In order to eliminate cumbersome coefficients in the formulas we use the normalization of the generators which differs from the more standard one from [11].
| (2) |
where the index runs over the set of simple roots of and and are certain special bases in the commutative subalgebra . The -character of a representation has the schematic form (we gloss over some technical details such as prefactors)
| (3) |
where is a certain projection operator whose job is effectively to eliminate factors. The untraced generators commute and can be viewed as parameters of the -character.
A more compact way to pack the parameters is to introduce their generating functions (where ), which look like
| (4) |
Since form a commuting set of operators, they can be simultaneously diagonalized and one can study their joint eigenspectra. The theorem proven in [11] is that in finite-dimensional representations of the eigenvalues have the form
| (5) |
where , are complex numbers and , are finite integers. Moreover, for the highest weight vector there are no ’s, i.e. .
Plugging Eq. (5) into Eq. (3) and comparing with Eq. (4) we find that the -character is a Laurent polynomial in , and that the highest weight of a finite-dimensional representation corresponds to a monomial with only positive powers of :
| (6) |
Properties of the -matrix guarantee that -characters are additive and multiplicative. The definition (3) of the character can be drawn as a picture:
| (7) |
In Eq. (7) the square on the intersection of the blue and black lines represents the -matrix of , the blue line is the representation over which one takes a trace, and the horizontal black line is the space in which the commuting operators act.
1.2 -characters and DIM algebra
In -characters the operators are no longer commuting. Instead they become vertex operators acting on (a tensor power of) the Fock space, the Hilbert space of a free boson.
To engineer a -character we start with the universal -matrix of the DIM algebra and evaluate it in the tensor product of the vertical and horizontal Fock spaces, which we denote by and respectively (see Appendix A for the definitions of the algebra and representations). The -matrix turns out to be equal to the refined topological string amplitude on degenerate resolved conifold [16]:
| (8) |
The lines in Eq. (8) have two different physical interpretations related by dualities in string theory.
-
1.
The lines may be viewed as forming a toric diagram of a toric Calabi-Yau (CY) three-fold, on which refined topological strings propagate. For example the second picture in Eq. (8) represents the resoved conifold (the total space of the bundle ). The Fock space associated with a leg of the diagram is the space of states of refined topological string wrapping the corresponding two-cycle inside the CY. Triple junctions in the picture are refined topological vertices [21]. The lines passing on top of each other without intersecting as in the first picture in Eq. (8) correspond to deformed conifold geometry. The second equality in Eq. (8) expresses the geometric transition between deformed and resolved conifold in refined topological string theory [22].
-
2.
Alternatively, the lines may be thought of as 5-branes in Type IIB string theory on a flat background333The equivalence between these two interpretations is shown in [23].. In this interpretation the Fock space on a leg of the diagram is the Hilbert spaces of BPS states bound to the corresponding 5-brane. The triple junctions in the picture are junctions of 5-branes. Two lines passing on top of each other without intersecting are simply branes lying in different two-dimensional planes. In gauge theories living on the worldvolumes of the branes this corresponds to passing to the Higgs branch.
We will use the terms lines and branes interchangeably henceforth.
Degenerate crossing Eq. (8) has special properties. Specifically, its matrix elements along the vertical Fock representation satisfy the following selection rule:
| (9) |
where and are Young diagrams labelling the states in the Fock space.
To get the -characters of type corresponding to the first fundamental representation we draw the toric diagram involving horizontal lines and a vertical ‘‘spectator’’ brane crossing the horizontal lines. The external states on the vertical line are and . For example for :
| (10) |
The external states are indicated above and below the vertical spectator brane. Every crossing in Eq. (10) is an -matrix insertion and a sum over intermediate states and is assumed. According to the selection rule Eq. (9) there are only three possibilities for and , namely , , and . As we will see in sec. 4 each of these possibilities produces a distinct combination of -operators acting in the tensor product of three horizontal Fock spaces. The resulting three terms reproduce the -character of the defining representation of .
To get -characters corresponding to higher representations one needs to insert several spectator branes. We explain the procedure in detail in sec. 6.
Notice how our approach is similar in spirit (the main object is the -matrix), but also markedly different from sec. 1.1:
-
1.
The -matrices belong to a larger algebra (DIM) with two quantum deformation parameters instead of one.
-
2.
The same -matrix is used to build the -characters of all types444We expect that all classical and affine series can in fact be treated in our framework..
-
3.
Instead of a trace one needs to take a matrix element of the -matrix.
-
4.
The representations of quantum affine Lie algebras are encoded in the external states living in the vertical Fock representations of DIM.
One could insert the spectator brane (10) into a given toric diagram to get an average of the corresponding -character. Some toric diagrams correspond to supersymmetric gauge theories, in which the -characters form a special class of observables called -observables as explained in [24]. For example, the diagram
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/045758e8-5d8e-41b2-9941-6118cc032288/x6.png) |
(11) |
corresponds to a pure gauge theory. Due to the properties of the -matrix, the spectator brane can be inserted anywhere in the picture, for example
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/045758e8-5d8e-41b2-9941-6118cc032288/x7.png) |
(12) |
We will demonstrate the appearance of the -observables from pictures such as Eq. (12) in sec. 4.
2 DIM -matrices as brane crossings
In this section we give a more technical description of DIM -matrices and provide an explicit formula for the crossing operator introduced in Eq. (8). According to [16], the -matrix for the tensor product of vertical and horizontal Fock spaces can be written as a composition of two intertwining operators, or refined topological vertices (see Appendix A for definitions of the Fock representations).
The formulas for the intertwiners were obtained in [25]. Up to prefactors they are given by the following vertex operators (see Eqs. (138), (139) in Appendix C for complete expressions):
| (13) |
| (14) |
where
| (15) |
and the free boson modes satisfy the -deformed Heisenberg commutation relations:
| (16) |
Combining the intertwiners Eqs. (13), (14) as drawn in Eq. (8) we get the (the matrix element of) the -matrix [26]:
| (17) |
where is given by Eq. (B) and
| (18) | ||||
| (19) | ||||
| (20) | ||||
| (21) |
Several remarks are in order:
- 1.
-
2.
DIM algebra has an infinite number of inequivalent coproducts labelled by an irrational slope in the lattice. Each of the coproducts gives rise to its own set of intertwining operators and -matrices. In all of the formulas in this paper the choice of DIM coproduct (also known as the preferred direction in refined topological strings) is understood to be vertical, .
- 3.
- 4.
-
5.
The additional terms that appear in for nontrivial and have the form of a product of vertex operators sitting at points corresponding to boxes of and , respectively.
-
6.
We will sometimes omit the and arguments in when there is no possibility for confusion.
The operator looks complicated, however in our present study we will need to evaluate it only for , equal to or . Due to the selection rule Eq. (9) there are three cases of this type:
-
1.
, :
(22) It is important that the exponent in Eq. (22) contains only negative bosonic modes, so it acts trivially on the bra vacuum state .
- 2.
- 3.
Having the basic ingredients — the crossings (22), (23) and (24) — we can proceed to combine them. Naturally, there are two ways:
-
1.
One can stack crossings on top of each other, so that a single vertical line crosses a number of horizontal ones. This will produce the -characters of the first fundamental representation of which we investigate in sec. 3.
-
2.
The crossings can be joined along the horizontal legs. This will produce -characters of higher representations as described in sec. 6.
3 DIM coproduct and fundamental -characters from brane crossings
Consider a vertical spectator brane intersecting horizontal ones as shown in Eq. (10) with external state on top and at the bottom. Every brane intersection gives rise to the -matrix operator Eq. (17). We claim that such an intersection produces the -character of the defining representation of algebra.
To simplify our presentation in this section we restrict ourselves to the case when the branes intersecting the vertical brane are strictly horizontal, i.e. correspond to Fock representations of type . However, the same arguments work for lines too. Let us follow the example of Eq. (10), where there are three horizontal lines and two diagrams on the intermediate edges and .
As we have mentioned in sec. 1.2, selection rules severely restrict the set of Young diagrams on the intermediate vertical edges. There are three possible pairs contributing to the answer. Let us write down the operators corresponding to each of these pairs:
-
1.
:
(25) which can alternatively be expressed using Eq. (23) as
(26) where , are three sets of bosonic operators acting on three horizontal lines and the operator is defined in Eq. (114). The ‘‘empty crossing’’ part is given by
(27) where we have defined the ‘‘diagonal part’’ of the bosonic modes
(28) Notice that has a natural algebraic meaning of its own: it corresponds to the crossing with a vertical spectator brane, but with empty external states on it. In that case the selection rule (9) dictates that the Young diagrams on the intermediate edges should all be empty. Therefore the operator factorizes into a product of operators each acting on its own horizontal brane (see sec. 4.3 of [16]).
-
2.
:
(29) which can be similarly expressed in terms of the operator and another operator acting on the tensor product of three horizontal Fock spaces,
(30) where
(31) is the inverse of the norm of Macdonald polynomial corresponding to the intermediate state on the vertical brane () and is defined in Eq. (117).
-
3.
:
(32) which can be rewritten as
(33)
Collecting the terms for each pair of intermediate diagrams we get the following result for the crossing:
| (34) |
where in the last line we have used the formula for the coproduct of the generating current which can be found in Eq. (107) in Appendix A.
At this point we would like to use some of the results of [17] summarized in Appendix A. It was shown there that the insertion of the current of the algebra acting in the tensor product of horizontal Fock representations generates the fundamental -character of type. In Eq. (34) we get almost the same result from the vertical brane insertion, but with an additional operator . This factor, however, will not affect most of the formulas that we get for the following reason. We will consider the insertion of the -matrix/-character into some ‘‘background’’ network of intertwining operators (refined topological vertices). As we will see in sec. 4 the extra operator has very simple commutation relations with refined topological vertices placed elsewhere in the diagram. This will allow us to effectively get rid of it in any given -character calculation by moving to the very left of the diagram, where it annihilates the bra vacuum state. Thus, we will dismiss the in most of the formulas.
To understand why the coproduct appears in Eq. (34) we have to recall the Khoroshkin-Tolstoy formula [20] for the universal -matrix. The formula has the form:
| (35) |
where is the permutation operator exchanging the two factors in the tensor product. The other three factors are
| (36) | ||||
| (37) | ||||
| (38) |
Let us explain the notations in Eqs. (36)–(38) (see Appendix A for basic definitions related to the DIM algebra):
-
1.
are generators of the DIM algebra,
-
2.
, are the two central charges of the algebra,
-
3.
, are the grading operators,
-
4.
,
-
5.
are DIM generating currents.
- 6.
The universal -matrix (35) satisfies the fundamental identity
| (39) |
where is the coproduct given by Eqs. (109)–(111) and (resp. ) represents acting on the first two (res. first and third) factors in the triple tensor product.
It is the property in Eq. (39) that explains the appearance of the coproduct of in Eq. (34). Indeed, consider acting in the tensor product of two representations: one is a vertical Fock space and the other is itself a tensor product of three horizontal Fock spaces (see Appendix A for the definitions of the relevant Fock representations). Due to the identity (39) the -matrix acting on the tensor product is
| (40) |
Let us compute the matrix element of the two sides of Eq. (40) between the states and in the vertical Fock representation. The r.h.s. gives the diagram in Eq. (34) while the l.h.s. can be evaluated using the formulas (36)–(38):
| (41) |
Using explicit formulas (109)–(113) for the coproduct and the Fock representations from Appendix A we find that the second line of Eq. (41) is given by
| (42) |
Notice that the product acts diagonally on the state with empty Young diagram on the vertical line, but exchanges the two tensor factors (due to operator) and shifts the spectral parameter of the representation from to (due to the piece involving grading operators). What remains is to evaluate the third line of Eq. (41):
| (43) |
where we have used the explicit action of in the vertical representation
| (44) |
which follows from the definition (121). In the second line of Eq. (43) we have also used the fact that the identity term in the definition (38) of does not contribute to the matrix element since it cannot turn into . A more nontrivial observation is that all the higher terms from Eq. (38) also don’t contribute: they all subtract two or more boxes from the diagram so that it vanishes.
This explains why we get the coproduct of the current from the brane crossing (10) and ensures that the resulting operator is indeed the -character, or -algebra generator as shown in [17] (and recalled in Appendix A).
In the next section we will see that an insertion of the vertical brane (10) into a toric diagram corresponding to a gauge theory gives the Nekrasov formulas for the -characters.
4 Normal ordering and commutation relations
To connect with the works of Nekrasov on the gauge theory origin of -characters [24], we need to insert the -character operator into a toric diagram corresponding to a gauge theory. The resulting expressions will have the form of sums (averages) over Young diagrams, or instanton series with brane insertion producing an extra contribution to the measure.
Since the vertical brane insertion (10) is essentially a sum of several free field vertex operators, its contribution to a refined topological string partition function is easy to calculate using Wick’s theorem. The expressions for the refined topological vertices in terms of free boson generators are written out in Eqs. (13), (14).
The normal ordering of (Eq. (17)) with a product of -type and -type operators is given by:
-
1.
, :
(46) i.e. the normal ordering coefficient is trivial.
-
2.
, :
(47) with the so-called -functions defined as
(48) where (the number of or intertwiners on a given horizontal brane) corresponds to the rank of the gauge group on a given node of the quiver theory and is the Nekrasov factor given by Eq. (B). -functions (48) are natural observables in gauge theory [24].
-
3.
, :
(49) In this case again no normal ordering corrections are produced.
In Eqs. (46)–(48) the vertical brane insertion has been placed to the left of all the other vertices. However, we can also do a similar computation using Wick’s theorem for the brane inserted at any other point in the ‘‘background’’ brane diagram. It would be more economical, however, to investigate directly the commutation relations of the vertical brane insertion of the formx (10) with other vertical edges on a toric diagram.
The crucial observation [16] is that due to the properties of the -matrix and the vertices, the vertical brane commutes with internal edges:
| (50) |
This can also be verified by a direct computation which we perform in sec. 5.1.2.
Another consequence of the properties of the -matrix is that the commutation of the vertical brane with external semi-infinite vertical legs of the diagram produce only an inessential prefactor which does not depend on the Young diagrams residing on the internal edges of the toric diagram.
In the next section we present the simplest example a -character computed using the operator formalism we have developed.
5 Fundamental -characters from the operator formalism and refined topological strings
In this section, we apply our operator formalism to explicitly calculate the -characters in different theories. We also do the same calculation in topological string theory using the formalism of refined vertex [21].
5.1 Fundamental -character of type
5.1.1 Operator formalism
The type -character can be obtained by inserting a vertical spectator brane into the brane diagram corresponding to the toric diagram of the local or local for gauge theory with Chern-Simons level 0 and 1, respectively. The calculation of the instanton partition function of the theory using the intertwining operators are briefly sketched in Appendix C for both cases.
-character in pure gauge theory without the Chern-Simons term.
Let us calculate the instanton partition function in the presence of the vertical brane with no Chern-Simons term. We can use the normal ordering identities (46), (2) and (49) to obtain the partition function with the spectator brane insertion:
| (51) |
where is the instanton counting parameter and
| (52) |
is the vector multiplet contribution for to the instanton partition function. In the last line of Eq. (51) the average is understood as the sum over pairs of Young diagrams with weight . Eq. (51) exactly reproduces the fundamental -character of type [11] (see also [24], [30]).
-character in a theory with Chern-Simons level 1.
Let us find the -character of the gauge theory with the Chern-Simons term of level 1 using the operator formalism. The modification compared to Eq. (51) is minor: the contractions between the -matrix and the intertwining operators are the same, only the prefactors change. We obtain the following -character for Chern-Simons level 1:
| (53) |
-character in a theory with hypermultiplets.
The algebraic formalism allows us to compute the -character with the matter hypermultiplets coupled to the gauge theory. As an example, we will compute the fundamental character of in the presence of four fundamental matter hypermultiplets. The contractions we have already computed are enough to evaluate the character:
| (54) |
where is a new factor accounting for the matter multiplets that depend on their masses encoded in the spectral parameters , ,
| (55) |
The instanton counting parameter is also slightly modified in the presence of matter fields,
| (56) |
5.1.2 Refined vertex computation
In [25] the refined topological vertex has been shown to be equal to the matrix element of certain intertwining operator of the DIM algebra . This provided an algebraic approach to compute the topological string amplitudes on local toric Calabi-Yau threefolds. Using this relation, we want to show how the -characters can be geometrically engineered. To introduce our approach we will treat our first example, the -character of the fundamental representation of using theory in five dimension, in some detail.
The -characters have been computed using the geometric transition before [19]. In that work the authors focused on geometries that initially engineer a higher rank gauge theory and studied open topological string amplitudes by taking certain limits of the appropriate Kähler classes corresponding to the geometric transition, thus obtaining a lower rank theory with an operator insertion. A different limit needed to be taken for each term in the -character, in other words, the character was a linear combination of amplitudes on different geometries. Although we study the open topological amplitudes too, our approach is different in the sense that all terms of the -character are produced from a single geometry as one or more infinite sums over Young diagrams truncate to a finite number of terms. To the best of our knowledge, this type of truncation is used for the first time in the literature.
-character in pure gauge theory without the Chern-Simons term.
For the -character of fundamental representation of theory with Chern-Simons level 0, we start with the toric threefold that engineers theory with two matter multiplets, one in the fundamental and the other in the anti-fundamental representation. Recalling the algebraic approach from sec. 5.1.1, this should be expected: inserting an extra D5 brane would correspond to an increase in the rank of the gauge theory and possibly new matter multiplets upon resolving singularities. In addition, having a non-trivial states along the additional brane translates into computing ‘‘open’’ amplitudes, depicted in Figure 2. We obtain the -character by imposing a ‘‘degeneration’’ condition in accordance with the definition of the -matrix Eq. (8). We note that the external legs of the toric diagram engineering the theory with two matter multiplets extend asymptotically in the same way as in the geometry which engineers the gauge theory with Chern-Simons level 0 (local ) depicted in Fig. 1 a). Fig. 1 b) shows the toric diagram after resolving the singularity.


The refined topological string partition function corresponding to Fig. 2 takes the following form after some slight modifications to match it identically to instanton counting,555We set the preferred direction to vertical in all the refined topological string computations throughout this paper.
| (57) |
where is defined in Eq. (20), is the Nekrasov factor Eq. (B) and
| (58) |
To obtain the -character we need to set the external representations to and and pick special ‘‘degenerate’’ values for the Kähler parameters
| (59) |
which correspond to the geometric transtion from Fig. 1. The sum over Young diagrams truncates to a sum consisting of only two terms due to the identity
| (60) |
which we prove in Appendix B. Note that the -character of the fundamental representation of has indeed two terms, as we also argued in the algebraic approach in sec. 5.1.1. In what follows we show that the extra factors arising from the brane insertion give rise to the -operators. The remaining instanton sums are used to evaluate their expectation values.
-
(i)
Consider . After some cancellations we end up with the following additional factors under the gauge theory instanton sum:
(61) where is defined in Eq. (48).
We need to make an identification between the physical parameters of the gauge theory and the geometric quantities, Kähler parameters, used in the vertex computation. Using the following identification,
(62) it can be seen that the first term in the -character that we had found earlier is indeed reproduced (up to the , which as we will show now gives only an overall factor).
-
(ii)
The second and last term in the sum over is when . This time we get
(63) which is identical to the second term in the -character we had found earlier. We would like to emphasize that this result is the ‘‘open’’ topological string amplitude of a single toric diagram, although we compute it in two steps: first the (two-term) sum over and then over , .
We can alternatively choose a different degeneration scheme by setting and . The selection rule for then follows from another choice of the Kähler classes and . It can be shown that in that case the same -character is reproduced. One can argue more generally that the second degeneration scheme gives the -characters for conjugate representations, so for the fundamental representation of which is isomorphic to its conjugate the answer remains the same.
-character in pure gauge theory without the Chern-Simons term. Alternative spectator brane position.
In sec. 4 we have noted that from general algebraic arguments it follows that the vertical spectator brane corresponding to the -matrix commutes with internal edges of the toric diagram. Now we would like to demonstrate it by a direct computation in refined topological string theory. If we commute the vertical brane with the internal edges we end up with a different toric diagram depicted in Fig. 3. However, if we properly modify the identification between the algebraic and geometric variables after the commutation, we end up with the same -character.

The open topological string amplitude corresponding to Fig. 3 is again expressed in terms of three infinite sums over Young diagrams which corresponds to gluing two strip geometries together. This amplitude can be manipulated to take the form of the instanton counting of the theory, with respect to which we will compute the expectation values of the -operators. Setting the Kähler parameters , to the degenerate values (59) with the same choice of boundary conditions as before, and , we get
| (64) |
which agrees with the -character (51) found earlier provided that we identify
| (65) |
Let us note that we also get the same -character if we choose and with , .
-character in a theory with Chern-Simons level 1.
We can compute the -character in the presence of a Chern-Simons term using the topological vertex as well. The toric diagram is depicted in Fig. 4. We start with the local which engineers the theory at Chern-Simons level 1 and insert a D5 brane as before.

The topological sting amplitude represented by Fig. 4 after taking , , and becomes:
| (66) |
We have almost the same map between the algebraic and geometric parameters as in the absence of the Chern-Simons term (cf. Eq. (62)):
| (67) |
with the same instanton parameter . With the identification Eq. (67) the refined topological string amplitude (66) reproduces the character (53).
-character in a theory with Chern-Simons level 1. Alternative spectator brane position.
We argued in sec. 4 that the exact point at which the vertical brane (representing the -matrix) is inserted into a toric diagram does not affect the form of the -character, but slightly modifies the identification between the Kähler parameters of the CY and the spectral parameters of the DIM representations. Let us demonstrate that the same is true for the case of nontrivial Chern-Simons level as well. The toric diagram corresponding to an alternative vertical brane insertion is depicted in Fig. 5.

The topological string amplitude is reduced to,
| (68) |
when the boundary conditions are set to and with . With the alternative insertion of the vertical brane we obtain the same -character as in Eq. (65) if we identify
| (69) |
as in the case of vanishing Chern-Simons level.
The ‘‘opposite’’ degeneration scheme with , is also possible for the non-vanishing Chern-Simons level, and the two alternatives give rise to the same -character.
-character in a theory with hypermultiplets.
As in the previous cases in this section, the -character with additional matter hypermultiplets can be obtained from refined topological strings. The corresponding toric diagram is shown in Fig. 6.

We set the boundary conditions as before, and with and , so that the topological string partition functions reduces to
| (70) |
We obtain a match with the -character (54) by setting the map between the algebraic and geometric parameters as follows
| (71) |
5.2 Fundamental -character of type
5.2.1 Operator formalism
Our formalism also produces -characters for higher rank -type root systems. The procedure is similar to the case described in sec. 5.1. We start with a network of DIM intertwiners corresponding to a quiver gauge theory of type , insert the -matrix into it and take its matrix element. We would like to demonstrate this approach on a simple example of . The network of intertwiners is depicted in Fig. 7.

Leaving out the details of the calculation, we give the answer for the matrix element of the network from Fig. 7 which indeed has the form of the -character:
| (72) |
5.2.2 Refined vertex computation
The same -character as in sec. 5.2.1 can also be calculated following the refined topological vertex approach. The toric diagram with the -matrix insertion is drawn in Fig. 8.

The degeneration needed to reproduce the -character occurs at and . The map between the Kähler parameters and the spectral parameters is given by
| (73) |
6 Multiple vertical brane insertions and higher -characters
In this section we consider several vertical ‘‘spectator’’ branes (representing the -matrices) inserted into the same network of intertwiners. We show that this gives rise to -characters of higher representations of algebras. As in sec. 5 we first derive our results in the algebraic approach employing DIM intertwining operators and then give the parallel ‘‘geometric’’ computation using refined topological vertex formalism.
6.1 Operator formalism
To understand how to combine several vertical branes together let us start with the simplest example with two vertical ‘‘spectator’’ branes intersecting two horizontal lines:
| (74) |
where has been defined in Eq. (27) and is given by Eq. (109). Using the formulas Eqs. (114)–(119) for the horizontal Fock representation and the normal ordering identities from sec. 4 we find that
| (75) | |||
| (76) | |||
| (77) |
| (78) |
where the ‘‘structure function’’ is defined as
| (79) |
Inserting the resulting operator Eq. (74) into a toric diagram corresponding to a pure gauge theory gives
| (80) |
which exactly reproduces weight -character of type corresponding to symmetric representation [30].
To get the -character corresponding to antisymmetric representation of (which is trivial) we need to consider a degeneration of Eq. (80):
| (81) |
The value is a pole of the function , therefore, to get a meaningful answer we have to multiply the character under the limit by something proportional to . Only one term survives:
| (82) |
which is indeed equal to the -character of the trivial representation of .
The degeneration pattern of higher -characters Eq. (82) is in fact general. For example, one can get the -characters of all the fundamental representations of by considering vertical branes with coordinates , intersecting horizontal lines in the toric diagram and sending
| (83) |
It is curious to notice which Young diagrams on the intermediate legs (the analogs of and in Eq. (80)) survive the degeneration. The pattern of intermediate diagrams is shown below
| (84) |
The only sets of or which give nontrival contributions to the -character Eq. (84) are
| (85) | |||
| (86) |
where we set and . Let us give an example of an allowed pattern of ’s for ,
| (87) |
It is evident that for there are no allowed configurations of . Indeed, at the top of the pattern there is a row of boxes, while at the bottom there is an empty row, and at every step down at most one box is eliminated. There is no way the total of boxes can be eliminated after steps. This fits with the fact that the corresponding representations vanish identically.
6.2 Refined vertex computation
The geometric approach involving refined topological vertices allows us to calculate the -characters of higher representations too. As an illustrative example, we calculate the character of the symmetric representation of . We insert branes at two different locations associated with two parameters of the -character. The corresponding toric Calabi-Yau threefold before the degeneration of the Kähler parameters, whose toric diagram is depicted in Figure 9, engineers a gauge theory with two fundamental and two anti-fundamental matter hypermultiplets.

To get the -character we calculate the open topological string amplitude for and with the Kähler parameters set to degenerate values and . Due to the degeneration two out of four infinite sums over all Young diagrams in the instanton sum of the theory truncate so that each of them consists of only two terms making up the four terms in the character:
| (88) |
where the ‘‘structure function’’ is the same as in Eq. (79). In the calculation leading to Eq. (88) the following alternative formula for through the Nekrasov factors Eq. (B) is useful:
| (89) |
The instanton counting parameter in Eq. (88) is given by
| (90) |
while the map between the Kähler parameters and the parameters of hte representation is similar to (62).
7 Elliptic generalization of -characters
Our algebraic approach can be generalized to produce the version of the -characters introduced in [17], [31]. This is achieved by taking the elliptic deformation of the DIM algebra and intertwining operators [36]. We review the basics of the procedure in Appendix D. The deformation is equivalent to the ‘‘partial compactification’’ of the toric CY giving rise to an elliptic fibration [32]. M-theory compactified on the fibration engineers the gauge theory on , hence the notion of -characters.
7.1 Operator formalism
The intertwining operators are vertex operators involving free bosonic modes obeying the -deformed Heisenberg algebra (16). In the elliptic deformation of the DIM algebra we introduce an extra parameter into the commutation relations [36], [33]. It turns out that to survive the deformation, the horizontal Fock representation defined in Appendix A needs to be ‘‘doubled’’, i.e. one needs to introduce the second set of independent Heisenberg generators in addition to . More details are provided in Appendix D.
Due to the doubling of the modes the elliptic deformation of each vertex operator becomes a product of two vertex operators: one expressed in terms of the old Heisenberg generators and the other in terms of the new ones . The elliptic version of the intertwining operator (13) takes the form666We denote the elliptic intertwining operators by and to distinguish them from the undeformed ones, which we call , .,
| (91) |
while its dual Eq. (14) becomes
| (92) |
where we denote the ‘‘doubled’’ Fock representations by thick lines, is defined by Eq. (15) and we have skipped the prefactors which are the same as in the undeformed case (see Eqs. (138), (139)). The Heisenberg generators and satisfy the elliptically deformed commutation relations (149). One can check that the vertex operators (91), (92) are indeed the intertwining operators between the vertical and horizontal Fock representations of the elliptic DIM algebra as defined in Appendix D.
We can use the deformed intertwining operators (91), (92) to compute the elliptic deformation of the -matrix (17) which we denote by ,
| (93) |
where the Nekrasov factors are given by Eq. (B), , and are defined by Eqs. (15), (18) and (20) respectively.
The selection rule for and in Eq. (93) is the same as in sec. 2: when the other representation can be either or for to be nonzero. The prefactor in the first line of Eq. (93) is slightly different from that of the original -matrix (17) — it is missing the factors. The reason behind this difference is our choice of basis in the vertical Fock representation. In the elliptic calculations in this section we use a more convenient (orthogonal) basis in which the norm is given by
| (94) |
where is defined by Eq. (21).
The norm (94) is proportional to the vector multiplet contribution to the Nekrasov partition function of the gauge theory. Moreover, for it reduces to the familiar integral form normalization of Macdonald polynomials ,
| (95) |
One can evaluate the Wick contractions of the -matrix Eq. (93) with the intertwining operators (91), (92) and show that the only non-trivial contributions (apart from the possible prefactors) happens when and . The contraction has the same form as in the undeformed case (Eq. (2)) but with modified functions which we denote by ,
| (96) |
In the definition (96) we have used the Jacobi theta function (Eq. (153)) instead of the more conventional one . The explicit expressions for the -characters are the same up to a multiplicative factor in front of them when written in terms of either of these functions.
Fundamental elliptic -character.
We would like to compute the elliptic (or ) -character of the fundamental representation for the group. In the case to avoid anomaly we need to make sure that the theory is conformal. The simplest nonabelian gauge group is just , so to have vanishing beta function we need to add four matter hypermultiplets in fundamental representations. First, let us present the computation using the elliptic deformation of the intertwining operators given by Eqs. (91), (92). The network of intertwiners corresponding to the theory is depicted in Fig. 10. Notice that the diagrams for the networks corresponding to the and theories are the same, only the intertwining operators , are replaced with their elliptic deformations , .

Similarly to the trigonometric case, we can normal order all the operators (the -matrices and triple intertwiners) in the network and obtain the following -character:
| (97) |
Here, is the elliptic version of the factor introduced in Eq. (55),
| (98) |
where is the insertion point of the intertwining operators corresponding to the matter hypermultiplets. If the elliptic deformation parameter is sent to zero, we obviously get back to the trigonometric result from sec. 5.1.1 [24], [17].
Higher elliptic -character.
The elliptic version of our algebraic approach can be extended to multiple brane insertions as well. As an example we would like to insert two -matrices into the diagram corresponding to the gauge theory. The DIM network is depicted in Fig. 11.

The network produces the elliptic -character corresponding to the first symmetric representation of :
| (99) |
where is given by Eq. (98) and we have defined the elliptic version of the structure function (Eq. (79)),
| (100) |
Note that we have defined the elliptic versions of all the functions featuring in the -characters using the Jacobi theta function instead of . It is easy to check that the functional form of the -character would not have changed if we had defined them using .
7.2 Refined vertex computation
Let us also comment on an alternative derivation of the elliptic -character (97). As shown in [32], [33], the elliptic deformation of a vacuum matrix element of a network of intertwiners can be achieved by taking the trace of the network instead. To this end we need to evaluate the matrix elements associated with external horizontal lines (Fock representations) in the diagram from Fig. 6 of the form , where ‘‘’’ stand for a product of the intertwining operators and . We then perform the sum over all possible Young diagrams with the weight . To get back the undeformed expression (54) one needs to take so that only the vacuum matrix element contributes to the sum.
This approach is parallel to the refined topological vertex computation in which one studies the ‘‘compactified’’ toric diagram [40], i.e. the diagram drawn on a cylinder instead of a plane. To be able to glue the external lines in the toric diagram together one needs to ensure that their slopes match. This turns out to be equivalent to requiring that the corresponding gauge theory is superconformal (cf. the diagram which cannot be compactified, e.g. from Fig. 4). Let us demonstrate how it works in several examples.
Fundamental elliptic -character and gauge theory.
We have pointed out before that the -matrix commutes with the vertex operators, which manifests itself in different possible degeneration schemes of the toric diagrams leading to the same -character. In the following we would like to present two different toric diagrams that give rise to the fundamental elliptic -character. The first version is depicted in Fig. 12.

After applying the degeneration condition , and fixing , one can show that the refined topological string partition function reproduces the elliptic -character (97) obtained in the algebraic approach. In the process one also fixes the identification between the Kähler parameters of the CY background and the spectral parameters of Fock representations of the algebra :
| (101) |
and for the insertion point of the spectator brane one gets
| (102) |
Fundamental elliptic -character and gauge theory. Alternative spectator brane position.
The second type of degeneration of the toric diagram leading to the elliptic -character is when the vertical spectator brane is placed in the compact four cycle, as depicted in Fig. 13.
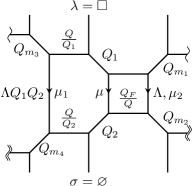
The topological string partition function is identical to the elliptic -character with the same dictionary between spectral parameters and Kähler parameters as in Eq. (101) and the slightly different Kähler class used to parametrize the insertion of the extra brane,
| (103) |
Higher elliptic -character and gauge theory.
Again, we can reproduce the -character (99) obtained in the algebraic approach from refined topological string. To this end we should compute the amplitude corresponding to the diagram depicted in Fig. 14.

8 Conclusions
We have presented a new description of -characters using the -matrix of the DIM algebra. Our approach is inspired by the correspondence between Type IIB branes and representations of the DIM algebra [25], [16] in which the -matrix is viewed as a spectator brane insertion. This allows for a compact uniform description of all -characters of the series both for fundamental (defining) representation and higher representations. We also provide an uplift of the formalism to elliptic -characters.
Several further lines of investigation are apparent. In the present paper we have considered the insertions of the spectator brane with external states and only. One can ask if other choices of external states also correspond to some -characters. The preliminary answer is affirmative, in particular we believe that the exchange of the two external states leads to the -character of the conjugate representation.
A more radical generalization would be to consider the spectator brane that is not a 5-brane, but a 7-brane. It is reasonable to conjecture that in this case the MacMahon -matrix put forward in [34] should appear, giving rise to new -characters. There is a large class of DIM representations arising from degenerations of the MacMahon representation which includes the among others the Fock representation. The MacMahon -matrix will allow one to study -characters corresponding to this class of DIM representations.
The uniform treatment of the series of -characters resembles the uniform approach of [35] to quantum affine Lie algebras. In that case the integrals of motion for all algebras are obtained uniformly in by building the transfer-matrices from a more elementary higher-dimensional object, the Zamolodchikov tetrahedron operator. It would be interesting to investigate if the -characters can be viewed in the same way with certain tetrahedron operator replacing the DIM -matrix.
From a gauge theory perspective it would be desirable to study the connection of our current approach with the work [38] where the -characters were interpreted as partition functions of a coupled - field theory system. The degrees of freedom represent the Wilson line in a gauge theory which looks similar to how the spectator brane producing the -character is coupled to the 5-brane system in our -matrix formalism. This connection definitely merits further investigation.
Recently the algebraic approach to -characters using DIM algebra has been extended to gauge theories with gauge groups from the classical series , and [39]. We believe that our -matrix formalism can also be extended to these cases putting them in the unified framework with the examples presented here. We plan to study such an extension in our next works.
Acknowledgments
YZ is grateful to CK and to Boğaziçi University where this work has been initiated. CK would like to thank the warm hospitality of Niels Bohr Institute where this work was finished. This work is partly supported by the joint grant RFBR 21-51-46010 and TÜBİTAK 220N106. CK’s research is also supported by TÜBİTAK grants 120F184. Mehmet Batu Bayındırlı is supported by TÜBİTAK grant 220N106. This article is based upon work from COST Action 21109 CaLISTA, supported by COST (European Cooperation in Science and Technology).
Appendix A Basic facts about the DIM algebra
In this Appendix we give a short summary of the Ding-Iohara-Miki (DIM) algebra . We will skip many technical details which can be found e.g. in [17], [27], [28].
Definition.
The algebra can be viewed as the quantum deformation of the universal enveloping algebra of a Lie algebra generated by the elements with satisfying
| (105) |
where are two central elements. The Lie algebra is doubly graded with having grading . We denote the grading operators by and respectively:
| (106) |
The automorphism group acts on so that the indices of the generators and the central charges transform in the fundamental two-dimensional representation and its conjugate respectively.
The quantum deformation of is controlled by the parameter . When is equal to one, the Lie algebra relations (105) are reproduced. We will keep the notation for the elements of the quantum deformed universal enveloping algebra corresponding to the elements of the Lie algebra, though the relations between them will become nonlinear after the deformation. We will not write these complicated relations explicitly here (see e.g. [28]).
The double grading survives the quantum deformation, while the action is uplifted to the action of its universal cover . Another nontrivial property of the algebra is that the parameter of , the deformation parameter and their inverse product enter the commutation relations only as symmetric combinations.
The automorphism group and the symmetry under the permutation of the deformation parameters imply that the set of representations of is organized into orbits of the group action.
Coproduct(s).
The DIM algebra is a nontrivial Hopf algebra. To write out the coproduct it will be convenient to introduce the generating currents
| (107) | ||||
| (108) |
where , and and are the central element of the DIM algebra corresponding to the central elements and of respectively.
In terms of the currents (107), (108) the coproduct can be written as
| (109) | ||||
| (110) | ||||
| (111) | ||||
| (112) | ||||
| (113) |
where , . In fact, the coproduct is one of infinitely many non-equivalent coproducts on the DIM algebra. In the literature on refined topological strings the choice of coproduct is known as the choice preferred direction (the coproducts are parametrized by directions in the two-dimensional plane). For the sake of brevity we will not explore here the issue of multiple coproducts, but simply use Eqs. (109)–(111) throughout the whole paper.
Fock representations.
There exist representations of on the Fock space of a free chiral boson with momentum (also called spectral parameter). As we have mentioned above, the representations of the algebra are organized into orbits. The family of Fock representations corresponds to the product of the orbit of the vector under action777The extra part of the universal cover can be absorbed by the shift of the spectral parameter and the rescaling of the generators. and the orbit of a pair under permutations of . Hence, a Fock representation is characterized by a pair of coprime integers and a choice of two out of three deformation parameters.
The two examples of () and will be particularly important for our investigation and we write them out explicitly. The two representations are of course related by the action, so one may wonder why consider them separately. The reason for this is that we know the action of on Fock representations only in terms of the generating currents , on which (unlike on for general ) the action of is not explicit.
-
1.
usually called the horizontal Fock representation. The states of the Fock representation, which we denote , are labelled by Young diagrams . They are in one to one correspondence with monomials of the form , where , are the creation and annihilation operators satisfying the commutation relations (16) and is the vacuum state annihilated by with .
The action of the generating currents in this representation is [25]
(114) (115) (116) (117) (118) (119) -
2.
also known as the vertical Fock representation. It is convenient write down the action of the generating currents in this representation in the basis of Macodnald polynomials [29], i.e. assume that :
(120) (121) (122) (123) where denotes the Young diagram with replaced by , is defined in Eq. (15) and
(124) (125) (126) and
(127)
-reduction and -characters.
Using the coproduct (109)–(111) one defines the action of the DIM algebra on a tensor product of horizontal Fock representations with different spectral parameters .
The generators of the DIM algebra in this representation can be expressed in terms of the currents of the smaller algebra: the -algebra and an extra Heisenberg algebra. -algebra is generated by currents of spins , which schematically look as follows
| (128) |
where are certain free field vertex operators acting on the tensor product of Fock representations. We denote the additional Heisenberg current by .
The currents are in fact the -characters [11] of type corresponding to fundamental representations . In -character approach the vertex operators are written in terms of the so-called -operators, certain elementary free boson exponents,
| (129) |
where one assumes that .
The action of the DIM current on can be expressed through the two lowest spin -currents, the Hiesnberg current and -deformed Virasoro stress-energy tensor . Schematically we have (see [17] for explicit formulas)
| (130) |
The Heisenberg current commutes with other -currents, and thus can be ignored in most formulas888Notice, how this property of the current is similar to that of the “empty crossing” from sec. 3 given by Eq. (27). Indeed, depends on the same “diagonal” combination of free bosons as the Heisenberg current. However, it includes only the positive modes, whereas is a standard free field exponent depending on both positive and negative modes..
Appendix B Conventions and identities
In this Appendix we summarize some conventions and identities used in the main text. The instanton counting partition function for (quiver) gauge theories with hypermultiplets in (anti)fundamental, bi-fundamental and adjoint representations can be obtained using standard Nekrasov formulas [41]. The partition function is expressed as a sum over -tuples of Young diagrams for each node in the quiver while the summand is given by the products of factors corresponding to each multiplet, which are built from the following combinatorial factor :
| (131) |
There exist more representations of the factor , but we will only use these three. It is evident from the first expression in Eq. (B) that the factor is a polynomial. It also obeys some nice identities:
| (132) |
where denotes the total number of boxes in the Young diagram , with is the number of non-empty rows of , and is a shorthand for .
In our calculations, we have used an alternative expression for the contributions of the -operators which follows from the identity
| (133) |
The identity (133) can be proven using the representation of the Nekrasov factor in terms of -Pochhammer symbols from the third line of Eq. (B).
These factors (133) have convenient degeneration properties, and we make extensive use one of them:
| (134) |
Indeed, one can see that the boundary box in the first row, , produces a vanishing contribution to the product in unless . Thus, to get a nonvanishing answer for the Young diagram should have the form . Furthermore, a box with coordinates if present also contributes a vanishing factor, so that the only nontrivial possibility for is either or . This property will allow us to truncate a sum over infinitely many Young diagrams to a finite sum with only two terms.
Appendix C Algebraic engineering of the theory
In the main text we have introduced the algebraic approach to calculating -characters based on the intertwining operators of the DIM algebra . For the sake of completeness, we review in this section the calculation of the instanton partition function of the pure theory without spectator brane insertions using similar technique which may be called algebraic engineering. In [25], the refined topological vertices [21] were shown to be matrix elements of intertwining operators of the DIM algebra between triplets of Fock spaces each labelled by a pair of integers and a spectral parameter. From the Type IIB string view point, these integers are the -charges of 5-branes corresponding to Fock representations, while in M-theory they encode the degeneration loci of a toric diagram. The definitions of the Fock representations of the algebra are collected in Appendix A.
In our calculations, we use the following intertwining operators between triplets of Fock representations:
| (138) |
and its dual
| (139) |
where , , and are defined by Eqs.(15), (18)–(20) respectively, and we have used the identity Eq. (136). Note that the -type Fock space , whose states are labelled by the diagrams and in Eqs. (138), (139), is associated with the so-called preferred direction of the refined topological vertex.
The network giving rise to the gauge theory is depicted in Fig. 15. It consists of two intertwining intertwining operators and two dual intertwining operators .

There are two possible choices for the ‘‘Chern-Simons level’’ for the theory, which is reflected in the choices for the levels of the Fock representations in Fig. 15: and corresponds to vanishing Chern-Simons level, and and gives rise to level one, all other choices being either inconsistent or equivalent to one of those two.
Generically, the sums over Young diagrams living on the edges along the preferred directions (vertical in Fig. 15) cannot be performed in a closed form for toric geometries with compact four-cycles. Instead they correspond to the instanton sums in the gauge theory that the toric diagram engineers. The same is true in the algebraic approach as well and we will end up with the same instanton sums over Young diagrams. In this Appendix we consider a quiver with a single gauge node, hence a single set of vertical edges stretched between two horizontal branes each associated with a Fock space. On these Fock spaces act two sets of Heisenberg generators commuting with each other:
| (140) | |||
| (141) |
where the superscripts label the horizontal lines. Two such lines are ‘‘glued’’ to each other along a vertical edge by inserting a complete basis of states in the vertical Fock representation, the basis of Macdonald polynomials,
| (142) |
where is defined in Eq. (31). The sums over , living on the vertical edges in Fig. 15 will turn into instanton sums in the gauge theory partition function.
As depicted in Fig. 15 we keep the external states in the horizontal Fock spaces empty, i.e. we calculate the vacuum-to-vacuum matrix elements of the form . We can proceed in two different ways. We either insert complete sets of states between all the intertwining operators in the picture and calculate matrix elements of the individual operators before performing the sums over intermediate states explicitly, or we construct the screening charges by combining an intertwining operator with the dual one coupled through a vertical edge. We choose the second method and find that the partition function is given by the vacuum matrix element of the following two operators
| (143) |
where the screening charge is
| (144) |
and are deformed Heisenberg generators and can be expressed as a linear combination of , generators,
| (145) |
Using the Wick’s theorem for the bosons (145) we get
| (146) |
The normal ordered part in the right hand side of Eq. (146) gives a simple factor when evaluated between the vacuum states. After some straightforward manipulations, we get the following expression for general and :
| (147) |
which reproduces the instanton partition function for gauge theory after certain identifications between the algebraic and gauge theoretic variables.
Appendix D Elliptic deformation of vertex operators and DIM algebra
Elliptic deformation of the DIM algebra as well as its free field representation were introduced in [36]. The deformation of the algebra is written in terms of the generating currents (107), (108) with rational factors in their commutation relations being replaced by Jacobi theta functions with elliptic modulus . The coproduct is formally given by the same formulas (109)–(113) as in the undeformed case.
In this Appendix we briefly review the elliptic deformation prescription for free field vertex operators (see [33] for more details) which produces the elliptic version of the horizontal Fock representation of DIM algebra starting from the formulas of Appendix A. We also review the elliptic deformation of the vertical Fock representation introduced in [37].
Elliptic deformation of the horizontal Fock representation.
Suppose a vertex operator has the following generic mode expansion,
| (148) |
where are the -deformed Heisenberg generators satisfying the commutation relations (16). Notice that the generating currents of DIM algebra in the horizontal Fock representation (120)–(123) also have the form (148).
It turns out that to reproduce elliptically deformed DIM commutation relations it is not enough to deform the commutation relations (16) of the generators . One also has to introduce another set of Heisenberg generators which commute with the original generators and have slightly different commutation relations among themselves. The elliptically deformed commutation relations for the Heisenberg generators with elliptic parameter are as follows:
| (149) |
The the elliptic version of the vertex operator (148) can be expressed as a product of two vertex operators in terms of both sets of Heisenberg generators,
| (150) |
where
| (151) | ||||
| (152) |
Applying the prescription (150)–(152) to DIM algebra generators in the horizontal Fock representation (114)–(117) we obtain the horizontal Fock representation of the elliptic DIM algebra.
Elliptic deformation of the vertical Fock representation.
References
- [1] V. G. Drinfeld, Proc. ICM Berkeley (1986), 798–820.
- [2] M. Jimbo, Lett. Math. Phys. 10 (1985), 63–69.
- [3] R. J. Baxter, Exactly solved models in statistical mechanics, doi:10.1142/9789814415255_0002
- [4] E. Witten, Commun. Math. Phys. 121 (1989), 351–399 doi:10.1007/BF01217730
- [5] J. A. Minahan, J. Phys. A 39 (2006), 12657–12677 doi:10.1088/0305-4470/39/41/S02
- [6] N. A. Nekrasov and S. L. Shatashvili, Prog. Theor. Phys. Suppl. 177 (2009), 105–119 doi:10.1143/PTPS.177.105 [arXiv:0901.4748 [hep-th]].
- [7] V. V. Bazhanov, S. L. Lukyanov and A. B. Zamolodchikov, Commun. Math. Phys. 177 (1996), 381–398 doi:10.1007/BF02101898 [arXiv:hep-th/9412229 [hep-th]].
- [8] V. V. Bazhanov, S. L. Lukyanov and A. B. Zamolodchikov, Commun. Math. Phys. 190 (1997), 247–278 doi:10.1007/s002200050240 [arXiv:hep-th/9604044 [hep-th]].
- [9] V. V. Bazhanov, S. L. Lukyanov and A. B. Zamolodchikov, Commun. Math. Phys. 200 (1999), 297–324 doi:10.1007/s002200050531 [arXiv:hep-th/9805008 [hep-th]].
- [10] H. Knight, Journal of Algebra, 174 (1995) 1, 187–196, ISSN 0021-8693, https://doi.org/10.1006/jabr.1995.1123.
-
[11]
E. Frenkel and
N. Reshetikhin, [arXiv:q-alg/9708006 [q-alg]]
E. Frenkel and N. Reshetikhin, [arXiv:math/9810055 [math.QA]]. -
[12]
H. Nakajima, Physics and Combinatorics, 196–219 (2001),
https://doi.org/10.1142/9789812810007_0009,
[arXiv:math/0009231 [math.QA]]
H. Nakajima, [arXiv:math/0105173 [math.QA]]
H. Nakajima, [arXiv:math/0204184 [math.QA]] - [13] H. Liu, SIGMA 18 (2022), 090, https://doi.org/10.3842/SIGMA.2022.090 [arXiv:2203.07072 [math.QA]]
-
[14]
J. Ding, K.
Iohara, Lett. Math. Phys. 41 (1997) 181–193, q-alg/9608002
K. Miki, J. Math. Phys. 48 (2007) 123520 -
[15]
H. Awata, H. Kanno, A. Mironov, A. Morozov, A. Morozov, Y. Ohkubo and Y. Zenkevich,
JHEP 10 (2016), 047
doi:10.1007/JHEP10(2016)047
[arXiv:1608.05351 [hep-th]].
H. Awata, H. Kanno, A. Mironov, A. Morozov, A. Morozov, Y. Ohkubo and Y. Zenkevich, Nucl. Phys. B 918 (2017), 358-385 doi:10.1016/j.nuclphysb.2017.03.003 [arXiv:1611.07304 [hep-th]]. - [16] Y. Zenkevich, JHEP 12 (2021), 027 doi:10.1007/JHEP12(2021)027 [arXiv:2012.15563 [hep-th]].
- [17] A. Mironov, A. Morozov and Y. Zenkevich, Phys. Lett. B 762 (2016), 196-208 doi:10.1016/j.physletb.2016.09.033 [arXiv:1603.05467 [hep-th]].
- [18] J. E. Bourgine, M. Fukuda, K. Harada, Y. Matsuo and R. D. Zhu, JHEP 11 (2017), 034 doi:10.1007/JHEP11(2017)034 [arXiv:1703.10759 [hep-th]].
- [19] T. Kimura, H. Mori and Y. Sugimoto, JHEP 01 (2018), 025 doi:10.1007/JHEP01(2018)025 [arXiv:1705.03467 [hep-th]].
-
[20]
S. M. Khoroshkin, V. N. Tolstoy, V. N. Tolstoy,
S. M. Khoroshkin, Commun. Math. Phys. 141, 599–617 (1991). https://doi.org/10.1007/BF02102819
Functional Analysis and Its Applications 26, 69–71 (1992). https://doi.org/10.1007/BF01077085 -
[21]
H. Awata and H. Kanno,
JHEP 05 (2005), 039
doi:10.1088/1126-6708/2005/05/039
[arXiv:hep-th/0502061 [hep-th]].
A. Iqbal, C. Kozcaz and C. Vafa, JHEP 0910 (2009) 069 doi:10.1088/1126-6708/2009/10/069 [hep-th/0701156]. - [22] R. Gopakumar and C. Vafa, Adv. Theor. Math. Phys. 3, 1415-1443 (1999) doi:10.4310/ATMP.1999.v3.n5.a5 [arXiv:hep-th/9811131 [hep-th]].
- [23] N. C. Leung and C. Vafa, Adv. Theor. Math. Phys. 2, 91-118 (1998) doi:10.4310/ATMP.1998.v2.n1.a4 [arXiv:hep-th/9711013 [hep-th]].
-
[24]
N. Nekrasov,
JHEP 1603 (2016) 181 doi:10.1007/JHEP03(2016)181
[arXiv:1512.05388 [hep-th]].
N. Nekrasov, Adv. Theor. Math. Phys. 21 (2017) 503 doi:10.4310/ATMP.2017.v21.n2.a4 [arXiv:1608.07272 [hep-th]].
N. Nekrasov, Commun. Math. Phys. 358 (2018) no.3, 863 doi:10.1007/s00220-017-3057-9 [arXiv:1701.00189 [hep-th]].
N. Nekrasov, arXiv:1711.11011 [hep-th], arXiv:1711.11582 [hep-th]. - [25] H. Awata, B. Feigin and J. Shiraishi, JHEP 03 (2012), 041 doi:10.1007/JHEP03(2012)041 [arXiv:1112.6074 [hep-th]].
- [26] Y. Zenkevich, [arXiv:2212.14808 [hep-th]].
- [27] Y. Zenkevich, JHEP 08 (2021), 149 doi:10.1007/JHEP08(2021)149 [arXiv:1812.11961 [hep-th]].
- [28] Y. Zenkevich, JHEP 03 (2023), 193 doi:10.1007/JHEP03(2023)193 [arXiv:2112.14687 [math.QA]].
- [29] I. G. Macdonald, Symmetric functions and Hall polynomials, Second Edition, Oxford University Press, 1995
-
[30]
T. Kimura and V. Pestun,
arXiv:1512.08533 [hep-th].
T. Kimura and V. Pestun, arXiv:1705.04410 [hep-th]. - [31] T. Kimura and V. Pestun, arXiv:1608.04651 [hep-th].
-
[32]
F. Nieri,
Lett. Math. Phys. 107 (2017) no.11, 2147-2187
doi:10.1007/s11005-017-0986-3 [arXiv:1511.00574 [hep-th]].
A. Iqbal, C. Kozcaz and S. T. Yau, [arXiv:1511.00458 [hep-th]]. - [33] M. Ghoneim, C. Kozçaz, K. Kurşun and Y. Zenkevich, Nucl. Phys. B 978 (2022), 115740 doi:10.1016/j.nuclphysb.2022.115740 [arXiv:2012.15352 [hep-th]].
- [34] H. Awata, H. Kanno, A. Mironov, A. Morozov, K. Suetake and Y. Zenkevich, JHEP 04 (2019), 097 doi:10.1007/JHEP04(2019)097 [arXiv:1810.07676 [hep-th]].
- [35] V. V. Bazhanov and S. M. Sergeev, J. Phys. A 39 (2006), 3295-3310 doi:10.1088/0305-4470/39/13/009 [arXiv:hep-th/0509181 [hep-th]].
- [36] Y. Saito, [arXiv:1301.4912 [math.QA]].
- [37] L. Wang, K. Wu, , J. Yang, Z. Yang, Front. Math. China 15, 155–166 (2020). https://doi.org/10.1007/s11464-020-0815-3
- [38] N. Haouzi and C. Kozçaz, Commun. Math. Phys. 393 (2022) no.2, 669-779 doi:10.1007/s00220-022-04375-0 [arXiv:1907.03838 [hep-th]].
- [39] S. Nawata, K. Zhang and R. D. Zhu, [arXiv:2302.00525 [hep-th]].
- [40] T. J. Hollowood, A. Iqbal and C. Vafa, JHEP 03 (2008), 069 doi:10.1088/1126-6708/2008/03/069 [arXiv:hep-th/0310272 [hep-th]].
- [41] N. A. Nekrasov, Adv. Theor. Math. Phys. 7 (2003) no.5, 831-864 doi:10.4310/ATMP.2003.v7.n5.a4 [arXiv:hep-th/0206161 [hep-th]].