On rigidity of Coxeter systems up to finite twists and separations of Coxeter generating sets
Abstract.
In this paper, we study the twist-conjecture for Coxeter systems and rigidity of Coxeter systems up to finite twists. For Coxeter systems and , under the untangle-condition for conjugate subsets, we investigate separations and type(I) and type(II) subsets of and and give an equivalent condition of and that are conjugate up to finite twists. We provide one direction of approach to solving the twist-conjecture and the isomorphism problem for Coxeter groups of finite ranks.
Key words and phrases:
Coxeter groups; Coxeter systems; the isomorphism problem for Coxeter groups; rigidity of Coxeter systems; twists of Coxeter systems2010 Mathematics Subject Classification:
20F551. Introduction and preliminaries
The purpose of this paper is to investigate the twist-conjecture for Coxeter systems and rigidity of Coxeter systems up to finite twists. Definitions and details of Coxeter groups and Coxeter systems are found in [1] and [11]. In this paper, we suppose that all Coxeter groups are of finite ranks. The isomorphism problem for Coxeter groups is open.
Problem 1.1 (The isomorphism problem for Coxeter groups).
For given Coxeter systems and , find an algorithm to determine whether the Coxeter groups and are isomorphic or not.
For a Coxeter system and a subset of , is defined as the subgroup generated by in . It is well known that also becomes a Coxeter system. A subset of is said to be spherical, if the subgroup is finite. If is a spherical subset of , then it is known that there exists a unique longest length element in that is denoted by . For a subset of , we denote . For a Coxeter group , a subset of is called a Coxeter generating set for , if is a Coxeter system.
Recent research on the isomorphism problem for Coxeter groups and rigidity of Coxeter groups and Coxeter systems can be found in [2], [4], [5], [10], [12], [14], [15], [16], [17] and [18].
A Coxeter system is said to be reflection-rigid, if it is determined by the Coxeter group and the set of reflections
up to isomorphisms; that is, for any Coxeter generating set for such that the reflection sets and are equal, two Coxeter systems and are isomorphic.
Also a Coxeter system is said to be strongly-reflection-rigid, if is determined by the Coxeter group and the reflection set up to conjugate; that is, for any Coxeter generating set for such that the reflection sets and are equal, two Coxeter generating sets and are conjugate in .
Let be a Coxeter group. Two Coxeter generating sets and for are said to be angle-compatible [5] (or sharp-angled [12]), if for any as there exists as such that and are conjugate in . Here for , is the order of in the group . We say that a Coxeter system is angle-rigid, if for any Coxeter generating set for such that and are angle-compatible, two Coxeter systems and are isomorphic. Also a Coxeter system is said to be strongly-angle-rigid, if for any Coxeter generating set for such that and are angle-compatible, two Coxeter generating sets and are conjugate in .
It is known that if two Coxeter generating sets and for are angle-compatible then the reflection sets and are equal (see [5]). Hence if a Coxeter system is (strongly-)reflection-rigid, then it is (strongly-)angle-rigid.
Recently, Marquis and Mühlherr have proved the following.
Theorem 1.2 ([12, Corollary 1.1]).
The isomorphism problem for Coxeter groups is solved as soon as the following problem is solved.
Problem 1.3 ([12]).
Let be a Coxeter system. Find all Coxeter generating sets such that is sharp-angled with respect to .
Thus if for a given Coxeter system we can output all Coxeter generating sets for such that and are angle-compatible, then the isomorphism problem for Coxeter groups is solved.
Caprace and Przytycki have given the following.
Theorem 1.4 ([5, Theorem 1.1]).
Let and be angle-compatible Coxeter generating sets for a group . If is twist-rigid, then and are conjugate.
Hence, every twist-rigid Coxeter system is strongly-angle-rigid.
Here (and ) is said to be twist-rigid, if has no elementary twist [5]. We give a definition and detail of a “twist” later.
Definition 1.5.
Let be a Coxeter system and let be a subset of . We consider the irreducible decomposition
where is a disjoint union and each is an irreducible Coxeter system. Here each is either finite or infinite. We define
Then is a disjoint union, is finite, is infinite (if is non-empty), and .
Let be a Coxeter system. We say that a subset of is a spherical-product subset of , if is non-empty and for some non-empty spherical subset of . Here if is a spherical-product subset of , then either
-
(1)
and (where is spherical),
-
(2)
and (where ), or
-
(3)
and (where for a spherical subset of such that , if we put then and ).
A subset of is said to be connected, if for any as , there exists a sequence in such that is finite for any (that is, the nerve of is connected). Also we often say that a spherical-product subset separates , if is connected and is not connected (that is, the nerve of separates the connected nerve of to some at least two components).
If a spherical-product subset of separates , then for some non-empty subsets and of ,
-
(1)
that is a disjoint union and
-
(2)
for any and .
There is a spherical subset of such that . Here if is non-empty then we take . Then and we obtain a Coxeter generating set for as
that is an elementary twist ([2], [3], [5], [13], [14]). Also in the case that is not connected, we can consider that separates . If that is a disjoint union and for any and , then for any we obtain a Coxeter generating set for that is also an elementary twist ([2], [3], [5], [6], [14]).
Hence, is twist-rigid if and only if is connected and any spherical-product subset does not separate .
More generally, let be a spherical-product subset of that separates and let and be non-empty subsets of such that
-
(1)
that is a disjoint union,
-
(2)
for any and and
-
(3)
for some .
Then we obtain a Coxeter generating set for as
that is called a general-twist. Here there is a possibility that every twist can be denoted by some elementary-twists. The author does not know whether this always holds.
In this paper, we often say that a Coxeter generating set is obtained from by some finite twists, if there exists a sequence of Coxeter generating sets for such that each is obtained from by some twist. We also say that Coxeter generating sets and for are conjugate up to finite twists, if there exists a Coxeter generating set for such that is obtained from by some finite twists and is conjugate to . Here Coxeter generating sets and for are conjugate up to finite twists if and only if there exist Coxeter generating sets and for such that and are obtained from and by some finite twists respectively and is conjugate to .
Now we define new concepts “separations” and “untangle-conjugate” on Coxeter systems. These definitions are technical. The purpose of this paper is to give a further reduction of the isomorphism problem for Coxeter groups. These definitions are designed and constructed as the main results in this paper hold and as two Coxeter generating sets with some conditions using them are conjugate up to finite twists.
First, the following lemma is known.
Lemma 1.6 (cf. [2]).
Let and be Coxeter systems. For each maximal spherical subset of , there exists a unique maximal spherical subset of such that and are conjugate in .
Here we say that two Coxeter systems and are maximal-spherical-subset-compatible, if for each maximal spherical subset of , there exists a maximal spherical subset of such that and are conjugate in (where is unique by Lemma 1.6). If two Coxeter systems are maximal-spherical-subset-compatible then they are angle-compatible. Indeed for each as , there exists a maximal spherical subset of containing . If is a maximal spherical subset of such that and are conjugate in then some subset is conjugate to .
For a Coxeter system as is connected and for , we say that is a twist-rigid subset of , if is connected and if there does not exist a spherical-product subset of such that separates and separates . Here we note that need not be a twist-rigid Coxeter system in general (see examples in Section 2).
Let be a Coxeter system. We suppose that is connected. Let be a set of subsets of such that
-
(1)
,
-
(2)
each is connected and a union of some maximal twist-rigid subsets of , and
-
(3)
for each maximal twist-rigid subset of , there exists a unique element such that .
A subset of is called a separator of , if the following conditions (i)–(v) hold:
-
(i)
is a spherical-product subset of .
-
(ii)
separates .
-
(iii)
For any , there exists a unique such that . Here and are the connected components of and we define for each .
-
(iv)
There exist such that , and for some as .
-
(v)
Let . For any distinct elements such that , if is maximal in
for any , then for some .
A set of subsets of is called a separation of , if the following conditions (1)–(4) hold:
-
(1)
.
-
(2)
Each is connected and a union of some maximal twist-rigid subsets of .
-
(3)
For each maximal twist-rigid subset of , there exists a unique element such that .
-
(4)
For distinct elements , if is maximal in
for any , then for each ,
-
(a)
is a separator of , and
-
(b)
and for some as , where and are the connected components of .
-
(a)
In the case that is not connected, a set of subsets of is called a separation of , if for the connected components of (that is, each is a maximal connected subset of and is a disjoint union), is a separation of for any .
For two sets and of subsets of , we denote , if for any , for some .
A separation of is said to be minimal, if
-
there does not exist a separation of such that and any is contained in some .
A minimal separation is “minimal” with respect to the partial order “”.
Let be a Coxeter system and let be a set of subsets of . We consider a twist
where is a spherical-product subset of and such that , separates as that is a disjoint union and for any and . A twist is said to be preserving , if for any , or (that is, there does not exist such that and ). If the twist is preserving then
is a set of subsets of and is called the set induced by and the twist.
Here if is a separation of , then the induced set is a separation of and it is called the separation induced by and the twist.
Let be a set of subsets of . We often say that is obtained from by some finite twists preserving , if there exists a sequence of Coxeter generating sets for such that is a twist of preserving for each where and is the set of subsets of induced by and the twist for each .
Definition 1.7.
Let and be Coxeter systems and let and be separations of and respectively. We say that and are compatible on separations and , if
-
(i)
each is conjugate to some unique and
-
(ii)
each is conjugate to some unique .
We define that two Coxeter systems and are some-separation-compatible, if and are compatible on some separations and of and respectively.
Every spherical subset of is not separated by any spherical(-product) subset of . Hence is a twist-rigid subset of and for some maximal twist-rigid subset of .
If two Coxeter systems are some-separation-compatible, then they are maximal-twist-rigid-subset-compatible and maximal-spherical-subset-compatible, hence they are angle-compatible.
We define and investigate type(I)-type(II)-compatible later.
In this paper, we study when are Coxeter generating sets conjugate up to finite twists under “the untangle-condition” on conjugate subsets.
Let be a Coxeter system. We define “untangle-conjugate”.
Definition 1.8.
For spherical subsets , and of as , we denote , if .
Let and be non-empty subsets of . They are uniquely denoted by and . For a spherical subset of as , we denote , if , and for any and .
Here if , then and are conjugate and
Also if
then and are conjugate and for ,
We say that conjugate subsets and of are untangle, if the following statements (1) and (2) hold:
-
(1)
In the case that , there exist a sequence of subsets of and a sequence of spherical subsets of such that
-
(2)
In the case that , for as , we define the bijective map by for any . For any as , for , or, there exist a sequence of subsets of and a sequence of spherical subsets of such that
and for .
Now we define “the untangle-conjugate-condition” and “the untangle-condition”.
Definition 1.9.
We say that a Coxeter system has the untangle-conjugate-condition, if all conjugate subsets and of are untangle and the following holds:
-
()
Let be a Coxeter generating set for , let be the connected components of and let be the connected components of (that is, ). If and are conjugate in for any , then there exists a Coxeter generating set for such that is obtained from by some finite twists and and are conjugate.
Also we say that a Coxeter system has the untangle-condition, if all Coxeter systems obtained from by some finite twists have the untangle-conjugate-condition.
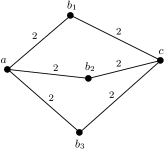
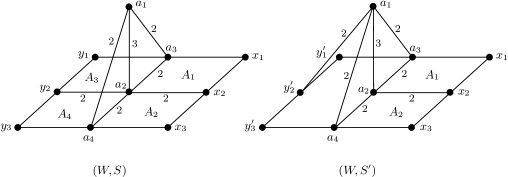
Example 1.10.
We consider a Coxeter system defined by Figure 1 (i) or (ii).
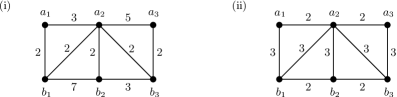
Here is the vertex set of the figure and for any . If two vertices as do not span any edge in the figure then we define . If two vertices as span an edge numbering then define .
Let , , , and . Also let , , and .
Then and are untangle-conjugate and
in both cases (i) and (ii).
In the case (ii), for ,
Then . Here and . Hence is the bijective map such that and .
Example 1.11.
We consider a Coxeter system defined by Figure 2.
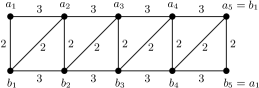
Here we identify and . (The nerve of is a triangulation of the Möbius band.)
Let , , , , , , and . Also let , , , , , , and .
Then
For , we have that . Here and .
For example, if , , , , , , or , then .
For any as , if [ and ] then for . Also if [ and ] then as above.
The author does not know whether there is an example of non-untangle-conjugate subsets of a Coxeter generating set.
Theorem 1.12.
Let and be Coxeter systems with the untangle-condition. If and are some-separation-compatible, then and are conjugate up to finite twists.
We obtain a corollary from Theorem 1.12.
Corollary 1.13.
For Coxeter systems and with the untangle-condition, the following statements are equivalent
-
(i)
and are conjugate up to finite twists.
-
(ii)
and are some-separation-compatible for some Coxeter generating set obtained from by finite twists.
Now we define “type(I)” and “type(II)” subsets and “the standard-separation” of a Coxeter generating set.
Definition 1.14.
Let be a Coxeter system. For each minimal separation of , we define as the set of separators of . Let
Then we define the separation of by as follows.
Let be the set of maximal twist-rigid subsets of . For , we denote if any does not separate and ; that is, there exist a minimal separation of and an element such that . Then “” is an equivalence relation on the set . Let that is the equivalence class for . Here
for some as if . Let
for each . Then we define
In Section 5, we show that is a separation of . We say that is the standard separation of .
A subset of is said to be type(I), if holds for any minimal separation of . Let be the set of type(I) subsets of ; that is,
We also define
and every element is called a type(II) subset of .
Then is a disjoint union. Here , and are uniquely determined by the Coxeter system .
Let be a Coxeter system. We say that for a subset of , is a twist of that induces some twist of , if there exist a spherical-product subset of and such that , separates , is a twist of obtained by and , separates and some twist of is obtained by and . We also say that is obtained from by some finite twists that induces some twist of , if there exist a sequence and a sequence of Coxeter generating sets for such that for any and is a twist of that induces a twist of for each .
We define “type(II)-compatible”.
Definition 1.15.
Let and be Coxeter systems. We say that and are type(II)-compatible, if
-
there exists obtained from by some finite twists that induce some twists of preserving such that and are conjugate in .
This means that the type(II) subsets and are conjugate up to finite twists that induce some twists of preserving .
Now we define “type(I)-type(II)-compatible”.
Definition 1.16.
Two Coxeter systems and are said to be type(I)-type(II)-compatible, if for the standard separations and of and respectively,
-
(i)
each is conjugate to some unique ,
-
(ii)
each is conjugate to some unique ,
-
(iii)
for each , there exists a unique such that and are type(II)-compatible, and
-
(iv)
for each , there exists a unique such that and are type(II)-compatible.
In Section 6, we show that if two Coxeter systems with the untangle-condition are type(I)-type(II)-compatible, then they are some-separation-compatible up to finite twists. Thus, if two Coxeter systems and with the untangle-condition are type(I)-type(II)-compatible, then and are conjugate up to finite twists by Theorem 1.12.
We show the following theorem in Section 6.
Theorem 1.17.
For Coxeter systems and with the untangle-condition, the following two statements are equivalent
-
(i)
and are conjugate up to finite twists.
-
(ii)
and are type(I)-type(II)-compatible.
For given Coxeter systems and , it seems that to consider whether
-
(a)
and are type(I)-type(II)-compatible
is more simple than to consider whether
-
(b)
and are some-separation-compatible for some Coxeter generating set obtained from by finite twists.
In Theorem 1.17, we use two conditions as “the untangle-condition” and “type(I)-type(II)-compatible” for Coxeter systems.
Problem 1.18.
The untangle-conjugate-condition will always hold for all Coxeter systems ?
Problem 1.19.
Angle-compatible Coxeter systems and will be always type(I)-type(II)-compatible?
If there exist counter-examples of angle-compatible Coxeter systems and such that any and obtained from and by some finite twists respectively are not type(I)-type(II)-compatible, or a Coxeter system that does not have the untangle-conjugate-condition, then they are meaningful examples.
If Problems 1.18 and 1.19 both can be solved affirmatively, then the twist-conjecture for Coxeter systems can be solved affirmatively from Theorem 1.17. Also if Problem 1.3 can be solved from the twist-conjecture for Coxeter systems affirmatively, then the isomorphism problem for Coxeter groups of finite ranks can be solved by Theorem 1.2.
2. Remarks and examples on separations
We introduce some remarks and examples on separations of Coxeter generating sets.
Remark 2.1.
Let be a Coxeter system as is connected. Let be a separation of and let . Then we may denote such that for each , is maximal in
Here by the definition of a separation of , is a separator of and it is a spherical-product subset of that separates for any . Hence has a structure as
Remark 2.2.
Let be a Coxeter system as is connected and let be a spherical-product subset of that separates . Let be the set of maximal twist-rigid subsets of . Suppose that are the connected components of and is a disjoint union. Let
| for each and let | ||||
Here each (and ) is connected and it is a union of some maximal twist-rigid subsets of (if is non-empty). Let if is non-empty, and let if is empty. Then is a separation of . We say that is the induced separation of by .
Let be a minimal separation of such that . Then does not separate any . Thus we can obtain a minimal separation of from a spherical-product subset of that separates such that does not separate any .
Let be the set of spherical-product subsets of that separate . By the above argument, we obtain the separation of induced by each . If is non-empty (that is, if is not a twist-rigid Coxeter system), then for any minimal separation of , for some . Hence, from considering the set of spherical-product subsets that separate and the induced separations , we can obtain all minimal separations of .
We give some examples.
Example 2.3.
We consider Coxeter systems () defined by Figure 3.
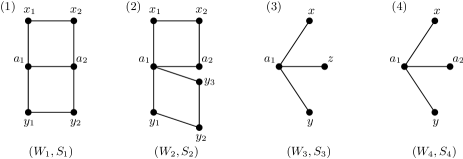
Here , , and are the vertex sets of the figures , , and respectively in Figure 3. Let . We define for any . If two vertices as do not span any edge in the figure then we define . If two vertices as span an edge then we consider that has some (arbitrary) finite number at least . Then a Coxeter system is obtained.
(1) Let , and in . Then is a spherical-product subset of that separates and where and are the connected components of . Then and . Here is the separation of induced by , and is a separator of .
(2) Let , and in . Then is a spherical-product subset of that separates and where and are the connected components of . Then and . Here is the separation of induced by , and is a separator of (here is not a separator of ).
(3) Let , , and in . Then is a spherical-product subset of that separates and where , and are the connected components of . Then , and . Here is the separation of induced by , and is a separator of .
(4) Let , and in . Then is a spherical-product subset of that separates and where and are the connected components of . Then , and . Here is the separation of induced by , and is a separator of (here is not a separator of ).
Example 2.4.
We consider a Coxeter system defined by Figure 4.
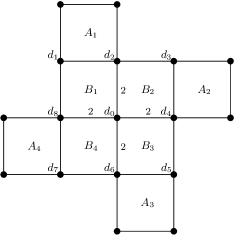
Here is the vertex set of the figure. Let for any . If two vertices as do not span any edge in the figure then we define . If two vertices as span an edge numbering then define . Also if two vertices as span an edge with no numbering then we consider that has some (arbitrary) finite number at least . Then a Coxeter system is obtained.
Let be the set of -vertices around “” in the figure and let be the set of -vertices around “” in the figure for each .
-
(a)
The set of maximal twist-rigid subsets of is
Here
is not a twist-rigid subset of . Indeed for example is a spherical-product subset of that separates and separates . We also note that is a twist-rigid Coxeter system.
-
(b)
The minimal separations of are the 4-sets as
-
(1)
,
-
(2)
,
-
(3)
and
-
(4)
.
-
(1)
-
(c)
The set of type(I) subsets of is
-
(d)
The set of type(II) subsets of is
-
(e)
The standard separation of is
Example 2.5.
We consider a Coxeter system defined by Figure 5.
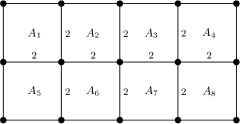
Here is the vertex set of the figure and is defined as in Example 2.4.
Let be the set of -vertices around “” in the figure for each .
-
(a)
The set of maximal twist-rigid subsets of is
-
(b)
The minimal separations of are the 9-sets as
-
(1)
,
-
(2)
,
-
(3)
,
-
(4)
,
-
(5)
,
-
(6)
,
-
(7)
,
-
(8)
and
-
(9)
.
-
(1)
-
(c)
The set of type(I) subsets of is empty.
-
(d)
The set of type(II) subsets of is
where and .
-
(e)
The standard separation of is
Example 2.6.
We consider the Coxeter system defined by Figure 6. Here .
Let , , , and .
-
(a)
The set of maximal twist-rigid subsets of is
-
(b)
The minimal separations of are the 2-sets as
-
(1)
and
-
(2)
.
-
(1)
-
(c)
The set of type(I) subsets of is empty.
-
(d)
The set of type(II) subsets of is .
-
(e)
The standard separation of is .
Example 2.7.
We consider a Coxeter system defined by Figure 7. Here is the vertex set of the figure; that is,
and we define .
Let
Then
is a separation of . For example,
Also , and are separators of and they are spherical-product subsets of that separate . Here we note that , and are spherical-product subsets that do not separate .
The spherical-product subsets of that separate are the 3-sets as
Each induces the separation of as in Remark 2.2. Then for any minimal separation of , for some . Here holds for any , where . Hence is the unique minimal separation of . Thus, there are no type(II) subsets of and
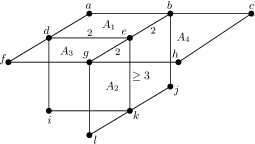
Example 2.8.
We consider a Coxeter system defined by Figure 8. Here is the vertex set of the figure; that is,
Then can be considered as a standard subgroup of in Example 2.7 generated by .
Let
Then the spherical-product subsets of that separate are the 3-sets as
Each induces the separation of as in Remark 2.2. Then for any minimal separation of , for some . Here we note that the set is not a separation of . Then the minimal separations of are the 3-sets as
Hence, there are no type(I) subsets of and
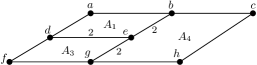
Example 2.9.
We consider Coxeter systems and defined by Figure 9. Here and are the vertex sets of the corresponding figures and we define .
Let , , , and . Here , and . Then is a twist of by and (where for ).
In , let be the set of -vertices around “” in the figure for each . Then the minimal separations of are the 9-sets as
-
(1)
,
-
(2)
,
-
(3)
,
-
(4)
,
-
(5)
,
-
(6)
,
-
(7)
,
-
(8)
and
-
(9)
.
The Coxeter system is denoted by Figure 10.
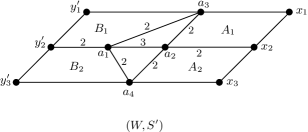
In , let and be the sets of -vertices around “” and “” in the figure for each respectively. Then the minimal separations of are the 9-sets as
-
(1)
,
-
(2)
,
-
(3)
,
-
(4)
,
-
(5)
,
-
(6)
,
-
(7)
,
-
(8)
and
-
(9)
.
Here is a spherical-product subset that separates and both. We consider the separations and of and induced by respectively. Then and are compatible on the separations and . Thus and are some-separation-compatible.
In , there are no type(I) subsets of and
The Coxeter system is denoted by Figure 10. In , there are no type(I) subsets of and
Then the type(II) subsets and are type(II)-compatible. Hence and are type(I)-type(II)-compatible. Here and are not compatible on their standard separations.
3. On separations of Coxeter generating sets and compatible Coxeter systems
Let be a Coxeter system. A maximal spherical subset of is not separated by any subset of . Hence every maximal spherical subset is a twist-rigid subset of . Also for a maximal spherical subset of , there exists a maximal twist-rigid subset of such that .
We consider that two Coxeter systems and are maximal-twist-rigid-subset-compatible, if each maximal twist-rigid subset of is conjugate to some unique maximal twist-rigid subset of and each maximal twist-rigid subset of is conjugate to some unique maximal twist-rigid subset of .
By the above argument, if two Coxeter systems are maximal-twist-rigid-subset-compatible, then they are maximal-spherical-subset-compatible. Also by the argument in Section 1, if two Coxeter systems are maximal-spherical-subset-compatible, then they are angle-compatible.
Question 3.1.
-
(i)
Angle-compatible Coxeter systems and will be maximal-spherical-subset-compatible?
-
(ii)
Maximal-spherical-subset-compatible Coxeter systems and will be maximal-twist-rigid-subset-compatible?
The following technical lemma and remark are used in the proof of the main theorem.
Lemma 3.2.
Let be a Coxeter system and let be a separation of . Suppose that the following statements (1)–(4) hold:
-
(1)
.
-
(2)
is maximal in
for any .
-
(3)
.
-
(4)
.
Then there exists a subset of such that is a separator of and separates and ; that is, for the connected components of (where is a disjoint union), and for some as .
Proof.
We suppose that the statements (1)–(4) hold.
Let such that is maximal in .
If separates and , then we obtain and this lemma is proved, since is a subset of and is a separator of by the definition of a separation.
We suppose that does not separate and .
Let such that is maximal in
for any and separates and . Here we may suppose that is the minimum number as separates and ; that is, does not separate and for any .
Let that is a separator of and separates and . Here if then we obtain and this lemma is proved.
We suppose that .
We consider the connected components of where is a disjoint union. We may suppose that and . By the definition of a separator, there exists () such that . Since , we have that .
(a) Since separates and , for any and , any path form to in the nerve of intersects .
(b) Let that is a separator of and does not separate and . We consider the connected components of where is a disjoint union. We may suppose that and . Here and . Hence there exist and . Since is connected, there exists a path from to in the nerve of . Here , since . Thus the path does not intersect . In particular, the path does not intersect , because . This contradicts (a).
Thus, and we obtain . This lemma is proved. ∎
The following remark is obtained from Lemma 3.2.
Remark 3.3.
Let be a Coxeter system with the untangle-conjugate-condition and let be a separation of . We suppose that the following statements (1)–(8) hold:
-
(1)
.
-
(2)
is maximal in
for any .
-
(3)
.
-
(4)
.
-
(5)
is a spherical-product subset of such that is non-empty and .
-
(6)
is a spherical-product subset of such that .
-
(7)
and are conjugate and .
-
(8)
.
Then by (7) and the untangle-conjugate-condition, there exist a sequence of subsets of and a sequence of spherical subsets of such that
Here .
Since by (7), . We suppose that for any and for any .
By Lemma 3.2, there exists a subset of such that is a separator of and separates and .
By the above untangle-conjugate sequence, is connected. Here for each . Also by (5) and by (6). Then and . Also .
For any , is connected and there exists a path from to some point of in , because each is spherical and for any .
Hence , since separates and .
We show that for some as . Let be the connected components of and let for each . Here if . Since is a separator of , there exist such that , and for some as by (iv) in the definition of a separator. Here for some . Then or , since . We suppose that . Then and , because and (here ). Hence for some as .
Thus by (8). Hence we have that , because .
Then separates , and separates . Here for any and .
Let and be subsets of such that is a disjoint union, , and for any and . Then we can obtain a twist
Here for each , or . Hence the twist is preserving and fixing . Let be the induced separation of by and the twist. Then . Let , let for and let for . Then in , we obtain that and . Also
in . Here we can iterate this argument.
4. Some-separation-compatible Coxeter generating sets are conjugate up to finite twists
We prove that two some-separation-compatible Coxeter generating sets are conjugate up to finite twists.
Theorem 4.1.
Let and be Coxeter systems with the untangle-condition. If and are some-separation-compatible, then and are conjugate up to finite twists.
Proof.
We suppose that and are some-separation-compatible and suppose that and are connected. Then there exist separations and of and respectively such that and are compatible on the separations and ; that is, each is conjugate to some unique and each is conjugate to some unique .
We note that if and are Coxeter generating sets for that are obtained from and by some finite twists preserving and respectively, then also each is conjugate to some unique and each is conjugate to some unique .
Now we show that the following statement holds for each , where .
-
There exist Coxeter generating sets and for such that and are obtained from and by some finite twists preserving and respectively and and are conjugate in , where is a union of some -th elements of in as is maximal in
for any , and is a union of some -th elements of in as is maximal in
for any .
We prove by induction on .
Let and . For , there exists a unique such that and are conjugate. Let and . Then holds.
Let . We suppose that holds; that is, there exist Coxeter generating sets and for such that and are obtained from and by some finite twists preserving and respectively and and are conjugate, where is a union of some -th elements of in as is maximal in
for any , and is a union of some -th elements of in as is maximal in
for any .
Then we show that holds.
Let
Since and are connected, and are connected. Hence and .
Now we suppose that .
Then there exists such that and . Let and let . Here is preserving and fixing . Also is obtained from by some finite twists preserving . We also note that is a union of some -th elements of in .
Let be the element of such that and are conjugate in . Let . Then since , is a spherical-product subset of and separates by the definition of a separation, because is a separation of .
Since and are conjugate in , for some . Then and . Also since and are conjugate in , for some . Then and . Here and are conjugate spherical-product subsets of in . Hence they are untangle by the untangle-condition. Here if is empty then .
(a) We consider the case that .
Then and , since and . Hence , is maximal in
and separates .
Here and . Hence
We define the bijective map by for any .
By the untangle-conjugate-condition, for , or, there exist a sequence of subsets of and a sequence of spherical subsets of such that
for any and for .
(a-1) Suppose that . Then in is conjugate to in where and are unions of some -th elements of and respectively. Let and . Here is maximal in
and is maximal in
because .
(a-2) Suppose that there exist a sequence of subsets of and a sequence of spherical subsets of such that
for any and for .
Then we will attach to by gluing and by some finite twists of (preserving and fixing ) induced by the above untangle-conjugate sequence from to .
Since separates , separates . For some two subsets and of ,
-
(1)
that is a disjoint union,
-
(2)
for any and ,
-
(3)
and
-
(4)
.
Here for any , or , since is a separator of and .
Then is a twist of preserving and fixing . Let be the separation of induced by and the twist.
Let that is conjugate to and . Then
and
Since separates and separates and , we have that separates and separates and in . Hence separates and separates and in .
We iterate this argument for . Then we obtain a Coxeter generating set from by some finite twists preserving and fixing such that for and that is conjugate to and ,
where is the separation of induced by and the twists.
Let and . Here is maximal in
and is maximal in
because . Here in is conjugate to in where is the element of that is conjugate to and . Thus we obtain that holds.
(b) We consider the case that .
Here and are non-empty. Then there exists a sequence of spherical-product subsets
in . Here are spherical subsets of such that for , for , and for any and . Also and .
Let for each . Then
We will attach to by gluing and by some finite twists of (preserving and fixing ) induced by the untangle-conjugate sequence from to .
We first suppose that (that is, ). Let be the number as and for any . For , and .
Let . Here for any and . Then is a spherical subset and is a spherical-product subset of . Also and .
Then by Remark 3.3, separates and separates and in .
Thus separates and separates and . For some two subsets and of ,
-
(1)
that is a disjoint union,
-
(2)
for any and ,
-
(3)
and
-
(4)
.
Here for any , or , since and . Then is a twist of preserving and fixing . Let be the separation of induced by and the twist.
Then and . Hence moves one step toward by this twist. Let and for each and let for (that are the corresponding subsets of to , and in respectively). Then
and
in where . Here is conjugate to and , and holds.
We iterate this argument. Then we obtain a Coxeter generating set from by some finite twists preserving and fixing such that the above sequence of spherical-product subsets transforms to
in where is the separation of induced by and the twist, and for that is conjugate to and . Here and by the assumption and the definition of the number .
Then and . Hence separates . Thus if then for , separates and we have a twist of by and preserving and fixing . Then moves one step toward by this twist. Here is conjugate to and , and in .
Since separates and separates and in , we have that separates and separates and in . Hence separates and separates and in .
We can iterate this argument for .
By iterating this argument and by (a), we obtain a Coxeter generating set from by some finite twists preserving and fixing such that in is conjugate to in where is the element of that is conjugate to and . Hence, we obtain that holds.
Thus holds for any .
Then implies that there exist Coxeter generating sets and for such that and are obtained from and by some finite twists respectively and and are conjugate, because the unions of the -th elements of in and in are just and respectively.
Therefore, and are conjugate up to finite twists.
In the case that and are connected, we showed that if and are some-separation-compatible, then and are conjugate up to finite twists.
We suppose that and are not connected.
Let be the connected components of and let be the connected components of ; that is,
where the numbers of the connected components of and are equal.
By the same argument as above (in the case that and are connected), we can obtain Coxeter generating sets and for such that and are obtained from and by some finite twists respectively and and are conjugate for any , where are the connected components of and are the connected components of .
Then by the untangle-condition, there exists a Coxeter generating set for such that is obtained from by some finite twists and and are conjugate.
Therefore, and are conjugate up to finite twists. ∎
We obtain the following corollary from Theorem 4.1.
Corollary 4.2.
For Coxeter systems and with the untangle-condition, the following two statements are equivalent:
-
(i)
and are conjugate up to finite twists.
-
(ii)
and are some-separation-compatible for some Coxeter generating set obtained from by finite twists.
5. is a separation of
In this section, we prove the following proposition.
Proposition 5.1.
Let be a Coxeter system and let be the set of subsets of in Definition 1.14. Then is a separation of .
Let be a Coxeter system and let be the set of maximal twist-rigid subsets of . We suppose that is connected. For , we show the statements (1)–(4) of the definition of a separation (in Section 1) hold.
(1) and (3): For each , there exists a unique such that . (Here we can denote by Definition 1.14.) Hence .
(2) Let . Then for some by Definition 1.14. Hence is a union of some maximal twist-rigid subsets of . Also is connected by the definition of the equivalence relation “” on .
To prove (4) in the definition of a separation for , we show some lemmas.
Let be a minimal separation of (and fix ).
Lemma 5.2.
Let . Let be the distinct elements of such that for any . Then .
Proof.
We can denote for some . Let (where as ). For each , for some unique , since is a separation of . Here need not be different all together.
We show that for any .
Let . Here and . Hence . Let as . Then by the definition of the equivalence relation “” on , since and . Thus . We obtain that . Hence
Thus for any .
Then (in fact, the equality holds) and
Also obviously holds. Thus . ∎
Now we say that a sequence satisfies the condition in , if
-
is maximal in
for any .
We next show the following.
Lemma 5.3.
Let . Let be the distinct elements of such that for any . Then there exists a bijective map such that the sequence satisfies the condition in .
Proof.
Let that is arbitrary. Let such that is maximal in . Then we show that is maximal in . Indeed if this does not hold, then there exists such that is maximal in and . Here and . Hence some separates and , where is the separators set as in Definition 1.14. Here “ separates and ” means that and for some as , where are the connected components of and .
Then separates and . Thus separates and , because . This contradicts that . Thus is maximal in .
Let such that is maximal in
Then we show that is maximal in
Indeed if this does not hold, then there exists such that is maximal in
and
Here and . Hence some separates and , and separates and . Then separates and , because . This contradicts that .
By iterating this argument, we obtain a sequence that satisfies the condition in . ∎
Lemma 5.4.
Let such that the sequence satisfies the condition in . Then there exists a sequence
satisfying the condition in such that
Also for any .
Proof.
In the case that , by Lemma 5.3, there exists a sequence satisfying the condition in such that .
Let . Suppose that satisfies the condition in , a sequence
satisfies the condition in and
Here and is maximal in
Since , by the definition of , there exists such that and where is a disjoint union, are the connected components of and for . Here is a separator of . For , by (v) in the definition of a separator, there exists such that . Then by (iv) in the definition of a separator, the following equation holds;
Let . Then
Hence . Thus
Here is maximal in
By the above argument, is maximal in
and it is maximal in
Hence the sequence
satisfies the condition in . Here is a separator of .
Let be the set of such that for any . By Lemma 5.2, . By Lemma 5.3, we may suppose that and the sequence satisfies the condition in . Then
We show that
for any . Let . Then
where and . Also here and . Obviously holds.
Then is maximal in
for any . Hence is maximal in
for any .
Thus the sequence
satisfies the condition in . ∎
(4) Now we show that (4) in the definition of a separation of holds for .
Suppose that is a sequence satisfying the condition in . Then we show that is a separator of for any .
Let and let . By Lemma 5.4, is a separator of .
(i) and (ii): Then is a spherical-product subset of and separates .
(iii) Suppose that is a disjoint union and are the connected components of . Let
for each .
By the definition of , each is not separated by any separator of a minimal separation of . Hence for any , does not separate and for some unique . Then and hold.
Here holds for any , because each is denoted by (where are the elements of such that ) and each is contained in some unique .
(iv) Since is a separator of , there exist such that , and for some as . Then and for some unique . Here and . Then holds.
(v) Let . Suppose that satisfies the condition in and . By Lemma 5.4, there exists a sequence
satisfying the condition in such that
Since is a separator of , we have that for some . Here for some . Then .
Thus from the above (i)–(v), is a separator of .
We show (b) on (4) in the definition of a separation for ; that is, and for some as .
Since is a separation, by Lemma 5.4, we obtain that and for some as . Since is a separator of , does not separate . Hence .
Thus (4) in the definition of a separation of holds for .
Therefore is a separation of .
6. Type(I)-type(II)-compatible and conjugate up to finite twists
We investigate on type(I)-type(II)-compatible Coxeter systems and conjugate up to finite twists. We show that for Coxeter systems and with the untangle-condition, and are conjugate up to finite twists if and only if and are type(I)-type(II)-compatible.
We show a lemma on conjugate spherical-product subsets.
Lemma 6.1.
Let be a Coxeter system and let be a spherical-product subset of . If for some , then and .
Proof.
Suppose that for some . Then
Here and are the minimal standard (parabolic) subgroups of finite index in and respectively (see [9]). Since and , we have that . Hence . Thus and . ∎
We show a lemma on spherical subsets and type(II) subsets.
Lemma 6.2.
Let be a Coxeter system. If is a spherical subset of that separates , then does not separate any type(II) subset of .
Proof.
Let be a spherical subset of that separates . We can denote where are the connected components of .
Then for any maximal twist-rigid subset of , does not separate and for some . Also for any minimal separation of and for any , does not separate and for some . (Indeed if separates some , then there exists a separation of induced by from such that . This contradicts that is minimal.)
Hence does not separate any type(II) subset of . ∎
Now we show the following.
Lemma 6.3.
Let be a Coxeter system with the untangle-condition and let be a Coxeter system obtained from by some twist. Then and are type(I)-type(II)-compatible.
Proof.
It is sufficient to show this lemma in the case that and are connected. Now we suppose this.
Let be a spherical-product subset of and let such that separates , and is obtained from by some twist of and . There exist non-empty subsets and of such that , , for any and , and .
Let and be the sets of maximal twist-rigid subsets of and respectively. Here for each , if we put (if ) and (if ), then . Hence
By the definition of type(I) subsets and Remark 2.2, each is not separated by any spherical-product subset that separates .
Let . Here is not separated by . We consider the subset of as (if ) and (if ). Then since separates , there is an induced separation of by as in Remark 2.2. Then is not separated by any spherical-product subset that separates . Indeed, suppose that is separated by some spherical-product subset that separates . Here either does not separate any or separates some . In both cases, or . For (if ) and (if ), is a spherical-product subset of that separates and has to separate that is a contradiction. Hence .
Also by the same argument, for each , if is the subset of defined by (if ) and (if ) then .
Thus
and .
(a) We first suppose that does not separate any .
Then for any minimal separation of , is a twist of that is preserving and the separation of induced by and the twist is minimal. Also for any minimal separation of , the separation of induced by and the twist is minimal. Hence
Thus and are type(I)-type(II)-compatible.
(b) We suppose that separates some unique . Here does not separate any .
Let
where and are the sets of separators of minimal separations and of and respectively. The standard separations and are defined by the separator sets and respectively.
Then for any minimal separation of , is a twist of that is preserving ; that is, or for each as . Also for any minimal separation of , is a twist of that is preserving where ; that is, or for each as .
Hence for any as , . Also for any as , .
Let . We consider the subset of as (if ) and (if ). Then by the above argument. Here and are type(II)-compatible, since and are conjugate. Hence
Thus , because and there is a possibility that the corresponding subset of to in is a union of some type(II) subsets. Also since is a twist of , by the same argument, . Hence . This implies that
is a type(II) subset of . Here is a twist of that induces the twist of .
Thus, if separates some unique then and are type(I)-type(II)-compatible.
(c) We suppose that separates some that is not unique. Let be the type(II) subsets of such that (also ) separates for .
For each , we show that separates unique . We suppose that separates some as . Then separates . The standard separation of is defined by the separator-set . Here for some . Then . Since separates , we have that separates . This contradicts that does not separate any .
Now is connected. Let be the connected components of . Then and that are disjoint unions.
Let be the maximal twist-rigid subset of , let be the induced separation of by as Remark 2.2, and let be a minimal separation of such that .
Let and let
Then
Since is a separation of , there exists such that is a separator of and for some . Then separates . (Also separates .) Here is uniquely determined.
Hence and the map is bijective on the set . We may suppose that for any . Then for each , is a separator of and .
Let for each . Since separates , separates . Here holds. Then and by Lemma 6.1. Hence for any by the untangle-condition. Thus
for any .
Here separates . Indeed
We show that separates the unique element of . We suppose that separates as . Then
separates . Since the spherical subset does not separate the type(II) subset by Lemma 6.2, and . Hence is connected. There exists the separation induced by as in Remark 2.2 and we can obtain a minimal separation as . Here the spherical-product subset separates and separates by hypothesis. This contradicts that and are distinct type(II) subsets of . Thus separates unique .
For each and for , that is a disjoint union and for any and . Here
is a disjoint union and as above.
Let that is a twist of by and . Then separates unique by the above argument. Hence and are type(I)-type(II)-compatible by the above argument (b). Then
For the corresponding subset of to the subset of , separates unique in . Also for the corresponding subset of to the subset of , is a disjoint union.
Let that is a twist of by and . Then separates unique in . Hence and are type(I)-type(II)-compatible by the above argument (b). Here
By iterating this argument, we obtain a sequence of Coxeter generating sets such that is some twist of by and for each . Here separates unique in for any , where is the type(II) subset of corresponding to in . Then and are type(I)-type(II)-compatible for each by the above argument (b). Here
Thus, we obtain that and are type(I)-type(II)-compatible. ∎
Remark 6.4.
Let be a Coxeter system. Let and be spherical-product subsets of that separate such that for each ,
-
does not separate any , or
-
separates some unique .
We consider a twist of by and . Here we suppose that , is a disjoint union and for any and .
Then we investigate a spherical-product subset of corresponding to in from the proof of Lemma 6.3.
If
-
does not separate any ,
then for (if ) and (if ), is the spherical-product subset of corresponding to in .
We suppose that
-
separates some unique .
If
-
does not separate any ,
then for (if ) and (if ), is the spherical-product subset of corresponding to in . Also if
-
separates some unique
and if , then for (if ) and (if ), is the spherical-product subset of corresponding to in .
Suppose that
-
separates some unique and
-
separates some unique
and suppose that . In this case, and both separate the unique type(II) subset .
Theorem 6.5.
Let be a Coxeter system with the untangle-condition and let be a Coxeter generating set for obtained from by some finite twists. Then and are type(I)-type(II)-compatible.
Proof.
There exists a sequence of Coxeter generating sets for such that is obtained from by some twist for any . We suppose that the twist of is obtained by a spherical-product subset of and as for each . Here by the proof of Lemma 6.3, for each , either
-
(a)
does not separate any ,
-
(b)
separates some unique , or
-
(c)
separates some that is not unique.
Here if (c) separates some that is not unique, then by the proof of Lemma 6.3, there exist a sequence of spherical-product subsets and a sequence of Coxeter generating set for such that each is obtained from by some twist induced by and as and separates some unique .
Thus there exists a sequence of Coxeter generating sets for such that for any , is obtained from by some twist of some spherical-product subset of and as and either
-
(a)
does not separate any , or
-
(b)
separates some unique .
We show the following theorem.
Theorem 6.6.
Let and be Coxeter systems with the untangle-condition. If and are type(I)-type(II)-compatible, then there exists a Coxeter generating set obtained from by some finite twists such that and are compatible on the standard separations and (hence they are some-separation-compatible).
Proof.
Let and such that and are type(II)-compatible. There exists obtained from by some finite twists that induce some twists of preserving such that and are conjugate in . Let be the Coxeter generating set for obtained from by the induced finite twists preserving such that in is conjugate to in .
Then by the proofs of Lemma 6.3 and Theorem 6.5, and are type(I)-type(II)-compatible, is a type(II) subset of and
where is the set of the corresponding conjugate subsets of to the elements of in .
Hence
-
(1)
and are type(I)-type(II)-compatible,
-
(2)
is conjugate to and
-
(3)
.
Let and such that and are type(II)-compatible. Let be the corresponding conjugate subset of to in .
There exists obtained from by some finite twists that induce some twists of preserving such that and are conjugate. Let be the induced Coxeter generating set.
Then by the proofs of Lemma 6.3 and Theorem 6.5, and are type(I)-type(II)-compatible, is a type(II) subset of and
where is the corresponding conjugate subset of to in , and (and ) is the set of the corresponding conjugate subsets of to the elements of in (and in respectively).
Hence
-
(1)
and are type(I)-type(II)-compatible,
-
(2)
is conjugate to ,
-
(3)
is conjugate to and
-
(4)
.
By iterating this argument, we obtain a Coxeter generating set for from by some finite twists preserving such that for each , the corresponding subset is conjugate to some unique .
Also by the definition of type(I)-type(II)-compatible and the above argument, each is conjugate to some unique .
Thus, and are compatible on the standard separations and . ∎
Theorem 6.7.
Let and be Coxeter systems with the untangle-condition. Then the following two statements are equivalent
-
(i)
and are conjugate up to finite twists.
-
(ii)
and are type(I)-type(II)-compatible.
Proof.
By Theorem 6.5, if and are conjugate up to finite twists, then and are type(I)-type(II)-compatible.
References
- [1] N. Bourbaki, Éléments de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitre IV: Groupes de Coxeter et systèmes de Tits. Chapitre V: Groupes engendrés par des réflexions. Chapitre VI: systèmes de racines, Actualités Scientifiques et Industrielles, No. 1337, Hermann, Paris, 1968.
- [2] N. Brady, J.P. McCammond, B. Mühlherr and W.D. Neumann, Rigidity of Coxeter groups and Artin groups, Geom. Dedicata 94 (2002), 91–109.
- [3] B. Brink and R.B. Howlett, Normalizers of parabolic subgroups in Coxeter groups, Inv. Math. 136 (1999), 323–351.
- [4] P.-E. Caprace and B. Mühlherr, Reflection rigidity of 2-spherical Coxeter groups, Proc. Lond. Math. Soc. (3) 94 (2007), no. 2, 520–542.
- [5] P.-E. Caprace and P. Przytycki, Twist-rigid Coxeter groups, Geom. Topol. 14 (2010), no. 4, 2243–2275.
- [6] R. Charney and M.W. Davis, When is a Coxeter system determined by its Coxeter group? J. Lond. Math. Soc., II. Ser. 61 (2000), no. 2, 441–461.
- [7] M.W. Davis, The cohomology of a Coxeter group with group ring coefficients, Duke Math. J. 91 (1998), no. 2, 297–314.
- [8] V.V. Deodhar, On the root system of a Coxeter group, Comm. Algebra 10 (1982), 611–630.
- [9] T. Hosaka, Parabolic subgroups of finite index in Coxeter groups, J. Pure Appl. Algebra 169 (2002), 215–227.
- [10] J. Huang and P. Przytycki, A step towards twist conjecture, arXiv preprint arXiv:1708.00960, 2017.
- [11] J.E. Humphreys, Reflection groups and Coxeter groups, Cambridge Studies in Advanced Mathematics 29, Cambridge University Press, Cambridge, 1992.
- [12] T. Marquis and B. Mühlherr, Angle-deformations in Coxeter groups, Algebr. Geom. Topol. 8 (2008), no. 4, 2175–2208.
- [13] B. Mühlherr, On isomorphisms between Coxeter groups, Des. Codes Cryptogr. 21 (2000), 189–189.
- [14] B. Mühlherr, The isomorphism problem for Coxeter groups, Davis, Chandler (ed.) et al., The Coxeter legacy. Reflections and projections. American Mathematical Society, Providence, RI, 2006, pp. 1–15.
- [15] B. Mühlherr and R. Weidmann, Rigidity of skew-angled Coxeter groups, Adv. Geom. 2 (2002), no. 4, 391–415.
- [16] K. Nuida, On the isomorphism problem for Coxeter groups and related topics, Narasimha Sastry, N.S. (ed.), Groups of exceptional type, Coxeter groups and related geometries, Springer Proceedings in Mathematics & Statistics 82, Springer, 2014, pp. 217–238.
- [17] J.G. Ratcliffe and S.T. Tschantz, Chordal Coxeter groups, Geom. Dedicata 136 (2008), 57–77.
- [18] C.J.Weigel, The twist conjecture for Coxeter groups without small triangle subgroups, Innov. Incidence Geom. 12 (2011), 111–140.