On Decidability of Existence of Nonblocking Supervisors Resilient to Smart Sensor Attacks

Cyber-attack resilience refers to properties of service availability and data integrity. With the continuous advancement of information and communications technology (ICT), in particular, the recent 5G-based IoT technologies, we are enjoying unprecedented connectivity around the world. Nevertheless, the threat of cyber attacks that may potentially cause significant damage to human lives and properties has more frequently become the center of attention, and has been attracting lots of research from different communities. Basically, an attacker aims to inflict damage on a target system by disrupting its control loop. This could be achieved either by intercepting and changing the controller’s input signals (in terms of sensor attacks), or by intercepting and changing the controller’s output signals (in terms of actuator attacks), or by completely blocking the data transmission between the controller and the plant (in terms of denial-of-service attacks). An attack can be either brute-force, e.g., via hardware destruction or signal jamming, or covert (or stealthy), i.e., to inflict damage without being detected by relevant monitoring mechanisms.

A good survey of cyber attacks and cyber defence with a systems-and-control perspective can be found in [1]. Typically, linear systems are considered in existing works that rely on system identification and control techniques. Within the DES community, most works rely on the control system setup introduced in the Ramadge-Wonham supervisory control paradigm [23], where the plant generates observable outputs, received by the supervisor via an observation channel, and each control command specified as a set of allowed (or disallowed) events is generated by the supervisor and fed to the plant via a command channel. The plant nondeterministically picks one event from a received control command and executes it. The event execution process is assumed to be asynchronous, i.e., up to one event execution at each time instant, and instantaneous. Unlike attacks in time-driven systems described in [1], attacks under consideration in a DES aim to change the sequence of events in specific system runs.

There are two different streams of research on cyber attacks and resilient control. The first stream refers to a set of black-box methods that treat attacks as undesirable (either intentional or unintentional) uncontrollable and mostly unobservable disturbances to a given closed-loop system. Existing works include, e.g., a game theoretical approach [29], fault-tolerance based approaches such as [5] and [19] on sensor attacks, [2] on actuator attacks, and [3] [6] [4] on sensor+actuator attacks, and transducer-based modelling and synthesis approaches such as [7] [8]. In the black-box methods, system vulnerability is typically modelled by concepts similar to diagnosability described in, e.g., [34], and system resilience bears similarity to fault tolerant control described in, e.g., [28] [32], that concerns whether there is a supervisor that can perform satisfactorily under the worst case attack scenarios. The second stream refers to a set of white-box methods, aiming to develop a specific “smart” attack model that ensures certain intuitive properties such as covertness and guaranteed (strong or weak) damage infliction. Existing works include, e.g., [9] [10] [11] [13] [12] [12] [20] on smart sensor attacks, [14] [18] and [17] on smart actuator attacks, and [16] [21] and [15] on smart sensor+actuator attacks. With such smart attack models, existing research works address the impact of a specific attack on the closed-loop behaviour, the vulnerability of a system to such an attack, and finally the resilience of a supervisor to a concerned attack.

After examining those existing works on smart cyber attacks, it is clear that most works focus on how to derive a proper smart attack model. Various synthesis algorithms have been proposed under relevant assumptions. Nevertheless, the existence of a supervisor that is resilient to all possible smart cyber attacks is still open for research. In [35] [36] the authors present synthesis methods for resilient control against a specific sensor attack model described by a finite-state automaton in different scenarios. Thus, the synthesized supervisor is not designed to be resilient to all possible smart sensor attacks. In case of a worst-case sensor attack scenario, no smartness in terms of, e.g., covertness, is considered by the authors. There are a few heuristic synthesis approaches proposed in the literature, e.g., [10] proposes one algorithm against smart sensor attacks, [16] proposes one algorithm that generates a resilient supervisor whose state set is bounded by a known value, and [18] presents an algorithm to synthesize a supervisor, which is control equivalent to an original supervisor and resilient to smart actuator attacks. But none of those existing algorithms can guarantee to find one resilient supervisor, if it exists. That is, when those algorithms terminate and return an empty solution, it does not necessarily mean that there is no solution.

Before any attempt of overcoming a complexity challenge in order to derive a resilient solution, it is critical to answer a computability question first, that is, how to decide whether a solution exists. To address this important decidability issue, in this paper we focus only on sensor attacks, but hoping that our derived result may shed light on research of other types of attacks. We follow a sensor attack model proposed in [10], which associates each observed sequence from the plant $G$ with an altered observable sequence that becomes the input of a given supervisor. After slightly improving the concept of attackability originally introduced in [10] and the corresponding definition of smart sensor attacks, our first contribution is to identify conditions that ensure the existence of a smart sensor attack. It turns out that the existence of a smart weak sensor attack, which is not necessarily regular (i.e., representable by a finite-state automaton), is solely determined by the existence of at least one risky pair that consists of a damage string desired by the attacker and an observable sequence feasible in the supervisor such that the latter induces a sequence of control patterns, which allows the concerned damage string to happen. Because any strong sensor attack is also a weak attack, the existence of such a risky pair becomes the sufficient and necessary condition for the existence of a smart sensor attack. In [9] and its journal version [10], by imposing language normality to the closed-loop behaviour, it is shown that the supremal smart sensor attack language can be synthesized, whenever it exists, upon which a specific smart sensor attack model can be derived. In [11] and its journal version [12], the language normality is dropped, and it is shown that a smart sensor attack model (not necessarily supremal) can be synthesized via a special insertion-deletion attack structure, whenever it exists. However, none of these works reveals the aforementioned demand-supply relationship reflected in risky pairs that capture the nature of sensor attacks. Due to this insightful concept of risky pairs, our second contribution is to show that the existence of a nonblocking controllable and observable supervisor that is resilient to all regular smart sensor attacks is decidable. To this end, we develop a genuine encoding mechanism that reveals all possible sequences of control patterns required by a regular sensor attack and all sequences of control patterns feasible in the plant, allowing us to remove the set of all risky pairs from the plant behaviour. After that, we introduce a language-based concept of nonblocking resilient supervisor candidate and its automaton-counterpart control feasible sub-automaton that does not contain any risky pair, upon which we are able to decide the existence of a resilient supervisor. As our third contribution, the proposed decision process renders a concrete synthesis procedure that guarantees to compute a nonblocking supervisor resilient to smart sensor attacks, whenever it exists.

The remainder of the paper is organized as follows. In Section 2 we present a motivation example. Then in Section 3 we review the basic concepts and operations of discrete event systems introduced in [26], followed by a specific smart sensor attack model, where the concept of attackability is introduced. Then we present a sufficient and necessary condition to ensure a smart sensor attack in Section 4, where the key concept of risky pairs is introduced. After that, we present a sufficient and necessary condition for the existence of a nonblocking supervisor that is resilient to smart sensor attacks in Section 5, and show that this sufficient and necessary condition is verifiable in Section 6, which finally establishes the decidability result for the existence of a resilient supervisor. Conclusions are drawn in Section 7. Long proofs for Theorems 1-4 are shown in the Appendix.

Image that Bob would like to ride his autonomous car from his home to his office. There is a GPS navigator installed inside his car. The navigator first generates a shortest path based on traffic conditions, then guides the vehicle to make required turns at planned junctions. However, Bob’s friend Peter plans to play a prank on Bob by tricking the navigator to lead Bob’s car to another location via GPS spoofing, shown in Figure 1.

Peter has the city road map and also knows Bob’s home address and office address. In addition, he has a navigator of the same model as the one installed in Bob’s car. Thus, by running his own navigator over the same origin-destination pair, Peter will know Bob’s route plan. Figure 2 depicts the system setup,

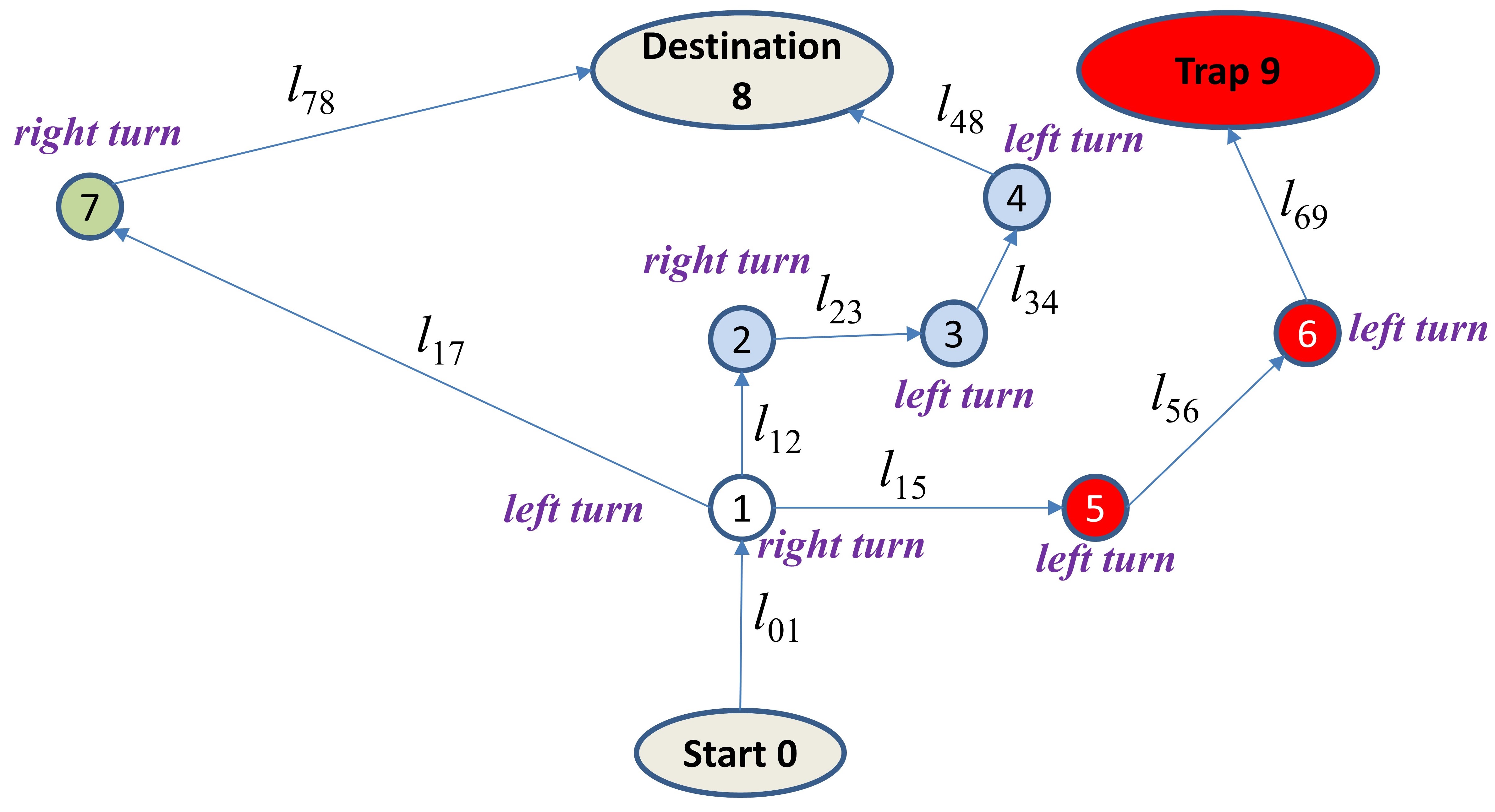
where Bob’s home is at “start 0” node, his office is at “Destination 8” node, and the prank location is at “Trap 9” node. Each symbol “$l_{ij}$” denotes the length of the road segment between node $i$ and node $j$. In addition, the position of each node in the map is publicly known. By simply running the navigator of the same model, Peter knows that Bob’s car will choose the shortest path “$0\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow 4\rightarrow 8$”, which leads to the following navigation commands: (1) right turn (at node 2), followed by (2) left turn (at node 3), followed by (3) left turn (at node 4). To trick the navigator to issue the same sequence of commands but at incorrect junctions, say, right turn at node 1, followed by left turn at node 5, and followed by left turn at node 6, Peter only needs to buy a GPS spoofing device available in the market that can send fake GPS position signals to Bob’s navigator. Peter can easily determine the spoofed GPS position signal as follows. Assume that $p_{0}$ denotes the position of “start 0” node, and $p(t)\in\mathbb{R}^{2}$ and $p^{a}(t)\in\mathbb{R}^{2}$ denote the actual and spoofed GPS positions in a 2D map. The travel distance made by Bob’s car between time $t_{0}$ and time $t$ ($t\geq t_{0}$) can be calculated by a simple line integral shown below:

where $p(t)$ is the parametric function of the path from node “start 0” to node 1, $p(t_{0})=p_{0}$, $||p(t)||$ denotes the magnitude of $p(t)$ and ‘$\cdot$’ is the dot product of vectors. For each $p(t)$, Peter uniquely determines the value of $p^{a}(t)$, which is the parametric function of the path from node “start 0” to node 2 with $p^{a}(t_{0})=p_{0}$, such that

which ensures that, when the navigator receives the spoofed signal, indicating that node 2 is reached, the actual node reached is node 1. With a similar GPS position spoofing scheme, Peter can misguide Bob’s car to reach node 9, instead of node 8, without being detected. Such GPS spoofing is one specific example of a smart sensor attack, whose formal definition will be given in the next section. Intuitively, it contains the following basic characteristics: by knowing sufficient information in advance, an attacker can trick a victim to issue the correct order of commands but at incorrect states (or locations), which leads to an unwanted consequence.

If Bob somehow knows that Peter will use GPS spoofing to play a trick on his car, he can simply choose the path “$0\rightarrow 1\rightarrow 7\rightarrow 8$”. In this case, even Peter knows this new path, he cannot spoof the GPS signals to trick Bob’s car to node 9 without being detected, as the new path generates a new sequence of navigation commands: (1) left turn (at node 1), then (2) right turn (at node 7), which, no matter how Peter changes GPS position signals, cannot bring Bob to node 9. Such a path plan is a specific example of a resilient supervisor against smart sensor attacks, whose definition will be given later in this paper. Intuitively, a resilient supervisor will ensure that, for any sensor attack, either it can be detected before inflicting damage, or it will not lead to any damage.

One big question is, for an arbitrary network, see, e.g., a road map of a small region in Singapore shown in Figure 3,

how to decide whether a resilient path plan (or navigation supervisor) exists. In this paper, we will investigate this decidability problem against smart sensor attacks. The computational efficiency, i.e., the complexity issue, however, will not be addressed here.

In this section we first recall basic concepts used in the Ramadge-Wonham supervisory control paradigm [23]. Then we recall a smart sensor attack model introduced in [10]. Most notations in this paper follow [26].

Let us start with a small example, which is depicted in Figure 6.

Assume that the attacker $A$ wants to achieve a string $abc\in L_{dam}$, which leads to a damage state. Assume that event $a$ is contained in control pattern $\gamma_{1}$, event $b$ is in control pattern $\gamma_{2}$, and event $c$ in control pattern $\gamma_{3}$. After event $a$ fires, the attacker wants the control pattern $\gamma_{2}$ to be issued. Since event $a$ does not lead to control pattern $\gamma_{2}$, but event $d$ does, the attacker $A$ will replace event $a$ with $d$ to trick the supervisor $S$ to generate $\gamma_{2}$. Assume that $b$ is fired afterwards. The attacker wants $\gamma_{3}$ to be issued. Since event $b$ does not lead to $\gamma_{3}$, instead, event $e$ does, the attacker $A$ replaces event $b$ with event $e$ to trick the supervisor $S$ to issue $\gamma_{3}$, if event $c$ happens afterwards, the attacker achieves his/her goal without being detected by the supervisor. The attacker could continue this trick as long as it is possible. So essentially, by faking some observable string, the attacker hopes to trick the supervisor to issue a sequence of control patterns, which contain some damaging strings, without being detected by the supervisor. We now generalize this idea. For notational simplicity, given a string $t=\nu_{1}\cdots\nu_{n}\in\Sigma^{*}$ with $n\in\mathbb{N}$, for each $i\in\{1,\cdots,n\}$, we use $t^{i}$ to denote the prefix substring $\nu_{1}\cdots\nu_{i}$. By convention, $t^{0}:=\epsilon$.

As an illustration, in Example 1 depicted in Figure 6, we can see that $r=3$, $\sigma_{1}=a$, $\sigma_{2}=b$, $\sigma_{3}=c$, $\nu_{1}=d$, $\nu_{2}=e$, $u_{1}=u_{2}=u_{3}=u_{4}=\epsilon$.

The strings $s$ and $t$ in Theorem 1 form a risky pair $(s,t)\in L_{dam}\times\Delta_{n}^{*}$ such that, by mapping $P_{o}(s)$ to $t$, the attacker can rely on the existing supervisor $V$ to inflict a weak attack on the plant $G$, without being detected by the supervisor. Since the existence of a risky pair is sufficient and necessary for the existence of a smart weak sensor attack, we will use this fact to determine the existence of a resilient supervisor. But before that, we would like to state the following result about the decidability of the existence of a regular smart weak sensor attack.

By the proof of Theorem 2 shown in the Appendix, the computational complexity of deciding the existence of a regular smart weak sensor attack is $O(|\Sigma|^{2}|\Delta_{n}|2^{|G||S||D|})$, where $S$ is an automaton realization of $V$ and $D$ is an automaton recognizing $L_{dam}$.

In [12] the authors have shown that a deterministic attack function that ensures the covertness and weak damage infliction can always be synthesized, when it exists. But since the attack model adopted in this paper is different from the one used in [12], e.g., the latter does not requires $A(\epsilon)=\epsilon$ (thus, non-existence of an attack model in our definition does not necessarily means the non-existence of an attack model in [12]), and encodes attack moves differently, Theorem 2 has its own value by providing another way of synthesizing a regular deterministic smart weak sensor attack, whenever it exists.

In this section we explore whether there exists a sufficient and necessary condition to ensure the existence of a supervisor that is resilient to all regular smart sensor attacks, i.e., the closed-loop system is not attackable by any regular smart sensor attack. In Section 3 we have shown that there is a sufficient and necessary condition for the existence of a smart weak sensor attack shown in Theorem 1. Since each strong attack is also a weak attack, if we can effectively eliminate those risky pairs described in Theorem 1, we shall be able to prevent the existence of any smart sensor attack. Since, given a plant $G$ and a requirement $Spec$, we can always synthesize a controllable and observable sublanguage of $L_{m}(G)\cap L_{m}(Spec)$, without loss of generality, we assume that the plant $G$ satisfies all given requirements. Thus, we will only focus on the following problem.

To solve this problem, we first intend to find a proper way of encoding all risky pairs. Given a string $s\in\Sigma^{*}$, we use $s^{\uparrow}$ to denote the last event of $s$. If $s=\epsilon$, by convention, $s^{\uparrow}:=\epsilon$. In addition, we use $s_{o}$ to denote the longest prefix substring of $s$, whose last event is observable, i.e., $s_{o}\in\overline{\{s\}}\cap(\Sigma_{uo}^{*}\Sigma_{o})^{*}\cap P_{o}^{-1}(P_{o}(\{s\}))$. Thus, if $s\in\Sigma_{uo}^{*}$, then we can derive that $s_{o}=\epsilon$.

Let $\iota:\Sigma^{*}\rightarrow 2^{(\Sigma\times\Gamma)^{*}}$ be a partial mapping, where

• •

  $\iota(\epsilon):={\color[rgb]{0,0,0}\{\epsilon\}}$;

• •

  $(\forall s\in\Sigma^{*})(\forall\sigma\in\Sigma)\,\iota(s\sigma):=\iota(s)\{(\sigma,\gamma)|\sigma\in\gamma\}$.

In Example 1, we have $(a,\gamma_{1})(b,\gamma_{2})(c,\gamma_{3})\in\iota(abc)$. What the map $\iota$ does is to map each string $s\in\Sigma^{*}$ to a set of sequences of control patterns such that each derived control pattern sequence, say $\gamma_{1}\cdots\gamma_{r}\in\Gamma^{*}$, contains the string $s$ in the sense that $s\in\gamma_{1}\cdots\gamma_{r}\subseteq\Sigma^{*}$. By applying the map $\iota$ to the damage language $L_{dam}$, the result $\iota(L_{dam}):=\cup_{s\in L_{dam}}\iota(s)$ presents all possible sequences of control patterns, each of which contains at least one string in $L_{dam}$ - in other words, each string in $\iota(L_{dam})$ may potentially result in damage.

To further illustrate how this function works, we introduce another simple example depicted in Figure 7,

where $\Sigma=\{a,b,c,d,v\}$, $\Sigma_{c}=\{a,b,d\}$ and $\Sigma_{o}=\{a,b,c,d\}$. To simplify our illustration, in this example we assume that $\Delta_{n}=\Sigma_{o}^{\epsilon}$, i.e., $n=1$. The damage language $L_{dam}=\{ad\}$, which is shown by a dashed line leading to state 3. Figure 8 depicts the outcome of $\iota({\color[rgb]{0,0,0}L_{dam}})$.

A smart sensor attack replaces each intercepted observable event $\sigma\in\Sigma_{o}$ with a string in $\Delta_{n}$, unless $\sigma$ is silent, i.e., $\sigma=\epsilon$. To capture the impact of such changes on the control pattern sequences, we introduce a mapping $\psi:(\Sigma\times\Gamma)^{*}\rightarrow 2^{((\Sigma\cup\Delta_{n})\times\Gamma)^{*}}$, where

• •

  $\psi(\epsilon):={\color[rgb]{0,0,0}\{\epsilon\}}$;

• •

  For each $\mu\in(\Sigma\times\Gamma)^{*}$ and $(\sigma,\gamma)\in\Sigma\times\Gamma$, we have

  $$\psi(\mu(\sigma,\gamma)):=\left\{\begin{array}[]{ll}\psi(\mu)\{(\sigma,\gamma)\}&\textrm{if $\sigma\in\Sigma_{uo}$,}\\ \psi(\mu)(\Delta_{n}\times\{\gamma\})&\textrm{otherwise.}\end{array}\right.$$

We extend the domain of $\psi$ to languages in the usual way, i.e., for all $L\subseteq(\Sigma\times\Gamma)^{*}$, $\psi(L):=\cup_{s\in L}\psi(s)$.

To explicitly describe how a smart attack may utilize possible sequences of control patterns, we introduce one more mapping

where

• •

  $\nu(\epsilon):={\color[rgb]{0,0,0}\{\epsilon\}}$;

• •

  For all $(\sigma,\gamma)\in(\Sigma\cup\{\epsilon\})\times\Gamma$,

  $$\nu(\sigma,\gamma)=\left\{\begin{array}[]{ll}(\sigma,\gamma)&\textrm{if $\sigma\in\Sigma_{o}\wedge\sigma\in\gamma$;}\\ (\epsilon,\gamma)&\textrm{if $\sigma\in\Sigma_{uo}\wedge\sigma\in\gamma$;}\\ \varnothing&\textrm{otherwise.}\end{array}\right.$$

• •

  For all $s=\sigma_{1}\cdots\sigma_{r}\in\Delta_{n}$, ${\color[rgb]{0,0,0}|P_{o}(s)|}=r\geq 2$, and $\gamma\in\Gamma$,

  $\nu(s,\gamma):=\{(\sigma_{1},\gamma_{1})\cdots(\sigma_{r},\gamma)|\sigma_{r}\in\gamma\wedge$

  $(\forall i\in\{1,\cdots,r-1\})\sigma_{i}\in\gamma_{r-1}\in\Gamma\}.$

• •

  $(\forall\mu(s,\gamma)\in((\Sigma\cup\Delta_{n})\times\Gamma)^{+})\,\nu(\mu(s,\gamma))=\nu(\mu)\nu(s,\gamma)$.

As an illustration, we apply the map $\psi$ to the damage language $\iota(L_{dam})$ in Figure 8, where $n=1$. To simplify illustration, we assume that an attacker can, but prefers not to, change events $c$ and $d$. The outcome is depicted in Figure 9. Notice that when event $a$ is intercepted by the attacker, it can be replaced by any other strings in $\Delta_{n}$. Because $n=1$, we have $\Delta_{1}=\Sigma_{o}\cup\{\epsilon\}=\{a,b,c,d,\epsilon\}$ - in this case, the outcome of $\nu(\psi(\iota(L(G))))$ equals $\psi(\iota(L(G)))$.

Next, we determine all control pattern sequences in the plant $G$ that may be used by a smart attack. Let $\Upsilon_{G}:L(G)\times\Sigma^{*}\times\Gamma\rightarrow\{0,1\}$ be a Boolean map, where for each $(s,t,\gamma)\in L(G)\times\Sigma^{*}\times\Gamma$,

For each $\gamma\in\Gamma$, let

This definition of $\zeta$ indicates that, except for control patterns generated initially, i.e., when $s=\epsilon$, each control pattern will be changed only after an observable event is received, i.e., when $st\in\Sigma^{*}\Sigma_{o}\cap L(G)$. This matches the definition of a supervisor $V$ that changes its output only when a new observation is received. In addition, if a control pattern $\gamma$ contains unobservable events, it will be contained in a self-loop of the augmented event $(\epsilon,\gamma)$, i.e., $\{(\epsilon,\gamma)\}^{*}$, denoting that the control pattern $\gamma$ may be used more than once by the plant, as long as no new observable event has been received. Again, this matches the Ramadge-Wonham supervisory control paradigm, where execution of any unobservable transition allowed by the current control pattern will not change the current control pattern - recall that in a finite-state automaton realization of $V$, unobservable events are self-looped at relevant states.

As an illustration, we apply $\zeta$ to the plant model $L(G)$ depicted in Figure 7. Part of the outcome is depicted in Figure 10.

Because the total state set is $X\times\Sigma_{o}^{\epsilon}\times\Gamma$, which is too big to be shown entirely in the picture, we only include states that have at least one future extension, unless they are marker states (i.e., states $(3,d,\{v,c\})$, $(5,c,\{v,c\})$ and $(7,d,\{v,c\})$), except for one blocking state $(2,b,\{v,c\})$, which is left there for an illustration purpose that will be explained shortly. The marker states in Figure 10 denote the augmented marked behaviour of $G$ in Example 2.

Till now, we have provide sufficient means to describe all risky pairs, which are captured by $\nu(\psi(\iota(L_{dam})))$ at the attacker’s demand side, and $\zeta(L(G))$ at the plant’s supply side. To avoid such risky pairs, we only need to remove $p^{-1}(p(\nu(\psi(\iota(L_{dam}))))(\Sigma_{o}^{\epsilon}\times\Gamma)^{*}$ from $\zeta(L(G))$. The reason why we concatenate $(\Sigma_{o}^{\epsilon}\times\Gamma)^{*}$ at the end of $p^{-1}(p(\nu(\psi(\iota(L_{dam}))))$ is to denote all possible augmented strings that may contain some strings in $p^{-1}(p(\nu(\psi(\iota(L_{dam}))))$ as prefix substrings. Thus, all safe supervisory control pattern sequences shall be contained in $\hat{H}:=\zeta(L(G))-p^{-1}(p(\nu(\psi(\iota(L_{dam}))))(\Sigma_{o}^{\epsilon}\times\Gamma)^{*}$ in order to prevent any sequence of control patterns from being used by an attacker.