[1]\fnmM. A. \surBotchev

[1]\orgnameKeldysh Institute of Applied Mathematics of Russian Academy of Sciences, \orgaddress\streetMiusskaya Sq., 4, \cityMoscow, \postcode125047, \countryRussia

On convergence of waveform relaxation for nonlinear systems of ordinary differential equations

To the memory of Willem Hundsdorfer

[email protected] *

(April 4, 2024)

Abstract

To integrate large systems of nonlinear differential equations in time, we consider a variant of nonlinear waveform relaxation (also known as dynamic iteration or Picard–Lindelöf iteration), where at each iteration a linear inhomogeneous system of differential equations has to be solved. This is done by the exponential block Krylov subspace (EBK) method. Thus, we have an inner-outer iterative method, where iterative approximations are determined over a certain time interval, with no time stepping involved. This approach has recently been shown to be efficient as a time-parallel integrator within the PARAEXP framework. In this paper, convergence behavior of this method is assessed theoretically and practically. We examine efficiency of the method by testing it on nonlinear Burgers, three-dimensional Liouville–Bratu–Gelfand, and three-dimensional nonlinear heat conduction equations and comparing its performance with that of conventional time-stepping integrators.

keywords:

waveform relaxation, Krylov subspaces, exponential time integrators, time-parallel methods, Burgers equation, Liouville–Bratu–Gelfand equation

1 Introduction

Large systems of time-dependent ordinary differential equations arise in various applications and in many cases have to be integrated in time by implicit methods, see e.g. [1, 2]. Last decennia the niche of implicit methods has been gradually taken up by exponential time integrators [3]. For implicit and exponential methods the key issue is how to solve arising nonlinear systems and (or) to evaluate related matrix functions efficiently. To achieve efficiency, different approaches exist and widely applied, such as inexact Newton methods combined with powerful linear preconditioned solvers [4, 5, 6], splitting and Rosenbrock methods [7, 8, 9, 10, 1] and approximate iterative implicit schemes (which can be seen as stabilized explicit schemes) [11, 12, 13, 14, 15, 16, 17, 18, 19].

Another important approach to achieve efficiency in implicit and exponential time integrators is based on waveform relaxation methods [20, 21, 22], where iterative approximations are time dependent functions rather than time step values of a numerical solution. These methods have also been known as dynamic iteration or Picard–Lindelöf iteration [23]. They have been developed since the 80s [21, 24, 25, 26, 27] and have received attention recently in connection to the time-parallel exponential method PARAEXP [28] and its extension to nonlinear problems [29, 30].

Typically matrix function evaluations within exponential integrators are carried out by special linear algebra iterative procedures (often these are Krylov subspace or Chebyshev polynomial methods) [31, 32, 33, 14, 34, 35, 36]. The key attractive feature of the waveform relaxation methods is that they employ this linear algebra machinery across a certain time interval rather than within a time step, so that computational costs are distributed across time. This leads to a higher computational efficiency as well as to a parallelism across time [22].

One promising time-integration exponential method of this class is the nonlinear EBK (exponential block Krylov) method [29, 30]. It is based on block Krylov subspace projections [37] combined with waveform relaxation iteration employed to handle nonlinearities. The nonlinear EBK method possesses an across-time parallelism, and, in its parallel implementation, can be seen as an efficient version of the time-parallel PARAEXP method [29, 30].

Convergence of the waveform relaxation methods has been studied in different settings, in particular, for linear initial-value problems, for nonlinear Gauss–Seidel and Jacobi iterations (the working horses of classical waveform relaxation) and for time-discretized settings, see [23, 22] for a survey. Convergence results for waveform relaxation in general nonlinear settings are scarce, and it is often assumed that “studying the linear case carefully … might be what users really need” [23]. Except book [22], containing some general introductory convergence results, one of the papers where nonlinear waveform relaxation is studied is [38]. Below, in Remark 2, we comment more specifically on the results presented there. The aim of this paper is to extend convergence results for waveform relaxation to a nonlinear setting employed in the EBK method. This also yields an insight on its convergence behavior in practice.

The paper is organized as follows. In Section 2.1 a problem setting and the assumptions made are formulated. Main convergence results are presented in Section 2.2. Since the results are formulated for the error function which is in general unknown, in Section 2.3 an error estimate in terms of a computable nonlinear residual is formulated. At each waveform relaxation iteration a linear initial-value problem (IVP) has to be solved which, in current setting, is done by an iterative block Krylov subspace method (the linear EBK method). Therefore, in Section 2.4 we show how the nonlinear iteration convergence is affected if the linear IVP is solved inexactly. In Section 2.5 implementation issues are briefly discussed. Numerical experiments are described in Section 3.1 (for a 1D Burgers equation), Section 3.2 (for a 3D Liouville–Bratu–Gelfand equation), and Section 3.3 (for a 3D nonlinear heat conduction problem). We finish the paper with conclusions drawn in Section 4.

2 Nonlinear waveform relaxation and its convergence

2.1 Problem setting, assumptions and notation

We consider an IVP for nonlinear ODE system

y^{\prime}(t)=\Phi(t,y(t)),\quad y(0)=v,\quad t\in[0,T]

(1)

where $\Phi:\mathbb{R}\times\mathbb{R}^{N}\rightarrow\mathbb{R}^{N}$ , $v\in\mathbb{R}^{N}$ and $T>0$ are given. Without loss of generality, we assume that the time dependence in the right hand side function $\Phi$ is of the form

\Phi(t,y)=\bar{\Phi}(y)+g(t),\quad\bar{\Phi}:\mathbb{R}^{N}\rightarrow\mathbb{R}^{N},\quad g:\mathbb{R}\rightarrow\mathbb{R}^{N}.

(2)

Otherwise, we can transform (1) to an equivalent autonomous form (usually this is done by extending the unknown vector function $y(t)$ with an additional $(N+1)$ -th coordinate $y_{N+1}(t)=t$ and adding an ODE $y_{N+1}^{\prime}(t)=1$ to the system).

Iterative methods considered in this note are based on a family of splittings

\Phi(t,y)=-A_{k}y+f_{k}(y)+g(t),\qquad\forall\;y\in\mathbb{R}^{N},\;t\geqslant 0,

(3)

with $k$ being the iteration number, so that matrices $A_{k}\in\mathbb{R}^{N\times N}$ and mappings $f_{k}:\mathbb{R}^{N}\rightarrow\mathbb{R}^{N}$ may vary from iteration to iteration. The mappings $f_{k}$ in (3) are all assumed to be Lipschitz continuous with a common Lipschitz constant $L$ , i.e.,

\forall k:\quad\|f_{k}(u)-f_{k}(v)\|\leqslant L\|u-v\|,\qquad\forall\;u,v\in\mathbb{R}^{N}.

(4)

Here and throughout the paper $\|\cdot\|$ denotes a vector norm in $\mathbb{C}^{N}$ or a corresponding induced matrix norm. Furthermore, we assume that for all the matrices $A_{k}$ in (3) there exist constants $C>0$ and $\omega\geqslant 0$ such that

\|\exp(-tA_{k})\|\leqslant Ce^{-\omega t},\qquad t\geqslant 0.

(5)

For a particular matrix $A=A_{k}$ , condition (5) holds, for instance, in the 2-norm if the numerical range of $A$ lies in the complex halfplane $\{z=x+iy\;|\;x\geqslant 0,y\in\mathbb{R},i^{2}=-1\}$ . In this case $C=1$ and $\omega$ is the smallest eigenvalue of the symmetric part $\frac{1}{2}(A+A^{T})$ of $A$ . Condition (5) is closely related to the concept of the matrix logarithmic norm, see, e.g., [39, 1]. In particular, if $\mu(-A)$ is the logarithmic norm of $-A$ then condition (5) holds, with $C=1$ and for all $t\geqslant 0$ , if and only if [1, Theorem I.2.4]

\mu(-A)\leqslant-\omega.

In the analysis below, we also use functions $\varphi_{j}$ [3, relation (2.10)], defined for $j=0,1,2,\dots$ as

\varphi_{j+1}(z)=\frac{\varphi_{j}(z)-\varphi_{j}(0)}{z},\qquad\varphi_{0}(z)=e^{z},

(6)

where we set $\varphi_{j}(0)=1/j!$ , which makes $\varphi_{j}$ entire functions. In this paper, the following variation-of-constants formula (see, e.g., [1, Section I.2.3], [3, relation (1.5)]) is instrumental:

y(t)=\exp(-tA_{k})v+\int_{0}^{t}\exp(-(t-s)A_{k})\left[f_{k}(y(s))+g(s)\right]\mathrm{d}s,\quad t\in[0,T],

(7)

where $y(t)$ is solution of IVP (1),(3).

2.2 Nonlinear waveform relaxation

Let $y_{0}(t)$ be an approximation to the unknown function $y(t)$ for $t\in[0,T]$ , with $y_{0}(0)=v$ . Usually $y_{0}(t)$ is taken to be $y_{0}(t)\equiv v$ for all $t\in[0,T]$ . To solve (1), in this paper we consider nonlinear waveform relaxation iteration where we solve successfully, for $k=0,1,2,\dots$ , a linear inhomogeneous IVP

y_{k+1}^{\prime}(t)=-A_{k}y_{k+1}(t)+f_{k}(y_{k}(t))+g(t),\quad y_{k+1}(0)=v,\quad t\in[0,T].

(8)

Here the matrices $A_{k}\in\mathbb{R}^{N\times N}$ and the mappings $f_{k}:\mathbb{R}^{N}\rightarrow\mathbb{R}^{N}$ form a splitting of $\Phi$ , see (3), and satisfy, for all $k$ , the assumptions (4),(5). We emphasize that at each iteration an approximation $y_{k+1}(t)$ is computed and stored for the whole time range $t\in[0,T]$ . In Section 2.5 below we briefly discuss how to do this efficiently.

The following proposition provides a sufficient condition for iteration (8) to converge.

Proposition 1.

Let IVP (1) be solved iteratively by (8) and let assumptions (4),(5) hold for $A_{k}$ and $f_{k}$ in (8), $k=0,1,\dots$ . Then for the error $\epsilon_{k+1}(t)\equiv y(t)-y_{k+1}(t)$ of the iterative approximation $y_{k+1}(t)$ holds, for $k=0,1,\dots$ ,

\|\epsilon_{k+1}(t)\|\leqslant CLt\varphi_{1}(-\omega t)\max_{s\in[0,t]}\|\epsilon_{k}(s)\|,\quad\forall t\in[0,T],

(9)

and nonlinear waveform relaxation (8) converges for $t\in[0,T]$ to solution $y(t)$ of IVP (1),(3) provided that

CLT\varphi_{1}(-\omega T)<1.

(10)

Proof.

Subtracting the iteration formula (8) from the ODE $y^{\prime}(t)=-A_{k}y(t)+f_{k}(y(t))+g(t)$ and taking into account that $y(0)=y_{k+1}(0)=v$ , we see that the error $\epsilon_{k+1}(t)$ satisfies IVP

\epsilon_{k+1}^{\prime}(t)=-A_{k}\epsilon_{k+1}(t)+f_{k}(y(t))-f_{k}(y_{k}(t)),\quad\epsilon_{k+1}(0)=0.

(11)

Then, applying the variation-of-constants formula (7) to IVP (11), we obtain

\epsilon_{k+1}(t)=\int_{0}^{t}\exp(-(t-s)A_{k})\left[f_{k}(y(s))-f_{k}(y_{k}(s))\right]\mathrm{d}s.

Therefore, using (4) and (5), we can bound

	$\displaystyle\\|\epsilon_{k+1}(t)\\|$	$\displaystyle\leqslant\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,\\|\left[f_{k}(y(s))-f_{k}(y_{k}(s))\right]\\|\mathrm{d}s$
		$\displaystyle\leqslant\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,L\\|y(s))-y_{k}(s)\\|\mathrm{d}s$
		$\displaystyle\leqslant L\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,\mathrm{d}s$
		$\displaystyle\leqslant CL\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|\int_{0}^{t}e^{-\omega(t-s)}\,\mathrm{d}s=CLt\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|.$

Thus, (9) is proved. Taking into account that $t\varphi_{1}(-\omega t)$ is a monotonically increasing function of $t$ , we obtain (10). ∎

Remark 1.

Proposition 1 shows that we can choose a length $T$ of the time interval $[0,T]$ such that the nonlinear waveform relaxation converges. The larger the Lipschitz constant $L$ , the smaller $T$ should be taken.

Remark 2.

To solve an initial-value problem for an autonomous ODE system

C(y)y^{\prime}(t)-\bar{F}(y(t))=0,

in [38] a nonlinear waveform iteration

y^{\prime}_{k+1}(t)-\bar{F}(y_{k+1}(t))=\widehat{g}(y^{\prime}_{k}(t))

(12)

is considered, where $C(y)$ is a matrix and $C(y)y^{\prime}=y^{\prime}-\widehat{g}(y^{\prime})$ . A convergence analysis of (12) is given in assumption that $\widehat{g}$ is Lipschitz-continuous with a Lipschitz constant less than one. In [38], a particular case of (12) is also considered with $\bar{F}(y)=-Ay+f(y)$ , i.e.,

y^{\prime}_{k+1}(t)+Ay_{k+1}(t)-f(y_{k+1}(t))=\widehat{g}(y^{\prime}_{k}(t)).

Hence, our results here do not overlap with the results in [38].

In case $f(y)$ is linear, waveform relaxation (8) is known to have an attractive property to converge superlinearly for final $T$ , see, e.g., [40, Theorem 5.1] and, for inexact waveform relaxation, [41, Theorem 2]. The following result shows that the superlinear convergence property is shared by nonlinear waveform relaxation (8).

Proposition 2.

Let IVP (1) be solved iteratively by (8) and let assumptions (4),(5) hold for $A_{k}$ and $f_{k}$ in (8), $k=0,1,\dots$ . Then for the error $\epsilon_{k}(t)$ of the iterative approximation $y_{k}(t)$ holds, for $k=1,2,\dots$ ,

	$\displaystyle\\|\epsilon_{k}(t)\\|$	$\displaystyle\leqslant(CL)^{k}t^{k}e^{-\omega t}\varphi_{k}(\omega t)\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|$		(13)
		$\displaystyle\leqslant(CL)^{k}\frac{t^{k}}{k!}\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|,\quad\forall t\in[0,T].$		(13)

Proof.

The proof is very similar to the proof of [40, Theorem 5.1], where a linear equivalent of (1),(8) is considered. The estimate (13) will be proven by induction. Note that $t\varphi_{1}(-\omega t)=te^{-\omega t}\varphi_{1}(\omega t)$ . Therefore, the estimate (13) for $k=1$ holds, as it coincides with (9) for $k=0$ . Assume that (13) holds for a certain $k$ . From the proof of Proposition 1, we see that

	$\displaystyle\\|\epsilon_{k+1}(t)\\|$	$\displaystyle\leqslant CL\int_{0}^{t}e^{-(t-s)\omega}\\|\epsilon_{k}(s)\\|\mathrm{d}s$
and, by the induction assumption,
		$\displaystyle\leqslant CL\int_{0}^{t}e^{-(t-s)\omega}(CL)^{k}s^{k}e^{-\omega s}\varphi_{k}(\omega s)\max_{\tilde{s}\in[0,s]}\\|\epsilon_{0}(\tilde{s})\\|\mathrm{d}s$
		$\displaystyle=(CL)^{k+1}e^{-\omega t}\int_{0}^{t}s^{k}\varphi_{k}(\omega s)\max_{\tilde{s}\in[0,s]}\\|\epsilon_{0}(\tilde{s})\\|\mathrm{d}s$
		$\displaystyle\leqslant(CL)^{k+1}e^{-\omega t}\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|\int_{0}^{t}s^{k}\varphi_{k}(\omega s)\mathrm{d}s$
		$\displaystyle=(CL)^{k+1}t^{k+1}e^{-\omega t}\varphi_{k+1}(\omega t)\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|,$

where the relation $\int_{0}^{t}s^{k}\varphi_{k}(\omega s)\mathrm{d}s=t^{k+1}\varphi_{k+1}(\omega t)$ is employed. Thus, the induction step is done. Finally, using the definition of $\varphi_{k}$ and the fact that $\omega\geqslant 0$ , it is not difficult to check that

t^{k}e^{-\omega t}\varphi_{k}(\omega t)\leqslant\frac{t^{k}}{k!},\quad t\geqslant 0,

which proves the second inequality in (13). ∎

2.3 Residual of the nonlinear problem

To control convergence of waveform relaxation (8) in practice, it is natural to consider a residual $r_{k}(t)$ of an iterative approximation $y_{k}(t)$ in (8). Since $y_{k}(t)$ is defined by (8),(3) written for $k-1$ , it is natural to define the residual with respect to IVP (1) combined with splitting (3) for $k-1$ , i.e., for IVP

y^{\prime}(t)=-A_{k-1}y(t)+f_{k-1}(y(t))+g(t),\quad y(0)=v,\quad t\in[0,T].

(14)

Hence, we define

r_{k}(t)\equiv-A_{k-1}y_{k}(t)+f_{k-1}(y_{k}(t))+g(t)-y_{k}^{\prime}(t),\quad t\in[0,T],

(15)

and write

$\displaystyle r_{k}(t)$	$\displaystyle=-A_{k-1}y_{k}(t)+f_{k-1}(y_{k}(t))+g(t)-y_{k}^{\prime}(t)\pm f_{k-1}(y_{k-1}(t))$	(16)
	$\displaystyle=\underbrace{-A_{k-1}y_{k}(t)+f_{k-1}(y_{k-1}(t))+g(t)-y_{k}^{\prime}(t)}_{=0}+f_{k-1}(y_{k}(t))-f_{k-1}(y_{k-1}(t))$
	$\displaystyle=f_{k-1}(y_{k}(t))-f_{k-1}(y_{k-1}(t)),\quad t\in[0,T],\quad k=1,2,\dots.$

Note that the residual $r_{k}(t)$ possesses the backward error property, i.e., iterative approximation $y_{k}(t)$ can be viewed as the exact solution of a perturbed IVP (14)

y_{k}^{\prime}(t)=-A_{k-1}y_{k}(t)+f_{k-1}(y_{k}(t))+g(t)-r_{k}(t),\quad y_{k}(0)=v\quad t\in[0,T].

(17)

Subtracting the ODE of this problem from the ODE in (14), we obtain an IVP for the error $\epsilon_{k}(t)$

\epsilon_{k}^{\prime}(t)=-A_{k-1}\epsilon_{k}(t)+f_{k-1}(y(t))-f_{k-1}(y_{k}(t))+r_{k}(t),\quad\epsilon_{k}(0)=0,

(18)

which is equivalent to the IVP (11). The following proposition shows that the residual can be seen as an upper bound bound for the error.

Proposition 3.

Let IVP (1) be solved iteratively by (8) and let assumptions (4),(5) hold for $A_{k}$ and $f_{k}$ in (8), $k=0,1,\dots$ . Let $T>0$ be chosen such that the sufficient condition (10) for convergence of (8) holds

CLT\varphi_{1}(-\omega T)\leqslant\delta<1,

(19)

for a certain constant $\delta\in(0,1)$ . Then, for $\forall t\in[0,T]$ ,

\max_{s\in[0,t]}\|\epsilon_{k}(s)\|\leqslant\frac{Ct\varphi_{1}(-\omega t)}{1-CLt\varphi_{1}(-\omega t)}\max_{s\in[0,t]}\|r_{k}(s)\|\leqslant\frac{\delta}{(1-\delta)L}\max_{s\in[0,t]}\|r_{k}(s)\|.

(20)

Note that $T\varphi_{1}(-\omega T)$ increases with $T$ monotonically.

Proof.

Employing the variation-of-constants formula for IVP (18), we can bound

	$\displaystyle\\|\epsilon_{k}(t)\\|$	$\displaystyle\leqslant\int_{0}^{t}\left\\|\exp(-(t-s)A_{k-1})\left[f_{k-1}(y(s))-f_{k-1}(y_{k}(s))+r_{k}(s)\right]\right\\|\mathrm{d}s$
		$\displaystyle\leqslant\max_{s\in[0,t]}\left\\|f_{k-1}(y(s))-f_{k-1}(y_{k}(s))+r_{k}(s)\right\\|\int_{0}^{t}\\|\exp(-(t-s)A_{k-1})\\|\,\mathrm{d}s$
		$\displaystyle\leqslant\max_{s\in[0,t]}\left\\|f_{k-1}(y(s))-f_{k-1}(y_{k}(s))+r_{k}(s)\right\\|\,Ct\varphi_{1}(-\omega t)$
		$\displaystyle\leqslant\left(L\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|+\max_{s\in[0,t]}\\|r_{k}(s)\\|\right)\,Ct\varphi_{1}(-\omega t)$
		$\displaystyle\leqslant CLt\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|+Ct\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|r_{k}(s)\\|.$

Taking into account that $CLt\varphi_{1}(-\omega t)\leqslant CLT\varphi_{1}(-\omega T)\leqslant\delta<1$ for $t\in[0,T]$ , we obtain

	$\displaystyle(1-CLt\varphi_{1}(-\omega t))\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|$	$\displaystyle\leqslant Ct\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|r_{k}(s)\\|$
	$\displaystyle\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|$	$\displaystyle\leqslant\frac{Ct\varphi_{1}(-\omega t)}{1-CLt\varphi_{1}(-\omega t)}\max_{s\in[0,t]}\\|r_{k}(s)\\|,$

which yields (20). ∎

As stated by proposition below, an upper bound for the nonlinear residual can be obtained in terms of the error at the previous iteration.

Proposition 4.

Let IVP (1) be solved iteratively by (8) and let assumptions (4),(5) hold for $A_{k}$ and $f_{k}$ in (8), $k=0,1,\dots$ . Then, for $k=1,2,\dots$ ,

	$\displaystyle\\|r_{k}(t)\\|$	$\displaystyle\leqslant(1+CLt\varphi_{1}(-\omega t))L\max_{s\in[0,t]}\\|\epsilon_{k-1}(s)\\|,\quad\forall t\in[0,T],$	(21)
If, in addition, convergence condition (19) is satisfied, we have
	$\displaystyle\\|r_{k}(t)\\|$	$\displaystyle\leqslant(1+\delta)L\max_{s\in[0,t]}\\|\epsilon_{k-1}(s)\\|<2L\max_{s\in[0,t]}\\|\epsilon_{k-1}(s)\\|,\quad\forall t\in[0,T].$	(22)

Proof.

Using relation (16), we can write, for $t\in[0,T]$ ,

	$\displaystyle r_{k}(t)$	$\displaystyle=f_{k-1}(y_{k}(t))-f_{k-1}(y(t))+f_{k-1}(y(t))-f_{k-1}(y_{k-1}(t)),$
	$\displaystyle r_{k}(t)$	$\displaystyle\leqslant\\|f_{k-1}(y_{k}(t))-f_{k-1}(y(t))\\|+\\|f_{k-1}(y(t))-f_{k-1}(y_{k-1}(t))\\|$
		$\displaystyle\leqslant L\\|y_{k}(t))-y(t)\\|+L\\|y(t)-y_{k-1}(t)\\|=L(\\|e_{k}(t)\\|+\\|e_{k-1}(t)\\|)$
		$\displaystyle\leqslant L\left(CLt\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|e_{k-1}(s)\\|+\\|e_{k-1}(t)\\|\right),$

which leads to (21),(22). ∎

2.4 Linear inner iteration and its residual

In practice, the linear ODE system (8) at each waveform relaxation iteration can be solved by any suitable integrator inexactly, with a certain accuracy tolerance. In the context of the time-parallel PARAEXP scheme, the nonlinear waveform relaxation appeared to be efficient for fluid dynamics problems [29, 30], with linear IVP (8) solved by the exponential block Krylov subspace (EBK) method [37]. Thus, in this setting we have an inner-outer iterative process where each nonlinear waveform relaxation iteration (8) involves an inner Krylov subspace iterative process $\tilde{y}_{k+1,\ell}(t)\rightarrow y_{k+1}(t)$ , with $\ell$ being the inner iteration number. For notation simplicity we omit the dependence on the inner iteration number $\ell$ in $\tilde{y}_{k+1,\ell}(t)$ and write $\tilde{y}_{k+1}(t)$ . These inner EBK iterations are controled by checking the norm of a residual defined, for $\tilde{y}_{k+1}(t)\approx y_{k+1}(t)$ , as

r^{\mathsf{lin}}_{k+1}(t)\equiv-A_{k}\tilde{y}_{k+1}(t)+f_{k}(\tilde{y}_{k}(t))+g(t)-\tilde{y}^{\prime}_{k+1}(t),\quad t\in[0,T].

(23)

Here we assume that the previous iterative approximation is also computed inexactly and therefore we replace $y_{k}(t)$ by $\tilde{y}_{k}(t)$ . The inner iterations stop after a certain number $\ell$ of inner iterations as soon as the linear residual $r^{\mathsf{lin}}_{k+1}(t)$ , defined by (23), is small enough in norm. The residual $\tilde{r}_{k+1}(t)$ turns out to be easily computable as a by-product of the block Krylov subspace method [37]. Moreover, the residual in (23) can be used as a controller for the error in the linear IVP (8), see [37, relation (16)].

As Proposition 5 below shows, convergence in the nonlinear waveform relaxation is retained if the IVP (8) at each nonlinear iteration is solved approximately, such that residual (23) is small enough in norm. To formulate the proposition, it is convenient to assume that the linear residual is bounded in norm by the error achieved at a previous nonlinear iteration, cf. (24).

Proposition 5.

Let IVP (1) be solved iteratively by (8) and let assumptions (4),(5) and convergence condition (19) hold. Furthermore, let the IVP (8) at each nonlinear iteration $k=0,1,\dots$ be solved approximately with $\ell$ inner iterations such that for the inner iteration residual (23) one of the following two conditions holds:

	$\displaystyle\mathrm{(a)}$	$\displaystyle\\|r^{\mathsf{lin}}_{k+1}(t)\\|\leqslant\eta\max_{s\in[0,t]}\\|f_{k}(\tilde{y}_{k+1}(s))-f_{k}(\tilde{y}_{k}(s))\\|,\quad t\in[0,T],$		(24)
	$\displaystyle\mathrm{(b)}$	$\displaystyle\\|r^{\mathsf{lin}}_{k+1}(t)\\|\leqslant\eta L\max_{s\in[0,t]}\\|\tilde{y}_{k+1}(s)-\tilde{y}_{k}(s)\\|,\quad t\in[0,T],$		(24)

with a constant $\eta\in(0,1)$ . Then for the error $\tilde{\epsilon}_{k+1}(t)\equiv y(t)-\tilde{y}_{k+1}(t)$ of the iterative solution $\tilde{y}_{k+1}(t)$ in inexact inner-outer iteration (8),(23) holds, for $k=0,1,\dots$ ,

\|\tilde{\epsilon}_{k+1}(t)\|\leqslant\frac{(1+\eta)CLt\varphi_{1}(-\omega t)}{1-\eta CLt\varphi_{1}(-\omega t)}\max_{s\in[0,t]}\|\tilde{\epsilon}_{k}(s)\|,\quad\forall t\in[0,T].

(25)

Moreover, the inexact iteration (8),(23) converges for $t\in[0,T]$ to solution $y(t)$ of IVP (1),(3) provided that

\eta<\frac{1-\delta}{2\delta}.

(26)

Proof.

Note that, due to (4),

\|f_{k}(\tilde{y}_{k+1}(t))-f_{k}(\tilde{y}_{k}(t))\|\leqslant L\|\tilde{y}_{k+1}(t)-\tilde{y}_{k}(t)\|

and, hence, condition (24),(b) follows from condition (24),(a) Therefore, without loss of generality, we assume that (24),(a) holds. It follows from (23) that $\tilde{y}_{k+1}(t)$ solves a perturbed ODE system

\tilde{y}^{\prime}_{k+1}(t)=-A_{k}\tilde{y}_{k+1}(t)+f_{k}(\tilde{y}_{k}(t))+g(t)-r^{\mathsf{lin}}_{k+1}(t).

(27)

Subtracting this equation from the original nonlinear ODE $y^{\prime}(t)=-A_{k}y(t)+f_{k}(y(t))+g(t)$ and taking into account that $\tilde{y}_{k+1}(0)=y(0)=v$ , we obtain an IVP for the error $\tilde{\epsilon}_{k+1}(t)\equiv y(t)-\tilde{y}_{k+1}(t)$ (cf. (11)):

\tilde{\epsilon}^{\prime}_{k+1}(t)=-A_{k}\tilde{\epsilon}_{k+1}(t)+f_{k}(y(t))-f_{k}(\tilde{y}_{k}(t))+r^{\mathsf{lin}}_{k+1}(t),\quad\tilde{\epsilon}_{k+1}(0)=0.

Application of variation-of-constants formula (7) leads to

\tilde{\epsilon}_{k+1}(t)=\int_{0}^{t}\exp(-(t-s)A_{k})\left[f_{k}(y(s))-f_{k}(\tilde{y}_{k}(s))+r^{\mathsf{lin}}_{k+1}(s)\right]\mathrm{d}s.

Then, using (4),(5),(24) we get, for $t\in[0,T]$ ,

	$\displaystyle\\|\tilde{\epsilon}_{k+1}(t)\\|$	$\displaystyle\leqslant\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,\left\\|f_{k}(y(s))-f_{k}(\tilde{y}_{k}(s))+r^{\mathsf{lin}}_{k+1}(s)\right\\|\mathrm{d}s$
		$\displaystyle\leqslant Ct\varphi_{1}(-\omega t)\left[L\max_{s\in[0,t]}\\|\tilde{\epsilon}_{k}(s)\\|+\max_{s\in[0,t]}\\|r^{\mathsf{lin}}_{k+1}(s)\\|\right]$
		$\displaystyle\leqslant Ct\varphi_{1}(-\omega t)\left[L\max_{s\in[0,t]}\\|\tilde{\epsilon}_{k}(s)\\|+\eta L\max_{s\in[0,t]}\\|\tilde{y}_{k+1}(s)-\tilde{y}_{k}(s)\\|\right].$

Furthermore,

\max_{s\in[0,t]}\|\tilde{y}_{k+1}(s)-\tilde{y}_{k}(s)\pm y(s)\|\leqslant\max_{s\in[0,t]}\|\tilde{\epsilon}_{k+1}(s)\|+\max_{s\in[0,t]}\|\tilde{\epsilon}_{k}(s)\|,

so that, for $t\in[0,T]$ ,

	$\displaystyle\\|\tilde{\epsilon}_{k+1}(t)\\|\leqslant CLt\varphi_{1}(-\omega t)\left[(1+\eta)\max_{s\in[0,t]}\\|\tilde{\epsilon}_{k}(s)\\|+\eta\max_{s\in[0,t]}\\|\tilde{\epsilon}_{k+1}(s)\\|\right],$
	$\displaystyle(1-CLt\varphi_{1}(-\omega t)\eta)\max_{s\in[0,t]}\\|\tilde{\epsilon}_{k+1}(s)\\|\leqslant CLt\varphi_{1}(-\omega t)(1+\eta)\max_{s\in[0,t]}\\|\tilde{\epsilon}_{k}(s)\\|.$

Taking into account that $CLt\varphi_{1}(-\omega t)\leqslant CLT\varphi_{1}(-\omega T)\leqslant\delta<1$ and $0<\eta<1$ , we then obtain

\max_{s\in[0,t]}\|\tilde{\epsilon}_{k+1}(s)\|\leqslant\frac{CLt\varphi_{1}(-\omega t)(1+\eta)}{1-CLt\varphi_{1}(-\omega t)\eta}\max_{s\in[0,t]}\|\tilde{\epsilon}_{k}(s)\|\leqslant\frac{\delta(1+\eta)}{1-\delta\eta}\max_{s\in[0,t]}\|\tilde{\epsilon}_{k}(s)\|.

This yields (25). Condition (26) is equivalent to $\frac{\delta(1+\eta)}{1-\delta\eta}<1$ . ∎

Remark 3.

Note that for $\eta\rightarrow 0$ the obtained convergence condition (26) transforms into (19). In general, condition (24),(b) is probably easier to check in practice than (24),(a). However, IVPs where (24),(a) is easy to compute may occur as well. Since $\tilde{y}_{k}(t)$ and $\tilde{y}_{k+1}(t)$ are solutions of IVPs with the same initial vector $v$ , we may expect that $\max_{s\in[0,t]}\|\tilde{y}_{k+1}(s)-\tilde{y}_{k}(s)\|\approx\|\tilde{y}_{k+1}(t)-\tilde{y}_{k}(t)\|$ .

Nevertheless, employment of condition (24) in practice does not seem to be necessary: as numerical tests below demonstrate, simple stopping criteria (cf. (33),(40)) based on smallness of $\|r^{\mathsf{lin}}_{k+1}(t)\|$ work fine in practice, leading to an efficient inner-outer iteration method.

2.5 Implementation of nonlinear waveform relaxation

We take initial guess function $y_{0}(t)$ identically (i.e., for all $t\in[0,T]$ ) equal to the initial vector $y_{0}(t)\equiv v$ . Then, at each iteration (8) we set $\tilde{g}(t):=f_{k}(y_{k}(t))+g(t)$ and solve a linear IVP

y^{\prime}_{k+1}(t)=-A_{k}y_{k+1}(t)+\tilde{g}(t),\quad y_{k+1}(0)=v,\quad t\in[0,T].

(28)

Since this IVP is solved by the EBK method [37], the solution $y_{k+1}(t)$ at every iteration is obtained as a linear combination of Krylov subspace vectors, stored columnwise in a matrix $V_{\ell\cdot m}\in\mathbb{R}^{N\times\ell m}$ , with $\ell$ being the number of inner iterations,

y_{k+1}(t)=V_{\ell\cdot m}u_{k+1}(t),\quad t\in[0,T],\quad u_{k+1}:\mathbb{R}\rightarrow\mathbb{R}^{\ell\cdot m},

where $u_{k+1}(t)$ of is solution of a small-sized projected IVP (see [37] for details). This allows to store $y_{k+1}(t)$ in a compact way for all $t\in[0,T]$ . At each nonlinear iteration $k$ the EBK method stops as soon as the residual (23) is small enough in norm. The residual norm is easily computable and is checked for several values of $t\in[0,T]$ .

Starting with the second iteration $k=1$ , before the IVP (28) is solved, the vector function $\tilde{g}(t)\equiv f_{k}(y_{k}(t))+g(t):\mathbb{R}\rightarrow\mathbb{R}^{N}$ is sampled at $n_{s}$ points $t_{1}$ , …, $t_{n_{s}}$ covering the time interval $[0,T]$ . Usually, it is sensible to take $t_{1}=0$ , $t_{n_{s}}=T$ and the other $t_{j}$ to be the Chebyshev polynomial roots:

t_{j}=\frac{T}{2}\left(1-\cos\frac{\pi(j-3/2)}{s-2}\right),\quad j=2,\dots,n_{s}-1.

The number of sample points $n_{s}$ should be taken such that $\tilde{g}(t)$ is sufficiently well approximated by its linear interpolation at $t_{1}$ , …, $t_{n_{s}}$ . The computed samples $\tilde{g}(t_{j})$ , $j=1,\dots,{n_{s}}$ , are then stored as the columns of a matrix $\tilde{G}\in\mathbb{R}^{N\times n_{s}}$ and the thin singular value decomposition of $\tilde{G}$ is employed to obtain a low rank representation

\tilde{g}(t)\approx Up(t),\quad U\in\mathbb{R}^{N\times m},\quad t\in[0,T],

(29)

where typically $m<10$ . For more details of this procedure we refer to [37] or to [29]. Usually the computational work needed to obtain representation $\tilde{g}(t)\approx Up(t)$ is negligible with respect to the other work in the EBK method. The nonlinear iteration (8) is stopped as soon as the nonlinear residual (16) is small enough in norm (in our limited experience, in practice it suffice to check the residual norm at final time $t=T$ only). The resulting algorithm is outlined below.

  Algorithm 1 Given: IVP (1), initial value vector $v$ , tolerance tol, block size $m$ , sample number $n_{s}$ .
Result: numerical solution $y(T)$ of IVP (1).
Initialize nonlinear iteration:
$y_{0}(t):=v$ (constant in time)
for $k=0,1,2,\dots$ (main iteration loop)
    if ( $k=0$ ) then
       $\texttt{resnorm}:=\|r_{0}(T)\|=\|\Phi(T,v)\|$
    else
       $\texttt{resnorm}:=\|r_{k}(T)\|=\|f_{k-1}(y_{k}(T))-f_{k-1}(y_{k-1}(T))\|$
    endif
    if resnorm is small enough (cf. (32),(39)) then
       stop iteration
    endif
    define $f_{k}(y)$ , $A_{k}$ , $\tilde{g}(t):=f_{k}(y_{k}(t))+g(t)$
    set inner iteration tolerance $\texttt{tol}_{\mathtt{lin}}$ (cf. (33),(40))
    compute the low rank approximation (29), $\tilde{g}(t)\approx Up(t)$
    solve linear IVP (28) by inner block Krylov subspace iteration (linear EBK)
    $\Rightarrow$ obtain $y_{k+1}(t)=V_{\ell\cdot m}u_{k+1}(t)$ , $t\in[0,T]$
endfor (main iteration loop)

3 Numerical experiments

3.1 1D Burgers equation

This IVP is taken from [42, Ch. IV.10]. To find unknown function $u(x,t)$ , we solve a 1D Burgers equation

u_{t}=\nu u_{xx}-uu_{x},\quad 0\leqslant x\leqslant 1,\quad 0\leqslant t\leqslant T,

with viscosity $\nu=3\cdot 10^{-4}$ and $\nu=3\cdot 10^{-5}$ . Initial and boundary conditions are

u(x,0)=\frac{3}{2}x(1-x)^{2},\quad u(0,t)=u(1,t)=0,

and the final time $T$ is set to $0.5$ , $1.0$ , and $1.5$ . We discretize the Burgers equation by finite differences on a uniform mesh with $N$ internal nodes $x_{j}=j\Delta x$ , $j=1,\dots,n$ , $\Delta x=1/(N+1)$ . To avoid numerical energy dissipation and to guarantee that a discretization of the advection term $uu_{x}$ results in a skew-symmetric matrix [43], we apply the standard second-order central differences in the following way

uu_{x}=\frac{1}{3}uu_{x}+\frac{2}{3}\left(\frac{u^{2}}{2}\right)_{x}\approx\frac{1}{3}u_{i}\frac{u_{i+1}-u_{i-1}}{2\Delta x}+\frac{2}{3}\frac{u_{i+1}^{2}-u_{i-1}^{2}}{4\Delta x}.

The diffusion term $\nu u_{xx}$ is discretized by second-order central differences in the usual way. Then this finite difference discretization leads to an IVP of the form

y^{\prime}(t)=-A_{\mathrm{symm}}y(t)-A_{\mathrm{skew}}(y(t))y(t),\quad y(0)=v,

(30)

where

A_{\mathrm{symm}}y\approx-\nu u_{xx},\quad A_{\mathrm{skew}}(y)y\approx uu_{x},

$A_{\mathrm{symm}}=A_{\mathrm{symm}}^{T}\in\mathbb{R}^{N\times N}$ is positive definite and $(A_{\mathrm{skew}}(y))^{T}=-A_{\mathrm{skew}}(y)\in\mathbb{R}^{N\times N}$ for all $y\in\mathbb{R}^{N}$ . It is important to make sure that discretization of the convective term results in a skew-symmetric matrix [43, 44]. Otherwise, there are contributions of the convective term to the symmetric part of the Jacobian matrix which distort the proper energy dissipation in the ODE system and may prevent the the symmetric part from being positive semidefinite. In the context of this paper, this would mean that $\omega\geqslant 0$ is not guaranteed anymore.

A straightforward way to apply the nonlinear iteration (8) to (30) would be setting in (3) $A_{k}:=A_{\mathrm{symm}}$ , $f_{k}(y):=-A_{\mathrm{skew}}(y)y$ . However, to decrease the Lipschitz constant of $f_{k}(y)$ (cf. condition (10)), we also include a linear part of $-A_{\mathrm{skew}}(y)y$ to the $-A_{k}y$ term in (3). More specifically, we apply the nonlinear iteration (8) to semidiscrete Burgers equation (30) in the form

	$\displaystyle y_{k+1}^{\prime}(t)=-(\,\underbrace{A_{\mathrm{symm}}+A_{\mathrm{skew}}(\bar{y}_{k})}_{\displaystyle A_{k}}\,)y_{k+1}(t)+\underbrace{\left[A_{\mathrm{skew}}(\bar{y}_{k})-A_{\mathrm{skew}}(y_{k}(t))\right]y_{k}(t)}_{\displaystyle f_{k}(y_{k}(t))},$		(31)
	$\displaystyle k=0,1,2,\dots,$		(31)

where $\bar{y}_{k}=y_{k}(T)$ . The nonlinear residual (16) in this case reads, for $k=0,1,\dots$ ,

	$\displaystyle r_{k+1}(t)$	$\displaystyle=f_{k}(y_{k+1}(t))-f_{k}(y_{k}(t))$
		$\displaystyle=\left[A_{\mathrm{skew}}(\bar{y}_{k})-A_{\mathrm{skew}}(y_{k+1}(t))\right]y_{k+1}(t)-\left[A_{\mathrm{skew}}(\bar{y}_{k})-A_{\mathrm{skew}}(y_{k}(t))\right]y_{k}(t),$
	$\displaystyle r_{k+1}(T)$	$\displaystyle=\left[A_{\mathrm{skew}}(\bar{y}_{k})-A_{\mathrm{skew}}(y_{k+1}(T))\right]y_{k+1}(T).$

Since the symmetric part of the matrix $A_{k}$ is $\frac{1}{2}(A_{k}+A_{k}^{T})=A_{\mathrm{symm}}$ , the $\omega$ value is the smallest eigenvalue of $A_{\mathrm{symm}}$ . The lowest eigenmodes should be well approximated even on the coarsest grid. Indeed, computing $\omega$ numerically (which is easy for this one-dimensional problem) yields approximately the same result on all grids: we get $\omega\approx\texttt{2.96e-03}$ for $\nu=3\cdot 10^{-4}$ and $\omega\approx\texttt{2.96e-04}$ for $\nu=3\cdot 10^{-5}$ . We stop our nonlinear iterative process (8) as soon as

\|r_{k}(T)\|\leqslant\texttt{tol},

(32)

where tol is a tolerance value. As we primarily aim at solving IVPs stemming from space discretization of PDEs, where space discretization error is significant, we settle for a moderate tolerance value $\texttt{tol}=10^{-3}$ in this test. To obtain the low rank representation (29) at each iteration $k$ we use $n_{s}=100$ sample points $t_{j}$ , $j=1,\dots,n_{s}$ and set the number $m$ of singular vectors to $m=7$ . The largest truncated singular value $\sigma_{m+1}$ , serving as an indicator of the relative low rank representation error in (29), is then of order $10^{-6}$ for $T=0.5$ and of order $10^{-3}$ for $T=1.5$ .

For the inner iterative solver EBK employed to solve (8) we set the residual tolerance to $\texttt{tol}_{\mathtt{lin}}=\texttt{tol}$ , which means that inner iterations are stopped as soon as the inner linear residual $r^{\mathsf{lin}}_{k+1}(t)$ satisfies

\|r^{\mathsf{lin}}_{k+1}(T)\|\leqslant\texttt{tol}_{\mathtt{lin}}.

(33)

Krylov subspace dimension is set to $10$ . As the block size in the Krylov subspace process is $m=7$ , the EBK solver requires $m(10+1)=77$ vectors to store. Since the problem becomes stiffer as the spatial grid gets finer, we use the EBK solver in the shift-and-invert (SAI) mode [45, 46], i.e., the block Krylov subspace is computed for the SAI matrix $(I+\gamma A_{k})^{-1}$ , $\gamma=T/10$ , with $A_{k}$ defined in (31). A sparse (banded in this test) LU factorization of $I+\gamma A_{k}$ is computed once at each nonlinear iteration and used every time an action of $(I+\gamma A_{k})^{-1}$ is required.

To compare our nonlinear iterative EBK solver to another solver, we also solve this test with a MATLAB stiff ODE solver ode15s. This is a variable step size and variable order implicit multistep method [47]. The ode15s solver is run with absolute and relative tolerances set, respectively, to $\texttt{AbsTol}=\texttt{tol}$ and $\texttt{RelTol}=10^{4}\texttt{tol}$ , with $\texttt{tol}=10^{-9}$ . For these tolerance values both ode15s and our nonlinear EBK deliver a comparable accuracy. The relative error values reported below are computed as

\frac{\|y-y_{\mathrm{ref}}\|}{\|y_{\mathrm{ref}}\|},

(34)

where $y$ is a numerical solution at final time $T$ and $y_{\mathrm{ref}}$ is a reference solution computed at final time by the ode15s solver run with strict tolerance values $\texttt{AbsTol}=10^{-12}$ and $\texttt{RelTol}=10^{-8}$ . As $y_{\mathrm{ref}}$ is computed on the same spatial grid as $y$ , the error value can be seen as a reliable measure of time accuracy [13].

Actual delivered accuracies and corresponding required computational work for both solvers are reported in Table 1 (for viscosity $\nu=3\cdot 10^{-4}$ ) and Table 2 (for $\nu=3\cdot 10^{-5}$ ). For our nonlinear EBK solver the work is reported as the number of nonlinear iterations, with one LU factorization and one matrix-vector product (matvec) per iteration, and the total number of linear systems solutions (which equals the total number of Krylov steps times the block size $m$ ). The reported total number of LU applications is not necessarily a multiple of the block size $m=7$ because at the first nonlinear iteration the approximate solution is constant in time and, hence, we set $m=1$ in (29) at the first iteration. The computational work for the ode15s solver is reported as the number of time steps, computed LU factorizations and the ODE right hand side function evaluations (fevals). In Tables 1 and 2 we also report the norm of $A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))$ which can be seen as a measure of the ODE system stiffness.

Table 1: The 1D Burgers test problem, viscosity

\nu=3\cdot 10^{-4}

. Attained error and computational work for our nonlinear EBK method and the ode15s solver. For the EBK method the work is reported as the nonlinear iteration number, number of LU factorizations, their applications and matvecs. For the ode15s solver the work is measured the as the number of time steps, LU factorizations, their applications and fevals.

	method,	iter./	LUs (LUs applic.),	relative
$T$	tolerance	steps	matvecs/fevals	error
grid $N=500$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 300$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (141), 5	5.17e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	7	7 (220), 7	2.03e-05
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	10	10 (340), 10	5.31e-05
$0.5$	ode15s, 1e-09	59	14 (73), 575	1.93e-06
$1.0$	ode15s, 1e-09	70	16 (86), 588	8.38e-06
$1.5$	ode15s, 1e-09	83	19 (118), 620	2.21e-05
grid $N=1000$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 1\,200$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (170), 5	5.06e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	7	7 (256), 7	2.00e-05
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	10	10 (389), 10	5.30e-05
$0.5$	ode15s, 1e-09	67	15 (83), 1085	1.76e-06
$1.0$	ode15s, 1e-09	78	17 (104), 1106	1.13e-05
$1.5$	ode15s, 1e-09	91	19 (134), 1136	2.48e-05
grid $N=2000$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 4\,800$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (177), 5	5.07e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	7	7 (277), 7	2.00e-05
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	11	11 (452), 11	4.38e-05
$0.5$	ode15s, 1e-09	73	16 (91), 2093	2.29e-06
$1.0$	ode15s, 1e-09	85	19 (107), 2109	7.96e-06
$1.5$	ode15s, 1e-09	98	22 (139), 2141	2.22e-05
grid $N=4000$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 19\,200$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (193), 5	5.06e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	8	8 (347), 8	4.82e-06
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	11	11 (501), 11	4.38e-05
$0.5$	ode15s, 1e-09	79	18 (99), 4101	1.93e-06
$1.0$	ode15s, 1e-09	90	20 (112), 4114	8.25e-06
$1.5$	ode15s, 1e-09	103	23 (144), 4146	2.21e-05

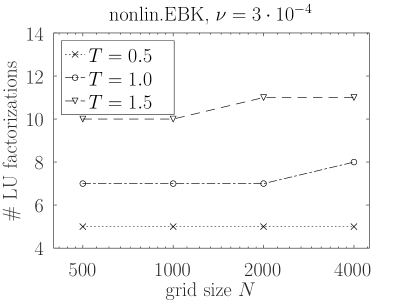
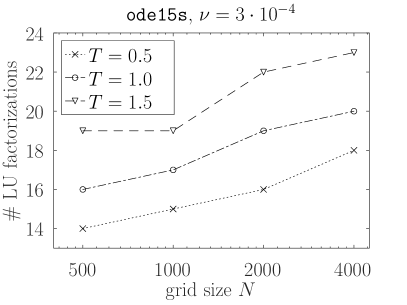
As we can see in Tables 1 and 2, our solver requires less LU factorizations than the ode15s solver. It does require more LU factorization actions but these are relatively cheap. Moreover, in EBK they are carried out simultaneously for blocks of $m$ right hand sides. For both solvers, in Figure 1 we plot the numbers of LU factorizations (presented in the tables) versus the grid size. The number of nonlinear iterations in the EBK solver (with one LU factorization per iteration) remains practically constant as the grid gets finer, whereas the number of LU factorizations in ode15s increases with the grid size. Furthermore, we see that the ode15s solver requires more time steps and significantly more fevals on the finer grids. $T=1.5$ is approximately the largest possible time for which our nonlinear EBK solver converges in this test. From Figure 1 we see that a higher efficiency is reached for larger $T$ values. Indeed, on the finest grid $N=4000$ $5\times 2=10$ LU factorizations per unit time are required for $T=0.5$ , $8$ LU factorizations for $T=1$ and $11/1.5\approx 7$ factorizations for $T=1.5$ .

Comparing Tables 1 and 2, we see that performance of the ode15s solver improves for the smaller viscosity value $\nu=3\cdot 10^{-5}$ . This is expected as the stiffness of the space-discretized Burgers equation decreases with $\nu$ . Indeed, on finer grids, where contributions of $A_{\mathrm{symm}}$ (proportional to $(\Delta x)^{-2}$ ) dominate those of $A_{\mathrm{skew}}(t)$ (proportional to $(\Delta x)^{-1}$ ), we have $\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(t)\|\approx\mathcal{O}(\nu)$ , see the values $\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(T)\|$ reported in the tables.

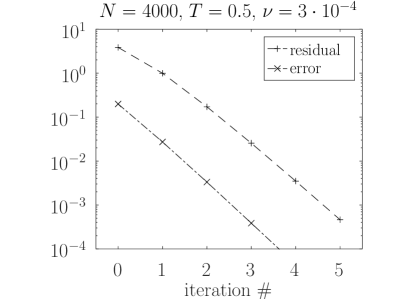
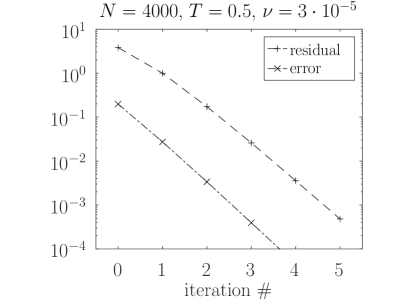
In Figure 2 we plot the reference solution $y_{\mathrm{ref}}(T)$ and the first three iterative approximations $y_{0}(T)=v$ , $y_{1}(T)$ and $y_{2}(T)$ . Convergence plots of the residual and error norms are shown in Figure 3. There, the shown residual norm is computed at $t=T$ according to (16) and the error norm is the relative norm defined in (34). As we see, the residual turns out to be a reliable measure of the error. Furthermore, convergence behavior is not influenced by viscosity $\nu$ , which is in accordance with theory: $\nu$ does not change the nonlinear term $f_{k}$ in (8) and its Lipschitz constant.

Table 2: The 1D Burgers test problem, viscosity

\nu=3\cdot 10^{-5}

	method,	iter./	LUs (LUs applic.),	relative
$T$	tolerance	steps	matvecs/fevals	error
grid $N=500$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 90$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (69), 5	1.82e-05
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	7	7 (139), 7	2.26e-05
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	13	13 (414), 13	1.10e-04
$0.5$	ode15s, 1e-09	28	7 (38), 540	3.71e-06
$1.0$	ode15s, 1e-09	38	9 (53), 555	1.23e-05
$1.5$	ode15s, 1e-09	52	13 (89), 591	3.38e-05
grid $N=1000$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 210$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (90), 5	6.20e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	7	7 (176), 7	2.25e-05
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	12	12 (430), 12	1.07e-04
$0.5$	ode15s, 1e-09	35	9 (44), 1046	2.44e-06
$1.0$	ode15s, 1e-09	45	10 (60), 1062	1.64e-05
$1.5$	ode15s, 1e-09	59	15 (99), 2102	3.83e-05
grid $N=2000$ , $\\|A_{\mathrm{symm}}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 540$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (120), 5	5.29e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	7	7 (190), 7	2.22e-05
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	12	12 (494), 12	1.06e-04
$0.5$	ode15s, 1e-09	42	10 (55), 2057	3.91e-06
$1.0$	ode15s, 1e-09	52	12 (70), 2072	1.32e-05
$1.5$	ode15s, 1e-09	66	17 (108), 4111	3.32e-05
grid $N=4000$ , $\\|A_{0}+A_{\mathrm{skew}}(y(T))\\|_{1}\approx 1\,920$
$0.5$	nonlin.EBK( $m=7$ ), 1e-03	5	5 (149), 5	5.24e-06
$1.0$	nonlin.EBK( $m=7$ ), 1e-03	8	8 (276), 8	5.52e-06
$1.5$	nonlin.EBK( $m=7$ ), 1e-03	12	12 (578), 12	1.07e-04
$0.5$	ode15s, 1e-09	47	11 (61), 4063	3.86e-06
$1.0$	ode15s, 1e-09	58	15 (80), 4082	1.22e-05
$1.5$	ode15s, 1e-09	71	18 (112), 8115	3.36e-05

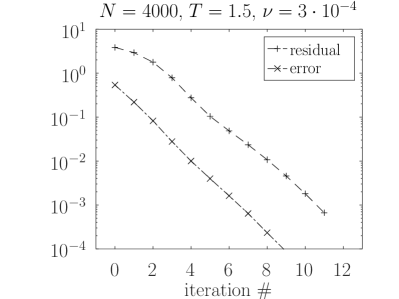
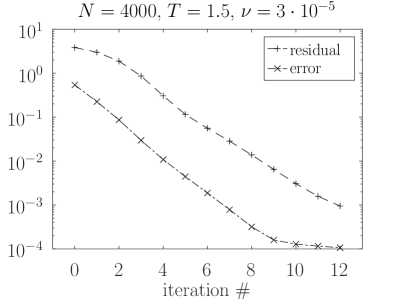
Refer to caption — Figure 1: The Burgers test. Number of required LU factorizations versus the grid size in the nonlinear EBK solver (left) and ode15s (right) for different final time values $T$ and viscosity $\nu=3\cdot 10^{-4}$

3.2 3D Bratu test problem

We now consider a nonstationary IVP for Liouville–Bratu–Gelfand equation [48]: find $u=u(x,y,z,t)$ such that

		$\displaystyle u_{t}=10^{4}u_{xx}+10^{2}u_{yy}+u_{zz}+Ce^{u}+g^{\mathsf{src}}(x,y,z,t),$		(35)
		$\displaystyle\qquad\qquad(x,y,z)\in\Omega=[0,1]^{3},\quad 0\leqslant t\leqslant T,\quad C=3\cdot 10^{4},$
		$\displaystyle u(x,y,z,0)=e^{-100\left((x-0.2)^{2}+(y-0.4)^{2}+(z-0.5)^{2}\right)},\quad u\bigl{\|}_{\partial\Omega}=0.$

Here the source function $g^{\mathsf{src}}$ is defined as

	$\displaystyle g^{\mathsf{src}}(x,y,z,t)=\begin{cases}e^{-100((x-x_{0}(t))^{2}+(y-y_{0}(t))^{2}+(z-0.5)^{2})}+Cu(x,y,z,0),\;&t\leqslant 5\cdot 10^{-5},\\ e^{-100((x-x_{0}(t))^{2}+(y-y_{0}(t))^{2}+(z-0.5)^{2})},\;&t>5\cdot 10^{-5},\end{cases}$
	$\displaystyle x_{0}(t)=0.5+0.3\cos(2000\pi t),\quad y_{0}(t)=0.5+0.3\sin(2000\pi t),$

and the final time $T$ is either $T=5\cdot 10^{-5}$ or $T=1\cdot 10^{-4}$ . Solution to (35) is shown in Figure 4.

The regular second order finite-difference discretization of the spatial derivatives in (35) on a uniform grid yields an IVP

y^{\prime}(t)=-Ay(t)+\hat{f}(y(t))+g(t),\quad y(0)=v,

(36)

where the entries of the vector functions $y(t)$ and $g(t)$ contain the values of the numerical solution and function $g^{\mathsf{src}}(x,y,z,t)$ at the grid nodes, respectively, and

Ay(t)\approx-(10^{4}u_{xx}+10^{2}u_{yy}+u_{zz}).

(37)

Furthermore, the components $[\hat{f}(y)]_{i}$ of the vector function $\hat{f}(y)$ are defined as

\left[\hat{f}(y)\right]_{i}=Ce^{y_{i}},\quad i=1,\dots,N.

To apply nonlinear waveform relaxation (8) for solving (36), one could have chosen to set $A_{k}:=A$ and $f_{k}(y):=\hat{f}(y)$ . However, to have a smaller Lipschitz constant $L$ in $f_{k}(y)$ , we supplement $A_{k}$ with a linear part of $\hat{f}$ , setting

	$\displaystyle y_{k+1}^{\prime}(t)=-(\,\underbrace{A-J(\bar{y}_{k})}_{\displaystyle A_{k}}\,)y_{k+1}(t)+\underbrace{\left[\hat{f}(y_{k}(t))-J(\bar{y}_{k})y_{k}(t)\right]}_{\displaystyle f_{k}(y_{k}(t))}+g(t),$		(38)
	$\displaystyle k=0,1,2,\dots,$		(38)

where $J(\bar{y}_{k})$ is the Jacobian matrix of $\hat{f}(y)$ evaluated at $\bar{y}_{k}=y_{k}(T)$ and an approximation

\hat{f}(y_{k+1}(t))\approx\hat{f}(y_{k}(t))+J(\bar{y}_{k})(y_{k+1}(t)-y_{k}(t))

is used. The nonlinear residual (16) takes in this case the form, for $k=0,1,\dots$ ,

	$\displaystyle r_{k+1}(t)$	$\displaystyle=f_{k}(y_{k+1}(t))-f_{k}(y_{k}(t))$
		$\displaystyle=\left[\hat{f}(y_{k+1}(t))-J(\bar{y}_{k})y_{k+1}(t)\right]-\left[\hat{f}(y_{k}(t))-J(\bar{y}_{k})y_{k}(t)\right]$
		$\displaystyle=\hat{f}(y_{k+1}(t))-\hat{f}(y_{k}(t))-J(\bar{y}_{k})(y_{k+1}(t)-y_{k}(t)).$

Since this IVP is stiff and anisotropic, the nonlinear residual norm can be very large in norm, $\mathcal{O}(10^{8})$ . Therefore we switch from the absolute stopping criterion $\|r_{k}(T)\|\leqslant\texttt{tol}$ used in the previous test to a relative stopping criterion

\|r_{k}(T)\|\leqslant\texttt{tol}\|r_{0}(T)\|,

(39)

with tolerances tol varying in this test from $10^{-2}$ to $10^{-4}$ (the specific values are reported in Table 3 discussed below). Note that $y_{0}(t)\equiv v$ , as discussed in Section 2.5.

The low rank representation (29) at each iteration $k$ is computed at $n_{s}=100$ sample points $t_{j}$ , $j=1,\dots,n_{s}$ for either $m=4$ or $m=5$ low rank terms. The EBK solver applied to solve (8) is stopped as soon as

\|r^{\mathsf{lin}}_{k+1}(T)\|\leqslant\texttt{tol}_{\mathtt{lin}}=\|f_{k}(y_{k}(0))+g(0)\|\,\texttt{tol}/10,

(40)

which means that the linear residual should be small with respect to the other terms in the perturbed ODE (27). We switch from the absolute inner stopping criterion (33) to (40) because in this stiff anisotropic problem the term $f_{k}(y_{k}(t))+g(t)$ can be very large in norm. Krylov subspace dimension is set to $10$ . Hence, for the block size $m=5$ , the EBK solver has to store $5\cdot(10+1)=55$ vectors. Since the problem is stiff, just as in the previous test, the EBK solver is employed in the SAI mode, with a sparse LU factorization of $I+\gamma A_{k}$ computed and applied throughout each nonlinear iteration. The relative error values we report below are computed according to (34).

We compare our nonlinear EBK solver to the two-stage Rosenbrock method ROS2, see [10] or [1, Chapter IV.5]. For IVP (1), it can be written as

$\displaystyle y^{\ell+1}$	$\displaystyle=y^{\ell}+\frac{3}{2}\tau k_{1}+\frac{1}{2}\tau k_{2},$	(41)
$\displaystyle(I-\gamma\tau\widehat{A})k_{1}$	$\displaystyle=\Phi(t_{\ell},y^{\ell}),$
$\displaystyle(I-\gamma\tau\widehat{A})k_{2}$	$\displaystyle=\Phi(t_{\ell+1},y^{\ell}+\tau k_{1})-2k_{1}.$

Here $y^{\ell}\approx y(\ell\tau)$ is numerical solution at time step $\ell=0,1,2,\dots$ ( $y^{0}=v$ ) obtained with a time step size $\tau>0$ . This scheme is second order consistent for any matrix $\widehat{A}\in\mathbb{R}^{N\times N}$ . Here we take $\widehat{A}$ to be the Jacobian matrix of $\Phi$ computed at $t_{\ell}=\ell\tau$ and $y_{\ell}$ . At each time step a sparse LU factorization of $I-\gamma\tau\widehat{A}$ can be computed and used to solve the two linear systems in $k_{1,2}$ . The numerical tests presented here are carried in Matlab and, as it turns out, for the grid sizes used, it is much faster to compute the action of the matrix $(I-\gamma\tau\widehat{A})^{-1}$ by the Matlab backslash operator \ than to compute a sparse LU factorization first and to apply it twice¹¹1To solve a linear system Ax=b with a square nonsingular matrix A, one can use the Matlab backslash operator $\mathtt{\backslash}$ as x=A $\mathtt{\backslash}$ b, in which case the operator computes and applies an LU factorization.. This is apparently because Matlab creates an overhead to call sparse LU factorization routines (of the UMFPACK software [49, 50]) and then to store the computed LU factors as Matlab variables. Note that both the backslash operator as well as the LU factorization for large sparse matrices in Matlab are based on UMFPACK.

Comparison results of our nonlinear EBK solver and ROS2 method are presented in Table 3. The results clearly show that, for this test problem, the nonlinear EBK solver is much more efficient than the ROS2 method both in terms of required LU factorizations (and their actions) and the CPU time. We also see that the number of nonlinear waveform relaxation iterations hardly changes with grid size and with final time $T$ (see also Table 4). While the convergence independence on the grid size is expected (as the grid size does not affect the nonlinear part $Ce^{u}$ in the ODE), the weak convergence dependence on $T$ is probably a property of the specific test problem. From plots in Figure 5 we see that convergence behavior does depend on $T$ .

Table 3: The 3D Bratu test problem. Attained error and computational work for our nonlinear EBK method and the ROS2 solver. For the EBK method the work is reported as the nonlinear iteration number, number of LU factorizations, their applications and matvecs. For the ROS2 solver the work is shown as as the number of time steps, LU factorizations, their applications and fevals.

method, time steps (t.s.)	iter./	LUs (LUs applic.),	relative	CPU
tolerance / $\tau$	steps	matvecs/fevals	error	time, s
grid $40\times 40\times 40$ , $T=5\cdot 10^{-5}$ , $T\\|A(y(T))\\|_{1}\approx\texttt{3.40e+03}$
nonlin.EBK( $m=4$ ), 1 t.s., 1e-02	2	2 (37), 2	1.17e-04	6.3
nonlin.EBK( $m=5$ ), 1 t.s., 1e-04	3	3 (111), 3	4.04e-05	12.9
ROS2, $\tau=T/320$	320	320 (640), 640	2.36e-04	225
ROS2, $\tau=T/640$	640	640 (1280), 1280	5.73e-07	442
grid $40\times 40\times 40$ , $T=1\cdot 10^{-4}$ , $T\\|A(y(T))\\|_{1}\approx\texttt{6.79e+03}$
nonlin.EBK( $m=4$ ), 1 t.s., 1e-03	3	3 (70), 3	2.09e-05	10.4
nonlin.EBK( $m=5$ ), 1 t.s., 1e-03	3	3 (80), 3	1.38e-05	11.1
ROS2, $\tau=T/320$	320	320 (640), 640	1.51e-05	201
ROS2, $\tau=T/640$	320	640 (1280), 1280	7.51e-06	401
grid $40\times 40\times 40$ , $T=1\cdot 10^{-3}$ , $T\\|A(y(T))\\|_{1}\approx\texttt{6.79e+04}$
nonlin.EBK( $m=5$ ), 20 t.s., 1e-03	46	46 (908), 46	1.34e-05	148
nonlin.EBK( $m=5$ ), 10 t.s., 1e-03	30	30 (646), 30	1.19e-05	102
ROS2, 3200 t.s., $\tau=T/3200$	3200	3200 (6400), 3200	2.19e-06	2007
grid $60\times 60\times 60$ , $T=5\cdot 10^{-5}$ , $T\\|A(y(T))\\|_{1}\approx\texttt{7.50e+03}$
nonlin.EBK( $m=4$ ), 1 t.s., 1e-02	2	2 (41), 2	1.18e-04	51.5
nonlin.EBK( $m=4$ ), 1 t.s., 1e-04	3	3 (91), 3	6.91e-05	90
ROS2, $\tau=T/320$	320	320 (640), 640	2.35e-04	2177
ROS2, $\tau=T/640$	640	640 (1280), 1280	1.66e-05	4790
grid $60\times 60\times 60$ , $T=1\cdot 10^{-4}$ , $T\\|A(y(T))\\|_{1}\approx\texttt{1.50e+04}$
nonlin.EBK( $m=4$ ), 1 t.s., 1e-02	2	2 (38), 2	3.48e-03	51
nonlin.EBK( $m=4$ ), 1 t.s., 1e-03	3	3 (74), 3	2.05e-05	83
ROS2, $\tau=T/320$	320	320 (640), 640	2.11e-05	2013
ROS2, $\tau=T/640$	640	640 (1280), 1280	1.66e-05	4368
grid $60\times 60\times 60$ , $T=1\cdot 10^{-3}$ , $T\\|A(y(T))\\|_{1}\approx\texttt{1.50e+05}$
nonlin.EBK( $m=5$ ), 10 t.s., 1e-04	30	30 (671), 30	1.18e-05	800
ROS2, $\tau=T/3200$	3200	3200 (6400), 3200	2.18e-06	20017

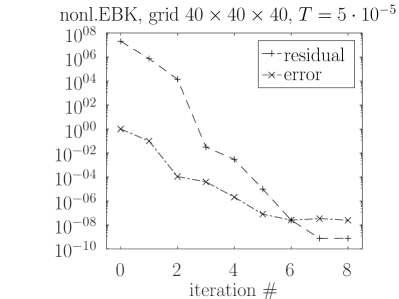
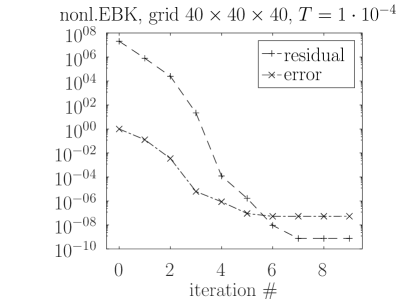
Results presented in Table 3 for the nonlinear EBK solver are obtained with the block size $m=4$ and $m=5$ . The value $m=4$ is marginally acceptable for the accuracy point of view but does yield an acceptable error values. Therefore, the plots in Figure 5, made to get an insight in the error convergence, are produced with a larger block size $m=32$ and $n_{s}=300$ samples. A convergence stagnation is clearly visible in both plots. Although we do not have a precise explanation for the stagnation, we note that it disappears if we switch off the strong anisotropy in (37), taking $A$ to be a Laplacian. The accuracy level at which stagnation occurs, appears to be related to the condition number of the Jacobian of the ODE system being solved. The nonlinear EBK solver relies on repeatedly made low-rank approximations which are instrumental for the inner block Krylov subspace solver. Another source of possible inaccuracies is linear system solution within the block Krylov subspace solver where linear systems with matrices $I+\gamma A_{k}$ are solved for $\gamma>0$ orders of magnitude larger than typical time step sizes in implicit time integrators. Nevertheless, the convergence stagnation is observed at an accuracy level $\approx 10^{-8}$ which seems to be by far acceptable for PDE solvers.

Finally, we briefly comment on convergence of the ROS2 method. Since its convergence order can not be seen from error values shown in Table 3, we give an error convergence plot in Figure 6, where relative error values, computed as given in (34), are plotted versus the total number of time steps. The second order convergence is clearly seen.

Table 4: Number of nonlinear EBK iterations needed to converge to relative tolerance

\texttt{tol}=10^{-3}

, cf. (39), for different grid sizes and

T

	$20\times 20\times 20$	$40\times 40\times 40$	$60\times 60\times 60$
$T=2.5\cdot 10^{-5}$	2	2	2
$T=5\cdot 10^{-5}$	2	2	3
$T=1\cdot 10^{-4}$	3	3	3

3.3 3D nonlinear heat conduction

In the previous tests the ODE right hand side function has a linear part (namely, $-A_{\mathrm{symm}}y(t)$ in the first test and $-Ay(t)$ in the second one, see (30) and (36), respectively). To examine whether our nonlinear EBK solver is able to handle nonlinear problems with no linear part, we now consider the following nonlinear heat conduction problem, described in [51]: find unknown $u=u(x,y,z,t)$ which satisfies

\begin{gathered}u_{t}=(k^{(x)}(u)u_{x})_{x}+(k^{(y)}(u)u_{y})_{y}+(k^{(z)}(u)u_{z})_{z},\\ (x,y,z)\in[0,1]^{3},\quad 0\leqslant t\leqslant T,\\ u\bigl{|}_{x=0}=u\bigl{|}_{x=1},\quad u\bigl{|}_{y=0}=900,\quad u\bigl{|}_{y=1}=300,\quad u_{z}\bigl{|}_{z=0}=u_{z}\bigl{|}_{z=1}=0,\\ u(x,y,z,0)=1800\,e^{-60((x-0.5)^{2}+(y-0.5)^{2}+(z-0.5)^{2})},\\ k^{(x)}(u)=u/300,\quad k^{(y)}(u)=k^{(z)}(u)=k^{(x)}(u)/10.\end{gathered}

(42)

We discretize this initial boundary value problem on a regular grid of $n_{x}\times n_{y}\times n_{z}$ nodes $(x_{i},y_{j},z_{k})$ , $x_{i}=ih_{x}$ , $i=1,\dots,n_{x}$ , $y_{j}=jh_{y}$ , $j=1,\dots,n_{y}$ , $z_{k}=(k-1/2)h_{z}$ , $k=1,\dots,n_{z}$ , with grid widths $h_{x,y}=1/(n_{x,y}+1)$ and $h_{z}=1/n_{z}$ . The shifted grid nodes are taken for the $z$ direction to accommodate the Neumann boundary conditions. The standard second order finite difference approximation is employed, which reads, for the $x$ derivative,

(k^{(x)}(u)u_{x})_{x}\bigl{|}_{i,j,k}\approx\frac{k^{(x)}(u_{i+1/2,j,k})(u_{i+1,j,k}-u_{i,j,k})-k^{(x)}(u_{i-1/2,j,k})(u_{i,j,k}-u_{i-1,j,k})}{h_{x}^{2}},

where $u_{i\pm 1/2,j,k}=(u_{i\pm 1,j,k}+u_{i,j,k})/2$ . The same finite difference approximations are applied in $y$ and $z$ directions. This space discretization of the initial boundary value problem (42) yields an IVP

y^{\prime}(t)=-A(y(t))y(t)+g,\quad y(0)=v,

(43)

where the entries of the vector function $y(t)$ contain the numerical solution values and the constant in time vector $g$ contains the inhomogeneous boundary condition contributions. The waveform relaxation iteration is applied with the splitting (3) where we set, for $\bar{y}_{k}=y_{k}(T)$ ,

A_{k}=A(\bar{y}_{k}),\quad f_{k}(y)=A(\bar{y}_{k})y-A(y)y.

In this relation, it is not difficult to recognize the same splitting as is used for the Burgers equation test (with $A_{\mathrm{symm}}=0$ and $A_{\mathrm{skew}}=A$ ).

The EBK inner-outer iterations are applied exactly in the same setting as in the previous test, with the same stopping criteria, see (39), (40) and the same number of samples $n_{s}$ . As in the previous test, we compare the EBK solver with the ROS2 integrator. The results of the test runs are presented in Table 5. As we see, on the grid $40\times 40\times 40$ the two time integration schemes perform equally well in terms of the CPU time. Note that the EBK solver requires much fewer LU factorizations. On the finer $60\times 60\times 60$ the EBK solver clearly outperforms ROS2, both in terms of the CPU time and required LU factorizations. When switching to the finer grid, to keep convergence in the EBK scheme, we have to decrease the time interval $T$ from $T=0.01$ to $T=0.005$ . Hence, we observe a deterioration of the EBK convergence in this test. There is also a moderate increase in the required number of nonlinear iterations: with $T=0.005$ EBK needs in total 73 and 94 iterations on the two grids, respectively.

Table 5: The 3D nonlinear heat conduction test. Attained error and computational work for our nonlinear EBK method and the ROS2 solver. For the EBK method the work is reported as the nonlinear iteration number, number of LU factorizations, their applications and matvecs. For the ROS2 solver the work is shown as as the number of time steps, LU factorizations, their applications and fevals.

method, time steps (t.s.)	iter./	LUs (LUs applic.),	relative	CPU
tolerance / $\tau$	steps	matvecs/fevals	error	time, s
grid $40\times 40\times 40$ , $T=0.1$ , $T\\|A(y(T))\\|_{1}\approx\texttt{2.19e+03}$
nonlin.EBK( $m=6$ ), 10 t.s., 1e-02	52	52 (1223), 52	1.30e-04	387
nonlin.EBK( $m=10$ ), 10 t.s., 1e-02	52	52 (1936), 52	5.91e-05	448
ROS2, $\tau=T/250$	250	250 (500)	7.26e-05	347
ROS2, $\tau=T/500$	500	500 (1000)	2.02e-05	821
grid $60\times 60\times 60$ , $T=0.1$ , $T\\|A(y(T))\\|_{1}\approx\texttt{4.96e+04}$
nonlin.EBK( $m=6$ ), 20 t.s., 1e-02	94	94 (2068), 94	4.41e-05	8229
ROS2, $\tau=T/500$	500	500 (1000)	3.99e-05	19578

4 Conclusions

In this paper nonlinear waveform relaxation iterations and their block Krylov subspace implementation (the nonlinear EBK method) are examined theoretically and practically. Theoretically we have shown that convergence of the considered nonlinear waveform relaxation iteration is determined by the Lipschitz constant $L$ of the nonlinear term $f_{k}$ in (3), the logarithmic norm bound $\omega$ of the linear term matrix $A_{k}$ and the time interval length $T$ , see relation (10). We have also established a superlinear convergence of our nonlinear iteration, which is known to hold in the linear case, see Proposition 2. Furthermore, we have linked the residual convergence in the nonlinear iteration to the error convergence, see relation (20). Finally, it is shown that inexact solution of the linear initial-value problem arising at each waveform relaxation iteration leads to a process whose convergence is equivalent to convergence of the exact waveform relaxation iteration with an increased Lipschitz constant $L+l$ , with $l$ being the inexactness tolerance.

Practical performance of nonlinear waveform relaxation heavily depends on the ability to solve the arising linear initial-value problem at each relaxation iteration quickly and to handle the iterative across-time solutions efficiently. As we show here, both these goals can be successfully reached by employing the exponential block Krylov subspace method EBK [37]. In the presented experiments the EBK method is used in the shift-and-invert (SAI) mode, i.e., it has been assumed that the SAI linear systems (similar to those arising in implicit time stepping) can be solved efficiently.

Comparisons with implicit time integration methods demonstrated superiority and potential of our EBK-SAI based nonlinear waveform relaxation iterations. The presented nonlinear residual stopping criterion has been proven to be a reliable way to control convergence and to estimate accuracy. Moreover, as the first two numerical tests demonstrate, the grid independent convergence of linear SAI Krylov subspace exponential time integrators (see [45, 46, 52]) can be inherited by the nonlinear waveform relaxation iterations.

As numerical tests and our experience suggest, the presented method has its limitations. First, it is not intended for strongly nonlinear problems with rapidly changing solutions. The method clearly profits if the right hand side function of the ODE system contains a linear part. Second, the linear systems arising in the presented nonlinear EBK method have a structure similar to linear systems occuring in implicit time integrators with significantly increased time step sizes. Therefore, the overall efficiency of the method for a particular application heavily depends on availability of efficient linear solvers. Third, the nonlinear EBK method is aimed at solving initial-value problems with a moderate accuracy (of order $10^{-4}$ or $10^{-5}$ ), which is usually enough for solving PDE problems. The accuracy of the presented method can be limited by the built-in low rank approximations and solving large ill-conditioned linear systems. Finally, some tuning (such as a proper choice of the block size $m$ and the time interval length) is required to apply the proposed approach successfully. Some of these issues can be addressed in more details in a future.

Nevertheless, as results in this paper show, the presented framework seems to be promising, has a potential and is of interest for the numerical community. Recently, an alternative approach based on exponential Krylov subspace integrators has been presented in [53, 54] for nonlinear heat equations. In this problem a rapid change in the solution seems to exclude using waveform relaxation with block Krylov subspaces as presented here. A further research should be done to get an insight on when to switch between the block Krylov subspace approach discussed here and the approach of [53]. Finally, it seems to be useful to gain more insight how these two approaches compare to other exponential time integrators for nonlinear initial-value problems [3, 55, 56].

Acknowledgments

The author thanks the anonymous reviewer for careful reading and suggesting several valuable improvements. We acknowledge the use of the hybrid supercomputer K-100 facilities installed in the Supercomputer center of collective usage at Keldysh Institute of Applied Mathematics of Russian Academy of Sciences.

References

\bibcommenthead
[1] W. Hundsdorfer, J.G. Verwer, Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations (Springer Verlag, 2003)
[2] H.C. Elman, D.J. Silvester, A.J. Wathen, Finite Elements and Fast Iterative Solvers with Applications in Incompressible Fluid Dynamics (Oxford University Press, Oxford, 2005)
[3] M. Hochbruck, A. Ostermann, Exponential integrators. Acta Numer. 19, 209–286 (2010). 10.1017/S0962492910000048
[4] P.N. Brown, Y. Saad, Convergence theory of nonlinear Newton–Krylov algorithms. SIAM J. Optimization 4(2), 297–330 (1994)
[5] R. Choquet, J. Erhel, Newton–GMRES algorithm applied to compressible flows. Int. J. Numer. Meth. Fluids 23, 177–190 (1996)
[6] D. Tromeur-Dervout, Y. Vassilevski, Choice of initial guess in iterative solution of series of systems arising in fluid flow simulations. Journal of Computational Physics 219(1), 210–227 (2006). https://doi.org/10.1016/j.jcp.2006.03.014. URL https://www.sciencedirect.com/science/article/pii/S0021999106001483
[7] N.N. Yanenko, The method of fractional steps. The solution of problems of mathematical physics in several variables (Springer-Verlag, New York, 1971), pp. viii+160
[8] E.G. D’yakonov, Difference systems of second order accuracy with a divided operator for parabolic equations without mixed derivatives. USSR Comput. Math. Math. Phys. 4(5), 206–216 (1964)
[9] P. Csomós, I. Faragó, A. Havasi, Weighted sequential splittings and their analysis. Comput. Math. Appl. pp. 1017–1031 (2005)
[10] J.G. Verwer, E.J. Spee, J.G. Blom, W. Hundsdorfer, A second order Rosenbrock method applied to photochemical dispersion problems. SIAM J. Sci. Comput. 20, 456–480 (1999)
[11] P.J. van der Houwen, B.P. Sommeijer, On the internal stability of explicit $m$ -stage Runge–Kutta methods for large values of $m$ . Z. Angew. Math. Mech. 60, 479–485 (1980)
[12] V.O. Lokutsievskii, O.V. Lokutsievskii, On numerical solution of boundary value problems for equations of parabolic type. Soviet Math. Dokl. 34(3), 512–516 (1987)
[13] B.P. Sommeijer, L.F. Shampine, J.G. Verwer, RKC: An explicit solver for parabolic PDEs. J. Comput. Appl. Math. 88, 315–326 (1998)
[14] H. Tal-Ezer, Spectral methods in time for parabolic problems. SIAM J. Numer. Anal. 26(1), 1–11 (1989)
[15] V.I. Lebedev, Explicit difference schemes for solving stiff systems of ODEs and PDEs with complex spectrum. Russian J. Numer. Anal. Math. Modelling 13(2), 107–116 (1998). 10.1515/rnam.1998.13.2.107
[16] J.G. Verwer, B.P. Sommeijer, W. Hundsdorfer, RKC time-stepping for advection–diffusion–reaction problems. Journal of Computational Physics 201(1), 61–79 (2004). https://doi.org/10.1016/j.jcp.2004.05.002. URL https://www.sciencedirect.com/science/article/pii/S0021999104001925
[17] M.A. Botchev, G.L.G. Sleijpen, H.A. van der Vorst, Stability control for approximate implicit time stepping schemes with minimum residual iterations. Appl. Numer. Math. 31(3), 239–253 (1999). https://doi.org/10.1016/S0168-9274(98)00138-X
[18] M.A. Botchev, H.A. van der Vorst, A parallel nearly implicit scheme. Journal of Computational and Applied Mathematics 137, 229–243 (2001). https://doi.org/10.1016/S0377-0427(01)00358-2
[19] V.T. Zhukov, Explicit methods of numerical integration for parabolic equations. Mathematical Models and Computer Simulations 3(3), 311–332 (2011). https://doi.org/10.1134/S2070048211030136
[20] E. Lelarasmee, A.E. Ruehli, A.L. Sangiovanni-Vincentelli, The waveform relaxation method for time-domain analysis of large scale integrated circuits. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 1(3), 131–145 (1982). 10.1109/TCAD.1982.1270004
[21] A.R. Newton, A.L. Sangiovanni-Vincentelli, Relaxation-based electrical simulation. IEEE Transactions on Electron Devices 30(9), 1184–1207 (1983). 10.1109/T-ED.1983.21275
[22] S. Vandewalle, Parallel Multigrid Waveform Relaxation for Parabolic Problems (Teubner, Stuttgart, 1993)
[23] U. Miekkala, O. Nevanlinna, Iterative solution of systems of linear differential equations. Acta Numerica 5, 259–307 (1996). https://doi.org/10.1017/S096249290000266X
[24] J. White, F. Odeh, A.L. Sangiovanni-Vincentelli, A. Ruehli, Waveform relaxation: Theory and practice. Tech. Rep. UCB/ERL M85/65, EECS Department, University of California, Berkeley (1985). www.eecs.berkeley.edu/Pubs/TechRpts/1985/543.html
[25] U. Miekkala, O. Nevanlinna, Convergence of dynamic iteration methods for initial value problems. SIAM Journal on Scientific and Statistical Computing 8(4), 459–482 (1987). https://doi.org/10.1137/0908046
[26] C. Lubich, A. Ostermann, Multi-grid dynamic iteration for parabolic equations. BIT Numerical Mathematics 27, 216–234 (1987). URL http://doi.org/10.1007/BF01934186. 10.1007/BF01934186
[27] J. Janssen, S. Vandewalle, Multigrid waveform relaxation of spatial finite element meshes: The continuous-time case. SIAM J. Numer. Anal. 33(2), 456–474 (1996). 10.1137/0733024
[28] M.J. Gander, S. Güttel, PARAEXP: A parallel integrator for linear initial-value problems. SIAM Journal on Scientific Computing 35(2), C123–C142 (2013)
[29] G.L. Kooij, M.A. Botchev, B.J. Geurts, A block Krylov subspace implementation of the time-parallel Paraexp method and its extension for nonlinear partial differential equations. Journal of Computational and Applied Mathematics 316(Supplement C), 229–246 (2017). https://doi.org/10.1016/j.cam.2016.09.036
[30] G. Kooij, M.A. Botchev, B.J. Geurts, An exponential time integrator for the incompressible Navier–Stokes equation. SIAM J. Sci. Comput. 40(3), B684–B705 (2018). https://doi.org/10.1137/17M1121950
[31] T.J. Park, J.C. Light, Unitary quantum time evolution by iterative Lanczos reduction. J. Chem. Phys. 85, 5870–5876 (1986)
[32] H.A. van der Vorst, An iterative solution method for solving $f(A)x=b$ , using Krylov subspace information obtained for the symmetric positive definite matrix $A$ . J. Comput. Appl. Math. 18, 249–263 (1987)
[33] V.L. Druskin, L.A. Knizhnerman, Two polynomial methods of calculating functions of symmetric matrices. U.S.S.R. Comput. Maths. Math. Phys. 29(6), 112–121 (1989)
[34] E. Gallopoulos, Y. Saad, Efficient solution of parabolic equations by Krylov approximation methods. SIAM J. Sci. Statist. Comput. 13(5), 1236–1264 (1992). http://doi.org/10.1137/0913071
[35] V.L. Druskin, L.A. Knizhnerman, Krylov subspace approximations of eigenpairs and matrix functions in exact and computer arithmetic. Numer. Lin. Alg. Appl. 2, 205–217 (1995)
[36] M. Hochbruck, C. Lubich, On Krylov subspace approximations to the matrix exponential operator. SIAM J. Numer. Anal. 34(5), 1911–1925 (1997)
[37] M.A. Botchev, A block Krylov subspace time-exact solution method for linear ordinary differential equation systems. Numer. Linear Algebra Appl. 20(4), 557–574 (2013). http://doi.org/10.1002/nla.1865
[38] O. Nevanlinna, F. Odeh, Remarks on the convergence of waveform relaxation method. Numerical functional analysis and optimization 9(3-4), 435–445 (1987). https://doi.org/10.1080/01630568708816241
[39] K. Dekker, J.G. Verwer, Stability of Runge–Kutta methods for stiff non-linear differential equations (North-Holland Elsevier Science Publishers, 1984)
[40] M.A. Botchev, V. Grimm, M. Hochbruck, Residual, restarting and Richardson iteration for the matrix exponential. SIAM J. Sci. Comput. 35(3), A1376–A1397 (2013). http://doi.org/10.1137/110820191
[41] M.A. Botchev, I.V. Oseledets, E.E. Tyrtyshnikov, Iterative across-time solution of linear differential equations: Krylov subspace versus waveform relaxation. Computers & Mathematics with Applications 67(12), 2088–2098 (2014). http://doi.org/10.1016/j.camwa.2014.03.002
[42] E. Hairer, G. Wanner, Solving Ordinary Differential Equations II. Stiff and Differential–Algebraic Problems, 2nd edn. Springer Series in Computational Mathematics 14 (Springer–Verlag, 1996)
[43] L.A. Krukier, Implicit difference schemes and an iterative method for solving them for a certain class of systems of quasi-linear equations. Sov. Math. 23(7), 43–55 (1979). Translation from Izv. Vyssh. Uchebn. Zaved., Mat. 1979, No. 7(206), 41–52 (1979)
[44] R.W.C.P. Verstappen, A.E.P. Veldman, Symmetry-preserving discretization of turbulent flow. J. Comput. Phys. 187(1), 343–368 (2003). http://doi.org/10.1016/S0021-9991(03)00126-8
[45] I. Moret, P. Novati, RD rational approximations of the matrix exponential. BIT 44, 595–615 (2004)
[46] J. van den Eshof, M. Hochbruck, Preconditioning Lanczos approximations to the matrix exponential. SIAM J. Sci. Comput. 27(4), 1438–1457 (2006)
[47] L.F. Shampine, M.W. Reichelt, The MATLAB ODE suite. SIAM J. Sci. Comput. 18(1), 1–22 (1997). Available at www.mathworks.com
[48] J. Jon, S. Klaus, The Liouville–Bratu–Gelfand problem for radial operators. Journal of Differential Equations 184, 283–298 (2002). https://doi.org/10.1006/jdeq.2001.4151
[49] T.A. Davis, A column pre-ordering strategy for the unsymmetric-pattern multifrontal method. ACM Trans. Math. Software 30(2), 167–195 (2004). 10.1145/992200.992205
[50] T.A. Davis, Algorithm 832: UMFPACK V4.3—an unsymmetric-pattern multifrontal method. ACM Trans. Math. Software 30(2), 196–199 (2004). 10.1145/992200.992206
[51] V.T. Zhukov, N. Novikova, O.B. Feodoritova, On direct solving conjugate heat transfer of gas mixture and solid body. KIAM Preprint 2023(12) (2023). https://doi.org/10.20948/prepr-2023-12
[52] V. Grimm, Resolvent Krylov subspace approximation to operator functions. BIT 52(3), 639–659 (2012). 10.1007/s10543-011-0367-8
[53] M.A. Botchev, V.T. Zhukov, Exponential Euler and backward Euler methods for nonlinear heat conduction problems. Lobachevskii Journal of Mathematics 44(1), 10–19 (2023). https://doi.org/10.1134/S1995080223010067
[54] M.A. Botchev, V.T. Zhukov, Adaptive iterative explicit time integration for nonlinear heat conduction problems. Lobachevskii Journal of Mathematics 45(1), 12–20 (2024). https://doi.org/10.1134/S1995080224010086
[55] D. Hipp, M. Hochbruck, A. Ostermann, An exponential integrator for non-autonomous parabolic problems. ETNA 41, 497–511 (2014). http://etna.mcs.kent.edu/volumes/2011-2020/vol41/
[56] E. Hansen, A. Ostermann, High-order splitting schemes for semilinear evolution equations. BIT Numerical Mathematics 56(4), 1303–1316 (2016)

	$\displaystyle\\|\epsilon_{k+1}(t)\\|$	$\displaystyle\leqslant\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,\\|\left[f_{k}(y(s))-f_{k}(y_{k}(s))\right]\\|\mathrm{d}s$
		$\displaystyle\leqslant\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,L\\|y(s))-y_{k}(s)\\|\mathrm{d}s$
		$\displaystyle\leqslant L\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|\int_{0}^{t}\\|\exp(-(t-s)A_{k})\\|\,\mathrm{d}s$
		$\displaystyle\leqslant CL\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|\int_{0}^{t}e^{-\omega(t-s)}\,\mathrm{d}s=CLt\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|.$

	$\displaystyle\\|\epsilon_{k}(t)\\|$	$\displaystyle\leqslant(CL)^{k}t^{k}e^{-\omega t}\varphi_{k}(\omega t)\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|$		(13)
		$\displaystyle\leqslant(CL)^{k}\frac{t^{k}}{k!}\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|,\quad\forall t\in[0,T].$		(13)

	$\displaystyle\\|\epsilon_{k+1}(t)\\|$	$\displaystyle\leqslant CL\int_{0}^{t}e^{-(t-s)\omega}\\|\epsilon_{k}(s)\\|\mathrm{d}s$
and, by the induction assumption,
		$\displaystyle\leqslant CL\int_{0}^{t}e^{-(t-s)\omega}(CL)^{k}s^{k}e^{-\omega s}\varphi_{k}(\omega s)\max_{\tilde{s}\in[0,s]}\\|\epsilon_{0}(\tilde{s})\\|\mathrm{d}s$
		$\displaystyle=(CL)^{k+1}e^{-\omega t}\int_{0}^{t}s^{k}\varphi_{k}(\omega s)\max_{\tilde{s}\in[0,s]}\\|\epsilon_{0}(\tilde{s})\\|\mathrm{d}s$
		$\displaystyle\leqslant(CL)^{k+1}e^{-\omega t}\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|\int_{0}^{t}s^{k}\varphi_{k}(\omega s)\mathrm{d}s$
		$\displaystyle=(CL)^{k+1}t^{k+1}e^{-\omega t}\varphi_{k+1}(\omega t)\max_{s\in[0,t]}\\|\epsilon_{0}(s)\\|,$

	$\displaystyle\\|\epsilon_{k}(t)\\|$	$\displaystyle\leqslant\int_{0}^{t}\left\\|\exp(-(t-s)A_{k-1})\left[f_{k-1}(y(s))-f_{k-1}(y_{k}(s))+r_{k}(s)\right]\right\\|\mathrm{d}s$
		$\displaystyle\leqslant\max_{s\in[0,t]}\left\\|f_{k-1}(y(s))-f_{k-1}(y_{k}(s))+r_{k}(s)\right\\|\int_{0}^{t}\\|\exp(-(t-s)A_{k-1})\\|\,\mathrm{d}s$
		$\displaystyle\leqslant\max_{s\in[0,t]}\left\\|f_{k-1}(y(s))-f_{k-1}(y_{k}(s))+r_{k}(s)\right\\|\,Ct\varphi_{1}(-\omega t)$
		$\displaystyle\leqslant\left(L\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|+\max_{s\in[0,t]}\\|r_{k}(s)\\|\right)\,Ct\varphi_{1}(-\omega t)$
		$\displaystyle\leqslant CLt\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|+Ct\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|r_{k}(s)\\|.$

	$\displaystyle(1-CLt\varphi_{1}(-\omega t))\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|$	$\displaystyle\leqslant Ct\varphi_{1}(-\omega t)\max_{s\in[0,t]}\\|r_{k}(s)\\|$
	$\displaystyle\max_{s\in[0,t]}\\|\epsilon_{k}(s)\\|$	$\displaystyle\leqslant\frac{Ct\varphi_{1}(-\omega t)}{1-CLt\varphi_{1}(-\omega t)}\max_{s\in[0,t]}\\|r_{k}(s)\\|,$