On connected components with many edges
Abstract.
We prove that if is a subgraph of a complete multipartite graph , then contains a connected component satisfying . We use this to prove that every three-coloring of the edges of a complete graph contains a monochromatic connected subgraph with at least of the edges. We further show that such a coloring has a monochromatic circuit with a fraction of the edges. This verifies a conjecture of Conlon and Tyomkyn. Moreover, for general , we show that every -coloring of the edges of contains a monochromatic connected subgraph with at least edges.
Supported by NSF GRFP Grant DGE-1656518. Email: [email protected].
1. Introduction
A classical observation of Erdős and Rado is that in any two-coloring of the edges of the complete graph , one of the color classes forms a connected graph. In [3], Gyárfás proves the following generalization of this observation: For any , in every -coloring of the edges of , there is a monochromatic connected component with at least vertices. This observation has since been extended in numerous ways, such as by replacing with a graph of high minimum degree [5] or with a nearly-complete bipartite graph [2], or adding a constraint on the diameter of the large monochromatic component [7]. See [4] for a survey of earlier work on the subject.
The arguments used in this subject tend to focus on sparse spanning structures like double stars. As such, there is a surprising lack of progress on the corresponding question about edges in a monochromatic connected component. That is, what is the largest value of such that every -edge-coloring of has a monochromatic connected component with at least edges?
This question was raised by Conlon and Tyomkyn in [1], in the context of determining the multicolor Ramsey numbers for trails (see Section 3.2 for the relevant definitions). After showing that , they sketch a simple argument that shows for all ; with a slightly more careful analysis, their argument in fact yields . In the other direction, they examine a construction of Gyárfás in [4] to show that for infinitely many values of (specifically, when is a prime power), conjecturing that this upper bound is tight in the case .
In this note, we improve the general lower bound on , as well as a corresponding lower bound for the trail Ramsey problem, bringing it to asymptotically within a factor of the upper bound for infinitely many values of .
Theorem 1.
For any , in every -coloring of the edges of , there is a monochromatic connected component with at least edges.
By building on the overarching ideas in [4] and introducing some key new insights, we manage to strengthen this lower bound in the case to prove the tight lower bound conjectured by Conlon and Tyomkyn.
Theorem 2.
In every -coloring of the edges of , there is a monochromatic component containing at least a sixth of the edges. That is, . Moreover, for sufficiently large, this bound is sharp.
While equality holds in this bound for sufficiently large , there are, as we will see from the proof, small values of for which . In particular, equality holds for all , but not for .
The key result we use is a new inequality that may be of independent interest. Given a subgraph of a complete multipartite graph , it relates the edge counts of and to the largest edge count of a connected component of .
Theorem 3.
Let be a complete -partite graph for some , and let be a subgraph of . Then contains a connected component satisfying
In effect, this result settles the density analogue of the coloring question of determining . Instead of partitioning the edges of a graph into color classes, we are fixing a subgraph of with a given fraction of its edges, and asking about the component of with the most edges. Theorem 3 can then be restated as: if , then contains a connected component with . Equality can be attained asymptotically when for any positive integer : Let be an -partition of , split each into (roughly) equally sized vertex sets , and for , let be the subgraph of induced on . Then indeed, is a subgraph of whose components have edge counts
The simplest case of Theorem 3, when , already immediately implies an improvement over previously known lower bounds on .
Corollary 4.
In every -coloring of the edges of , there is a monochromatic connected component with at least edges.
Proof.
2. Proof of Theorem 3
In the case , the proof of Theorem 3 is very simple, but nevertheless includes a key insight: Instead of taking a component that maximizes the number of edges right away, we consider a component with maximum average degree . Two observations are crucial here: First, by the so-called generalized mediant inequality, this highest average degree must be at least the average degree of the whole graph , since
where the sums are over connected components of , and the right hand side is a generalized mediant of the average degrees of the individual components. Second, the number of vertices of is at least one more than its maximum degree, so . Letting , we then obtain the bound
as desired.
The general case will use both of these observations in a modified setting. Instead of the average degree, we will work with a slightly different quantity whose denominator is a weighted vertex count; we will then, perhaps counterintuitively, lower bound this weighted vertex count by the modified analogue of the average degree, in order to obtain the bound we seek. The core of our proof is the following general inequality.
Lemma 5.
If and are nonnegative real numbers, then
Proof.
The Cauchy-Schwarz inequality yields
This last quantity is clearly nonnegative, since and . So,
where the last inequality is an application of the AM-GM inequality. ∎
Given a graph and vertex sets , let
We write for when the graph in question is unambiguous. Let denote the induced subgraph of on the vertex set . Lemma 5 immediately implies the following.
Corollary 6.
Let be a complete multipartite graph. For any , we have
Proof.
Suppose that is -partite. Let be a partition of the vertices of into independent sets. Let and , so
while
Then Lemma 5 indeed yields , as desired. ∎
Proof of Theorem 3.
Let be a partition of the vertices of into independent sets, let be the connected components of , and let . We have
For any subset , define . Note that
so can be viewed as a weighted vertex count for , with the property that
Then by the generalized mediant inequality, for some we have
Now, Corollary 6 applied with , yields , so that
which rearranges to the desired inequality. ∎
3. Coloring problems
We can now apply Theorem 3 to the corresponding coloring problems. We have already seen that applying Theorem 3 with readily yields the simple lower bound on given in Corollary 4. We now discuss how to improve this lower bound, before turning to a closely related problem on monochromatic trails and circuits.
3.1. Lower bound on for general
Our strategy for improving the lower bound on is as follows: First, assuming that no monochromatic component has too many edges, we show that in the color with the highest density (say, red), we can upper bound the number of vertices covered by any set of components (or else we can finish with an average degree argument on the rest of the red components). Through a smoothing argument, this yields an upper bound on the sum of squares of the number of vertices in each red component, and thus a lower bound on the number of edges in the complete multipartite graph formed by deleting from all edges within the vertex sets of the red components. We finish by applying Theorem 3 to to find a non-red component with many edges.
Proof of Theorem 1.
Fix a -coloring of the edges of , and suppose that the largest number of edges in a monochromatic connected component in this coloring is . Without loss of generality, let red be the color with the most edges, so there are at least red edges in our coloring. Let be the set of red components, with
| (3.1) |
Let , so . By assumption, for . As in the proof of Corollary 4, applying Theorem 3 with as and its red color class (i.e. the spanning subgraph formed by its red edges) as yields a red component with at least edges, so by assumption we have . Define , so .
For any , let be the complete graph on , with its coloring induced by . Applying Theorem 3 with as and the red color class of as yields a red connected component with . Since
while , we have
Since , this implies
Since , and the function is increasing for , this then implies
| (3.2) |
We can now give an upper bound on by solving the corresponding convex optimization problem. The proof of the following technical lemma will be deferred until the end of the section.
Lemma 7.
Let . Subject to the constraints , , and
the quantity is maximized when , for , , and for .
Let . Since (3.1) and (3.2) hold, we can apply Lemma 7 to obtain
so that we have
Finally, let be the complete -partite graph obtained from by removing all edges within each , with its coloring induced by . There are no red edges in , so by the pigeonhole principle, one of the remaining colors has at least edges in . Let be the spanning subgraph of induced by the edges in that color. Applying Theorem 3 then yields a monochromatic connected component with at least edges. Then by assumption we have
which rearranges to give
The right hand side is a quadratic in that is decreasing for . Since by assumption , we then have
Substituting in yields
which upon rearrangement becomes
This implies
so that . Thus, the coloring contains a monochromatic connected component with at least edges, where
as desired. ∎
Proof of Lemma 7.
Since the feasible region is compact, there exists a choice of the such that the desired maximum is attained. Fix such a maximizing choice of the . For , let denote the given constraint on , and let be the set of for which equality holds in . Let . Since , the constraints for cannot be tight, so . For any and any , replacing with increases the value of , so by maximality, no such “smoothing” operation is possible. That is, we can assume the following equality condition for all with : Either , or , or . If , then we are in exactly the maximizing case described (since by the equality conditions for we have for all ), so assume otherwise.
First, suppose there is some such that , and pick the smallest such index . Let be the largest index such that , and note that since . Then we have and . But as for any , we have , contradicting the equality condition for . So, we can assume for all . In particular, if for some , then we recursively obtain for all , so .
Thus, we can assume , i.e. . By the equality condition for , we must then have . Let be the smallest index such that . By the equality condition for , there is some . Then
which implies . But then , violating . This is a contradiction, so in fact , and we are in the desired maximizing case. ∎
We remark that in Gyárfás’s construction, after removing all edges contained in the vertex set of each red component, each non-red component is left with approximately edges. Since , this suggests that the method used to prove Theorem 1 cannot show a lower bound on better than without introducing additional ideas.
3.2. Multicolor Ramsey numbers of trails and circuits
A trail is a walk without repeated edges, and a circuit is a trail with the same first and last vertex. The (-color) Ramsey problem for trails is the question of finding the largest such that every -coloring of the edges of contains a monochromatic trail of length .
Answering a question of Osumi [6], Conlon and Tyomkyn [1] show that every -coloring of the edges of contains a monochromatic circuit with at least edges, and this is asymptotically tight. For the case of general , they observe that by deleting a forest in each color class of a -coloring of to make each color class Eulerian (i.e. ensuring every vertex has even degree in each color), one can reduce this Ramsey problem to a variant of the problem of determining . Where previously we colored the edges of and found a large monochromatic component, we now apply the same procedure to the graph obtained by deleting at most edges from . We now prove a lower bound for the general case of this problem, analogous to the bound on given in Theorem 1.
Corollary 8.
Every -coloring of the edges of contains a monochromatic circuit (and hence a monochromatic trail) of length at least .
Proof.
Fix a -coloring of . As in [1], we can remove from each color class a forest that meets all odd degree vertices, leaving a coloring where every color class, and hence every monochromatic connected component, is Eulerian. Let be the resulting partial -coloring of , where the (at most ) removed edges are left uncolored, and let be the largest number of edges in a monochromatic component in this coloring. It suffices to show that , since every monochromatic component is Eulerian, and thus contains an Eulerian circuit. Fix a color (say, red) with edges, where . As before, applying Theorem 3 with immediately yields . Note that this means there is a monochromatic circuit with at least edges.
To improve this lower bound further, we proceed as in the proof of Theorem 1. Letting be the red components, such that (3.1) holds, we obtain (3.2) in the same manner as before, so we can once again apply Lemma 7 to obtain the same upper bound on in terms of and . Let be the complete -partite graph with parts , with its partial coloring induced by . Since has no red edges, and at most edges are uncolored, one of its color classes has at least edges. Applying Theorem 3 as before yields
Letting and noting that , we can perform the same rearrangements and substitutions as in the proof of Theorem 1, simply separating out the terms at each step, to derive the inequality , and thus
Then the coloring contains a monochromatic connected component, and hence a monochromatic Eulerian circuit, with at least edges, as claimed. ∎
3.3. Three colors
In this section, we prove the lower and upper bounds on in separate lemmas in order to establish Theorem 2. We then discuss the behavior of for small values of , and conclude by describing how to adapt our proofs to obtain asymptotically tight bounds for the Ramsey numbers of trails and circuits in three colors.
Lemma 9.
Every -coloring of the edges of contains a monochromatic component with at least edges.
Proof.
Let , and call the three colors red, green, and blue. First, suppose one of the color classes (say, red) is connected. If there are at least red edges, we are done. Otherwise, the other two colors together have at least edges, so one of them has at least edges. Applying Theorem 3 with to the graph in that color then gives a monochromatic component with at least edges, so we are again done.
Thus, we can assume every color has at least two components. Without loss of generality, let red be the color with the most edges, so the red graph has at least edges. Let be the component of with the highest average degree, so . We can assume ; otherwise, we would have . Let and , and let be the bipartite graph induced by between and , so has at least edges, all of which must be green or blue.
Fix an edge in and consider the monochromatic component of containing this edge. Without loss of generality, assume is green. Suppose covers all of . Since every green edge in intersects , this means there is exactly one green component of with a nonzero number of edges. Since there are at least two green components in , there is a vertex not in . Then all edges between and must be blue, so all vertices of are in the same blue component in . This implies that there is also exactly one blue component of with nonzeroly many edges. Thus, all edges of are in one of two monochromatic components, one of which then has at least edges, as desired.
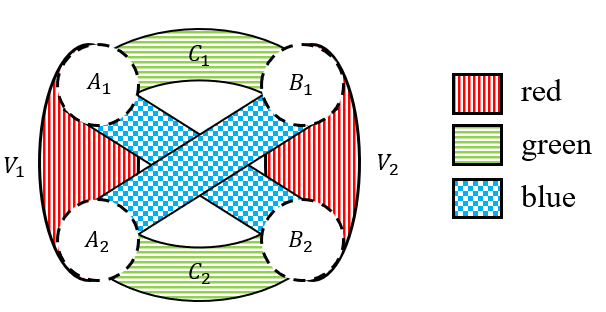
We are likewise done if covers all of , so we can assume and are both nonempty. Let , , , . Then all edges between and , or between and , can only be blue. Then there are at most two blue components, and thus by assumption exactly two. This in turn implies that all edges between and , or between and , can only be green, so there are exactly two green components and . Finally, all edges between and can only be red, so we conclude that there are exactly two red components, and ; see Figure 1.
Since each of the three colors has exactly two components, one of the components has at least edges, as desired. ∎
Lemma 10.
For sufficiently large , there exists a -coloring of the edges of such that every monochromatic component contains at most edges.
Proof.

We consider the following modification of a construction by Gyárfás: Let be a partition of the vertices of into four parts, with
Letting denote the set of edges between vertex sets and , color red, green, and blue. For large enough , for , so it remains to extend this partial coloring by coloring the edges within each of the such that each monochromatic component has at most edges at the end. It is natural to attempt the simple approach of distributing the edges within each as evenly as possible among the three colors. However, the possibility of a slight difference in size among the can yield a difference among the numbers of edges in each component if we are not sufficiently careful; a different coloring strategy will turn out to be simpler to analyze.
We call an extension of the above partial coloring nice if each green or blue component contains exactly edges. At least one nice coloring exists: we can color exactly of the edges within and of the edges within green, and exactly of the edges within and of the edges within blue (there are enough edges within each to do this when is sufficiently large), and color all remaining edges red. See Figure 2 for a diagram of this coloring. Fix a nice coloring where the larger of the two red components contains as few edges as possible.
Suppose one of the red components in this coloring, without loss of generality the one on , has more than edges. Then must have less than red edges. Without loss of generality let contain a red edge . If either contains a green edge, or contains a blue edge, we can switch the color of that edge with edge , preserving the sizes of the green and blue components while decreasing the size of the larger red component by one. Otherwise, is entirely blue and red, and is entirely green and red. Since the red component on has less than edges, neither nor can be entirely red (for sufficiently large , ). Then if contains a red edge, we can similarly switch two edges to reduce the size of the larger red component by one, so we can assume is entirely green and blue. But then there is one component of each color (including the larger red component) that does not have any edges within , which means there are at least edges incident to , a contradiction since
for sufficiently large . Thus indeed there is a construction of this form where every monochromatic component has at most edges. ∎
The construction in the proof of Lemma 10 is well-defined for all . A more careful analysis, splitting into cases based on the value of modulo and then using a more explicit construction in each case, shows that in fact for all except . However, the lower bound from Lemma 9 is not sharp for some of these small values of . Closely inspecting each step of our proof for , for example, we can deduce that , instead of the expected ; indeed, all of the bounds before the final step in the proof of Lemma 9 are loose enough to yield a component with at least edges unless we are in the case depicted in Figure 1, where one of the vertex sets or has size , and the other three sets have size . The set of size then contains internal edges, some of which are in the same color, yielding a component with edges as claimed. This shows a genuine difference in the behavior of for these small values of due to integer-related constraints in the extremal configurations.
We can adjust the proof of Lemma 9 to give a lower bound on the size of the largest monochromatic circuit in a -coloring of the edges of , as follows. First, as before, we can remove a forest in each color and leave each color class Eulerian. The resulting graph has at least edges, so all but at most of the vertices have degree at least . We then pass to the induced subgraph on these vertices; the minimum degree of is at least when is sufficiently large. The argument then proceeds largely as in the proof of Lemma 9, except that the condition of every green or blue component intersecting both and is strengthened by requiring every green or blue component to intersect each of and in more than vertices. The proof then concludes as before, reducing to the case where there are exactly two components in each color. When the edges between and are added back in, it remains true that there are at most two components in each color with a positive number of edges. So, at least one monochromatic component in has at least edges. Since this component of is Eulerian, we have a circuit, and hence a trail, of the desired length, for all sufficiently large . The upper bound from Lemma 10 likewise applies to the size of the longest circuit, showing that the lower bound is asymptotically tight.
Acknowledgments. I would like to thank my advisor Jacob Fox for introducing me to this problem and for helpful conversations along the way, as well as David Conlon and Mykhaylo Tyomkyn for the insights from our later joint work that served as inspiration for some of the strengthened arguments in the revised version of this paper. In addition, I would like to thank the anonymous referees for their careful reading and helpful comments, including a specific suggestion that led to a significant strengthening in the bound for general in Theorem 1.
References
- [1] Conlon, D., and Tyomkyn, M. Ramsey numbers of trails and circuits. arXiv preprint arXiv:2109.02633 (2021).
- [2] DeBiasio, L., Krueger, R. A., and Sárközy, G. N. Large monochromatic components in multicolored bipartite graphs. J. Graph Theory 94, 1 (2020), 117–130.
- [3] Gyárfás, A. Partition coverings and blocking sets in hypergraphs. Communications of the Computer and Automation Institute of the Hungarian Academy of Sciences 71 (1977), 62.
- [4] Gyárfás, A. Large monochromatic components in edge colorings of graphs: a survey. In Ramsey theory, vol. 285 of Progr. Math. Birkhäuser/Springer, New York, 2011, pp. 77–96.
- [5] Gyárfás, A., and Sárközy, G. N. Large monochromatic components in edge colored graphs with a minimum degree condition. Electron. J. Combin. 24, 3 (2017), Paper No. 3.54, 14.
- [6] Osumi, M. Ramsey numbers of trails. arXiv preprint arXiv:2109.00734 (2021).
- [7] Ruszinkó, M. Large components in -edge-colorings of have diameter at most five. J. Graph Theory 69, 3 (2012), 337–340.