On Comparing Fair Classifiers under Data Bias
Abstract
In this paper, we consider a theoretical model for injecting data bias, namely, under-representation and label bias (Blum & Stangl, 2019). We empirically study the effect of varying data biases on the accuracy and fairness of fair classifiers. Through extensive experiments on both synthetic and real-world datasets (e.g., Adult, German Credit, Bank Marketing, COMPAS), we empirically audit pre-, in-, and post-processing fair classifiers from standard fairness toolkits for their fairness and accuracy by injecting varying amounts of under-representation and label bias in their training data (but not the test data). Our main observations are: 1. The fairness and accuracy of many standard fair classifiers degrade severely as the bias injected in their training data increases, 2. A simple logistic regression model trained on the right data can often outperform, in both accuracy and fairness, most fair classifiers trained on biased training data, and 3. A few, simple fairness techniques (e.g., reweighing, exponentiated gradients) seem to offer stable accuracy and fairness guarantees even when their training data is injected with under-representation and label bias . Our experiments also show how to integrate a measure of data bias risk in the existing fairness dashboards for real-world deployments.
1 Introduction
Fairness in AI and machine learning is an important problem because automated decision-making in highly sensitive domains such as justice, healthcare, banking, and education can proliferate social and economic harms [17, 29, 4, 45]. Fair and representative data is a foremost requirement to train and validate fair models. However, most collected and labeled datasets invariably contain historical and systemic biases [5], resulting in unfair and unreliable performance after deployment [58, 13, 61]. Even many standard datasets used to evaluate and compare bias mitigation techniques are not perfectly fair and representative [21, 48].
Recent literature in fair classification has studied the failure of fairness and accuracy guarantees under distribution shifts (e.g., covariate shift, label shift) between the training and test distributions and proposed fixes under reasonable assumptions [57, 20, 54, 59, 44, 22, 10, 56]. In this paper, we consider a simple, natural data bias model that incorporates under-representation, over-representation, and label biases [12], and study the change in accuracy and fairness of various classifiers as we inject bias in their training data. The central question we ask is: Among the various fair classifiers available in the standard fairness toolkits (e.g., [7]), which ones are less vulnerable to data bias?
The definitions of fairness prevalent in literature fall into two broad types: individual fairness and group fairness [24, 6, 50, 27, 50, 33, 62, 8]. Individual fairness promises similar treatment to similar individuals. Our focus is group-fair classification, which promises equal or near-equal outcomes across different sensitive groups (e.g., race, gender). Examples of group fairness include Equal Opportunity (equal false negative rates across groups) and Statistical Parity (equal acceptance rate across groups). Various bias mitigation techniques have been proposed for group-fair classification motivated by different applications and stages of the machine learning pipeline [69, 29, 45]. They are broadly categorized into three types: 1. Pre-Processing, where one transforms the input data, independent of the subsequent stages of training, and validation [37, 25, 15], 2. In-Processing, where models are trained by fairness-constrained optimization [14, 39, 64, 63, 66, 1, 16], and 3. Post-Processing, where the output predictions are adjusted afterward to improve fairness [38, 33, 52] . These techniques appear side by side in standard fairness toolkits with little normative prescription about which technique to choose under data bias. Furthermore, it’s unclear what happens to such standard fair classifiers when they are trained and exposed to varying amounts of data bias over time in the training or deployment environments. We attempt to close this gap by providing an auditing method to compare different fair classifiers under a simple model of data bias.
To examine the effect of data bias on group-fair classifiers, we use a theoretical model by Blum & Stangl [12] for under-representation and label bias. It is a simple model for demographic under-/over-sampling and implicit label bias seen in real-world data [58, 13, 61, 32, 41]. Given a train-test data split, we create biased training data by injecting under-representation and label bias in the training data (but not the test data). We then study the error rates and (un)fairness metrics of various pre-, in-, and post-processing fair classifiers on the original test data, as we vary the amount of bias in their training data. We inject two types of under-representation biases in the training data: -bias, where we undersample the positive labeled population of the minority group by a multiplicative factor of , and -bias, where we undersample the negative labeled population of the minority group by a multiplicative factor of . We examine the effect of increasing the parameters and separately as well as together. We also investigate the effect of label bias parameter , where we flip the positive labels of the minority group to negative ones with probability . We cannot hope to re-create real-world data bias scenarios via this synthetic pipeline [13, 61], but our findings on stability/instability of various classifiers can be somewhat useful towards designing fair pipelines in the presence of various data biases.
Our Contributions:
Our main contributions and observations can be summarized as follows.
-
•
Using synthetic and real-world datasets, we show that the fairness and accuracy guarantees of many fair classifiers from standard fairness toolkits are highly vulnerable to under-representation and label bias. In fact, often, an unfair classifier (e.g., logistic regression classifier) trained on the correct data can be more accurate and fairer than fair classifiers trained on biased data.
-
•
Some fair classification techniques (viz., reweighing [37], exponentiated gradients [1], adaptive reweighing [36]) have stable accuracy and fairness guarantees even when their training data in injected with under-representation and label bias. We provide a theoretical justification to support the empirically observed stability of the reweighing classifier [37]; see Theorem 1.
-
•
Our experimental pipeline can be leveraged to create audit and test suites to check the vulnerability of fair classifiers to simple models of data bias before their real-world deployment.
The rest of the paper is organized as follows. Section 2 explains related work to set the context for our work. Section 3 explains our experimental setup, and Section 4 discusses our key empirical observations. Section 5 contains some relevant theorems and proof outlines. Section 6 discusses our work in the context of other research directions on data bias in fair machine learning.
2 Related Work
The robustness of machine learning models when there is a mismatch between their training and test distributions has been studied under various theoretical models of distribution shifts, e.g., covariate shift and label shift. Recent works have studied fair classification subject to these distribution shifts and proposed solutions under reasonable assumptions on the data distribution [19, 57, 12, 54, 59, 20, 10, 22, 44, 31]. As pointed out in the introduction, our goal is different, so we defer the critical contributions of these works to Appendix A.1. However, later in Section 6, we discuss different distribution shifts and their relation to the data bias model of Blum & Stangl [12] used in our paper.
Our work builds on the under-representation and label bias model proposed in Blum & Stangl [12]. Under this model, they prove that the optimal fair classifier that maximizes accuracy subject to fairness constraints (equal opportunity constraints, to be precise) on the biased data distribution gives the maximum accuracy on the unbiased data distribution. For under-representation bias, the above result can be achieved by equalized odds and equal opportunity constraints but not by demographic parity constraints. Along similar lines, Maity et al. [44] derive necessary and sufficient conditions about when performance parity constraints in the presence of subpopulation shifts give better accuracy on the test distribution. Jiang et al. [36] have also considered the label bias model, although we look at the aggregate effect over varying amounts of label bias. Our observations on label bias also corroborate various findings by other works investigating the role of label noise in fair classification [43, 28, 60, 42]. Under-representation bias can also be studied as a targeted Sample Selection Bias mechanism [18]. There is some work done on fair sample selection bias [22, 67], which we elaborate on in Appendix A.1.
Parallel to our work, a recent preprint by Akpinar et al. [2] proposes a simulation toolbox based on the under-representation setting from Blum & Stangl [12] to stress test four different fairness interventions with user-controlled synthetic data and data biases. On the other hand, our work uses the under-representation framework from Blum & Stangl [12] to extensively examine the stability of different types of fair classifiers on various synthetic and real-world datasets. While Akpinar et al. [2] focus on proposing a simulation framework to extensively test all findings of Blum & Stangl [12], we focus on using the under-representation framework to highlight the differences in performance between various fair classifiers and theoretically investigating the stability of one of the fair classifiers.
We compare various fair classifiers in the presence of under-representation and label bias, which complements some expository surveys in fair machine learning [69, 45, 49, 26] and some benchmarking on important aspects like the choice of data processing, splits, data errors, and data pre-processing choices [29, 10, 53, 35]. We elaborate on these works in the Appendix A.2.
3 Experimental Setup
For our analysis, we select a comprehensive suite of commonly used fair classifiers implemented in the open-source AI Fairness 360 (AIF-360) toolkit [7]. From the available choice of pre-processing classifiers, we include two: 1. Reweighing (‘rew’) [37], and 2. Adaptive Reweighing (‘jiang_nachum’) [36] . Since ‘jiang_nachum’ is not a part of AIF-360, we use the authors’ implementation111https://github.com/google-research/google-research/tree/master/label_bias. Among the in-processing classifiers in AIF-360, we choose three: 1. Prejudice Remover classifier (‘prej_remover’) [39], 2. Exponentiated Gradient Reduction classifier (‘exp_grad’), and its deterministic version (‘grid_search’) [1] and 3. the method from Kearns et al. (‘gerry_fair’) [40] . From post-processing classifiers, we choose three: 1. the Reject Option classifier (‘reject’) [38], 2. the Equalized Odds classifier (‘eq’) [33], and 3. the Calibrated Equalized Odds algorithm (‘cal_eq’) [52] . We omitted the use of some classifiers in the AIF360 toolkit for two reasons: resource constraints and their extreme sensitivity to the choice of hyperparameters.
All fair classifiers use a base classifier, which it uses in its optimization routine to mitigate unfairness. We experiment with two base classifiers: a logistic regression (LR) model and a Linear SVM classifier with Platt’s scaling [51] for probability outputs. We use the Scikit-learn toolkit to implement the base classifiers [47]. The ‘prej_remover’ and ‘gerry_fair’ classifiers do not support SVM as a base classifier; hence, we only show results for those on LR.
The fairness metric we use in the main paper is Equalized Odds (EODDS) [33], which is defined as the difference of False positive and False negative Rates, and we measure an equally weighted combination of both to report our results , where denotes the predicted label, denotes a binary class label, and denotes a binary sensitive attribute. Blum & Stangl [12] suggest that equal opportunity and equalized odds constraints on biased data can be more beneficial than demographic parity constraints. Therefore, we use the equalized odds constraint for ‘jiang_nachum’ and ‘exp_grad’. Different classifiers have been proposed for different fairness metrics and definitions. However, we often compare different methods with one or two standard metrics in practice. Since most of the methods used in this paper were trained for Equalized Odds, we report Equalized Odds results in the main text and report average Equal Opportunity Difference (EOD) and Statistical Parity Difference (SPD) results over under-representation bias settings to report a complete picture of the effect on data bias on fairness and error rate. EOD is defined as the True Positive Rate difference: , while SPD is defined as . For both metrics, values closer to mean better fairness, whereas values closer to indicate extreme parity difference between the two sensitive groups and .
We train on multiple datasets to perform our analysis. We consider four standard real-world datasets from fair classification literature: the Adult Income dataset [23], the Bank Marketing dataset [46], the COMPAS dataset [3], and the German Credit dataset [23]. We also consider a synthetic dataset setup from Zeng et al. [65], which consists of a binary label and a binary sensitive attribute setting . We take the original train-test split for a given dataset, or in its absence, a 70%-30% stratified split on the subgroups. Appendix B gives specific details for all datasets.
To perform our analysis, we use the data bias model from Blum & Stangl [12] and inject varying amounts of under-representation and label bias into the original training data before giving it to a classifier. We summarize our experimental setup in Algorithm , presented in Appendix C. Let represent the label, and represent the sensitive attribute. Let be the probability of retaining samples from the subgroup defined by the favorable label and underprivileged group (-subgroup). Similarly, let be the probability of retaining samples from the unfavorable label and underprivileged group (-subgroup). We inject under-representation bias into the training data by retaining samples from the -subgroup and the -subgroup with probability and , respectively. We consider ten different values each for and varying over . This results in different settings ( factors x factors) for training data bias. We separately inject ten different levels of label bias by flipping the favorable label of the underprivileged group to an unfavorable one () with a probability varying over . The test set for all settings is the original split test set, either provided at the original dataset source or taken out separately beforehand. This results in different datasets corresponding to different data bias settings, and consequently different results each for a particular fair classifier. Finally, the training of all classifiers and the procedures to create biased training data using , , and is performed times to account for randomness in sampling and optimization procedures.
We also note that some fair classifiers in our list, like ‘exp_grad’ and ‘cal_eq’, are randomized classifiers. Therefore, repeating the entire pipeline multiple times and reporting means and standard deviations normalizes the random behavior of these methods to some extent, apart from the measures taken during the implementation of these methods in widely used toolkits like the one we are using, AIF360 [7]. The code to train and reproduce the results is available here 222https://github.com/mohitsharma29/comparision_data_bias_fairness.
4 Stability of Fair Classifiers: Under-Representation and Label Bias
In this section, we present our experimental results about the stability of fairness and accuracy guarantees of various fair classifiers after injecting under-representation and label bias in their training data. Stability means whether the error rate and unfairness show high variance/spread in response to increasing or decreasing under-representation or label bias. A stable behavior is indicated by small changes in error rate and unfairness, as change.

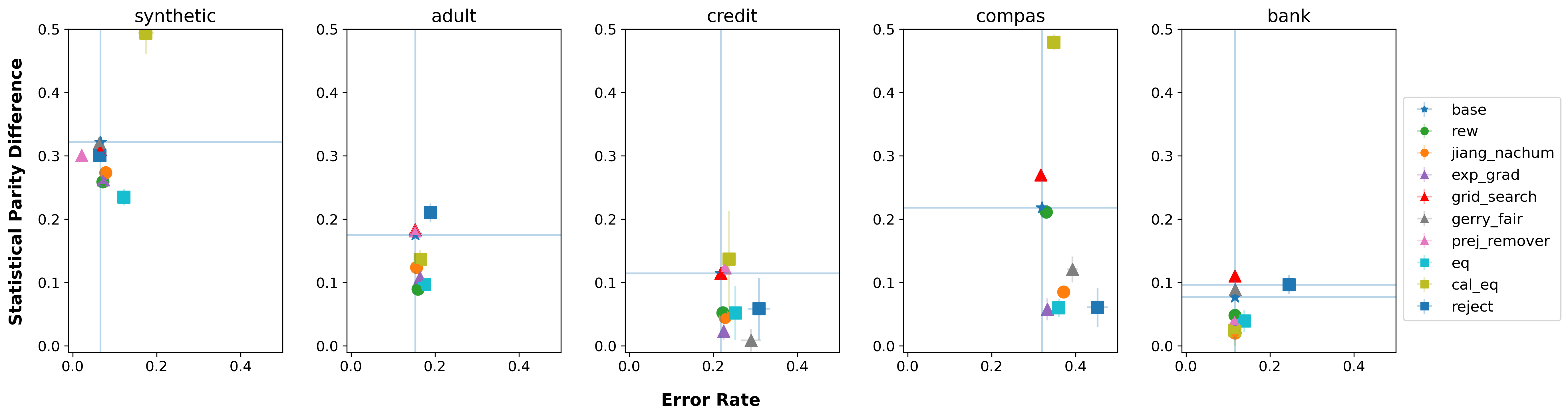
We first plot the unfairness (Equalized Odds) and error rates of various fair classifiers on the original training splits. Figure 1 shows the results of various fair classifiers with a logistic regression model on original dataset splits without any explicitly injected under-representation or label bias. While most fair classifiers exhibit an expected behavior of trading off some accuracy to minimize unfairness, some classifiers perform worse in mitigating unfairness than the unfair LR model. We attribute this reason to the strong effects of different kinds of data preprocessing on the performance of fair classifiers, as noted in previous works [29, 11]. Other results with SVM as a base classifier, Equal Opportunity Difference, and Statistical Parity Difference are given in Appendix D.
We can also inspect Figure 1 and other figures later in the paper by looking at the four quadrants formed by the blue horizontal and vertical lines corresponding to the unfairness and error rate of the base LR model. Following a Cartesian coordinate system, most fair classifiers, when trained on the original training set without explicit under-representation or label bias, lie in the fourth quadrant, as they trade-off some accuracy to mitigate unfairness. Any method lying in the first quadrant is poor, as it is worse than the base LR model in terms of both error rate and unfairness. Finally, any method lying in the third quadrant is excellent as it improves over both error rate and unfairness compared to the LR model.
 (a)
(a)
 (b)
Algo.
Err.
SPD
EOD
base
lr
0.324 0.011
0.206 0.011
0.126 0.024
svm
0.338 0.013
0.186 0.014
0.106 0.028
rew
lr
0.327 0.006
0.198 0.026
0.123 0.037
svm
0.343 0.008
0.177 0.027
0.101 0.04
jiang nachum
lr
0.39 0.014
0.066 0.017
0.018 0.009
svm
0.389 0.011
0.068 0.018
0.016 0.006
exp grad
lr
0.333 0.009
0.07 0.025
0.029 0.022
svm
0.354 0.017
0.057 0.02
0.029 0.021
grid search
lr
0.336 0.016
0.194 0.107
0.163 0.096
svm
0.358 0.025
0.163 0.092
0.13 0.089
gerry fair
lr
0.41 0.037
0.113 0.057
0.097 0.082
svm
-
-
-
prej remover
lr
0.654 0.024
0.303 0.137
0.246 0.118
svm
-
-
-
eq
lr
0.37 0.012
0.05 0.016
0.044 0.021
svm
0.381 0.014
0.046 0.018
0.043 0.022
cal_eq
lr
0.343 0.022
0.251 0.141
0.171 0.092
svm
0.353 0.022
0.216 0.114
0.144 0.083
reject
lr
0.415 0.019
0.079 0.027
0.038 0.019
svm
0.413 0.021
0.081 0.026
0.041 0.018
(a)
Figure 2: Stability analysis of various fair classifiers on the Compas dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds(EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
(b)
Algo.
Err.
SPD
EOD
base
lr
0.324 0.011
0.206 0.011
0.126 0.024
svm
0.338 0.013
0.186 0.014
0.106 0.028
rew
lr
0.327 0.006
0.198 0.026
0.123 0.037
svm
0.343 0.008
0.177 0.027
0.101 0.04
jiang nachum
lr
0.39 0.014
0.066 0.017
0.018 0.009
svm
0.389 0.011
0.068 0.018
0.016 0.006
exp grad
lr
0.333 0.009
0.07 0.025
0.029 0.022
svm
0.354 0.017
0.057 0.02
0.029 0.021
grid search
lr
0.336 0.016
0.194 0.107
0.163 0.096
svm
0.358 0.025
0.163 0.092
0.13 0.089
gerry fair
lr
0.41 0.037
0.113 0.057
0.097 0.082
svm
-
-
-
prej remover
lr
0.654 0.024
0.303 0.137
0.246 0.118
svm
-
-
-
eq
lr
0.37 0.012
0.05 0.016
0.044 0.021
svm
0.381 0.014
0.046 0.018
0.043 0.022
cal_eq
lr
0.343 0.022
0.251 0.141
0.171 0.092
svm
0.353 0.022
0.216 0.114
0.144 0.083
reject
lr
0.415 0.019
0.079 0.027
0.038 0.019
svm
0.413 0.021
0.081 0.026
0.041 0.018
(a)
Figure 2: Stability analysis of various fair classifiers on the Compas dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds(EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
Figure 1 shows how various fair classifiers perform without explicit under-representation and label bias. In this figure, we try to summarize all the available pieces of results for a given dataset in various ways to get a holistic picture. We show the stability of error rates and Equalized Odds unfairness and look at the average stability of the other two metrics: Equal Opportunity and Statistical Parity Difference, since many times in practice, we care about the performance of methods against a fixed set of metrics. We now look at the individual effects of both under-representation factors (, and label bias ()), with the LR model as a reference, denoted by the vertical and the horizontal error rate and Equal Opportunity Difference (EOD) lines respectively. Figure 2(a) shows those results for the Compas dataset. The results for the Adult, Synthetic, Bank Marketing, and Credit datasets are given in Appendix E. We first observe that many fair classifiers exhibit a large variance in the unfairness-error rate plane and often become unfair as the bias factors increase. This is also indicated by how the fair classifiers jump from quadrant four to quadrant one, as , , or increase. In fact, for the ‘prej_remover’ classifier, the results lie outside the plot limits, indicating its instability. Even when its average SPD is measured in Figure 2(c) (‘prej_remover’ is implicitly optimized for SPD), we observe that it does not perform well.
However, ‘rew’, ‘jiang_nachum’, and ‘exp_grad’ fair classifiers remain stable across all three kinds of biases for both error rate and EOD and show a minimal spread across both the error rate and unfairness (EOD) axes. They tend to remain in the same quadrant with varying bias factors. This remains true on other datasets as well (as shown in Appendix E). Furthermore, it’s interesting to note that a simple logistic regression model tends to stay relatively stable in the presence of under-representation and label biases, and on many occasions, more fair than many fair classifiers in our analysis.
We can also look at the combined effect of and in Figure 2(b) with the help of heatmaps. Each cell in the heatmap denotes a possible setting, thus covering all the possible settings. Darker color values in cells denote lower error rates and unfairness. For this analysis, to examine stability with heatmaps, we look for uniformity of colors in the entire grid, which means that the error rate and unfairness values do not change with different values.
Figure 2(b) again confirm the stability of ‘rew’, ‘jiang_nachum’ and ‘exp_grad’ fair classifiers even when they are trained on datasets with combined and biases. However, ‘jiang_nachum’ and ‘exp_grad’ emerge as stable and better classifiers in terms of their unfairness values than the ‘rew’ classifier because they have darker uniform colors across their entire error rate and unfairness grid. The ‘eq’ classifier also remains stable for unfairness, except on the Credit dataset (shown in Appendix E). Amongst the classifiers optimized for Equalized Odds (‘jiang_nachum’, ‘exp_grad’, ‘eq’ and ‘cal_eq’), ‘jiang_nachum’ and ‘exp_grad’ emerge out to be most stable ones in terms of error rate and unfairness.
To quantitatively summarize the findings from the heatmap plots and to show this statistic with other choices of base classifiers (LR and SVM) and unfairness metrics (SPD and EOD), we look at the average performance across different settings of and in Figure 2(c) for the Compas dataset. An indication of stability with these results is whether the mean error rate and unfairness across different under-representation settings stay low and whether this mean performance has a low standard deviation. Because we run the whole experimental setup times with different random seeds for reproducibility, the values represent the mean value of the mean across runs for each setting, and its standard deviation over the settings. We embolden the top- mean and top- standard deviation values for each column, where the top- means the lowest error rate and the unfairness metrics (SPD and EOD).
For all datasets, the observations across all emboldened values corroborate our findings from the heatmap plots. For both unfairness metrics (SPD and EOD), ‘exp_grad’ and ‘jiang_nachum’ often appear in the top- mean performance across all settings, whereas ‘rew’, ‘jiang_nachum’ and ‘exp_grad’ often appear in the top- smallest standard deviation values, indicating their stability. Furthermore, ‘rew’ and ‘jiang_nachum’ often appear in the top- mean and standard deviation list for error rate. ‘rew’ often appears in the top- mean performance for Statistical Parity Difference (SPD). As expected, the unfair base classifier often appears in the top- mean error rate list since its objective is always to minimize error rates without regard for unfairness. Finally, when looking over all the datasets’ results, we find that ‘exp_grad’ and ‘jiang_nachum’ often emerge to be the most stable classifiers for other metrics like EOD and SPD, despite not being trained to minimize those metrics, further solidifying the evidence for their stable behavior.
Another interesting observation across the results of all datasets is that the deterministic version of the ‘exp_grad’ fair algorithm, the ’grid_search’ classifier [1], is very unstable compared to the ’exp_grad’ classifier, which is the most stable amongst the lot, indicating that in the face of data bias, randomness might help. Other results, such as Figure 2 (a,b) with SPD as the unfairness metric, cannot be included in the manuscript.
Finally, it is worth noting that the stability of ‘rew’ and ‘exp_grad’ has also been reported in another benchmarking study about testing various fair classifiers in the presence of varying sensitive attribute noise [30]. This indicates towards a potentially stable performance from reweighing-based approaches in the presence of varying kinds of data biases and noises in the training data.
5 Stability Theorems for Reweighing Classifier
The following theorems give a theoretical justification for the stability of test accuracy when the reweighing classifier [37] is trained even on data injected with extreme under-representation such as or .
Theorem 1.
Let be the original data distribution and . Let be the biased data distribution after injecting under-representation bias in using (or similarly ). Let be any binary classifier and be any non-negative loss function on the prediction of and the true label. Let denote the reweighed loss optimized by the reweighing classifier [37]. Then
where denotes the subgroup imbalance in the original distribution .
The proof for this theorem is given in Appendix F. The proof involves bounding subgroup and group/label probabilities using , and with a reasonable assumption that in in . The main take-away from Theorem 1 is the following: when we reweigh a given non-negative loss function using the Reweighing scheme from Kamiran & Calders [37] on samples from , we always lie in some constant ‘radius’ of the expected loss on the true distribution for any classifier . This does not tell us anything about the expected loss on itself, but rather, about the ability of the reweighed loss to recover from any arbitrary under-representation bias . However, the constant factors depend on , the worst case imbalance between the subgroups for a given distribution.
Remark 1.
Whenever is small, Theorem 1 says that the expected reweighed loss on the biased distribution will also be small, for any classifier . This means that if we are given a non-negative loss function which also subsumes a given fairness constraint (let’s call it ), then reweighing with can give us low unfairness and stable classifiers.
Using Theorem 1, we prove the following bound on the expected loss of the reweighing classifier that is obtained by empirical minimization of the reweighed loss on the biased distribution but tested on the original distribution .
Theorem 2.
For any , let the classifier obtained by empirical minimization of the reweighed loss on samples from the biased distribution defined as in Theorem 1. Then, with probability at least , we have
where is the Bayes optimal classifier on the original distribution , is the subgroup imbalance as in Theorem 1.
The proof for this theorem is given in Appendix F. It uses a generalized version of the Hoeffding’s inequality [34], proof of Theorem of Zhu et al. [68] and Theorem 1. Note that Theorem 2 implies that given any and , we can get the guarantee
with probability at least , by simply choosing the number of samples from in the empirical reweighed loss minimization to be large enough so that
6 Discussion
In this section, we discuss where our results stand in the context of related works on distribution shifts and data bias in real-world AI/ML models and make a few practical recommendations based on our work.
6.1 Under-Representation and Distribution Shifts
Let and define the probabilities for training and testing distributions, respectively, with a random data point denoted by with features , sensitive attribute , and class label . Let be the favorable label and be the underprivileged group. A covariate shift in fair classification is defined as [54]. Singh et al. [59] look at fairness and covariate shift from a causal perspective using the notion of a separating set of features that induce a covariate shift. Coston et al. [19] look at covariate shift and domain adaptation when sensitive attributes are not available at source (train) or target (test).
Distribution shifts can also be induced via class labels. Dai et al. [20] present a more general model for label bias, building upon the work of Blum et al. [12]. They present a model for label shift where , but . Biswas et al. [10] study model shifts in prior probability, where but . Our work is also different from sample selection bias [18] (selection of training samples at random vs. sensitive group dependent under-sampling and label flipping), but may have some connections to fair sample selection bias [22], where the objective is to train only on selected samples(), but generalize well for fairness and accuracy on the overall population (unselected samples and ). An interesting question one can ask in this regard is to design fair classifiers which are stable against a range of malicious sample selection biases.
The under-representation model used in our paper comes from Blum et al. [12] and can be thought of as the following distribution shift: , while the other two subgroups () and () are left untouched. Overall, the distribution of remains unchanged, while the distribution of changes only for the underprivileged group . The above distribution shift is different from covariate and label shifts in that it affects both the joint marginal and .
In a broader sense beyond the mathematical definition used in our work, under-representation of a demographic and implicit bias in the labels are known problems observed in real-world data. Shankar et al. [58] highlight geographic over-representation issues in public image datasets and how that can harm use cases concerning prediction tasks involving developing countries. Buolamwini et al. [13] highlight a similar under-representation issue with gender classification systems trained on over-represented lighter-skinned individuals. Wilson et al. [61] highlight similar disparities for pedestrian detection tasks. Biased labels in the training data have also been observed in the context of implicit bias in the literature [32, 41].
6.2 Practical Recommendations
We show that the performance guarantees of commonly used fair classifiers can be highly unstable when their training data has under-representation and label bias. Our experimental setup serves as a template of a dashboard to check the vulnerability of fair classifiers to data bias by injecting bias using simple models similar to Blum & Stangl [12].
Our work motivates the importance of creating test suites for robustness to data bias and incorporating them with modern fairness toolkits such as AIF-360 [7]. Our results complement previous studies on the stability across different train-test splits [29] or different data pre-processing strategies [11]. We experiment with a range of and factors. In practice, this can be done with a user-supplied range of under-representation and label bias relevant for specific use cases. The ability to measure the stability of chosen fairness metrics across dynamically specified bias factors can be a great first step towards safe deployment of fair classifiers, similar to recent works like Shifty [31].
Our results show that some classifiers like ‘jiang_nachum’ [36] and ‘exp_grad’ [1] can remain relatively unscathed in the presence of varying under-representation and label biases. The stability is maintained even when they are trained and tested on mismatching fairness metrics. This motivates using such reweighing methodologies when the level of data biases our model might see is unknown.
Motivated by the same setup of Blum & Stangl [12], Akpinar et al. [2] also propose a toolkit and dashboard to stress test fair algorithms under a user-controlled synthetic setup, which allows the user to control various aspects of the simulation. A handy addition to existing fairness toolkits such as AIF360 [7], and Fairlearn [9] can be to incorporate input distribution stability routines from our work and Akpinar et al. [2], along with some comparative analysis routines from Friedler et al. [29] to create a practical checklist for any fairness algorithm. Finally, our experimental setup can provide an additional tool for checking the robustness of models to data bias, along with the existing robustness test suites, e.g., CheckList [55].
7 Conclusion
We show that many state-of-the-art fair classifiers exhibit a large variance in their performance when their training data is injected with under-representation and label bias. We propose an experimental setup to compare different fair classifiers under data bias. We show how the Bayes Optimal unfair and fair classifiers react with under-representation bias and propose a reweighing scheme to recover the true fair Bayes Optimal classifiers while optimizing over biased distributions with a known bias. We give a theoretical bound on the accuracy of the reweighing classifier [37] that holds even under extreme data bias. Finally, we discuss our work in the broader context of data bias literature and make practical recommendations.
A limitation of our work is that we use a simple model for injecting under-representation and label bias, with which one cannot hope to address the root cause behind different kinds of biases in real-world data. Thinking about the causal origin of data bias instead may allow one to model more types of biases and obtain better fixes for them under reasonable assumptions. Theoretically explaining the stability of the ‘exp_grad’ [1], and ‘jiang_nachum’ [36] fair classifiers with under-representation bias is also an interesting future work.
References
- [1] Alekh Agarwal, Alina Beygelzimer, Miroslav Dudík, John Langford, and Hanna Wallach. A reductions approach to fair classification. In International Conference on Machine Learning, pages 60–69. PMLR, 2018.
- [2] Nil-Jana Akpinar, Manish Nagireddy, Logan Stapleton, Hao-Fei Cheng, Haiyi Zhu, Steven Wu, and Hoda Heidari. A sandbox tool to bias (stress)-test fairness algorithms. arXiv preprint arXiv:2204.10233, 2022.
- [3] Julia Angwin, Jeff Larson, Surya Mattu, and Lauren Kirchner. Machine bias. ProPublica, May, 23(2016):139–159, 2016.
- [4] Solon Barocas, Moritz Hardt, and Arvind Narayanan. Fairness in machine learning. Nips tutorial, 1:2017, 2017.
- [5] Solon Barocas and Andrew D Selbst. Big data’s disparate impact. Calif. L. Rev., 104:671, 2016.
- [6] Yahav Bechavod, Christopher Jung, and Zhiwei Steven Wu. Metric-free individual fairness in online learning. In Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020.
- [7] Rachel K. E. Bellamy, Kuntal Dey, Michael Hind, Samuel C. Hoffman, Stephanie Houde, Kalapriya Kannan, Pranay Lohia, Jacquelyn Martino, Sameep Mehta, Aleksandra Mojsilovic, Seema Nagar, Karthikeyan Natesan Ramamurthy, John Richards, Diptikalyan Saha, Prasanna Sattigeri, Moninder Singh, Kush R. Varshney, and Yunfeng Zhang. AI Fairness 360: An extensible toolkit for detecting, understanding, and mitigating unwanted algorithmic bias, October 2018.
- [8] Reuben Binns. On the apparent conflict between individual and group fairness. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, FAT* ’20, page 514–524. Association for Computing Machinery, 2020.
- [9] Sarah Bird, Miro Dudík, Richard Edgar, Brandon Horn, Roman Lutz, Vanessa Milan, Mehrnoosh Sameki, Hanna Wallach, and Kathleen Walker. Fairlearn: A toolkit for assessing and improving fairness in ai. Microsoft, Tech. Rep. MSR-TR-2020-32, 2020.
- [10] Arpita Biswas and Suvam Mukherjee. Ensuring fairness under prior probability shifts. In Proceedings of the 2021 AAAI/ACM Conference on AI, Ethics, and Society, pages 414–424, 2021.
- [11] Sumon Biswas and Hridesh Rajan. Fair preprocessing: Towards understanding compositional fairness of data transformers in machine learning pipeline. arXiv preprint arXiv:2106.06054, 2021.
- [12] Avrim Blum and Kevin Stangl. Recovering from biased data: Can fairness constraints improve accuracy? arXiv preprint arXiv:1912.01094, 2019.
- [13] Joy Buolamwini and Timnit Gebru. Gender shades: Intersectional accuracy disparities in commercial gender classification. In Conference on fairness, accountability and transparency, pages 77–91. PMLR, 2018.
- [14] Toon Calders and Sicco Verwer. Three naive bayes approaches for discrimination-free classification. Data mining and knowledge discovery, 21(2):277–292, 2010.
- [15] Flavio P Calmon, Dennis Wei, Bhanukiran Vinzamuri, Karthikeyan Natesan Ramamurthy, and Kush R Varshney. Optimized pre-processing for discrimination prevention. In Proceedings of the 31st International Conference on Neural Information Processing Systems, pages 3995–4004, 2017.
- [16] L Elisa Celis, Lingxiao Huang, Vijay Keswani, and Nisheeth K Vishnoi. Classification with fairness constraints: A meta-algorithm with provable guarantees. In Proceedings of the conference on fairness, accountability, and transparency, pages 319–328, 2019.
- [17] Alexandra Chouldechova and Aaron Roth. The frontiers of fairness in machine learning. arXiv preprint arXiv:1810.08810, 2018.
- [18] Corinna Cortes, Mehryar Mohri, Michael Riley, and Afshin Rostamizadeh. Sample selection bias correction theory. In International conference on algorithmic learning theory, pages 38–53. Springer, 2008.
- [19] Amanda Coston, Karthikeyan Natesan Ramamurthy, Dennis Wei, Kush R Varshney, Skyler Speakman, Zairah Mustahsan, and Supriyo Chakraborty. Fair transfer learning with missing protected attributes. In Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, pages 91–98, 2019.
- [20] Jessica Dai and Sarah M Brown. Label bias, label shift: Fair machine learning with unreliable labels. In NeurIPS 2020 Workshop on Consequential Decision Making in Dynamic Environments, volume 12, 2020.
- [21] Frances Ding, Moritz Hardt, John Miller, and Ludwig Schmidt. Retiring adult: New datasets for fair machine learning. arxiv preprint arxiv:2108.04884, 2021.
- [22] Wei Du and Xintao Wu. Fair and robust classification under sample selection bias. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, pages 2999–3003, 2021.
- [23] Dheeru Dua and Casey Graff. UCI machine learning repository, 2017.
- [24] Cynthia Dwork, Moritz Hardt, Toniann Pitassi, Omer Reingold, and Richard Zemel. Fairness through awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science (ITCS) Conference, page 214–226. Association for Computing Machinery, 2012.
- [25] Michael Feldman, Sorelle A Friedler, John Moeller, Carlos Scheidegger, and Suresh Venkatasubramanian. Certifying and removing disparate impact. In proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pages 259–268, 2015.
- [26] Qizhang Feng, Mengnan Du, Na Zou, and Xia Hu. Fair machine learning in healthcare: A review. arXiv preprint arXiv:2206.14397, 2022.
- [27] Will Fleisher. What’s Fair about Individual Fairness?, page 480–490. Association for Computing Machinery, 2021.
- [28] Riccardo Fogliato, Alexandra Chouldechova, and Max G’Sell. Fairness evaluation in presence of biased noisy labels. In International Conference on Artificial Intelligence and Statistics, pages 2325–2336. PMLR, 2020.
- [29] Sorelle A Friedler, Carlos Scheidegger, Suresh Venkatasubramanian, Sonam Choudhary, Evan P Hamilton, and Derek Roth. A comparative study of fairness-enhancing interventions in machine learning. In Proceedings of the conference on fairness, accountability, and transparency, pages 329–338, 2019.
- [30] Avijit Ghosh, Pablo Kvitca, and Christo Wilson. When fair classification meets noisy protected attributes. In Proceedings of the 2023 AAAI/ACM Conference on AI, Ethics, and Society, pages 679–690, 2023.
- [31] Stephen Giguere, Blossom Metevier, Bruno Castro da Silva, Yuriy Brun, Philip S Thomas, and Scott Niekum. Fairness guarantees under demographic shift. In International Conference on Learning Representations, 2022.
- [32] Anthony G Greenwald and Linda Hamilton Krieger. Implicit bias: Scientific foundations. California law review, 94(4):945–967, 2006.
- [33] Moritz Hardt, Eric Price, and Nati Srebro. Equality of opportunity in supervised learning. Advances in neural information processing systems, 29:3315–3323, 2016.
- [34] Wassily Hoeffding. Probability inequalities for sums of bounded random variables. Journal of the American statistical association, 58(301):13–30, 1963.
- [35] Maliha Tashfia Islam, Anna Fariha, Alexandra Meliou, and Babak Salimi. Through the data management lens: Experimental analysis and evaluation of fair classification. In Proceedings of the 2022 International Conference on Management of Data, pages 232–246, 2022.
- [36] Heinrich Jiang and Ofir Nachum. Identifying and correcting label bias in machine learning. In International Conference on Artificial Intelligence and Statistics, pages 702–712. PMLR, 2020.
- [37] Faisal Kamiran and Toon Calders. Data preprocessing techniques for classification without discrimination. Knowledge and Information Systems, 33(1):1–33, 2012.
- [38] Faisal Kamiran, Asim Karim, and Xiangliang Zhang. Decision theory for discrimination-aware classification. In 2012 IEEE 12th International Conference on Data Mining, pages 924–929. IEEE, 2012.
- [39] Toshihiro Kamishima, Shotaro Akaho, Hideki Asoh, and Jun Sakuma. Fairness-aware classifier with prejudice remover regularizer. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pages 35–50. Springer, 2012.
- [40] Michael Kearns, Seth Neel, Aaron Roth, and Zhiwei Steven Wu. Preventing fairness gerrymandering: Auditing and learning for subgroup fairness. In International Conference on Machine Learning, pages 2564–2572. PMLR, 2018.
- [41] Jon Kleinberg and Manish Raghavan. Selection problems in the presence of implicit bias. arXiv preprint arXiv:1801.03533, 2018.
- [42] Nikola Konstantinov and Christoph H Lampert. On the impossibility of fairness-aware learning from corrupted data. In Algorithmic Fairness through the Lens of Causality and Robustness workshop, pages 59–83. PMLR, 2022.
- [43] Alex Lamy, Ziyuan Zhong, Aditya K Menon, and Nakul Verma. Noise-tolerant fair classification. Advances in Neural Information Processing Systems, 32, 2019.
- [44] Subha Maity, Debarghya Mukherjee, Mikhail Yurochkin, and Yuekai Sun. Does enforcing fairness mitigate biases caused by subpopulation shift? Advances in Neural Information Processing Systems, 34, 2021.
- [45] Ninareh Mehrabi, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, and Aram Galstyan. A survey on bias and fairness in machine learning. ACM Computing Surveys (CSUR), 54(6):1–35, 2021.
- [46] Sérgio Moro, Paulo Cortez, and Paulo Rita. A data-driven approach to predict the success of bank telemarketing. Decision Support Systems, 62:22–31, 2014.
- [47] Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort, Vincent Michel, Bertrand Thirion, Olivier Grisel, Mathieu Blondel, Peter Prettenhofer, Ron Weiss, Vincent Dubourg, et al. Scikit-learn: Machine learning in python. the Journal of machine Learning research, 12:2825–2830, 2011.
- [48] Kenneth L Peng, Arunesh Mathur, and Arvind Narayanan. Mitigating dataset harms requires stewardship: Lessons from 1000 papers. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), 2021.
- [49] Dana Pessach and Erez Shmueli. A review on fairness in machine learning. ACM Computing Surveys (CSUR), 55(3):1–44, 2022.
- [50] Felix Petersen, Debarghya Mukherjee, Yuekai Sun, and Mikhail Yurochkin. Post-processing for individual fairness. Advances in Neural Information Processing Systems, 34, 2021.
- [51] John Platt et al. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in large margin classifiers, 10(3):61–74, 1999.
- [52] Geoff Pleiss, Manish Raghavan, Felix Wu, Jon Kleinberg, and Kilian Q Weinberger. On fairness and calibration. arXiv preprint arXiv:1709.02012, 2017.
- [53] Shangshu Qian, Hung Pham, Thibaud Lutellier, Zeou Hu, Jungwon Kim, Lin Tan, Yaoliang Yu, Jiahao Chen, and Sameena Shah. Are my deep learning systems fair? an empirical study of fixed-seed training. Advances in Neural Information Processing Systems, 34, 2021.
- [54] Ashkan Rezaei, Anqi Liu, Omid Memarrast, and Brian D Ziebart. Robust fairness under covariate shift. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pages 9419–9427, 2021.
- [55] Marco Tulio Ribeiro, Tongshuang Wu, Carlos Guestrin, and Sameer Singh. Beyond accuracy: Behavioral testing of nlp models with checklist. arXiv preprint arXiv:2005.04118, 2020.
- [56] Jessica Schrouff, Natalie Harris, Oluwasanmi Koyejo, Ibrahim Alabdulmohsin, Eva Schnider, Krista Opsahl-Ong, Alex Brown, Subhrajit Roy, Diana Mincu, Christina Chen, et al. Maintaining fairness across distribution shift: do we have viable solutions for real-world applications? arXiv preprint arXiv:2202.01034, 2022.
- [57] Candice Schumann, Xuezhi Wang, Alex Beutel, Jilin Chen, Hai Qian, and Ed H Chi. Transfer of machine learning fairness across domains. arXiv preprint arXiv:1906.09688, 2019.
- [58] Shreya Shankar, Yoni Halpern, Eric Breck, James Atwood, Jimbo Wilson, and D Sculley. No classification without representation: Assessing geodiversity issues in open data sets for the developing world. arXiv preprint arXiv:1711.08536, 2017.
- [59] Harvineet Singh, Rina Singh, Vishwali Mhasawade, and Rumi Chunara. Fairness violations and mitigation under covariate shift. In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, pages 3–13, 2021.
- [60] Jialu Wang, Yang Liu, and Caleb Levy. Fair classification with group-dependent label noise. In Proceedings of the 2021 ACM conference on fairness, accountability, and transparency, pages 526–536, 2021.
- [61] Benjamin Wilson, Judy Hoffman, and Jamie Morgenstern. Predictive inequity in object detection. arXiv preprint arXiv:1902.11097, 2019.
- [62] Muhammad Bilal Zafar, Isabel Valera, Manuel Gomez Rodriguez, and Krishna P. Gummadi. Fairness beyond disparate treatment & disparate impact: Learning classification without disparate mistreatment. In Proceedings of the 26th International Conference on World Wide Web (WWW), WWW’17, page 1171–1180, 2017.
- [63] Muhammad Bilal Zafar, Isabel Valera, Manuel Gomez Rogriguez, and Krishna P Gummadi. Fairness constraints: Mechanisms for fair classification. In Artificial Intelligence and Statistics, pages 962–970. PMLR, 2017.
- [64] Rich Zemel, Yu Wu, Kevin Swersky, Toni Pitassi, and Cynthia Dwork. Learning fair representations. In International conference on machine learning, pages 325–333. PMLR, 2013.
- [65] Xianli Zeng, Edgar Dobriban, and Guang Cheng. Bayes-optimal classifiers under group fairness. arXiv preprint arXiv:2202.09724, 2022.
- [66] Brian Hu Zhang, Blake Lemoine, and Margaret Mitchell. Mitigating unwanted biases with adversarial learning. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, pages 335–340, 2018.
- [67] Jiongli Zhu, Sainyam Galhotra, Nazanin Sabri, and Babak Salimi. Consistent range approximation for fair predictive modeling. Proceedings of the VLDB Endowment, 16(11):2925–2938, 2023.
- [68] Zhaowei Zhu, Tianyi Luo, and Yang Liu. The rich get richer: Disparate impact of semi-supervised learning. arXiv preprint arXiv:2110.06282, 2021.
- [69] Indre Zliobaite. A survey on measuring indirect discrimination in machine learning. arXiv preprint arXiv:1511.00148, 2015.
Appendix A Detailed Related Work
A.1 Prior Work on Distribution Shifts
The robustness of ML models when there is a mismatch between the training and test distributions has been studied under various theoretical models of distribution shifts, e.g., covariate shift and label shift. Recent works have studied fair classification subject to these distribution shifts and proposed solutions under reasonable assumptions on the data distribution [19, 57, 12, 54, 59, 20, 10, 22, 44, 31].
Coston et al. [19] study the problem of fair transfer learning with covariate shift under two conditions: availability of protected attributes in the source or target data, and propose to solve these problems by weighted classification and using loss functions with twice differentiable score disparity terms. Schumann et al. [57] present theoretical guarantees on different scenarios of fair transfer learning for equalized odds and equal opportunity through a domain adaptation framework. Rezaei et al. [54] propose an adversarial framework to learn fair predictors in the presence of covariate shift by formulating a game between choosing fair minimizing and maximizing target conditional label distributions, formulating a convex optimization problem which they ultimately solve using batch gradient descent. Singh et al. [59] proposes to learn stable models with respect to fairness and accuracy in the presence of shifts in data distribution using a causal graph modeling the shift, using the framework of causal domain adaptation, deriving solutions that are worst-case optimal for some kinds of covariate shift. Dai et al. [20] talk about the impact of label bias and label shift on standard fair classification algorithms. They study label bias and label shift through a common framework where they assume the availability of a trained fair classifier on true labels and analyze its performance at test time when either the true label distribution changes or when the new test time labels are biased. Biswas et al. [10] focus on addressing the effects of prior probability shifts on fairness and propose an algorithm and a metric called Prevalence Difference, which, when minimized, ensures Proportional Equality.
Finally, Du et al. [22] propose a framework to realize classifiers robust to sample selection bias using reweighing and minimax robust estimation. The selection of samples is indicated by . The aim is to train using a part of the distribution where but generalize well for fairness and accuracy on the overall population (both and ). Du et al. [22] show that robust and fair classifiers on the overall population can be obtained by solving a reweighed optimization problem. Giguere et al. [31] consider demographic shift where a certain group can become more or less probable in the test distribution than the training distribution. They output a classifier that retains fairness guarantees for given user-specified bounds on these probabilities. Zhu et al. [67] study the fair sample selection bias problem and propose the CRAB framework, which constructs a causal graph based on the background knowledge about the data collection process and external data sources.
We tackle a related problem to the above works, where we only look at the performance of fair classifiers in varying amounts of under-representation bias (or subgroups imbalance) and label bias, which is a very straightforward case of distribution shift.
A.2 Prior Work on Comparative Analysis of Fair Methods
We compare various fair classifiers in the presence of under-representation and label bias. Our work complements the surveys in fair machine learning that compare different methods either conceptually [69, 45, 49, 26] or empirically, on important aspects like the choice of data processing, splits, data errors, and data pre-processing choices [29, 10, 53, 35]. Friedler et al. [29] compare some fair classification methods in terms of how the data is prepared and preprocessed for training, how different fairness metrics correlate with each other, stability with respect to slight changes in the training data, and the usage of multiple sensitive attributes. Islam et al. [35] conceptually compare various fairness metrics and further use that to empirically compare fair classification approaches on their fairness-accuracy tradeoffs, scalability with respect to the size of dataset and dimensionality, robustness against training data errors such as swapped and missing feature values, and variability of results with multiple training data partitions. On the other hand, we compare various classifiers with respect to changes in the distribution while keeping most things like base classifiers and data preprocessing the same across methods.
Appendix B Dataset Information
Table 1 list all information pertaining to the datasets used in our experiments. We choose to drop columns which either introduce a lot of empty values, or represent some other sensitive attribute. The reason to drop the non-primary sensitive attributes is to avoid unintended disparate treatment. The choice of sensitive attributes for each dataset is motivated from previous works in fair ML literature [63, 1, 29, 36].
The synthetic dataset setup from Zeng et al. [65] consists of a binary label and a binary sensitive attribute setting . We sample data from subgroup-specific -dimensional Gaussian distributions where denotes a identity matrix and all entries of are sampled from . We sample training examples and test examples.
| Dataset | # Data Pts. | Outcome (Y) | Sensitive Attribute(S) | Dropped Columns |
|---|---|---|---|---|
| Adult [23] | Income(>, <=) | Sex (Male, Female) | fnlwgt, education-num, race | |
| Bank [46] | Term Deposit (Yes, No) | Age (<=, >) | poutcome, contact | |
| Compas [3] | Recidivate (Yes,No) | Race(African-American, Caucasian) | sex | |
| Credit [23] | Credit Risk (good, bad) | Sex (Male, Female) | age, foreign_worker | |
| Synthetic [65] | NA |
Appendix C Algorithm to create different Data Bias scenarios
Algorithm 1 gives a detailed description of how we inject varying amounts of under-representation and label bias for the considered fair classifiers.
Appendix D Original Split results for other settings
Figures 4, 5 and 6 show the results of all fair classifiers when we use either a Logistic Regression model or an SVM model, and measure unfairness using Statistical Parity or Equal Opportunity Difference as a metric. Note that ‘gerry_fair’ and ‘prej_remover’ are missing from Figures 5 and 6 because these two classifiers do not support SVM as a base classifier for their fairness routines.



Appendix E Stability Analysis for remaining datasets
Figures 7, 8, 9 and 10 show the scatter plot, heatmap and average results for the Synthetic, Adult, Credit and Bank Marketing datasets respectively.
 (a)
(a)
 (b)
Algo.
Err.
SPD
EOD
base
lr
0.075 0.009
0.311 0.073
0.206 0.107
svm
0.074 0.009
0.325 0.074
0.218 0.115
rew
lr
0.077 0.006
0.241 0.018
0.122 0.033
svm
0.074 0.006
0.258 0.023
0.131 0.04
jiang nachum
lr
0.075 0.006
0.291 0.041
0.086 0.079
svm
0.083 0.009
0.289 0.046
0.086 0.093
exp grad
lr
0.076 0.003
0.259 0.009
0.029 0.011
svm
0.079 0.005
0.257 0.01
0.026 0.01
grid search
lr
0.078 0.012
0.301 0.111
0.207 0.149
svm
0.078 0.013
0.315 0.119
0.22 0.167
gerry fair
lr
0.099 0.032
0.368 0.144
0.354 0.245
svm
-
-
-
prej remover
lr
0.022 0.001
0.296 0.009
0.022 0.008
svm
-
-
-
eq
lr
0.192 0.052
0.187 0.029
0.025 0.017
svm
0.191 0.052
0.188 0.028
0.025 0.017
cal_eq
lr
0.218 0.042
0.534 0.132
0.219 0.11
svm
0.22 0.042
0.535 0.132
0.22 0.111
reject
lr
0.075 0.008
0.278 0.028
0.168 0.043
svm
0.075 0.008
0.276 0.028
0.167 0.046
(a)
Figure 7: Stability analysis of various fair classifiers on the Synthetic dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds (EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
(b)
Algo.
Err.
SPD
EOD
base
lr
0.075 0.009
0.311 0.073
0.206 0.107
svm
0.074 0.009
0.325 0.074
0.218 0.115
rew
lr
0.077 0.006
0.241 0.018
0.122 0.033
svm
0.074 0.006
0.258 0.023
0.131 0.04
jiang nachum
lr
0.075 0.006
0.291 0.041
0.086 0.079
svm
0.083 0.009
0.289 0.046
0.086 0.093
exp grad
lr
0.076 0.003
0.259 0.009
0.029 0.011
svm
0.079 0.005
0.257 0.01
0.026 0.01
grid search
lr
0.078 0.012
0.301 0.111
0.207 0.149
svm
0.078 0.013
0.315 0.119
0.22 0.167
gerry fair
lr
0.099 0.032
0.368 0.144
0.354 0.245
svm
-
-
-
prej remover
lr
0.022 0.001
0.296 0.009
0.022 0.008
svm
-
-
-
eq
lr
0.192 0.052
0.187 0.029
0.025 0.017
svm
0.191 0.052
0.188 0.028
0.025 0.017
cal_eq
lr
0.218 0.042
0.534 0.132
0.219 0.11
svm
0.22 0.042
0.535 0.132
0.22 0.111
reject
lr
0.075 0.008
0.278 0.028
0.168 0.043
svm
0.075 0.008
0.276 0.028
0.167 0.046
(a)
Figure 7: Stability analysis of various fair classifiers on the Synthetic dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds (EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
 (a)
(a)
 (b)
Algo.
Err.
SPD
EOD
base
lr
0.156 0.003
0.171 0.035
0.134 0.111
svm
0.155 0.003
0.179 0.036
0.172 0.131
rew
lr
0.16 0.001
0.101 0.012
0.109 0.02
svm
0.159 0.001
0.103 0.02
0.105 0.029
jiang nachum
lr
0.156 0.001
0.125 0.011
0.019 0.011
svm
0.159 0.003
0.136 0.012
0.049 0.013
exp grad
lr
0.166 0.002
0.107 0.003
0.016 0.008
svm
0.168 0.002
0.109 0.003
0.017 0.008
grid search
lr
0.156 0.005
0.176 0.048
0.169 0.131
svm
0.208 0.041
0.056 0.067
0.051 0.064
gerry fair
lr
0.412 0.287
0.071 0.068
0.064 0.087
svm
-
-
-
prej remover
lr
0.156 0.005
0.174 0.05
0.172 0.135
svm
-
-
-
eq
lr
0.184 0.013
0.085 0.019
0.038 0.02
svm
0.182 0.013
0.085 0.017
0.038 0.021
cal_eq
lr
0.183 0.034
0.125 0.075
0.088 0.063
svm
0.183 0.036
0.123 0.081
0.091 0.066
reject
lr
0.199 0.008
0.192 0.025
0.027 0.018
svm
0.203 0.008
0.191 0.024
0.027 0.02
(a)
Figure 8: Stability analysis of various fair classifiers on the Adult dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equal Opportunity Difference(EOD) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EOD across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
(b)
Algo.
Err.
SPD
EOD
base
lr
0.156 0.003
0.171 0.035
0.134 0.111
svm
0.155 0.003
0.179 0.036
0.172 0.131
rew
lr
0.16 0.001
0.101 0.012
0.109 0.02
svm
0.159 0.001
0.103 0.02
0.105 0.029
jiang nachum
lr
0.156 0.001
0.125 0.011
0.019 0.011
svm
0.159 0.003
0.136 0.012
0.049 0.013
exp grad
lr
0.166 0.002
0.107 0.003
0.016 0.008
svm
0.168 0.002
0.109 0.003
0.017 0.008
grid search
lr
0.156 0.005
0.176 0.048
0.169 0.131
svm
0.208 0.041
0.056 0.067
0.051 0.064
gerry fair
lr
0.412 0.287
0.071 0.068
0.064 0.087
svm
-
-
-
prej remover
lr
0.156 0.005
0.174 0.05
0.172 0.135
svm
-
-
-
eq
lr
0.184 0.013
0.085 0.019
0.038 0.02
svm
0.182 0.013
0.085 0.017
0.038 0.021
cal_eq
lr
0.183 0.034
0.125 0.075
0.088 0.063
svm
0.183 0.036
0.123 0.081
0.091 0.066
reject
lr
0.199 0.008
0.192 0.025
0.027 0.018
svm
0.203 0.008
0.191 0.024
0.027 0.02
(a)
Figure 8: Stability analysis of various fair classifiers on the Adult dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equal Opportunity Difference(EOD) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EOD across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
 (a)
(a)
 (b)
Algo.
Err.
SPD
EOD
base
lr
0.235 0.012
0.156 0.125
0.103 0.11
svm
0.235 0.011
0.17 0.143
0.115 0.111
rew
lr
0.234 0.006
0.043 0.012
0.018 0.009
svm
0.234 0.007
0.071 0.045
0.047 0.024
jiang nachum
lr
0.236 0.008
0.038 0.012
0.023 0.011
svm
0.236 0.011
0.046 0.025
0.031 0.018
exp grad
lr
0.239 0.008
0.045 0.022
0.027 0.014
svm
0.261 0.044
0.045 0.019
0.034 0.015
grid search
lr
0.24 0.027
0.153 0.117
0.102 0.105
svm
0.291 0.029
0.026 0.028
0.021 0.021
gerry fair
lr
0.263 0.031
0.039 0.038
0.024 0.024
svm
-
-
-
prej remover
lr
0.247 0.022
0.153 0.112
0.112 0.114
svm
-
-
-
eq
lr
0.318 0.074
0.057 0.032
0.074 0.045
svm
0.336 0.084
0.045 0.035
0.059 0.05
cal_eq
lr
0.261 0.013
0.255 0.163
0.151 0.124
svm
0.255 0.011
0.186 0.154
0.106 0.111
reject
lr
0.312 0.031
0.084 0.038
0.098 0.051
svm
0.317 0.037
0.089 0.04
0.105 0.046
(a)
Figure 9: Stability analysis of various fair classifiers on the Credit dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds (EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
(b)
Algo.
Err.
SPD
EOD
base
lr
0.235 0.012
0.156 0.125
0.103 0.11
svm
0.235 0.011
0.17 0.143
0.115 0.111
rew
lr
0.234 0.006
0.043 0.012
0.018 0.009
svm
0.234 0.007
0.071 0.045
0.047 0.024
jiang nachum
lr
0.236 0.008
0.038 0.012
0.023 0.011
svm
0.236 0.011
0.046 0.025
0.031 0.018
exp grad
lr
0.239 0.008
0.045 0.022
0.027 0.014
svm
0.261 0.044
0.045 0.019
0.034 0.015
grid search
lr
0.24 0.027
0.153 0.117
0.102 0.105
svm
0.291 0.029
0.026 0.028
0.021 0.021
gerry fair
lr
0.263 0.031
0.039 0.038
0.024 0.024
svm
-
-
-
prej remover
lr
0.247 0.022
0.153 0.112
0.112 0.114
svm
-
-
-
eq
lr
0.318 0.074
0.057 0.032
0.074 0.045
svm
0.336 0.084
0.045 0.035
0.059 0.05
cal_eq
lr
0.261 0.013
0.255 0.163
0.151 0.124
svm
0.255 0.011
0.186 0.154
0.106 0.111
reject
lr
0.312 0.031
0.084 0.038
0.098 0.051
svm
0.317 0.037
0.089 0.04
0.105 0.046
(a)
Figure 9: Stability analysis of various fair classifiers on the Credit dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds (EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
 (a)
(a)
 (b)
Algo.
Err.
SPD
EOD
base
lr
0.116 0.000
0.069 0.021
0.12 0.05
svm
0.116 0.000
0.069 0.007
0.096 0.014
rew
lr
0.116 0.000
0.053 0.008
0.088 0.011
svm
0.116 0.000
0.067 0.003
0.092 0.008
jiang nachum
lr
0.116 0.000
0.033 0.016
0.039 0.031
svm
0.116 0.000
0.05 0.017
0.051 0.023
exp grad
lr
0.117 0.001
0.023 0.007
0.03 0.011
svm
0.124 0.018
0.022 0.006
0.031 0.012
grid search
lr
0.12 0.012
0.153 0.14
0.255 0.184
svm
0.116 0.001
0.002 0.01
0.003 0.015
gerry fair
lr
0.117 0.003
0.146 0.215
0.224 0.238
svm
-
-
-
prej remover
lr
0.116 0.001
0.09 0.123
0.174 0.175
svm
-
-
-
eq
lr
0.227 0.125
0.026 0.01
0.069 0.027
svm
0.209 0.093
0.028 0.01
0.067 0.019
cal_eq
lr
0.116 0.000
0.05 0.028
0.099 0.054
svm
0.116 0.000
0.054 0.019
0.091 0.025
reject
lr
0.394 0.126
0.123 0.025
0.118 0.04
svm
0.35 0.115
0.116 0.026
0.117 0.035
(a)
Figure 10: Stability analysis of various fair classifiers on the Bank dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds (EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
(b)
Algo.
Err.
SPD
EOD
base
lr
0.116 0.000
0.069 0.021
0.12 0.05
svm
0.116 0.000
0.069 0.007
0.096 0.014
rew
lr
0.116 0.000
0.053 0.008
0.088 0.011
svm
0.116 0.000
0.067 0.003
0.092 0.008
jiang nachum
lr
0.116 0.000
0.033 0.016
0.039 0.031
svm
0.116 0.000
0.05 0.017
0.051 0.023
exp grad
lr
0.117 0.001
0.023 0.007
0.03 0.011
svm
0.124 0.018
0.022 0.006
0.031 0.012
grid search
lr
0.12 0.012
0.153 0.14
0.255 0.184
svm
0.116 0.001
0.002 0.01
0.003 0.015
gerry fair
lr
0.117 0.003
0.146 0.215
0.224 0.238
svm
-
-
-
prej remover
lr
0.116 0.001
0.09 0.123
0.174 0.175
svm
-
-
-
eq
lr
0.227 0.125
0.026 0.01
0.069 0.027
svm
0.209 0.093
0.028 0.01
0.067 0.019
cal_eq
lr
0.116 0.000
0.05 0.028
0.099 0.054
svm
0.116 0.000
0.054 0.019
0.091 0.025
reject
lr
0.394 0.126
0.123 0.025
0.118 0.04
svm
0.35 0.115
0.116 0.026
0.117 0.035
(a)
Figure 10: Stability analysis of various fair classifiers on the Bank dataset (Lighter the shade, more the under-representation and label bias): (a) The spread of error rates and Equalized Odds (EODDS) of various fair classifiers as we vary , and label bias separately. The vertical and horizontal reference blue lines denote the performance of an unfair logistic regression model on the original dataset without any under-representation or label bias. (b) Heatmap for Error Rate and EODDS across all different settings of and . Darker values denote lower error rates and unfairness. Uniform values across the grid indicate stability to different and . (c) Mean error rates, Statistical Parity Difference (SPD), and Equal Opportunity Difference (EOD) across all and settings for both kinds of base classifiers (SVM and LR).
Appendix F Proofs
F.1 Proof for Theorem 1
Proof.
We show the proof for binary label and sensitive attribute . The proof works out in a similar manner for multiple labels and sensitive attributes.
Assume that the subgroup probabilities on are denoted by : .
For the loss , we can write its expectation under distribution as:
Let , , and .
For the rest of the proof, we will assume an under-representation bias on subgroup with bias . The proof for bias on subgroup will work out similarly.
We denote by the distribution induced because of the under-representation bias on subgroup, where , and for rest of the subgroups.
For the reweighing loss , the reweighing weight is given by the following expression [37]:
Now we can write
Thus, we have
because in remains the same as in even after injecting under-representation.
For the distribution , assume that the normalization constant for the subgroup probabilities is .
We can write down individual label and sensitive attribute probabilities as follows in : , , and .
We will now attempt to lower and upper bound
in terms of , for any and any . Let . For example, for we get
using , and the definition of and . Similarly working out the upper and lower bounds for each of the four probability terms in the expected reweighed loss expression above, we get a common bound
for any . Now we can plug in these bounds in the following expression for .
Using the sandwich bound with the final form of , we get:
∎
F.2 Proof of Theorem 2
Before proving Theorem 1, we prove a small proposition that will be useful for later results.
Proposition 1.
Let L be a non-negative bounded loss between . Let be the empirical risk minimizing classifier with loss with samples: , where are i.i.d. samples from . Let . Then with probability of at least , we have
Proof.
The proof follows directly from the proof of Thm. 1 in [68], and a general form of Hoeffding’s inequality for any non-negative bounded loss333http://cs229.stanford.edu/extra-notes/hoeffding.pdf. ∎
We are now ready to prove Theorem 2.
Proof.
Using the results from Theorem 1, for any and , we can write
For , we can use the lower bound from Theorem 1 to get
| (1) |
We now assume that is a bounded loss between . if not, we can rescale it to lie in . Using , , and , we can show that the reweighing factor
for all . This can be done by using the upper bound from Theorem 1 and the fact that in the worst case ( here), .
Thus, the reweighed loss is bounded between . Now, using Proposition 1 and that is the empirical minimizer of the reweighed loss on samples from the biased distribution , we obtain that
where is the Bayes optimal classifier for the reweighed loss on the biased distribution . Now let be the Bayes optimal classifier for the loss on the original distribution . Thus, , and we get
| (2) |
Combining (1) and (2), we have
where we use the upper bound in Theorem 1 to get the last inequality. That completes the proof of Theorem 2. ∎