Odd-parity spin-loop-current order mediated by transverse spin fluctuations
in cuprates and related electron systems
Abstract
Unconventional symmetry-breaking phenomena due to nontrivial order parameters attract increasing attention in strongly correlated electron systems. Here, we predict theoretically the occurrence of nanoscale spontaneous spin-current, called the spin loop-current (sLC) order, as a promising origin of the pseudogap and electronic nematicity in cuprates. We reveal that the sLC is driven by the odd-parity electron-hole condensation that are mediated by transverse spin fluctuations around the pseudogap temperature . At the same temperature, odd-parity magnon pair condensation occurs. The sLC order is “hidden” in that neither internal magnetic field nor charge density modulation is induced, whereas the predicted sLC with finite wavenumber naturally gives the Fermi arc structure. In addition, the fluctuations of sLC order work as attractive pairing interaction between adjacent hot spots, which enlarges the -wave superconducting transition temperature . The sLC state will be a key ingredient in understanding the pseudogap, electronic nematicity as well as superconductivity in cuprates and other strongly correlated metals.
I Introduction
Various unconventional symmetry-breaking phenomena, such as violations of rotational and parity symmetries, have been discovered in many strongly correlated metals recently. This fact strongly indicates the emergence of exotic density-wave orders, which are totally different from usual spin/charge density waves. Various exotic symmetry-breaking phenomena, such as violations of rotational and parity symmetries, are the central issues in cuprate high- superconductors. However, their microscopic mechanisms still remain as unsolved issues. Figure 1 (a) shows a schematic phase diagram of cuprate superconductors. Below K, a stripe charge-channel density-wave emerges at finite wavevector in many compounds Y-Xray1 ; Bi-Xray1 ; STM-Kohsaka ; STM-Fujita , which produces the Fermi arc structure and causes a reduction in the density-of-states (DOS). However, it cannot be the origin of the pseudogap temperature since . Short quasiparticle lifetime due to spin or charge fluctuations could reduce the DOS Tremblay ; Scalapino ; Moriya .
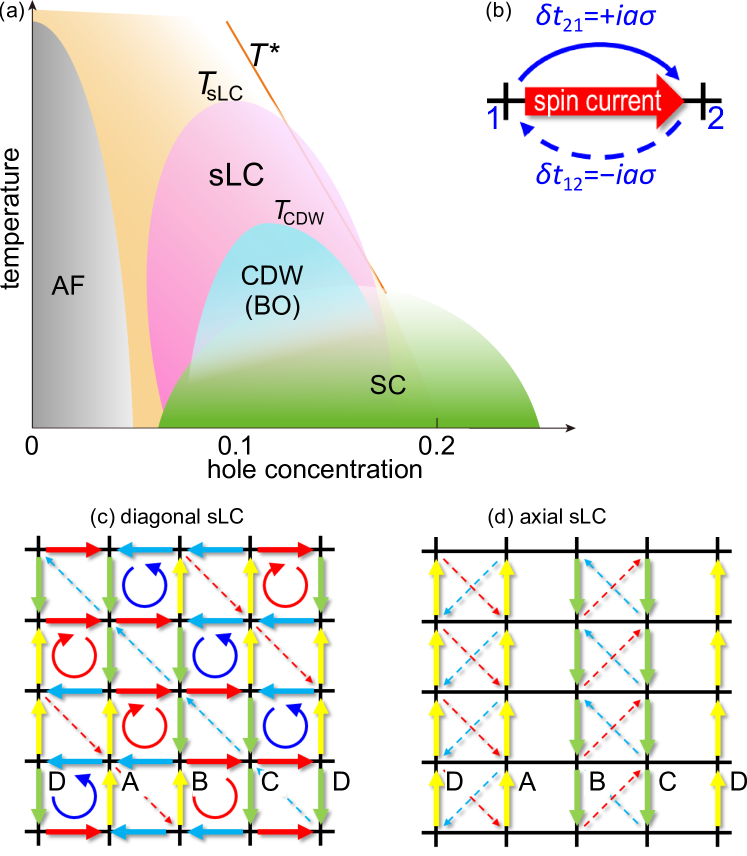
Recently, much experimental evidence for the phase transition at has been accumulated RUS ; ARPES-Science2011 ; Y-Sato ; Hg-Murayama ; Fujimori-nematic ; Shibauchi-nematic . Various fascinating order parameters have been proposed and actively investigated, such as the CDW or bond-order (BO) Bulut ; Chubukov ; Chubukov-AL ; Sachdev ; Metzner ; DHLee-PNAS ; Kivelson-NJP ; Yamakawa-CDW ; Tsuchiizu-CDW ; Kawaguchi-CDW , the pair-density-wave PALee ; Agterberg , and the charge loop-current (cLC) order Varma ; Affleck ; FCZhang ; Schultz . At present, the symmetries of the hidden order in the pseudo-gap phase are not yet confirmed experimentally. Thus, it is necessary to study various possibilities without prejudice based on advanced many-body theories Chubukov ; Chubukov-AL ; Sachdev ; Metzner ; DHLee-PNAS ; Kivelson-NJP ; Yamakawa-CDW ; Tsuchiizu-CDW ; Kawaguchi-CDW ; PALee ; Agterberg ; Varma ; Affleck ; FCZhang ; Schultz .
Let us discuss the symmetry breaking in the correlated hopping between sites and ; , where is the order parameter. Then, the BO is given by a real and even-parity Bulut ; Chubukov ; Sachdev ; Metzner ; DHLee-PNAS ; Kivelson-NJP ; Yamakawa-CDW ; Tsuchiizu-CDW ; Kawaguchi-CDW . A spin-fluctuation mechanism Tsuchiizu-CDW ; Kawaguchi-CDW predicts the ferro () -wave BO state at and stripe () BO at . The former order explains the experimental nematic transition Y-Sato ; Shibauchi-nematic . However, simple translational symmetry preserving ferro-BO does not explain the pseudogap formation. OAlso, the cLC order is given by a pure imaginary and odd-parity Varma ; Affleck ; FCZhang ; Schultz . Both order parameters have been actively investigated.
In contrast, spin current flows if pure imaginary order parameter is odd under space and spin inversions; as shown in Fig. 1 (b) Schultz ; Nersesyan ; Ozaki ; Ikeda ; Fujimoto ; Sr2IrO4 . Here, represents the spin of the electron. Figures 1 (c) and (d) depict the spin loop-current (sLC) order at the wavevectors and that at with , respectively. The sLC is a hidden order in the sense that no internal magnetic field appears, and charge density modulation is quite small. Nonetheless, the sLC is very attracting since the pseudogap and Fermi surface (FS) reconstruction are induced by band-folding if .
In this paper, we discover the emergence of “hidden symmetry breaking” accompanied by finite spin current at . This sLC order originates from the spin-flipping magnon-exchange process, called the Aslamazov-Larkin (AL) process Onari-SCVC ; Onari-FeSe ; Yamakawa-FeSe ; Chubukov-AL . The sLC order is hidden in that neither internal magnetic field nor charge density modulation is induced, while the band-folding by these sLC orders produces the Fermi arc structure and pseudogap in the DOS ARPES-Science2011 ; Yoshida-arc . The derived transition temperature is higher than that of the stripe-BO, and comparable to that of the ferro-BO. The sLC order will be responsible for the pseudogap and electronic nematicity not only in cuprates, but also in iridates and -electron systems Sr2IrO4 ; Sr2IrO4-ARPES ; Ikeda ; Fujimoto .
The emergence of the sLC has been discussed in various electronic systems Schultz ; Ozaki ; Nersesyan ; Sr2IrO4 ; Ikeda . From the microscopic viewpoint, however, the mechanism of the sLC is highly nontrivial, since the realization condition of the sLC order is very severe in the extended -- Hubbard model within the mean-field theory Nersesyan . In addition, only the case was analyzed in previous works. The present study can explain the sLC order based on a simple Hubbard model with on-site , without assuming the wavevector .
II Spin-fluctuation-driven unconventional orders
II.1 Model Hamiltonian
Here, we analyze the single-orbital square-lattice Hubbard model
| (1) |
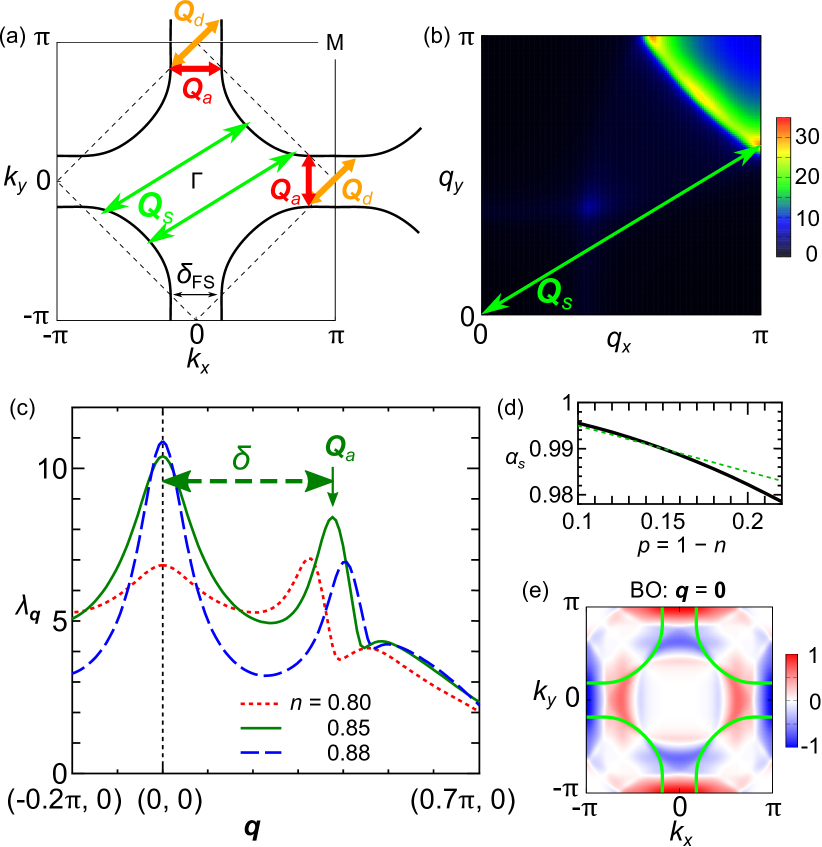
We denote the hopping integrals , where is the -th nearest hopping integral Kontani-ROP ; Springer . Hereafter, we set the unit of energy as , which corresponds to [K] in cuprates, and fix the temperature . The FS at filling is given in Fig. 2 (a). The spin susceptibility in the random-phase-approximation (RPA) is , where is the irreducible susceptibility without and . The spin Stoner factor is defined as . Figure 2 (b) shows the obtained at (). Here, [] [], which is still smaller than Im [] at K in 60K YBCO neutron . Thus, in real compounds. Owing to the Mermin-Wagner theorem, the relation is naturally satisfied for without any fine tuning of by considering the spin-fluctuation-induced self-energy self-consistently Kontani-ROP .
II.2 Introduction of singlet and triplet DW equations
From now on, we investigate possible exotic density-wave (DW) states for both charge- and spin-channels with general wavevector (), which is generally expressed as Nersesyan
| (2) | |||||
where , and is the charge (spin) channel order parameter. It induces the symmetry breaking in the self-energy:
| (3) |
which we call the form factors in this paper. Below, we assume without losing generality. The DW is interpreted as the electron-hole pairing condensation Nersesyan .
Here, is given by the Fourier transformation of the spin-independent hopping modulation . When , the relation holds. Also, is given by the spin-dependent modulation . The even-parity and the odd-parity respectively correspond to the BO state and the sLC state. Both states preserve the time-reversal symmetry.
To find possible DW in an unbiased way, we generalize the DW equation Kawaguchi-CDW for both spin/charge channels:
| (4) | |||
| (5) |
where () is the eigenvalue that represents the charge (spin) channel DW instability, , (, are fermion Matsubara frequencies). These DW equations are interpreted as the “spin/charge channel electron-hole pairing equations”.
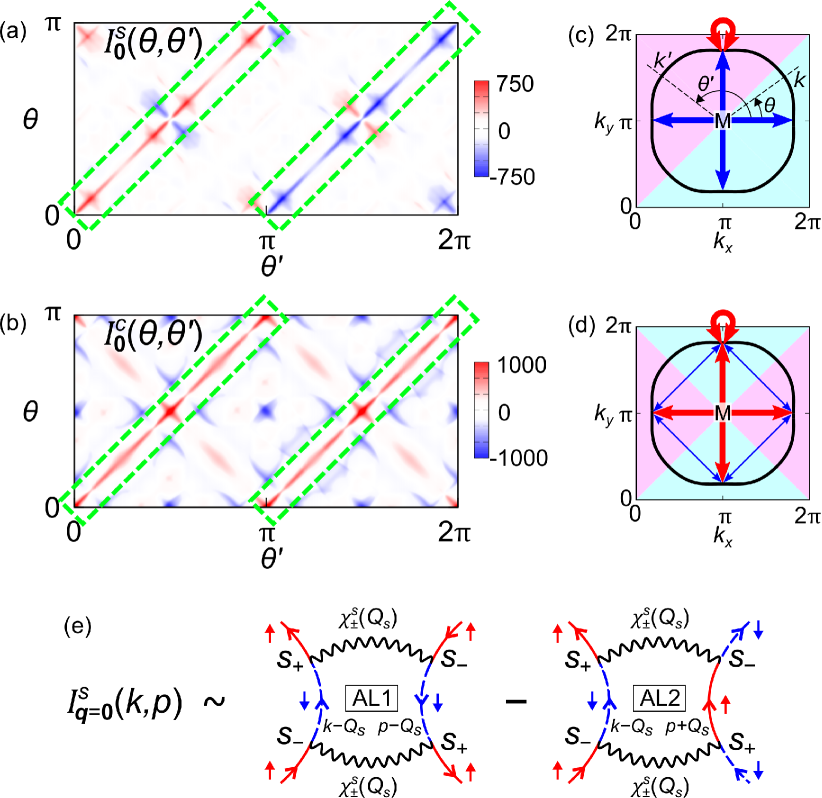
The charge (spin) channel kernel function is ; at is given by the Ward identity , which is composed of one single-magnon exchange term and two double-magnon exchange ones: The former and the latter are called the Maki-Thompson (MT) term and the AL terms; see Fig. 7 in Appendix A. The lowest order Hartree term in gives the RPA contribution. while the AL terms are significant for in various strongy correlated systems Onari-SCVC ; Kawaguchi-CDW ; Tazai-CeCu2Si2 ; Tazai-CeB6 . The significance of the AL processes have been revealed by the functional-renormalization-group (fRG) study, in which higher-order vertex corrections are produced in an unbiased way Tsuchiizu-CDW ; Tsuchiizu-PRL ; Tazai-FRG ; Tazai-kappa . Note that the MT term is important for the superconducting gap equation, transport phenomena Kontani-ROP , and cLC order Tazai-cLC .
Figure 2 (c) shows the charge-channel eigenvalue derived from the DW eq. (4) Kawaguchi-CDW ; Onari-B2g ; Onari-AFB . Hereafter, we put to satisfy the relation with , shown as full line in Fig. 2 (d). The obtained form factor at , shown in Fig. 2 (e), belongs to symmetry BO, consistently with previous studies Kawaguchi-CDW ; Tsuchiizu-CDW . As we discuss in Appendix B, the large eigenvalue in Fig. 2 (c) (and Fig. 3 (a)) is strongly suppressed to by considering the small quasiparticle weight due to the self-energy in cuprates Kawaguchi-CDW ; Onari-B2g .
III Derivation of sLC order based on triplet DW equation
III.1 Origin of sLC order
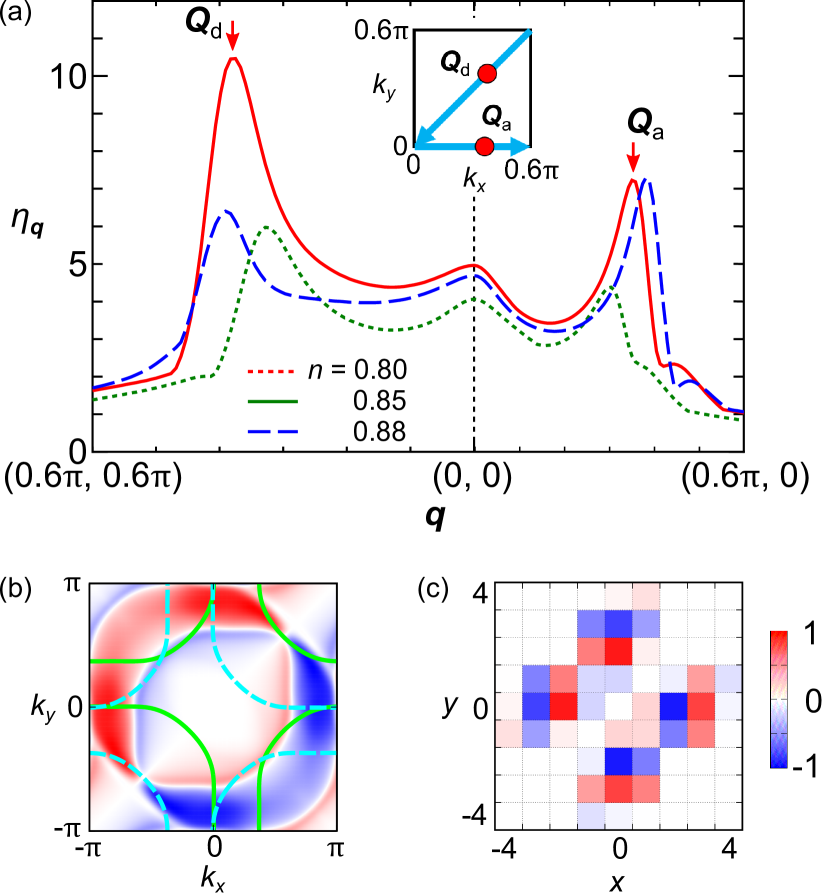
Next, we discuss the spin-fluctuation-driven sLC order, which is the main issue of this manuscript. Figure 3 (a) exhibits the spin-channel eigenvalue derived from the DW eq. (5). Peaks of are located at the nesting vectors (diagonal) and (axial). The obtained form factor at (diagonal sLC) is shown in Fig. 3 (b). The odd-parity solution means the emergence of the sLC order. The reason for large is that all hot spots contribute to the diagonal sLC as shown in Fig. 3 (b). Figure 3 (c) shows the form factor in real space with . Here, .
To understand why sLC state is obtained, we simplify Eq. (5) by taking the Matsubara summation analytically by approximating that and are static:
| (6) |
where is a positive function, and is Fermi distribution function; see Appendix A. In general, the peak positions of in Eq. (6) are located at and/or nesting vectors with small wavelength ( in the present model). The reason is that by AL terms is large for small , and is large for wide area of when is a nesting vector.
To understand why odd-parity form factor is obtained, we show the spin-channel “electron-hole pairing interaction” on the FS in Fig. 4 (a). The charge-channel one is also shown in Fig.4 (b). Here, represents the position of shown in Figs. 4 (c) and (d). in Fig. 4 (a) gives large attractive interaction for and large repulsive one for . In this case, we naturally obtain -wave form factor shown in Fig. 3 (b), as we explain in Fig. 4 (c). Here, red (blue) arrows represent the attractive (repulsive) interaction.
The strong -dependence of originates from the AL1 and AL2 terms in Fig. 4 (e), or Fig. 7 (a) in Appendix A. Owing to the spin-conservation law, AL terms in originates from the spin-flipping processes due to transverse spin fluctuations in Fig. 4 (e), in proportion to . (In , the spin non-flipping AL processes in proportion to are exactly canceled out.) Therefore, . The AL1 term with the p-h (anti-parallel) pair Green functions causes large attractive interaction for , and the AL2 term with the p-p (parallel) ones does for , as explained in Ref. Onari-B2g in detail. Thus, -dependence in Fig. 4 (a) and resultant odd-parity solution is understood naturally.
In contrast, the charge channel kernel gives an attractive interaction for both as shown in Fig. 4 (b), beucase . Then, we obtain -wave form factor in Fig. 2 (e), as we explain in Fig. 4 (d) Kawaguchi-CDW ; Onari-B2g .
In the present transverse spin fluctuation mechanism, the -vector will be parallel to -direction when (XY-anisotropy) due to the spin-orbit interaction (SOI). When the XY-anisotropy of is very large, due to AL terms is multiplied by whereas is unchanged, so it is suitable condition for the sLC order.
III.2 Filling dependences of sLC/BO instabilities
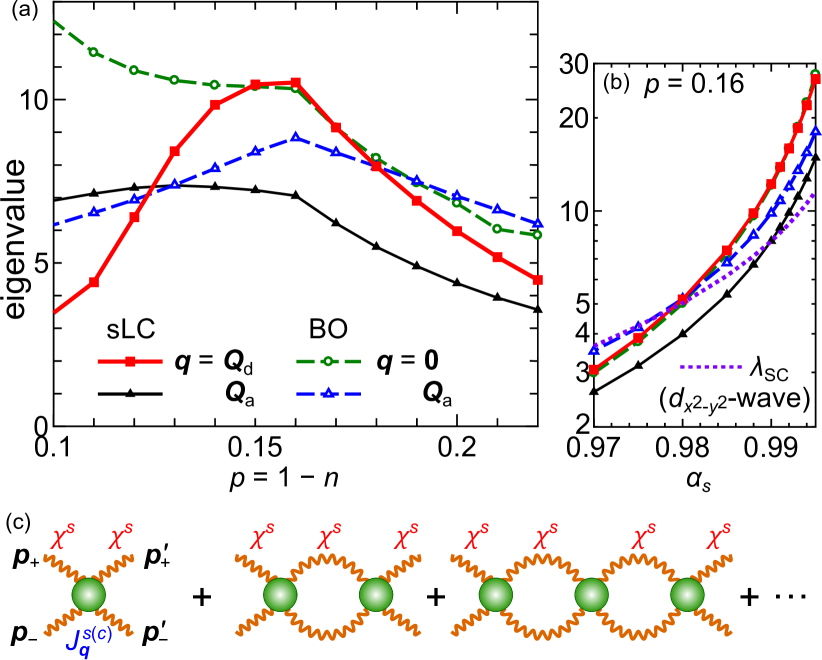
The sLC and BO eigenvalues are summarized in Fig. 5 (a). The relation around the optimal doping () means that the sLC transition temperature is higher than , as in Fig. 1 (a). The robustness of Fig. 5 (a) is verified in Appendix B. We also verify in Fig. 5 (b) that both and are larger than the -wave superconducting eigenvalue for . Here, is derived from the gap equation
| (7) |
where is the MT-type kernel d-wave . Note that if AL terms are dropped Norman . The large eigenvalues in Fig. 5 are suppressed to by small ; see Refs. Kawaguchi-CDW ; Onari-B2g ; Kontani-ROP and Appendix B. We stress that sLC is not suppressed by the ferro-BO that induces neither Fermi arc nor pseudogap, as explained in Appendix B.
Here, we analyzed the sLC/BO in terms of the electron-hole pairing. Another physical interpretation of the sLC/BO is the “condensation of odd/even parity magnon-pairs”, which is the origin of the nematic order in quantum spin systems Andreev ; Coleman ; Shannon . In fact, the two-magnon propagator shown in Fig. 5 (c) diverges when the eigenvalue of DW equation reaches unity, as we explain in Appendix C. That is, triplet (singlet) magnon-pair condensation occurs at . Thus, the sLC/BO discussed here and the spin nematic order in quantum spin systems are essentially the same phenomenon.
III.3 Fermi arc and pseudogap under sLC order
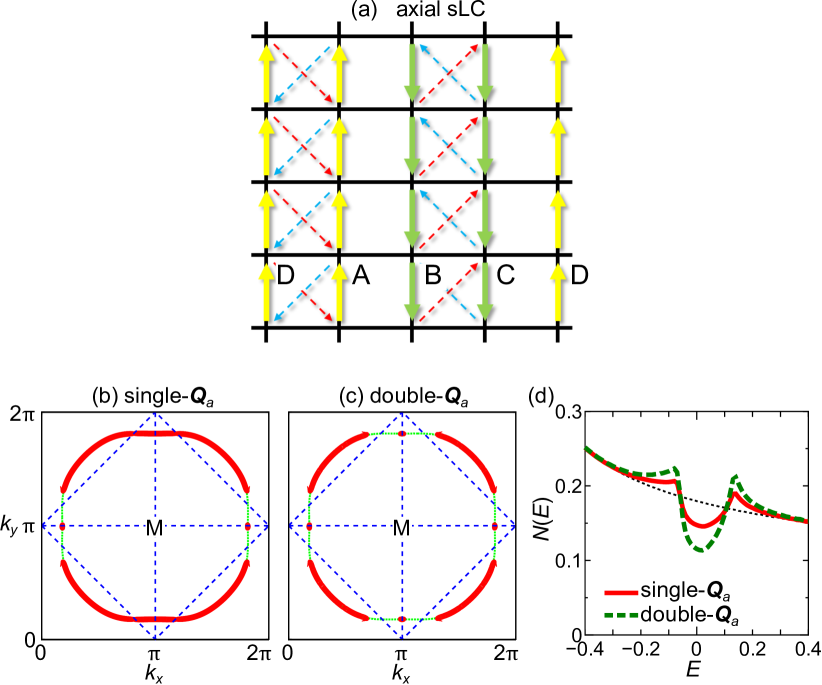
Now, we discuss the band-folding and hybridization gap due to the diagonal sLC order. Figures 6 (a) and (b) show the Fermi arc structures in the cases of (a) single- and (b) double- orders. We set . Here, the folded band structure under the sLC order with finite is “unfolded” into the original Brillouin zone by following Ref. Ku to make a comparison with ARPES results. The Fermi arc due to the single- order in Fig. 6 (a) belongs to symmetry. In contrast, the Fermi arc due to the double- order in Fig. 6 (b) preserves the symmetry. The resultant pseudogap in the DOS is shown in Fig. 6 (c). The unfolded band structure in the single- sLC order is displayed in Fig. 12 in Appendix B.
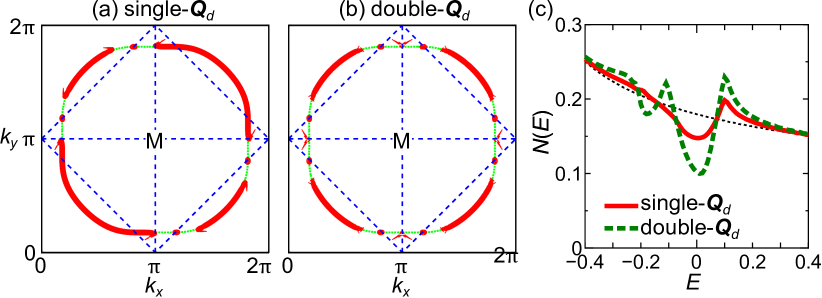
Recent magnetic torque measurements revealed the symmetry breaking at occurs in YBCO Y-Sato , while one appears in Hg-based cuprates Hg-Murayama . To understand different symmetry breakings, we examine the dependence of DW equation solution in Appendix B 2: As shown in Figs. 9 (b)-(e), the sLC wavevector changes from to for larger . When , the symmetry of the Fermi arc is in Fig. 6 (a). On the other hand, the Fermi arc has symmetry in the axial sLC order in Fig. 1 (d), as we show in Fig. 10 (b).
Since the van Vleck susceptibility becomes anisotropic when symmetry of the FS is broken Kawaguchi-B2g , the reported compound-dependent symmetry breaking Y-Sato ; Hg-Murayama would be explained by the sLC order scenario. This is an important future issue.
III.4 Spin-current pattern under sLC order
Next, we investigate the spin current in real space, which is driven by a fictitious Peierls phase due to the “spin-dependent self-energy” . As shown in Fig. 3 (c), is purely imaginary and odd with respect to . The conservation law directly leads to the definition the spin current operator from site to site as , where . Then, the spontaneous spin current from to is .
Here, we calculate the spin current for the commensurate sLC order at , which is achieved by putting . Then, the unit cell are composed four sites A-D. In Fig. 14 in Appendix D, we show the obtained spin current from the center site (-) to different site in Fig. 1 (c). The derived spin current pattern between the nearest and second-nearest sites is depicted in Fig. 1 (c).
The Fermi arc structure and the DOS in Fig. 6 are independent of the phase shift . In contrast, the real space current pattern depends on the phase shift. We discuss other possible sLC patterns in Appendix D. The charge modulation due to the sLC is just for since . Thus, experimental detection of translational symmetry breaking by sLC order may be difficult. However, the cLC is induced by applying uniform magnetic field parallel to . In the present sLC state, under 10 T magnetic field, the induced cLC gives Oe when , which may be measurable by NMR or SR study.
III.5 sLC fluctuation mediated superconductivity
Finally, we discuss that the sLC fluctuations can contribute to the -wave pairing mechanism. The sLC fluctuations connects the close hot spots at and in Fig. 2 (a). At both points, the -wave gap function has the same sign. The pairing interaction mediated by the spin-channel sLC fluctuations between singlet pairs and is
| (8) |
where and . is the sLC susceptibility and is its form factor. Thus, Eq. (8) give positive (=attractive) pairing interaction between close hot spots. The derivation of Eq. (8) is given in Appendix A and in SM F of Ref. Onari-AFB . This mechanism may be important for slightly over-doped cuprates with .
IV Summary
In summary we proposed a novel and long-sought formation mechanism for the nanoscale spin-current order, which violates the parity and translational symmetry while time-reversal symmetry is preserved. It was revealed that the formation of triplet odd-parity electron-hole pairs that is mediated by spin fluctuations, and therefore the spontaneous sLC is established at . In the present spin-fluctuation mechanism, the condensation of odd-parity magnon-pairs occurs simultaneously. The band-folding by the sLC orders results in the formations of the Fermi arc structure and pseudogap at . In the sLC state, a staggered moment is expected to appear under the uniform magnetic field. The sLC order will be a key ingredient in understanding pseudogap phase and electronic nematicity not only in cuprates, but also in iridates Sr2IrO4 ; Sr2IrO4-ARPES and heavy-fermion compound. It is an important future issue to incorporate the self-energy effect into the present theory.
Acknowledgements.
The authors are grateful to Y. Matsuda, K. Yamada, T. Moriya, and A. Kobayashi for the fruitful comments and discussions. This work was supported by the “Quantum Liquid Crystals” No. JP19H05825 KAKENHI on Innovative Areas from JSPS of Japan, and JSPS KAKENHI (JP18H01175, JP20K22328, JP20K03858, JP17K05543).Appendix A Derivation of singlet and triplet DW equations
Here, we discuss the linearized density-wave (DW) equation driven by spin fluctuations. For this purpose, we introduce the irreducible four-point vertex function . It is given by the Ward identity at , that is, . Here, we use the one-loop self-energy given as
| (9) |
where and are longitudinal and transverse susceptibilities. They are given as
| (10) | |||||
| (11) |
where and are longitudinal and transverse irreducible susceptibilities. Then, the irreducible vertex function given by the Ward identity is composed of one MT term and two AL terms in Fig. 7 (a). Note that contains the lowest order Hartree term .
First, we derive the charge-channel (singlet) DW equation in the absence of the magnetic field, where the form factor is independent of spin: . The singlet DW equation was introduced in the study of Fe-based superconductors Onari-B2g and cuprate superconductors Kawaguchi-CDW . It is given as
| (12) |
which is shown in Fig. 7 (b), and . Here, . It is given as
| (13) |
where , , and . The first, the second, the third terms in Eq. (13) corresponds to the MT, AL1 and AL2 terms in Fig. 7 (a).
In cuprates, Eq. (12) gives even-parity solution with wavevector and . This singlet and even-parity electron-hole condensation is interpreted as the BO.
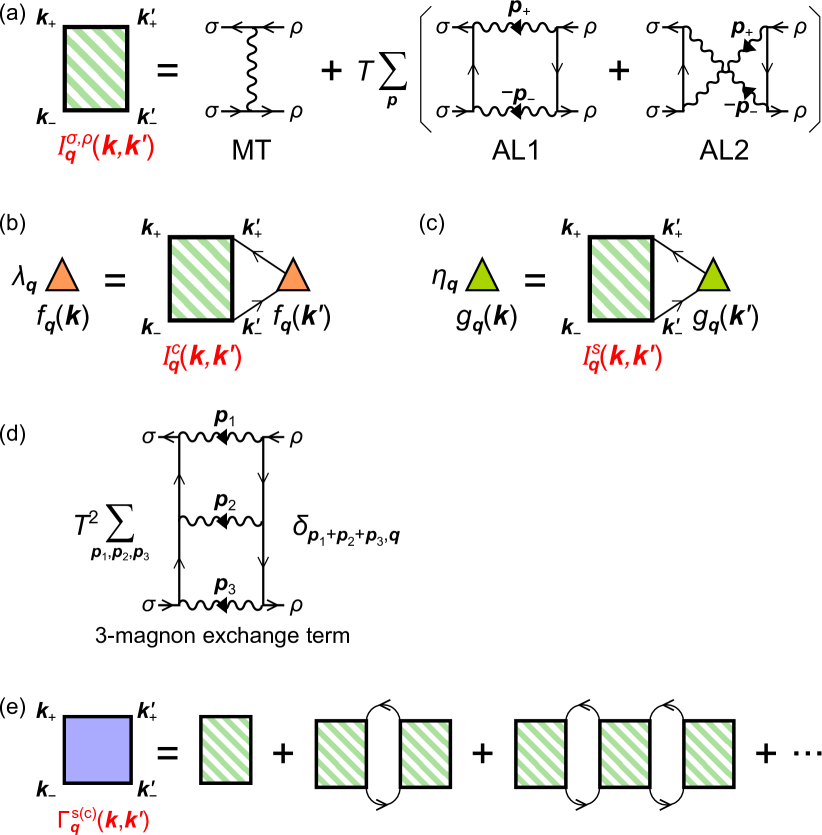
Next, we derive the spin-channel (triplet) DW equation in the absence of the magnetic field, the spin-dependent form factor is . It is given as
| (14) |
which is shown in Fig. 7 (c). Here, . It is given as
| (15) |
where the first, the second, the third terms in Eq. (13) corresponds to the MT, AL1 and AL2 terms in Fig. 7 (a). The AL terms with are shown in Fig. 4 (e). In cuprates, Eq. (14) gives the odd-parity solution at wavevector and . This triplet and odd-parity electron-hole pairing is interpreted as the spin-loop-current (sLC).
In both Eqs. (13) and (15), the AL terms are proportional to . The AL terms are significant when the spin fluctuations are large, since both and take large value simultaneously when in the case of . If we put at zero Matsubara frequency, where is the magnetic correlation length, in two-dimensional systems. Therefore, double-magnon exchange (AL) terms induce not only BO, but also the sLC order when . A three-magnon exchange term shown in Fig. 7 (d) is proportional to . Then, in two-dimensional systems for , which is smaller than at low temperatures . Thus, the AL process would be the most significant, which is also indicated by functional-renormalization-group studies Tsuchiizu-CDW .
The electron-hole pairing order is generally expressed in real space as follows Nersesyan :
| (16) | |||||
where , and () is spin singlet (triplet) pairing. It induces the symmetry breaking in the self-energy:
| (17) |
which we call the form factors in this paper. The BO is given by real even-parity function , and the sLC is given by pure imaginary odd-parity vector . Both orders preserve the time-reversal symmetry. Note that and in Eqs. (12) and (14) correspond to and , respectively.
Finally, we discuss the effective interaction driven by the BO/sLC fluctuations. By solving the DW equation (12), we obtain the full four-point vertex function that is composed of and shown in Fig. 7 (e), which increases in proportion to . Thus, we obtain the relation , which is well satisfied when is close to unity. Here, . In the same way, we obtain the relation . Thus, it is apparent that the sLC order (BO ) emerges when diverges.
The pairing interaction due to the sLC fluctuations is given by the full four-point vertex. It is approximately expressed as . Since is odd-function, the sLC fluctuations cause attractive interaction: .
Appendix B Additional numerical results of DW equations
B.1 Enhancement of the sLC instability under the finite ferro BO
In Figs. 5 (a) and (b) in the main text, the sLC eigenvalue is comparable to the BO eigenvalue for a wide doping range. This result means that the sLC order at and the ferro-BO occur at almost the same temperature . Here, we discuss the possibility of coexistence of sLC order and ferro-BO.
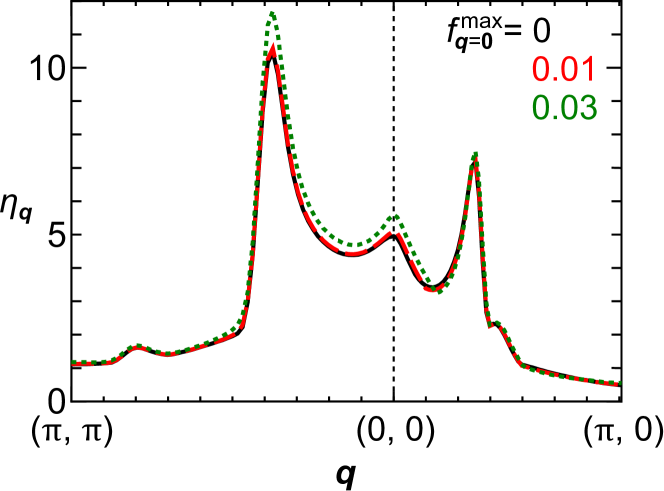
Since the ferro-BO does not induce the band-folding and pseudogap, the sLC order will emerge even if the ferro-BO transiting temperature is higher. To verify this expectation, we calculated the triplet DW equation (14) under the ferro-BO with . Figure 8 shows the eigenvalue of sLC as function of for and () under the ferro-BO form factor obtained by the spin-singlet DW equation (12). It is verified that the ferro-BO does not prohibit the emergence of the sLC order. The eigenvalue slightly increases with , since the spin Stoner factor is enlarged by the ferro-BO Kawaguchi-CDW ; Tsuchiizu-CDW .
B.2 Change in the phase diagram by
In the main text, we show that the sLC eigenvalue at develops as large as the ferro-BO eigenvalue near the optimally-doping case (), based on the Hubbard model with the hopping integrals . The obtained Fermi surface (FS) has the flat part near the Brillouin zone boundary, which captures the characteristic of YBCO compounds.
Here, we examine a key model parameter for the phase diagram, and reveal that the sLC instability is sensitively controlled by . Figure 9 (a) shows the FSs for in the case of and . The shape of the flat part of the FS near the BZ, which is significant for the density wave (DW) instabilities at , is sensitively modified by .
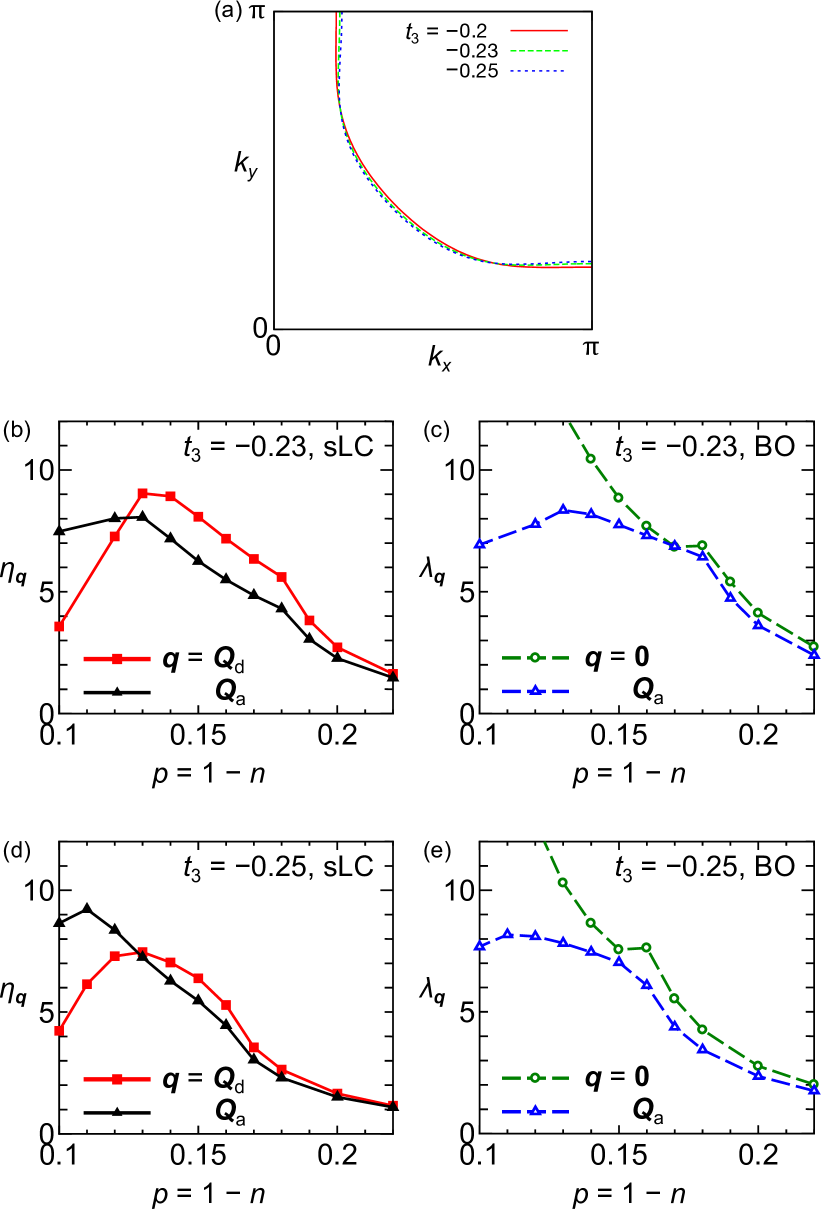
Figures 9 (b)-(e) shows the obtained spin-channel eigenvalue and the charge-channel one in the cases of ((b) and (c)) and ((d) and (e)). (We set the condition by following the main text.) With increasing , the peak of sLC instability is found to shift to the under-doped region. Interestingly, the SLC eigenvalue at becomes larger than that at for . Its spin current pattern in real space is shown in Fig. 10 (a).
We note that recent experiments indicate that the phase diagram of cuprate superconductors is very diverse and rich. For example, the in-plain anisotropy of the ferro-magnetic susceptibility at is in YBCO Y-Sato , whereas in Hg-compound Hg-Murayama . Also, the antiferro-magnetic susceptibility in slightly under-doped YBCO exhibits a clear symmetry breaking at a temperate between and Keimer . The present sensitive dependent sLC may give important hint to understand diverse symmetry breaking in cuprates.
Here, we discuss the band-folding and hybridization gap in the axial sLC phase. Figures 10 (b) and (c) show the Fermi arc structures induced by the axial sLC order in the cases of (a) single- and (b) double- orders. We set . Here, the folded band structure under the sLC order with finite is “unfolded” to make a comparison with ARPES results. The Fermi arc due to the single- order in Fig. 10 (b) belongs to the symmetry. The resultant pseudogap in the DOS is shown in Fig. 10 (d).
B.3 Reduction of eigenvalues by
In the present work, we study the mechanism of exotic DW orders due to the interference between paramagnons based on the linearized DW equation. The obtained form factor represents the characteristics and the symmetry of the DW, and the eigenvalue expresses the strength of the DW instability. In the present numerical study, we drop the self-energy in the DW equation. Then, the obtained eigenvalues shown in Fig. 5 and Fig. 9 are much larger than unity. In addition, the eigenvalue of the superconducting gap equation, , shown in Fig. 5 (b) is also very large.
The self-energy gives the quasiparticle weight as , and is the mass-enhancement. The effect of the self-energy in the DW equation has been studied in Ref Onari-AFB for Fe-based superconductors (), and it was revealed that the eigenvalue of the orbital fluctuations is reduced by the self-energy, and the orbital order temperature is reduced to K, consistently with experiments.
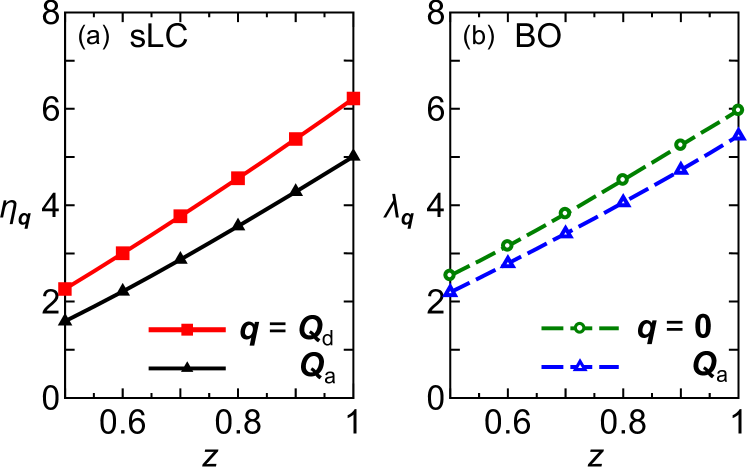
Here, we study the effect of the renormalization factor on the eigenvalues in the present single-orbital Hubbard model. Then, the Green function is given as
| (18) |
First, we discuss the effect of on , by replacing two ’s in Eq. (7) with given by Eq. (18). On the other hand, we do not include in the susceptibilities in in the pairing interaction, in order not to change the Stoner factor . Then, it is well known that is reduced as based on the Eliashberg equation Allen .
Next, we discuss the effect of on () by replacing four ’s in Eqs. (12) and (13) (in Eqs. (14) and (15)) with given by Eq. (18). The obtained -dependences of the eigenvalues at are shown in Fig. 11. It is verified that both and are reduced in proportion to . Although this approximation may be justified only for , the obtained results strongly indicate that both and are reduced to in the case of , which is realized in cuprate superconductors.
B.4 Unfolded band structure under the sLC order
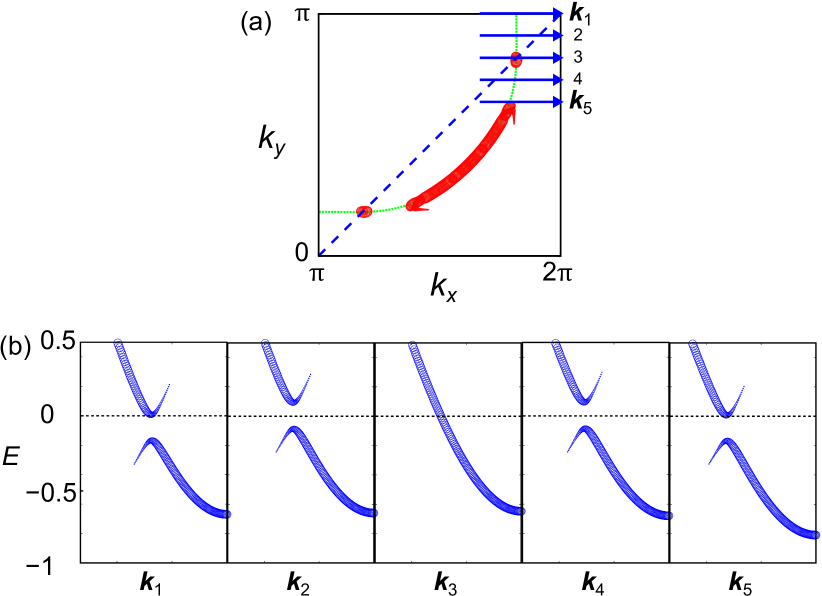
Here, we examine the experimentally observed band structure in the sLC ordered state, by applying the unfolding procedure proposed in Ref. Ku . Figure 12 shows the “unfolded” band structure in the single- sLC order at , which corresponds to Fig. 6 (a) in the main text. The pseudogap closes on the X-Y line owing to the odd-parity form factor. This Dirac point which will be smeared out for because of very large inelastic scattering at the hot spot Kontani-ROP ; Tremblay ; Scalapino ; Moriya . In addition, the Dirac point should be masked by the -wave BO below .
Appendix C BO/sLC order as magnon-pair condensation
We explain that the sLC order is exactly the same as the magnon-pair condensation. The following spin quadrupole order occurs owing to the magnon-pair condensation Andreev :
| (19) |
where , and the relation holds. We will explain that the even-parity function (with ) corresponds the BO state, and the odd-parity function (with ) corresponds the sLC order.
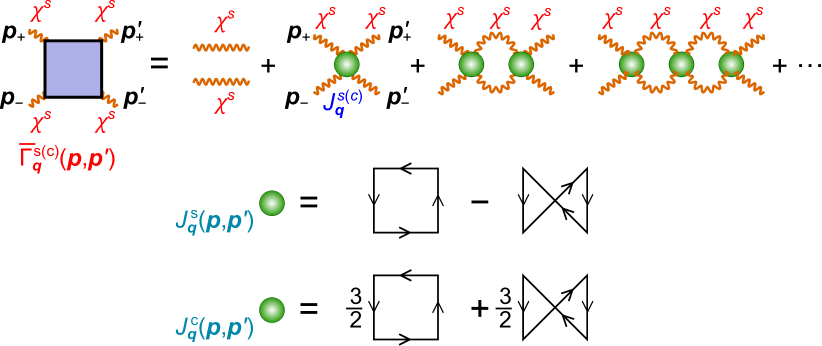
Here, we explain that due to the AL processes represents the scattering between two-magnons. To simplify the discussion, we drop the MT term, and consider only AL terms with two s. Then, we define by the following relation; . Figure 13 shows the diagrammatic expression of , which represents the scattering process of magnon pair amplitude () through the interaction , which is a moderate function of . With decreasing temperatures, diverges when singlet (triplet) magnon pairs with momentum condensate, and the critical temperature corresponds to ().
Here, we introduce and , where , and and are form factors of the DW equations. Then, the DW equations are rewritten as
| (20) | |||||
| (21) |
where the kernel function is given in Fig. 13. These equations means that () corresponds to the singlet (triplet) magnon pair condensation. Therefore, their Fourier transformations correspond to and , respectively.
To summarize, in the present double spin-flip mechanism, magnon-pair condensation occurs at . Therefore, the sLC/BO given by the present mechanism is exactly the same as “condensation of odd/even parity magnon pairs”.
Appendix D Spontaneous spin current in the sLC phase
D.1 Calculation of the spin current
Here, we investigate the spin current in real space due to the “spin-dependent self-energy” shown in Fig. 3 (c), which is purely imaginary and odd with respect to . The spin current operator from site to site is , where . Then, the spin current from to is given as .
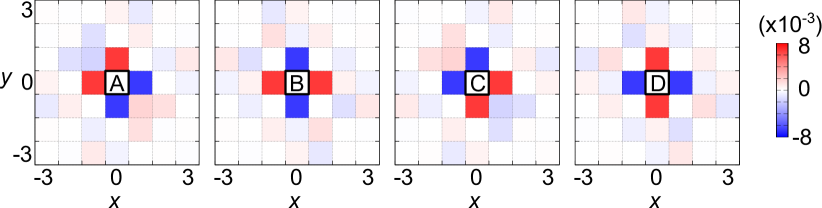
Here, we calculate the spin current for the commensurate sLC order at , which is achieved by putting . Then, the unit cell are composed four sites A-D. Figure 14 shows the obtained spin current from the center site (-) to different site in Fig. 1 (c), by setting . The obtained current is in unit . The derived spin current pattern between the nearest and second-nearest sites is depicted in Fig. 1 (c). The spin current is exactly conserved at each site.
D.2 Possible diagonal sLC patterns in real space
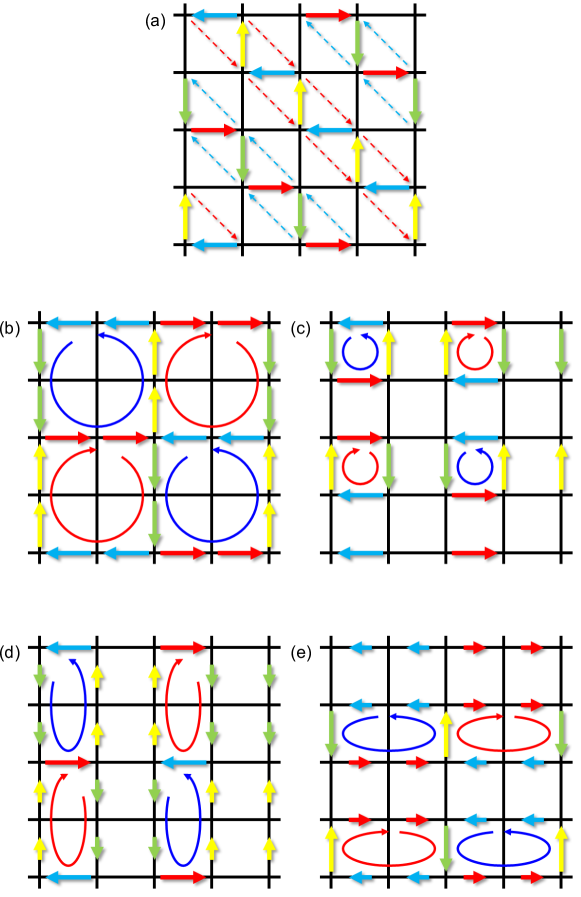
Next, we explain that the spin current pattern derived from the form factor in Fig. 3 (b) is not uniquely determined. In fact, the form factor in real space is given as , where is an arbitrary phase. Here, we discuss other possible spin current patterns by choosing .
First, we discuss the real space pattern for . We assume that Fig. 1 (c) corresponds to . Then, the single- spin current pattern for is given in Fig. 15 (a). The double- spin current order is given by the combination of the sLC order at and that at with arbitrary phase factors. Figure 15 (b)-(c) are given by the combination of Fig. 1 (c) with its -rotation, and Figs. 15 (d)-(e) are given by the combination of Figs. 15 (a) with its -rotation. We stress that the magnitude of spin current in Fig. 15 (b)-(c) has symmetry, whereas that in Fig. 15 (d)-(e) breaks the symmetry.
References
- (1) G. Ghiringhelli, M. L. Tacon, M. Minola, S. Blanco-Canosa, C. Mazzoli, N. B. Brookes, G. M. D. Luca, A. Frano, D. G. Hawthorn, F. He, T. Loew, M. M. Sala, D. C. Peets, M. Salluzzo, E. Schierle, R. Sutarto, G. A. Sawatzky, E. Weschke, B. Keimer, and L. Braicovich, Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x, Science 337, 821 (2012).
- (2) R. Comin, A. Frano, M. M. Yee, Y. Yoshida, H. Eisaki, E. Schierle, E. Weschke, . Sutarto, F. He, A. Soumyanarayanan, Y. He, M. L. Tacon, I. S. Elfimov, J. E. Hffman, G. A. Sawatzky, B. Keimer, and A. Damascelli, Charge order driven by Fermi-arc instability in Bi2Sr2-xLaxCuO+δ, Science 343, 390 (2014).
- (3) Y. Kohsaka, T. Hanaguri, M. Azuma, M. Takano, J. C. Davis, and H. Takagi, Visualization of the emergence of the pseudogap state and the evolution to superconductivity in a lightly hole-doped Mott insulator, Nature Physics 8, 534 (2012).
- (4) K. Fujita, M. H. Hamidian, S. D. Edkins, C. K. Kim, Y. Kohsaka, M. Azuma, M. Takano, H. Takagi, H. Eisaki, S. Uchida, A. Allais, M. J. Lawler, E.-A. Kim, S. Sachdev, and J. C. S. Davis, Direct phase-sensitive identification of a -form factor density wave in underdoped cuprates, Proc. Natl. Acad. Sci. USA, 111, E3026 (2014).
- (5) B. Kyung, S. S. Kancharla, D. Senechal, A.-M. S. Tremblay, M. Civelli, and G. Kotliar, Pseudogap induced by short-range spin correlations in a doped Mott insulator, Phys. Rev. B 73, 165114 (2006).
- (6) T.A. Maier, M.S. Jarrell, and D.J. Scalapino, Understanding high-temperature superconductors with quantum cluster theories, Physica C, 460-462, 13 (2007).
- (7) T. Moriya and K. Ueda, Spin fluctuations and high temperature superconductivity, Adv. Phys. 49, 555 (2000).
- (8) A.Shekhter, B. J. Ramshaw, R. Liang, W. N. Hardy, D. A. Bonn, F. F. Balakirev, R. D. McDonald, J. B. Betts, S. C. Riggs, and A. Migliori, Bounding the pseudogap with a line of phase transitions in YBa2Cu3O6+δ, Nature 498, 75 (2013).
- (9) R.-H. He, M. Hashimoto, H. Karapetyan, J. D. Koralek, J. P. Hinton, J. P. Testaud, V. Nathan, Y. Yoshida, H. Yao, K. Tanaka, W. Meevasana, R. G. Moore, D. H. Lu, S.-K. Mo, M. Ishikado, H. Eisaki, Z. Hussain, T. P. Devereaux, S. A. Kivelson, J. Orenstein, A. Kapitulnik, and Z.-X. Shen, From a Single-Band Metal to a High-Temperature Superconductor via Two Thermal Phase Transitions, Science 331, 1579 (2011).
- (10) Y. Sato, S. Kasahara, H. Murayama, Y. Kasahara, E. -G. Moon, T. Nishizaki, T. Loew, J. Porras, B. Keimer, T. Shibauchi, and Y. Matsuda, Thermodynamic evidence for a nematic phase transition at the onset of the pseudogap in YBa2Cu3Oy, Nature Physics 13, 1074 (2017).
- (11) H. Murayama, Y. Sato, R. Kurihara, S. Kasahara, Y. Mizukami, Y. Kasahara, H. Uchiyama, A. Yamamoto, E. -G. Moon, J. Cai, J. Freyermuth, M. Greven, T. Shibauchi, and Y. Matsuda, Diagonal nematicity in the pseudogap phase of HgBa2CuO4+δ, Nat. Commun. 10, 3282 (2019).
- (12) S. Nakata, M. Horio, K. Koshiishi, K. Hagiwara, C. Lin, M. Suzuki, S. Ideta, K. Tanaka, D. Song, Y. Yoshida, H. Eisaki, and A. Fujimori, Nematicity in the pseudogap state of cuprate superconductors revealed by angle-resolved photoemission spectroscopy, arXiv:1811.10028.
- (13) K. Ishida, S. Hosoi, Y. Teramoto, T. Usui, Y. Mizukami, K. Itaka, Y. Matsuda, T. Watanabe, and T. Shibauchi, Divergent nematic susceptibility near the pseudogap critical point in a cuprate superconductor, J. Phys. Soc. Jpn. 89, 064707 (2020).
- (14) S. Bulut, W.A. Atkinson and A.P. Kampf, Spatially modulated electronic nematicity in the three-band model of cuprate superconductors Phys. Rev. B 88, 155132 (2013).
- (15) Y. Wang and A.V. Chubukov, Charge-density-wave order with momentum and within the spin-fermion model: Continuous and discrete symmetry breaking, preemptive composite order, and relation to pseudogap in hole-doped cuprates, Phys. Rev. B 90, 035149 (2014).
- (16) R.-Q. Xing, L. Classen, and A. V. Chubukov, Orbital order in FeSe: The case for vertex renormalization, Phys. Rev. B 98, 041108(R) (2018).
- (17) M.A. Metlitski and S. Sachdev, Instabilities near the onset of spin density wave order in metals, New J. Phys. 12, 105007 (2010); S. Sachdev and R. La Placa, Bond Order in Two-Dimensional Metals with Antiferromagnetic Exchange Interactions, Phys. Rev. Lett. 111, 027202 (2013).
- (18) W. Metzner, M. Salmhofer, C. Honerkamp, V. Meden, and K. Schönhammer, Functional renormalization group approach to correlated fermion systems, Rev. Mod. Phys. 84, 299 (2012); C. Husemann and W. Metzner, Incommensurate nematic fluctuations in the two-dimensional Hubbard model, Phys. Rev. B 86, 085113 (2012); T. Holder and W. Metzner, Incommensurate nematic fluctuations in two-dimensional metals, Phys. Rev. B 85, 165130 (2012); C. Honerkamp, Charge instabilities at the metamagnetic transition of itinerant electron systems, Phys. Rev. B 72, 115103 (2005).
- (19) J. C. S. Davis and D.-H. Lee, Concepts relating magnetic interactions, intertwined electronic orders, and strongly correlated superconductivity, Proc. Natl. Acad. Sci. USA, 110, 17623 (2013).
- (20) E. Berg, E. Fradkin, S. A. Kivelson, and J. M. Tranquada, Striped superconductors: how spin, charge and superconducting orders intertwine in the cuprates, New J. Phys. 11, 115004 (2009).
- (21) Y. Yamakawa, and H. Kontani, Spin-Fluctuation-Driven Nematic Charge-Density Wave in Cuprate Superconductors: Impact of Aslamazov-Larkin Vertex Corrections, Phys. Rev. Lett. 114, 257001 (2015).
- (22) M. Tsuchiizu, K. Kawaguchi, Y. Yamakawa, and H. Kontani, Multistage electronic nematic transitions in cuprate superconductors: A functional-renormalization-group analysis, Phys. Rev. B 97, 165131 (2018).
- (23) K. Kawaguchi, Y. Yamakawa, M. Tsuchiizu, and H. Kontani, Competing Unconventional Charge-Density-Wave States in Cuprate Superconductors: Spin-Fluctuation-Driven Mechanism, J. Phys. Soc. Jpn. 86, 063707 (2017).
- (24) P. A. Lee, Amperean Pairing and the Pseudogap Phase of Cuprate Superconductors, Phys. Rev. X 4, 031017 (2014).
- (25) D. F. Agterberg, J. C. S. Davis, S. D. Edkins, E. Fradkin, D. J. Van Harlingen, S. A. Kivelson, P. A. Lee, L. Radzihovsky, J. M. Tranquada, and Y. Wang, The Physics of Pair Density Waves, Annu. Rev. Condens. Matter Phys. 11, 231 (2020).
- (26) C. M. Varma, Non-Fermi-liquid states and pairing instability of a general model of copper oxide metals, Phys. Rev. B 55, 14554 (1997).
- (27) I. Affleck and J. B. Marston, Large- limit of the Heisenberg-Hubbard model: Implications for high- superconductors, Phys. Rev. B 37, 3774(R) (1988).
- (28) F. C. Zhang, Superconducting instability of staggered-flux phase in the t-J model, Phys. Rev. Lett. 64, 974 (1990).
- (29) H. J. Schulz, Fermi-surface instabilities of a generalized two-dimensional Hubbard model, Phys. Rev. B 39, 2940(R) (1989).
- (30) A. A. Nersesyan, G. I. Japaridze, and I. G. Kimeridze, Low-temperature magnetic properties of a two-dimensional spin nematic state, J. Phys.: Condens. Matter 3, 3353 (1991).
- (31) M. Ozaki, Broken Symmetry Solutions of the Extended Hubbard Model, Int. J. Quantum. Chem. 42, 55 (1992).
- (32) S. Zhou, K. Jiang, H. Chen, and Z. Wang, Correlation Effects and Hidden Spin-Orbit Entangled Electronic Order in Parent and Electron-Doped Iridates Sr2IrO4, Phys. Rev. X 7, 041018 (2017).
- (33) H. Ikeda and Y. Ohashi, Theory of Unconventional Spin Density Wave: A Possible Mechanism of the Micromagnetism in U-based Heavy Fermion Compounds, Phys. Rev. Lett. 81, 3723 (1998).
- (34) S. Fujimoto, Spin Nematic State as a Candidate of the Hidden Order Phase of URu2Si2, Phys. Rev. Lett. 106, 196407 (2011).
- (35) S. Onari and H. Kontani, Self-consistent Vertex Correction Analysis for Iron-based Superconductors: Mechanism of Coulomb Interaction-Driven Orbital Fluctuations, Phys. Rev. Lett. 109, 137001 (2012).
- (36) S. Onari, Y. Yamakawa, and H. Kontani, Sign-Reversing Orbital Polarization in the Nematic Phase of FeSe due to the Symmetry Breaking in the Self-Energy, Phys. Rev. Lett. 116, 227001 (2016).
- (37) Y. Yamakawa, S. Onari, and H. Kontani, Nematicity and Magnetism in FeSe and Other Families of Fe-Based Superconductors, Phys. Rev. X 6, 021032 (2016).
- (38) T. Yoshida, M. Hashimoto, I. M. Vishik, Z. X. Shen, and A. Fujimori, Pseudogap, Superconducting Gap, and Fermi Arc in High- Cuprates Revealed by Angle-Resolved Photoemission Spectroscopy, J. Phys. Soc. Jpn. 81, 011006 (2011).
- (39) Y. K. Kim, O. Krupin, J. D. Denlinger, A. Bostwick, E. Rotenberg, Q. Zhao, J. F. Mitchell, J. W. Allen, an B. J. Kim, Fermi arcs in a doped pseudospin-1/2 Heisenberg antiferromagnet, Science 345, 187 (2014).
- (40) H. Kontani, Anomalous Transport Phenomena in Fermi Liquids with Strong Magnetic Fluctuations, Rep. Prog. Phys. 71, 026501 (2008);
- (41) H. Kontani, Transport Phenomena in Strongly Correlated Fermi Liquids (Springer-Verlag Berlin and Heidelberg GmbH & Co. K, 2013).
- (42) C. Stock, W. J. L. Buyers, R. Liang, D. Peets, Z. Tun, D. Bonn, W. N. Hardy, and R. J. Birgeneau, Dynamic stripes and resonance in the superconducting and normal phases of YBa2Cu3O6.5 ortho-II superconductor, Phys. Rev. B 69, 014502 (2004).
- (43) Hexadecapole Fluctuation Mechanism for s-wave Heavy Fermion Superconductor CeCu2Si2: Interplay between Intra- and Inter-Orbital Cooper Pairs J. Phys. Soc. Jpn. 88, 063701 (2019); R. Tazai, Y. Yamakawa, and H. Kontani, Plain s-wave superconductivity near the magnetic criticality: Enhancement of attractive electron-boson coupling vertex corrections, J. Phys. Soc. Jpn. 86, 073703 (2017).
- (44) R. Tazai and H. Kontani, Multipole fluctuation theory for heavy fermion systems: Application to multipole orders in CeB6, Phys. Rev. B 100, 241103(R) (2019).
- (45) M. Tsuchiizu, Y. Ohno, S. Onari, and H. Kontani, Orbital Nematic Instability in the Two-Orbital Hubbard Model: Renormalization-Group + Constrained RPA Analysis, Phys. Rev. Lett. 111, 057003 (2013).
- (46) R. Tazai, Y. Yamakawa, M. Tsuchiizu, and H. Kontani, Functional renormalization group study of orbital fluctuation mediated superconductivity: Impact of the electron-boson coupling vertex corrections, Phys. Rev. B 94, 115155 (2016).
- (47) R. Tazai, Y. Yamakawa, M. Tsuchiizu, and H. Kontani, Prediction of -wave bond-order and pseudogap in organic superconductor -(BEDT-TTF)2X: Similarities to cuprate superconductors, arXiv:2010.15516.
- (48) R. Tazai, Y. Yamakawa, and H. Kontani, Emergence of Charge Loop Current in Geometrically Frustrated Hubbard Model: Functional Renormalization Group Study, arXiv:2010.16109.
- (49) S. Onari and H. Kontani, Origin of diverse nematic orders in Fe-based superconductors: 45 degree rotated nematicity in AFe2As2 (A=Sc,Rb), Phys. Rev. B 100, 020507(R) (2019).
- (50) S. Onari and H. Kontani, Hidden antiferro-nematic order in Fe-based superconductor BaFe2As2 and NaFeAs above , Phys. Rev. Research 2, 042005 (2020).
- (51) D. J. Scalapino, E. Loh, and J. E. Hirsch, d-wave pairing near a spin-density-wave instability, Phys. Rev. B 34, 8190 (1986).
- (52) V. Mishra and M. R. Norman, Strong coupling critique of spin fluctuation driven charge order in underdoped cuprates, Phys. Rev. B 92, 060507(R) (2015).
- (53) A. F. Andreev and I. A. Grishchuk, Spin nematics, Zh. Eksp. Teor. Fiz. 87, 467 (1984).
- (54) P. Chandra and P. Coleman, Quantum spin nematics: Moment-free magnetism, Phys. Rev. Lett. 66, 100 (1991).
- (55) N. Shannon, T. Momoi, and P. Sindzingre, Nematic Order in Square Lattice Frustrated Ferromagnets, Phys. Rev. Lett. 96, 027213 (2006).
- (56) W. Ku, T. Berlijn, and C.-C. Lee, Unfolding First-Principles Band Structures, Phys. Rev. Lett. 104, 216401 (2010).
- (57) K. Kawaguchi and H. Kontani, Spin-fluctuation-driven and Bond Order and Induced In-plane Anisotropy in Magnetic Susceptibility in Cuprate Superconductors: Impact of Hot-/Cold-spot Structure on Bond-order Symmetry, J. Phys. Soc. Jpn. 89, 124704 (2020).
- (58) V. Hinkov, D. Haug, B. Fauque, P. Bourges, Y. Sidis, A. Ivanov, C. Bernhard, C. T. Lin, and B. Keimer, Electronic Liquid Crystal State in the High-Temperature Superconductor YBa2Cu3O6.45, Science 319, 597 (2008).
- (59) P. B. Allen and B. Mitrovic, Theory of Superconducting , Solid State Physics, 37, 1 (1983)