Observing individual thermal motions of ions, and molecules in water with light

All matter gives rise to thermal motions at the molecular level, which can be observed, for instance, indirectly through Brownian motion. Diffusion manifests thermal motions macroscopically, and is important not only to physics, but also to chemistry, biology, technology, as well as culinary scienceCussler . Being able to “see” the motion of individual particles directly, is not only fascinating, but should contribute to a better understanding of the microscopic structure that underlies macroscopic diffusion. Previously, nucleation processesnucleation1 ; nucleation2 , and motions of gold atoms in ion liquidMiyata2017 were observed at the atomic level, using electron tomography.

In the present work, we shine light through liquids, and observe the thermal motions of individual ethanol molecules, and NaCl ions in water, through the intensity variations in the transmitted light they cause, for the first time. This method is referred to as transmission fluctuation spectroscopy (TFS), below. The thermal motions are characterized through the averaged spectra of light intensity variations, and using the theory of random motions of particles, we relate the properties of these spectra to the macroscopic diffusive behavior of NaCl, ethanol, and water. TFS was previously applied to rubidium gas, where averaged random motions of individual atoms were observed through their shadows, using resonant extinctionrbWalk . Our intent here is to study “everyday” substances, at room temperature, and pressure. Such properties of of NaCl solutions, and ethanol-water mixtures are of interest to a broad range of fields, and belong to a classic, yet active area of research.water1 ; saltWater1 ; saltWater2 ; alcWater1 ; alcWater3 .

TFS is complementary to dynamic light scattering (DLS), which has been, and is a powerful method to study properties of matterDLS . In DLS, one usually studies light scattered by matter, away from the forward direction. In TFS, one studies light intensity variations in the forward direction, caused by light extinction in its path. In TFS, since the vast majority of the light is neither scattered nor absorbed, shot-noise, often referred to as the standard quantum limit (SQL), can dominate the intensity variations, if left as is. This noise needs to be substantially reduced to measure minuscule variations caused by light extinction due to ions, and molecules in water, especially since the extinction is non-resonant for the materials we study.

The principle underlying the experiment is illustrated in Fig. 1(a): Light extinction due to a particle in the light beam changes the beam intensity that depends on the location of the particle. In the experimental setup (Fig. 1(b)), laser beam is shone on the fluid in a cell (depth 1 mm), and the light in the forward direction is detected by a dual element photo diode (DEPD, S4204, Hamamatsu Photonics). The motion of a particle causes intensity variations which show up as time dependent photocurrent differences in the two elements of the photodiode. The spectrum is obtained by averaging, and Fourier transforming these variations in the photocurrent. We use two light sources with different wavelengths, and then take the correlation of the intensity variation measurements from the two DEPDs, corresponding to the two wavelengths, to statistically reduce all uncorrelated noise in the two DEPD measurementsMA1 . This principle is effective in reducing any uncorrelated noise in the two DEPD measurements, including the shot-noiseMA1 ; rbWalk ; Pottier17 . The magnitude of the spectrum is normalized by the shot-noise level determined from the measured photocurrents.

The thermal motions of one particle in a fluid can be modeled by a random walk process. Using a theory similar to that for the transmission intensity variations caused by one particle derived in rbWalk , the spectrum corresponding to our current experiment is

$$S(f)={\left\langle|\Delta\tilde{\cal P}|^{2}\right\rangle\over{\cal P}^{2}}=AF(\pi w^{2}f/D)\ .$$

(1)

Here, ${\cal P}$, $\Delta{\cal P}$ are the (average) power of the light beam at the two elements of DEPD, their difference, and tilde denotes the Fourier transform. $D$ is the diffusion constant, $w$ the beam radius, and $f$ the frequency. $F(x)=2-2{\rm\,Im}\left[xe^{ix}{\rm Ei}(-ix)\right]$, where ${\rm Ei}(x)$ is the exponential integral functionGradshteyn . It is important to note that the shape of the spectrum is uniquely determined by the two parameters, $D$, and $w$.

In Fig. 2, the measured TFS spectra for polystyrene beads in water, with radii 25 nm (Polysciences, Inc.) , and 11 nm (Thermo Fisher Scientific) are shown. The difference in the index of refraction for polystyrene, and water causes light extinction, leading to the observed intensity fluctuations due to Brownian motion. The Einstein relation $D=k_{\scriptscriptstyle\rm B}T/(6\pi\eta a)$, ($\eta$: water viscosityCRC , $a$: particle radius) lets us compute the diffusion constant, which was used in the theoretical spectra, Eq. (1) in Fig. 2. Here, effective $w$ was deduced from the experimental spectra. The spectral shapes match well between the theory, and the experiment, over six orders of magnitude. From SQL indicated in Fig. 2, it can be seen that such dynamic range is achieved only by using the reduction of shot-noise. $w$ estimated from the two spectra are consistent with each other, and also with the design of the experiment. The magnitudes of the spectra were obtained from the experimental spectra. These spectral measurements of particles of known size provide us with a method to measure $w$, whose precise value can vary slightly under the experimental conditions, and is also difficult to measure directly. In the subsequent measurements of other samples, $w$ is determined from TFS spectra of $a=25\,$nm polystyrene beads, prior to, and after the sample measurement, where $w$ varied from $0.99$ to $1.07\,\mu$m. There is a mismatch between the theoretical, and the experimental spectra below the magnitude $10^{-16}$ /Hz, due to temperature fluctuations of water, as explained below.

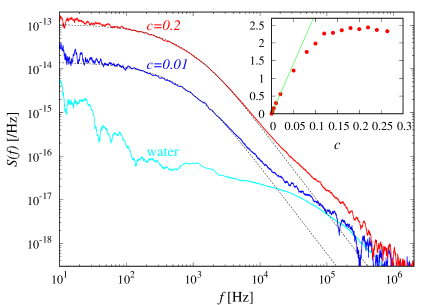
In Fig. 3, the experimentally measured TFS spectra are shown for aqueous solutions of NaCl, with mass fractions, $c=0.2,0.01$, and for water. The theoretical spectrum, Eq. (1), is seen to describe the measured spectra well for $f\lesssim 10^{4}$ Hz. For $f\gtrsim 10^{4}$ Hz, the temperature fluctuations of water also contributes. Since $w$ is known from the polystyrene bead spectra, we can deduce the only remaining parameter determining the spectral shape, the diffusion constant, $D$, corresponding to each spectrum. Binary diffusion spectra are pronounced at around $f=300$ Hz, and the spectral magnitudes there increases linearly with the concentration, reflecting linearity with respect to the number of particles, and saturates at higher concentrations (Fig. 3 Inset).

TFS spectra for ethanol are shown in Fig. 4 at $c=0.9,0.4,0.02$, along with that for water. The theoretical spectrum agree well with the measured spectra, for $f\lesssim 10^{3}$ Hz, from which $D$ can be computed. For $f\gtrsim 10^{4}\,$Hz, the spectrum due to temperature fluctuations in water becomes dominant, and its theoretical spectrum, discussed below, is seen to describe the experimental spectrum well. The spectral magnitude at $f=300$ Hz (Fig. 3 Inset) exhibits intriguing behavior; for $c\lesssim 0.2$, the behavior is linear with respect to $c$, similarly to NaCl solution above. In the high concentration limit, there is no binary diffusion, and the corresponding spectrum should decrease, which explains this overall behavior. There is interesting non-monotonous behavior at $c\simeq 0.95$, which warrants further investigation.

The measured diffusion constants from TFS spectra for NaCl solutions, and ethanol–water mixtures at various concentrations are shown in Fig. 5, along with their corresponding values in the previous literaturenaclD1 ; naclD2 ; ethanolD1 ; ethanolD3 , which are consistent with each other. While it seems reasonable to expect that the random thermal motions of molecules are directly responsible for the diffusive behavior in liquid mixtures, and solutions, we find it beautiful to see that this physics picture works so well.

In matter, there inevitably exist temperature and density fluctuations, microscopically, that are responsible for Rayleigh scattering, for instanceLandauEM . These fluctuations should give rise to local, and time varying thermal gradients, resulting in microscopic thermal diffusive processes, in addition to binary diffusion process discussed above. Unlike binary diffusion, thermal diffusion does not necessarily require mass diffusion, especially in liquids, at least at the macroscopic level, since momentum transfer can occur without actual movement at macroscopic scales. The microscopic behavior underlying thermal diffusion in liquids is not well understood, especially in mixturesCussler ; tDiffusion , but the origin of these momentum transfer processes should lie in the thermal motions of molecules. Density fluctuations give rise to local, and time dependent inhomogeneities in the susceptibility, causing light extinction, even in pure liquids. A priori, it is unclear whether these local thermal motions are directly observable, and even if so, whether they reflect the properties of the thermal diffusion process in a simple manner. In studying TFS spectra of ethanol, and water, the spectra due to to the random thermal motion of molecules, Eq. (1), are observed (Fig. 6). The diffusion constants extracted from the TFS spectra agree with their corresponding values predicted from theory, $\kappa/(\rho C_{\rm V})$ within few percent. Here, $\kappa$, is the thermal conductivity, $\rho$ the density, and $C_{\rm V}$ is the specific heatCRC . Furthermore, the diffusion constants were measured at various ethanol concentrations in water, and compared to previously measured values (albeit few degrees different)ethanolTD1 , in Fig. 6 (Inset), and agree within 10%. Most of the measured spectra, or all for the case of water, lie well below the shot-noise level, so that its reduction was crucial for these measurements.

The magnitudes of TFS spectra reflect the cross sections of the particles observed, and allow us to estimate the sizes of the particles. Here, we assume a simple power behavior with respect to the particle radius, $a$, for the spectral magnitude per particle, $A/n=Ca^{p}$ (Eq. (1)), where $n$ is the particle number density. Using the size information of polystyrene beads, this leads to $p=7.5$, and $a=0.30\,$nm, and $0.25$ nm for NaCl (Fig. 3), and ethanol (Fig. 4), respectively. While these estimates are crude, they have the merit of relying on a simple relation, with no further assumptions. The unit of motion in diffusion, which has some hydration, is a topic of active research, and the measured sizes are consistent with previous theories saltWater2 ; alcWater3 ; molSize . Studying this property in more detail through this new window is of interest. We note that the binary diffusion constant also leads to an estimate of the size of the particle with the same order through the Einstein relation, but the above estimate is optical, and is independent from it, experimentally. The power, $p$, is consistent with extinction mainly due to absorption, which should dominate for smaller particlesHulst : The cross sections due to absorption behave as $a^{3}$, and $A/n$ should be proportional to its square. There is $1/D$ factor multiplying this from the structure of the spectrum Eq. (1)rbWalk , leading $p=7$. The value of $p$ found above is slightly larger, which is consistent with some scattering contribution for larger beads, since the relevant small particle expansion parameter is $ka=0.30$ for them ($k$: wave number), and cross sections behave as $a^{6}$ for Rayleigh scatteringHulst , leading to $p=13$.

In this work, we observed averaged thermal motions of ions, and molecules that underlie binary diffusion, and thermal diffusion, as well as thermal motions polystyrene particles, at the individual particle level. This was made possible by TFS, which we propose as a method for the detection of particle motions in fluids at the atomic scale. We believe that being able to observe molecular motions at the atomic scale complement previously available methods, and provides us with an important window into the dynamical microscopic structure of liquids. The binary diffusion constants, and thermal diffusivity deduced from the TFS spectra agreed with those previously measured through macroscopic methods. We obtained estimates of the sizes of ions, and molecules in water, from the spectral magnitudes, that are consistent with those obtained from other methods. We find the emergent picture of the diffusive processes, from microscopic, to macroscopic quite satisfying, and intriguing.