Observation of the near-threshold intruder resonance in 12Be
Abstract
A resonant state at MeV, located just above the one-neutron separation threshold, was observed for the first time in 12Be from the 11Be Be one-neutron transfer reaction in inverse kinematics. This state is assigned a spin-parity of , according to the distorted-wave Born approximation (DWBA) and decay-width analysis. Gamow coupled-channel (GCC) and Gamow shell-model (GSM) calculations show the importance of the continuum-coupling, which dramatically influences the excitation energy and ordering of low-lying states. Various exotic structures associated with cross-shell intruding configurations in 12Be and in its isotonic nucleus 11Li are comparably discussed.
In weakly-bound nuclear systems approaching the drip-line, several exotic structures can emerge, including cross-shell intruder states and halo structures Johnson et al. (2020). Well known examples include the ground states (g.s.) of the one-neutron halo nucleus 11Be Talmi and Unna (1960); Schmitt et al. (2012); Aumann et al. (2000) and the two-neutron halo nucleus 11Li Tanihata et al. (2008); Simon et al. (1999), which are characterized by the intrusion of the orbital around the traditional neutron magic number . This kind of orbital reordering should naturally lead to exotic structures not only in the g.s., but also in the low-lying exited states of the weak-binding nuclei. One outstanding example is 12Be, in which the low-lying excited states appear at 2.109 (), 2.251 (), and 2.715 () MeV Iwasaki et al. (2000); Shimoura et al. (2003); Imai et al. (2009); Alburger et al. (1978); Fortune et al. (1994). These energies are dramatically reduced compared with their counterparts in the isotone 14C Ajzenberg-selove (1991), for which the lowest low-lying states are located at 6–7 MeV, indicating strong intrusion of the -orbitals and the disappearance of the magic number.
In principle, for weakly-bound nuclei, low-lying intruder states may approach the particle-separation threshold or even appear as resonances above it. As a result, these single-particle states should strongly couple to the continuum, where open quantum phenomena will emerge Persson et al. (2000); Okołowicz et al. (2020); Mazumdar et al. (2006). Although the reordering of some close-threshold orbits can be reproduced phenomenologically by the simple potential model (Woods-Saxon form) Ozawa et al. (2000); Hoffman et al. (2016, 2014), the systematic description and understanding of the open quantum system require explicit treatment of the effective interactions and coupling to the continuum Dobaczewski et al. (2007). Over the years, particular attention has been paid to narrow resonances at the vicinity of the particle-separation threshold Okołowicz et al. (2020); Ikeda et al. (1968); Yang et al. (2014); Liu et al. (2020); Jiang et al. (2020), associated with phenomena such as resonance trapping Persson et al. (2000), aligned eigenstates Okołowicz et al. (2020) and Efimov states Mazumdar et al. (2006).
Traditional nuclear structure models Yuan et al. (2012); Warburton and Brown (1992); Blanchon et al. (2010); Kanada-En’yo and Horiuchi (2003); Garrido et al. (2012); Romero-Redondo et al. (2008) have inherent difficulties to self-consistently account for the continuum coupling effects Wang et al. (2019) and to correctly reproduce the low-lying states in weakly-bound nuclear systems. In recent years, new theoretical approaches have been developed to incorporate the continuum-coupling effect, which greatly improves the description of the weakly-bound nuclei Michel et al. (2009, 2002); Webb et al. (2019); Wang et al. (2019). For instance, the Gamow coupled-channel (GCC) approach may handle continuum-coupling and deformed core in a self-consistent way Webb et al. (2019); Wang et al. (2019). The negative-parity states in weakly-bound nuclei around , which have cross-shell one-particle one-hole (1p-1h) configuration, should provide a sensitive testing ground to these theoretical calculations.
With one neutron in the intruder -orbital and the other in the normal -orbital, the and states in 12Be are expected to have extended spatial distributions and should strongly couple to the continuum Johnson et al. (2020). The state was observed at 2.715 MeV Iwasaki et al. (2000), whereas the state has been predicted by various theoretical approaches with an extremely large uncertainty, namely from 2.5 – 9.0 MeV Yuan et al. (2012); Warburton and Brown (1992); Garrido et al. (2012); Romero-Redondo et al. (2008); Blanchon et al. (2010); Kanada-En’yo and Horiuchi (2003); Fortune (2014). However, in spite of a large number of experimental studies, no bound state below the one-neutron separation energy ( MeV) has been found Iwasaki et al. (2000); Shimoura et al. (2003); Imai et al. (2009); Alburger et al. (1978); Fortune et al. (1994); Johansen et al. (2013); Kanungo et al. (2010). As outlined in Fortune (2014), one neutron adding reaction on the nucleus 11Be, such as 11Be, is a favorable way to populate the 1p-1h unnatural-parity state in 12Be Fortune (2014); Garrido et al. (2012). However, the previous 11Be () experiments at energies of 2.8 Johansen et al. (2013) and 5 MeV/u Kanungo et al. (2010), focused on the bound states in 12Be and were insensitive to the coincident detection of Be residues related to a 12Be resonance decay.
In this letter, we report on the first observation of the unbound state in 12Be from a 11Be () reaction at 26.9 MeV/u using a specially designed telescope centered 0∘. The experiment was carried out in inverse kinematics at the exotic nuclei (EN) beam line, Research Center for Nuclear Physics (RCNP), Osaka University Shimoda et al. (1992); Ong (2014). The secondary beam 11Be with an intensity of particle per second (pps) and a purity of was tracked onto a 4.00-mg/cm2 (CD thick reaction target by using two upstream parallel-plate avalanche counters (PPACs). A set of annular double-sided silicon detectors (ADSSD) was used to detect the protons from the reaction, covering the backward angular range of in the laboratory system. Froward-moving Be isotopes (see inset of Fig. 1) were measured and identified by a downstream zero-degree telescope comprised of several layers of silicon detectors. The coincidence between the protons with the projectile-like Be ions emitting within is essential to select the reaction channel and to reduce the background. The protons were identified by their time of flight from the target to the annular silicon detector Chen et al. (2018a); Liu et al. (2020). More details of the experimental setup can be found in Chen et al. (2018a).
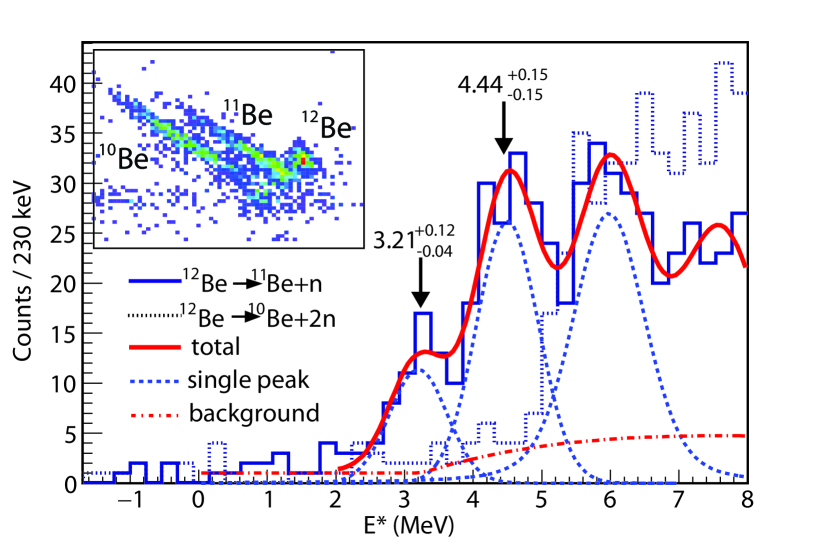
The events identified as 12Be in the inset of Fig. 1 were used to select the 11Be reactions populating the bound states of 12Be as previously reported in Chen et al. (2018a). The 11Be and 10Be isotopes have much broader energy distributions, coming mostly from the reactions leading to one-neutron and two-neutron decays of the 12Be neutron-unbound states. Fig. 1 shows the excitation energy spectrum of 12Be, deduced from the energies and angles of the protons using the missing mass method and gated on the forward-moving 11Be or 10Be ions. The detection and calibration methods were validated from the study of the bound states as detailed in Chen et al. (2018a).
| (MeV)) | (MeV) | ||
|---|---|---|---|
| 1 | 0-0.37 | ||
| 1 | () | 0-0.43 |
The Breit-Wingner(BW) function Lane and Thomas (1958); Cao et al. (2012) with energy dependent width is convoluted by the energy response function of the detection system to fit the excitation energy spectrum from the 11Be Be Be reaction. The energy response function at each excitation energy possesses approximately a Gaussian shape with its width deduced from the simulation Chen et al. (2018a). A resolution of 1.0 – 1.2 MeV (FWHM), and a constant acceptance of were obtained for the states in the excitation energy range of 2.0 – 6.0 MeV. The non-resonant background from direct breakup process was simulated from random sampling of 11Be+Be++ reaction in a three-body phase space and by tracking the particles into the detector system with smeared energies according to the energy resolution Brown et al. (2012). In addition, the random coincidence background was estimated using the event mixing method Yang et al. (2014). The excitation energy spectrum is fitted with the resonance energies and the corresponding widths left as free parameters by using the least-square method Olive (2014). The extracted results are listed in Table I and partially indicated in Fig. 1.
The lowest energy peak at MeV, is located just above . The existence of this resonant peak was confirmed by applying various cuts on 11Be isotopes (inset of Fig. 1) as well as on different angular ranges. The next peak at MeV lies above two-neutron separation threshold, MeV. The relative branching ratios for its decay to one- and two-neutron final channels are determined by the ratios of the proton counts in coincidence with 11Be or 10Be ions, with the former being more than four times larger than the latter. Due to the complexity of the 10Be decay channel and the decreasing acceptance at higher excitation energies, we concentrate only on the analysis of the - and -MeV peaks in the present work.
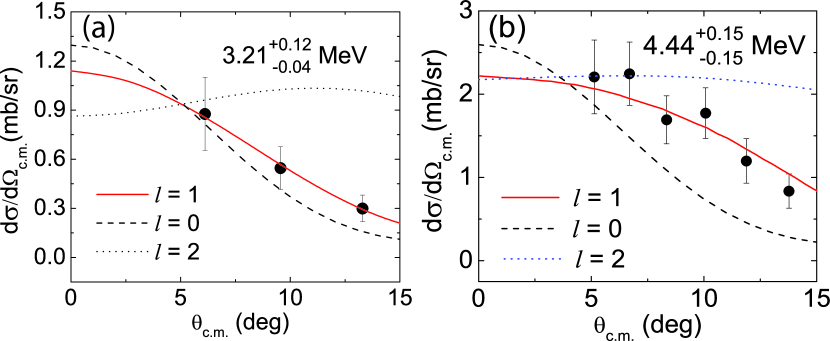
The differential cross section shown in Fig. 2 was extracted from the corresponding resonant peak at each angular bin Liu et al. (2020). The systematic uncertainty is estimated to be around , contributed mainly from a reasonable variation of the 11Be cuts ( 6), the influence of the fitting procedure ( ) and the uncertainty in target thickness ( ).
The distorted-wave Born approximation (DWBA) calculations with transferred orbital angular momentum and (Fig. 2) were performed with an expanded version of the code DWUCK Kunz , modified by Comfort Comfort to include the Vincent-Fortune technique Vincent and Fortune (1970) for stripping to unbound states. The curves for were calculated with a binding energy of 0.01 MeV Vincent and Fortune (1970). The optical model parameters (OMP) are the same as in Chen et al. (2018a). For the -MeV state, the determination between or seems marginal, with the corresponding minimum values of 1.54 and 0.23, respectively. However, the transfer to the -MeV state can be excluded by the systematics of the level scheme in the isotones (refer to Fig. 5) and by the extracted narrow resonance width Bertsch et al. (1998); Simon et al. (2007); swa . An assignment limits the possible spin-parities to , or . The state has already been experimentally identified at 2.71 MeV Iwasaki et al. (2000), whereas the state should lie at much higher energy than the state, similar to the case of 14C Fortune (2014) and also considering the theoretical calculations shown in Fig. 3. Hence, the -MeV state is assigned a spin-parity of . Based on comparison between the measured differential cross sections and the DWBA calculation Chen et al. (2018a, b), a spectroscopic factor of 0.78(23) is deduced. This state possesses predominantly a cross-shell configuration 11Be, similar to the state, consistent with its large value in the 11Be reaction. Combined with the following theoretical discussions, the -MeV state is tentatively assigned a single state with . The uncertainty of is typically around 20, resulted mainly from the variation of the OMPs Kay et al. (2013).
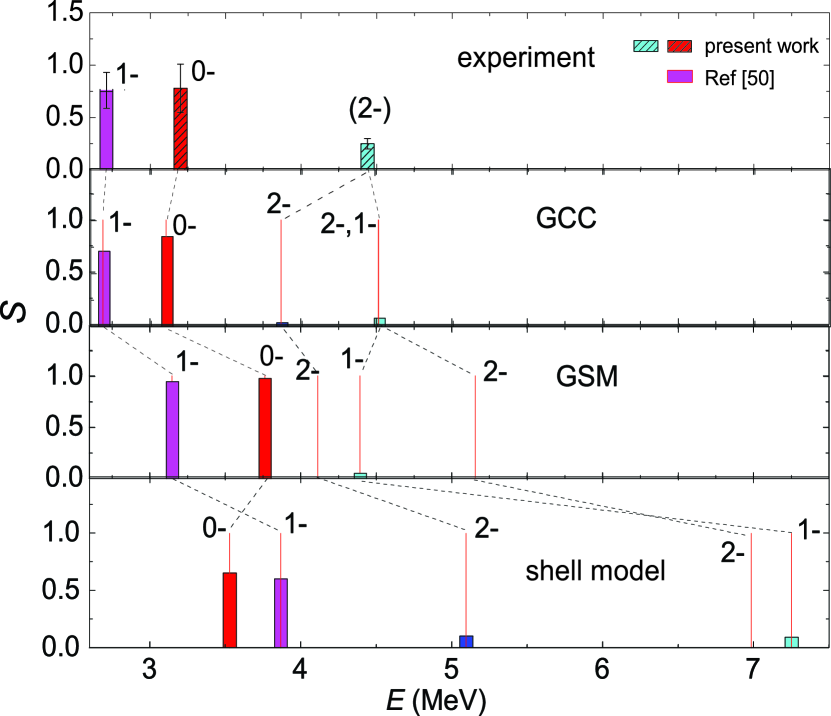
In Fig. 3, the calculated energy spectra and values are compared with the experimental results. The latest YSOX interaction Yuan et al. (2012); Chen et al. (2018a) was used in the shell model calculations. The energies of the and states are predicted much higher than the experimental value and are inverted with respect to each other. As a matter of fact, considering the weakly-bound and intruding mechanisms of 12Be, its low-lying negative-parity states should be dominated by (, ) or (, ) configurations and thus strongly coupled to the continuum. This coupling is difficult to be dealt with using the shell model based on the harmonic oscillator (HO) basis. Gamow shell-model (GSM) incorporates continuum-coupling by assuming a 8He core mimicked by a Woods-Saxon (WS) potential with an optimized Furutani-Horiuchi-Tamagaki (FHT) force Furutani et al. (1979). As shown in Fig. 3, the excitation energies of the and states are clearly reduced and the level ordering of the and states is restored, showing the importance of the continuum-coupling. However, there still exist some considerable discrepancies between the GSM calculations and the observations, possibly originating from the insufficiency of realistic interaction.
For the negative-parity and states populated with a significant strength in the one-neutron adding reaction on the -wave intruding 11Be g.s., it is natural to expect a dominant three-body structure with two weakly-bound neutrons occupying and orbitals coupled to the 10Be core. Accordingly, we performed calculations within Gamow coupled-channel (GCC) approach assuming a system of 10Be core plus two neutrons, together with the continuum-coupling Wang et al. (2019); Webb et al. (2019). The calculation uses the same interaction and model space as in Wang et al. (2019). We choose 10Be as a deformed core including a non-adiabatic coupling with low-lying rotational states. The effective core-valence potential and the interaction between the two valence nucleons are taken in a deformed WS shape including the spherical spin-orbit term and the finite-range Minnesota force, respectively. This interaction has successfully reproduced the excitation spectra of 11N-11Be and 12O-12Be mirror nuclei Wang et al. (2019); Webb et al. (2019). The wave functions are constructed in Jacobi coordinates with a complex-energy basis, which exhibit unique three-body features and provide a compelling approach to study the interplay between the single-particle structure and two-neutron correlations. As shown in Fig. 3, the spectra of 12Be and corresponding calculated in the framework of GCC are in good agreement with experimental data, including the previously known state and the currently determined state.
Furthermore, the width of the state has also been checked using the Wentzel–Kramers–Brillouin (WKB) approximation with single-particle tunnelling through a WS potential with a reduced radius fm and a diffuseness fm, plus a centrifugal potential for . Taking into account , the width of the state was estimated to be 0.012(3) MeV, fairly within the experimental upper limit. This further confirms the selection of transfer in the reaction and the assignment of for the -MeV state.
Looking at the excitation energy spectra predicted by the GCC approach, there are three possible candidates (, and ) for the observed -MeV state. However, based on the comparison between the DWBA calculation and the experimental differential cross sections, the for a pure state is clearly larger than that for a pure state. As a result, the assignment would lead to an resonance width largely exceeding the experimental limit. Therefore, we adopt a tentative assignment of to the -MeV resonance.
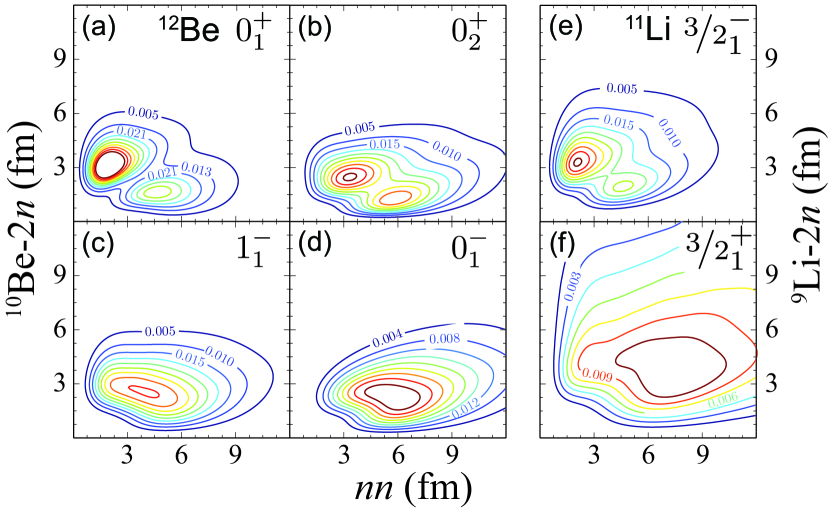
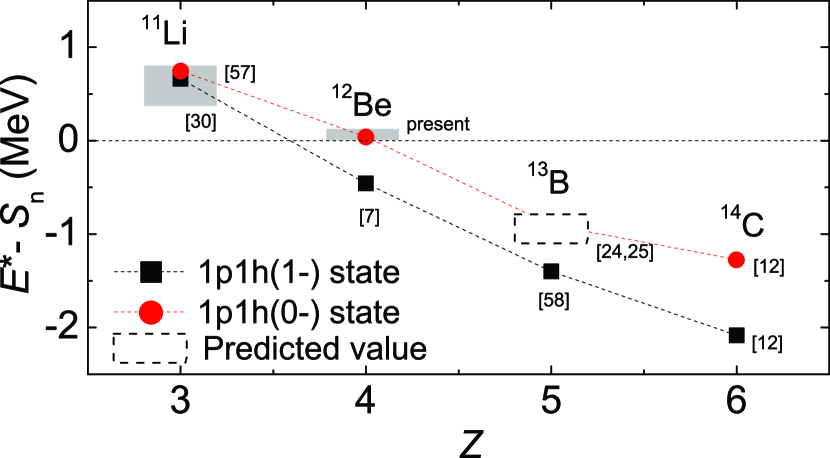
Since the low-lying and 1p-1h states have been found in 14C and 12Be, it is interesting to investigate similar states in the even less bound isotone 11Li Hagino and Sagawa (2005); Wang et al. (2019). We show in Fig. 4 the Jacobi-coordinate density distributions for the g.s. and low-lying states of 12Be and 11Li, as calculated in the GCC approach. The density distribution of the 12Be g.s., as shown in Fig. 4(a), exhibits a mixture of dineutron-like and cigar-like configurations Hagino et al. (2007). Its GCC-predicted single-particle configuration is mainly the pairing-featured mixture of , in line with previous observations Chen et al. (2018a); Meharchand et al. (2012); Pain et al. (2006). The density distribution of the state of 12Be (Fig. 4(b)) still exhibits a two-component distribution, but is more spatially expanded due most likely to the much smaller binding energy and the reduction of the -wave in its configuration (). This state in 12Be is similar to the two-neutron halo structure of the 11Li g.s., shown in Fig. 4(e) with a configuration . As for the and states in 12Be (Fig. 4(c) and (d)), the density distributions are diffused into one large component, reflecting the pair-broken 1p-1h configuration. The GCC-predicted main wave function configuration is with and probability for the and states, respectively. This large -wave neutron content is reminiscent of the one-neutron halo structure of the 11Be g.s. ( intruder -wave ). We see here the rich effects of the continuum-induced shell melting and cross-shell intrusion, which lead to exotic structures not only in the pair-coupled states, but also in the pair-broken 1p-1h low-lying states at the vicinity of the particle-separation threshold. For the isotone 11Li, according to the GCC calculation, the 1p-1h low-lying resonances are the ( = 0.906 MeV, MeV) and ( MeV, MeV) states Webb et al. (2019); Wang et al. (2019), corresponding to and in 12Be, respectively. As an example, we plot the density distribution of the state in Fig. 4(f). The overall shape of the distribution is similar to that for 12Be, but dramatically expanded in space, which may be attributed to the higher relative energy above the particle-separation threshold and the different core property together with the related core-valence interaction Webb et al. (2019); Wang et al. (2019). The latest finding of the soft dipole resonance might be the predicted 1p-1h states (either , or ) Kanungo et al. (2015). Further experimental confirmation of very exotic 1p-1h resonances in 11Li would be of special interest. Combining these theoretical and experimental results, we show in Fig. 5 the binding energy of the 1p-1h states relative to , as a function of increasing for proton-deficient isotones Iwasaki et al. (2000); Back et al. (2010); Ajzenberg-selove (1991); Kanungo et al. (2015). The nearly linear trend reflects the sensitivity of using these states to test model calculations with explicit coupling to the continuum.
It is worth noting that the currently observed at MeV is located very close to the . This means the state can only decay to the g.s. of 11Be through a -wave, which makes the state narrow and relatively stable. If the energy of the state was higher, the decay channel to the of 11Be at keV would open, leading to much broader resonance or even a virtual resonance. In fact, it is the -intruding 11Be sub-system and the threshold effect of the valence particle, which allows to generate the convenient location for the current narrow resonance. Recently it has been indicated that the formation of narrow resonances at the close proximity of the corresponding decay threshold is a quite general phenomenon, resulted from the coupling between the internal configuration mixing and the open decay channel mixing Okołowicz et al. (2020); Ikeda et al. (1968). These threshold aligned states may form a relatively stable structure carrying characteristics of the nearby decay channel. The present observation of the narrow near-threshold resonance, together with the extracted sizable , provides a new evidence for this “alignment” effect, in addition to, for example, the 7.654-MeV Hoyle state in 12C Freer and Fynbo (2014); Freer et al. (2018), and the 11.425-MeV state in 11B Ayyad et al. (2019).
In summary, using the 11Be Be reaction, some low-lying unbound states in 12Be are investigated. A resonance at MeV, just above 1n-separation threshold, was observed for the first time. Based on the DWBA and decay-width analysis, a spin-parity of is assigned to this threshold aligned state, corresponding to a 1p-1h configuration. The successful reproduction of the low-lying states using the GCC approach demonstrates the essential role of the continuum-coupling for weakly-bound and unbound nuclear systems. Further studies for more resonant states in 12Be, 11Li and other light unstable nuclei are expected in order to promote understanding of the new aspects of open quantum many-body systems.
The authors would like to acknowledge the operation staff at RCNP and EN course for providing the beam. The authors from Peking University acknowledge local support. This work is supported by the National Key RD Program of China (Contract No. 2018YFA0404403), the National Natural Science Foundation of China (Contracts No. 11775004, No. U1867214, No. 11775013, No. 11775316, No. 11875074, No. 11961141003, No. 11835001, No. 11921006, and No. 11975282). This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under award number DE-SC0013365, Grant No. DE-SC0020451 and Cooperative agreement DE-SC0000661, the State of Michigan and Michigan State University. D.T.T. and C.J. appreciate the support of the Nishimura International Scholarship Foundation and RCNP Visiting Young Scientist Support Program, respectively.
References
- Johnson et al. (2020) C. W. Johnson et al., Journal of Physics G: Nuclear and Particle Physics 47, 123001 (2020).
- Talmi and Unna (1960) I. Talmi and I. Unna, Phys. Rev. Lett. 4, 469 (1960).
- Schmitt et al. (2012) K. T. Schmitt et al., Phys. Rev. Lett. 108, 192701 (2012).
- Aumann et al. (2000) T. Aumann et al., Phys. Rev. Lett. 84, 35 (2000).
- Tanihata et al. (2008) I. Tanihata et al., Phys. Rev. Lett. 100, 192502 (2008).
- Simon et al. (1999) H. Simon et al., Phys. Rev. Lett. 83, 496 (1999).
- Iwasaki et al. (2000) H. Iwasaki et al., Phys. Lett. B 491, 8 (2000).
- Shimoura et al. (2003) S. Shimoura et al., Phys. Lett. B 560, 31 (2003).
- Imai et al. (2009) N. Imai et al., Phys. Lett. B 673, 179 (2009).
- Alburger et al. (1978) D. E. Alburger et al., Phys. Rev. C 17, 1525 (1978).
- Fortune et al. (1994) H. T. Fortune, G.-B. Liu, and D. E. Alburger, Phys. Rev. C 50, 1355 (1994).
- Ajzenberg-selove (1991) F. Ajzenberg-selove, Nucl. Phys. A 523 (1991).
- Persson et al. (2000) E. Persson et al., Phys. Rev. Lett. 85, 2478 (2000).
- Okołowicz et al. (2020) J. Okołowicz, M. Płoszajczak, and W. Nazarewicz, Phys. Rev. Lett. 124, 042502 (2020).
- Mazumdar et al. (2006) I. Mazumdar, A. R. P. Rau, and V. S. Bhasin, Phys. Rev. Lett. 97, 062503 (2006).
- Ozawa et al. (2000) A. Ozawa, T. Kobayashi, T. Suzuki, K. Yoshida, and I. Tanihata, Phys. Rev. Lett. 84, 5493 (2000).
- Hoffman et al. (2016) C. R. Hoffman, B. P. Kay, and J. P. Schiffer, Phys. Rev. C 94, 024330 (2016).
- Hoffman et al. (2014) C. R. Hoffman, B. P. Kay, and J. P. Schiffer, Phys. Rev. C 89, 061305 (2014).
- Dobaczewski et al. (2007) J. Dobaczewski, N. Michel, W. Nazarewicz, M. Płoszajczak, and J. Rotureau, Progress in Particle and Nuclear Physics 59, 432 (2007), international Workshop on Nuclear Physics 28th Course.
- Ikeda et al. (1968) K. Ikeda et al., Prog. Theor. Phys. Suppl. E68, 464 (1968).
- Yang et al. (2014) Z. H. Yang, Y. L. Ye, Z. H. Li, et al., Phys. Rev. Lett. 112, 162501 (2014).
- Liu et al. (2020) Y. Liu, Y. L. Ye, J. L. Lou, et al., Phys. Rev. Lett. 124, 192501 (2020).
- Jiang et al. (2020) W. Jiang, Y. L. Ye, C. J. Lin, et al., Phys. Rev. C 101, 031304 (2020).
- Yuan et al. (2012) C. Yuan et al., Phys. Rev. C 85, 064324 (2012).
- Warburton and Brown (1992) E. K. Warburton and B. A. Brown, Phys. Rev. C 46, 923 (1992).
- Blanchon et al. (2010) G. Blanchon, N. V. Mau, A. Bonaccorso, M. Dupuis, and N. Pillet, Phys. Rev. C 82, 034313 (2010).
- Kanada-En’yo and Horiuchi (2003) Y. Kanada-En’yo and H. Horiuchi, Phys. Rev. C 68, 014319 (2003).
- Garrido et al. (2012) E. Garrido et al., Phys. Rev. C 86, 024310 (2012).
- Romero-Redondo et al. (2008) C. Romero-Redondo et al., Phys. Rev. C 77, 054313 (2008).
- Wang et al. (2019) S. M. Wang et al., Phys. Rev. C 99, 054302 (2019).
- Michel et al. (2009) N. Michel et al., Jour. Phys. G. Nucl. Part. Phys. 36, 013101 (2009).
- Michel et al. (2002) N. Michel et al., Phys. Rev. Lett. 89, 042502 (2002).
- Webb et al. (2019) T. B. Webb et al., Phys. Rev. Lett. 122, 122501 (2019).
- Fortune (2014) H. T. Fortune, Phys. Rev. C 89, 017302 (2014).
- Johansen et al. (2013) J. G. Johansen et al., Phys. Rev. C 88, 044619 (2013).
- Kanungo et al. (2010) R. Kanungo et al., Phys. Lett. B 682, 391 (2010).
- Shimoda et al. (1992) T. Shimoda, H. Miyatake, and S. Morinobu, Nucl. Instrum. Methods Phys. Res., Sect. B 70, 320 (1992).
- Ong (2014) H. J. Ong, AIP Conference Proceedings 1588, 146 (2014).
- Chen et al. (2018a) J. Chen et al., Phys. Lett. B 781, 412 (2018a).
- Lane and Thomas (1958) A. M. Lane and R. G. Thomas, Rev. Mod. Phys. 30, 257 (1958).
- Cao et al. (2012) Z. Cao, Y. Ye, et al., Phys. lett. B 707, 46 (2012).
- Brown et al. (2012) S. M. Brown et al., Phys. Rev. C 85, 011302 (2012).
- Olive (2014) K. Olive, Chinese Phys. C 38, 090001 (2014).
- (44) P. D. Kunz, private communication.
- (45) J. R. Comfort, private communication.
- Vincent and Fortune (1970) C. M. Vincent and H. T. Fortune, Phys. Rev. C 2, 782 (1970).
- Bertsch et al. (1998) G. F. Bertsch, K. Hencken, and H. Esbensen, Phys. Rev. C 57, 1366 (1998).
- Simon et al. (2007) H. Simon, M. Meister, T. Aumann, et al., Nuclear Physics A 791, 267 (2007).
- (49) The would be 6.90 for the s-wave vritual state distribution, much larger than the BW distribution with minimum equals to 4.50.
- Chen et al. (2018b) J. Chen, J. L. Lou, Y. L. Ye, et al., Phys. Rev. C 98, 014616 (2018b).
- Kay et al. (2013) B. P. Kay, J. P. Schiffer, and S. J. Freeman, Phys. Rev. Lett. 111, 042502 (2013).
- Furutani et al. (1979) H. Furutani, H. Horiuchi, and R. Tamagaki, Prog. Theor. Phys. 62, 981 (1979).
- Hagino and Sagawa (2005) K. Hagino and H. Sagawa, Phys. Rev. C 72, 044321 (2005).
- Hagino et al. (2007) K. Hagino, H. Sagawa, J. Carbonell, and P. Schuck, Phys. Rev. Lett. 99, 022506 (2007).
- Meharchand et al. (2012) R. Meharchand et al., Phys. Rev. Lett. 108, 122501 (2012).
- Pain et al. (2006) S. D. Pain et al., Phys. Rev. Lett. 96, 032502 (2006).
- Kanungo et al. (2015) R. Kanungo et al., Phys. Rev. Lett. 114, 192502 (2015).
- Back et al. (2010) B. B. Back et al., Phys. Rev. Lett. 104, 132501 (2010).
- Freer and Fynbo (2014) M. Freer and H. Fynbo, Prog. Part. Nucl. Phys. 78, 1 (2014).
- Freer et al. (2018) Freer et al., Rev. Mod. Phys. 90, 035004 (2018).
- Ayyad et al. (2019) Y. Ayyad, B. Olaizola, W. Mittig, et al., Phys. Rev. Lett. 123, 082501 (2019).