Observation of interaction-induced mobility edge in a disordered atomic wire
Abstract
Mobility edge, a critical energy separating localized and extended excitations, is a key concept for understanding quantum localization. Aubry-André (AA) model, a paradigm for exploring quantum localization, does not naturally allow mobility edges due to self-duality. Using the momentum-state lattice of quantum gas of Cs atoms to synthesize a nonlinear AA model, we provide experimental evidence for mobility edge induced by interactions. By identifying the extended-to-localized transition of different energy eigenstates, we construct a mobility-edge phase diagram. The location of mobility edge in the low- or high-energy region is tunable via repulsive or attractive interactions. Our observation is in good agreement with the theory, and supports an interpretation of such interaction-induced mobility edge via a generalized AA model. Our work also offers new possibilities to engineer quantum transport and phase transitions in disordered systems.
Introduction – The concept of mobility edge (ME), a critical energy separating extended and exponentially localized energy eigen-states in the excitation spectrum, is key for understanding Anderson localization Anderson1958 ; Dalichaouch1991 ; Wiersma1997 ; Chabanov2000 ; Strzer2006 ; Schwartz2007 ; Julien2008 ; Lahini2008 ; Billy2008 ; Kondov2011 ; Jendrzejewski2012 ; Isam2015 ; White2020 induced by random disorder in three dimensions (3D) Abrahams1979 . In low dimensions, arbitrarily weak random disorder can make all single-particle eigenstates localize, hence ME is absent. Localization phenomena have also been actively studied in quasi-periodic lattice systems with incommensurate modulations Aubry1980 ; Grempel1982 ; Kohmoto1983a ; Kohmoto1983b ; DasSarma1986 ; Thouless1988 ; Modugno2009 ; Biddle2009 ; Biddle2011 ; Yan2021 , such as those described by Aubry-André (AA) model Aubry1980 .
Realization of the AA model in cold atoms has led to the first observation of the localization transition of a noninteracting Bose-Einstein condensate (BEC) Roati2008 . As the AA model has self-dual symmetry Aubry1980 , the localization transition is energy-independent (i.e., no ME), with all eigenstates being localized across a single critical point. Intriguingly, variants of AA model which have broken self-duality, such as the generalized Aubry-André (GAA) model Ganeshan2015 , can host ME already in one dimension (1D). So far, the existence of ME has been mainly conjectured in noninteracting quasi-periodic lattice systems DasSarma1988 ; Goedeke2007 ; Biddle2010 ; Ganeshan2015 ; Li2017 ; Yao2019 ; Deng2019 ; Li2020 ; Wang2020 ; Roy2021 , and experimentally confirmed with cold atoms in optical lattices Lschen2018 .
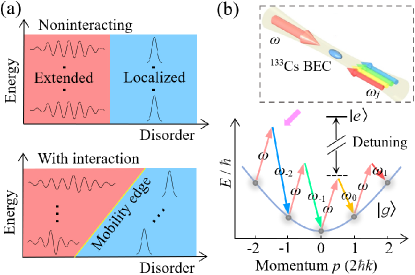
Beyond noninteracting systems, the realization and control of ME are of fundamental interests, but are generally challenging. Recently, some atomic experiments in this direction have been carried out, showing how single-particle MEs are affected by weak interactions An2018a ; An2021a , and many-body ME has been discussed in the context of many-body localization Kohlert2019 . In these experiments, however, ME is already expected without interactions. It is thus highly desired to understand MEs based on systems with tunable interactions.
In this work, we demonstrate that ME can be induced and tuned by interaction; the physical picture is shown in Fig. 1(a): weak interaction can have different dressing effects on different energy eigenstates of the AA model, resulting in a suppressed or enhanced localization of an eigenstate, thus a critical energy (i.e., ME) is expected in the excitation spectrum.
Experimentally, we observe signatures of ME based on the momentum-state lattice of quasi-1D 133Cs BEC that simulates a nonlinear AA model [Fig. 1(b)]. Exploiting the tunable scattering length of Cs atoms with Feshbach resonances Weber2003 ; Kraemer2004 ; Chin2004 ; Chin2010 , we realize a disordered wire with a wide range of interaction, and observe the extended-to-localized transition in the excitation spectrum. In particular, the controllability of all the system parameters including interactions allows us to access the highest excited state, which can be viewed as the ground state of the associated negative Hamiltonian. We demonstrate that interactions can enhance the localization of either low- or high-energy eigenstates, depending on the sign of the interactions. We further construct a mobility-edge phase diagram, which agrees well with the theory.
Such interaction-induced ME can be understood through an effective noninteracting GAA model. While the nonlinear AA model and its variants Lahini2009 ; Deissler2010 ; Lucioni2011 ; An2017 have been studied before in optical and atomic setups McKenna1992 ; Pikovsky2008 ; Deissler2010 ; Lucioni2011 ; Lellouch2014 ; Schwartz2007 ; Lahini2008 ; Lahini2009 ; An2017 ; Deissler2010 ; Lucioni2011 , the exploration of ME in the model remains elusive.
ME in the nonlinear AA model – We start by theoretically showing how ME arises in the nonlinear AA model
| (1) | |||||
Here is the reduced Planck’s constant, is the wave function at site in a lattice of size with , and is the nearest-neighbor coupling. The on-site modulation with has an amplitude and phase , which plays the role of disorder. The nonlinear term characterized by in our subsequent discussion arises from the atomic interaction. When , Eq. (1) reduces to the AA model, with all eigenstates extended for and localized for .
We are interested in the weak interaction regime where the self-trapping Smerzi1997 ; Albiez2005 does not occur, and every eigenstate has a correspondence in the noninteracting counterpart Wu2005 . Insights can be obtained by noting that the combination of the nonlinear term and the disorder results in a density-dependent potential , with the density . As the density distribution is shaped by the incommensurate modulation, contains multiple harmonics of the quasi-periodicity (i.e., ), which breaks the self-duality and leads to ME. For , perturbative analysis suggests is effectively a GAA lattice potential. For instance, when , by Fourier expanding the density up to the second harmonics of the quasi-periodicity, we have (apart from some constant), with the expansion coefficients and . It approximates the GAA lattice potential Ganeshan2015
| (2) |
with and , up to the second harmonics. Thus the physics of Eq. (1) may be understood via an effective noninteracting GAA model: . As the GAA model hosts an exact ME Ganeshan2015 , the location of ME in a weakly nonlinear AA model is expected to be
| (3) |
where sgn denotes the sign function. Because , we expect the location of ME in the low- or high-energy region is swapped when .
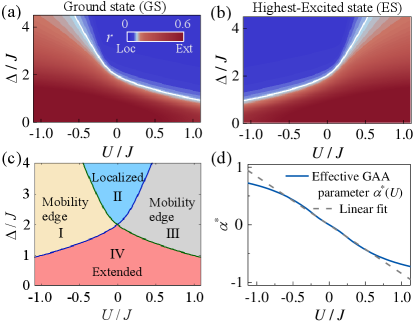
The above analysis is supported by numerical calculations. We focus on the ground state (GS) and the highest excited state (ES) of the nonlinear AA model footnote1 , and characterize their degree of localization via the participation ratio
| (4) |
For a localized state, ; for an extended state, the maximum possible is . Figure 2(a) and (b) show the participation ratio as a function of and for GS and ES, respectively. To identify the transition from the extended to the localized, we use the critical value of at in the noninteracting limit (see white curves) footnote2 ; for sites, the critical value is . We see that while the transition points of GS and ES coincide without interaction, they differ in the presence of interaction, suggesting the transition is energy-dependent. Moreover, adding enhances localization of GS but delocalizes ES, whereas the opposite occurs for . The critical points of GS and ES divide the parameter space into four regimes [Fig. 2(c)]. In phase II (IV), all states are localized (extended). But in both phases I and III, extended and localized states coexist, signaling the existence of ME. When increasing disorder, ME emerges from the high-energy regime in I (), while it emerges from the low-energy regime in III ().
We validate the effective GAA model through numerical simulations. We calculate the effective parameter based on Eq. (3), where () denotes the energy of GS (ES) at their critical point (), representing where ME coincides with the lowest (highest) energy. Figure 2(d) shows as a function of (blue curve). It is linear for small interactions, confirming the previous conjecture. In the linear regime, we expect the location of ME to be given by Eq. (3). When the linearity breaks down, the effective model is no longer suitable.
Experimental realization of the model – We experimentally realize the nonlinear AA model using the momentum-state lattice of 133Cs BEC that contains atoms in the hyperfine state [Fig. 1(b)] Wang2021 . We start with a BEC confined in a quasi-1D optical trap Supp . Two counter-propagating laser beams with the wavelength nm are applied, one with a frequency , while the other containing multi-frequency components , . They drive a series of two-photon Bragg transitions to couple discrete momentum states with the momentum increment of (with ), which simulates AA model of sites with the nearest-neighbor coupling Meier2016 . The disorder is realized by engineering to yield an on-site energy Supp with both and controllable via Bragg lasers. We employ a broad Feshbach resonance centered at magnetic field G to tune the atomic -wave scattering length Weber2003 ; Kraemer2004 ; Chin2004 ; Chin2010 . According to the mean-field theory of the momentum-lattice system Chen ; An2021a ; An2018 ; An2021b , the atomic interaction leads to the nonlinear term in Eq. (1), with , where is the atomic mass and is an effective atomic density Supp . We note that a quasi-1D BEC can be stable for BECBOOK ; Experimentally, we do not observe the collapse of BEC for on the time scale of ms relevant for our measurements. To avoid significant three-body loss Kraemer2006 , we restrict ourselves to ( is the Bohr radius).
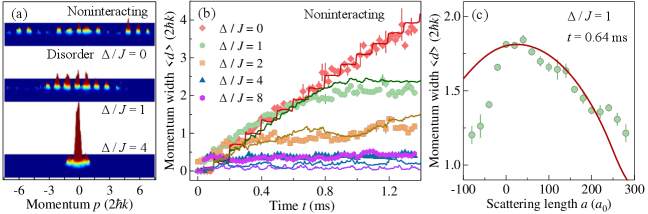
To confirm the realization of the nonlinear AA model, we first tune and observe the transport of the noninteracting BEC by controlling the disorder strength. Initially, the BEC with zero momentum is prepared at momentum-state lattice site , before the Bragg lasers are switched on. After an evolution time , the momentum distribution is measured through the time-of-flight (TOF) technique Supp . TOF images for ms under different disorder strength are illustrated in Fig. 3(a). As expected from the AA model, atoms spread over several lattice sites for , but localizing sharply near the initial position for . Figure 3(b) measures the time-dependent momentum width, , where is the measured fraction of atomic population at the momentum state at time . We observe the familiar crossover from the ballistic transport to localization with increasing disorder, in agreement with the numerical simulations (solid lines) based on Gross-Pitaevskii (GP) equation Supp .
Next, we tune the scattering length from to using the broad Feshbach resonance and fix the disorder at . Figure 3(c) shows the measured momentum width at ms under various interactions. We observe decreases with the interaction strength, regardless of its sign, suggesting an increased degree of localization. The experiment agrees qualitatively with the GP calculations Supp (red curve).
Construction of ME phase diagram – Important for our study is the preparation of GS and ES under various disorder and interaction. We prepare GS following the adiabatic protocol in Ref. An2021a . It consists of switching off the laser coupling between lattice sites and initializing atoms in the ground state at zero-momentum site . Then, by linearly ramping the coupling from to Hz in ms and holding there for ms, the initial state is transferred to GS of the lattice system.
A reliable preparation of ES, however, was nontrivial due to non-adiabatic effects An2021a . Here we adopt a strategy which is motivated by the fact that ES of a Hamiltonian can be viewed as GS of . Experimentally, in preparing ES of a system with desired , and we instead realize an associated “negative Hamiltonian” (i.e., ) with , and . To realize , we introduce a relative phase in the two-photon Bragg transition coupling neighboring momentum states [c.f. Fig. 1(b)]. The is achieved by tuning . Crucially, the conversion from to is uniquely enabled by Feshbach tuning of the interaction of Cs atoms. Then we adiabatically prepare GS of the negative system similarly as before: after switching off the laser coupling and initializing atoms at a site with the lowest energy, we linearly ramp up , thus achieving ES of the original system.
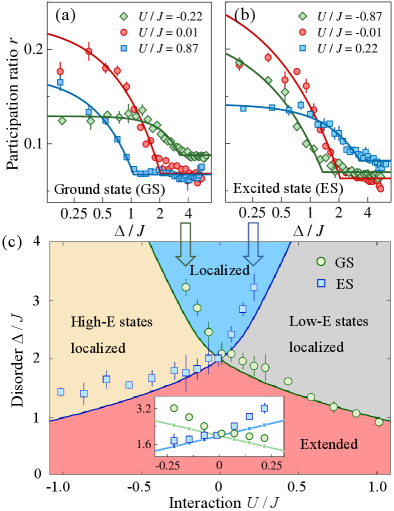
After the state preparation, we measure the population in each momentum mode to obtain the participation ratio according to Eq. (4). We identify the potential extended-to-localized transition by numerically fitting the experimental data of as a function of Supp , as shown in Figs. 4(a)-(b). For , the transition is at for both GS and ES, as expected. Comparing Figs. 4(a) and (b) shows that the localization of GS is enhanced (suppressed) under (), whereas the opposite occurs for ES, in agreement with the predictions. Owing to the non-adiabatic effect in the experimental ramp, the participation ratio is generically smaller than the idealized value expected from Eq. (1) Supp . Moreover, the experimental deep in the localized phase is slightly higher than due to the residual population. Nevertheless, these imperfections and finite-size effect do not qualitatively change the transitions Supp .
Finally, to construct the phase diagram, we collect the extracted transition points of GS and ES under various interactions into Fig. 4(c). The good agreement between the experiment and theory provides strong evidences on the existence of interaction-induced ME. It also confirms that, depending on whether the atomic interaction is attractive or repulsive, ME emerges from the high- or low-energy region of the excitation spectrum. In the inset of Fig. 4(c), we compare the experimental data with the predictions from the effective GAA model [c.f. Fig. 2(d)]. As shown, the effective model provides a good explanation of the data for , suggesting the location of ME in this regime is given by Eq. (3).
Conclusion – In this work we have provided experimental evidence that ME can be induced and controlled by interactions. The interaction-induced ME is different from the single-particle ME in noninteracting models and from the many-body ME Abanin2019 ; Deng2017 ; Li2015 . Our observations shed new light on the interplay between disorder and interaction. The widely tunable atomic interaction featured in our experiment enables the first observation of this intriguing phenomena, which presents new opportunities for engineering the quantum transport and quantum phase transitions in disordered systems.
Acknowledgement – We acknowledge helpful discussions with Biao Wu, Xiaopeng Li, Zhihao Xu and Shuai Chen. This research is funded by National Key R&D Program of China (Grant No. 2017YFA0304203), National Natural Science Foundation of China (Grant No. 62020106014, 92165106, 62175140, 12104276, 11874038, 12034012, 12074234). CC acknowledges support by the National Science Foundation (Grant No. PHY-2103542).
References
- (1) P. W. Anderson, Absence of diffusion in certain random lattices, Phys. Rev. 109, 1492 (1958).
- (2) R. Dalichaouch, J. P. Armstrong, S. Schultz, P. M. Platzman, and S. L. McCall, Microwave localization by two-dimensional random scattering, Nature 354, 53 (1991).
- (3) D. Wiersma, P. Bartolini, A. Lagendijk, and R. Righini, Localization of light in a disordered medium, Nature 390, 671 (1997).
- (4) A. A. Chabanov, M. Stoytchev, and A. Z. Genack, Statistical signatures of photon localization, Nature 404, 850 (2000).
- (5) M. Störzer, P. Gross, C. Aegerter, and G. Maret, Observation of the critical regime near Anderson localization of light, Phys. Rev. Lett. 96, 063904 (2006).
- (6) T. Schwartz, G. Bartal, S. Fishman, and M. Segev, Transport and Anderson localization in disordered two-dimensional photonic lattices, Nature 446, 52 (2007).
- (7) J. Chabé, G. Lemarié, B. Grémaud, D. Delande, P. Szriftgiser, and J. C. Garreau, Experimental observation of the Anderson metal-insulator transition with atomic matter waves, Phys. Rev. Lett. 101, 255702 (2008).
- (8) Y. Lahini, A. Avidan, F. Pozzi, M. Sorel, R. Morandotti, D. Christodoulides, and Y. Silberberg, Anderson localization and nonlinearity in one-dimensional disordered photonic lattices, Phys. Rev. Lett. 100, 013906 (2008).
- (9) J. Billy, V. Josse, Z. C. Zuo, A. Bernard, B. Hambrecht, P. Lugan, D. Clément, L. Sanchez-Palencia, P. Bouyer, and A. Aspect, Direct observation of Anderson localization of matter waves in a controlled disorder, Nature 453, 891 (2008).
- (10) S. S. Kondov, W. R. McGehee, J. J. Zirbel, and B. DeMarco, Three-dimensional Anderson localization of ultracold matter, Science 334, 66 (2011).
- (11) F. Jendrzejewski, A. Bernard, K. Müller, P. Cheinet, V. Josse, M. Piraud, L. Pezzé, L. Sanchez-Palencia, A. Aspect, and P. Bouyer, Three-dimensional localization of ultracold atoms in an optical disordered potential, Nat. Phys. 8, 398 (2012).
- (12) I. Manai, J. Clément, R. Chicireanu, C. Hainaut, J. C. Garreau, P. Szriftgiser, and D. Delande, Experimental observation of two-dimensional Anderson localization with the atomic kicked rotor, Phys. Rev. Lett. 115, 240603 (2015).
- (13) D. White, T. Haase, D. Brown, M. Hoogerland, M. Najafabadi, J. Helm, C. Gies, D. Schumayer, and D. W. Hutchinson, Observation of two-dimensional Anderson localisation of ultracold atoms, Nat. Commun. 11, 4942 (2020).
- (14) E. Abrahams, P. W. Anderson, D. C. Licciardello, and T. V. Ramakrishnan, Scaling theory of localization: Absence of quantum diffusion in two dimensions, Phys. Rev. Lett. 42, 673 (1979).
- (15) S. Aubry and G. André, Analyticity breaking and Anderson localization in incommensurate lattices, Ann. Israel Phys. Soc. 3, 18 (1980).
- (16) D. R. Grempel, S. Fishman, and R. E. Prange, Localization in an incommensurate potential: An exactly solvable model, Phys. Rev. Lett. 49, 833 (1982).
- (17) M. Kohmoto, L. Kadanoff, and C. Tang, Localization problem in one dimension: Mapping and escape, Phys. Rev. Lett. 50, 1870 (1983).
- (18) M. Kohmoto, Metal-insulator transition and scaling for incommensurate systems, Phys. Rev. Lett. 51, 1198 (1983).
- (19) S. D. Sarma, A. Kobayashi, and R. E. Prange, Proposed experimental realization of Anderson localization in random and incommensurate artificially layered systems, Phys. Rev. Lett. 56, 1280 (1986).
- (20) D. J. Thouless, Localization by a potential with slowly varying period, Phys. Rev. Lett. 61, 2141 (1988).
- (21) M. Modugno, Exponential localization in one-dimensional quasi-periodic optical lattices, New J. Phys. 11, 033023 (2009).
- (22) J. Biddle, B. Wang, D. J. Priour, Jr., and S. D. Sarma, Localization in one-dimensional incommensurate lattices beyond the Aubry-André model, Phys. Rev. A 80, 021603(R) (2009).
- (23) J. Biddle, D. J. Priour, Jr., B. Wang, and S. D. Sarma, Localization in one-dimensional lattices with non-nearest-neighbor hopping: Generalized Anderson and Aubry-André models, Phys. Rev. B 83, 075105 (2011).
- (24) T. Xiao, D. Z. Xie, Z. L. Dong, T. Chen, W. Yi, and B. Yan, Observation of topological phase with critical localization in a quasi-periodic lattice, Sci. Bull. 66, 2175 (2021).
- (25) G. Roati, C. D’Errico, L. Fallani, M. Fattori, C. Fort, M. Zaccanti, G. Modugno, M. Modugno, and M. Inguscio, Anderson localization of a non-interacting Bose-Einstein condensate, Nature 453, 895 (2008).
- (26) S. Ganeshan, J. H. Pixley, and S. D. Sarma, Nearest neighbor tight binding models with an exact mobility edge in one dimension, Phys. Rev. Lett. 114, 146601 (2015).
- (27) S. D. Sarma, S. He, and X. C. Xie, Mobility edge in a model one-dimensional potential, Phys. Rev. Lett. 61, 2144 (1988).
- (28) D. J. Boers, B. Goedeke, D. Hinrichs, and M. Holthaus, Mobility edges in bichromatic optical lattices, Phys. Rev. A 75, 063404 (2007).
- (29) J. Biddle and S. D. Sarma, Predicted mobility edges in one-dimensional incommensurate optical lattices: An exactly solvable model of Anderson localization, Phys. Rev. Lett. 104, 070601 (2010).
- (30) X. Li, X. P. Li, and S. D. Sarma, Mobility edges in one-dimensional bichromatic incommensurate potentials, Phys. Rev. B 96, 085119 (2017).
- (31) H. P. Yao, H. Khoudli, L. Bresque, and L. Sanchez-Palencia, Critical behavior and fractality in shallow one-dimensional quasiperiodic potentials, Phys. Rev. Lett. 123, 070405 (2019).
- (32) X. Deng, S. Ray, S. Sinha, G. V. Shlyapnikov, and L. Santos, One-dimensional quasicrystals with Power-Law hopping, Phys. Rev. Lett. 123, 025301 (2019).
- (33) X. Li and S. D. Sarma, Mobility edge and intermediate phase in one-dimensional incommensurate lattice potentials, Phys. Rev. B 101, 064203 (2020).
- (34) Y. C. Wang, X. Xia, L. Zhang, H. P. Yao, S. Chen, J. G. You, Q. Zhou, and X. J. Liu, One-dimensional quasiperiodic mosaic lattice with exact mobility edges, Phys. Rev. Lett. 125, 196604 (2020).
- (35) S. Roy, T. Mishra, B. Tanatar, and S. Basu, Reentrant localization transition in a quasiperiodic chain, Phys. Rev. Lett. 126, 106803 (2021).
- (36) H. Lüschen, S. Scherg, T. Kohlert, M. Schreiber, P. Bordia, X. Li, S. D. Sarma, and I. Bloch, Single-particle mobility edge in a one-dimensional quasiperiodic optical lattice, Phys. Rev. Lett. 120, 160404 (2018).
- (37) F. A. An, E. J. Meier, and B. Gadway, Engineering a flux-dependent mobility edge in disordered Zigzag chains, Phys. Rev. X 8, 031045 (2018).
- (38) F. A. An, K. Padavić, E. J. Meier, S. Hegde, S. Ganeshan, J. H. Pixley, S. Vishveshwara, and B. Gadway, Interactions and mobility edges: Observing the generalized Aubry-André model, Phys. Rev. Lett. 126, 040603 (2021).
- (39) T. Kohlert, S. Scherg, X. Li, H. Lüschen, S. D. Sarma, I. Bloch, and M. Aidelsburger, Observation of many-body localization in a one-dimensional system with a single-particle mobility edge, Phys. Rev. Lett. 122, 170403 (2019).
- (40) T. Weber, J. Herbig, M. Mark, H. -C. Nägerl, and R. Grimm, Bose-Einstein condensation of cesium, Science 299, 232 (2003).
- (41) T. Kraemer, J. Herbig, M. Mark, T. Weber, C. Chin, H. -C. Nägerl, and R. Grimm, Optimized production of a cesium Bose-Einstein condensate, Appl. Phys. B 79, 1013 (2004).
- (42) C. Chin, V. Vuletić, A. Kerman, S. Chu, E. Tiesinga, P. Leo, and C. Williams, Precision feshbach spectroscopy of ultracold Cs2, Phys. Rev. A 70, 032701 (2004).
- (43) C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, Feshbach resonances in ultracold gases, Rev. Mod. Phys. 82, 1225 (2010).
- (44) Y. Lahini, R. Pugatch, F. Pozzi, M. Sorel, R. Morandotti, N. Davidson, and Y. Silberberg, Observation of a localization transition in quasiperiodic photonic lattices, Phys. Rev. Lett. 103, 013901 (2009).
- (45) F. A. An, E. J. Meier, and B. Gadway, Diffusive and arrested transport of atoms under tailored disorder, Nat. Commun. 8, 325 (2017).
- (46) B. Deissler, M. Zaccanti, G. Roati, C. D’Errico, M. Fattori, M. Modugno, G. Modugno, and M. Inguscio, Delocalization of a disordered bosonic system by repulsive interactions, Nat. Phys. 6, 354 (2010).
- (47) E. Lucioni, B. Deissler, L. Tanzi, G. Roati, M. Zaccanti, M. Modugno, M. Larcher, F. Dalfovo, M. Inguscio, and G. Modugno, Observation of subdiffusion in a disordered interacting system, Phys. Rev. Lett. 106, 230403 (2011).
- (48) M. J. McKenna, R. L. Stanley, and J. D. Maynard, Effects of nonlinearity on Anderson localization, Phys. Rev. Lett. 69, 1807 (1992).
- (49) A. S. Pikovsky and D. L. Shepelyansky, Destruction of Anderson localization by a weak nonlinearity, Phys. Rev. Lett. 100, 094101 (2008).
- (50) S. Lellouch and L. Sanchez-Palencia, Localization transition in weakly interacting Bose superfluids in one-dimensional quasiperdiodic lattices, Phys. Rev. A 90, 061602(R) (2014).
- (51) A. Smerzi, S. Fantoni, S. Giovanazzi, and S. R. Shenoy, Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates, Phys. Rev. Lett. 79, 4950 (1997).
- (52) M. Albiez, R. Gati, J. Fölling, S. Hunsmann, M. Cristiani, and M. Oberthaler, Direct observation of tunneling and nonlinear self-trapping in a single bosonic Josephson junction, Phys. Rev. Lett. 95, 010402 (2005).
- (53) B. Wu and Q. Niu, Superfluidity of Bose-Einstein condensate in an optical lattice: Landau-Zener tunnelling and dynamical instability, New. J. Phys. 5, 104 (2003).
- (54) To numerically calculate the highest excited state, we invert the sign of all the system parameters in the nonlinear AA model and use imaginary time evolution to find its ground state.
- (55) This provides a convenient way for numerically identifying the critical point when the system is small. It is consistent with the more generic approach using power-law fitting to identify the transition, as we did later in the experiment.
- (56) Y. F. Wang, Y. Q. Li, J. Z. Wu, W. L. Liu, J. Z. Hu, J. Ma, L. T. Xiao, and S. T. Jia, Hybrid evaporative cooling of 133Cs atoms to Bose-Einstein condensation, Opt. Express 29, 13960 (2021).
- (57) Details are provided in the Supplementary Materials.
- (58) E. J. Meier, F. A. An, and B. Gadway, Atom-optics simulator of lattice transport phenomena, Phys. Rev. A 93, 051602(R) (2016).
- (59) T. Chen, D. Z. Xie, B. Gadway, and B. Yan, A Gross-Pitaevskii-equation description of the momentum-state lattice: roles of the trap and many-body interactions. arXiv:2103.14205v2.
- (60) F. A. An, E. J. Meier, J. Ang’ong’a, and B. Gadway, Correlated dynamics in a synthetic lattice of momentum states, Phys. Rev. Lett. 120, 040407 (2018).
- (61) F. A. An, B. Sundar, J. P. Hou, X. W. Luo, E. J. Meier, C. W. Zhang, K. A. Hazzard, and B. Gadway, Nonlinear dynamics in a synthetic momentum-state lattice, Phys. Rev. Lett. 127, 130401 (2021).
- (62) C. J. Pethick and H. Smith, Bose-Einstein Condensation in Dilute Gases (Cambridge University Press, Cambridge, 2008).
- (63) T. Kraemer, M. Mark, P. Waldburger, J. G. Danzl, C. Chin, B. Engeser, A. D. Lange, K. Pilch, A. Jaakkola, H. -C. Nägerl, and R. Grimm, Evidence for Efimov quantum states in an ultracold gas of caesium atoms, Nature 440, 315 (2006).
- (64) D. A. Abanin, E. Altman, I. Bloch, and M. Serbyn, Many-body localization, thermalization, and entanglement, Rev. Mod. Phys. 91, 021001 (2019).
- (65) D. L. Deng, S. Ganeshan, X. P. Li, R. Modak, S. Mukerjee, and J. H. Pixley, Many-body localization in incommensurate models with a mobility edge, Ann. Phys. 529, 1600399 (2017).
- (66) X. P. Li, S. Ganeshan, J. H. Pixley, and S. D. Sarma, Many-body localization and quantum nonergodicity in a model with a single-particle mobility edge, Phys. Rev. Lett. 115, 186601 (2015).