Observation of gamma rays up to 320 TeV from the middle-aged TeV pulsar wind nebula HESS J1849-000
Abstract
Gamma rays from HESS J1849000, a middle-aged TeV pulsar wind nebula (PWN), are observed by the Tibet air shower array and the muon detector array. The detection significance of gamma rays reaches and levels above and , respectively, in units of Gaussian standard deviation . The energy spectrum measured between for the first time is described with a simple power-law function of . The gamma-ray energy spectrum from the sub-TeV () to sub-PeV () ranges including the results of previous studies can be modeled with the leptonic scenario, inverse Compton scattering by high-energy electrons accelerated by the PWN of PSR J18490001. On the other hand, the gamma-ray energy spectrum can also be modeled with the hadronic scenario in which gamma rays are generated from the decay of neutral pions produced by collisions between accelerated cosmic-ray protons and the ambient molecular cloud found in the gamma-ray emitting region. The cutoff energy of cosmic-ray protons is estimated at , suggesting that protons are accelerated up to the PeV energy range. Our study thus proposes that HESS J1849000 should be further investigated as a new candidate for a Galactic PeV cosmic-ray accelerator, PeVatron.
1 Introduction
The origin of the knee at around in the cosmic-ray (CR) energy spectrum has been an open question since its discovery (Kulikov & Kristiansen, 1958). One of the major approaches to the problem is observing sub-PeV -decay gamma rays generated by collisions of PeV CRs accelerated by a source with the ambient interstellar medium. This strategy helps us discover several candidates of Galactic PeV CR accelerators, “PeVatrons”, including supernova remnants (SNR), star-forming regions, and unidentified sources (Amenomori et al., 2021; Cao et al., 2021a; Albert et al., 2021a; Abeysekara et al., 2021; Fang et al., 2022). On the other hand, many of the TeV and sub-PeV gamma-ray sources are pulsar wind nebulae (PWNe), representing the accelerators of high-energy electrons and positrons (H.E.S.S. collaboration, 2018a, b; Amenomori et al., 2019; Albert et al., 2021b). In particular, middle-aged PWNe harboring pulsars with characteristic ages of occupy a large fraction of PWNe (for example, see H.E.S.S. Collaboration et al. (2019a, b)). Some theories also discuss that many unidentified sources bright in gamma rays could be middle-aged or old PWNe (Tibolla et al., 2013; Vorster et al., 2013; Kaufmann & Tibolla, 2018). Moreover, in terms of CR acceleration, a PWN inside its precursor SNR could accelerate PeV CRs (Ohira et al., 2018). Therefore, detailed observations of individual middle-aged PWNe are crucial not only to study the majority of Galactic gamma-ray sources but also to elucidate the origin of CRs around the knee energy range.
HESS J1849000 is a TeV gamma-ray source detected by H.E.S.S. (Terrier et al., 2008; H.E.S.S. collaboration, 2018a). The TeV emission is nearly centered at an X-ray pulsar PSR J18490001, which is surrounded by a diffuse synchrotron X-ray PWN found by previous studies (Terrier et al., 2008; Gotthelf et al., 2011; Kuiper & Hermsen, 2015; Vleeschower Calas et al., 2018). The spin period, spin-down luminosity, and characteristic age of PSR J18490001 are , , and , respectively (Gotthelf et al., 2011). Due to the positional coincidence of the TeV gamma-ray emission with the pulsar and the energetic nature of the pulsar, HESS J1849000 is interpreted as the PWN which is powered by PSR J18490001 and is in transition from a young, synchrotron-dominated phase to an evolved, inverse-Compton dominated phase from the comparison of the energy fluxes of the diffuse keV X-ray and TeV gamma-ray emissions H.E.S.S. collaboration (2018a). The differential spectrum of the TeV emission has a relatively hard index of (H.E.S.S. collaboration, 2018a, b), which may allow the detection of nearby gamma-ray sources in the ultra-high energy range by HAWC (eHWC J1850001 in ) and LHAASO (LHAASO J18490001 at ) (Abeysekara et al., 2020; Cao et al., 2021a). In particular, the HAWC collaboration also implies the association of the observed gamma-ray emission with J18490001 and points out that such a high-energy gamma-ray emission may be ubiquitous around powerful pulsars with (Albert et al., 2021b). However, the current situation of the ultra-high-energy gamma-ray observations still lacks studies of the particle acceleration taking place in this middle-aged PWN through detailed analysis.
This paper presents the observation of gamma rays from HESS J1849000 up to the sub-PeV energy range by the Tibet air shower array and the muon detector array and proposes some possible mechanisms of the gamma-ray emission through detailed data analysis and discussion. First, Section 2 briefly introduces the experiment. After presenting the results of the data analysis and the discussion in Sections 3 and 4, respectively, the conclusion is made in Section 5.
2 Experiment
Tibet air shower (AS) array has been observing CRs above the TeV energy range since 1991 (Amenomori et al., 1992, 1999, 2009, 2019) at Yangbajing (, , a.s.l.) in Tibet, China. The surface array consists of 597 plastic scintillation detectors covering a total geometrical area of . These detectors record the number of secondary particles in ASs and the timings of detection of these particles to reconstruct the energy and arrival direction of primary CRs. The surface array is equipped with an underground water-Cherenkov-type muon detector (MD) array with a geometrical area of to improve the sensitivity to celestial gamma rays (Sako et al., 2009; Amenomori et al., 2019). This work utilizes data taken by the Tibet AS array and the MD array from 2014 February to 2017 May (719 live days). The data analysis and the Monte Carlo simulation performed in this work are described in Appendices A and B, respectively.
3 Results
3.1 Detection of gamma rays from HESS J1849000
Events are taken by opening a circular ON-source window with an angular radius of centered at HESS J1849000, in the J2000 coordinates (H.E.S.S. collaboration, 2018a). On the other hand, the background is estimated by counting events in 20 OFF windows, each of which has the same size as the ON-source window, opened with the equi-zenith angle method (Amenomori et al., 2003). The events in the ON-source and OFF windows are then binned by energy into five logarithmically equal bins per decade. After the event selection described in Appendix A, the detection significance of gamma rays from HESS J1849000 reaches and levels above and , respectively, in units of Gaussian standard deviation (Li & Ma, 1983).
Figure 1 shows the significance maps of the HESS J1849000 region above (top) and (bottom) pixelized by pixels. The map is smoothed with the point-spread function (PSF) of the experiment. In the map above , the pixel with the maximum significance (let us call it “the brightest pixel”) is found at , deviating by from HESS J1849000. A toy Monte Carlo simulation shows that the statistical uncertainty in the brightest pixel’s orientation is . The pointing systematics of the experiment along the right ascension and the declination are also estimated at and , respectively, from the data analysis of the gamma rays coming from the Crab Nebula; see Appendix C. From the above statistical and systematic uncertainties, the total uncertainty in the center position of the observed gamma-ray emission with the confidence level is estimated at following the methodology used in the previous studies (H.E.S.S. collaboration, 2018a; Amenomori et al., 2022). Therefore, the center position of the sub-PeV gamma-ray emission observed in this study is consistent with that of HESS J1849000. On the other hand, HESS J1852000 (H.E.S.S. collaboration, 2018a) deviates by in angular distance from the brightest pixel, and the deviation corresponds to significance taking into account both the uncertainty in the center position of the observed sub-PeV gamma-ray emission () and that in the position of HESS J1852000. The result thus disfavors HESS J1852000 as the origin of the sub-PeV gamma rays.
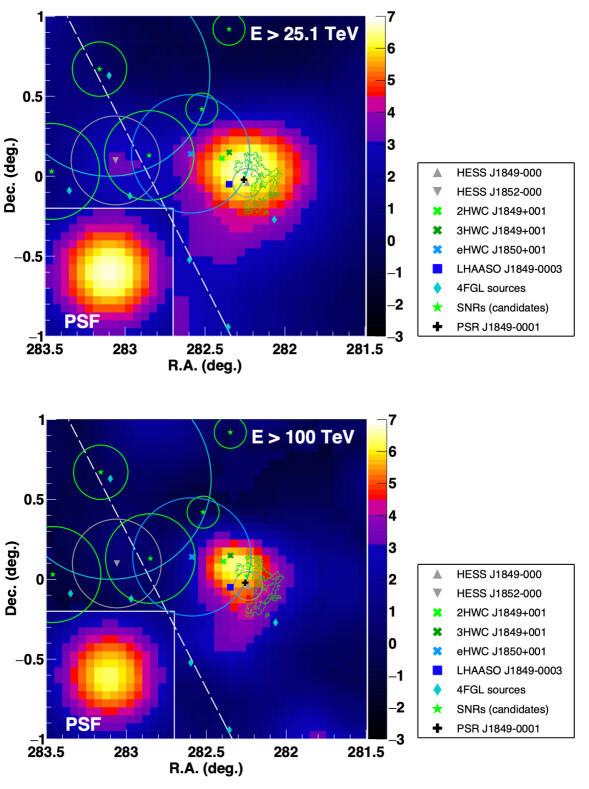
3.2 Energy spectrum
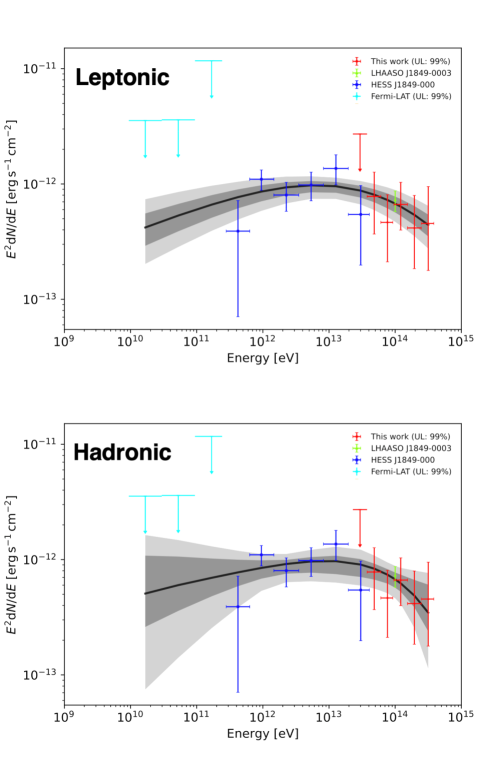
The energy spectrum of gamma rays from HESS J1849000 is measured for the first time in an energy range between as shown with the red points in Figure 2. The differential energy flux in each energy bin is calculated only if the detection significance of gamma rays exceeds , otherwise, the upper limit on the flux is calculated. Table 1 summarizes the result of the calculation. A simple power-law (PL) function can be fitted to the measured spectrum and the best-fit result is with . The experiment’s absolute energy scale uncertainty of (Amenomori et al., 2009) dominates the systematic uncertainty in the flux normalization of . The fraction of contamination to the number of events above from the lower energy range due to the finite energy resolution is estimated at . Furthermore, there may be a spillover of gamma rays from the nearby gamma-ray source HESS J1852000 into the ON-source window (see also Figure 1). Assuming a two-dimensional Gaussian with a extension for the morphology of HESSJ1852000 (H.E.S.S. collaboration, 2018a), the 95% upper limit on its integral gamma-ray flux above is calculated as if the spectrum extends beyond the sub-PeV range. The spillover into the ON-source window is thus estimated at , which is less than of the integral flux of HESS J1849000 above , . According to Vernetto & Lipari (2016), the attenuation of gamma rays due to the interactions with the interstellar radiations on the way to Earth is at if the distance to HESS J1849000 is assumed as (H.E.S.S. collaboration, 2018b).
| () | Flux () | Significance () |
|---|---|---|
| 2.1 | ||
| 2.3 | ||
| 3.8 | ||
| 2.8 | ||
| 2.7 |
Note. — The third column presents the significance of the event excess in the ON-source window over the background calculated with Equation (17) of Li & Ma (1983), which corresponds to the detection significance of gamma rays from HESS J1849000
4 Discussion
4.1 Leptonic scenario
The gamma-ray energy spectrum from the sub-TeV () to the sub-PeV ranges observed by Fermi-LAT (Acero et al., 2013), H.E.S.S. (H.E.S.S. collaboration, 2018a), LHAASO (Cao et al., 2021a), and this work is modeled with the leptonic scenario using Naima (Zabalza, 2015). In this scenario, gamma rays are generated from inverse Compton scattering (ICS) off the interstellar radiations by high-energy electrons (Khangulyan et al., 2014). The target radiation field is assumed to consist of the cosmic microwave background and near- (temperature of and energy density of ) and far-infrared blackbody components ( and ) whose energy densities are determined using GALPROP (Porter et al., 2017). The distance to HESS J1849000 is assumed as , the same as that assumed for PSR J18490001 in previous studies (Gotthelf et al., 2011; H.E.S.S. collaboration, 2018b). The energy spectrum of parent electrons is assumed to follow a simple PL function
| (1) |
where the normalization constant and the spectral index are free parameters. Under the above model assumptions, Naima computes the posterior distributions of the parameters and gives the median value and its uncertainty corresponding to the central of each distribution. The best-fit result of the modeling is shown with the black curve in the top panel of Figure 2 and the spectral parameters are estimated at and . Assuming a PL function with an exponential cutoff (ECPL) for the electron spectrum does not improve the goodness of fit, and the lower limit on the cutoff energy is estimated at . The obtained limit is extremely high but is not implausible because the acceleration of PeV electrons takes place in the Crab Nebula (Cao et al., 2021b). A broken PL function is not significantly preferred as the electron spectrum either and the current gamma-ray observations can be well explained with ICS by electrons following a simple PL spectrum.
In the leptonic scenario considered above, the gamma rays observed can be interpreted as ICS radiations from high-energy electrons accelerated by the PWN of PSR J18490001. On the other hand, the total energy of electrons above is calculated as , which occupies only of the total spin-down energy of PSR J18490001 (). If the rest of the spin-down energy is assigned to the magnetic field inside the diffuse X-ray nebula around the pulsar ( in radius or at the distance of according to Gotthelf et al. (2011)), then the magnetic field strength in the nebula would be . Such a strong field, however, leads to the synchrotron X-ray nebula far outshining that observed with the energy flux of in (Gotthelf et al., 2011; Kuiper & Hermsen, 2015; Vleeschower Calas et al., 2018), which can be reproduced with under a simple one-zone model in the spectral fit assuming the aforementioned PL electron population. Furthermore, the one-zone model would not be adequate to interpret the observations since the extensions of the X-ray nebula and TeV gamma-ray emission (, H.E.S.S. collaboration (2018b)) are much different, and more detailed theoretical modeling is thus required when one considers the leptonic scenario.
4.2 Hadronic scenario
On the other hand, the gamma-ray energy spectrum can also be explained in the context of the hadronic scenario. This scenario supposes that CR protons generate -decay gamma rays through interactions with the ambient interstellar medium (Kafexhiu et al., 2014). To investigate the environment around the source, archive data of the line emission published by the FUGIN survey (Umemoto et al., 2017) is analyzed. The analysis finds a size molecular cloud in the velocity range of corresponding to the distance around , which resides at the west side of HESS J1849000 as shown by green contours in Figure 1. The cloud has the line intensity of and can provide a gas density of protons assuming the canonical CO-to- factor of (Bolatto et al., 2013). A wealthy amount of target material for CRs is also implied by the high hydrogen column density of toward the source direction (Gotthelf et al., 2011). The region bright in gamma rays above shown in Figure 1 is positionally consistent with the cloud within the uncertainty discussed in Section 3.1.
The modeling of the gamma-ray energy spectrum from the sub-TeV to the sub-PeV ranges is performed under the hadronic scenario assuming an ECPL function for the spectrum of CR protons:
| (2) |
where the normalization constant , the spectral index , and the cutoff energy are free parameters. The density of the interstellar medium is assumed as protons based on the aforementioned radio data analysis. The result of the modeling is shown in the bottom panel of Figure 2, and the spectral parameters are determined as , , and , respectively; it is suggested that the cutoff energy reaches the PeV range. The total energy of the CR protons between is calculated as .
The aforementioned spectral index () implies CR protons are accelerated by shock waves of the PWN or the precursor SNR. However, given the high cutoff energy beyond , the acceleration of CR protons in a PWN-SNR composite system may provide an adequate explanation. Ohira et al. (2018) pointed out that the PWN adiabatically compressed by the reverse shock of the precursor SNR can produce PeV CR protons. The total energy of given to particles by the PWN-SNR system (Gelfand et al., 2009) is also consistent with our result. Moreover, such a composite system can also accelerate and leptons and would produce an X-ray nebula as observed in the adiabatically compressed PWN with the amplified magnetic field (Gelfand et al., 2009; Ohira et al., 2018). On the other hand, there are still no theories that systematically study the distribution of high-energy particles generated in a PWN-SNR system simulating detailed particle acceleration processes and the resultant spectrum of their non-thermal radiations. Neutrinos inevitably generated in the hadronic interaction are not currently detected and the contribution to gamma-ray flux from hadrons is not well constrained (Huang & Li, 2022). Future deep observation of neutrinos by IceCube-Gen2 (Aartsen et al., 2021) and of sub-PeV gamma rays by ALPACA (Kato et al., 2021), CTA (The Cherenkov Telescope Array Consortium, 2017), and SWGO (Hinton & the SWGO Collaboration, 2021) have great importance to find clear evidence for the acceleration of PeV CRs in this energetic source.
5 Conclusion
This paper presents the results of the observation of gamma rays from HESS J1849000 by the Tibet AS array and the MD array and discusses the origin of the observed gamma-ray emission. The detection significance of gamma rays above and reaches and levels, respectively. The energy spectrum first measured between is described with a simple power-law function of . The gamma-ray energy spectrum from the sub-TeV to sub-PeV range including the results of previous studies can be modeled with the leptonic scenario in which high-energy electrons accelerated by the PWN of PSR J18490001 radiate gamma rays through ICS. However, the scenario requires detailed theoretical modeling other than the one-zone model to explain the compact X-ray nebula around PSR J18490001 and the relatively small energy given to the electrons above ( of the spin-down power of PSR J18490001). On the other hand, the hadronic scenario can also model the spectrum, suggested by the detection of a molecular cloud found in the gamma-ray emitting region. The cutoff energy of CR protons is estimated at , suggesting that CR protons are accelerated up to the PeV energy range in HESS J1849000. As a possible way to explain the observed gamma rays, it is proposed that HESS J1849000 may be a PWN-SNR composite system. The PWN-SNR system can provide the site to accelerate both PeV CR protons and high-energy leptons and realize the observed complex of non-thermal radiations from the X-ray to sub-PeV gamma-ray range. Note that, however, there is still much room to theoretically study the particle distribution and the resultant non-thermal radiation spectra in such a composite system. In addition, future observations of neutrinos and gamma rays in the higher energy range than explored in this work are important to determine the dominant contribution from hadrons or leptons to the observed gamma-ray radiations and to obtain evidence for the acceleration of PeV CRs. It is worth emphasizing that HESS J1849000 needs to be further investigated as one of the PeVatron candidates from the aspects of both theories and observations.
Appendix A Data analysis
Selection criteria for AS events are the same as those introduced by Amenomori et al. (2019), except for the maximum of the analyzed zenith-angle range, the threshold energy, and the cut using the total number of muons recorded by the MD array. The first condition is changed from to to improve statistics because HESS J1849000 culminates only at the meridian zenith of at the Tibet site. Our analysis using the Monte Carlo (MC) simulation described in Appendix B finds that this extension increases the photon statistics by above , and accordingly the threshold energy of the analysis is fixed at . Second, the MD cut condition is optimized for this work with the method presented by Amenomori et al. (2022) using gamma-ray events generated with the MC simulation and the background events from the experimental data. The resultant cut requires events to satisfy or where denotes the total number of muons recorded with the MD array and is the sum of particle number densities recorded with the scintillation detectors of the AS array. The MD cut can reject more than of background CRs in the gamma-ray equivalent energy range above while keeping of gamma rays from HESS J1849000 in the same energy range. The energy and angular resolutions of the AS array for gamma rays after the event selection are evaluated as and (50% containment), respectively. After the event selection, events are left for later analysis.
Appendix B Monte Carlo simulation
Using the air-shower simulation software Corsika v7.4000 (Heck et al., 1998), a total number of gamma rays following a power-law spectrum with an index of 2 are generated between and injected into the atmosphere from a hypothetical point source at . The air-shower development in the atmosphere is simulated until they reach the altitude of the Tibet AS array. The source extension, spectral index, and flux normalization of HESS J1849000 are appropriately taken into account in the MC data analysis.
The air-shower events are randomly thrown over the circle with a radius centered at the AS array, and the detector responses for these events are simulated with Geant 4 v10.0 (Agostinelli et al., 2003). The energy loss of shower particles in the scintillation detectors and the soil layer is calculated. For the particles that reach MDs, their Cherenkov photon emission in the water layer of MDs is simulated. The photons are reflected on the walls and floor of each MD and collected by a 20-inch photomultiplier suspended downward at the ceiling, where the number of photoelectrons is counted. The simulation data are processed through our analysis pipeline in the same way as the experimental data.
Appendix C Pointing systematics of the experiment
To estimate the pointing systematics of the experiment, events from the direction of the Crab Nebula are analyzed in the zenith-angle range larger than the meridian zenith of HESS J1849000 (). The center of the gamma-ray emission above from the direction of the nebula is determined with the two-dimensional unbinned maximum likelihood analysis by fitting an axisymmetric Gaussian to the distribution of events. The resultant center is , deviated by and in real angle along the right ascension and the declination, respectively, from the position of the Crab pulsar of 111http://simbad.u-strasbg.fr/simbad/sim-id?Ident=Crab+Pulsar. The pointing systematics is estimated by summing the apparent deviation and its statistical error in quadrature, which results in and along the right ascension and the declination, respectively.
References
- Aartsen et al. (2021) Aartsen, M. G., Abbasi, R., Ackermann, M., et al. 2021, Journal of Physics G: Nuclear and Particle Physics, 48, 060501, doi: 10.1088/1361-6471/abbd48
- Abdollahi et al. (2020) Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, The Astrophysical Journal Supplement Series, 247, 33, doi: 10.3847/1538-4365/ab6bcb
- Abeysekara et al. (2021) Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2021, 5, 465, doi: https://doi.org/10.1038/s41550-021-01318-y
- Abeysekara et al. (2017) —. 2017, The Astrophysical Journal, 843, 40, doi: 10.3847/1538-4357/aa7556
- Abeysekara et al. (2020) —. 2020, Phys. Rev. Lett., 124, 021102, doi: 10.1103/PhysRevLett.124.021102
- Acero et al. (2013) Acero, F., Ackermann, M., Ajello, M., et al. 2013, The Astrophysical Journal, 773, 77, doi: 10.1088/0004-637x/773/1/77
- Agostinelli et al. (2003) Agostinelli, S., Allison, J., Amako, K., et al. 2003, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506, 250, doi: https://doi.org/10.1016/S0168-9002(03)01368-8
- Albert et al. (2020) Albert, A., Alfaro, R., Alvarez, C., et al. 2020, The Astrophysical Journal, 905, 76, doi: 10.3847/1538-4357/abc2d8
- Albert et al. (2021a) —. 2021a, The Astrophysical Journal, 907, L30, doi: 10.3847/2041-8213/abd77b
- Albert et al. (2021b) Albert, A., et al. 2021b, The Astrophysical Journal, 911, 27, doi: 10.3847/2041-8213/abf4dc
- Amenomori et al. (2021) Amenomori, M., Bao, Y. W., Bi, X. J., et al. 2021, Nature Astronomy, 5, 460, doi: 10.1038/s41550-020-01294-9
- Amenomori et al. (1992) Amenomori, M., Cao, Z., Ding, L. K., et al. 1992, Phys. Rev. Lett., 69, 2468, doi: 10.1103/PhysRevLett.69.2468
- Amenomori et al. (1999) Amenomori, M., Ayabe, S., Cao, P. Y., et al. 1999, The Astrophysical Journal, 525, L93, doi: 10.1086/312342
- Amenomori et al. (2003) Amenomori, M., Ayabe, S., Cui, S. W., et al. 2003, The Astrophysical Journal, 598, 242, doi: 10.1086/378350
- Amenomori et al. (2009) Amenomori, M., Bi, X. J., Chen, D., et al. 2009, The Astrophysical Journal, 692, 61, doi: 10.1088/0004-637x/692/1/61
- Amenomori et al. (2019) Amenomori, M., Bao, Y. W., Bi, X. J., et al. 2019, Phys. Rev. Lett., 123, 051101, doi: 10.1103/PhysRevLett.123.051101
- Amenomori et al. (2022) Amenomori, M., Asano, S., Bao, Y. W., et al. 2022, The Astrophysical Journal, 932, 120, doi: 10.3847/1538-4357/ac6ef4
- Anderson et al. (2017) Anderson, L. D., Wang, Y., Bihr, S., et al. 2017, A&A, 605, A58, doi: 10.1051/0004-6361/201731019
- Bolatto et al. (2013) Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, Annual Review of Astronomy and Astrophysics, 51, 207, doi: 10.1146/annurev-astro-082812-140944
- Cao et al. (2021a) Cao, Z., Aharonian, F. A., An, Q., et al. 2021a, Nature, 594, 33, doi: 10.1038/s41586-021-03498-z
- Cao et al. (2021b) Cao, Z., Aharonian, F., An, Q., et al. 2021b, Science, 373, 425, doi: 10.1126/science.abg5137
- Fang et al. (2022) Fang, K., Kerr, M., Blandford, R., Fleischhack, H., & Charles, E. 2022, Phys. Rev. Lett., 129, 071101, doi: 10.1103/PhysRevLett.129.071101
- Gelfand et al. (2009) Gelfand, J. D., Slane, P. O., & Zhang, W. 2009, The Astrophysical Journal, 703, 2051, doi: 10.1088/0004-637x/703/2/2051
- Gotthelf et al. (2011) Gotthelf, E. V., Halpern, J. P., Terrier, R., & Mattana, F. 2011, The Astrophysical Journal, 729, L16, doi: 10.1088/2041-8205/729/2/l16
- Heck et al. (1998) Heck, D., Knapp, J., Capdevielle, J. N., Schats, G., & Thouw, T. 1998
- H.E.S.S. collaboration (2018a) H.E.S.S. collaboration. 2018a, Astronomy & Astrophysics, 612, A1, doi: 10.1051/0004-6361/201732098
- H.E.S.S. collaboration (2018b) —. 2018b, Astronomy & Astrophysics, 612, A2, doi: 10.1051/0004-6361/201629377
- H.E.S.S. Collaboration et al. (2019a) H.E.S.S. Collaboration, Abdalla, H., Aharonian, F., et al. 2019a, A&A, 627, A100, doi: 10.1051/0004-6361/201935458
- H.E.S.S. Collaboration et al. (2019b) —. 2019b, A&A, 621, A116, doi: 10.1051/0004-6361/201834335
- Hinton & the SWGO Collaboration (2021) Hinton, J., & the SWGO Collaboration. 2021, Proc. 37th International Cosmic Ray Conference; PoS(ICRC2021)023, doi: 10.22323/1.395.0023
- Huang & Li (2022) Huang, T.-Q., & Li, Z. 2022, The Astrophysical Journal, 925, 85, doi: 10.3847/1538-4357/ac423d
- Kafexhiu et al. (2014) Kafexhiu, E., Aharonian, F., Taylor, A. M., & Vila, G. S. 2014, Phys. Rev. D, 90, 123014, doi: 10.1103/PhysRevD.90.123014
- Kato et al. (2021) Kato, S., Condori, C. A. H., d.l. Fuente, E., et al. 2021, Experimental Astronomy, 52, 85, doi: 10.1007/s10686-021-09796-8
- Kaufmann & Tibolla (2018) Kaufmann, S., & Tibolla, O. 2018, Nuclear and Particle Physics Proceedings, 297-299, 91, doi: https://doi.org/10.1016/j.nuclphysbps.2018.07.014
- Khangulyan et al. (2014) Khangulyan, D., Aharonian, F. A., & Kelner, S. R. 2014, The Astrophysical Journal, 783, 100, doi: 10.1088/0004-637x/783/2/100
- Kuiper & Hermsen (2015) Kuiper, L., & Hermsen, W. 2015, Monthly Notices of the Royal Astronomical Society, 449, 3827, doi: 10.1093/mnras/stv426
- Kulikov & Kristiansen (1958) Kulikov, G. V., & Kristiansen, G. B. 1958, Zh. Eksp. Teor. Fis., 35, 635
- Li & Ma (1983) Li, T.-P., & Ma, Y.-Q. 1983, The Astrophysical Journal, 272, 317, doi: 10.1086/161295
- Manchester et al. (2005) Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, The Astronomical Journal, 129, 1993, doi: 10.1086/428488
- Ohira et al. (2018) Ohira, Y., Kisaka, S., & Yamazaki, R. 2018, Monthly Notices of the Royal Astronomical Society, 478, 926, doi: 10.1093/mnras/sty1159
- Porter et al. (2017) Porter, T. A., Jóhannesson, G., & Moskalenko, I. V. 2017, The Astrophysical Journal, 846, 67, doi: 10.3847/1538-4357/aa844d
- Sako et al. (2009) Sako, T. K., Kawata, K., Ohnishi, M., et al. 2009, Astroparticle Physics, 32, 177, doi: 10.1016/j.astropartphys.2009.07.006
- Terrier et al. (2008) Terrier, R., Mattana, F., Djannati-Atai, A., et al. 2008, AIP Conference Proceedings, 1085, 312, doi: https://doi.org/10.1063/1.3076669
- The Cherenkov Telescope Array Consortium (2017) The Cherenkov Telescope Array Consortium. 2017, ArXiv e-prints. https://arxiv.org/pdf/1709.07997
- Tibolla et al. (2013) Tibolla, O., Vorster, M., Kaufmann, S., Ferreira, S., & Mannheim, K. 2013, arXiv:1306.6833v1. https://arxiv.org/pdf/1306.6833.pdf
- Umemoto et al. (2017) Umemoto, T., Minamidani, T., Kuno, N., et al. 2017, Publications of the Astronomical Society of Japan, 69, doi: 10.1093/pasj/psx061
- Vernetto & Lipari (2016) Vernetto, S., & Lipari, P. 2016, Phys. Rev. D, 94, 063009, doi: 10.1103/PhysRevD.94.063009
- Vleeschower Calas et al. (2018) Vleeschower Calas, L., Kaufmann, S., Álvarez Ochoa, C., & Tibolla, O. 2018, Nuclear and Particle Physics Proceedings, 297-299, 102, doi: https://doi.org/10.1016/j.nuclphysbps.2018.07.016
- Vorster et al. (2013) Vorster, M. J., Tibolla, O., Ferreira, S. E. S., & Kaufmann, S. 2013, The Astrophysical Journal, 773, 139, doi: 10.1088/0004-637x/773/2/139
- Zabalza (2015) Zabalza, V. 2015, Proc. of International Cosmic Ray Conference 2015, 922