Observation of an excitonic Mott transition through ultrafast core-cum-conduction photoemission spectroscopy
Abstract
Time-resolved soft-X-ray photoemission spectroscopy is used to simultaneously measure the ultrafast dynamics of core-level spectral functions and excited states upon excitation of excitons in WSe2. We present a many-body approximation for the Green’s function, which excellently describes the transient core-hole spectral function. The relative dynamics of excited-state signal and core levels reveals a delayed core-hole renormalization due to screening by excited quasi-free carriers, revealing an excitonic Mott transition. These findings establish time-resolved core-level photoelectron spectroscopy as a sensitive probe of subtle electronic many-body interactions and an ultrafast electronic phase transition.
Optoelectronic properties of semiconductors are largely governed by two types of excitations – excitons Mueller and Malic (2018), the bosonic quasiparticles comprised of an electron and a hole bound by Coulomb interaction, and quasi-free carriers (QFCs) of single-particle character Steinhoff et al. (2017); Guerci et al. (2019). While the interplay between excitons and QFCs has been studied experimentally with terahertz and optical spectroscopies Kaindl et al. (2003); Huber et al. (2001), these techniques are restricted to optically allowed transitions and do not provide direct information about the underlying many-body interactions. In this letter, we show that detailed information about the dynamics of both excitons and QFCs can be deduced from the simultaneous measurement of the core-hole spectral function and the excited state population with ultrafast time-resolved X-ray photoelectron spectroscopy (trXPS) Pietzsch et al. (2008). We observe strong renormalization of the W spectral function after optical excitation of WSe2 bulk crystals. The transient spectral function is excellently reproduced using a many-body approximation for the Green’s function Stefanucci and van Leeuwen (2013), which accounts for the core-hole screening by photo-excited QFCs. The simultaneous measurement of the excited-state population in the conduction band (CB) reveals an 100 fs delay of the core-hole screening compared to the initial build-up of exciton population, which we ascribe to an ultrafast Mott transition from optically-prepared excitons to an uncorrelated QFC plasma.
Static XPS has been a workhorse of surface science by driving the understanding of catalytic processes Ertl and Thiele (1979); Ertl et al. (1980); Asahi et al. (2001), chemical states of interfaces Biesinger et al. (2011), and functional materials Xu et al. (2009). The measured photoelectron distribution is proportional to the core-hole spectral function and carries information about the many-body interactions such as Auger scattering, electron-phonon coupling, plasmonic excitations and local screening Citrin et al. (1977); Hüfner (2003); Mahan (2000); Lizzit et al. (1998). The XPS lineshape of metals is usually asymmetric and phenomenologically well-described by the Doniach-Šunjić (DS) function Doniach and Sunjic (1970), where the characteristic heavy tail towards higher binding energy originates from the core-hole screening by conduction electrons. For semiconductors, on the other hand, the observed lineshape is typically symmetric and can be described by a Voigt profile Dendzik et al. (2015, 2017). In the presence of excited carriers, a semiconductor becomes partially-metallic and one can expect a renormalization of the core-hole lineshape. This opens up the possibility of studying non-equilibrium dynamics with XPS. Recently, technological advances of femtosecond X-ray sources Ackermann et al. (2007) and photoelectron detectors Schönhense et al. (2015) enabled ultrafast trXPS experiments to be conducted. These include the observation of melting of charge-density wave states in Mott insulators Hellmann et al. (2010); Ishizaka et al. (2011), charge-transfer dynamics at semiconductor interfaces Siefermann et al. (2014) or transient surface-photovoltage control Liu et al. (2018). Nevertheless, an accurate theoretical description of the out-of-equilibrium core-hole spectral function is still missing and applying the DS theory to the dynamic case is problematic. In this work, we generalize the DS theory to cover the case of a photo-excited semiconductor, which enables a quantitative description of the fundamental processes governing the experimentally observed core-hole spectral changes.
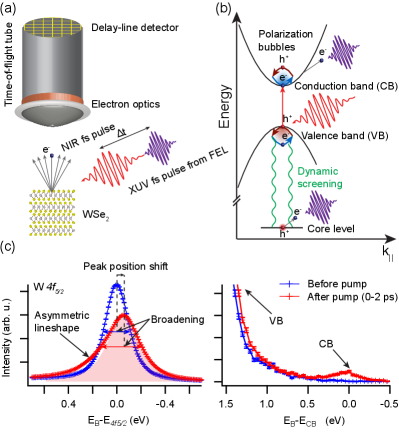
We performed core-cum-conduction trXPS experiments of WSe2 using the FLASH free-electron laser and optical pump pulses tuned to the optical A-exciton resonance at 1.6 eV at room temperature. A time-of-flight (ToF) momentum microscope was used as a photoelectron analyzer, which enabled us to simultaneously probe a 40 eV-broad spectral window including the excited states, valence band and the highest W and Se core levels SM ; Kutnyakhov et al. (2020). Schematics of the setup and of a model conduction-core energy level diagram are shown in the Figs. 1(a-b). The observed time-dependent trXPS spectra of W shown in Fig. 1(c) exhibit distinct dynamics with respect to pump-probe delay time, showing characteristic changes of photoemission peak position and width. In addition, we observed a build-up of asymmetry (skewness) which resembles the DS asymmetry. Simultaneosly, we observed a transient population of excited carriers which is responsible for the core-hole lineshape modifications.
In order to understand the origin of the observed trXPS spectral changes, we propose a theoretical model to describe the dynamical screening of the core hole due to the photo-induced valence holes and conduction electrons. We refer the reader to SM for details. Briefly, the core-level photoemission signal is proportional to the core-hole spectral function Hüfner (2003)
| (1) |
with being the core-hole Green’s function:
| (2) |
Here, is the core energy, is the correlation self-energy due to scatterings between the core electron and conduction/valence electrons and quantifies the broadening due to other decay channels, such as Auger or phonon scattering. According to the DS theory, the non-interacting lineshape is mainly renormalized by dynamical screening effects. In the diagramatic formalism, this means that the self-energy is dominated by the GW term Hed , where is the screened interaction in the random phase approximation. In this work, we show that screening the interaction with the single polarization bubble of QFCs (see Fig. 1b) is enough to reproduce the core-level shift and the asymmetric lineshape. The screening due to excitons is much weaker in comparison to QFCs for transition metal dichalcogenide (TMDC) materials Steinhoff et al. (2017) and it is therefore neglected. The resulting self-energy takes the form
| (3) |
where is a parameter proportional to the average of conduction and valence bandwidths, while the renormalized core energy reads
| (4) |
In Eq. (4), is the Lambert function, is the effective mass at the band edge (the average value of conduction and valence band effective masses), is the quasi-free carrier density and is the average Coulomb interaction between the core electron and the valence/conduction electrons. In the absence of QFCs, reduces to a Lorentzian profile with width dictated by , while at a finite QFC density, the real and imaginary parts of the self-energy are responsible for the shift of the core energy and the asymmetric lineshape.
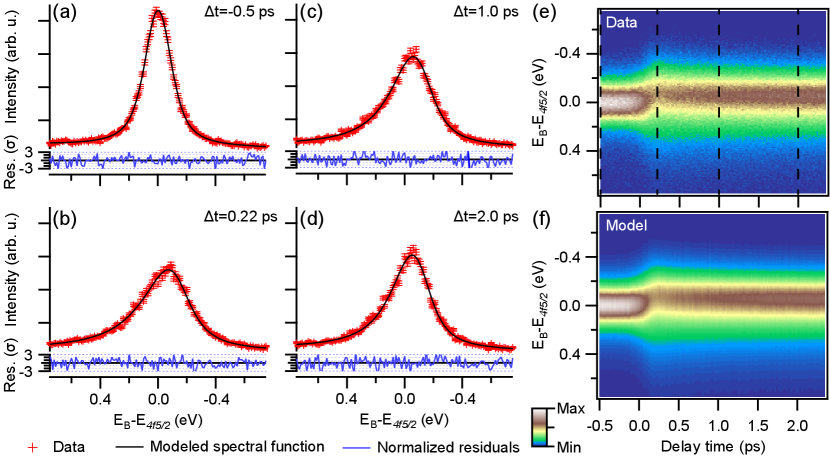
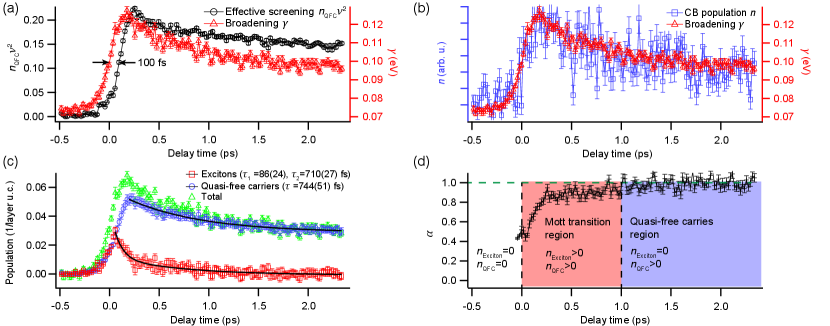
The modeled spectral function (Eqs. 1-4), convoluted with a constant Gaussian to account for the experimental energy resolution, excellently reproduces the experimental data, as presented in Fig. 2. This is evidenced by the featureless normalized residuals, shown for four representative time delays in Figs. 2(a-d). The entire time series (see Figs. 2(e-f)) can be reproduced by fixing the average bandwidth and effective mass of the material and solely fitting the broadening and the product (the average interaction is independent of time) for every delay time . The transient spectral function can thus be described by just two independent parameters, as couples the experimentally observed peak shift and asymmetry of the lineshape and describes the symmetric broadening. Interestingly, these parameters exhibit drastically different dynamics, with rising ca. 100 fs later and decaying slower than (see Fig. 3(a)). This effect is not induced by the applied model, as the same behaviour is present in model-independent quantities such as the higher moments of the photoelectron distribution SM .
The ToF momentum microscope allows simultaneous detection of photoelectrons over a large energy range, spanning electrons from the core levels, valence band and excited population in the CB, within a single experiment (see fig. 1). Therefore, it is possible to directly compare the dynamics of with the build-up of the excited-state population , and we find a strong correlation between the two quantities (see Fig. 3(b)), i.e. the core-level broadening immediately follows the buildup of excited carriers which includes contributions from both excitons Christiansen et al. (2019) and QFCs in the CB. In contrast, the core-hole lineshape renormalization governed by the quasi-particle screening shows a clear delay in buildup compared to and . This is consistent with the prediction that the pump energy tuned to the excitonic resonance should favor the creation of excitons Perfetto et al. (2019) up to a critical density Steinleitner et al. (2017), and can be explained by means of an excitonic Mott transition – the initial stage of the dynamics is dominated by excitons which subsequently break into a QFC plasma. An estimation of the excitation density per layer, cm-2 SM , used in our experiment indeed significantly exceeds the predicted critical excitation density of approximately cm-2 Steinhoff et al. (2017), and is close to the density of cm-2 reported for experimental observation of excitonic Mott transition in single-layered WS2 Chernikov et al. (2015).
The simultaneous acquisition of both excited states population in the whole surface Brillouin zone and renormalized core-hole spectral function enables us to exclude the effect of space-charge, often observed in ultrafast photoemission experiments Hellmann et al. (2012); Oloff et al. (2014), as space-charge would not contribute to the CB population. We also exclude the influence of the inter-band scattering due to much faster dynamics of ca. 15 fs Puppin (2018). Moreover, we exclude surface-photovoltage observed before for WSe2 Liu et al. (2018) as origin of the observed renormalization. This effect can influence the peak position, but not the asymmetry of the XPS spectra. Finally, the effect of laser-assisted photoemission is minimized by the choice of s-polarization for the pump. All these observations strongly suggest the electronic excitation as origin of the lineshape renormalization.
Based on the Mott transition interpretation and the assumption that screening by excitons is negligible compared to QFCs Steinhoff et al. (2017), we can effectively disentangle both of these populations, as presented in the Fig. 3(c) SM . The result indicates that the excitonic population reaches the critical value within the pump pulse envelope, which is then followed by a rapid decay with a lifetime of fs. The remaining exciton population decays at much lower rate ( fs). In contrast, the QFC population continues to rise even after excitation as a result of exciton dissociation, and decays with a lifetime fs. Interestingly, this decay seems to correlate with the slow component of exciton decay which is likely due to diffusion into the bulk, as excited-carrier lifetimes are typically observed on 100 ps time scale Tokudomi et al. (2007).
Previous experimental studies of the excitonic Mott transition in TMDCs have observed either continuous Chernikov et al. (2015) or discontinuous behaviour Bataller et al. (2019), while theory predicts that both of these cases can be realized depending on the interaction strength Guerci et al. (2019). Our results shed new light into the ultrafast dynamics of the exciton-QFC transition (see Fig. 3(d)). The observed degree of ionization stays in the range of 0.5-1 for the first 1 ps after photo-excitation. For longer time delays, the excited carriers are found exclusively in the QFC state. The observation is indicative of a continuous transition with coexisting phases. It should be underlined that details of the transition will depend on the excitation density. Additional data acquired simultaneously, but with 25% lower pump fluence indicate that both and the initial decay of exciton population depend on the total excitation density, corroborating our data interpretation SM .
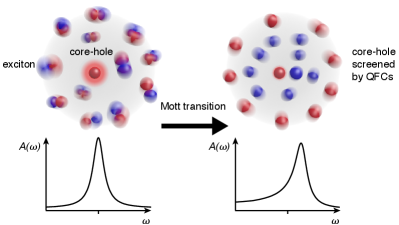
The possibility to disentangle the dynamics of excitons and QFCs by trXPS is quite surprising due to the small energy difference between these two phases, typically 50 meV, in comparison to the characteristic core-state energy scale of tens of eV. However, it was shown before that small changes in the valence band structure can have a dramatic influence on the shape of core-level spectra Dendzik et al. (2017). Discrimination of excitons and QFCs is based on the different screening of the core-hole created during the photoemission process (see Fig 4). This can be understood quite intuitively – excitons, being localized charge dipoles, are expected to interact much weaker with the suddenly created core-hole potential than delocalized QFCs. The most cogent manifestation of this effect is the fs delay of the core-level peak-position shift with respect to the peak-width increase (see Fig. 3(a) for the dynamics of closely-related parameters). The detailed interpretation of this result relies on the proposed theoretical model which ,we believe, is general enough to be successfully applied to further ultrafast studies of many-body states as well as electronic phase transitions. This seems to be especially appealing in combination with hard x-ray photoemission due to its larger probing depth, providing access to buried interfaces in realistic semiconducting devices.
This work is dedicated to Wilfried Wurth, who passed away on May 8, 2019. We acknowledge support by the scientific and technical staff of FLASH and valuable discussions with Karsten Horn and Lucia Reining.
This work was funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant No. ERC-2015-CoG-682843, No. 676598, No. 824143, and No. 654360), the German Research Foundation (DFG) within the Emmy Noether program (Grant No. RE 3977/1), through the SFB/TRR 227 ”Ultrafast Spin Dynamics” (projects A09 and B07), the SFB 925 ”Lichtinduzierte Dynamik und Kontrolle korrelierter Quantensysteme” (project B2), and the Max Planck Society. F.P. acknowledges funding from the excellence cluster “The Hamburg Centre for Ultrafast Imaging - Structure, Dynamics and Control of Matter at the Atomic Scale” of the Deutsche Forschungsgemeinschaft (DFG EXC 1074). M.D., R.E., and L.R. acknowledge funding from NFFA Europe (project 879). G.S., D.S., A.M., and E.P. acknowledge funding from MIUR PRIN Grant No.20173B72NB. This work was supported by VILLUM FONDEN via the Centre of Excellence for Dirac Materials (Grant No. 11744).
References
References
- Mueller and Malic (2018) T. Mueller and E. Malic, npj 2D Materials and Applications 2, 29 (2018), URL http://dx.doi.org/10.1038/s41699-018-0074-2.
- Steinhoff et al. (2017) A. Steinhoff, M. Florian, M. Rösner, G. Schönhoff, T. O. Wehling, and F. Jahnke, Nature Communications 8, 1166 (2017), URL http://dx.doi.org/10.1038/s41467-017-01298-6.
- Guerci et al. (2019) D. Guerci, M. Capone, and M. Fabrizio, Physical Review Materials 3, 054605 (2019), URL http://dx.doi.org/10.1103/PhysRevMaterials.3.054605.
- Kaindl et al. (2003) R. A. Kaindl, M. A. Carnahan, D. Hägele, R. Lövenich, and D. S. Chemla, Nature 423, 734 (2003), URL http://dx.doi.org/10.1038/nature01676.
- Huber et al. (2001) R. Huber, F. Tauser, A. Brodschelm, M. Bichler, G. Abstreiter, and A. Leitenstorfer, Nature 414, 286 (2001), URL http://dx.doi.org/10.1038/35104522.
- Pietzsch et al. (2008) A. Pietzsch, A. Föhlisch, M. Beye, M. Deppe, F. Hennies, M. Nagasono, E. Suljoti, W. Wurth, C. Gahl, K. Döbrich, et al., New Journal of Physics 10, 033004 (2008), URL http://dx.doi.org/10.1088/1367-2630/10/3/033004.
- Stefanucci and van Leeuwen (2013) G. Stefanucci and R. van Leeuwen, Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction (Cambridge University Press, 2013), ISBN 9781139023979, URL http://doi.org/10.1017/CBO9781139023979.
- Ertl and Thiele (1979) G. Ertl and N. Thiele, Applications of Surface Science 3, 99 (1979), URL http://doi.org/10.1016/0378-5963(79)90064-3.
- Ertl et al. (1980) G. Ertl, R. Hierl, H. Knözinger, N. Thiele, and H. Urbach, Applications of Surface Science 5, 49 (1980), URL https://doi.org/10.1016/0378-5963(80)90117-8.
- Asahi et al. (2001) R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki, and Y. Taga, Science 293, 269 (2001), URL https://science.sciencemag.org/content/293/5528/269.
- Biesinger et al. (2011) M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. Lau, A. R. Gerson, and R. S. Smart, Applied Surface Science 257, 2717 (2011), URL http://dx.doi.org/10.1016/j.apsusc.2010.10.051.
- Xu et al. (2009) Z. Xu, L.-M. Chen, G. Yang, C.-H. Huang, J. Hou, Y. Wu, G. Li, C.-S. Hsu, and Y. Yang, Advanced Functional Materials 19, 1227 (2009), URL http://dx.doi.org/10.1002/adfm.200801286.
- Citrin et al. (1977) P. H. Citrin, G. K. Wertheim, and Y. Baer, Physical Review B 16, 4256 (1977), URL http://dx.doi.org/10.1103/PhysRevB.16.4256.
- Hüfner (2003) S. Hüfner, Photoelectron Spectroscopy (Springer Berlin Heidelberg, 2003), URL https://doi.org/10.1007/978-3-662-09280-4.
- Mahan (2000) G. D. Mahan, Many-Particle Physics (Springer US, 2000), URL https://doi.org/10.1007/978-1-4757-5714-9.
- Lizzit et al. (1998) S. Lizzit, K. Pohl, A. Baraldi, G. Comelli, V. Fritzsche, E. W. Plummer, R. Stumpf, and P. Hofmann, Physical Review Letters 81, 3271 (1998), URL http://dx.doi.org/10.1103/PhysRevLett.81.3271.
- Doniach and Sunjic (1970) S. Doniach and M. Sunjic, Journal of Physics C: Solid State Physics 3, 285 (1970), URL http://dx.doi.org/10.1088/0022-3719/3/2/010.
- Dendzik et al. (2015) M. Dendzik, M. Michiardi, C. Sanders, M. Bianchi, J. A. Miwa, S. S. Grønborg, J. V. Lauritsen, A. Bruix, B. Hammer, and P. Hofmann, Physical Review B 92, 245442 (2015), URL http://dx.doi.org/10.1103/PhysRevB.92.245442.
- Dendzik et al. (2017) M. Dendzik, A. Bruix, M. Michiardi, A. S. Ngankeu, M. Bianchi, J. A. Miwa, B. Hammer, P. Hofmann, and C. E. Sanders, Physical Review B 96, 235440 (2017), URL http://dx.doi.org/10.1103/PhysRevB.96.235440.
- Ackermann et al. (2007) W. Ackermann, G. Asova, V. Ayvazyan, A. Azima, N. Baboi, J. Bähr, V. Balandin, B. Beutner, A. Brandt, A. Bolzmann, et al., Nature Photonics 1, 336 (2007), URL http://dx.doi.org/10.1038/nphoton.2007.76.
- Schönhense et al. (2015) G. Schönhense, K. Medjanik, and H.-J. Elmers, Journal of Electron Spectroscopy and Related Phenomena 200, 94 (2015), URL http://dx.doi.org/10.1016/j.elspec.2015.05.016.
- Hellmann et al. (2010) S. Hellmann, M. Beye, C. Sohrt, T. Rohwer, F. Sorgenfrei, H. Redlin, M. Kalläne, M. Marczynski-Bühlow, F. Hennies, M. Bauer, et al., Physical Review Letters 105, 187401 (2010), URL http://dx.doi.org/10.1103/PhysRevLett.105.187401.
- Ishizaka et al. (2011) K. Ishizaka, T. Kiss, T. Yamamoto, Y. Ishida, T. Saitoh, M. Matsunami, R. Eguchi, T. Ohtsuki, A. Kosuge, T. Kanai, et al., Physical Review B 83, 081104 (2011), URL http://dx.doi.org/10.1103/PhysRevB.83.081104.
- Siefermann et al. (2014) K. R. Siefermann, C. D. Pemmaraju, S. Neppl, A. Shavorskiy, A. A. Cordones, J. Vura-Weis, D. S. Slaughter, F. P. Sturm, F. Weise, H. Bluhm, et al., The Journal of Physical Chemistry Letters 5, 2753 (2014), URL http://dx.doi.org/10.1021/jz501264x.
- Liu et al. (2018) R.-Y. Liu, K. Ozawa, N. Terashima, Y. Natsui, B. Feng, S. Ito, W.-C. Chen, C.-M. Cheng, S. Yamamoto, H. Kato, et al., Applied Physics Letters 112, 211603 (2018), URL http://dx.doi.org/10.1063/1.5026351.
- (26) See Supplemental Material at … for additional information on the experimental details, theoretical model derivation, model-independent analysis, excitation density estimation and data processing.
- Kutnyakhov et al. (2020) D. Kutnyakhov, R. P. Xian, M. Dendzik, M. Heber, F. Pressacco, S. Y. Agustsson, L. Wenthaus, H. Meyer, S. Gieschen, G. Mercurio, et al., Review of Scientific Instruments 91, 013109 (2020), URL http://dx.doi.org/10.1063/1.5118777.
- (28) L. Hedin, B. Lundqvist, and S. Lundqvist, Electron Den- sity of States, ed I. H. Bennet (Washington, DC: Natl Bur. Stand.). Special Publication No 323 pp 233-47 (1971).
- Christiansen et al. (2019) D. Christiansen, M. Selig, E. Malic, R. Ernstorfer, and A. Knorr, Physical Review B 100, 205401 (2019), URL http://dx.doi.org/10.1103/PhysRevB.100.205401.
- Perfetto et al. (2019) E. Perfetto, D. Sangalli, A. Marini, and G. Stefanucci, Physical Review Materials 3, 124601 (2019), URL http://dx.doi.org/10.1103/PhysRevMaterials.3.124601.
- Steinleitner et al. (2017) P. Steinleitner, P. Merkl, P. Nagler, J. Mornhinweg, C. Schüller, T. Korn, A. Chernikov, and R. Huber, Nano Letters 17, 1455 (2017), URL http://dx.doi.org/10.1021/acs.nanolett.6b04422.
- Chernikov et al. (2015) A. Chernikov, C. Ruppert, H. M. Hill, A. F. Rigosi, and T. F. Heinz, Nature Photonics 9, 466 (2015), URL http://dx.doi.org/10.1038/NPHOTON.2015.104.
- Hellmann et al. (2012) S. Hellmann, C. Sohrt, M. Beye, T. Rohwer, F. Sorgenfrei, M. Marczynski-Bühlow, M. Kalläne, H. Redlin, F. Hennies, M. Bauer, et al., New Journal of Physics 14, 013062 (2012), URL http://dx.doi.org/10.1088/1367-2630/14/1/013062.
- Oloff et al. (2014) L.-P. Oloff, M. Oura, K. Rossnagel, A. Chainani, M. Matsunami, R. Eguchi, T. Kiss, Y. Nakatani, T. Yamaguchi, J. Miyawaki, et al., New Journal of Physics 16, 123045 (2014), URL http://dx.doi.org/10.1088/1367-2630/16/12/123045.
- Puppin (2018) M. Puppin, Ph.D. thesis (2018), URL http://dx.doi.org/10.17169/refubium-804.
- Tokudomi et al. (2007) S. Tokudomi, J. Azuma, K. Takahashi, and M. Kamada, Journal of the Physical Society of Japan 76, 104710 (2007), URL http://dx.doi.org/10.1143/JPSJ.76.104710.
- Bataller et al. (2019) A. W. Bataller, R. A. Younts, A. Rustagi, Y. Yu, H. Ardekani, A. Kemper, L. Cao, and K. Gundogdu, Nano Letters 19, 1104 (2019), URL http://dx.doi.org/10.1021/acs.nanolett.8b04408.