num_style

One notable class of the topological non-trivial states—nodal line semimetals—are the neighbor states to various topological quantum phases, such as three-dimensional Dirac semimetals, Weyl semimetals, topological insulators, spinful Weyl nodal line semimetals, and hence it is regarded as an ideal platform to study and control the quantum topological phase transition by breaking symmetriesYang2018 . 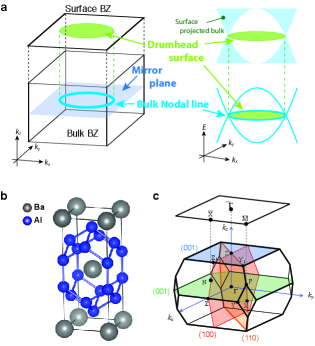In a topological nodal line semimetal, the linearly degenerate bands cross each other on a mirror plane giving rise to a nodal line in the momentum space (see cartoon in Fig. 1(a)). The crossing bands on the mirror plane cannot hybridize since they have opposite mirror eigenvalues, resulting in a stable nodal loop/line on the mirror plane. The projection of these bulk nodal lines onto the surface fills the inside of the nodal lines and generates the so-called drumhead surface stateChiu2016 ; Burkov2011 ; Zhao2013 ; Ryu2002 ; Bian2016 ; Kim2015 ; Ma2018 , given its resemblance to the head of an open drum. The peculiar momentum space structure of these states, flat in both energy and momentum, is critical for the realization of novel phenomenaTang2014 ; Kopnin2011 ; Magda2014 ; Shapourian2018 ; Sur2016 ; Wang2017a ; Imada2000 ; Peotta2015 ; Huber2010 ; Wu2007 ; Tasaki1992 ; Wang2016 ; Sun2011 ; Neupert2011 ; Pezzini2017 ; Matusiak2017 , such as topological superconductivityShapourian2018 ; Sur2016 ; Wang2017a ; Kopnin2011 ; Volovik2015 and magnetismMagda2014 . In the case of superconductivity, for example, the momentum extension of the drumhead state (area) is proportional to the pairing strength, and hence $T_{\text{c}}$Kopnin2011 ; Volovik2015 . Therefore, topological semimetals exhibiting drumhead surface states present a significant expansion of topological materials beyond topological insulators and nodal-point Dirac/Weyl semimetals.

Recently, BaAl₄ has been reported to have topological semimetallic features with 3D Dirac dispersions and possible nodal lines protected by crystal symmetryWangMori2021 . While this can explain several of the observed transport properties, it cannot fully account for the extremely large magnetoresistance, including quantum oscillationsWangMori2021 . In this paper, we use angle-resolved photoemission spectroscopy (ARPES) to study in detail the electronic structure of BaAl₄, focusing on the surface localized bands. BaAl₄ has the body-centered tetragonal structure in the space group of $I4/mmm$ (No. 139) as shown in Fig. 1(b), also known as a prototype parent crystal of a large family of compoundsWangMori2021 ; Paglione2010 ; Steglich1979 ; Stewart1984 ; Kneidinger2014 . The bulk and (001) surface projected BZs with high-symmetry points labelled are shown in Fig. 1(c). The crystal has three non-equivalent mirror-reflection planes $m_{001}$ (green and blue planes), $m_{110}$ (orange plane), and $m_{100}$ (red plane) (see Fig. 1(c)). The $m_{110}$ plane and $m_{100}$ plane have equivalent mirror planes along the orthogonal directions. Therefore, a number of Dirac nodal lines can exist on these planes when spin-orbit coupling (SOC) is negligible, leading to the presence of drumhead surface states.

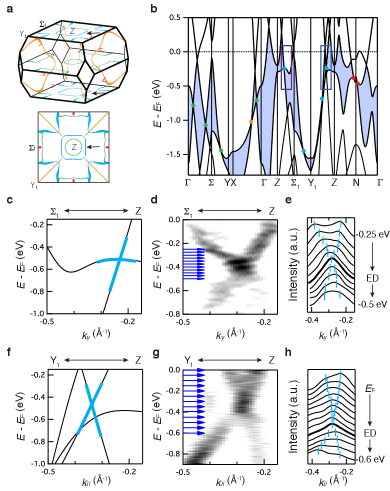
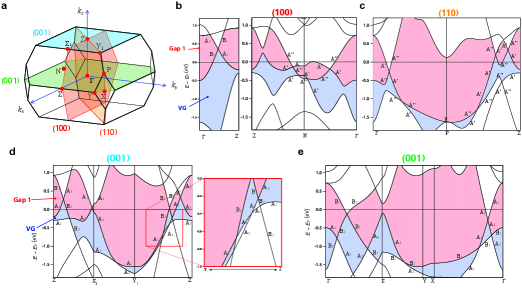
Fig. 2 shows the bulk electronic structure of BaAl₄. Panel (a) shows the theoretical bulk nodal lines without SOC. The energy and momentum dispersions along the high symmetry directions reveal the presence of several nodal points within the valence bands for each mirror plane (see dots in panel (b)). These nodal points, developing between the highest valence band and the second-highest valence band (Valence Gap (VG)), give rise to a variety of nodal lines in each mirror plane (see colored lines in panel (a)). The colors used in panels (a) and (b) for the nodal points/lines correspond to the same color scale used to represent the respective mirror plane (Fig. 1(c)). A detailed analysis of the irreducible representations for each crossing is shown in Supplementary Fig. 1 in the Supplementary Information (SI). Panels (c) and (d) show the calculated and experimental momentum and energy dispersions along the $\Sigma_{1}-$Z direction in the $k_{z}=2{\pi}/c$ plane. Following the maximum intensity, a Dirac like linear-shaped dispersion can be observed, in agreement with the theoretical calculation in panel (c). The dispersion can be better extracted by following the peak positions in the momentum distribution curves (MDCs) shown in panel (e) where two peaks disperse linearly throughout the entire energy range and cross at $\sim-0.4$ eV, namely the Dirac point. The non-gap linear feature is further confirmed in Supplementary Fig. 5 in the SI where the only one side of Dirac dispersion is observed due to the matrix element effectChen2012 ; Damascelli2003 . Panels (f)-(h) show the same as panels (c)-(e), respectively, but the momentum direction is the $\text{Y}_{1}-$Z direction in the $k_{z}=2{\pi}/c$ plane. Similar to the $\Sigma_{1}-$Z direction, the Dirac like linear dispersion can also be observed in the $\text{Y}_{1}-$Z direction and is confirmed by the MDCs spectra, where the two peaks disperse linearly and cross at the ED. Those Dirac nodes belong to one of the nodal loops in the $k_{z}=2{\pi}/c$ plane (see the black arrows in panel (a)). The lack of a gap in the spectra can be due to the absence of hybridization between the two spins and/or weak SOC as in this case, where the bands near $E_{\text{F}}$ in the VG region are mainly composed of Al $s$ and $p$ orbitals (see details in Supplementary Fig. 2 of the SI). Once SOC is introduced, the two spins are coupled and allowed to hybridize, resulting in a gap opening at each of the Dirac points/lines. This is true for each high symmetry directions, unless the $\Gamma-$Z direction where the two bands belong to different representation of the symmetry group, and therefore, their intersection is protected by the crystalline symmetry, $C_{4v}$. The details of the crystal symmetric information and topological nature with SOC are found in RefWangMori2021 . In the presence of weak SOC, the gap size becomes negligible, and this may be the case for the VG.

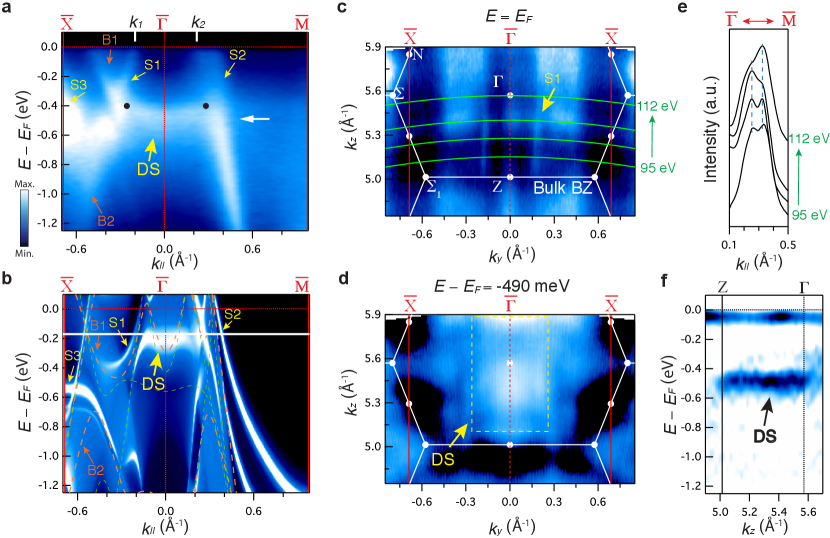
We now turn our attention to the surface localized electronic states. Thanks to the matrix element effect, the bulk and surface electronic structures can be characterized selectively (see the detail in Supplementary Fig. 4 in the SI). Fig. 3 shows the surface electronic structure within the surface BZ projected onto (001) plane. In addition to the bulk states identified in panel (b) (labelled as B1-B2), three new sets of features are observed in panel (a): sharp linearly dispersive states (labelled as S1-S2), a hole-like dispersion state (labelled as S3), and a weakly dispersive state (labelled as DS state). Similar features are observed in the surface states calculations shown in panel (b), pointing to their surface origin (see also Method section and Supplementary Fig. 3 in the SI for more details about the calculation). These multiple surface states, originating from the Dirac nodal lines, indicate their topologically protected nature. Note that the surface states calculation is sensitive to details of the simulations as reportedCucchi2020 , and surface effects, such as potential band bending and structural relaxation effects, are not included in the calculation. These effects might lead to apparent discrepancy between the experimental data (panel (a)) and theory (panel (b)). Other potential discrepancy could arise from matrix element effectsChen2012 ; Damascelli2003 . These effects can however be minimized by changing photon energy (see Supplementary Fig. 6 in the SI), revealing different features. The surface origin of these states is further supported by their photon energy dependence (i.e., $k_{z}$ dependence) as shown in panels (c–f). Throughout the whole range, negligible dispersions are observed for each of these states, confirming their surface state origin. Indeed, S1 and S2 states form straight vertical lines as indicated by yellow arrows in panel (c) and blue dashed line in panel (e), indicative of lack of $k_{z}$ dispersion. On the other hand, the DS state defines a sheet in the ($k_{y}$, $k_{z}$) plane (see dashed yellow rectangle in panel (d)), indicative of a localized state in $k_{z}$. This can be directly seen in panel (f), where the energy vs $k_{z}$ dispersion along the $\text{Z}-\Gamma$ direction shows a localized two-dimensional state.

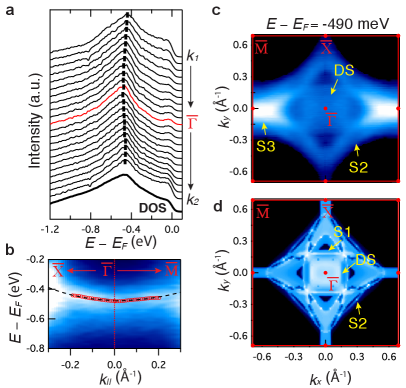
Among all the surface states, of particular interest is the DS state, which is the one appearing at $E=-0.49$ eV. Indeed, this state emerges out and connects the two Dirac bulk nodal lines, as expected in the case of a drumhead surface state (see also Fig. 3(a)). Fig. 4 presents its full momentum and energy characterization. The energy vs momentum dispersion (panel (b)), extracted from the peak position of the energy distribution curves (EDC) (panel (a)), appears weakly dispersing along both the $\bar{\Gamma}-\bar{\text{X}}$ and $\bar{\Gamma}-\bar{\text{M}}$ direction, with an overall bandwidth less than $38$ meV and $23$ meV respectively in the momentum range ($k_{1}-k_{2}$). This gives rise to an almost flat surface state with an effective mass of $m^{*}\simeq 4.0m_{e}$ and $6.1m_{e}$ and a peak in the density of state at the energy of the DS state (see the bold line in panel (a)). In panel (c), we show the momentum extension of the DS state. The constant energy map ($k_{y}$ vs $k_{x}$) at DS state shows that the DS state is localized in momentum along a well-defined filled square-shaped region, centered at the BZ center. The topology of the DS state is consistent with the confirmed bulk nodal loop (see Fig. 2(a)) and is confined within an area of $\sim$0.16 Å^-2, which corresponds to $\sim$8.5 % of the BZ. Additionally, the momentum location of the surface states S2-S3 is also visible in this energy window. In contrast, the main contribution of the S1 state appears near $E_{\text{F}}$ and is localized along a square-shaped region (see Supplementary Fig. S6 in the SI). The topology of these states is qualitatively consistent with the theoretical constant energy map shown in panel (d). All the data reported so far supports the existence of a strongly localized drumhead surface state in BaAl₄ and reveals its extended location in momentum space.

The localized nature of this state makes it unique with respect to previous studiesBian2016 ; Belopolski2019 ; Lou2018 ; Muechler2020 , where highly dispersive DS states have been reported. Indeed the flatness of our DS state drives a large density of states, as shown in Fig. 3–4, enhancing interaction effects significantly. The large area of the DS state is also promising in view of the enhancing the electrons’ interactionKopnin2011 ; Volovik2015 , although the first step would be to engineer the DS state close to the Fermi level. Finally, it is noteworthy to point out that the observed bulk nodal line might be also responsible for the reported transport anomaly, including the quantum oscillation and extremely large magnetoresistanceWangMori2021 . A complete quantification of the gap size in BaAl₄, and hence the topological classification of BaAl₄, requires more detailed calculations and further measurements. Even a small amount of lattice strain can tune the gap sizeTang2011 ; Winterfeld2013 ; Rodin2014 ; Teshome2018 ; Owerre2018 , resulting in a new type of Dirac semimetal, where both Dirac point and Dirac nodal lines may coexist.

In summary, by combining surface-sensitive ARPES experiments with the theoretical calculations, we have provided direct evidence for the existence of a flat extended surface state in a topological semimetal, BaAl₄. We present that the flat surface state fills inside of the bulk square-shaped nodal line by showing the full momentum space topology of such state. All the data reported here support that the observed flat band is directly associated with the observed Dirac nodal line, and therefore, the topological drumhead surface states. These results enable the exploration of such states for the realization of a number of novel correlated phases of matterShapourian2018 ; Sur2016 ; Wang2017a ; Kopnin2011 ; Volovik2015 ; Peotta2015 ; BERGHOLTZ2013 ; Wang2016 ; Peotta2015 ; Sun2011 ; Neupert2011 ; Tang2014 ; Magda2014 .

Methods

Single crystals of BaAl₄ were synthesized by a high-temperature self-flux method and characterized by X-ray diffraction at room temperature with Cu K_α ($\lambda=0.15418$ nm) radiation in a powder diffractometerWangMori2021 .

Electronic structure calculations were performed within the framework of the density functional theory (DFT) with the PAW pseudopotentials, as implemented in the Quantum Espresso packageGiannozzi2009 . The generalized gradient approximation (GGA) with the Perder-Burke-Ernzerhof parameterization (PBE) was usedPerdew1996 . A plane wave energy cut-off 40 Ry and 24$\times$24$\times$24 $k$-mesh to sample the BZ were used for the bulk calculations. Total energies were converged to smaller than $10^{-10}$. The experimental crystal data ($a=b=4.566$ Å, $c=11.278$ Å) were usedBruzzone1975 . The calculation of surface electronic structures was carried out with momentum resolved local density of states of a semi-infinite surface by employing a tight-binding (TB) model obtained by using the Wannier90Mostofi2014 and WannierTools suite of codeWu2018 . The quality of the Wannier function based TB model was checked by comparing it with the DFT calculation (see Supplementary Fig. S3 in the SI). The comparison of our experimental spectra with the theory-calculated surface states shows a good agreement with a 25 % expansion in the energy dimension of the calculation result. VESTA package was used for visualization of the crystal structureMomma2011 .

ARPES measurements on single crystalline samples of BaAl₄ were performed at the Beamline 4.0.3. end station of the Advanced Light Source in Berkley California. Samples were cleaved in situ to yield clean (001) surfaces and measured at 20 K in an ultra-high vacuum better than $3\times 10^{-11}$ Torr using the photon energy of 80-128 eV with Scienta R8000 analyzer. The energy resolution was 20-30 meV and the angular resolution was better than $0.2^{\circ}$ for all measurements. According to this photon energy dependence measurements, the inner potential of BaAl₄ is estimated to 10.5 eV.

Acknowledgments

This work was primarily funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05-CH11231 (Quantum materials KC2202) and used resources of the Advanced Light Source, a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. Research at the University of Maryland was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF9071, and the Maryland Quantum Materials Center. TM was supported by JST PRESTO (JPMJPR19L9), and JST CREST (JPMJCR19T3).

Author contributions

A.L., J.P., and R.M. initiated and directed this research project. R.M. carried out ARPES measurements with the assistance of J.D.D. R.M. calculated the band structure and analyzed the ARPES data. A.L. and R.M. wrote the text, with feedback from all authors. The samples were grown and characterized by K.W. T.M. provided theoretical insight.

Competing Interests

The authors declare that they have no competing financial interests.

Correspondence

Correspondence and requests for materials should be addressed to A.L. (email: [email protected]).

Data availability

The data that support the finding of this study are available from the corresponding author upon request.

Supplementary Note 1: Irreducible representations of crossing points

Supplementary Fig. 1 shows the irreducible representations of the band structures for each crossing point. The crystal structure of BaAl₄ has three non-equivalent mirror-reflection planes $m_{001}$ (green and light-blue planes), $m_{110}$ (orange plane), and $m_{100}$ (red plane). The $m_{110}$ plane and $m_{100}$ plane have equivalent mirror planes along the orthogonal directions. The crossing bands on these mirror planes cannot hybridize because of the different irreducible representations of the space group where the two crossing bands belong to opposite mirror eigenvalues. Therefore, these crossing bands form nodal loops/lines on mirror planes.

Supplementary Note 2: Orbital contribution near $E_{F}$

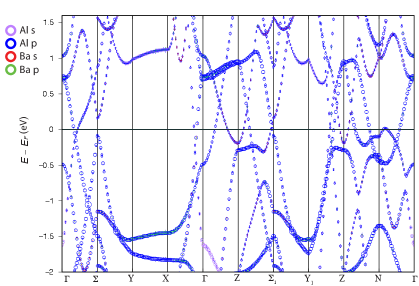
To see the orbital contribution for the band structures near $E_{\text{F}}$, the orbital projected band dispersions are calculated as shown in Supplementary Fig. 2. The size of circles represents the relative weight of orbital projection onto Al-$p$, Al-$s$, Ba-$s$, and Ba-$p$ orbitals. The bands near $E_{\text{F}}$ are composed mainly of Al-$p$ and Al-$s$ orbital, resulting in small SOC effects. Once SOC is included in the calculation, hybridization leads to gap opening. The size of the gap is directly related to the strength of SOC.

Supplementary Note 3: Wannier function for tight-binding

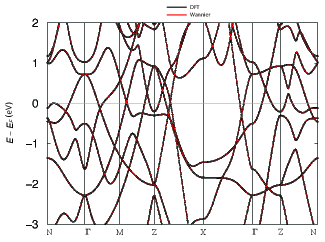
To help understand the observed electronic structures in the main text, we create Wannier function based tight-binding model. Supplementary Fig. 3 shows the band dispersions based on DFT (black lines) and Wannier functions (red lines). This tight-binding model can well reproduce the energy bands near $E_{\text{F}}$, which are crucial to the band topology. This Wannier function-based model is used in the surface electronic structure calculation shown in the main text.

Supplementary Note 4: Bulk and surface electronic structures

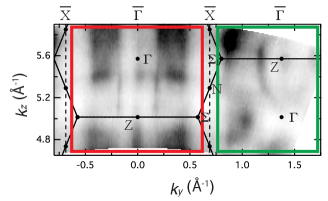
Thanks to the matrix element effect, the bulk and surface electronic structures can be characterized selectively. In Supplementary Fig. 4, we show the out-of-plane Fermi surface mapping taken with the different photon energies. In the red square region in the panel, negligible dispersions are observed throughout the whole range, confirming their surface state origin. On the contrary, the dispersive electronic structures are observed in the different BZ (see the green square region), suggesting their bulk state origin. The observed bulk states here are consistent well with the calculated Fermi surface (see RefWangMori2021 for more details about the bulk structure).

Supplementary Note 5: Bulk Dirac nodes

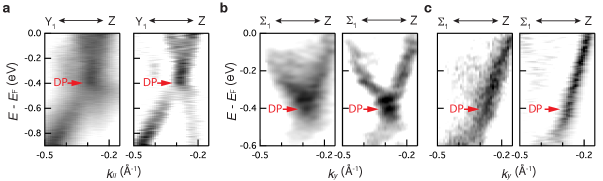
As shown in Fig. 2 in the main text, the bulk Dirac nodes along two high-symmetric lines in $k_{z}=2{\pi}/c$ plane are observed. Supplementary Fig. 5(a)-(b) show the raw normalized spectra and their second derivative along $\text{Y}_{1}-$Z direction. and $\Sigma_{1}-$Z, respectively. Panel (c) shows the experimental result along $\Sigma_{1}-$Z direction (the same direction as panel (b)), but taken in the different BZ. In this BZ, the only one side of Dirac dispersion is observed due to the matrix element effect, further confirming the non-gap linear dispersion.

Supplementary Note 6: Photon energy dependence of bulk and surface states

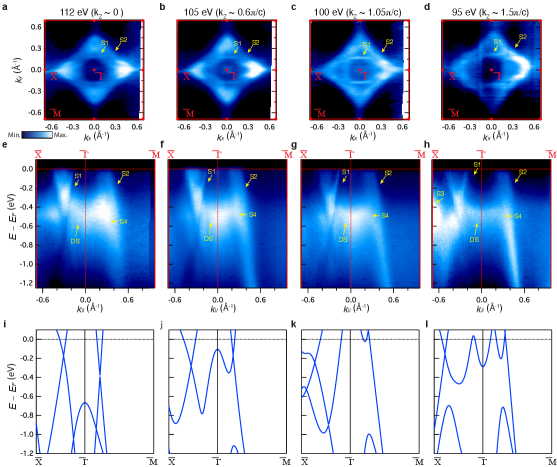
Photon energy dependence is a powerful way to extract the $k_{z}$ dependence of electronic structures. The $k_{z}$ dependence can be obtained by changing photon energy using the free-electron final state approximation:

where $m_{e}$ is the free electron mass, $E_{i}$ is the energy of the initial state, $h\nu$ is the photon energy, $\Phi$ is the work function, $\theta$ is the emission angle of photoelectrons, and $V_{0}$ is the inner potential. Electronic structures taken with the different photon energies resolve the surface nature of the observed spectra; surface states are two-dimensional states and hence showing no $k_{z}$ dependence, while bulk states show $k_{z}$ dispersive three-dimensional feature.

Supplementary Fig. 6 shows the experimental spectra (panels (a–h)) and the calculated bulk structures for several different photon energies, corresponding to different $k_{z}$ values in panels (i–l); $k_{z}\sim 0$ ($h\nu=112$ eV in (i)), $k_{z}~{}\sim 0.6\pi/c$ ($h\nu=105$ eV in (j)), $k_{z}~{}\sim 1.05\pi/c$ ($h\nu=100$ eV in (k)), and $k_{z}~{}\sim 1.5\pi/c$ ($h\nu=95$ eV in (l)). The Fermi surface mappings (panels (a)-(d)) confirm that the topology of the observed surface states (S1-S2) near $E_{\text{F}}$ is consistent with the theoretical constant energy map shown in Fig. 4(d) in the main text. By comparing the experimental spectra (panels (e)-(h)) and the bulk calculations (panels (i)-(l)), the S1–S4 states and the DS state are clearly distinguished from the bulk electronic features, validating their surface origins. Note that the matrix element effects play a different role for different photon energy, leading to the different appearance of these states. Indeed, S4 appears in panels (e)-(g) and the intensity is suppressed in panel (h), and S3 appears in panel (h).