Observation of 4- and 6-magnon bound-states in the spin-anisotropic frustrated antiferromagnet FeI₂

Spin-waves e.g. magnons are the conventional elementary excitations of ordered magnets. However, other possibilities exist. For instance, magnon bound-states can arise due to attractive magnon-magnon interactions and drastically impact the static and dynamic properties of materials Torrance and Tinkham (1969); Hoogerbeets et al. (1984). Here, we demonstrate a zoo of distinct multi-magnon quasiparticles in the frustrated spin-1 triangular antiferromagnet FeI₂ using time-domain terahertz spectroscopy. The energy-magnetic field excitation spectrum contains signatures of one-, two-, four- and six-magnon bound-states, which we analyze using an exact diagonalization approach for a dilute gas of interacting magnons. The two-magnon single-ion bound states occur due to strong anisotropy and the preponderance of even higher order excitations arises from the tendency of the single-ion bound states to themselves form bound states due to their very flat dispersion. This menagerie of tunable interacting quasiparticles provides a unique platform in a condensed matter setting that is reminiscent of the few-body quantum phenomena central to cold-atom, nuclear, and particle physics experiments.

Insulating spin systems are widely studied for their unconventional ground states, exotic magnetic excitations and spin textures. Geometrically frustrated lattices, like the 2D antiferromagnetic triangular lattice, can lead to the suppression of magnetic order at low temperatures and the emergence of fractionalized excitations Broholm et al. (2020); Gingras and McClarty (2014). But even a long-range ordered magnetic phase can exhibit excitations that are entirely distinct from conventional magnons. For instance, depending on spin-space anisotropies and the range of magnetic interactions, single-magnon quasiparticles can interact attractively with each other, generating multi-magnon bound states. The existence of such bound states was first predicted in the 1930s by Bethe Bethe (1931) in 1D quantum magnets, using a spin-1/2 Heisenberg model. These exchange-driven bound-states are usually observed in 1D ferromagnetic spin chains with S $\leq$ 1 Torrance and Tinkham (1969); Hoogerbeets et al. (1984); Chauhan et al. (2020). Although two-magnon bound states have been detected in experiments, evidence for even higher order magnon bound states remains scarce. Recently, a 3-magnon bound state was observed in a quasi-1D antiferromagnetic spin chain system with $S\!=\!2$ Dally et al. (2020). Because of their potential for a deeper understanding of fundamental phenomena in magnetism and of few-body problems (i.e. quantum mechanics of a finite number n$>$2 of interacting particles), such excitations are of intense current interest in the study of insulating magnets Nishida et al. (2013); Kato et al. (2020); Wang et al. (2018); Keselman et al. (2020); Yoshida et al. (2017); Pradhan et al. (2020); Ward et al. (2017); Wulferding et al. (2020). But they are also important for potential technological applications since they can for example strongly affect the transport properties in a one-dimensional chain of qubits Subrahmanyam (2004).

Here we study multi-magnon bound state excitations in the spin-anisotropic triangular lattice antiferromagnet FeI₂. The magnetic Fe²⁺ ions in this compound carry $S\!=\!1$ and are distributed on hexagonal planes (Fig. 1). In zero magnetic field, FeI₂ orders spontaneously in a striped antiferromagnetic phase below $T_{N}$ $\approx$ 9 K Fert et al. (1973). One distinctive feature for the $S\!=\!1$ spins in FeI₂ is that the energy of two spin deviations on a single-site – a particular form of 2-magnon excitation called single-ion bound-state (SIBS, Fig. 1d) – is comparable or even lower than the energy of a single magnon (Fig. 1c). Recent neutron scattering experiments in zero magnetic field at T $<$ $T_{N}$ revealed that this effect stems primarily from the balance between strong easy-axis single-ion anisotropy $D$ and nearest-neighbor ferromagnetic exchange interaction $J_{1}$ Bai et al. (2020), although competing further-neighbor exchange interactions are necessary to explain the complex magnetic structure and details of the excitation spectrum. Modeling of these neutron scattering measurements also evinced that the large spectral weight and weak dispersion of the SIBS originates from a hybridization with the single-magnon band through off-diagonal exchange interactions. As we will see below, the almost flat band nature of the SIBS promotes further bound states formation and allows for a very rich phenomenology to develop.

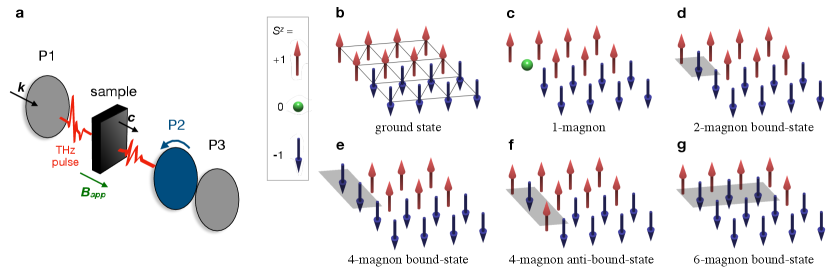
In the presence of a $\boldsymbol{c}$-axis magnetic field, FeI₂ undergoes several metamagnetic transitions Wiedenmann et al. (1988); we only study the low-field antiferromagnetic phase here (at T $=$ 4 K and $\mu_{0}$H $<$ 5 T). Using time-domain THz spectroscopy (TDTS) we find evidence for a variety of low energy multi-magnon excitations (up to 6-magnon character), along with interactions and hybridization between them. Through a comparison with exact diagonalization calculations for a generalized spin-wave Hamiltonian, our work elucidates how hybridization and interactions between magnetic excitations with different quantum numbers stabilize a low-energy subspace with at least 4 distinct types of quasiparticles. The presence of distinct low-energy excitations that can be tuned by magnetic field is of general interest for the comprehensive understanding of interacting quasiparticles in materials.

We conducted TDTS measurements as a function of magnetic field ($\mu_{0}H\leq 5$ T along the crystal $\boldsymbol{c}$ axis) to study the low-energy magnetic excitations of FeI₂ ($\nu\leq 1.5$ THz $\equiv 6.2$ meV) in the antiferromagnetic phase at $T\!=\!4$ K. The Faraday geometry of the experiment (Fig. 1a) allows extracting the transmission eigenstates for both left-handed (LCP) and right-handed circular polarization (RCP) via the polarization modulation technique (see Methods). Employing long time scans of $50$ ps along with reference spectra at higher temperatures Morris et al. (2014) yields a high-frequency resolution appropriate for distinguishing resonance peaks separated by $\Delta\nu\approx 0.02$ THz (0.08 meV). While this procedure allows measuring fine features in frequency-dependent spectra, it does not allow us to extract the magnitude of the transmission coefficients with quantitative precision. We thus normalize intensity plots to their maximum value.

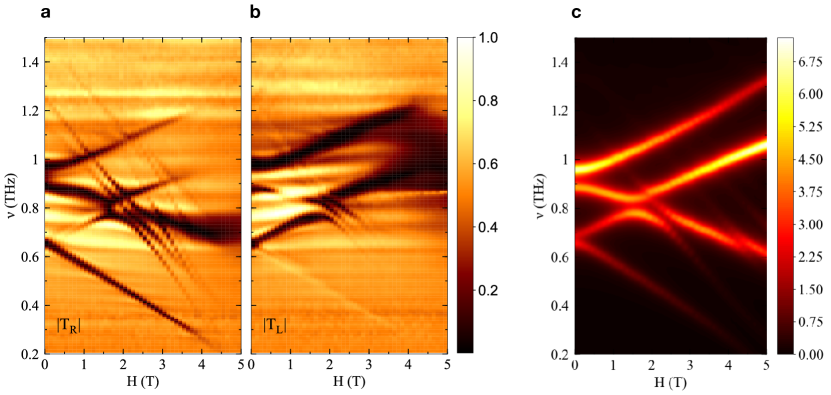
The frequency ($\nu$) and magnetic-field ($\mu_{0}H$) dependence of the complex transmission functions, plotted in magnitude as $|T_{R}|$ (RCP, Fig. 2a) and $|T_{L}|$ (LCP, Fig. 2b) shows dark regions corresponding to strong absorption. We associate these absorption lines with a wealth of distinct magnetic excitations with several crossings and apparent hybridizations. At fixed frequency and magnetic field, most branches show a different response in the RCP and LCP channels; several resonances are present in both channels. The steep field-slope of several branches is clear evidence for their multi-magnon character, as discussed further below. Earlier far-infrared spectroscopy and electron spin resonance studies Petitgrand et al. (1980); Katsumata et al. (2000) observed the zero-field absorption branches at $\nu=0.65,0.88$ and $0.97$ THz. The high energy and field resolution of our experiments uncover new and very steep branches, as well as additional details that are important to fully understand the low-energy excitations of FeI₂ (see Supplemental Information for comparison to earlier results).

To gain further insight, we extract the absorption lines’ position by inspecting the spectra for both polarization channels (Fig. 3a). Weak modes are sometimes difficult to track from these spectra, and we infer their energies from 2D intensity plots, along with error-bar estimates. In addition to elucidating the slope of all observed branches, i.e. the different $\boldsymbol{c}$-axis magnetization $S^{z}$ of the underlying excitations, this data elucidates crossing and hybridization between modes with different slopes. Given that the uniform magnetization is small below $5$ T, these excitations can be further characterized via the sign of $S^{z}$ relative to the magnetic field. In Faraday geometry, this is related to the circular dichroism of the material, which we plot using the imaginary part of the complex angle $\theta_{F}=\arctan[(T_{R}-T_{L})/i(T_{R}+T_{L})]$, the ellipticity (see Methods), as a function of frequency and magnetic field (Fig. 3b). As absorptions mainly appear in either the RCP or LCP channel, this accentuates the fact that different excitation branches exhibit different signs of $S^{z}$ (Fig. 3b).

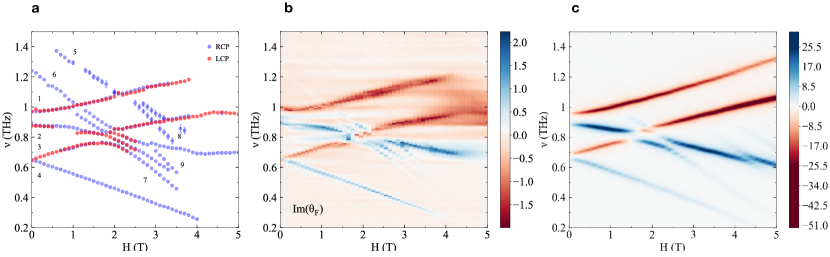
The evolution of the excitation energies with the magnetic field yields effective g-factors (see SI for extracted values) from which we identify at least four different kinds of excitations, including the previously reported single modes and 2-magnon excitations (branches labeled #1 to #4 in Fig. 3a), the latter with single-ion bound-state (SIBS) character (Fig. 1c–d). Given that the SIBS excitations have an almost flat dispersion throughout the Brillouin Zone Bai et al. (2020), and given the ferromagnetic nature of nearest-neighbor exchange interactions, SIBS display a strong propensity to form bound states with themselves. As a result, we infer that excitations with the highest effective g-factors (branches labeled #5 to #9 in Fig. 3a) are exchange bound states comprising primarily two and three SIBS, i.e. 4-magnon (Fig. 1e) and 6-magnon bound states (Fig. 1g), respectively. For all excitations, we observe effective g-factors that do not reach precisely the maximum hypothetical values of twice, four times, or six times that of single magnon excitations. We associate this effect to the hybridization between the different excitations, e.g. a 4-magnon bound state can still be regarded as a bound state of two SIBS, but other states mix in when proximate in energy. In fact, similar to neutron scattering experiments Bai et al. (2020), the multi-magnon bound states in FeI₂ only become detectable in TDTS due to their hybridization with single magnon modes.

Additional insight on the role of multi-magnon hybridization in FeI₂ is gained by calculating the absorption spectra using the microscopic spin-exchange Hamiltonian

where $Q_{i}^{zz}=(S_{i}^{z})^{2}-2/3$, the values of the exchange parameters ${\cal J}_{ij}^{\mu\nu}$ and single-ion anisotropy $D$ have been established from the neutron scattering data Bai et al. (2020), and $g=3.2$ Petitgrand et al. (1980). As previously demonstrated, the nearest-neighbor interactions in FeI₂ are spatially-anisotropic and include symmetric off-diagonal terms, $J_{1}^{z\pm}$ and $J_{1}^{\pm\pm}$, that are responsible for the hybridization between states with different $S^{z}$, such as the single-magnon and SIBS. A generalized spin-wave Hamiltonian describes the model’s low-energy spectrum as a dilute gas of interacting single-magnon and SIBS quasiparticles, which are treated on equal footing Muniz et al. (2014); Bai et al. (2020). To study this problem beyond linear spin-wave theory, we enforce the dilute limit by eliminating states with more than two quasiparticles from the Hilbert space (see SI) and perform an exact diagonalization (ED) of the restricted spin-wave Hamiltonian on a finite lattice of $5\times 5\times 5$ unit cells (500 spins). As the Hilbert space dimension becomes prohibitively large for ED if we include states with three quasiparticles, our calculation can only account for 1-, 2- and 4-magnon excitations and ignores the 6-magnon states.

The results of our theoretical calculations are shown through the angular average of the frequency-weighted susceptibility $\omega\left[\chi^{\prime\prime}_{xx}(q=0,\omega)+\chi^{\prime\prime}_{yy}(q=0,\omega)\right]$ (Fig. 2c) and as the difference between the absorption in the right and the left channels via $\omega\left[\chi^{\prime\prime}_{+-}(q=0,\omega)-\chi^{\prime\prime}_{-+}(q=0,\omega)\right]$ (Fig. 3c). Both plots exhibit a remarkable correspondence with the experimental data (excepting the absence of 6-magnon excitations in the ED). Compared to the linear generalized spin-wave approach of Ref. Bai et al. (2020), ED includes non-linear interactions that slightly renormalize quasiparticle energies. Therefore, precisely reproducing the energies of the low-energy modes in zero-field requires us to slightly adjust the parameters in Eq. 1 (see SI) compared to Ref. Bai et al. (2020).

ED calculations give the absolute value of the change in $\boldsymbol{c}$-axis magnetization, $|\Delta S^{z}|$, for each excitation branch as a function of frequency and magnetic field (Fig. 4). Given that the striped magnetic structure of FeI₂ has several sub-lattices, we expect various branches to be present for each magnon sector, some of which optically inactive due to sub-lattice effects. The color-coded expectation value of $|\Delta S^{z}|$ shows that in the absence of hybridization ($J_{1}^{z\pm}=J_{1}^{\pm\pm}=0$), excitations have a well defined $S^{z}$ character, with single and two-magnon modes in purple and blue, respectively (Fig. 4a). The four two-magnon branches are degenerate at zero field as SIBS are completely localized on each lattice site. The Zeeman term splits the zero-field SIBS quartet into two doublets. In the presence of the hybridization terms $J_{1}^{z\pm}$ and $J_{1}^{\pm\pm}$, the two SIBS doublets are split by the $J^{z\pm}$ term via hybridization with non-degenerate single-magnon modes (Fig. 4b). Including 4-magnon excitations yields a rich excitation spectrum with a sequence of hybridization effects between all types of excitations between 1 T and 4 T (Fig. 4c).

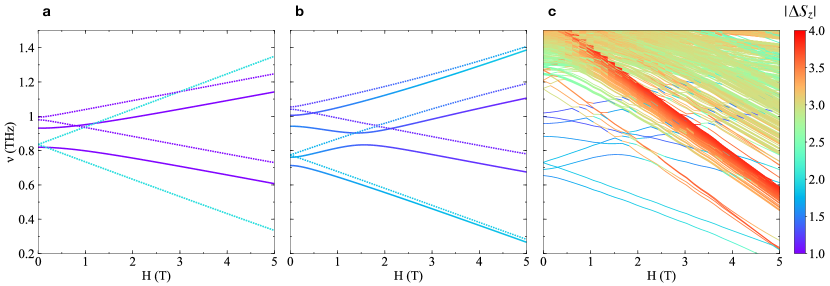
These results highlight that the character of magnetic excitations in FeI₂ in an applied magnetic field is profoundly affected by their strong mutual hybridization; most branches have a mixed and changing $|\Delta S^{z}|$ character. Therefore, even if the effective g-factors give some insight into the nature and degeneracies of the observed resonances, labeling excitations based on their $S^{z}$ is not possible. Given that excitation branches #5, #6 and #7 from Fig. 3a have primarily 4-magnon character by comparison to theoretical predictions (Fig. 4c), the even larger slope of excitation branches #8 and #9 indicate an even higher-order character, i.e. these are primarily 6-magnon bound states. The hybridization of 4- and 6-magnon bound states with lower-order excitations has three important consequences. First, they become detectable in TDTS in the proximity of energy crossings. Second, this explains why the effective g-factors of the steeper branches do not reach their hypothetical maximum values, as mentioned above. Finally, it explains why the four low-field branches, labeled #1 to #4 in Fig. 3a, have comparable absorption intensities and similar slopes. These are roughly equal mixtures of single and two-magnon excitations.

In summary, we have used high frequency-resolution time-domain terahertz spectroscopy in a magnetic field to study the spin-anisotropic frustrated compound FeI₂ and developed a quantitative understanding of the nature of its low-energy excitations for fields up to around 4 T. Our experiments unraveled a wealth of multi-magnon excitations, including 4-magnon and 6-magnon bound states. ED calculations of a generalized spin-wave Hamiltonian Bai et al. (2020) elucidated spectral contributions from each $|\Delta S^{z}|$ sector, enabling a complete understanding of the microscopic character of excitations up to 4-magnons. The strong hybridization that stems from spin-space anisotropy leads to a unique spectroscopic situation where bound states and their interactions can be tracked as a function of the magnetic field. Thus, FeI₂ is a promising field-tunable material platform to study fundamental quantum phenomena in magnetism and strongly-interacting few-body models encountered in various contexts such as excitons in semiconductors, cold atoms, and nuclear and particle physics.