Observable proton decay and gauge coupling unification in the improved missing doublet SU(5) model
Abstract
We investigate the possibility of observable proton decay within the improved missing doublet model (IMDM75), which utilizes a Higgs in 75 representation for gauge symmetry breaking. The realization of observable proton decay in IMDM75 is made feasible primarily due to chirality nonflipping color-triplet mediation, while chirality flipping mediation is adequately suppressed. Our predictions suggest a range of proton lifetimes between yr, which can be observed in upcoming experiments such as Hyper-K and DUNE, for a corresponding range of color-triplet mass parameter in the order of GeV. IMDM75 is shown to offer unique predictions for branching ratios when compared to other grand unified theory models. Finally, a realization of successful gauge coupling unification is achieved, even with the presence of particles at intermediate scales.
I Introduction
Proton decay serves as a very important discriminator in distinguishing among the various models of grand unified theories (GUTs) such as , flipped , Pati-Salam model, and , etc. Even different versions of the same model can lead to distinct predictions. Currently, Super-K sets a lower limit on proton lifetime [1, 2, 3, 4, 5, 6], while future experiments such as JUNO [7], DUNE [8, 9], and Hyper-K [10] with enhanced sensitivities are expected to distinguish between different GUT models.
The minimal supersymmetric model has been extensively studied in relation to proton decay, particularly with regard to the mediation of color triplets through dimension-five operators [11, 12, 13, 14, 15]. However, a major challenge is the doublet-triplet splitting problem, where both electroweak doublets and color triplets in 5-plets acquire masses of similar orders. A successful realization of electroweak symmetry breaking requires the electroweak doublets to be sufficiently light. On the other hand, to prevent rapid proton decay, it is necessary for the color triplets to have a sufficiently heavy mass. To address this issue, a missing partner mechanism was proposed, which involves replacing the standard GUT Higgs with a -plet and adding a pair of GUT mass -plets to the minimal matter content of the model [16]. This allows the color triplets in 5-plets to mix with those in 50-plets and acquire heavy masses, while the electroweak doublets remain light. However, the presence of large representations like the and -plets makes the model nonperturbative just above the GUT scale. A modified version [17, 18] overcomes this issue by assigning Planck-scale masses to the -plets and introducing additional pairs of 5 and 50-plets. To delve into the modified version and its variants that have undergone a phenomenologically acceptable treatment, one can refer to the following sources: [19, 20, 21, 22, 23, 24, 25].
This paper explores the improved missing doublet model (IMDM75) [20] in the context of searching for observable proton decay. Similar to the modified version, this improved model includes additional pairs of 5 and 50-plets. In addition, it employs an anomalous symmetry that solves the doublet-triplet problem without requiring any additional discrete or global symmetries. along with anomalous symmetry can be embedded in a realistic string theory, as the existence of such an anomalous symmetry does not imply an anomaly in the string theory [26]. The findings of this investigation show that IMDM75 predicts observable proton decay via chirality nonflipping color-triplet mediation, making it an important target for next-generation proton decay experiments. A detailed investigation of observable proton decay in IMDM75 along with a consistent two-loop gauge coupling unification is the prime focus of this paper.
The paper is structured as follows: Section II outlines the matter content and superpotential of IMDM75, along with the charge assignments under the anomalous symmetry. In Sec. III, we discuss the different modes of proton decay mediated by chirality flipping and nonflipping color triplets. Section IV provides a brief comparison of IMDM75’s predictions for proton decay with those of other GUT models. Section V describes a successful realization of gauge coupling unification, along with a discussion of the matching conditions in the presence of additional intermediate-scale particles beyond the minimal content of the minimal supersymmetric standard model (MSSM). Our conclusions are summarized in Sec. VI.
II IMDM75
The matter content of MSSM and the right-handed-neutrino superfield reside in and representations of respectively, as shown in Table 1. The GUT Higgs superfield is denoted by representation whereas the electroweak doublets arise from the mixing of and -plets. An anomalous symmetry, broken by the nonzero vacuum expectation value (VEV) of a gauge singlet field via anomalous D term[27, 28, 29], is imposed on the model, as described in [20]. The charge assignment under symmetry and matter parity for all superfields are provided in Table 2. Note that the field has a charge of under and takes values . The matter parity is utilized to eliminate undesired terms in the superpotential and to obtain a potential cold dark matter candidate. Interestingly, the appearance of matter parity can be an accidental by-product of the symmetry breaking, as discussed in [20]. It is noteworthy that for and , only the subgroup of the symmetry is sufficient to restrict the model. This implies a complete breakdown of the symmetry once obtains a VEV, eliminating any potential domain wall problems. An additional set of and -plets () is necessary to prevent rapid proton decay while maintaining gauge coupling unification (GCU), as explained in [20].
| + + | |
| + | |
| + | |
| + | |
| + + | |
| + + + | |
| + + + | |
| + + | |
| + + | |
| + + | |
| + + + | |
| + + | |
| + + + |
The superpotential for the IMDM75 model with symmetry, as shown in Table 2, is given by
| (1) | |||||
where generation indices have been suppressed. The first two terms in break the symmetry and attain the VEV of in the singlet direction of MSSM gauge symmetry . The Yukawa interactions of charged superfields are described by the terms in the second line, while the third and fourth lines provide heavy masses to the color triplets in 5- and 50-plets and leaving the electroweak doublets in 5-plets massless. This is the missing partner mechanism, which solves the doublet-triplet splitting problem without requiring parameter fine-tuning. The fifth line provides heavy masses of the order of GeV to 50-plets while keeping the model perturbative above the GUT scale. The first two terms in the last line explain tiny neutrino masses through the seesaw mechanism [30]. The last term, , includes all relevant nonrenormalizable terms that will be discussed later.
The symmetry in the IMDM75 model forbids the term, which leads to the electroweak doublets in and remaining massless up to all orders. To generate the MSSM term for the light electroweak doublets, the Giudice-Masiero mechanism [31] can be utilized, which is a consequence of supergravity breaking in the hidden sector. The term leads to same mass matrix for down type quark and charges leptons. This can be avoided by using nonrenormalizable term
| (2) |
Yukawa terms for quarks and charged leptons in superpotential of IMDM75 include
| (3) | |||||
where and are generation indices. After diagonalizing Yukawa couplings and calculating mass eigenstates, down-type quark and charged lepton Yukawa couplings are redefined as
| (4) | |||||
| (5) |
The Yukawa terms in the effective superpotential can be expressed in terms of mass eigenstates as
| (6) | |||||
here are color indices. are diagonalized Yukawa couplings effectively. Furthermore, fermion mass hierarchy is explained by introducing a generation-dependent horizontal symmetry and incorporating nonrenormalizable terms from in [20].
III Proton decay in IMDM75
Proton decay can occur via the color triplets through dimension-five and -six operators. On the other hand, GUT gauge bosons can mediate proton decay only through dimension-six operators at the leading order. Chirality flipping and nonflipping operators contribute to both dimension-five and -six levels. However, we can observe testable predictions only through the chirality nonflipping operators in color-triplet mediation as explained below.
III.1 Dimension-five proton decay
A detailed analysis of proton decay originated from the dimension-five operators is in order. In IMDM75 the renormalizable operators involving color triplets are
| (7) | |||||
| (8) | |||||
These Yukawa interactions along with chirality flipping mass term, , lead to dimension-five proton decay operator with two scalars and two fermions, as shown in Fig. 1.


If allowed the chirality flipping mass term, , leads to fast proton decay even with color-triplet masses of the order of GUT scale, thanks to the symmetry which forbids this term in IMDM75 up to all orders. This term, however, can arise indirectly via symmetry-breaking interactions induced by the VEV , as explained below.
As a matter of convenience, the mixing terms of the color triplets among, and in Eq. (1) are represented diagrammatically in Fig. 2.



Especially, the effective mass term, , is generated via as
| (9) |
where
| (10) |
and GeV is the reduced Planck mass. This term ensures that the electroweak doublets and the color triplets in -plets acquire the same masses, disregarding any mixing terms of the color triplets. Moreover, it results in an effective term, , as depicted in Fig. 3.

However, it is important to note that the effective term, , couples only the color triplets in and not the electroweak doublets, as there are no electroweak doublets in 50-plets.
The mass matrix relevant for chirality flipping color-triplet mediation is given by
| (11) |
where the mass matrix element relevant for proton decay via chirality flipping term is
| (12) |
The dimension-five proton decay interactions contribute in a loop diagram, which generates the effective dimension-six four-Fermi proton decay operator. The decay rate, aside from loop factors, varies as
| (13) |
where the mass arises from the term of the GM mechanism. We obtain GeV and for typical parameter values. Thus, we conclude that proton decay in IMDM75 through chirality flipping dimension-five operators is safe from rapid proton decay.
Next, we examine a different type of dimension-five operators for proton decay, which arise due to the intermixing of renormalizable and nonrenormalizable interactions from as follows
| (14) |
We will refer to the dimension-five proton decay operators, which result from the mixing of renormalizable and nonrenormalizable interactions in , as heterogeneous operators. The reason for this is that the color triplets involved in these operators originate from different representations of , namely, the - and -plets. Figure 4 depicts these operators diagrammatically.

Although potentially dangerous for proton decay, these heterogeneous operators do not significantly contribute to the decay rate due to an extra suppression factor. Specifically, for , this factor is . It is worth noting that the contribution of the dimension-five proton decay operator, which is induced by a Planck-scale suppressed operator , is suppressed by the symmetry, as also discussed in [20].
III.2 Observable chirality nonflipping dimension-six proton decay
Proton decay induced by the dimension-six operators is mediated through both the gauge bosons and the color triplets . The interaction terms for the gauge boson mediation arise from the following part of the Kähler potential
| (15) | |||||
where is a diagonal matrix such that and represents the Cabibbo-Kobayashi-Maskawa (CKM) matrix. Feynman diagrams for gauge boson mediated proton decay are shown in Fig. 5.


These interactions correspond to proton decay operators of the chirality type.
The proton decay operators of chirality type, mediated by color triplets, can be depicted through the diagrams in Fig. 6 for dimension-six.


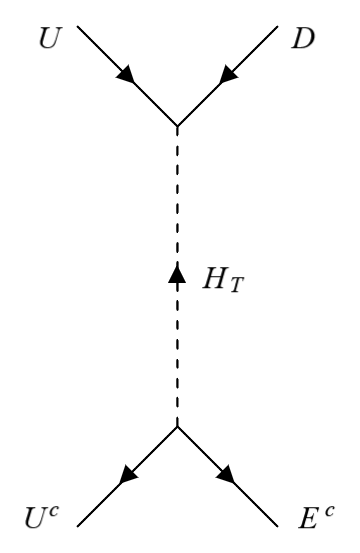

Even though Figs. 6a and 6b have two fermions and two scalars, they originate from the dimension-six operators, as clarified in [32]. These operators undergo further dressing in the box diagram to generate the four-Fermi proton decay operators effectively. Hence, their contribution to the proton decay rate is expected to be comparatively suppressed by loop factors as compared to tree-level four-fermion diagrams shown in Figs. 6c and 6d. Consequently, in the subsequent discussion, only the four-fermion diagrams of Figs. 6c and 6d will be considered for chirality nonflipping color-triplet mediation of type .
For chirality nonflipping dimension-six operators we need the corresponding interaction mass matrix for the color triplets.

The mass matrix relevant for chirality nonflipping color-triplet mediation is
| (16) |
Figure 7 illustrates a diagram for fermionic color-triplet mediation involving . The relevant mass matrix element for the mediation of can be expressed as follows
| (17) | |||||
Here, it is assumed that the couplings and are real, , and
| (18) |
Similarly for the mediation of , we obtain
| (19) |
where we assume couplings to be real. We also assume . For , and we get
| (20) |
This mediation leads to observable proton decay for as shown below.
The contributions of chirality nonflipping mediation via color triplets and gauge bosons are presented in the following dimension-six proton decay operators
| (21) |
where are the dimension-six proton decay operators defined as
| (22) | |||||
| (23) |
and are Wilson’s coefficients given by
| (24) | |||||
| (25) | |||||
Here is the phase angle, represents diagonalized Yukawa couplings, represents the CKM matrix, is gauge coupling at GUT scale, and is the mass of gauge bosons. The decay rates for charged lepton channels are
| (26) | |||||
| (27) |
where
| (28) |
| Decay channel | Super-K | Sensitivities | |||
|---|---|---|---|---|---|
| = Matrix element () | bound [6] | ( yr) | |||
| ( yr) | Hyper-K[10] | DUNE[9, 8] | |||
and represents hadronic matrix elements given in Table 3 [34]. Current experimental bounds from Super-K and future sensitivities of Hyper-K and DUNE on different proton decay channels are given in Table 3. For numerical estimates we assume and for convenience the mass matrix element in eqs. (17) and (19) is denoted by,
| (29) |
For natural values of , IMDM75 predicts intermediate masses of color triplets . The figures in Fig. 8 depict the partial lifetime of proton for charged lepton channels as a function of ranging from to . The lower horizontal red line in each plot represents the existing Super-K bounds, while the upper horizontal red line indicates the expected sensitivities in future experiments. The gray shaded region in each plot represents the range of proton lifetimes that have been excluded by previous experimental searches.




The decay rates for the neutral lepton channels are
| (30) | |||||
| (31) |


Figure 9 displays the estimated partial-lifetime values for the neutral lepton channels. For GeV, the gauge boson mediation becomes dominant over the color-triplet mediation, and the partial-lifetime estimates become independent of .
Using Super-K bounds on proton decay channels, lower bounds on the mass of color triplets and involved couplings can be derived as
| (32) | |||||
| (33) |
where and ,respectively, represents the lower bound on and for a given value and decay mode. Similarly, the observable range for and dependent on can be found using Hyper-K and DUNE bounds, as shown in Fig. 10. It is worth noting that IMDM75 predicts the observable range of proton-lifetime for the next-generation experiments with somewhat natural values of the coupling, .


IV IMDM75 versus other GUTs
To compare the proton decay predictions in IMDM75 with other GUT models, we consider the standard model with a -dimensional Higgs field [35] (), the flipped model () [32, 33], the Pati-Salam model () [36] and the Babu-Pati-Wilczek model [37]. One can find proton decay predictions from other models in references such as [38, 39, 40]. The branching fractions for various proton decay channels are plotted in Fig. 12 and 13. The left panel displays the relationship between the branching fraction and in IMDM75, while the right panel presents the corresponding predictions from the flipped model. While IMDM75 places an upper bound on the value of , the flipped model allows to extend up to without any such constraint.
We find a significant difference in the proton lifetime behavior for the channel compared to the predictions from the flipped model in [32]. Our plots exhibit a spread with respect to the values, and due to the contributions from gauge boson mediation, we notice saturation at GeV, which is in contrast to the flipped case where gauge boson mediation was absent and the spread in plots with respect to values was minimal for this channel. We conclude that the channel is expected to play a crucial role in differentiating between the and flipped models.
The red horizontal lines in the figures represent the predictions of different GUT models. Specifically, the line corresponding to represents the prediction where proton decay is mainly mediated via gauge bosons. On the other hand, the lines corresponding to the Pati-Salam () and Babu-Pati-Wilczek models represent the predictions where proton decay is dominantly mediated via color triplets. Thus, the IMDM75 model is found to make unique predictions for diverse branching ratios over a broad range of involved parameters, setting it apart from the three other GUT models.
V Gauge Coupling Unification
In this section, we present a comprehensive two-loop analysis of gauge coupling unification in IMDM75. Following the breaking of the GUT symmetry, we end up with a pair of electroweak doublets with a mass of and two pairs of color triplets, in addition to the minimal matter content of the MSSM. The color-triplet mass matrix in Eq. (11) has eigenvalues denoted by , where . It is worth noting that only one pair of color triplets acquires intermediate-scale masses, specifically and , while the other pair, with masses and , acquire GUT-scale masses. As a result, only one pair of color triplets, with masses , is pertinent for the renormalization group analysis below the GUT scale, while the other pair, with masses , is relevant for the renormalization group analysis above the GUT scale. We set as the unification scale where , and we match IMDM75 with MSSM at . The symmetry breaking into the symmetry results in the various components of acquiring masses (Table 4), as given below
| (34) |
With the gauge field strength chiral superfield , a Planck-scale suppressed dimension-five operator can be written as
| Mass | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| , |
| (35) |
The GUT scale matching conditions for the gauge couplings depend on the coupling of the above dimension-five operator [18, 41, 25, 42] and on the masses of order GUT scale or lower as,
| (36) | |||
| (37) | |||
| (38) |
By eliminating , we arrive at the following constraint,
| (39) |
where,
| (40) |

To investigate gauge coupling unification, we employ two-loop renormalization group equations (RGEs) for MSSM, with an extra pair of the electroweak doublet and the color-triplet at the intermediate scale, as depicted in Fig. 11. This analysis yields GeV, , and . At the GUT scale, applying Eq. (39) leads to the following constraint
| (41) |
Assuming and we obtain the following expression
| (42) |
To find the matching condition for we employ the following constraint
| (43) |
with
| (44) |
When evaluated at the GUT scale, the aforementioned constraint yields the following expression
| (45) |
In Fig. 11, we depict the behavior of the gauge coupling above the GUT scale for a value of , which is adequate to guarantee perturbative gauge coupling [25]. The presence of GUT multiplets with large representations leads to becoming nonperturbative just above the mass scale GeV.
VI Conclusion
The article investigates proton decay with partial lifetimes in IMDM75, improved missing doublet model, that can be tested in the next-generation experiments. The model incorporates an anomalous symmetry to prevent the occurrence of the term at all orders. For GUT symmetry breaking and implementation of the missing partner mechanism, a -plet GUT Higgs field () is utilized in the presence of two pairs of and -plet fields. To prevent fast proton decay and achieve successful GCU in the improved model, the presence of a second pair of and -plet fields is necessary. This allows an extra pair of electroweak doublets and one pair of color triplets to acquire masses naturally at the intermediate scale. The model predicts observable proton decay via the naturally obtained intermediate masses of chirality nonflipping mediation of color triplets, while the chirality flipping dimension-five proton decay mediated via color triplets is sufficiently suppressed to avoid fast proton decay. The model’s predictions for various branching ratios are compared with those of , , PS model, and , and in this regard the significance of the channel is emphasized. The model presented in this article provides unique predictions for different branching ratios over a broad range of involved parameters. Finally, the matching conditions for the gauge couplings involved are provided, and the compatibility of gauge coupling unification with observable proton decay lifetimes is demonstrated.
Acknowledgements.
M. M. thanks Zurab Tavartkiladze for useful discussion.References
- [1] K. Abe et al. Search for proton decay via and in 0.31 megaton·years exposure of the Super-Kamiokande water Cherenkov detector. Phys. Rev. D, 95(1):012004, 2017.
- [2] K. Abe et al. Search for Nucleon Decay via and in Super-Kamiokande. Phys. Rev. Lett., 113(12):121802, 2014.
- [3] C. Regis et al. Search for Proton Decay via in Super-Kamiokande I, II, and III. Phys. Rev. D, 86:012006, 2012.
- [4] K. Abe et al. Search for proton decay via using 260 kiloton·year data of Super-Kamiokande. Phys. Rev. D, 90(7):072005, 2014.
- [5] K. Kobayashi et al. Search for nucleon decay via modes favored by supersymmetric grand unification models in Super-Kamiokande-I. Phys. Rev. D, 72:052007, 2005.
- [6] M. Tanabashi et al. Review of Particle Physics. Phys. Rev. D, 98(3):030001, 2018.
- [7] Fengpeng An et al. Neutrino Physics with JUNO. J. Phys. G, 43(3):030401, 2016.
- [8] R. Acciarri et al. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report, Volume 2: The Physics Program for DUNE at LBNF. 12 2015.
- [9] Babak Abi et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics. 2 2020.
- [10] K. Abe et al. Hyper-Kamiokande Design Report. 5 2018.
- [11] J. Hisano, H. Murayama, and T. Yanagida. Nucleon decay in the minimal supersymmetric SU(5) grand unification. Nucl. Phys. B, 402:46–84, 1993.
- [12] Junji Hisano, Daiki Kobayashi, Takumi Kuwahara, and Natsumi Nagata. Decoupling Can Revive Minimal Supersymmetric SU(5). JHEP, 07:038, 2013.
- [13] Natsumi Nagata and Satoshi Shirai. Sfermion Flavor and Proton Decay in High-Scale Supersymmetry. JHEP, 03:049, 2014.
- [14] John Ellis, Jason L. Evans, Natsumi Nagata, Keith A. Olive, and Liliana Velasco-Sevilla. Supersymmetric proton decay revisited. Eur. Phys. J. C, 80(4):332, 2020.
- [15] K. S. Babu, Ilia Gogoladze, and Cem Salih Un. Proton lifetime in minimal SUSY SU(5) in light of LHC results. JHEP, 02:164, 2022.
- [16] A. Masiero, Dimitri V. Nanopoulos, K. Tamvakis, and T. Yanagida. Naturally Massless Higgs Doublets in Supersymmetric SU(5). Phys. Lett. B, 115:380–384, 1982.
- [17] J. Hisano, T. Moroi, K. Tobe, and T. Yanagida. Suppression of proton decay in the missing partner model for supersymmetric SU(5) GUT. Phys. Lett. B, 342:138–144, 1995.
- [18] J. Hisano, Yasunori Nomura, and T. Yanagida. Dimension-six proton decays in the modified missing doublet SU(5) model. Prog. Theor. Phys., 98:1385–1390, 1997.
- [19] C. Kounnas, D. V. Nanopoulos, M. Quiros and M. Srednicki, Natural Triplet - Doublet Splitting From Supergravity, Phys. Lett. B 127, 82-84 (1983) doi:10.1016/0370-2693(83)91634-9
- [20] Zurab Berezhiani and Zurab Tavartkiladze. Anomalous U(1) symmetry and missing doublet SU(5) model. Phys. Lett. B, 396:150–160, 1997.
- [21] Guido Altarelli, Ferruccio Feruglio, and Isabella Masina. From minimal to realistic supersymmetric SU(5) grand unification. JHEP, 11:040, 2000.
- [22] Stefan Antusch, Ivo de Medeiros Varzielas, Vinzenz Maurer, Constantin Sluka, and Martin Spinrath. Towards predictive flavour models in SUSY SU(5) GUTs with doublet-triplet splitting. JHEP, 09:141, 2014.
- [23] Borut Bajc, Junji Hisano, Takumi Kuwahara, and Yuji Omura. Threshold corrections to dimension-six proton decay operators in non-minimal SUSY SU (5) GUTs. Nucl. Phys. B, 910:1–22, 2016.
- [24] Stefan Pokorski, Krzysztof Rolbiecki, Graham G. Ross, and Kazuki Sakurai. A new approach to gauge coupling unification and proton decay. JHEP, 04:161, 2019.
- [25] John Ellis, Jason L. Evans, Natsumi Nagata, and Keith A. Olive. A minimal supersymmetric SU(5) missing-partner model. Eur. Phys. J. C, 81(6):543, 2021.
- [26] H. P. Nilles, Anomalous U(1) gauge symmetries and heterotic type I / II string duality, PoS tmr99, 037 (1999) doi:10.22323/1.004.0037 [arXiv:hep-th/0003152 [hep-th]].
- [27] M. Dine, N. Seiberg and E. Witten, Nucl. Phys. B 289, 589-598 (1987) doi:10.1016/0550-3213(87)90395-6
- [28] J. J. Atick, L. J. Dixon and A. Sen, Nucl. Phys. B 292, 109-149 (1987) doi:10.1016/0550-3213(87)90639-0
- [29] M. Dine, I. Ichinose and N. Seiberg, Nucl. Phys. B 293, 253-265 (1987) doi:10.1016/0550-3213(87)90072-1
- [30] R. N. Mohapatra and J. W. F. Valle. Neutrino Mass and Baryon Number Nonconservation in Superstring Models. Phys. Rev. D, 34:1642, 1986.
- [31] G. F. Giudice and A. Masiero. A Natural Solution to the mu Problem in Supergravity Theories. Phys. Lett. B, 206:480–484, 1988.
- [32] Maria Mehmood, Mansoor Ur Rehman, and Qaisar Shafi. Observable proton decay in flipped SU(5). JHEP, 02:181, 2021.
- [33] M. M. A. Abid, M. Mehmood, M. U. Rehman and Q. Shafi, Realistic inflation in no-scale U(1) R symmetric flipped SU(5), JCAP 10, 015 (2021) doi:10.1088/1475-7516/2021/10/015 [arXiv:2107.05678 [hep-ph]].
- [34] Yasumichi Aoki, Taku Izubuchi, Eigo Shintani, and Amarjit Soni. Improved lattice computation of proton decay matrix elements. Phys. Rev. D, 96(1):014506, 2017.
- [35] John Ellis, Marcos A. G. Garcia, Natsumi Nagata, Dimitri V. Nanopoulos, and Keith A. Olive. Proton Decay: Flipped vs Unflipped SU(5). JHEP, 05:021, 2020.
- [36] George Lazarides, Mansoor Ur Rehman, and Qaisar Shafi. Proton decay in supersymmetric . JHEP, 10:085, 2020.
- [37] K. S. Babu, Jogesh C. Pati, and Frank Wilczek. Suggested new modes in supersymmetric proton decay. Phys. Lett. B, 423:337–347, 1998.
- [38] K. S. Babu, Jogesh C. Pati, and Frank Wilczek. Fermion masses, neutrino oscillations, and proton decay in the light of Super-Kamiokande. Nucl. Phys. B, 566:33–91, 2000.
- [39] Naoyuki Haba, Yukihiro Mimura, and Toshifumi Yamada. Enhanced as a signature of minimal renormalizable SUSY (10) GUT. PTEP, 2020(9):093B01, 2020.
- [40] A. Djouadi, R. Fonseca, R. Ouyang and M. Raidal, Non-supersymmetric SO(10) models with Gauge and Yukawa coupling unification, Eur. Phys. J. C 83, no.6, 529 (2023) doi:10.1140/epjc/s10052-023-11696-4 [arXiv:2212.11315 [hep-ph]].
- [41] Katri Huitu, Yoshiharu Kawamura, Tatsuo Kobayashi, and Kai Puolamaki. Generic gravitational corrections to gauge couplings in SUSY SU(5) GUTs. Phys. Lett. B, 468:111–117, 1999.
- [42] Jason L. Evans and Tsutomu T. Yanagida. Upper limit on the proton lifetime in minimal supersymetric SU(5). Phys. Lett. B, 833:137359, 2022.











