Oblique corrections from leptoquarks

In this paper we consider a model of New Physics (NP), i.e. an extension of the Standard Model (SM), that has arbitrary numbers of scalars placed in triplets of colour-$SU(3)$ which are

$SU(2)$ singlets with weak hypercharge⁵⁵5We use the normalization $Y=Q-T_{3}$, where $Y$ is the weak hypercharge, $Q$ is the electric charge, and $T_{3}$ is the third component of weak isospin. $-1/3$

$$\sigma_{0,-2};$$

(1)

$SU(2)$ singlets with weak hypercharge $-4/3$

$$\sigma_{0,-8};$$

(2)

$SU(2)$ doublets with weak hypercharge $7/6$

$$\left(\begin{array}[]{c}\delta_{1,7}\\ \delta_{-1,7}\end{array}\right);$$

(3)

$SU(2)$ doublets with weak hypercharge $1/6$

$$\left(\begin{array}[]{c}\delta_{1,1}\\ \delta_{-1,1}\end{array}\right);$$

(4)

$SU(2)$ triplets with weak hypercharge $-1/3$

$$\left(\begin{array}[]{c}\tau_{2,-2}\\ \tau_{0,-2}\\ \tau_{-2,-2}\end{array}\right).$$

(5)

In Eqs. (1)–(5),

the letter $\sigma$ denotes singlets of gauge $SU(2)$, the letter $\delta$ stands for doublets, and the letter $\tau$ means triplets;

the first number in the subscript is two times the third component of weak isospin $T_{3}$;

the second number in the subscript is six times the weak hypercharge $Y$.

In the notation of the recent Ref. [1], which refers to the original Ref. [2],

the scalars in Eq. (1) are leptoquarks of type $\Phi_{1}$, viz. scalars placed in the representation $\left(\mathbf{3},\mathbf{1},-1/3\right)$ of the gauge group $SU(3)\times SU(2)\times U(1)$;

the scalars in Eq. (2) are leptoquarks of type $\Phi_{\tilde{1}}$, viz. scalars placed in the representation $\left(\mathbf{3},\mathbf{1},-4/3\right)$ of $SU(3)\times SU(2)\times U(1)$;

the scalars in Eq. (3) are leptoquarks of type $\Phi_{2}$, viz. scalars placed in the representation $\left(\mathbf{3},\mathbf{2},7/6\right)$ of the gauge group;

the scalars in Eq. (4) are leptoquarks of type $\Phi_{\tilde{2}}$, viz. scalars placed in the representation $\left(\mathbf{3},\mathbf{2},1/6\right)$;

the scalars in Eq. (5) are leptoquarks of type $\Phi_{3}$, viz. scalars placed in the representation $\left(\mathbf{3},\mathbf{3},-1/3\right)$ of $SU(3)\times SU(2)\times U(1)$.

Leptoquarks⁶⁶6In this paper we focus exclusively on scalar leptoquarks. Various authors use the term ‘leptoquarks’ to mean some vector, i.e. spin-one, fields. are scalars that are in multiplets of $SU(3)\times SU(2)\times U(1)$ such that they have (renormalizable) Yukawa couplings to one lepton multiplet and one quark multiplet of the SM. Leptoquarks have recently been much used in models that seek to explain one or more unexpected experimental results like those on the muon magnetic moment, the $W^{\pm}$ mass, the decays $b\to c\tau\nu$, and the decays $b\to s\ell^{+}\ell^{-}$; see for instance Refs. [3, 4, 5, 6, 7, 8, 9, 10].

The oblique parameters are defined as [11]⁷⁷7We use the sign conventions in Ref. [12]. Those conventions differ from the ones used in many other papers, viz. in Ref. [11]. For a resource paper on sign conventions, see Ref. [13]; using the notation of that paper, our convention has $\eta_{e}=\eta_{Z}=1$ and $\eta=-1$.^,888The definitions (6) build on, and generalize, previous work in Refs. [14, 15, 16]. They are appropriate for the case where the functions $A_{VV^{\prime}}\left(q^{2}\right)$ are not linear in the range $0<q^{2}<m_{Z}^{2}$. This means that, using those definitions, NP does not need to be much above the Fermi scale.

	$\displaystyle S$	$\displaystyle=$	$\displaystyle\frac{16\pi c_{W}^{2}}{g^{2}}\left[\frac{A_{ZZ}\left(m_{Z}^{2}\right)-A_{ZZ}\left(0\right)}{m_{Z}^{2}}-\left.\frac{\partial A_{\gamma\gamma}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right.$		(6a)
			$\displaystyle\left.+\frac{c_{W}^{2}-s_{W}^{2}}{c_{W}s_{W}}\,\left.\frac{\partial A_{\gamma Z}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right],$
	$\displaystyle T$	$\displaystyle=$	$\displaystyle\frac{4\pi}{g^{2}s_{W}^{2}}\left[\frac{A_{WW}\left(0\right)}{m_{W}^{2}}-\frac{A_{ZZ}\left(0\right)}{m_{Z}^{2}}\right],$		(6b)
	$\displaystyle U$	$\displaystyle=$	$\displaystyle\frac{16\pi}{g^{2}}\left[\frac{A_{WW}\left(m_{W}^{2}\right)-A_{WW}\left(0\right)}{m_{W}^{2}}-c_{W}^{2}\,\frac{A_{ZZ}\left(m_{Z}^{2}\right)-A_{ZZ}\left(0\right)}{m_{Z}^{2}}\right.$		(6c)
			$\displaystyle\left.-s_{W}^{2}\left.\frac{\partial A_{\gamma\gamma}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}+2c_{W}s_{W}\left.\frac{\partial A_{\gamma Z}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right],$
	$\displaystyle V$	$\displaystyle=$	$\displaystyle\frac{4\pi}{g^{2}s_{W}^{2}}\left[\left.\frac{\partial A_{ZZ}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=m_{Z}^{2}}-\frac{A_{ZZ}\left(m_{Z}^{2}\right)-A_{ZZ}\left(0\right)}{m_{Z}^{2}}\right],$		(6d)
	$\displaystyle W$	$\displaystyle=$	$\displaystyle\frac{4\pi}{g^{2}s_{W}^{2}}\left[\left.\frac{\partial A_{WW}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=m_{W}^{2}}-\frac{A_{WW}\left(m_{W}^{2}\right)-A_{WW}\left(0\right)}{m_{W}^{2}}\right],$		(6e)
	$\displaystyle X$	$\displaystyle=$	$\displaystyle\frac{4\pi c_{W}}{g^{2}s_{W}}\left[\left.\frac{\partial A_{\gamma Z}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}-\frac{A_{\gamma Z}\left(m_{Z}^{2}\right)-A_{\gamma Z}\left(0\right)}{m_{Z}^{2}}\right],$		(6f)

where $g$ is the $SU(2)$ gauge coupling constant and $c_{W}$ and $s_{W}$ are the cosine and the sine, respectively, of the Weinberg angle. The functions $A_{VV^{\prime}}\left(q^{2}\right)$ are the coefficients of the metric tensor $g^{\mu\nu}$ in the vacuum-polarization tensor

$$\Pi^{\mu\nu}_{VV^{\prime}}\left(q^{2}\right)=g^{\mu\nu}\,A_{VV^{\prime}}\left(q^{2}\right)+q^{\mu}q^{\nu}\,B_{VV^{\prime}}\left(q^{2}\right)$$

(7)

between gauge bosons $V_{\mu}$ and $V^{\prime}_{\nu}$ carrying four-momentum $q$. In $A_{VV^{\prime}}\left(q^{2}\right)$

one only takes into account the dispersive part—one discards the absorptive part;

one subtracts the SM contribution from the full result.⁹⁹9In this paper we do not need to perform this subtraction, since we are dealing with NP scalars that have non-integer electric charges and, therefore, do not mix with the SM scalars.

Note that

$$S+U=\frac{16\pi}{g^{2}}\left[\frac{A_{WW}\left(m_{W}^{2}\right)-A_{WW}\left(0\right)}{m_{W}^{2}}-\left.\frac{\partial A_{\gamma\gamma}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}+\frac{c_{W}}{s_{W}}\left.\frac{\partial A_{\gamma Z}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right]$$

(8)

has a somewhat simpler expression than $U$.

It is convenient to separate the parameters $S$ and $U$ in two parts:

$$S=S^{\prime}+S^{\prime\prime},\quad U=U^{\prime}+U^{\prime\prime}.$$

(9)

The parameters $S^{\prime}$ and $U^{\prime}$ are identical to the original $S$ and $U$, respectively, as they were defined in Ref. [14]:

	$\displaystyle S^{\prime}$	$\displaystyle=$	$\displaystyle\frac{16\pi c_{W}^{2}}{g^{2}}\left[\left.\frac{\partial A_{ZZ}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}-\left.\frac{\partial A_{\gamma\gamma}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}+\frac{c_{W}^{2}-s_{W}^{2}}{c_{W}s_{W}}\left.\frac{\partial A_{\gamma Z}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right],\hskip 19.91692pt$		(10a)
	$\displaystyle U^{\prime}$	$\displaystyle=$	$\displaystyle-S^{\prime}+\frac{16\pi}{g^{2}}\left[\left.\frac{\partial A_{WW}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}-\left.\frac{\partial A_{\gamma\gamma}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}+\frac{c_{W}}{s_{W}}\left.\frac{\partial A_{\gamma Z}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right].$		(10b)

Clearly then,

	$\displaystyle S^{\prime\prime}$	$\displaystyle=$	$\displaystyle\frac{16\pi c_{W}^{2}}{g^{2}}\left[\frac{A_{ZZ}\left(m_{Z}^{2}\right)-A_{ZZ}\left(0\right)}{m_{Z}^{2}}-\left.\frac{\partial A_{ZZ}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right],$		(11a)
	$\displaystyle U^{\prime\prime}$	$\displaystyle=$	$\displaystyle-S^{\prime\prime}+\frac{16\pi}{g^{2}}\left[\frac{A_{WW}\left(m_{W}^{2}\right)-A_{WW}\left(0\right)}{m_{W}^{2}}-\left.\frac{\partial A_{WW}\left(q^{2}\right)}{\partial q^{2}}\right|_{q^{2}=0}\right].$		(11b)

In this paper we compute the oblique parameters for a NP model with arbitrary numbers of leptoquarks, mixing arbitrarily among themselves. Our work generalizes earlier partial results in Refs. [17, 18, 19, 20, 21, 22]. At the end of this paper we present a generalization wherein the oblique parameters are computed for any NP model solely with extra scalars, whatever the representations of $SU(2)\times U(1)$ those new scalars are in—just assuming that no new scalar either develops a vacuum expectation value or mixes with the scalars of the SM.

In the next section we write the Lagrangian for the gauge interactions of the scalars, carefully defining the mixing matrices that appear in that Lagrangian. Section 3 performs the computation of the relevant diagrams and explicitly gives various functions that appear in the formulas for the oblique parameters. Those formulas are then given in Section 4. Section 5 presents a few illustrative examples of application of our formulas to simple models with leptoquarks. Section 6 generalizes our work to scalars in any representations of $SU(2)\times U(1)$. Section 7 summarizes our main results. In Appendices A and B we deal, respectively, with the counting of mixing parameters and with the parameterization of the mixing in models with leptoquarks. In Appendix C we explicitly demonstrate that $S^{\prime}$ and $U^{\prime}$ are finite as they should be.

There are in our NP model $n_{\sigma,-2}$ multiplets of type (1), $n_{\sigma,-8}$ multiplets of type (2), $n_{\delta,7}$ multiplets of type (3), $n_{\delta,1}$ multiplets of type (4), and $n_{\tau,-2}$ multiplets of type (5). All these five numbers $n_{\sigma,-2}$, $n_{\sigma,-8}$, $n_{\delta,7}$, $n_{\delta,1}$, and $n_{\tau,-2}$ must be multiples of three, since all the scalars are in triplets of $SU(3)$; otherwise, those numbers are free.

Our model has fractionary-charge scalars that we call

$h$-type scalars, viz. the ones that have electric charge $Q_{h}=5/3$;

$u$-type scalars, viz. the ones that have electric charge $Q_{u}=2/3$;

$d$-type scalars, viz. the ones that have electric charge $Q_{d}=-1/3$;

$l$-type scalars, viz. the ones that have electric charge $Q_{l}=-4/3$.

The total numbers of $h$-type scalars, $u$-type scalars, $d$-type scalars, and $l$-type scalars are

	$\displaystyle n_{h}$	$\displaystyle=$	$\displaystyle n_{\delta,7},$		(12a)
	$\displaystyle n_{u}$	$\displaystyle=$	$\displaystyle n_{\delta,7}+n_{\delta,1}+n_{\tau,-2},$		(12b)
	$\displaystyle n_{d}$	$\displaystyle=$	$\displaystyle n_{\sigma,-2}+n_{\delta,1}+n_{\tau,-2},$		(12c)
	$\displaystyle n_{l}$	$\displaystyle=$	$\displaystyle n_{\sigma,-8}+n_{\tau,-2},$		(12d)

respectively. Notice that

$$n_{d}\geq n_{u}-n_{h}\geq 0.$$

(13)

One bi-diagonalizes the leptoquark mass matrices by making

	$\displaystyle\delta_{1,7}$	$\displaystyle=$	$\displaystyle H_{1}h,$		(14a)
	$\displaystyle\left(\begin{array}[]{c}\delta_{-1,7}\\ \delta_{1,1}\\ \tau_{2,-2}\end{array}\right)$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{c}U_{1}\\ U_{2}\\ U_{3}\end{array}\right)u,$		(14h)
	$\displaystyle\left(\begin{array}[]{c}\sigma_{0,-2}\\ \delta_{-1,1}\\ \tau_{0,-2}\end{array}\right)$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{c}D_{1}\\ D_{2}\\ D_{3}\end{array}\right)d,$		(14o)
	$\displaystyle\left(\begin{array}[]{c}\sigma_{0,-8}\\ \tau_{-2,-2}\end{array}\right)$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{c}L_{1}\\ L_{2}\end{array}\right)l,$		(14t)

where $h$ in Eq. (14a) stands for a column matrix containing the $n_{h}$ $h$-type scalars; and analogously for $u$, $d$, and $l$ in the other three Eqs. (14). The matrices $H_{1}$, $U_{1}$, $U_{2}$, $U_{3}$, $D_{1}$, $D_{2}$, $D_{3}$, $L_{1}$, and $L_{2}$ have dimensions $n_{\delta,7}\times n_{h}$, $n_{\delta,7}\times n_{u}$, $n_{\delta,1}\times n_{u}$, $n_{\tau,-2}\times n_{u}$, $n_{\sigma,-2}\times n_{d}$, $n_{\delta,1}\times n_{d}$, $n_{\tau,-2}\times n_{d}$, $n_{\sigma,-8}\times n_{l}$, and $n_{\tau,-2}\times n_{l}$, respectively. The matrices

$$H_{1},\quad\left(\begin{array}[]{c}U_{1}\\ U_{2}\\ U_{3}\end{array}\right),\quad\left(\begin{array}[]{c}D_{1}\\ D_{2}\\ D_{3}\end{array}\right),\quad\mbox{and}\ \left(\begin{array}[]{c}L_{1}\\ L_{2}\end{array}\right)$$

(15)

are unitary.¹⁰¹⁰10Without loss of generality, one may chose a basis where $H_{1}$ is equal to the unit matrix. We refrain from doing that, in order to keep the notation as general as possible.

We next define the mixing matrices that appear in the charged-current interactions of the scalars. They are

	$\displaystyle\mathcal{N}$	$\displaystyle=$	$\displaystyle H_{1}^{\dagger}U_{1},$		(16a)
	$\displaystyle\mathcal{V}$	$\displaystyle=$	$\displaystyle U_{2}^{\dagger}D_{2}+\sqrt{2}\,U_{3}^{\dagger}D_{3},$		(16b)
	$\displaystyle\mathcal{Q}$	$\displaystyle=$	$\displaystyle\sqrt{2}\,D_{3}^{\dagger}L_{2},$		(16c)

respectively. The factors $\sqrt{2}$ in Eqs. (16) arise because the charged gauge interactions of the triplets are $\sqrt{2}$ times stronger than those of the doublets. The mixing matrices that appear in the neutral-current interactions of the scalars are

	$\displaystyle\bar{H}$	$\displaystyle=$	$\displaystyle\mathcal{H}-2Q_{h}s_{W}^{2}\times\mathbbm{1}_{n_{h}},$		(17a)
	$\displaystyle\bar{U}$	$\displaystyle=$	$\displaystyle\mathcal{U}-2Q_{u}s_{W}^{2}\times\mathbbm{1}_{n_{u}},$		(17b)
	$\displaystyle\bar{D}$	$\displaystyle=$	$\displaystyle\mathcal{D}+2Q_{d}s_{W}^{2}\times\mathbbm{1}_{n_{d}},$		(17c)
	$\displaystyle\bar{L}$	$\displaystyle=$	$\displaystyle\mathcal{L}+2Q_{l}s_{W}^{2}\times\mathbbm{1}_{n_{l}},$		(17d)

where $\mathbbm{1}_{m}$ denotes the $m\times m$ unit matrix and the matrices $\mathcal{H}$, $\mathcal{U}$, $\mathcal{D}$, and $\mathcal{L}$ are related to the mixing matrices in Eqs. (16) through

	$\displaystyle\mathcal{H}$	$\displaystyle=$	$\displaystyle\mathcal{N}\mathcal{N}^{\dagger},$		(18a)
	$\displaystyle\mathcal{U}$	$\displaystyle=$	$\displaystyle\mathcal{V}\mathcal{V}^{\dagger}-\mathcal{N}^{\dagger}\mathcal{N},$		(18b)
	$\displaystyle\mathcal{D}$	$\displaystyle=$	$\displaystyle\mathcal{V}^{\dagger}\mathcal{V}-\mathcal{Q}\mathcal{Q}^{\dagger},$		(18c)
	$\displaystyle\mathcal{L}$	$\displaystyle=$	$\displaystyle\mathcal{Q}^{\dagger}\mathcal{Q},$		(18d)

respectively.

The gauge interactions of the scalars are given by the following pieces of the Lagrangian:

	$\displaystyle\mathcal{L}_{ASS}$	$\displaystyle=$	$\displaystyle-igs_{W}A_{\theta}\left[Q_{h}\sum_{h}\left(h^{\ast}\partial^{\theta}h-h\partial^{\theta}h^{\ast}\right)+Q_{u}\sum_{u}\left(u^{\ast}\partial^{\theta}u-u\partial^{\theta}u^{\ast}\right)\right.$		(19a)
			$\displaystyle\left.+Q_{d}\sum_{d}\left(d^{\ast}\partial^{\theta}d-d\partial^{\theta}d^{\ast}\right)+Q_{l}\sum_{l}\left(l^{\ast}\partial^{\theta}l-l\partial^{\theta}l^{\ast}\right)\right],$
	$\displaystyle\mathcal{L}_{AASS}$	$\displaystyle=$	$\displaystyle g^{2}s_{W}^{2}A_{\theta}A^{\theta}\left(Q_{h}^{2}\,\sum_{h}hh^{\ast}+Q_{u}^{2}\,\sum_{u}uu^{\ast}+Q_{d}^{2}\,\sum_{d}dd^{\ast}+Q_{l}^{2}\,\sum_{l}ll^{\ast}\right),\hskip 8.53581pt$		(19b)
	$\displaystyle\mathcal{L}_{WSS}$	$\displaystyle=$	$\displaystyle i\,\frac{g}{\sqrt{2}}\,W_{\theta}^{+}\left[\sum_{h,u}\mathcal{N}_{hu}\left(h^{\ast}\partial^{\theta}u-u\partial^{\theta}h^{\ast}\right)+\sum_{u,d}\mathcal{V}_{ud}\left(u^{\ast}\partial^{\theta}d-d\partial^{\theta}u^{\ast}\right)\right.$		(19c)
			$\displaystyle\left.+\sum_{d,l}\mathcal{Q}_{dl}\left(d^{\ast}\partial^{\theta}l-l\partial^{\theta}d^{\ast}\right)\right]+\mathrm{H.c.},$
	$\displaystyle\mathcal{L}_{WWSS}$	$\displaystyle=$	$\displaystyle\frac{g^{2}}{2}\,W^{+}_{\theta}W^{-\theta}\left[\sum_{h,h^{\prime}}\left(\mathcal{N}\mathcal{N}^{\dagger}\right)_{hh^{\prime}}h^{\ast}h^{\prime}+\sum_{u,u^{\prime}}\left(\mathcal{N}^{\dagger}\mathcal{N}+\mathcal{V}\mathcal{V}^{\dagger}\right)_{uu^{\prime}}u^{\ast}u^{\prime}\right.$		(19d)
			$\displaystyle\left.+\sum_{d,d^{\prime}}\left(\mathcal{V}^{\dagger}\mathcal{V}+\mathcal{Q}\mathcal{Q}^{\dagger}\right)_{dd^{\prime}}d^{\ast}d^{\prime}+\sum_{l,l^{\prime}}\left(\mathcal{Q}^{\dagger}\mathcal{Q}\right)_{ll^{\prime}}l^{\ast}l^{\prime}\right],$
	$\displaystyle\mathcal{L}_{ZSS}$	$\displaystyle=$	$\displaystyle i\,\frac{g}{2c_{W}}\,Z_{\theta}\left[\sum_{h}\bar{H}_{hh^{\prime}}\left(h^{\ast}\partial^{\theta}h^{\prime}-h^{\prime}\partial^{\theta}h^{\ast}\right)+\sum_{u,u^{\prime}}\bar{U}_{uu^{\prime}}\left(u^{\ast}\,\partial^{\theta}u^{\prime}-u^{\prime}\,\partial^{\theta}u^{\ast}\right)\right.$		(19e)
			$\displaystyle\left.-\sum_{d,d^{\prime}}\bar{D}_{dd^{\prime}}\left(d^{\ast}\,\partial^{\theta}d^{\prime}-d^{\prime}\,\partial^{\theta}d^{\ast}\right)-\sum_{l,l^{\prime}}\bar{L}_{ll^{\prime}}\left(l^{\ast}\,\partial^{\theta}l^{\prime}-l^{\prime}\,\partial^{\theta}l^{\ast}\right)\right],$
	$\displaystyle\mathcal{L}_{ZZSS}$	$\displaystyle=$	$\displaystyle\frac{g^{2}}{4c_{W}^{2}}\,Z_{\theta}Z^{\theta}\left[\sum_{h,h^{\prime}}\left(\bar{H}^{2}\right)_{hh^{\prime}}h^{\ast}h^{\prime}+\sum_{u,u^{\prime}}\left(\bar{U}^{2}\right)_{uu^{\prime}}u^{\ast}u^{\prime}\right.$		(19f)
			$\displaystyle\left.+\sum_{d,d^{\prime}}\left(\bar{D}^{2}\right)_{dd^{\prime}}d^{\ast}d^{\prime}+\sum_{l,l^{\prime}}\left(\bar{L}^{2}\right)_{ll^{\prime}}l^{\ast}l^{\prime}\right],$
	$\displaystyle\mathcal{L}_{AZSS}$	$\displaystyle=$	$\displaystyle-\frac{g^{2}s_{W}}{c_{W}}\,A_{\theta}Z^{\theta}\left(Q_{h}\,\sum_{h,h^{\prime}}\bar{H}_{hh^{\prime}}\,h^{\ast}h^{\prime}+Q_{u}\,\sum_{u,u^{\prime}}\bar{U}_{uu^{\prime}}\,u^{\ast}u^{\prime}\right.$		(19g)
			$\displaystyle\left.-Q_{d}\,\sum_{d,d^{\prime}}\bar{D}_{dd^{\prime}}\,d^{\ast}d^{\prime}-Q_{l}\,\sum_{l,l^{\prime}}\bar{L}_{ll^{\prime}}\,l^{\ast}l^{\prime}\right).$

Notice the presence in Eqs. (19c) and (19d) of the matrices defined in Eqs. (16) and the presence in Eqs. (19e)–(19g) of the matrices defined in Eqs. (17). Also notice that, out of the four matrices in Eq. (19d), only $\mathcal{N}\mathcal{N}^{\dagger}=\mathcal{H}$ and $\mathcal{Q}^{\dagger}\mathcal{Q}=\mathcal{L}$ coincide with matrices in Eqs. (18).

The Passarino–Veltman (PV) functions [23] $B_{00}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)$ and $A_{0}\left(m_{1}^{2}\right)$ are defined by¹¹¹¹11We use the definitions of Ref. [24] for the PV functions.

	$\displaystyle\mu^{\epsilon}\int\frac{\mathrm{d}^{4-\epsilon}k}{\left(2\pi\right)^{4-\epsilon}}\ \,k^{\theta}k^{\psi}\,\frac{1}{k^{2}-m_{1}^{2}}\ \frac{1}{\left(k+q\right)^{2}-m_{2}^{2}}$	$\displaystyle=$	$\displaystyle\frac{i}{16\pi^{2}}\,\left[g^{\theta\psi}\,B_{00}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)\right.$		(20a)
			$\displaystyle\left.+q^{\theta}q^{\psi}\,B_{11}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)\right],\hskip 19.91692pt$
	$\displaystyle\mu^{\epsilon}\int\frac{\mathrm{d}^{4-\epsilon}k}{\left(2\pi\right)^{4-\epsilon}}\ \frac{1}{k^{2}-m_{1}^{2}}\$	$\displaystyle=$	$\displaystyle\frac{i}{16\pi^{2}}\ A_{0}\left(m_{1}^{2}\right),$		(20b)

respectively, where $\mu$ is an arbitrary quantity with mass dimension. The quantities $q^{2}$, $m_{1}^{2}$, and $m_{2}^{2}$ are assumed to be non-negative. The PV function $B_{11}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)$ in Eq. (20a) is not needed in this paper; on the other hand, we need

	$\displaystyle B_{00}^{\prime}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)$	$\displaystyle\equiv$	$\displaystyle\frac{\partial B_{00}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)}{\partial q^{2}},$		(21a)
	$\displaystyle\bar{B}_{00}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)$	$\displaystyle\equiv$	$\displaystyle\frac{B_{00}\left(q^{2},m_{1}^{2},m_{2}^{2}\right)-B_{00}\left(0,m_{1}^{2},m_{2}^{2}\right)}{q^{2}}.$		(21b)

The PV functions may be numerically evaluated by using softwares like LoopTools [24] and COLLIER [25].¹²¹²12For the present purposes, in the results given by those codes one should take only the real, viz. dispersive, parts of the PV functions, while dropping the absorptive parts, which have no relevance for the oblique parameters. They may also be evaluated through analytic formulas given in Ref. [26].

One has [26]

$$B^{\prime}_{00}\left(0,m_{1}^{2},m_{2}^{2}\right)=-\frac{\mathrm{div}}{12}+\frac{1}{24}\left[\ln{\frac{m_{1}^{2}}{\mu^{2}}}+\ln{\frac{m_{2}^{2}}{\mu^{2}}}+g\left(\frac{m_{1}^{2}}{m_{2}^{2}}\right)\right],$$

(22)

where $\mathrm{div}$ is a divergent quantity which is defined in Eq. (C3) and cancels out in the final results, and

$$g\left(x\right)=\left\{\begin{array}[]{lcl}{\displaystyle\frac{x^{3}-3x^{2}-3x+1}{\left(x-1\right)^{3}}\,\ln{x}-\frac{5x^{2}-22x+5}{3\left(x-1\right)^{2}}}&\Leftarrow&x\neq 1,\\[5.69054pt] 0&\Leftarrow&x=1\end{array}\right.$$

(23)

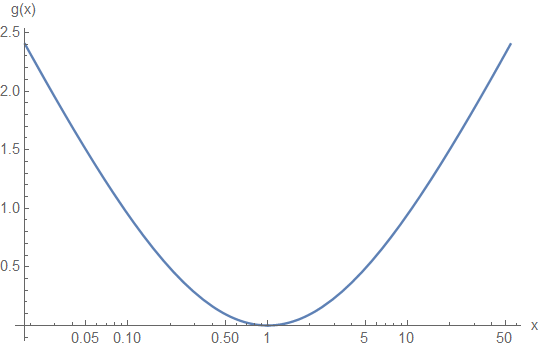
is a function that obeys $g\left(1\right)=0$ and $g\left(x\right)=g\left(1/x\right)$. This function is depicted in Fig. 1.

From the formulas in Ref. [26] one gathers that

$$B_{00}\left(0,m_{1}^{2},m_{2}^{2}\right)=\frac{A_{0}\left(m_{1}^{2}\right)+A_{0}\left(m_{2}^{2}\right)}{4}+\frac{\theta_{+}\left(m_{1}^{2},m_{2}^{2}\right)}{8},$$

(24)

where [27]

$$\theta_{+}\left(m_{1}^{2},m_{2}^{2}\right)\equiv\left\{\begin{array}[]{lcl}\displaystyle{m_{1}^{2}+m_{2}^{2}-\frac{2m_{1}^{2}m_{2}^{2}}{m_{1}^{2}-m_{2}^{2}}\,\ln{\frac{m_{1}^{2}}{m_{2}^{2}}}}&\Leftarrow&m_{1}^{2}\neq m_{2}^{2},\\[5.69054pt] 0&\Leftarrow&m_{1}^{2}=m_{2}^{2}.\end{array}\right.$$

(25)

We define the function $\rho\left(x,y\right)$—where $x$ and $y$ are positive—through

$$\rho\left(x,y\right)\equiv 2\left[B_{00}^{\prime}\left(q^{2},q^{2}x,q^{2}y\right)-\bar{B}_{00}\left(q^{2},q^{2}x,q^{2}y\right)\right],$$

(26)

which is $q^{2}$-independent. Using the analytic formulas in ref. [26] one finds that

$$\rho\left(x,y\right)=\left\{\begin{array}[]{lcl}\displaystyle{\frac{1}{6}-\frac{3\left(x+y\right)}{4}+\frac{\left(x-y\right)^{2}}{2}+\left[\frac{\left(y-x\right)^{3}}{4}+\frac{x^{2}+y^{2}}{4\left(y-x\right)}\right.}&&\\[5.69054pt] \displaystyle{\left.+\frac{x^{2}-y^{2}}{2}\right]\ln{\frac{x}{y}}+\frac{\left(x-y\right)^{2}-x-y}{4}\ f\left(x,y\right)}&\Leftarrow&x\neq y,\\[11.38109pt] \displaystyle{\frac{1}{6}-2x-\frac{x}{2}\ f\left(x,x\right)}&\Leftarrow&x=y.\end{array}\right.$$

(27)

In Eq. (27),

$$f\left(x,y\right)=\left\{\begin{array}[]{lcl}\displaystyle{\sqrt{\Delta\left(x,y\right)}\ \ln{\frac{x+y-1+\sqrt{\Delta\left(x,y\right)}}{x+y-1-\sqrt{\Delta\left(x,y\right)}}}}&\Leftarrow&\Delta\left(x,y\right)\geq 0,\\[11.38109pt] \displaystyle{-2\sqrt{-\Delta\left(x,y\right)}\left[\arctan{\frac{x-y+1}{\sqrt{-\Delta\left(x,y\right)}}}+\left(x\leftrightarrow y\right)\right]}&\Leftarrow&\Delta\left(x,y\right)<0,\end{array}\right.$$

(28)

where

$$\Delta\left(x,y\right)=1-2\left(x+y\right)+\left(x-y\right)^{2}.$$

(29)

The function $\zeta\left(x,y\right)$—where $x$ and $y$ are positive—is defined through

$$\zeta\left(x,y\right)\equiv 2\left[B_{00}^{\prime}\left(0,q^{2}x,q^{2}y\right)-\bar{B}_{00}\left(q^{2},q^{2}x,q^{2}y\right)\right],$$

(30)

which is $q^{2}$-independent. Using the analytic formulas in ref. [26] one finds that

$$\zeta\left(x,y\right)=\left\{\begin{array}[]{lcl}\displaystyle{\frac{11}{36}-\frac{5\left(x+y\right)}{12}+\frac{xy}{3\left(x-y\right)^{2}}+\frac{\left(x-y\right)^{2}}{6}+\left[\frac{x^{2}-y^{2}}{4}+\frac{\left(y-x\right)^{3}}{12}\right.}&&\\[5.69054pt] \displaystyle{\left.+\frac{x^{2}+y^{2}}{4\left(y-x\right)}+\frac{x+y}{12\left(x-y\right)}+\frac{xy\left(x+y\right)}{6\left(y-x\right)^{3}}\right]\ln{\frac{x}{y}}}&&\\[5.69054pt] \displaystyle{+\frac{\Delta\left(x,y\right)}{12}\ f\left(x,y\right)}&\Leftarrow&x\neq y,\\[8.53581pt] \displaystyle{\frac{4}{9}-\frac{4x}{3}+\frac{\Delta\left(x,x\right)}{12}\ f\left(x,x\right)}&\Leftarrow&x=y.\end{array}\right.$$

(31)

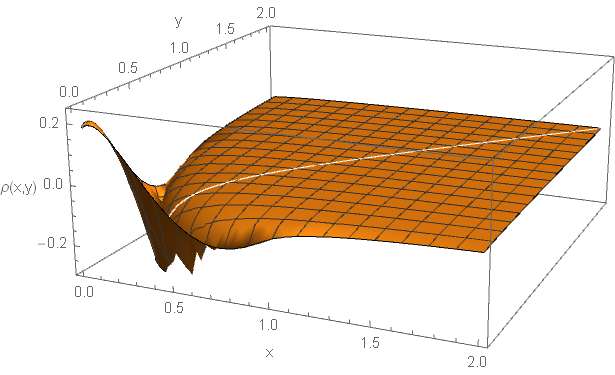
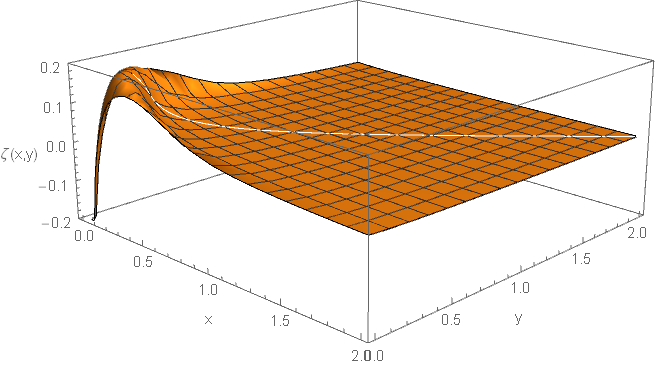
The functions $\rho\left(x,y\right)$ and $\zeta\left(x,y\right)$ are illustrated in Fig. 2. They are both very small when $x\gtrsim 1$ and $y\gtrsim 1$.

Suppose the vertices $V_{\mu}S_{1}S_{2}$ and $V_{\mu}V^{\prime}_{\nu}S_{1}S_{2}$ have Feynman rules

		$\displaystyle=iX\left(k-p\right)_{\mu},$		(32a)
	{fmfgraph*} (75,75) \fmflefti1,i2 \fmfrighto1,o2 \fmfdashesi1,w1 \fmfdashesi2,w1 \fmfphotonw1,o1 \fmfphotonw1,o2 \fmflabel$S_{2}$i1 \fmflabel$S_{1}$i2 \fmflabel$V_{\mu}$o2 \fmflabel$V_{\nu}^{\prime}$o1	$\displaystyle=iYg_{\mu\nu},$		(32b)

and

$$A^{VV^{\prime}S_{1}}\left(q^{2}\right)=-\frac{Y}{16\pi^{2}}\,A_{0}\left(m_{1}^{2}\right)$$

(32ah)

for diagrams of the form in Fig. 4.

In Eqs. (32ag) and (32ah), $q$ is the four-momentum of the gauge bosons.

For the oblique parameter $T$ we have

	$\displaystyle T$	$\displaystyle=$	$\displaystyle\frac{1}{8\pi s_{W}^{2}m_{W}^{2}}\left\{4\left[\sum_{h,u}\left|\mathcal{N}_{hu}\right|^{2}B_{00}(0,m_{h}^{2},m_{u}^{2})+\sum_{u,d}\left|\mathcal{V}_{ud}\right|^{2}B_{00}(0,m_{u}^{2},m_{d}^{2})\right.\right.$		(32aid)
			$\displaystyle\left.+\sum_{d,l}\left|\mathcal{Q}_{dl}\right|^{2}B_{00}(0,m_{d}^{2},m_{l}^{2})\right]$
			$\displaystyle-\sum_{h}\left(\mathcal{N}\mathcal{N}^{\dagger}\right)_{hh}\,A_{0}\left(m_{h}^{2}\right)-\sum_{u}\left(\mathcal{N}^{\dagger}\mathcal{N}+\mathcal{V}\mathcal{V}^{\dagger}\right)_{uu}\,A_{0}\left(m_{u}^{2}\right)$
			$\displaystyle-\sum_{d}\left(\mathcal{V}^{\dagger}\mathcal{V}+\mathcal{Q}\mathcal{Q}^{\dagger}\right)_{dd}\,A_{0}\left(m_{d}^{2}\right)-\sum_{l}\left(\mathcal{Q}^{\dagger}\mathcal{Q}\right)_{ll}\,A_{0}\left(m_{l}^{2}\right)$
			$\displaystyle-2\left[\sum_{h,h^{\prime}}\left|\bar{H}_{hh^{\prime}}\right|^{2}B_{00}\left(0,m_{h}^{2},m_{h^{\prime}}^{2}\right)+\sum_{u,u^{\prime}}\left|\bar{U}_{uu^{\prime}}\right|^{2}B_{00}\left(0,m_{u}^{2},m_{u^{\prime}}^{2}\right)\right.$
			$\displaystyle\left.+\sum_{d,d^{\prime}}\left|\bar{D}_{dd^{\prime}}\right|^{2}B_{00}\left(0,m_{d}^{2},m_{d^{\prime}}^{2}\right)+\sum_{l,l^{\prime}}\left|\bar{L}_{ll^{\prime}}\right|^{2}B_{00}\left(0,m_{l}^{2},m_{l^{\prime}}^{2}\right)\right]$
			$\displaystyle+\sum_{h}\left(\bar{H}^{2}\right)_{hh}\,A_{0}\left(m_{h}^{2}\right)+\sum_{u}\left(\bar{U}^{2}\right)_{uu}\,A_{0}\left(m_{u}^{2}\right)$
			$\displaystyle\left.+\sum_{d}\left(\bar{D}^{2}\right)_{dd}\,A_{0}\left(m_{d}^{2}\right)+\sum_{l}\left(\bar{L}^{2}\right)_{ll}\,A_{0}\left(m_{l}^{2}\right)\right\},$

where lines (32aid) and (32aid) originate in $A_{WW}\left(0\right)$ while lines (32aid) and (32aid) originate in $A_{ZZ}\left(0\right)$. Utilizing Eq. (24) on Eq. (32ai), we obtain

	$\displaystyle T$	$\displaystyle=$	$\displaystyle\frac{1}{16\pi s_{W}^{2}m_{W}^{2}}\left[\sum_{h,u}\left|\mathcal{N}_{hu}\right|^{2}\theta_{+}\left(m_{h}^{2},m_{u}^{2}\right)\right.$		(32aj)
			$\displaystyle+\sum_{u,d}\left|\mathcal{V}_{ud}\right|^{2}\theta_{+}\left(m_{u}^{2},m_{d}^{2}\right)+\sum_{d,l}\left|\mathcal{Q}_{dl}\right|^{2}\theta_{+}\left(m_{d}^{2},m_{l}^{2}\right)$
			$\displaystyle-\sum_{h<h^{\prime}}\left|\mathcal{H}_{hh^{\prime}}\right|^{2}\theta_{+}\left(m_{h}^{2},m_{h^{\prime}}^{2}\right)-\sum_{u<u^{\prime}}\left|\mathcal{U}_{uu^{\prime}}\right|^{2}\theta_{+}\left(m_{u}^{2},m_{u^{\prime}}^{2}\right)$
			$\displaystyle\left.-\sum_{d<d^{\prime}}\left|\mathcal{D}_{dd^{\prime}}\right|^{2}\theta_{+}\left(m_{d}^{2},m_{d^{\prime}}^{2}\right)-\sum_{l<l^{\prime}}\left|\mathcal{L}_{ll^{\prime}}\right|^{2}\theta_{+}\left(m_{l}^{2},m_{l^{\prime}}^{2}\right)\right],$

The function $\theta_{+}\left(m_{1}^{2},m_{2}^{2}\right)$ is given in Eq. (25). It is a finite function; thus, in Eq. (32aj) there are no divergences, contrary to what happens in Eq. (32ai), wherein the functions $B_{00}\left(0,m_{1}^{2},m_{2}^{2}\right)$ and $A_{0}\left(m_{3}^{2}\right)$ are divergent. The function $\theta_{+}\left(m_{1}^{2},m_{2}^{2}\right)$ is moreover positive definite; thus, the two first lines of Eq. (32aj) constitute a positive contribution to $T$, which always exists in a model with leptoquarks, while the two last lines of that equation are a negative contribution, which only exists if at least one of the matrices $\mathcal{H}$, $\mathcal{U}$, $\mathcal{D}$, and $\mathcal{L}$ has nonzero off-diagonal matrix elements.