This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Objectives Are All You Need:
Solving Deceptive Problems Without Explicit Diversity Maintenance

Ryan Boldi
University of Massachusetts Amherst
[email protected]
&Li Ding
University of Massachusetts Amherst
[email protected]
&Lee Spector
Amherst College
University of Massachusetts Amherst
[email protected]
Abstract

Navigating deceptive domains has often been a challenge in machine learning due to search algorithms getting stuck at sub-optimal local optima. Many algorithms have been proposed to navigate these domains by explicitly maintaining diversity or equivalently promoting exploration, such as Novelty Search or other so-called Quality Diversity algorithms. In this paper, we present an approach with promise to solve deceptive domains without explicit diversity maintenance by optimizing a potentially large set of defined objectives. These objectives can be extracted directly from the environment by sub-aggregating the raw performance of individuals in a variety of ways. We use lexicase selection to optimize for these objectives as it has been shown to implicitly maintain population diversity. We compare this technique with a varying number of objectives to a commonly used quality diversity algorithm, MAP-Elites, on a set of discrete optimization as well as reinforcement learning domains with varying degrees of deception. We find that decomposing objectives into many objectives and optimizing them outperforms MAP-Elites on the deceptive domains that we explore. Furthermore, we find that this technique results in competitive performance on the diversity-focused metrics of QD-Score and Coverage, without explicitly optimizing for these things. Our ablation study shows that this technique is robust to different subaggregation techniques. However, when it comes to non-deceptive, or “illumination” domains, quality diversity techniques generally outperform our objective-based framework with respect to exploration (but not exploitation), hinting at potential directions for future work.

1 Introduction

In the realm of machine learning, numerous problems exhibit inherent deceptiveness, i.e., direct optimization towards a given objective within these domains often yields suboptimal solutions. To traverse these intricate problems, algorithms have been developed to place significant emphasis on explicit diversity maintenance, such as quality diversity algorithms (Pugh et al., 2016). Such strategies improve exploration capabilities, thereby avoiding the deceptive characteristics inherent in these problems. Nevertheless, a notable limitation of these explicit diversity maintenance techniques is the need to define and measure certain diversity metrics during the process of optimization.

In this work, we present an alternative approach to navigating deceptive domains without explicit diversity maintenance. We propose a method that leverages multi-objective optimization (MOO) to implicitly maintain stepping stones to global solutions. Instead of directly optimizing for a single objective, we decompose the objective into multiple sub-objectives and optimize for different combinations of these in parallel. This allows us to explore the search space more comprehensively, potentially uncovering high-quality solutions that explicit diversity techniques might skip. We utilize lexicase selection (Helmuth et al., 2015; Spector, 2012) to perform this optimization, due to its demonstrated implicit diversity maintenance properties as well as its superior performance in MOO.

Our experimental results demonstrate that our objective-based approach outperforms MAP-Elites on the deceptive domains we examine. By decomposing the objectives and optimizing them independently, we are able to achieve better solution quality and explore the search space more effectively. Furthermore, our approach achieves competitive performance on diversity-focused metrics, such as QD-Score and Coverage, without explicitly optimizing for diversity. We also conduct an ablation study to assess the robustness of our subaggregation technique. The results show that different subaggregation methods yield similar performance, indicating the versatility of our approach.

Overall, our findings demonstrate the efficacy of implicit diversity maintenance using multi-objective optimization. By decomposing objectives and leveraging lexicase selection, we can effectively solve deceptive domains without the need for explicit diversity maintenance.

2 Related work

There exists a considerable literature of work surrounding finding solutions to deceptive problems. This work often is inspired by evolution in nature due to it being a fundamentally open-ended process. In this section, we outline the areas of research most relevant to this work, and provide references for a curious reader to learn more.

Diversity-Driven Optimization

Novelty Search (Lehman & Stanley, 2011a) was introduced as an algorithm to overcome highly deceptive fitness landscapes, where methods that follow objectives usually fail. Lehman & Stanley (2011a) found that by “abandoning objectives” and simply optimizing for novelty in the solutions, deceptive problems can be solved more consistently. Since then, large research efforts have been lead into using Novelty search to solve previously unsolvable deceptive problems (Mouret, 2011; Gomes et al., 2015; Risi et al., 2010; Lehman & Stanley, 2010).

Novelty Search with Local Competition enhances Novelty Search’s use by assessing individuals for both novelty and fitness (Lehman & Stanley, 2011b). This approach was among the first ”Quality Diversity” (QD) algorithms, simultaneously optimizing for performance and diversity (Pugh et al., 2016). Another method optimizes aggregate performance and diversity with a multi-objective evolutionary algorithm (Mouret, 2011).

The MAP-Elites algorithm maintains an archive of diverse individuals with respect to specific qualitative “measures”, with each cell housing individuals with the highest fitness found so far (Mouret & Clune, 2015). There have been many MAP-Elite variants that can exploit gradients (Fontaine & Nikolaidis, 2021; Tjanaka et al., 2022; Boige et al., 2023; Lim et al., 2023b), utilize advanced evolutionary algorithms (Fontaine & Nikolaidis, 2023), or apply policy-gradient-based techniques (Nilsson & Cully, 2021; Lim et al., 2023a).

QD algorithms typically solve deceptive problems, where there is a single optimal solution to find, and illuminative problems, where the goal is to span a series of qualitative “measures” or “descriptors” while maintaining high performance. A classic example of an illumination problem, that we consider in this work, is finding a set of reinforcement learning policies π​(s)\pi(s) that effectively reach a specific maze position (x,yx,y) while minimizing energy cost (Mouret & Clune, 2015; Cully et al., 2015).

Multi-Objective Optimization

The concept of multi-objectivation (Knowles et al., 2001) has been explored in traditional hill-climbing-style optimization methods to reduce the likelihood of becoming trapped in local optima. Our work further extends this concept with population-based optimization methods for implicit diversity maintenance, where the objectives are constructed according to different heuristics that may imply certain diversity characteristics. There has been a recent interest in combining Multi-Objective Optimization with Quality Diversity (Janmohamed et al., 2023; Pierrot et al., 2022). However, we consider large sets of objectives, which would cause dominance-based techniques like those in the literature to be ineffective due to the curse of dimensionality.

Another important aspect of this paper is lexicase selection, a popular parent selection algorithm developed for use in evolutionary computation systems (Helmuth et al., 2015; Spector, 2012). It has been shown to be effective at solving these problems when there are many objectives, as the domination-based MOOs suffer from the curse of dimensionality) La Cava et al. (2019). There also has been recent interest in comparing lexicase selection and quality diversity techniques (Boldi & Spector, 2023; Jundt & Helmuth, 2019). Lexicase selection continually filters down a population based on a random shuffle objectives by keeping individuals that are elite on the given test cases, in order. A more in depth description of lexicase selection can be found in Appendix A.

3 Optimization with Implicit Diversity

Diversity-driven algorithms have been praised for their ability to explore complex search spaces by actively preserving phenotypic differences in a population of solutions, which is often achieved by employing explicit diversity maintenance, e.g., MAP-Elites (Mouret & Clune, 2015). However, such explicit diversity maintenance has its limitations. It often needs prior knowledge to choose relevant diversity metrics. More importantly, in more complex or deceptive search spaces where the relationship between phenotypic traits and fitness is not straightforward, these explicit measures can inadvertently steer the search away from optimal or even satisfactory solutions.

This work introduces implicit diversity maintenance as a promising alternative in such scenarios. Instead of overtly measuring and preserving diversity, our method inherently promotes diversity through its structure and operation. In general, we propose an objective subaggregation approach that turns the search problem into a multi-objective optimization (MOO) problem, and utilizes lexicase selection, which has been shown to produce diverse solutions and maintain such diversity, to solve it. This leads to a more adaptive and efficient exploration of the search space, potentially uncovering solutions that explicit methods might miss, especially when the terrain of the search landscape is intricate or misleading.

3.1 Objective Subaggregation

In the realm of general search problems, the objectives are often framed as aggregated values over a series of steps or stages. For instance, in reinforcement learning (RL), the goal typically boils down to maximizing the cumulative reward over time, i.e., the sum of step rewards over the course of an episode, until termination. Similarly, in robotics problems such as navigation or control, the overarching goal is often to reach a desired endpoint of a trajectory, determined by an accumulation of individual position changes over time.

Delving deeper into this notion of aggregation, we introduce the concept of “objective subaggregation”. Instead of aggregating over all objective values, we focus on subsets of these values, where the subsets could be sampled based on certain heuristics or predefined rules. Given the set of steps or stages TT and nn heuristics, the it​hi^{th} heuristic hih_{i} samples a subset SiS_{i} where Si=hi​(T)S_{i}=h_{i}(T). The sub-aggregated objectives RR can be expressed as:

R={Ri}={∑t∈Sirt},i=1,2,⋯,nR=\{R_{i}\}=\Big{\{}\sum_{t\in S_{i}}r_{t}\Big{\}},i=1,2,\cdots,n (1)

where rtr_{t} is objective value at step/stage tt.

This objective subaggregation approach converts a single-objective optimization problem into a multi-objective or many-objective one, where the objectives can be used to promote diversity depending on the heuristics for sampling. This allows for more granular and targeted optimization that can potentially enhance the efficiency and effectiveness of the search process.

3.2 Multi-Objective Optimization with Implicit Diversity Maintenance

While the proposed objective subaggregation method can be potentially used to improve the diversity of solutions, another essential problem to solve is how to obtain and maintain such diversity during the optimization process. In this work, we utilize lexicase selection (Spector, 2012; Helmuth et al., 2015), which is a recently developed parent selection method in evolutionary computation. The idea of lexicase selection is that instead of compiling performance metrics over the training dataset, we can leverage individual performance to sift through a population via a sequence of randomly shuffled training cases. This strategy effectively tailors the selection pressure towards specific subsets of training cases that yield worse performance. Recent work also shows that by replacing individual performance with different objectives, lexicase selection can be used for multi-objective optimization, and outperforms state-of-the-art optimization algorithms (La Cava et al., 2019). A more in depth explanation of Lexicase Selection can be found in appendix A.

There are two main reasons for our specific choice of lexicase selection. Firstly, prior work (Helmuth et al., 2016) has shown that lexicase selection can maintain high diversity and re-diversify less-diverse populations. For complex search problems, the initial solutions (usually sampled from a Gaussian distribution) may not be diverse enough to drive the search, and may even lose diversity at certain points depending on the topology of the search space. Lexicase selection could potentially overcome these problems. Secondly, with different subaggregation strategies, the number of objectives for optimization after subaggregation may be large. Lexicase selection has shown to be the state-of-the-art method on many-objective optimization problems (La Cava et al., 2019) compared to other methods such as NSGA-II (Deb et al., 2002) and HypE (Bader & Zitzler, 2011) .

3.3 General Subaggregation Strategies

One important component in the proposed method is how the heuristics for subaggregation are chosen. We hereby introduce two general strategies that are used in this work and can be potentially extended to many other tasks in the RL, robotics, and beyond.

Space-based Subaggregation

Suppose there is some location information in each state tt that can be easily retrieved, e.g., the position of the agent or end-point of a robot arm, we denote it as (xt,yt)(x_{t},y_{t}) in a 2D space for simplicity. Each heuristic hih_{i} thus defines a sub-space (X,Y)(X,Y), and construct a sample Si={t∈T∣xt∈X​ and ​yt∈Y}S_{i}=\{t\in T\mid x_{t}\in X\text{ and }y_{t}\in Y\}. An example would be to split the 2D space into n×nn\times n blocks, and each block is a heuristic to construct the sample. This is often a cost-free approach as long as such location information is inherently contained in the state variables.

Time-based Subaggregation

Given the trajectory of states TT, we can define a subset directly based on its position. Here, each heuristic hih_{i} defines a sub-space T′T^{\prime}, and samples from Si={t∈T′}S_{i}=\{t\in T^{\prime}\}. An example would be to split the whole trajectory into nn pieces where each piece is the sample for subaggregation. This is an even more general strategy that can be applied to almost any optimization and search problem.

4 Domains

Refer to caption
Figure 1: Kheperax domain adapted from Grillotti & Cully (2023)

In order to test the problem solving performance of our implicit diversity maintenance technique, we consider two domains that are deceptive as search problems in general but vary in a few key aspects. We also present two variations of the latter domain to demonstrate robustness to task.

4.1 Knight’s Tour

A knight’s tour is a path through a chess board taken by a knight that satisfies the following conditions: a) the Knight doesn’t leave the board and b) Every tile is visited exactly once.

The Knight’s Tour domain is inherently deceptive. There exist many local optima that are easy to be trapped in. For example, consider a knight’s tour that visits all but 1 tile on the board. This knight’s tour is very nearly optimal. However, reaching this solution might not be very helpful in finding the tour that visits all tiles on the board, as that solution would likely be largely different. This is a good domain to test the problem solving ability of quality diversity algorithms, as well as lexicase selection. The maintenance of stepping stones is also very important to this domain, so the use of quality diversity algorithms here fits their usual use case in deceptive problems.

Objective and Subaggregation

The objective in the knight’s tour domain is to have the longest tour without breaking any rules. So, we define the fitness to be the size of the set of visited positions before the first rule break. The size of this set will range between 1 (worst) and 64 (best). This problem naturally lends itself to a space-based subaggregation where each heuristic hih_{i} references a quadtree decomposition of the positions of the board. For example, with 4 objectives, we split the 8×88\times 8 board into 4 smaller 4×44\times 4 portions, and aggregate the fitness achieved in these positions (i.e. the total number of tiles visited in this region). This leads to a four-dimensional objective vector, where each objective ranges from 0 to 16. In this work, we study objective counts of 1,4,16,641,4,16,64. For our MAP-Elites implementation, we use the measure function defined as the end position of the knight before a rule break, and we use the aggregated score as the objective value.

4.2 Maze

The Maze domain (Lehman & Stanley, 2011a) has often been cited as the motivating problem for novelty search based algorithms. In this maze (Figure 1) there is a reinforcement learning agent represented by a neural network policy πθ​(s)\pi_{\theta}(s). The goal for this agent is to reach the top left of the maze. It is clear that myopically optimizing to minimize the distance to the goal would result in the agent falling into one of many local minima on the map.

Other versions of this domain (Mouret & Doncieux, 2012; Grillotti & Cully, 2023) are presented with a slightly different purpose: to measure the “illumination” strength of these algorithms. This is a measure of how well the given algorithm can effectively spread across a given behavioral feature space. To do this, we must define the behavioral measures to be the end position of the robot. The objective then becomes some measure of the energy taken to reach this end position. A well performing illumination algorithm should find a large number of low energy consuming policies that result in reaching highly diverse parts of the maze. We decided to use this maze due to its historical precedence, as well as the fact that, with slight modifications to the reward function, it can be used as both a deceptive domain or an illumination domain.

Objective for Deceptive Maze

The objective in this task is to minimize the distance to the goal. As an objective, the agent must maximize the distance moved towards the goal at each time step. rt=dt−dt−1r_{t}=d_{t}-d_{t-1} where dtd_{t} is the distance from the agent to the goal at timestep tt.

Objective for Illumination Maze

The objective in this task is based on that used by Grillotti & Cully (2023). At each timestep, the agent receives a reward based on the energy consumption during that time-step. The agents actions 𝐚t\mathbf{a}_{t} can be characterized as:

𝐚t=clip​([Velocity command wheel 1Velocity command wheel 2],−1,1)×0.025\mathbf{a}_{t}=\text{clip}\left(\begin{bmatrix}\text{Velocity command wheel 1}\\ \text{Velocity command wheel 2}\end{bmatrix},-1,1\right)\times 0.025

and therefore, can assign the reward at each time step to be rt=−‖𝐚t‖22r_{t}=-||\mathbf{a}_{t}||_{2}^{2}. In order to get the total objective value or fitness ff, you can simply aggregate this reward over every time step f=∑t=1Trtf=\sum_{t=1}^{T}r_{t}.

Subaggregation

We follow the same subaggregation scheme for both types of maze domain. Since we get a single reward value per time-step, as well as a position of the agent at that time step, we follow a similar aggregation to that used in the knight’s domain. We perform a quadtree subaggregation of the rewards received when the agent is in certain parts of the state space. For example, when we have four objectives, we aggregate the reward received by the agent in each quadrant of the board, and end up with a four dimensional objective function. fi=∑t=1T𝟙​[Agent in quadrant i at time t]×rtf_{i}=\sum_{t=1}^{T}\mathds{1}\left[\text{Agent in quadrant $i$ at time $t$}\right]\times r_{t} where 𝟙\mathds{1} is the indicator function, that evaluates to 1 if the agent is in quadrant ii at time tt, or 0 otherwise. Since the agent can only be in one quadrant at a time, it becomes clear that f=∑i=0nrif=\sum_{i=0}^{n}r_{i} where nn is the number of objectives previously decided on, which satisfies our definition of a space based subaggregation. For both mazes, the measure function used for MAP-Elites is the end position of the robot, and the objective is the aggregated reward over the course of the trajectory.

5 Experiments

We perform a series of experiments to empirically validate the performance of our implicit diversity preservation algorithm. For each of the lexicase selection based systems, we instantiate a single population of solutions, and repeatedly select from them based on the objective subaggregation that is in use. Then, we perform mutation on the population members. These populations have a fixed size pp, and at each generation, we select (with replacement) pp individuals to be parents for the next generation. Note that this is different to the usual QD frameworks, where an archive of solutions is maintained over the course of the entire algorithm run. For the MAP-Elites based systems, we simply initialize an empty archive, and insert a series of solutions into the archive. Then, we select a batch of the elites from the archive, mutate them, and re-insert them if the cell that corresponds to their measure (xx and yy position for both domains) is empty or contains a worse solution. In these experiments, we set the batch size to be equal to the population size (pp) used in lexicase selection.

We hold a number of things constant for this investigation. We hold the total number of individual evaluations, solution representation and mutation scheme constant across both systems. Since lexicase selection operates on a population, we maintain an archive similar to that used in the MAP-Elites loop to report all of our statistics from. Every generation, we insert the current population of solutions into the archive in the same way as detailed by MAP-Elites, and use this for comparison.

From these successive archives, we report three different kinds of statistics. Best Score refers to the score that the best individual in the population/archive at that step has achieved. QD-Score is simply defined as the sum of the scores for each individual in the archive, corrected to account for negative values. Finally, coverage is simply the percentage of the cells in the archive that are full. For each of these metrics, we report the mean over 10 replicate runs, with standard deviation shaded at every step of our search procedure. Below, we outline the results of these experiments.

Refer to caption
(a) QD-Score
Refer to caption
(b) Best Score
Figure 2: Knight’s Tour results. We compare implicit diversity preservation approaches using lexicase selection and MAP-Elites across iterations. Lexicase selection shows an increasing performance given more objectives and outperforms MAP-Elites with 16 and 64 objectives.

5.1 Knights Tour

For this domain, we report the Best Score and the QD-Score over time for both algorithms. We did not include coverage results for this domain as all algorithms had full coverage of the defined measure archive for every iteration. We find that for the Knight’s tour domain, lexicase based approaches reach a solution that has a longer tour than MAP-Elites. This provides evidence that the MOO based approach is better at finding high performing solutions in the domain of choice. In terms of QD-Score, we also find that the lexicase selection based approaches outperform the MAP-Elites algorithm. The results for this can be found in Figure 2(a). This was a surprising result, as MAP-Elites operates directly to maximize this value, whilst lexicase selection is agnostic to the measures we use to measure diversity. This hints that lexicase selection is able to maintain diversity with respect to many human-chosen diversity metrics, demonstrating its’ potential applicability across a wide variety of domains.

5.2 Maze

Deceptive Maze

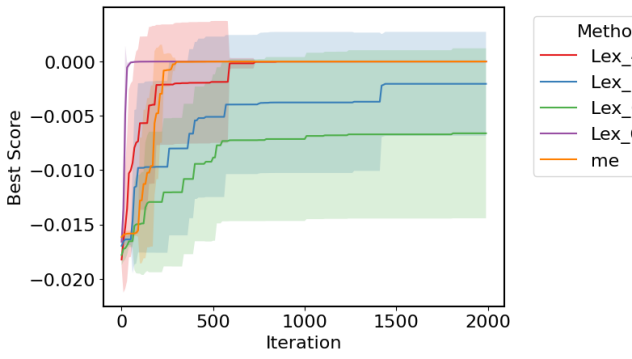
The results for our deceptive maze can be found in Figure 3. From these figures, it is clear that the objective-based techniques are outperforming MAP-Elites. With more objectives, we see better performance on this domain. This is likely due to the added diversity preservation that arises from a large number of objectives, which is one of the benefits of lexicase selection. We also see that, with all techniques but Lex-1 (single objective optimization), a policy is found that overcomes the deception of the maze and actually achieves the globally optimal score of 0. Surprisingly too do we see that the implicit diversity preservation techniques have a higher QD-Score than the archives for MAP-Elites, despite the fact that MAP-Elites is operating directly to optimize this metric.

Refer to caption
(a) QD-Score
Refer to caption
(b) Best Score
Figure 3: Deceptive Maze results. Implicit diversity preservation techniques have a higher QD-Score than the archives for MAP-Elites. They also find the best solution faster than MAP-Elites.

Illumination Maze

The results for the illumination maze can be found in Figure 4(a). We can see from these results a very similar conclusion to the prior two domains. Note that the objective is not designed to be deceptive and all algorithms very quickly reach the optimal score of 0 (can be seen in Appendix B.2). However, when it comes to the QD Score, it appears that lexicase selection with 64 objectives actually outperforms MAP-Elites. This result was especially surprising for us as this domain is not inherently deceptive, and so using an objective-based algorithm would not necessarily make sense in this context. However, we still find that the space-based subaggregation prioritizes exploration in the search space implicitly. We study whether this improvement holds across subaggregation strategies in our ablation study in Section 6.

Refer to caption
(a) Illumination Maze: QD-Score
Refer to caption
b1 Lexicase Selection w/ 64 Objs
Refer to caption
b2 MAP-Elites
(b) Archive Visualizations
Figure 4: Illumination Maze Archive results. (a) The QD-Score over time for a variety of methods. (b1) and (b2) show visualizations of the final archives for lexicase selection and MAP-Elites. A blank cell means that no individual was found with that given measure.

We also include a visualization of the archive to highlight the actual illumination abilities of each algorithm. Each position in the archive represents an individual that reaches that spot in the maze, and the fitness is determined by the energy used by the individual. Figures 4b1 and 4b2 shows two of the final archives from a randomly chosen replicate run. We can see that lexicase selection results in a better illumination of the measure space as more of the archive is filled with high performing solutions. The coverage results for both mazes are included in Appendix B.1. The results for coverage align well with the QD-Score metrics, as these two results are nearly directly correlated.

6 Ablation Study

In order to verify the robustness of our proposed methodology, we ablate the subaggregation we used on both the deceptive and illumination maze, and we compare the results. For this experiment, we replace the subaggregation used on the maze domain from a space-based one to a time-based one. This means, instead of the multiple objectives referring to the objective value collected at different locations on the maze, the multiple objectives refer to the time step that these values were collected in. For example, with 4 objectives, the time based aggregation would simply sum the rewards achieved in the first, second, third and fourth quarters of time-steps of the episode, treating each as a single objective. We suppose that this aggregation is generally very simply to apply to almost any time-step based RL domain.

The results of this ablation can be found in Figure 5. We see that the time-based subaggregation is competitive with the space based subaggregation when the domain is deceptive. This is because in the deceptive domain, the ultimate goal is to maximize an objective. Maintaining diversity is simply done in order to generate stepping stones to solve this problem. As long as the subaggregation scheme used is reasonable, it would result in added diversity preservation when used in conjunction with lexicase selection. We see that our algorithm detects the “correct kind” of diversity (i.e. lining up with the human hand-crafted measures) as evidenced by the increased QD-score on the deceptive domain. However, when the main goal in the space is illumination of a certain set of qualitative measures, one should try to design a subaggregation scheme with these measures in mind. Without it, using an uncorrelated subaggregation scheme might result in low exploration with respect to these measures, as one would expect.

Refer to caption
(a) Deceptive Maze: Best Score
Refer to caption
(b) Illuminative Maze: Best Score
Refer to caption
(c) Deceptive Maze: QD Score
Refer to caption
(d) Illuminative Maze: QD Score
Figure 5: Results of the ablation study. We compare time-based subaggregation with 4, 16 and 64 objectives to the space based subaggregation results we show above with 64 objectives and to MAP-Elites (me). When comparing problem solving performance (or the best score achieved throughout the search process), it is clear that lexicase is robust to the choice of subaggregation when using a deceptive domain.

7 Conclusion

In this work, we presented a technique to solve potentially deceptive problems without explicitly measuring or maintaining diversity. Given a domain, we sub-aggregate the objective as opposed to fully aggregating it, and solve this subaggregation of objectives with many objective optimization. We use lexicase selection perform this optimization, which has demonstrated implicit diversity preservation properties whilst also being able to operate on large numbers of objectives.

In experiments, we show that better search performance can be achieved using the objective-based approach than with explicit diversity methods such as MAP-Elites. This suggests that when domains are deceptive, using implicit diversity preservation techniques could result in better stepping stones for optimization. Furthermore, we find that our objective-based approaches also outperform the diversity-based approaches on evaluation metrics that are diversity-focused. For example, despite the fact that MAP-Elites is designed to optimize for QD-Score, our technique often performs better with respect to this metric without being directly tasked to do so. This gives good evidence for the applicability of our strategy to solve a variety of deceptive domains.

Our ablation study shows that our technique can be robust to changes in the subaggregation scheme for deceptive domains. However, we find that when the domains are non-deceptive, the exploration ability of our algorithm is subject to the subaggregation scheme used, and likely would require more careful choices regarding how to aggregate states (based on their location spatially or temporally).

Lehman & Stanley (2011a) end their seminal novelty search paper with the line “To achieve your highest goals, you must be willing to abandon them.” This work hints at an alternative view: “To achieve your highest goals, you must be willing to decompose them and work towards each component, in a potentially random order.”

References

  • Bader & Zitzler (2011) Johannes Bader and Eckart Zitzler. Hype: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary computation, 19(1):45–76, 2011.
  • Boige et al. (2023) Raphael Boige, Guillaume Richard, Jérémie Dona, Thomas Pierrot, and Antoine Cully. Gradient-informed quality diversity for the illumination of discrete spaces. arXiv preprint arXiv:2306.05138, 2023.
  • Boldi & Spector (2023) Ryan Boldi and Lee Spector. Can the Problem-Solving Benefits of Quality Diversity Be Obtained without Explicit Diversity Maintenance? Proceedings of the Companion Conference on Genetic and Evolutionary Computation, pp.  2152–2156, July 2023. doi: 10.1145/3583133.3596336. URL https://dl.acm.org/doi/10.1145/3583133.3596336.
  • Cully et al. (2015) Antoine Cully, Jeff Clune, Danesh Tarapore, and Jean-Baptiste Mouret. Robots that can adapt like animals. Nature, 521(7553):503–507, 2015.
  • Deb et al. (2002) Kalyanmoy Deb, Amrit Pratap, Sameer Agarwal, and TAMT Meyarivan. A fast and elitist multiobjective genetic algorithm: Nsga-ii. IEEE transactions on evolutionary computation, 6(2):182–197, 2002.
  • Fontaine & Nikolaidis (2021) Matthew Fontaine and Stefanos Nikolaidis. Differentiable quality diversity. Advances in Neural Information Processing Systems, 34:10040–10052, 2021.
  • Fontaine & Nikolaidis (2023) Matthew Fontaine and Stefanos Nikolaidis. Covariance matrix adaptation map-annealing. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO ’23, pp.  456–465, New York, NY, USA, 2023. Association for Computing Machinery. ISBN 9798400701191. doi: 10.1145/3583131.3590389. URL https://doi.org/10.1145/3583131.3590389.
  • Gomes et al. (2015) Jorge Gomes, Pedro Mariano, and Anders Lyhne Christensen. Devising effective novelty search algorithms: A comprehensive empirical study. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, pp.  943–950, 2015.
  • Grillotti & Cully (2023) Luca Grillotti and Antoine Cully. Kheperax: a Lightweight JAX-based Robot Control Environment for Benchmarking Quality-Diversity Algorithms. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation, pp.  2163–2165, Lisbon Portugal, July 2023. ACM. ISBN 9798400701207. doi: 10.1145/3583133.3596387. URL https://dl.acm.org/doi/10.1145/3583133.3596387.
  • Helmuth et al. (2015) Thomas Helmuth, Lee Spector, and James Matheson. Solving Uncompromising Problems With Lexicase Selection. IEEE Transactions on Evolutionary Computation, 19(5):630–643, October 2015. ISSN 1089-778X, 1089-778X, 1941-0026. doi: 10.1109/TEVC.2014.2362729. URL http://ieeexplore.ieee.org/document/6920034/.
  • Helmuth et al. (2016) Thomas Helmuth, Nicholas Freitag McPhee, and Lee Spector. Effects of lexicase and tournament selection on diversity recovery and maintenance. In Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion, pp.  983–990, 2016.
  • Janmohamed et al. (2023) Hannah Janmohamed, Thomas Pierrot, and Antoine Cully. Improving the data efficiency of multi-objective quality-diversity through gradient assistance and crowding exploration. arXiv preprint arXiv:2302.12668, 2023.
  • Jundt & Helmuth (2019) Lia Jundt and Thomas Helmuth. Comparing and combining lexicase selection and novelty search. In Proceedings of the Genetic and Evolutionary Computation Conference, pp.  1047–1055, 2019.
  • Knowles et al. (2001) Joshua D Knowles, Richard A Watson, and David W Corne. Reducing local optima in single-objective problems by multi-objectivization. In International conference on evolutionary multi-criterion optimization, pp.  269–283. Springer, 2001.
  • La Cava et al. (2019) William La Cava, Thomas Helmuth, Lee Spector, and Jason H. Moore. A Probabilistic and Multi-Objective Analysis of Lexicase Selection and ϵ\epsilon-Lexicase Selection. Evolutionary Computation, 27(3):377–402, 2019. ISSN 1530-9304. doi: 10.1162/evco˙a˙00224.
  • Lehman & Stanley (2010) Joel Lehman and Kenneth O. Stanley. Efficiently evolving programs through the search for novelty. In Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation, GECCO ’10, pp.  837–844, New York, NY, USA, 2010. Association for Computing Machinery. ISBN 9781450300728. doi: 10.1145/1830483.1830638. URL https://doi.org/10.1145/1830483.1830638.
  • Lehman & Stanley (2011a) Joel Lehman and Kenneth O Stanley. Abandoning objectives: Evolution through the search for novelty alone. Evolutionary computation, 19(2):189–223, 2011a.
  • Lehman & Stanley (2011b) Joel Lehman and Kenneth O Stanley. Evolving a diversity of virtual creatures through novelty search and local competition. In Proceedings of the 13th annual conference on Genetic and evolutionary computation, pp.  211–218, 2011b.
  • Lim et al. (2023a) Bryan Lim, Manon Flageat, and Antoine Cully. Understanding the synergies between quality-diversity and deep reinforcement learning. In Proceedings of the Genetic and Evolutionary Computation Conference. ACM, jul 2023a. doi: 10.1145/3583131.3590388. URL https://doi.org/10.1145%2F3583131.3590388.
  • Lim et al. (2023b) Bryan Lim, Manon Flageat, and Antoine Cully. Efficient exploration using model-based quality-diversity with gradients. In ALIFE 2023: Ghost in the Machine: Proceedings of the 2023 Artificial Life Conference. MIT Press, 2023b.
  • Mouret (2011) Jean-Baptiste Mouret. Novelty-based multiobjectivization. In New Horizons in Evolutionary Robotics: Extended Contributions from the 2009 EvoDeRob Workshop, pp.  139–154. Springer, 2011.
  • Mouret & Clune (2015) Jean-Baptiste Mouret and Jeff Clune. Illuminating search spaces by mapping elites. arXiv preprint arXiv:1504.04909, 2015.
  • Mouret & Doncieux (2012) Jean-Baptiste Mouret and Stéphane Doncieux. Encouraging Behavioral Diversity in Evolutionary Robotics: an Empirical Study. Evolutionary Computation, 20(1):91–133, 2012. doi: 10.1162/EVCO˙a˙00048. URL https://hal.science/hal-00687609. Publisher: Massachusetts Institute of Technology Press (MIT Press).
  • Nilsson & Cully (2021) Olle Nilsson and Antoine Cully. Policy gradient assisted map-elites. In Genetic and Evolutionary Computation Conference, 2021.
  • Pierrot et al. (2022) Thomas Pierrot, Guillaume Richard, Karim Beguir, and Antoine Cully. Multi-objective quality diversity optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, pp.  139–147, 2022.
  • Pugh et al. (2016) Justin K. Pugh, Lisa B. Soros, and Kenneth O. Stanley. Quality Diversity: A New Frontier for Evolutionary Computation. Frontiers in Robotics and AI, 3, July 2016. ISSN 2296-9144. doi: 10.3389/frobt.2016.00040. URL http://journal.frontiersin.org/Article/10.3389/frobt.2016.00040/abstract.
  • Risi et al. (2010) Sebastian Risi, Charles E Hughes, and Kenneth O Stanley. Evolving plastic neural networks with novelty search. Adaptive Behavior, 18(6):470–491, 2010.
  • Spector (2012) Lee Spector. Assessment of Problem Modality by Differential Performance of Lexicase Selection in Genetic Programming: A Preliminary Report. 2012.
  • Tjanaka et al. (2022) Bryon Tjanaka, Matthew C. Fontaine, Julian Togelius, and Stefanos Nikolaidis. Approximating gradients for differentiable quality diversity in reinforcement learning. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO ’22, pp.  1102–1111, New York, NY, USA, 2022. Association for Computing Machinery. ISBN 9781450392372. doi: 10.1145/3512290.3528705. URL https://doi.org/10.1145/3512290.3528705.

Appendix A Lexicase Selection

An outline of lexicase selection can be found in Algorithm 1. Given a series of objectives, lexicase selection randomly shuffles these objectives and considers them in order. The population is filtered down based on the performance of the individuals on these objectives by taking the individuals with the maximal performance on this objective when compared to the rest of the pool of candidates. Then, the next objective is used to filter this pool down further until there is either a single candidate remaining, or there are no more objectives to use. Then, this process is repeated with a new shuffle of objectives to select the next parent. This process is repeated until we have selected enough individuals to be parents for the next generation.

Data:
  • •

    objectives - a sequence of the objectives to be used in the selection

  • •

    candidates - the entire population of individuals

Result:
  • •

    A selected individual

shuffled_objs ←\leftarrow Shuffle(objectives)
for obj in shuffled_objs do
       results ←\leftarrow evaluate candidates with respect to obj
      candidates ←\leftarrow the subset of the current candidates that have exactly best performance on obj
      if candidates contains only one single candidate then
            return candidate
       end if
      
end for
candidate ←\leftarrow a randomly selected individual in candidates
return candidate
Algorithm 1 Lexicase Selection for Parent Selection

Appendix B Further Results

B.1 Coverage Results for the Two Maze Domains

We include results (Figure 6) for the coverage of the archive for each of these algorithms. The coverage is the fraction of the archive that is full at every step of the search procedure. For the deceptive domain, these results are directly proportional to the QD-Score results as the objective value at a given portion of the archive is entirely determined by it’s (x,y)(x,y) position. For the illumination maze, whilst not directly proportional, we expect the coverage to be highly correlated with the QD-Score, as discovering more solutions would lead to a higher QD-Score as well as coverage.

Refer to caption
(a) Deceptive Maze
Refer to caption
(b) Illuminative Maze
Figure 6: Percentage coverage of the mazes by solutions discovered by each algorithm.

B.2 Best Score for Illumination Maze

We include results (Figure 7) for the best performance of any individual produced using MAP-Elites versus those produced by Lexicase selection. It is clear that both of these algorithms rapidly discover solutions with the minimum energy expenditure of 0. This highlights the fact that this domain is not deceptive at all, as achieving a globally optimal solution is trivial (just staying still suffices to achieve this).

Refer to caption
Figure 7: Illumination Maze: Best performance achieved by each algorithm