Nuclear multipole responses from chiral effective field theory interaction
Abstract
We probe nuclear multipole resonances in the framework of the random-phase approximation by using the interaction obtained from the chiral effective field theory. The three-nucleon force is included in a form of the in-medium two-nucleon interaction which was derived from the chiral three-nucleon force. The isoscalar monopole, isoscalar dipole, isovector dipole and isoscalar quadrupole resonances of the closed-shell 56,68,78Ni have been investigated. The calculations reasonably reproduce the experimental multipole resonances of 56,68Ni, and well describe the pygmy dipole resonance and dipole polarizability measured in 68Ni. The multipole resonances of 78Ni, including pygmy dipole resonance and dipole polarizability, are predicted. The detailed effects of the tensor force and three-body force are analyzed by dissecting the chiral interaction. We find that in general the tensor force effect on electric giant resonances is not as significant as the effect from the three-body force, although the tensor force provides more than half of the binding energy. The effect from three-body force is strong in light nuclei. Particularly, three-body force is crucial for the formation of the pygmy resonance in calculations.
I Introduction
Giant resonances (GRs) in atomic nuclei are the most collective excitations in which many nucleons participate in a joint motion with various multipolarities and different spin-isospin quantum numbers. GRs are relevant to many physics problems, ranging from finite nuclei to infinite nuclear matter to neutron stars and supernovae Glendenning (1997); Harakeh and van der Woude (2001). The isoscalar giant monopole resonance (ISGMR) and isoscalar giant dipole resonance (ISGDR) provide direct way to probe the incompressibility of nuclei and nuclear matters Harakeh and van der Woude (2001); Garg and Colò (2018); Colò et al. (2014). The electric dipole polarizability quantifies the behavior of dipole response and is related to the neutron distribution Reinhard and Nazarewicz (2010); Hagen et al. (2016). The GRs of nuclei far from the valley of stability provide particular information on the structures of exotic nuclei and the equation of state (EOS) of neutron-rich matter.
The ISGMR in neutron-rich nuclei can be used to probe the density dependence of the symmetry energy because it is sensitive to the incompressibility of nuclear matter Fattoyev and Piekarewicz (2012); Piekarewicz and Centelles (2009); Hebeler and Schwenk (2014); Colò et al. (2014). For neutron-rich nuclei, there exist low-lying electric dipole responses with weak strengths, named pygmy dipole resonance (PDR) Brzosko et al. (1969); Savran et al. (2013). They are interpreted as the dipole oscillations of excess neutrons against a core made by all other nucleons Mohan et al. (1971). The PDR can be used to determine the neutron-skin thickness and the parameters of the EOS. Neutron capture cross sections in the astrophysical -process are also impacted by PDRs Goriely (1998); Savran et al. (2013). Studying the evolution of GRs along an isotopic chain is useful in both experiment and theory for understanding of the isotopes and EOS. Nickel isotopes provide an excellent laboratory for the investigation of the evolution. In 56Ni, Monrozeau et al. Monrozeau et al. (2008) implemented the first measurement of the isoscalar response. Recently, the multipole response strengths in the neutron-rich 68Ni were observed Rossi et al. (2013); Vandebrouck et al. (2014, 2015). 78Ni with an extreme neutron-proton asymmetry (28 protons and 50 neutrons) is claimed to be a doubly magic nucleus Taniuchi et al. (2019). It was commented that there is a competition between spherical and deformed shapes, which is challenging the current theory Taniuchi et al. (2019).
A variety of nonrelativistic and relativistic mean-field models have been successfully applied to the GRs of nuclei (see, e.g., Paar et al. (2007); Bai et al. (2010); Van Giai and Sagawa (1981a); Wang et al. (2017); Sagawa and Bertulani (1996); Litvinova and Wibowo (2018) and references therein). Calculations based on realistic nuclear forces have also made considerable progresses in the descriptions of the multipole responses, such as few-body approach Gazit et al. (2006); Bacca et al. (2015), no-core shell model Quaglioni and Navrátil (2007); Baker (2019), self-consistent Green’s function (SCGF) Raimondi and Barbieri (2019), coupled cluster combined with the Lorentz integral transform Bacca et al. (2013); Miorelli et al. (2016) and Hartree-Fock plus random-phase approximation (HF-RPA) Paar et al. (2006); Papakonstantinou et al. (2007); Wu et al. (2018).
In theory, the collective responses of nuclei are directly related to certain properties of the underlying nuclear force. The roles of the tensor force and three-nucleon force (3NF) have recently been highlighted in nuclear structure calculations. It has been claimed that the tensor force has a significant contribution to charge-exchange excitation Bai et al. (2009, 2010); Minato and Bai (2013). The 3NF has been known playing an important role in the first-principles calculations of nuclear matters and structures Sammarruca et al. (2012); Ekström et al. (2015); Jurgenson et al. (2009); Maris et al. (2011); Hergert et al. (2013); Ekström et al. (2014); Carlson et al. (2015); Ma et al. (2019). The chiral effective field theory (EFT) provides a robust framework to construct nucleon-nucleon interaction based on quantum chromodynamics Machleidt and Entem (2011). An important advantage of the chiral EFT is that it creates two- and three-nucleon forces on an equal footing. The chiral EFT interaction provides a good platform for analyzing the effects of the tensor force and 3NFs.
In the previous work Wu et al. (2018), we calculated the monopole, dipole and quadrupole resonances of the closed-shell nuclei 4He,16,22,24O and 40,48Ca using the chiral EFT NNLOsat interaction within the Hartree-Fock plus RPA (HF-RPA) approach. The HF-RPA can reproduce experimental multipole resonances reasonably. In this work, we extend the calculations to heavier nuclei, 56,68,78Ni, with particular focus on the roles of the tensor force and 3NF of the underlying realistic nuclear force in the giant resonances.
II The Hartree-Fock Random Phase Approximation (HF-RPA)
The intrinsic Hamiltonian of the -nucleon system reads
| (1) |
where is the two-body nucleon-nucleon () interaction, and is the three-nucleon force (3NF). The chiral EFT two-body interaction N3LO developed by Entem and Machleidt Entem and Machleidt (2003) is used. We include the 3NF via the in-medium two-body potential V that was derived from the chiral N2LO 3NF by integrating one nucleon over the Fermi sea (i.e., up to the Fermi momentum ) in symmetric nuclear matter Holt et al. (2009); *PhysRevC.81.024002; Hebeler and Schwenk (2010). The extra low-energy constants for the chiral effective N2LO 3NF are = 0.2 and = 0.735 with the effective cutoff = 500 MeV and the Fermi momentum = 0.95 fm-1, which are the same as given in Ref. Hagen et al. (2012). With the chiral NN interaction at N3LO Entem and Machleidt (2003) and the effective in-medium 3NFeff at N2LO, the coupled cluster calculations have well described binding energies and low-lying excitation energies of heavy -shell nuclei Hagen et al. (2012).
The chiral NN+3NFeff is expressed in 13 major harmonic oscillator (HO) shells with the commonly used oscillator frequency = 24 MeV Hagen et al. (2012); Hu et al. (2019); Henderson et al. (2018). With the interaction established thus, we perform the HF-RPA calculations for the isoscalar monopole, isoscalar dipole, isovector dipole and isoscalar quadrupole resonances of the closed-shell nuclei 56,68,78Ni. The detail of the HF-RPA approach can be found in our previous article Wu et al. (2018). The photo-absorption cross section and electric dipole polarizability are interesting observables for nuclear giant responses Raimondi and Barbieri (2019); Miorelli et al. (2016), which were not calculated in our previous paper on the He, O and Ca isotopes Wu et al. (2018). The and measure the responses to the isovector dipole resonance. We have
| (2) |
and
| (3) |
where is fine-structure constant and is the excitation energy of the resonance. is the response strength distribution of the transition,
| (4) |
where is the reduced electric dipole transition probability Wu et al. (2018). The summation is over all possible particle-hole excitation modes Wu et al. (2018). stands for the excitation energy of an excitation mode which is obtained in the HF-RPA calculation Wu et al. (2018). The discrete stength distributions is smoothed by using the Lorentzian function,
| (5) |
where the width of = 2 MeV Paar et al. (2006); Papakonstantinou et al. (2007); Wu et al. (2018) is used.
III Calculations and discussions
Figure 1 gives the HF-RPA results for 56Ni, compared with available experimental data Monrozeau et al. (2008). In the experiment Monrozeau et al. (2008), the centroid energies of the ISGMR and isoscalar giant quadrupole resonance (ISGQR) were measured at 19.30.5 MeV and 16.20.5 MeV via the 56Ni(,) reaction. The data provide useful information to test theoretical approaches and can be used to extract the nuclear matter incompressibility Harakeh and van der Woude (2001); Garg and Colò (2018); Colò et al. (2014). In order to dissect the roles of the different components of the interaction, we use the spin-tensor decomposition method Elliott et al. (1968); Kirson (1973); Umeya and Muto (2006) to decompose the interaction into central, tensor, and spin-orbit parts. The calculation without tensor force means that the tensor terms in NN+3NFeff are taken away by using the spin-tensor decomposition method. As shown in Fig. 1, the tensor force and 3NF have no significant effect on the IS monopole resonance, while their effects on other multipole resonances are seen clearly. The tensor force shifts the energy of the low-lying state by 2 MeV, and other IS quadrupole and IS dipole peaks are shifted within 5% (the percent of the peak-energy shift over the peak energy). It changes the centroid energy of the IV dipole resonance by 16%. It seems that the 3NF effects are more significant in the IS quadrupole and IS dipole resonances. The calculation without 3NF cannot clearly give the peak at 1 MeV in the IS quadrupole response distribution. The calculated RPA wave function shows that the low-lying state is caused by several one-particle one-hole excitations with the neutron or proton excited from to or . The peak seems to correspond to the experimental 2 excited state at 2.7 MeV nnd . For the state, the present HF-RPA gives a reduced E2 transition probability = 0.454 e2b2, larger than the experimental datum of 0.060(12) e2b2 Kraus et al. (1994). The discrepancy between the calculations and data would originate from missing higher-order correlations in RPA Wu et al. (2018).

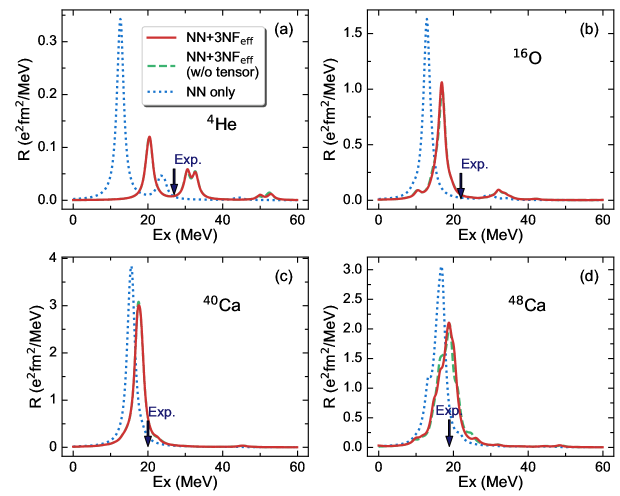
We find that the 3NF effect on giant resonances is more pronounced in light nuclei. In Fig. 2, we show the calculations of the IV dipole resonances for the closed-shell nuclei, 4He, 16O and 40,48Ca. The nuclei were investigated in our previous paper using the chiral NNLOsat with the 3NF being normal ordered at a two-body level Wu et al. (2018). Here, we recalculate their IV dipole resonances and analyze the 3NF effect by using the 3NFeff. Obtained results using the 3NFeff are similar to those given by using NNLOsat Wu et al. (2018). We see that the 3NF effects are significant, particularly in 4He and 16O. Since we have no NNLOsat interaction matrix elements for the heavy Ni isotopes, the N3LO(NN) and NNLO(3NFeff) are used in the present calculations.
In Table 1, we calculate the dipole polarizability for the nuclei, compared with data Pachucki and Moro (2007); Ahrens et al. (1975); Birkhan et al. (2017), coupled-cluster (CC) Miorelli et al. (2016); Hagen et al. (2016) and density functional theory (DFT) Colò et al. (2013) calculations. In the CC calculations Miorelli et al. (2016); Hagen et al. (2016), the chiral NNLOsat(NN+3NF) interaction was used. For the DFT results, the self-consistent RPA calculations with Skyrme forces SG Van Giai and Sagawa (1981b), SkM* Bartel et al. (1982), SkP Dobaczewski et al. (1984), Sk255 Agrawal et al. (2003), SLy4 Chabanat et al. (1998); *1998441, Sly5 Chabanat et al. (1998); *1998441 and LNS Cao et al. (2006) were performed by using the skyrme-rpa code Colò et al. (2013). The use of different Skyrme forces gives a range of the values, shown in Table 1. The present and DFT calculations overestimate slightly the dipole polarizability in 4He, 16O and 48Ca, while in 40Ca the is slightly underestimated in the present and CC calculations. The tensor force has no significant effect on the electric dipole polarizability , as shown in Table 1.
|
|
|
Exp. | CC | DFT | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4He | 0.2811 | 0.0892 | 0.0893 | 0.076(8) | 0.0735 | 0.11080.1333 | ||||||
| 16O | 1.2714 | 0.7618 | 0.7593 | 0.58(1) | 0.58 | 0.61540.6922 | ||||||
| 40Ca | 2.5866 | 2.0521 | 2.0507 | 2.23(3) | 2.08 | 2.01752.2508 | ||||||
| 48Ca | 2.8391 | 2.2231 | 2.2438 | 2.07(22) | 2.192.60 | 2.35942.5813 |
Figure 3 shows the results for 68Ni. It is seen that the effect of tensor force is similar to that in 58Ni. In the neutron-rich 68Ni, the isovector PDR (IVPDR) and isovector GDR (IVGDR) were observed recently by Rossi et al. Rossi et al. (2013) with peaks located at 9.55(17) MeV and 17.1(2) MeV, respectively. We see that the calculation with 3NF can give the IV PDR peaked at energy 10 MeV, while the calculation without 3NF does not show a clear PDR peak. However, the reduced electric dipole transition probability calculated without 3NF shows a possible weak PDR at energy 10 MeV. There is a strong resonance peak at 10 MeV in the IS channel, which overlaps with the weak IV peak. This indicates a mixing nature of isoscalar and isovector resonances in the dipole channel at low energy. The mixing was seen in our previous calculations Wu et al. (2018) for the neutron-rich 22,24O. Experimentally, the IS dipole resonance can be incurred by inelastic scatterings with an isoscalar particle (e.g., particle), while electromagnetic excitations (usually by electron scattering) give the total strength of the IS and IV resonances. The recent experiment Vandebrouck et al. (2015) has shown the possible IS dipole resonances in the energy range of 1129 MeV (see Fig. 3).

The experiment by Rossi et al. Rossi et al. (2013) presents the first measurement of the dipole polarizability in an unstable neutron-rich nucleus. Using the measured , the authors Rossi et al. (2013) deduced a neutron-skin thickness of 0.17(2) fm in 68Ni by taking a nearly linear relation between and neutron-skin thickness guided by the relativistic RPA calculation Piekarewicz (2011). The data provide further constraint on the isospin-asymmetric part of the EOS.
Table 2 lists the calculated isovector dipole polarizability, compared with the data Rossi et al. (2013), SCGF Raimondi and Barbieri (2019) and DFT Colò et al. (2013) calculations. The calculated dipole polarizability agrees well with the data Rossi et al. (2013) and SCGF Raimondi and Barbieri (2019). In the SCGF calculations, NNLOsat(NN+3NF) was used. There are two IV dipole resonance peaks at the low energies of 10.6 and 11.6 MeV, similar to the SCGF conclusions. The mean-field calculation Khan et al. (2011) predicted a possible soft monopole excitation in 68Ni. However, we do not see the soft monopole mode in the present calculations, while there is a low-lying IS quadrupole response peak at the energy of 4.2 MeV. The low-energy IS quadrupole peak would correspond to a soft resonance involving few-particle few-hole excitations or even one-particle one-hole excitation as happening in 22,24O Wu et al. (2018). These may need to be verified further by experiments and other models. In Table 2, we also show the results of 78Ni as prediction.
| 68Ni | 78Ni | |||||
| Exp. | Present | SCGF | DFT | Present | DFT | |
| (MeV) | 9.55(17) | 10.64 | 10.68 | 8.4110.60 | 11.03 | 8.7811.42 |
| 11.55 | 10.92 | |||||
| (%) | 2.8(5) Rossi et al. (2013); 5 Wieland et al. (2009) | 5.20 | 1.773.56 | 5.81 | 2.005.59 | |
| (MeV) | 17.1(2) | 18.64 | 18.10 | 16.4417.95 | 17.17 | 15.7118.72 |
| (fm3) | 3.40(23) | 3.40 | 3.60 | 3.994.52 | 3.76 | 4.485.26 |
The sum rule of the response strength distribution can be used to analyze the interaction in the momentum dependence and isospin exchange Erler et al. (2011). The energy-weighted sum rule (EWSR) is defined by Orlandini and Traini (1991)
| (6) |
where is the so-called enhancement factor which can be obtained by integrating the strength function Wu et al. (2018). As shown in Table 2, the present calculation with 3NFeff gives that, in 68Ni, the strength below 12 MeV exhausts 5.2% of the classical Thomas-Reiche-Kuhn (TRK) energy-weighted sum rule (EWSR), compared with the experimentally extracted value of Wieland et al. (2009) or 2.8(5)% Rossi et al. (2013). Note that the PDR peak at 10.64 MeV contributes about 2.0% of the EWSR, and the 11.55 MeV peak contributes about 3.2%. We predict that it is about 5.8% in 78Ni. Table 2 also gives the DFT results, as discussed in Table 1. The DFT calculations give smaller EWSR but larger than the present calculations in 68,78Ni.
Figure 4 displays the calculated ISGMR, ISGQR, ISGDR, and IVGDR for 78Ni, predicting a IV PDR peaked at 11 MeV. We see that the PDR is enhanced in the calculation with 3NF. The calculated centroid energies of the isovector PDR and GDR are given in Table 2. The isovector GDR energy in 78Ni is 1.5 MeV lower than the one in 68Ni. The dipole polarizability is also predicted in Table 2. 78Ni has been believed to be a doubly magic nucleus, with a high excitation energy at 2.6 MeV Taniuchi et al. (2019). The present HF-RPA calculation with 3NF gives 2.90 MeV for the excited state, which is consistent with the ab-initio coupled cluster and in-medium similarity renormalization group calculations given in Ref. Taniuchi et al. (2019).

From the calculations discussed above, we see that 3NF effects on collective multipole resonances are meaningful, particularly for light nuclei. The 3NF (including tensor ingredients) plays a crucial role in the formations of the PDRs in 68,78Ni. Fig. 5 plots the binding energies calculated within the RPA framework. In the binding energy calculation, the correction from the second-order perturbation Wu et al. (2018); Hu et al. (2016) is considered. We see that the tensor force provides more than 50% of the binding energy. If tensor components were taken away from the realistic interaction, we should not be able to describe the ground states of nuclei correctly. The 3NF also has a significant effect on binding energy, and improves the calculation, see Fig. 5. We find that the second-order many-body perturbation correction is not converged in 56Ni if only two-body interaction is considered in the calculation. This is why in Fig. 5 the 56Ni binding energy is missing in the NN-only cure.
In realistic nuclear forces, the tensor component is large. For example, in the chiral EFT leading-order term that consists of one-pion exchange and contact interactions, the tensor force has the same strength as the central force in the one-pion exchange Machleidt and Entem (2011); Tanihata (2013); Sagawa and Colò (2014). The leading-order term should be most important for the calculations of binding energy and other observables. The result that the tensor force provides a large proportion of the binding energy is quite general in calculations based on realistic forces. In Refs. Tanihata (2013); Sakai et al. (1974), the calculation with the Hamada-Johnston and Tamagaki interaction shows that about 50% of the 4He potential energy comes from the tensor force. In the Green-function Monte-Carlo calculations Pieper and Wiringa (2001), the one-pion exchange in the AV18 interaction provides 70%-80% of the nuclear potential energy for light nuclei. With the present method and interaction, we have also calculated the binding energies of 4He, 16O and 40,48Ca, giving the similar result, i.e., the tensor force provides about 50% of the binding energy.

IV Summary
Starting from the chiral effective field theory interaction N3LO(NN)+N2LO(3NFeff), we have performed the RPA calculations within the Hartree-Fock (HF) approach, to investigate the monopole, dipole and quadrupole resonances in 56,68,78Ni. The ground-state energies have also been calculated by incorporating the second-order perturbation correction into the HF-RPA energy. The present HF-RPA calculations reproduce reasonably the multipole resonances observed in 56,68Ni and their binding energies as well. The pygmy dipole resonance, the dipole polarizability and the sum rule in 68Ni have been discussed, and compared with experimental data available. The properties of 78Ni have been predicted.
We dissect the 3NF and tensor terms of the realistic interaction, to see their roles in the multipole resonances of nuclei. Although the tensor force may be important for charge-exchanged collective resonances, it is not such significant for the electric giant resonances. However, the tensor force provides more than half of binding energy using the chiral EFT interaction. The three-body force has a nonnegligible effect on multipole resonances, particularly on the formation of the pygmy resonance. The tensor force and three-body force hardly affect the isoscalar monopole giant resonance. In possible future work, we will extend the present framework to charge-exchange excitations.
Acknowledgements.
We thank Umesh Garg for his useful suggestions and discussions. This work has been supported by the National Key RD Program of China under Grant No. 2018YFA0404401; the National Natural Science Foundation of China under Grants No. 11921006, No. 11835001 and No. 11847203; China Postdoctoral Science Foundation under Grant No. 2018M630018; and the CUSTIPEN (China-U.S. Theory Institute for Physics with Exotic Nuclei) funded by the U.S. Department of Energy, Office of Science under Grant No. DE-SC0009971. We acknowledge the High-performance Computing Platform of Peking University for providing computational resources.References
- Glendenning (1997) N. K. Glendenning, Compact Stars (Springer-Verlag, New York, 1997).
- Harakeh and van der Woude (2001) M. N. Harakeh and A. van der Woude, Giant Resonances: Fundamental High-Frequency Modes of Nuclear Excitation (Oxford University Press, New York, 2001).
- Garg and Colò (2018) U. Garg and G. Colò, Prog. Part. Nucl. Phys. 101, 55 (2018).
- Colò et al. (2014) G. Colò, U. Garg, and H. Sagawa, Eur. Phys. J. A 50, 26 (2014).
- Reinhard and Nazarewicz (2010) P.-G. Reinhard and W. Nazarewicz, Phys. Rev. C 81, 051303(R) (2010).
- Hagen et al. (2016) G. Hagen et al., Nat. Phys. 12, 186 (2016).
- Fattoyev and Piekarewicz (2012) F. J. Fattoyev and J. Piekarewicz, Phys. Rev. C 86, 015802 (2012).
- Piekarewicz and Centelles (2009) J. Piekarewicz and M. Centelles, Phys. Rev. C 79, 054311 (2009).
- Hebeler and Schwenk (2014) K. Hebeler and A. Schwenk, Eur. Phys. J. A 50, 11 (2014).
- Brzosko et al. (1969) J. S. Brzosko, E. Gierlik, A. S. Jr., and Z. Wilhelmi, Can. J. Phys. 47, 2849 (1969).
- Savran et al. (2013) D. Savran, T. Aumann, and A. Zilges, Prog. Part. Nucl. Phys. 70, 210 (2013).
- Mohan et al. (1971) R. Mohan, M. Danos, and L. C. Biedenharn, Phys. Rev. C 3, 1740 (1971).
- Goriely (1998) S. Goriely, Phys. Lett. B 436, 10 (1998).
- Monrozeau et al. (2008) C. Monrozeau, E. Khan, Y. Blumenfeld, C. E. Demonchy, W. Mittig, P. Roussel-Chomaz, et al., Phys. Rev. Lett. 100, 042501 (2008).
- Rossi et al. (2013) D. M. Rossi, P. Adrich, F. Aksouh, H. Alvarez-Pol, T. Aumann, J. Benlliure, et al., Phys. Rev. Lett. 111, 242503 (2013).
- Vandebrouck et al. (2014) M. Vandebrouck, J. Gibelin, E. Khan, N. L. Achouri, H. Baba, D. Beaumel, et al., Phys. Rev. Lett. 113, 032504 (2014).
- Vandebrouck et al. (2015) M. Vandebrouck, J. Gibelin, E. Khan, N. L. Achouri, H. Baba, D. Beaumel, et al., Phys. Rev. C 92, 024316 (2015).
- Taniuchi et al. (2019) R. Taniuchi et al., Nature 569, 53 (2019).
- Paar et al. (2007) N. Paar, D. Vretenar, E. Khan, and G. Colò, Rep. Prog. Phys. 70, 691 (2007).
- Bai et al. (2010) C. L. Bai, H. Q. Zhang, H. Sagawa, X. Z. Zhang, G. Colò, and F. R. Xu, Phys. Rev. Lett. 105, 072501 (2010).
- Van Giai and Sagawa (1981a) N. Van Giai and H. Sagawa, Nucl. Phys. A 371, 1 (1981a).
- Wang et al. (2017) K. Wang, M. Kortelainen, and J. C. Pei, Phys. Rev. C 96, 031301(R) (2017).
- Sagawa and Bertulani (1996) H. Sagawa and C. A. Bertulani, Prog. Theor. Phys. Suppl. 124, 143 (1996).
- Litvinova and Wibowo (2018) E. Litvinova and H. Wibowo, Phys. Rev. Lett. 121, 082501 (2018).
- Gazit et al. (2006) D. Gazit, S. Bacca, N. Barnea, W. Leidemann, and G. Orlandini, Phys. Rev. Lett. 96, 112301 (2006).
- Bacca et al. (2015) S. Bacca, N. Barnea, W. Leidemann, and G. Orlandini, Phys. Rev. C 91, 024303 (2015).
- Quaglioni and Navrátil (2007) S. Quaglioni and P. Navrátil, Phys. Lett. B 652, 370 (2007).
- Baker (2019) R. Baker, LSU Doctoral Dissertations (2019).
- Raimondi and Barbieri (2019) F. Raimondi and C. Barbieri, Phys. Rev. C 99, 054327 (2019).
- Bacca et al. (2013) S. Bacca, N. Barnea, G. Hagen, G. Orlandini, and T. Papenbrock, Phys. Rev. Lett. 111, 122502 (2013).
- Miorelli et al. (2016) M. Miorelli, S. Bacca, N. Barnea, G. Hagen, G. R. Jansen, G. Orlandini, and T. Papenbrock, Phys. Rev. C 94, 034317 (2016).
- Paar et al. (2006) N. Paar, P. Papakonstantinou, H. Hergert, and R. Roth, Phys. Rev. C 74, 014318 (2006).
- Papakonstantinou et al. (2007) P. Papakonstantinou, R. Roth, and N. Paar, Phys. Rev. C 75, 014310 (2007).
- Wu et al. (2018) Q. Wu, B. S. Hu, F. R. Xu, Y. Z. Ma, S. J. Dai, Z. H. Sun, and G. R. Jansen, Phys. Rev. C 97, 054306 (2018).
- Bai et al. (2009) C. L. Bai, H. Sagawa, H. Q. Zhang, X. Z. Zhang, G. Colò, and F. R. Xu, Phys. Lett. B 675, 28 (2009).
- Minato and Bai (2013) F. Minato and C. L. Bai, Phys. Rev. Lett. 110, 122501 (2013).
- Sammarruca et al. (2012) F. Sammarruca, B. Chen, L. Coraggio, N. Itaco, and R. Machleidt, Phys. Rev. C 86, 054317 (2012).
- Ekström et al. (2015) A. Ekström, G. R. Jansen, K. A. Wendt, G. Hagen, T. Papenbrock, B. D. Carlsson, C. Forssén, M. Hjorth-Jensen, P. Navrátil, and W. Nazarewicz, Phys. Rev. C 91, 051301(R) (2015).
- Jurgenson et al. (2009) E. D. Jurgenson, P. Navrátil, and R. J. Furnstahl, Phys. Rev. Lett. 103, 082501 (2009).
- Maris et al. (2011) P. Maris, J. P. Vary, P. Navrátil, W. E. Ormand, H. Nam, and D. J. Dean, Phys. Rev. Lett. 106, 202502 (2011).
- Hergert et al. (2013) H. Hergert, S. Binder, A. Calci, J. Langhammer, and R. Roth, Phys. Rev. Lett. 110, 242501 (2013).
- Ekström et al. (2014) A. Ekström, G. R. Jansen, K. A. Wendt, G. Hagen, T. Papenbrock, S. Bacca, B. Carlsson, and D. Gazit, Phys. Rev. Lett. 113, 262504 (2014).
- Carlson et al. (2015) J. Carlson, S. Gandolfi, F. Pederiva, S. C. Pieper, R. Schiavilla, K. E. Schmidt, and R. B. Wiringa, Rev. Mod. Phys. 87, 1067 (2015).
- Ma et al. (2019) Y. Z. Ma, L. Coraggio, L. De Angelis, T. Fukui, A. Gargano, N. Itaco, and F. R. Xu, Phys. Rev. C 100, 034324 (2019).
- Machleidt and Entem (2011) R. Machleidt and D. R. Entem, Phys. Rep. 503, 1 (2011).
- Entem and Machleidt (2003) D. R. Entem and R. Machleidt, Phys. Rev. C 68, 041001(R) (2003).
- Holt et al. (2009) J. W. Holt, N. Kaiser, and W. Weise, Phys. Rev. C 79, 054331 (2009).
- Holt et al. (2010) J. W. Holt, N. Kaiser, and W. Weise, Phys. Rev. C 81, 024002 (2010).
- Hebeler and Schwenk (2010) K. Hebeler and A. Schwenk, Phys. Rev. C 82, 014314 (2010).
- Hagen et al. (2012) G. Hagen, M. Hjorth-Jensen, G. R. Jansen, R. Machleidt, and T. Papenbrock, Phys. Rev. Lett. 109, 032502 (2012).
- Hu et al. (2019) B. S. Hu, Q. Wu, Z. H. Sun, and F. R. Xu, Phys. Rev. C 99, 061302(R) (2019).
- Henderson et al. (2018) J. Henderson et al., Phys. Lett. B 782, 468 (2018).
- Elliott et al. (1968) J. P. Elliott, A. D. Jackson, H. A. Mavromatis, E. A. Sanderson, and B. Singh, Nucl. Phys. A 121, 241 (1968).
- Kirson (1973) M. W. Kirson, Phys. Lett. B 47, 110 (1973).
- Umeya and Muto (2006) A. Umeya and K. Muto, Phys. Rev. C 74, 034330 (2006).
- (56) Data extracted using the NNDC On-Line Data Service, http://www.nndc.bnl.gov/ .
- Kraus et al. (1994) G. Kraus, P. Egelhof, C. Fischer, H. Geissel, A. Himmler, F. Nickel, G. Münzenberg, W. Schwab, A. Weiss, J. Friese, A. Gillitzer, H. J. Körner, M. Peter, W. F. Henning, J. P. Schiffer, J. V. Kratz, L. Chulkov, M. Golovkov, A. Ogloblin, and B. A. Brown, Phys. Rev. Lett. 73, 1773 (1994).
- Pachucki and Moro (2007) K. Pachucki and A. M. Moro, Phys. Rev. A 75, 032521 (2007).
- Ahrens et al. (1975) J. Ahrens, H. Borchert, K. H. Czock, H. B. Eppler, H. Gimm, H. Gundrum, M. Kröning, P. Riehn, G. Sita Ram, A. Zieger, and B. Ziegler, Nucl. Phys. A 251, 479 (1975).
- Birkhan et al. (2017) J. Birkhan, M. Miorelli, S. Bacca, S. Bassauer, C. A. Bertulani, G. Hagen, H. Matsubara, P. von Neumann-Cosel, T. Papenbrock, N. Pietralla, V. Y. Ponomarev, A. Richter, A. Schwenk, and A. Tamii, Phys. Rev. Lett. 118, 252501 (2017).
- Colò et al. (2013) G. Colò, L. G. Cao, N. Van Giai, and L. Capelli, Comp. Phys. Comm. 184, 142 (2013).
- Van Giai and Sagawa (1981b) N. Van Giai and H. Sagawa, Phys. Lett. B 106, 379 (1981b).
- Bartel et al. (1982) J. Bartel, P. Quentin, M. Brack, C. Guet, and H.-B. Håkansson, Nucl. Phys. A 386, 79 (1982).
- Dobaczewski et al. (1984) J. Dobaczewski, H. Flocard, and J. Treiner, Nucl. Phys. A 422, 103 (1984).
- Agrawal et al. (2003) B. K. Agrawal, S. Shlomo, and V. Kim Au, Phys. Rev. C 68, 031304 (2003).
- Chabanat et al. (1998) E. Chabanat, P. Bonche, P. Haensel, J. Meyer, and R. Schaeffer, Nucl. Phys. A 635, 231 (1998).
- 199 (1998) Nucl. Phys. A 643, 441(E) (1998).
- Cao et al. (2006) L. G. Cao, U. Lombardo, C. W. Shen, and N. Van Giai, Phys. Rev. C 73, 014313 (2006).
- Berman and Fultz (1975) B. L. Berman and S. C. Fultz, Rev. Mod. Phys. 47, 713 (1975).
- Piekarewicz (2011) J. Piekarewicz, Phys. Rev. C 83, 034319 (2011).
- Khan et al. (2011) E. Khan, N. Paar, and D. Vretenar, Phys. Rev. C 84, 051301(R) (2011).
- Wieland et al. (2009) O. Wieland et al., Phys. Rev. Lett. 102, 092502 (2009).
- Erler et al. (2011) J. Erler, P. Klüpfel, and P.-G. Reinhard, J. Phys. G: Nucl. Part. Phys. 38, 033101 (2011).
- Orlandini and Traini (1991) G. Orlandini and M. Traini, Rep. Prog. Phys. 54, 257 (1991).
- Hu et al. (2016) B. S. Hu, F. R. Xu, Z. H. Sun, J. P. Vary, and T. Li, Phys. Rev. C 94, 014303 (2016).
- Tanihata (2013) I. Tanihata, Phys. Scr. T152, 014021 (2013).
- Sagawa and Colò (2014) H. Sagawa and G. Colò, Prog. Part. Nucl. Phys. 76, 76 (2014).
- Sakai et al. (1974) M. Sakai, I. Shimodaya, Y. Akaishi, J. Hiura, and H. Tanaka, Prog. Theor. Phys. Supp. 56, 32 (1974).
- Pieper and Wiringa (2001) S. C. Pieper and R. B. Wiringa, Annu. Rev. Nucl. Part. Sci. 51, 53 (2001).