This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Note on Minimization of Quasi \Mnat-convex Functions111 This work was supported by JSPS KAKENHI Grant Numbers JP23K11001 and JP23K10995.

Kazuo Murota222 The Institute of Statistical Mathematics, Tokyo 190-8562, Japan; and Faculty of Economics and Business Administration, Tokyo Metropolitan University, Tokyo 192-0397, Japan, [email protected]    Akiyoshi Shioura333 Department of Industrial Engineering and Economics, Tokyo Institute of Technology, Tokyo 152-8550, Japan [email protected]
(May 29, 2023 / June 18, 2023 / September 5, 2023 /November 27, 2023)
Abstract

For a class of discrete quasi convex functions called semi-strictly quasi \Mnat-convex functions, we investigate fundamental issues relating to minimization, such as optimality condition by local optimality, minimizer cut property, geodesic property, and proximity property. Emphasis is put on comparisons with (usual) \Mnat-convex functions. The same optimality condition and a weaker form of the minimizer cut property hold for semi-strictly quasi \Mnat-convex functions, while geodesic property and proximity property fail.

1 Introduction

In this paper, we deal with a class of discrete quasi convex functions called semi-strictly quasi \Mnat-convex functions [2] (see also [10]). The concept of semi-strictly quasi \Mnat-convex function is introduced as a “quasi convex” version of \Mnat-convex function [9], which is a major concept in the theory of discrete convex analysis introduced as a variant of M-convex function [5, 6, 8]. Application of (semi-strictly) quasi \Mnat-convex functions can be found in mathematical economics [2, 11] and operations research [1].

An M-convex function is defined as a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} satisfying a certain exchange axiom (see Section 4.2), which implies that the effective domain dom​f={x∈ℤn∣f​(x)<+∞}{\rm dom\,}f=\{x\in\mathbb{Z}^{n}\mid f(x)<+\infty\} is contained in a hyperplane of the form ∑i=1nx​(i)=r\sum_{i=1}^{n}x(i)=r for some r∈ℤr\in\mathbb{Z}. Due to this fact, it is natural to consider the projection of an M-convex function to the (n−1)(n-1)-dimensional space along a coordinate axis, which is called an \Mnat-convex function. A nontrivial argument shows that an \Mnat-convex function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} is characterized by the following exchange axiom:

(\Mnat-EXC) ∀x,y∈dom​f\forall x,y\in{\rm dom\,}f, ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)∪{0}\exists j\in{\rm supp}^{-}(x-y)\cup\{0\} such that

f​(x)+f​(y)≥f​(x−χi+χj)+f​(y+χi−χj),f(x)+f(y)\geq f(x-\chi_{i}+\chi_{j})+f(y+\chi_{i}-\chi_{j}), (1.1)

where N={1,2,…,n}N=\{1,2,\ldots,n\}, χi∈{0,1}n\chi_{i}\in\{0,1\}^{n} is the characteristic vector of i∈Ni\in N, χ0=0\chi_{0}=0, and

supp+​(x−y)={i∈N∣x​(i)>y​(i)},supp−​(x−y)={j∈N∣x​(j)<y​(j)}.\displaystyle{\rm supp}^{+}(x-y)=\{i\in N\mid x(i)>y(i)\},\qquad{\rm supp}^{-}(x-y)=\{j\in N\mid x(j)<y(j)\}.

The inequality (1.1) implies that at least one of the following three conditions holds:

f​(x−χi+χj)<f​(x),\displaystyle f(x-\chi_{i}+\chi_{j})<f(x), (1.2)
f​(y+χi−χj)<f​(y),\displaystyle f(y+\chi_{i}-\chi_{j})<f(y), (1.3)
f​(x−χi+χj)=f​(x)​ and ​f​(y+χi−χj)=f​(y).\displaystyle f(x-\chi_{i}+\chi_{j})=f(x)\mbox{ and }f(y+\chi_{i}-\chi_{j})=f(y). (1.4)

Using this, a semi-strictly quasi \Mnat-convex function (s.s. quasi \Mnat-convex function, for short) is defined as follows: f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} is called an s.s. quasi \Mnat-convex function if it satisfies the following exchange axiom:

(SSQM♮) ∀x,y∈dom​f\forall x,y\in{\rm dom\,}f, ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)∪{0}\exists j\in{\rm supp}^{-}(x-y)\cup\{0\} satisfying at least one of the conditions (1.2), (1.3), and (1.4).

The main aim of this paper is to investigate fundamental issues relating to minimization of an s.s. quasi \Mnat-convex function. It is known that minimizers of an M-convex function have various nice properties (to be described in Section A.1 of Appendix) such as

∙\bullet optimality condition by local optimality,
∙\bullet minimizer cut property,
∙\bullet geodesic property,
∙\bullet proximity property.

The definition of \Mnat-convex function implies that these properties of M-convex functions are inherited by \Mnat-convex functions, as shown in Section 2. In this paper, we examine which of the above properties are satisfied by s.s. quasi \Mnat-convex functions. For each of the properties, if it holds for s.s. quasi \Mnat-convex functions, we describe the precise statement of the property in question and give its proof; otherwise, we provide an example to show the failure of the property.

It is added that there is a notion called “s.s. quasi M-convex function” [8, 10], which corresponds directly to M-convexity. Although M-convex and \Mnat-convex functions are known to be essentially equivalent, it turns out that their quasi-convex versions, namely, s.s. quasi M-convexity and s.s. quasi \Mnat-convexity, are significantly different. We also discuss such subtle points in Section 4.2.

2 Properties on Minimization of Quasi \Mnat-convex Functions

2.1 Optimality Condition by Local Optimality

In this section we consider an optimality condition for minimization in terms of local optimality and also a minimization algorithm based on the optimality condition. Before dealing with quasi \Mnat-convex functions, we describe the existing results for \Mnat-convex functions.

A minimizer x∗x^{*} of an \Mnat-convex function ff can be characterized by the local minimality within the neighborhood consisting of vectors y∈ℤny\in\mathbb{Z}^{n} with ‖y−x∗‖1≤2\|y-x^{*}\|_{1}\leq 2.

Theorem 2.1 (cf. [5, Theorem 2.4], [7, Theorem 2.2]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function. A vector x∗∈dom​fx^{*}\in{\rm dom\,}f is a minimizer of ff if and only if

f​(x∗−χi+χj)≥f​(x∗)(i,j∈N∪{0}).\displaystyle f(x^{*}-\chi_{i}+\chi_{j})\geq f(x^{*})\qquad(i,j\in N\cup\{0\}). (2.1)

Theorem 2.1 makes it possible to apply the following steepest descent algorithm to find a minimizer of an \Mnat-convex function.

Algorithm BasicSteepestDescent

Step 0: Let x0∈dom​fx_{0}\in{\rm dom\,}f be an arbitrarily chosen initial vector. Set x:=x0x:=x_{0}.

Step 1: If f​(x−χi+χj)≥f​(x)f(x-\chi_{i}+\chi_{j})\geq f(x) for every i,j∈N∪{0}i,j\in N\cup\{0\}, then output xx and stop.

Step 2: Find i,j∈N∪{0}i,j\in N\cup\{0\} that minimize f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}).

Step 3: Set x:=x−χi+χjx:=x-\chi_{i}+\chi_{j} and go to Step 1.

Corollary 2.2 (cf. [12]).

For an \Mnat-convex function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} with arg⁡min⁡f≠∅\arg\min f\neq\emptyset, Algorithm BasicSteepestDescent finds a minimizer of ff in a finite number of iterations.

The optimality condition for \Mnat-convex functions in Theorem 2.1 can be generalized to s.s. quasi \Mnat-convex functions.

Theorem 2.3.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function satisfying (SSQM♮). A vector x∗∈dom​fx^{*}\in{\rm dom\,}f is a minimizer of ff if and only if the condition (2.1) holds.

The “only if” part of the theorem is easy to see. The “if” part is implied immediately by the following lemma.

Lemma 2.4.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function satisfying (SSQM♮). For x,y∈dom​fx,y\in{\rm dom\,}f, if f​(x)>f​(y)f(x)>f(y), then there exist some i∈supp+​(x−y)∪{0}i\in{\rm supp}^{+}(x-y)\cup\{0\} and j∈supp−​(x−y)∪{0}j\in{\rm supp}^{-}(x-y)\cup\{0\} satisfying f​(x)>f​(x−χi+χj)f(x)>f(x-\chi_{i}+\chi_{j}).

Proof.

Putting

α=∑i∈supp+​(x−y)|x​(i)−y​(i)|,β=∑j∈supp−​(x−y)|x​(j)−y​(j)|,\alpha=\sum_{i\in{\rm supp}^{+}(x-y)}|x(i)-y(i)|,\qquad\beta=\sum_{j\in{\rm supp}^{-}(x-y)}|x(j)-y(j)|,

we prove the lemma by induction on the pair of values (α,β)(\alpha,\beta). If α≤1\alpha\leq 1 and β≤1\beta\leq 1, then y=x−χi+χjy=x-\chi_{i}+\chi_{j} for some i,j∈N∪{0}i,j\in N\cup\{0\}, and therefore the claim holds immediately.

Suppose α≥2\alpha\geq 2 and let i∈supp+​(x−y)i\in{\rm supp}^{+}(x-y). By (SSQM♮) applied to xx, yy, and ii, there exists some j∈supp−​(x−y)∪{0}j\in{\rm supp}^{-}(x-y)\cup\{0\} satisfying f​(x−χi+χj)<f​(x)f(x-\chi_{i}+\chi_{j})<f(x) or f​(y+χi−χj)≤f​(y)f(y+\chi_{i}-\chi_{j})\leq f(y) (or both). In the former case, we are done. In the latter case, we can apply the induction hypothesis to xx and y′=y+χi−χjy^{\prime}=y+\chi_{i}-\chi_{j} to obtain some i′∈supp+​(x−y′)∪{0}⊆supp+​(x−y)∪{0}i^{\prime}\in{\rm supp}^{+}(x-y^{\prime})\cup\{0\}\subseteq{\rm supp}^{+}(x-y)\cup\{0\} and j′∈supp−​(x−y′)∪{0}⊆supp−​(x−y)∪{0}j^{\prime}\in{\rm supp}^{-}(x-y^{\prime})\cup\{0\}\subseteq{\rm supp}^{-}(x-y)\cup\{0\} satisfying f​(x)>f​(x−χi′+χj′)f(x)>f(x-\chi_{i^{\prime}}+\chi_{j^{\prime}}). The proof for the case β≥2\beta\geq 2 is similar. ∎

It follows from Theorem 2.3 that we can also apply the steepest descent algorithm to find a minimizer of an s.s. quasi \Mnat-convex function.

Corollary 2.5.

For a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} with arg⁡min⁡f≠∅\arg\min f\neq\emptyset satisfying (SSQM♮), Algorithm BasicSteepestDescent finds a minimizer of ff in a finite number of iterations.

2.2 Minimizer Cut Property

The minimizer cut property, originally shown for M-convex functions [12, Theorem 2.2] (see also Theorem A.2 in Appendix), states that a separating hyperplane between a given vector xx and some minimizer can be found by using the steepest descent direction at xx (i.e., vector −χi+χj-\chi_{i}+\chi_{j} with i,j∈Ni,j\in N that minimizes f​(x−χi+χj)f(x-\chi_{i}+\chi_{j})). By rewriting the minimizer cut property for M-convex functions based on the relationship between M-convexity and \Mnat-convexity, we obtain the following minimizer cut property for \Mnat-convex functions, where y​(N)=∑i∈Ny​(i)y(N)=\sum_{i\in N}y(i) for y∈ℤny\in\mathbb{Z}^{n}.

Theorem 2.6 (cf. [12, Theorem 2.2]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f be a vector with x∉arg⁡min⁡fx\not\in\arg\min f. For a pair (i,j)(i,j) of distinct elements in N∪{0}N\cup\{0\} minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1(if ​i,j∈N),x∗​(i)≤x​(i)−1,x∗​(N)≤x​(N)−1(if ​i∈N,j=0),x∗​(j)≥x​(j)+1,x∗​(N)≥x​(N)+1(if ​i=0,j∈N).\begin{cases}x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1&(\mbox{if }i,j\in N),\\ x^{*}(i)\leq x(i)-1,\ x^{*}(N)\leq x(N)-1&(\mbox{if }i\in N,\ j=0),\\ x^{*}(j)\geq x(j)+1,\ x^{*}(N)\geq x(N)+1&(\mbox{if }i=0,\ j\in N).\end{cases} (2.2)

Other variants of the minimizer cut property of \Mnat-convex functions are given in Section 4.1, which capture the technical core of Theorem 2.6.

Using Theorem 2.6 we can provide an upper bound for the number of iterations in the following variant of the steepest descent algorithm, where dom​f{\rm dom\,}f is assumed to be bounded, and the integer interval [ℓ,u]={x∈ℤn∣ℓ≤x≤u}[\ell,u]=\{x\in\mathbb{Z}^{n}\mid\ell\leq x\leq u\} always contains a minimizer of ff.

Algorithm ModifiedSteepestDescent

Step 0: Let x0∈dom​fx_{0}\in{\rm dom\,}f be an arbitrarily chosen initial vector. Set x:=x0x:=x_{0}.

Step 0: Let ℓ,u∈ℤn\ell,u\in\mathbb{Z}^{n} be vectors such that dom​f⊆[ℓ,u]{\rm dom\,}f\subseteq[\ell,u].

Step 1: If f​(x−χi+χj)≥f​(x)f(x-\chi_{i}+\chi_{j})\geq f(x) for every i,j∈N∪{0}i,j\in N\cup\{0\} with x−χi+χj∈[ℓ,u]x-\chi_{i}+\chi_{j}\in[\ell,u],

Step 0: then output xx and stop.

Step 2: Find i,j∈N∪{0}i,j\in N\cup\{0\} with x−χi+χj∈[ℓ,u]x-\chi_{i}+\chi_{j}\in[\ell,u] that minimize f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}).

Step 3: Set x:=x−χi+χjx:=x-\chi_{i}+\chi_{j}, u​(i):=x​(i)−1u(i):=x(i)-1 if i∈Ni\in N, and ℓ​(j):=x​(j)+1\ell(j):=x(j)+1 if j∈Nj\in N.

Step 0: Go to Step 1.

We define the L∞-diameter of a bounded set S⊆ℤnS\subseteq\mathbb{Z}^{n} by

L∞​(S)=max⁡{‖x−y‖∞∣x,y∈S}.L_{\infty}(S)=\max\{\|x-y\|_{\infty}\mid x,y\in S\}.
Corollary 2.7 (cf. [12, Section 2]).

For an \Mnat-convex function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} with a bounded effective domain, Algorithm ModifiedSteepestDescent finds a minimizer of ff in O​(n​L)O(nL) iterations with L=L∞​(dom​f)L=L_{\infty}({\rm dom\,}f).

While the number of iterations in the algorithm ModifiedSteepestDescent is proportional to the L∞-diameter of dom​f{\rm dom\,}f, the domain reduction approach in [12] (see Section 3.2; see also [8, Section 10.1.3]), combined with the minimizer cut property, makes it possible to speed up the computation of a minimizer.

Corollary 2.8 (cf. [12, Theorem 3.2]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function with a bounded effective domain, and suppose that a function evaluation oracle for ff and a vector in dom​f{\rm dom\,}f are available. Then, a minimizer of ff can be obtained in O​(n4​(log⁡L)2)O(n^{4}(\log L)^{2}) time with L=L∞​(dom​f)L=L_{\infty}({\rm dom\,}f).

Note that faster polynomial-time algorithms based on the scaling technique are also available for \Mnat-convex function minimization [13, 15].

An s.s. quasi \Mnat-convex function satisfies the following weaker statement than Theorem 2.6. To be specific, the inequality x∗​(N)≤x​(N)−1x^{*}(N)\leq x(N)-1 in the second case (i∈N,j=0i\in N,\;j=0) of (2.2) is missing in (2.3) below, and the inequality x∗​(N)≥x​(N)+1x^{*}(N)\geq x(N)+1 in the third case (i=0,j∈Ni=0,\;j\in N) of (2.2) is missing in (2.3); an example illustrating this difference is given later in Example 2.12.

Theorem 2.9.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function with (SSQM♮) satisfying arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f be a vector with x∉arg⁡min⁡fx\not\in\arg\min f. For a pair (i,j)(i,j) of distinct elements in N∪{0}N\cup\{0\} minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1(if ​i,j∈N),x∗​(i)≤x​(i)−1(if ​i∈N,j=0),x∗​(j)≥x​(j)+1(if ​i=0,j∈N).\left\{\begin{array}[]{ll}x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1&(\mbox{if }i,j\in N),\\ x^{*}(i)\leq x(i)-1&(\mbox{if }i\in N,\ j=0),\\ x^{*}(j)\geq x(j)+1&(\mbox{if }i=0,\ j\in N).\end{array}\right. (2.3)

A proof of this theorem is given in Section 3.1.

Using Theorem 2.9 we can obtain the same upper bound for the number of iterations in the algorithm ModifiedSteepestDescent applied to s.s. quasi \Mnat-convex functions.

Corollary 2.10.

For a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} with a bounded effective domain satisfying (SSQM♮), Algorithm ModifiedSteepestDescent finds a minimizer of ff in O​(n​L)O(nL) iterations with L=L∞​(dom​f)L=L_{\infty}({\rm dom\,}f).

A combination of Theorem 2.9 with the domain reduction approach (described in Section 3.2) makes it possible to find a minimizer of an s.s. quasi \Mnat-convex function in time polynomial in nn and log⁡L∞​(dom​f)\log L_{\infty}({\rm dom\,}f), provided that dom​f{\rm dom\,}f is an \Mnat-convex set. Note that the effective domain of an s.s. quasi \Mnat-convex function is not necessarily an \Mnat-convex set (see (3.11) in Section 3.2 for the definition of \Mnat-convex set).

Corollary 2.11.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function satisfying (SSQM♮), and suppose that the effective domain of ff is bounded and \Mnat-convex. Also, suppose that a function evaluation oracle for ff and a vector in dom​f{\rm dom\,}f are available. Then, a minimizer of ff can be obtained in O​(n4​(log⁡L)2)O(n^{4}(\log L)^{2}) time with L=L∞​(dom​f)L=L_{\infty}({\rm dom\,}f).

A proof of this corollary is given in Section 3.2.

Example 2.12.

This example shows that the statement of Theorem 2.6, stronger than Theorem 2.9, is not true for s.s. quasi \Mnat-convex functions. Consider the function f:ℤ3→ℝ∪{+∞}f:\mathbb{Z}^{3}\to\mathbb{R}\cup\{+\infty\} defined by

f​(2,1,0)=f​(2,0,1)=0,\displaystyle f(2,1,0)=f(2,0,1)=0, f​(1,1,0)=f​(1,0,1)=1,\displaystyle f(1,1,0)=f(1,0,1)=1,
f​(0,1,1)=f​(0,0,2)=2,\displaystyle f(0,1,1)=f(0,0,2)=2, f​(1,1,1)=f​(1,0,2)=3,\displaystyle f(1,1,1)=f(1,0,2)=3,
f​(0,1,2)=4,\displaystyle f(0,1,2)=4, f​(x1,x2,x3)=+∞​ otherwise\displaystyle f(x_{1},x_{2},x_{3})=+\infty\mbox{ otherwise}

(see Figure 1). This function ff satisfies (SSQM♮) and has two minimizers y∗=(2,1,0)y^{*}=(2,1,0) and y∗∗=(2,0,1)y^{**}=(2,0,1) (denoted by ○{\bf\bigcirc} in Figure 1).

Refer to caption
Figure 1: Values of function ff in Example 2.12.

For x=(0,1,2)x=(0,1,2), the pair (i,j)=(2,0)(i,j)=(2,0) is a valid choice in Theorem 2.9, since we have

x−χi+χj=(0,0,2),\displaystyle x-\chi_{i}+\chi_{j}=(0,0,2),
f​(x−χi+χj)=2=mini′,j′∈N∪{0}⁡f​(x−χi′+χj′).\displaystyle f(x-\chi_{i}+\chi_{j})=2=\min_{i^{\prime},j^{\prime}\in N\cup\{0\}}f(x-\chi_{i^{\prime}}+\chi_{j^{\prime}}).

However, neither of the two minimizers y∗=(2,1,0)y^{*}=(2,1,0) and y∗∗=(2,0,1)y^{**}=(2,0,1) satisfies the inequality x∗​(N)≤x​(N)−1x^{*}(N)\leq x(N)-1 in (2.2), while y∗∗=(2,0,1)y^{**}=(2,0,1) satisfies the inequality x∗​(i)≤x​(i)−1=0x^{*}(i)\leq x(i)-1=0 in (2.3). ∎

2.3 Geodesic Property

Geodesic property of a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} means that whenever a vector x∈dom​fx\in{\rm dom\,}f moves to a local minimizer x′∈N​(x)x^{\prime}\in N(x) in an appropriately defined neighborhood N​(x)N(x) of xx, the distance ‖x∗−x‖\|x^{*}-x\| to a nearest minimizer x∗x^{*} from the current solution xx decreases by ‖x′−x‖\|x^{\prime}-x\|, where ∥⋅∥\|\cdot\| is an appropriately chosen norm. It is known that M-convex functions have the geodesic property with respect to the L1-norm [14, Corollary 4.2], [3, Theorem 2.4]. We first point out that \Mnat-convex functions do not enjoy the geodesic property with respect to the L1-norm.

For a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} and a vector x∈dom​fx\in{\rm dom\,}f, we define

μ​(x)\displaystyle\mu(x) =min⁡{‖x∗−x‖1∣x∗∈arg⁡min⁡f},\displaystyle=\min\{\|x^{*}-x\|_{1}\mid x^{*}\in\arg\min f\}, (2.4)
M​(x)\displaystyle M(x) ={x∗∈ℤn∣x∗∈arg⁡min⁡f,‖x∗−x‖1=μ​(x)}.\displaystyle=\{x^{*}\in\mathbb{Z}^{n}\mid x^{*}\in\arg\min f,\ \|x^{*}-x\|_{1}=\mu(x)\}. (2.5)

The following is an expected plausible statement of the geodesic property for \Mnat-convex functions with respect to the L1-norm.

Statement A:  Let x∈dom​fx\in{\rm dom\,}f be a vector that is not a minimizer of ff. Also, let (i,j)(i,j) be a pair of distinct elements in N∪{0}N\cup\{0\} minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), and define

M′={{x∗∈M​(x)∣x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1}(if ​i,j∈N),{x∗∈M​(x)∣x∗​(i)≤x​(i)−1}(if ​i∈N,j=0),{x∗∈M​(x)∣x∗​(j)≥x​(j)+1}(if ​i=0,j∈N).{M}^{\prime}=\begin{cases}\{x^{*}\in M(x)\mid x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1\}&(\mbox{if }i,j\in N),\\ \{x^{*}\in M(x)\mid x^{*}(i)\leq x(i)-1\}&(\mbox{if }i\in N,\ j=0),\\ \{x^{*}\in M(x)\mid x^{*}(j)\geq x(j)+1\}&(\mbox{if }i=0,\ j\in N).\end{cases}

(i) There exists some x∗∈M​(x)x^{*}\in M(x) that is contained in M′{M}^{\prime}; we have M′≠∅{M}^{\prime}\neq\emptyset, in particular.
(ii) It holds that

μ​(x−χi+χj)\displaystyle\mu(x-\chi_{i}+\chi_{j}) ={μ​(x)−2(if ​i,j∈N),μ​(x)−1(if ​i=0​ or ​j=0),\displaystyle=\begin{cases}\mu(x)-2&(\mbox{if }i,j\in N),\\ \mu(x)-1&(\mbox{if }i=0\mbox{ or }j=0),\end{cases}
M​(x−χi+χj)\displaystyle M(x-\chi_{i}+\chi_{j}) =M′.\displaystyle={M}^{\prime}.

However, neither (i) nor (ii) of Statement A is true for \Mnat-convex functions, as shown by the following example.

Example 2.13.

This example shows that Statement A is not true for \Mnat-convex functions. Consider a function f:ℤ2→ℝ∪{+∞}f:\mathbb{Z}^{2}\to\mathbb{R}\cup\{+\infty\} given by

dom​f={x∈ℤ2∣0≤x​(1)≤2, 0≤x​(2)≤1},\displaystyle{\rm dom\,}f=\{x\in\mathbb{Z}^{2}\mid 0\leq x(1)\leq 2,\ 0\leq x(2)\leq 1\},
f​(x)=2−x​(1)(x∈dom​f)\displaystyle f(x)=2-x(1)\qquad(x\in{\rm dom\,}f)

(see Figure 2), for which arg⁡min⁡f={(2,0),(2,1)}\arg\min f=\{(2,0),(2,1)\}. Function ff satisfies the condition (\Mnat-EXC), and hence it is \Mnat-convex.

Refer to caption
Figure 2: Values of function ff in Example 2.13.

For x=(0,1)x=(0,1), we have

μ​(x)=‖(2,1)−(0,1)‖1=2,M​(x)={(2,1)}.\mu(x)=\|(2,1)-(0,1)\|_{1}=2,\qquad M(x)=\{(2,1)\}.

We see that (i,j)=(2,1)(i,j)=(2,1) is a possible choice to minimize the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}) among all i,j∈N∪{0}i,j\in N\cup\{0\}. Then, we have

x′\displaystyle x^{\prime} =x−χi+χj=(1,0),\displaystyle=x-\chi_{i}+\chi_{j}=(1,0),
M′\displaystyle{M}^{\prime} =M​(x)∩{x∗∈ℤ2∣x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1}\displaystyle=M(x)\cap\{x^{*}\in\mathbb{Z}^{2}\mid x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1\}
={(2,1)}∩{x∗∈ℤ2∣x∗​(2)≤0,x∗​(1)≥1}=∅,\displaystyle=\{(2,1)\}\cap\{x^{*}\in\mathbb{Z}^{2}\mid x^{*}(2)\leq 0,\ x^{*}(1)\geq 1\}=\emptyset,
μ​(x−χi+χj)\displaystyle\mu(x-\chi_{i}+\chi_{j}) =‖(2,0)−(1,0)‖1=1≠0=μ​(x)−2.\displaystyle=\|(2,0)-(1,0)\|_{1}=1\neq 0=\mu(x)-2.

That is, Statement A does not hold for this \Mnat-convex function ff. ∎

While Statement A fails for \Mnat-convex functions, an alternative geodesic property holds for \Mnat-convex functions, which can be obtained from the geodesic property for M-convex functions with respect to the L1-norm (see [14, Corollary 4.2], [3, Theorem 2.4]; see also Theorem A.3 in Appendix).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset. For x∈ℤnx\in\mathbb{Z}^{n}, we define

μ~​(x)\displaystyle\widetilde{\mu}(x) =min⁡{‖x∗−x‖1+|x∗​(N)−x​(N)|∣x∗∈arg⁡min⁡f},\displaystyle=\min\{\|x^{*}-x\|_{1}+|x^{*}(N)-x(N)|\mid x^{*}\in\arg\min f\},
M~​(x)\displaystyle\widetilde{M}(x) ={x∗∈ℤn∣x∗∈arg⁡min⁡f,‖x∗−x‖1+|x∗​(N)−x​(N)|=μ~​(x)}.\displaystyle=\{x^{*}\in\mathbb{Z}^{n}\mid x^{*}\in\arg\min f,\ \|x^{*}-x\|_{1}+|x^{*}(N)-x(N)|=\widetilde{\mu}(x)\}.

That is, μ~​(x)\widetilde{\mu}(x) is a kind of distance from xx to the nearest minimizer of ff, and M~​(x)\widetilde{M}(x) is the set of the minimizers of ff nearest to xx with respect to this distance.

Theorem 2.14 (cf. [14, Corollary 4.2], [3, Theorem 2.4]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f be a vector that is not a minimizer of ff, i.e., x∉arg⁡min⁡fx\not\in\arg\min f. Also, let (i,j)(i,j) be a pair of distinct elements in N∪{0}N\cup\{0\} minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), and define

M~′={{x∗∈M~​(x)∣x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1}(if ​i,j∈N),{x∗∈M~​(x)∣x∗​(i)≤x​(i)−1,x∗​(N)≤x​(N)−1}(if ​i∈N,j=0),{x∗∈M~​(x)∣x∗​(j)≥x​(j)+1,x∗​(N)≥x​(N)+1}(if ​i=0,j∈N).\widetilde{M}^{\prime}=\begin{cases}\{x^{*}\in\widetilde{M}(x)\mid x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1\}&(\mbox{if }i,j\in N),\\ \{x^{*}\in\widetilde{M}(x)\mid x^{*}(i)\leq x(i)-1,\ x^{*}(N)\leq x(N)-1\}&(\mbox{if }i\in N,\ j=0),\\ \{x^{*}\in\widetilde{M}(x)\mid x^{*}(j)\geq x(j)+1,\ x^{*}(N)\geq x(N)+1\}&(\mbox{if }i=0,\ j\in N).\end{cases} (2.6)

(i) There exists some x∗∈M~​(x)x^{*}\in\widetilde{M}(x) that is contained in M~′\widetilde{M}^{\prime}; we have M~′≠∅\widetilde{M}^{\prime}\neq\emptyset, in particular.
(ii) It holds that μ~​(x−χi+χj)=μ~​(x)−2\widetilde{\mu}(x-\chi_{i}+\chi_{j})=\widetilde{\mu}(x)-2 and M~​(x−χi+χj)=M~′\widetilde{M}(x-\chi_{i}+\chi_{j})=\widetilde{M}^{\prime}.

Note that the statement (i) immediately implies the minimizer cut property (Theorem 2.6) for \Mnat-convex functions. The statement (ii) implies that in each iteration of Algorithm BasicSteepestDescent applied to an \Mnat-convex function, the distance μ~​(x)\widetilde{\mu}(x) to the nearest minimizer reduces by two. This fact yields an exact number of iterations required by BasicSteepestDescent.

Corollary 2.15.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset. Suppose that Algorithm BasicSteepestDescent is applied to ff with the initial vector x0∈dom​fx_{0}\in{\rm dom\,}f. Then, the number of iterations is equal to μ~​(x0)/2\tilde{\mu}(x_{0})/2.

In contrast, s.s. quasi \Mnat-convex functions do not enjoy the geodesic property in the form of Theorem 2.14, as illustrated in the following example.

Example 2.16.

This example shows that the statement of Theorem 2.14 is not true for s.s. quasi \Mnat-convex functions in the case of i=0i=0 or j=0j=0. Consider the s.s. quasi \Mnat-convex function f:ℤ3→ℝ∪{+∞}f:\mathbb{Z}^{3}\to\mathbb{R}\cup\{+\infty\} in Example 2.12 (see Figure 1), for which arg⁡min⁡f={(2,1,0),(2,0,1)}\arg\min f=\{(2,1,0),(2,0,1)\}. For x=(0,1,2)x=(0,1,2), we have

μ~​(x)=‖(2,1,0)−(0,1,2)‖1=‖(2,0,1)−(0,1,2)‖1=4,M~​(x)={(2,1,0),(2,0,1)}.\widetilde{\mu}(x)=\|(2,1,0)-(0,1,2)\|_{1}=\|(2,0,1)-(0,1,2)\|_{1}=4,\quad\widetilde{M}(x)=\{(2,1,0),(2,0,1)\}.

For (i,j)=(2,0)(i,j)=(2,0), we have x−χi+χj=(0,0,2)x-\chi_{i}+\chi_{j}=(0,0,2) and

f​(x−χi+χj)=2=mini′,j′∈N∪{0}⁡f​(x−χi′+χj′).f(x-\chi_{i}+\chi_{j})=2=\min_{i^{\prime},j^{\prime}\in N\cup\{0\}}f(x-\chi_{i^{\prime}}+\chi_{j^{\prime}}).

However, we have

M~′\displaystyle\widetilde{M}^{\prime} =M~​(x)∩{x∗∈ℤ3∣x∗​(i)≤x​(i)−1,x∗​(N)≤x​(N)−1}\displaystyle=\widetilde{M}(x)\cap\{x^{*}\in\mathbb{Z}^{3}\mid x^{*}(i)\leq x(i)-1,\ x^{*}(N)\leq x(N)-1\}
={(2,1,0),(2,0,1)}∩{x∗∈ℤ3∣x∗​(2)≤0,x∗​(N)≤2}=∅,\displaystyle=\{(2,1,0),(2,0,1)\}\cap\{x^{*}\in\mathbb{Z}^{3}\mid x^{*}(2)\leq 0,\ x^{*}(N)\leq 2\}=\emptyset,
μ~​(x−χi+χj)\displaystyle\widetilde{\mu}(x-\chi_{i}+\chi_{j}) =‖(2,0,1)−(0,0,2)‖1=3≠2=μ~​(x)−2.\displaystyle=\|(2,0,1)-(0,0,2)\|_{1}=3\neq 2=\widetilde{\mu}(x)-2.

Thus, the statements (i) and (ii) in Theorem 2.14 fail for ff. ∎

2.4 Proximity Property

Given a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\}, x^∈dom​f\hat{x}\in{\rm dom\,}f, and an integer α≥2\alpha\geq 2, we consider the following scaled minimization problem:

(SP)  Minimize f​(x) subject to x=x^+α​y,y∈ℤn.\mbox{(SP) \quad Minimize }\quad f(x)\qquad\mbox{ subject to }\quad x=\hat{x}+\alpha y,\ y\in\mathbb{Z}^{n}.

It is expected that an appropriately chosen neighborhood of a global (or local) optimal solution of the scaled minimization problem (SP) contains some minimizer of ff; such a property is referred to as a proximity property in this paper. It is known that M-convex functions enjoy a proximity property [4, Theorem 3.4] (see also Theorem A.4 in Appendix), which can be rewritten in terms of \Mnat-convex functions as follows:

Theorem 2.17 (cf. [4, Theorem 3.4]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function and α≥2\alpha\geq 2 be an integer. For every vector x∈dom​f{x}\in{\rm dom\,}f satisfying

f​(x)≤min⁡[mini∈N⁡f​(x±α​χi),mini,j∈N⁡f​(x−α​(χi−χj))],f({x})\leq\min\Big{[}\min_{i\in N}f({x}\pm\alpha\chi_{i}),\ \min_{i,j\in N}f({x}-\alpha(\chi_{i}-\chi_{j}))\Big{]},

there exists some minimizer x∗x^{*} of ff satisfying

‖x∗−x‖∞≤n​(α−1),|x∗​(N)−x​(N)|≤n​(α−1).\|x^{*}-{x}\|_{\infty}\leq n(\alpha-1),\qquad|x^{*}(N)-{x}(N)|\leq n(\alpha-1).

This theorem, in particular, implies that for every optimal solution x{x} of (SP), there exists some minimizer x∗x^{*} of ff such that ‖x∗−x‖∞≤n​(α−1)\|x^{*}-{x}\|_{\infty}\leq n(\alpha-1).

In contrast, a proximity property of this form does not hold for s.s. quasi \Mnat-convex functions. Indeed, the following example shows that there exists a family of s.s. quasi \Mnat-convex functions such that the distance between an approximate global minimizer x^\hat{x} and a unique exact global minimizer x∗x^{*} can be arbitrarily large.

Example 2.18.

This example shows a function satisfying (SSQM♮) for which the statement of Theorem 2.17 does not hold. With an integer k≥2k\geq 2, define a function f:ℤ3→ℝ∪{+∞}f:\mathbb{Z}^{3}\to\mathbb{R}\cup\{+\infty\} as follows (see Figure 3 for the case of k=3k=3):

dom​f={x∈ℤ3∣0≤x1≤k, 0≤x2≤1, 0≤x3≤1},\displaystyle{\rm dom\,}f=\{x\in\mathbb{Z}^{3}\mid 0\leq x_{1}\leq k,\ 0\leq x_{2}\leq 1,\ 0\leq x_{3}\leq 1\},
f​(λ,0,0)=0(0≤λ≤k),\displaystyle f(\lambda,0,0)=0\qquad(0\leq\lambda\leq k),
f​(λ,1,0)=f​(λ,0,1)=λ−k−1(0≤λ≤k),\displaystyle f(\lambda,1,0)=f(\lambda,0,1)=\lambda-k-1\qquad(0\leq\lambda\leq k),
f​(λ,1,1)=2​(λ−k−1)(0≤λ≤k).\displaystyle f(\lambda,1,1)=2(\lambda-k-1)\qquad(0\leq\lambda\leq k).

It can be verified that ff satisfies the condition (SSQM♮). Note that the value f​(λ,0,0)f(\lambda,0,0) is constant for every λ\lambda with 0≤λ≤k0\leq\lambda\leq k, while f​(λ,1,0),f​(λ,0,1)f(\lambda,1,0),f(\lambda,0,1), and f​(λ,1,1)f(\lambda,1,1) are strictly increasing with respect to λ\lambda in the interval 0≤λ≤k0\leq\lambda\leq k. We also see that ff has a unique minimizer y∗=(0,1,1)y^{*}=(0,1,1).

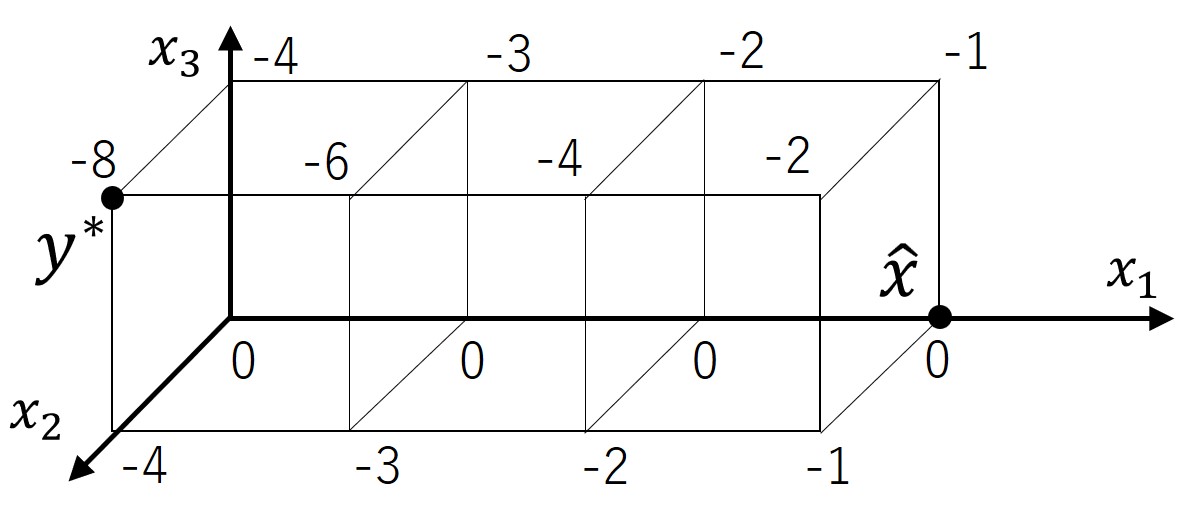
Refer to caption
Figure 3: Values of function ff in Example 2.18 with k=3k=3.

For the problem (SP) with x^=(k,0,0)\hat{x}=(k,0,0) and α=2\alpha=2, x^\hat{x} itself is an optimal solution. The distance between the unique minimizer y∗y^{*} of ff and x^\hat{x} is ‖x^−y∗‖∞=k\|\hat{x}-y^{*}\|_{\infty}=k, which can be arbitrarily large by taking a sufficiently large kk. ∎

3 Proofs

3.1 Minimizer Cut Property

We derive Theorem 2.9 from the following variants of the minimizer cut property for s.s. quasi \Mnat-convex functions.

Theorem 3.1.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function with (SSQM♮) satisfying arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f.
(i) Let i∈Ni\in N and suppose that the minimum of f​(x−χi+χj′)f(x-\chi_{i}+\chi_{j^{\prime}}) over j′∈N∪{0}j^{\prime}\in N\cup\{0\} is attained by some j∈Nj\in N (j≠0)(j\neq 0). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(j)≥x​(j)+1(if ​j∈N∖{i}),x∗​(i)≥x​(i)(if ​j=i).\begin{cases}x^{*}(j)\geq x(j)+1&(\mbox{if }j\in N\setminus\{i\}),\\ x^{*}(i)\geq x(i)&(\mbox{if }j=i).\end{cases}

(ii) Symmetrically to (i), let j∈Nj\in N and suppose that the minimum of f​(x−χi′+χj)f(x-\chi_{i^{\prime}}+\chi_{j}) over i′∈N∪{0}i^{\prime}\in N\cup\{0\} is attained by some i∈Ni\in N (i≠0)(i\neq 0). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(i)≤x​(i)−1(if ​i∈N∖{j}),x∗​(j)≤x​(j)(if ​i=j).\begin{cases}x^{*}(i)\leq x(i)-1&(\mbox{if }i\in N\setminus\{j\}),\\ x^{*}(j)\leq x(j)&(\mbox{if }i=j).\end{cases}

(iii) Suppose that the minimum of f​(x+χj′)f(x+\chi_{j^{\prime}}) over j′∈N∪{0}j^{\prime}\in N\cup\{0\} is attained by some j∈Nj\in N (j≠0)(j\neq 0). Then, there exists some minimizer x∗x^{*} of ff satisfying x∗​(j)≥x​(j)+1x^{*}(j)\geq x(j)+1.
(iv) Symmetrically to (iii), suppose that the minimum of f​(x−χi′)f(x-\chi_{i^{\prime}}) over i′∈N∪{0}i^{\prime}\in N\cup\{0\} is attained by some i∈Ni\in N (i≠0)(i\neq 0). Then, there exists some minimizer x∗x^{*} of ff satisfying x∗​(i)≤x​(i)−1x^{*}(i)\leq x(i)-1.

While postponing the proof of Theorem 3.1, we first give a proof of Theorem 2.9.

Proof of Theorem 2.9.

We first consider the case of j∈Nj\in N (i.e., j≠0j\neq 0 and i∈N∪{0}i\in N\cup\{0\}). By the choice of jj, we have f​(x−χi+χj)=minj′∈N∪{0}⁡f​(x−χi+χj′)f(x-\chi_{i}+\chi_{j})=\min_{j^{\prime}\in N\cup\{0\}}f(x-\chi_{i}+\chi_{j^{\prime}}). Hence, we can apply Theorem 3.1 (i) (if i≠0i\neq 0) or Theorem 3.1 (iii) (if i=0i=0) to obtain some x∗∈arg⁡min⁡fx^{*}\in\arg\min f such that x∗​(j)≥x​(j)+1x^{*}(j)\geq x(j)+1. If i=0i=0 then we are done since x∗x^{*} satisfies the desired condition (2.3).

We consider the case i≠0i\neq 0. Let f~:ℤn→ℝ∪{+∞}\tilde{f}:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be the restriction of ff to D={y∈ℤn∣y​(j)≥x​(j)+1}D=\{y\in\mathbb{Z}^{n}\mid y(j)\geq x(j)+1\}. Since x∗∈D∩arg⁡min⁡fx^{*}\in D\cap\arg\min f, it holds that

min⁡f~=min⁡f,arg⁡min⁡f~⊆arg⁡min⁡f.\min\tilde{f}=\min f,\qquad\arg\min\tilde{f}\subseteq\arg\min f.

We can check easily that f~\tilde{f} satisfies (SSQM♮) and i∈Ni\in N satisfies

f~​(x−χi+χj)=mini′∈N∪{0}⁡f~​(x−χi′+χj).\tilde{f}(x-\chi_{i}+\chi_{j})=\min_{i^{\prime}\in N\cup\{0\}}\tilde{f}(x-\chi_{i^{\prime}}+\chi_{j}).

Hence, we can apply Theorem 3.1 (ii) to obtain some minimizer x∗∗x^{**} of f~\tilde{f} satisfying x∗∗​(i)≤x​(i)−1x^{**}(i)\leq x(i)-1. This vector x∗∗x^{**} satisfies x∗∗​(i)≤x​(i)−1x^{**}(i)\leq x(i)-1 and x∗∗​(j)≥x​(j)+1x^{**}(j)\geq x(j)+1 as desired in (2.3). Note that x∗∗x^{**} is a minimizer of ff because x∗∗∈arg⁡min⁡f~⊆arg⁡min⁡fx^{**}\in\arg\min\tilde{f}\subseteq\arg\min f.

The remaining case (i.e., i∈Ni\in N and j=0j=0) can be treated similarly by using Theorem 3.1 (iv). ∎

We now give a proof of Theorem 3.1.

Proof of Theorem 3.1.

In the following, we give proofs of (i) and (iii); proofs of (ii) and (iv) can be obtained by applying (i) and (iii) to g​(x)=f​(−x)g(x)=f(-x), respectively.

[Proof of (i)]  Put x′=x−χi+χjx^{\prime}=x-\chi_{i}+\chi_{j}. It suffices to show that x∗​(j)≥x′​(j)x^{*}(j)\geq x^{\prime}(j) holds for some x∗∈arg⁡min⁡fx^{*}\in\arg\min f. Let x∗x^{*} be a vector in arg⁡min⁡f\arg\min f that maximizes the value x∗​(j)x^{*}(j). If x∗x^{*} satisfies x∗​(j)≥x′​(j)x^{*}(j)\geq x^{\prime}(j), then we are done. Hence, we assume, to the contrary, that x∗​(j)<x′​(j)x^{*}(j)<x^{\prime}(j), and derive a contradiction.

The condition (SSQM♮) applied to x′x^{\prime}, x∗x^{*}, and j∈supp+​(x′−x∗)j\in{\rm supp}^{+}(x^{\prime}-x^{*}) implies that there exists some r∈supp−​(x′−x∗)∪{0}r\in{\rm supp}^{-}(x^{\prime}-x^{*})\cup\{0\} such that

f​(x∗)>f​(x∗+χj−χr), or\displaystyle f(x^{*})>f(x^{*}+\chi_{j}-\chi_{r}),\quad\mbox{ or } (3.1)
f​(x′)>f​(x′−χj+χr), or\displaystyle f(x^{\prime})>f(x^{\prime}-\chi_{j}+\chi_{r}),\quad\mbox{ or } (3.2)
f​(x∗)=f​(x∗+χj−χr)​ and ​f​(x′)=f​(x′−χj+χr).\displaystyle f(x^{*})=f(x^{*}+\chi_{j}-\chi_{r})\mbox{ and }f(x^{\prime})=f(x^{\prime}-\chi_{j}+\chi_{r}). (3.3)

Note that r≠jr\neq j holds. Since x∗∈arg⁡min⁡fx^{*}\in\arg\min f, we have

f​(x∗)≤f​(x∗+χj−χr).f(x^{*})\leq f(x^{*}+\chi_{j}-\chi_{r}). (3.4)

By the choice of jj and x′=x−χi+χjx^{\prime}=x-\chi_{i}+\chi_{j}, we have

f​(x′)≤f​(x−χi+χr)=f​(x′−χj+χr),f(x^{\prime})\leq f(x-\chi_{i}+\chi_{r})=f(x^{\prime}-\chi_{j}+\chi_{r}), (3.5)

where x−χi+χr=x′−χj+χrx-\chi_{i}+\chi_{r}=x^{\prime}-\chi_{j}+\chi_{r}. The inequalities (3.4) and (3.5) exclude the possibilities of (3.1) and (3.2), respectively. Therefore, we have (3.3). The former equation in (3.3) implies that x∗+χj−χrx^{*}+\chi_{j}-\chi_{r} is also a minimizer of ff, a contradiction to the choice of x∗x^{*} since (x∗+χj−χr)​(j)=x∗​(j)+1>x∗​(j)(x^{*}+\chi_{j}-\chi_{r})(j)=x^{*}(j)+1>x^{*}(j).

[Proof of (iii)]  The proof given below is similar to that for (i). Put x′=x+χjx^{\prime}=x+\chi_{j}. It suffices to show that x∗​(j)≥x′​(j)x^{*}(j)\geq x^{\prime}(j) holds for some x∗∈arg⁡min⁡fx^{*}\in\arg\min f. Let x∗x^{*} be a vector in arg⁡min⁡f\arg\min f that maximizes the value x∗​(j)x^{*}(j). If x∗x^{*} satisfies x∗​(j)≥x′​(j)x^{*}(j)\geq x^{\prime}(j), then we are done. Hence, we assume, to the contrary, that x∗​(j)<x′​(j)x^{*}(j)<x^{\prime}(j), and derive a contradiction.

The condition (SSQM♮) applied to x′x^{\prime}, x∗x^{*}, and j∈supp+​(x′−x∗)j\in{\rm supp}^{+}(x^{\prime}-x^{*}) implies that there exists some r∈supp−​(x′−x∗)∪{0}r\in{\rm supp}^{-}(x^{\prime}-x^{*})\cup\{0\} such that

f​(x∗)>f​(x∗+χj−χr), or\displaystyle f(x^{*})>f(x^{*}+\chi_{j}-\chi_{r}),\quad\mbox{ or } (3.6)
f​(x′)>f​(x′−χj+χr), or\displaystyle f(x^{\prime})>f(x^{\prime}-\chi_{j}+\chi_{r}),\quad\mbox{ or } (3.7)
f​(x∗)=f​(x∗+χj−χr)​ and ​f​(x′)=f​(x′−χj+χr).\displaystyle f(x^{*})=f(x^{*}+\chi_{j}-\chi_{r})\mbox{ and }f(x^{\prime})=f(x^{\prime}-\chi_{j}+\chi_{r}). (3.8)

Note that r≠jr\neq j holds. Since x∗∈arg⁡min⁡fx^{*}\in\arg\min f, we have

f​(x∗)≤f​(x∗+χj−χr).f(x^{*})\leq f(x^{*}+\chi_{j}-\chi_{r}). (3.9)

By the choice of jj and x′=x+χjx^{\prime}=x+\chi_{j}, we have

f​(x′)≤f​(x+χr)=f​(x′−χj+χr),f(x^{\prime})\leq f(x+\chi_{r})=f(x^{\prime}-\chi_{j}+\chi_{r}), (3.10)

where x+χr=x′−χj+χrx+\chi_{r}=x^{\prime}-\chi_{j}+\chi_{r}. The inequalities (3.9) and (3.10) exclude the possibilities of (3.6) and (3.7), respectively. Therefore, we have (3.8). The former equation in (3.8) implies that x∗+χj−χrx^{*}+\chi_{j}-\chi_{r} is also a minimizer of ff, a contradiction to the choice of x∗x^{*} since (x∗+χj−χr)​(j)=x∗​(j)+1>x∗​(j)(x^{*}+\chi_{j}-\chi_{r})(j)=x^{*}(j)+1>x^{*}(j). ∎

3.2 Domain Reduction Algorithm

To prove Corollary 2.11, we need to explain the general framework of the domain reduction algorithm for minimization of a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} with bounded dom​f{\rm dom\,}f. For a nonempty bounded set S⊆ℤnS\subseteq\mathbb{Z}^{n}, we denote

ℓ​(S;i)=min⁡{x​(i)∣x∈S},u​(S;i)=max⁡{x​(i)∣x∈S}(i∈N).\displaystyle\ell(S;i)=\min\{x(i)\mid x\in S\},\qquad u(S;i)=\max\{x(i)\mid x\in S\}\qquad(i\in N).

We define the peeled set S^\widehat{S} of SS by

S^\displaystyle\widehat{S} ={x∈S∣ℓ′​(i)≤x​(i)≤u′​(i)​(i∈N)},\displaystyle=\{x\in S\mid\ell^{\prime}(i)\leq x(i)\leq u^{\prime}(i)\ (i\in N)\},
ℓ′​(i)\displaystyle\ell^{\prime}(i) =(1−1/n)​ℓ​(S;i)+(1/n)​u​(S;i)(i∈N),\displaystyle=(1-1/n)\ell(S;i)+(1/n)u(S;i)\qquad(i\in N),
u′​(i)\displaystyle u^{\prime}(i) =(1/n)​ℓ​(S;i)+(1−1/n)​u​(S;i)(i∈N).\displaystyle=(1/n)\ell(S;i)+(1-1/n)u(S;i)\qquad(i\in N).

The outline of the algorithm is described as follows.

Algorithm DomainReduction

Step 0: Let B:=dom​fB:={\rm dom\,}f.

Step 1: Find a vector xx in the peeled set B^\widehat{B}.

Step 2: If xx is a minimizer of ff, then output xx and stop.

Step 3: Find an axis-orthogonal hyperplane y​(i)=αy(i)=\alpha with some i∈Ni\in N and α∈ℤ\alpha\in\mathbb{Z} such that

(Case 1) arg⁡min⁡f∩{y∣y​(i)≥α}≠∅\arg\min f\cap\{y\mid y(i)\geq\alpha\}\neq\emptyset and x∉{y∣y​(i)≥α}x\notin\{y\mid y(i)\geq\alpha\}  or
  (Case 2) arg⁡min⁡f∩{y∣y​(i)≤α}≠∅\arg\min f\cap\{y\mid y(i)\leq\alpha\}\neq\emptyset and x∉{y∣y​(i)≤α}x\notin\{y\mid y(i)\leq\alpha\}.

Step 4: Set

B:={B∩{y∣y​(i)≥α}(Case 1),B∩{y∣y​(i)≤α}(Case 2)B:=\begin{cases}B\cap\{y\mid y(i)\geq\alpha\}&(\mbox{Case 1}),\\ B\cap\{y\mid y(i)\leq\alpha\}&(\mbox{Case 2})\end{cases}

Step 4:  and go to Step 1.

The algorithm successfully finds a minimizer of ff if the following are true in each iteration:

(DR1) the peeled set B^\widehat{B} in Step 1 is nonempty, and
(DR2) there exists a hyperplane satisfying the desired condition in Step 3.

These conditions hold indeed if ff is an s.s. quasi \Mnat-convex function, as we show later (after Lemma 3.2).

The number of iterations of the algorithm DomainReduction can be analyzed as follows.

Lemma 3.2 (cf. [12, Section 3]).

If the conditions (DR1) and (DR2) are satisfied in each iteration of DomainReduction, then the algorithm terminates in O​(n2​log⁡L)O(n^{2}\log L) iterations with L=L∞​(dom​f)L=L_{\infty}({\rm dom\,}f).

Proof.

We provide a proof for completeness. We first note that the set BB always contains a minimizer of ff. For an iteration of the algorithm, we say that it is of type ii if the hyperplane found in Step 3 is of the form y​(i)=αy(i)=\alpha. In an iteration of type ii, the value u​(B;i)−ℓ​(B;i)u(B;i)-\ell(B;i) decreases by (1/n)​(u​(B;i)−ℓ​(B;i))(1/n)(u(B;i)-\ell(B;i)) by the choices of the vector xx in Step 1 and the hyperplane in Step 3. This implies that after O​(n​log⁡L)O(n\log L) iterations of type ii, we have u​(B;i)−ℓ​(B;i)<1u(B;i)-\ell(B;i)<1, i.e., u​(B;i)=ℓ​(B;i)u(B;i)=\ell(B;i), and therefore an iteration of type ii never occurs afterwards. Hence, after O​(n2​log⁡L)O(n^{2}\log L) iterations we have u​(B;i)=ℓ​(B;i)u(B;i)=\ell(B;i) for all i∈Ni\in N, i.e., BB consists of a single vector, which must be a minimizer of ff. ∎

We now assume that ff is an s.s. quasi \Mnat-convex function (i.e., satisfies (SSQM♮)) such that the effective domain of ff is a bounded \Mnat-convex set, and show that the conditions (DR1) and (DR2) are satisfied in each iteration. The minimizer cut property (Theorem 2.9) guarantees the condition (DR2) for an s.s. quasi \Mnat-convex function. An axis-orthogonal hyperplane satisfying the condition in Step 3 can be found by evaluating function values O​(n2)O(n^{2}) times.

The condition (DR1), i.e., the nonemptiness of the peeled set B^\widehat{B}, can be shown as follows. We say that a set S⊆ℤnS\subseteq\mathbb{Z}^{n} is an \Mnat-convex set (see, e.g., [8, Section 4.7]) if it satisfies the following exchange axiom:

∀x,y∈S\forall x,y\in S, ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)∪{0}\exists j\in{\rm supp}^{-}(x-y)\cup\{0\} such that

x−χi+χj∈S,y+χi−χj∈S.x-\chi_{i}+\chi_{j}\in S,\qquad y+\chi_{i}-\chi_{j}\in S. (3.11)

It is known that for an \Mnat-convex set S⊆ℤnS\subseteq\mathbb{Z}^{n} and an integer interval [a,b](⊆ℤn)[a,b]\ (\subseteq\mathbb{Z}^{n}), their intersection S∩[a,b]S\cap[a,b] is again an \Mnat-convex set if it is nonempty. Hence, the set BB in each iteration of the algorithm is always an \Mnat-convex set as far as it is nonempty. The following lemma shows that the set BB is always nonempty.

Lemma 3.3.

For a bounded \Mnat-convex set B⊆ℤnB\subseteq\mathbb{Z}^{n}, the peeled set B^\widehat{B} is nonempty.

Proof.

The proof can be reduced to a similar statement known for an M-convex set (see, e.g., [8] for the definition of M-convex set). First note that a set B⊆ℤnB\subseteq\mathbb{Z}^{n} is an \Mnat-convex set if and only if the set S={(y,−y​(N))∣y∈B}S=\{(y,-y(N))\mid y\in B\} (⊆ℤn×ℤ)(\subseteq\mathbb{Z}^{n}\times\mathbb{Z}) is an M-convex set. For an \Mnat-convex set B⊆ℤnB\subseteq\mathbb{Z}^{n}, the peeled set S^\widehat{S} of the associated M-convex set SS is nonempty by [12, Theorem 2.4], whereas {y∣(y,−y​(N))∈S^}⊆B^\{y\mid(y,-y(N))\in\widehat{S}\}\subseteq\widehat{B}. Therefore, we have B^≠∅\widehat{B}\neq\emptyset. ∎

We note that for a bounded \Mnat-convex set B⊆ℤnB\subseteq\mathbb{Z}^{n}, a vector in the peeled set B^\widehat{B} can be found in O​(n2​log⁡L)O(n^{2}\log L) time with L=L∞​(dom​f)L=L_{\infty}({\rm dom\,}f) as in [12]. Hence, the condition (DR1) is also satisfied for s.s. quasi \Mnat-convex functions. By Theorem 2.3, Step 2 can be done in O​(n2)O(n^{2}) time. This concludes the proof of Corollary 2.11.

4 Concluding Remarks

4.1 Remarks on Minimizer Cut Property

We note that, in addition to Theorem 2.6, \Mnat-convex functions enjoy the following variants of the minimizer cut property, which are similar to, but stronger than, the statements of Theorem 3.1 for s.s. quasi \Mnat-convex functions. The statements in the theorem below can be obtained from the corresponding statements for M-convex functions [12, Theorem 2.2] (see Theorem A.2 (i), (ii) in Appendix).

Theorem 4.1 (cf. [12, Theorem 2.2]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an \Mnat-convex function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f.
(i) Let i∈Ni\in N and let jj be an element in N∪{0}N\cup\{0\} minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(j)≥x​(j)+1(if ​j∈N∖{i}),x∗​(i)≥x​(i)(if ​j=i),x∗​(N)≤x​(N)−1(if ​j=0).\begin{cases}x^{*}(j)\geq x(j)+1&(\mbox{if }j\in N\setminus\{i\}),\\ x^{*}(i)\geq x(i)&(\mbox{if }j=i),\\ x^{*}(N)\leq x(N)-1&(\mbox{if }j=0).\end{cases}

(ii) Symmetrically to (i), let j∈Nj\in N and let ii be an element in N∪{0}N\cup\{0\} minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(i)≤x​(i)−1(if ​i∈N∖{j}),x∗​(j)≤x​(j)(if ​i=j),x∗​(N)≥x​(N)+1(if ​i=0).\begin{cases}x^{*}(i)\leq x(i)-1&(\mbox{if }i\in N\setminus\{j\}),\\ x^{*}(j)\leq x(j)&(\mbox{if }i=j),\\ x^{*}(N)\geq x(N)+1&(\mbox{if }i=0).\end{cases}

(iii) Let jj be an element in N∪{0}N\cup\{0\} minimizing the value f​(x+χj)f(x+\chi_{j}). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(j)≥x​(j)+1(if ​j∈N),x∗​(N)≤x​(N)(if ​j=0).\begin{cases}x^{*}(j)\geq x(j)+1&(\mbox{if }j\in N),\\ x^{*}(N)\leq x(N)&(\mbox{if }j=0).\end{cases}

(iv) Symmetrically to (iii), let ii be an element in N∪{0}N\cup\{0\} minimizing the value f​(x−χi)f(x-\chi_{i}). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(i)≤x​(i)−1(if ​i∈N),x∗​(N)≥x​(N)(if ​i=0).\begin{cases}x^{*}(i)\leq x(i)-1&(\mbox{if }i\in N),\\ x^{*}(N)\geq x(N)&(\mbox{if }i=0).\end{cases}

It is in order here to dwell on the difference between Theorem 4.1 and Theorem 3.1 by focusing on the statement (i). The statement (i) of Theorem 4.1 for \Mnat-convex functions covers all possible cases of j∈N∪{0}j\in N\cup\{0\}. In contrast, the statement (i) of Theorem 3.1 for s.s. quasi \Mnat-convex functions puts an assumption that j≠0j\neq 0 attains the minimum, which means that we can obtain no conclusion if the minimum of f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}) over j∈N∪{0}j\in N\cup\{0\} is attained uniquely by j=0j=0. Thus, the statement (i) of Theorem 3.1 is strictly weaker than the statement (i) of Theorem 4.1.

We present an example to show that the statements (i) and (iii) of Theorem 4.1 in the case of j=0j=0 do not hold for s.s. quasi \Mnat-convex functions.

Refer to caption
Figure 4: Values of function ff in Example 4.2.
Example 4.2.

Here is an example to show that the statements (i) and (iii) of Theorem 4.1 in the case of j=0j=0 are not true for s.s. quasi \Mnat-convex functions. Consider the function f:ℤ2→ℝ∪{+∞}f:\mathbb{Z}^{2}\to\mathbb{R}\cup\{+\infty\} given by444 This function ff is an adaptation of the one in [11, Example 5.1] to a discrete quasi convex function. The function in [11, Example 5.1] is used in [11] to point out the difference between the weaker versions of (SSQM♮) and (SSQ\Mnat-EXC-PRJ); see also Section 4.2.

dom​f={(1,0),(2,0),(0,1),(1,1)},\displaystyle{\rm dom\,}f=\{(1,0),(2,0),(0,1),(1,1)\},
f​(1,0)=1,f​(2,0)=0,f​(0,1)=2,f​(1,1)=3\displaystyle f(1,0)=1,\ f(2,0)=0,\ f(0,1)=2,\ f(1,1)=3

(see Figure 4). Function ff satisfies the condition (SSQM♮).

For x=(1,1)x=(1,1) and i=1i=1, j=0j=0 minimizes the value f​(x−χ1+χj)f(x-\chi_{1}+\chi_{j}) among all j∈N∪{0}j\in N\cup\{0\}. However, the unique minimizer y∗=(2,0)y^{*}=(2,0) does not satisfy y∗​(N)≤x​(N)−1y^{*}(N)\leq x(N)-1, i.e., the statement (i) of Theorem 4.1 does not hold in the case of j=0j=0.

For y=(0,1)y=(0,1), j=0j=0 minimizes the value f​(y+χj)f(y+\chi_{j}) among all j∈N∪{0}j\in N\cup\{0\}. However, the unique minimizer y∗=(2,0)y^{*}=(2,0) does not satisfy y∗​(N)≤y​(N)y^{*}(N)\leq y(N), i.e., the statement (iii) of Theorem 4.1 does not hold in the case of j=0j=0. ∎

We can also show that the statements (ii) and (iv) of Theorem 3.1 in the case of i=0i=0 do not hold for s.s. quasi \Mnat-convex functions; a counterexample to the statements is given by the function g​(x)=f​(−x)g(x)=f(-x) with the function ff in Example 4.2.

4.2 Connection with Quasi M-convex Functions

As mentioned in Introduction, the concept of s.s. quasi M-convex function is proposed in [8, 10] as a quasi-convex version of M-convex function. We explain the subtle difference between s.s. quasi M-convexity and s.s. quasi \Mnat-convexity in this section555 The difference between the weaker versions of (SSQM♮) and (SSQ\Mnat-EXC-PRJ) is already pointed out by Murota and Yokoi [11]. .

Recall that the condition (SSQM♮) defining s.s. quasi \Mnat-convexity is obtained by relaxing the condition (\Mnat-EXC) for \Mnat-convex functions. Similarly, the concept of s.s. quasi M-convex function is defined by using the relaxed version of the exchange axiom for M-convex functions as follows.

A function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} is said to be M-convex if it satisfies the following exchange axiom:

(M-EXC) ∀x,y∈dom​f\forall x,y\in{\rm dom\,}f, ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)\exists j\in{\rm supp}^{-}(x-y) such that

f​(x)+f​(y)≥f​(x−χi+χj)+f​(y+χi−χj).f(x)+f(y)\geq f(x-\chi_{i}+\chi_{j})+f(y+\chi_{i}-\chi_{j}). (4.1)

A semi-strictly quasi M-convex function is defined as a function satisfying the following relaxed version of (M-EXC):

(SSQM) ∀x,y∈dom​f\forall x,y\in{\rm dom\,}f, ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)\exists j\in{\rm supp}^{-}(x-y) satisfying at least one of the three conditions:

f​(x−χi+χj)<f​(x),\displaystyle f(x-\chi_{i}+\chi_{j})<f(x), (4.2)
f​(y+χi−χj)<f​(y),\displaystyle f(y+\chi_{i}-\chi_{j})<f(y), (4.3)
f​(x−χi+χj)=f​(x)​ and ​f​(y+χi−χj)=f​(y).\displaystyle f(x-\chi_{i}+\chi_{j})=f(x)\mbox{ and }f(y+\chi_{i}-\chi_{j})=f(y). (4.4)

Recall also that an \Mnat-convex function is originally defined as the projection of an M-convex function: an \Mnat-convex function is defined as a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} such that the function f~:ℤn×ℤ→ℝ∪{+∞}\tilde{f}:\mathbb{Z}^{n}\times\mathbb{Z}\to\mathbb{R}\cup\{+\infty\} given by

f~​(x,x0)={f​(x)(if ​x0=−x​(N)),+∞(if ​x0≠−x​(N))\tilde{f}(x,x_{0})=\begin{cases}f(x)&(\mbox{if }x_{0}=-x(N)),\\ +\infty&(\mbox{if }x_{0}\neq-x(N))\end{cases} (4.5)

is M-convex (i.e., satisfies (M-EXC)). Hence, a function ff is \Mnat-convex if and only if it satisfies the following exchange axiom obtained by the projection of (M-EXC):

(\Mnat-EXC-PRJ) ∀x,y∈dom​f\forall x,y\in{\rm dom\,}f,
(i) if x​(N)>y​(N)x(N)>y(N), then ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)∪{0}\exists j\in{\rm supp}^{-}(x-y)\cup\{0\} satisfying (4.1),
(ii) if x​(N)≤y​(N)x(N)\leq y(N), then ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)\exists j\in{\rm supp}^{-}(x-y) satisfying (4.1),
(iii) if x​(N)<y​(N)x(N)<y(N), then ∃j∈supp−​(x−y)\exists j\in{\rm supp}^{-}(x-y) satisfying (4.1) with i=0i=0.

That is, the following equivalence holds for \Mnat-convex functions.

Theorem 4.3 ([9, Theorem 4.2]).

For f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\},

f~​ in (4.5) satisfies (M-EXC)⇔f​ satisfies (\Mnat-EXC-PRJ)⇔f​ satisfies (\Mnat-EXC).\tilde{f}\mbox{ in \eqref{eqn:def-tildef} satisfies {\rm(M-EXC)}}\iff f\mbox{ satisfies {\rm(\Mnat-EXC-PRJ)}}\iff f\mbox{ satisfies {\rm(\Mnat-EXC)}.} (4.6)

For s.s. quasi \Mnat-convex functions, we may similarly consider the function f~\tilde{f} in (4.5) and the projected version of (SSQM):

(SSQ\Mnat-EXC-PRJ) ∀x,y∈dom​f\forall x,y\in{\rm dom\,}f,
(i) if x​(N)>y​(N)x(N)>y(N), then ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)∪{0}\exists j\in{\rm supp}^{-}(x-y)\cup\{0\} satisfying at least one of (4.2), (4.3), and (4.4),
(ii) if x​(N)≤y​(N)x(N)\leq y(N), then ∀i∈supp+​(x−y)\forall i\in{\rm supp}^{+}(x-y), ∃j∈supp−​(x−y)\exists j\in{\rm supp}^{-}(x-y) satisfying at least one of (4.2), (4.3), and (4.4),
(iii) if x​(N)<y​(N)x(N)<y(N), then ∃j∈supp−​(x−y)\exists j\in{\rm supp}^{-}(x-y) satisfying at least one of (4.2), (4.3), and (4.4) with i=0i=0.

While the conditions (\Mnat-EXC-PRJ) and (\Mnat-EXC) are equivalent to each other, as mentioned in Theorem 4.3, the condition (SSQ\Mnat-EXC-PRJ) is not equivalent to, but strictly stronger than, (SSQM♮) for s.s. quasi \Mnat-convex functions. That is, we have

f~\tilde{f} in (4.5) satisfies (SSQM) ⇔\iff ff satisfies (SSQ\Mnat-EXC-PRJ) ⟹⟸／\begin{array}[]{l}\Longrightarrow\\ \Longleftarrow\!\!\!\!\!\!\not\end{array} ff satisfies (SSQM♮) (4.7)

in contrast to (4.6). To be more specific, it is easy to see that

∙\bullet (SSQ\Mnat-EXC-PRJ) (i) and (ii) together imply (SSQM♮),
∙\bullet (SSQM♮) implies (SSQ\Mnat-EXC-PRJ) (i),

but (SSQM♮) does not imply (ii) and (iii) of (SSQ\Mnat-EXC-PRJ), as shown in the examples below.

Example 4.4.

Consider the function f:ℤ2→ℝ∪{+∞}f:\mathbb{Z}^{2}\to\mathbb{R}\cup\{+\infty\} given by

dom​f={x∈ℤ2∣x​(1)≥0,x​(2)≥0,x​(1)+x​(2)≤2},\displaystyle{\rm dom\,}f=\{x\in\mathbb{Z}^{2}\mid x(1)\geq 0,\ x(2)\geq 0,\ x(1)+x(2)\leq 2\},
f​(0,0)=0,f​(1,0)=f​(0,1)=1,f​(0,2)=2,f​(2,0)=f​(1,1)=3\displaystyle f(0,0)=0,\ f(1,0)=f(0,1)=1,\ f(0,2)=2,\ f(2,0)=f(1,1)=3

(see Figure 5). Function ff satisfies the condition (SSQM♮). The condition (SSQ\Mnat-EXC-PRJ) (ii) fails for this function.

Refer to caption
Figure 5: Values of function ff in Example 4.4.

Indeed, for x=(0,2)x=(0,2), y=(2,0)y=(2,0), and i=2∈supp+​(x−y)i=2\in{\rm supp}^{+}(x-y), we have a unique element j=1∈supp−​(x−y)j=1\in{\rm supp}^{-}(x-y), for which

x−χi+χj=y+χi−χj=(1,1),\displaystyle x-\chi_{i}+\chi_{j}=y+\chi_{i}-\chi_{j}=(1,1),
f​(x)=2<3=f​(x−χi+χj),f​(y)=3=f​(y+χi−χj).\displaystyle f(x)=2<3=f(x-\chi_{i}+\chi_{j}),\qquad f(y)=3=f(y+\chi_{i}-\chi_{j}).

∎

Example 4.5.

Consider the function f:ℤ2→ℝ∪{+∞}f:\mathbb{Z}^{2}\to\mathbb{R}\cup\{+\infty\} in Example 4.2, which satisfies (SSQM♮). The condition (iii) of (SSQ\Mnat-EXC-PRJ) fails for this function. Indeed, for x=(0,1)x=(0,1) and y=(2,0)y=(2,0), we have x​(N)=1<2=y​(N)x(N)=1<2=y(N) and supp−​(x−y)={1}{\rm supp}^{-}(x-y)=\{1\}, but

x+χ1=(1,1),y−χ1=(1,0),\displaystyle x+\chi_{1}=(1,1),\quad y-\chi_{1}=(1,0),
f​(x+χ1)=3>2=f​(x),f​(y−χ1)=1>0=f​(y).\displaystyle f(x+\chi_{1})=3>2=f(x),\quad f(y-\chi_{1})=1>0=f(y).

We can also verify that f~\tilde{f} in (4.5) does not satisfy (SSQM), which is consistent with (4.7). ∎

It is known that an s.s. quasi M-convex function (i.e., function ff satisfying (SSQM)) satisfies the minimizer cut property [10, Theorem 4.3] and the proximity property [10, Theorem 4.4]; it can be shown that an s.s. quasi M-convex function also enjoys the geodesic property (see Section A.2 in Appendix). It follows from this fact that if a function f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} satisfies the (stronger) condition (SSQ\Mnat-EXC-PRJ), then it satisfies the same statements as in Theorem 2.6 (minimizer cut property), Theorem 2.14 (geodesic property), and Theorem 2.17 (proximity property) for \Mnat-convex functions. In this connection we emphasize that the s.s. quasi \Mnat-convex functions in Examples 2.12 and 2.18 do not satisfy (SSQ\Mnat-EXC-PRJ) (iii).

Appendix A Appendix

A.1 Properties on Minimization of M-convex Functions

For ease of comparison between M- and \Mnat-convexity, we recall four theorems for minimization of an M-convex function, which correspond, respectively, to Theorems 2.1, 2.6, 2.14, and 2.17 for an \Mnat-convex function.

Optimality Condition by Local Optimality

Theorem A.1 ([5, Theorem 2.4], [7, Theorem 2.2]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an M-convex function. A vector x∗∈dom​fx^{*}\in{\rm dom\,}f is a minimizer of ff if and only if

f​(x∗−χi+χj)≥f​(x∗)(i,j∈N).\displaystyle f(x^{*}-\chi_{i}+\chi_{j})\geq f(x^{*})\qquad(i,j\in N).

The same statement holds also for s.s. quasi M-convex functions [10, Theorem 4.2].

Minimizer Cut Property

Theorem A.2 ([12, Theorem 2.2]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an M-convex function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f be a vector with x∉arg⁡min⁡fx\not\in\arg\min f.
(i) For i∈Ni\in N, let j∈Nj\in N be an element minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(j)≥x​(j)+1(if ​j∈N∖{i}),x∗​(i)≥x​(i)(if ​j=i).\begin{cases}x^{*}(j)\geq x(j)+1&(\mbox{if }j\in N\setminus\{i\}),\\ x^{*}(i)\geq x(i)&(\mbox{if }j=i).\end{cases}

(ii) Symmetrically, for j∈Nj\in N, let i∈Ni\in N be an element minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}). Then, there exists some minimizer x∗x^{*} of ff satisfying

{x∗​(i)≤x​(i)−1(if ​i∈N∖{j}),x∗​(j)≤x​(j)(if ​i=j).\begin{cases}x^{*}(i)\leq x(i)-1&(\mbox{if }i\in N\setminus\{j\}),\\ x^{*}(j)\leq x(j)&(\mbox{if }i=j).\end{cases}

(iii) For a pair (i,j)(i,j) of distinct elements in NN minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), there exists some minimizer x∗x^{*} of ff satisfying x∗​(i)≤x​(i)−1x^{*}(i)\leq x(i)-1 and x∗​(j)≥x​(j)+1x^{*}(j)\geq x(j)+1.

The same statement holds also for s.s. quasi M-convex functions [10, Theorem 4.3].

Geodesic Property

Recall the definitions of μ​(x)\mu(x) and M​(x)M(x) in (2.4) and (2.5), respectively.

Theorem A.3 ([14, Corollary 4.2], [3, Theorem 2.4]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an M-convex function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset, and x∈dom​fx\in{\rm dom\,}f be a vector that is not a minimizer of ff. Also, let (i,j)(i,j) be a pair of distinct elements in NN minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), and define

M′={x∗∈M​(x)∣x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1}.{M}^{\prime}=\{x^{*}\in M(x)\mid x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1\}.

(i) There exists some x∗∈M​(x)x^{*}\in M(x) that is contained in M′{M}^{\prime}; we have M′≠∅{M}^{\prime}\neq\emptyset, in particular.
(ii) It holds that μ​(x−χi+χj)=μ​(x)−2\mu(x-\chi_{i}+\chi_{j})=\mu(x)-2 and M​(x−χi+χj)=M′M(x-\chi_{i}+\chi_{j})={M}^{\prime}.

The same statement holds also for s.s. quasi M-convex functions; see Section A.2 for a proof.

Proximity Property

Theorem A.4 ([4, Theorem 3.4], [10, Theorem 4.4]).

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be an M-convex function and α≥2\alpha\geq 2 be an integer. For every vector x∈dom​f{x}\in{\rm dom\,}f satisfying

f​(x)≤mini,j∈N⁡f​(x−α​(χi−χj)),f({x})\leq\min_{i,j\in N}f({x}-\alpha(\chi_{i}-\chi_{j})),

there exists some minimizer x∗x^{*} of ff such that ‖x∗−x‖∞≤(n−1)​(α−1)\|x^{*}-{x}\|_{\infty}\leq(n-1)(\alpha-1).

The same statement holds also for s.s. quasi M-convex functions [10, Theorem 4.4].

A.2 Proof of Geodesic Property for Quasi M-convex Functions

We give a proof for the following geodesic property for semi-strictly quasi M-convex functions.

Theorem A.5.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset satisfying (SSQM) (i.e., ff is semi-strictly quasi M-convex), and x∈dom​fx\in{\rm dom\,}f be a vector that is not a minimizer of ff. Also, let (i,j)(i,j) be a pair of distinct elements in NN minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}), and define

M′={x∗∈M​(x)∣x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1}.{M}^{\prime}=\{x^{*}\in M(x)\mid x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1\}.

(i) There exists some x∗∈M​(x)x^{*}\in M(x) that is contained in M′{M}^{\prime}; we have M′≠∅{M}^{\prime}\neq\emptyset, in particular.
(ii) It holds that μ​(x−χi+χj)=μ​(x)−2\mu(x-\chi_{i}+\chi_{j})=\mu(x)-2 and M​(x−χi+χj)=M′M(x-\chi_{i}+\chi_{j})={M}^{\prime}.

The proof given below is essentially the same as the one in [3] for Theorem A.3 on M-convex functions. In the proof of Theorem A.5 (i) we use the following lemma.

Lemma A.6.

Let f:ℤn→ℝ∪{+∞}f:\mathbb{Z}^{n}\to\mathbb{R}\cup\{+\infty\} be a function with arg⁡min⁡f≠∅\arg\min f\neq\emptyset satisfying (SSQM). Assume that x∈dom​fx\in{\rm dom\,}f is not a minimizer of ff, and let (i,j)(i,j) be a pair of distinct elements in NN minimizing the value f​(x−χi+χj)f(x-\chi_{i}+\chi_{j}). Define y=x−χi+χjy=x-\chi_{i}+\chi_{j}.
(i) For every x∗∈arg⁡min⁡fx^{*}\in\arg\min f with i∈supp+​(x∗−y)i\in{\rm supp}^{+}(x^{*}-y), there exists some h∈supp−​(x∗−y)h\in{\rm supp}^{-}(x^{*}-y) with h≠jh\neq j such that x∗−χi+χh∈arg⁡min⁡fx^{*}-\chi_{i}+\chi_{h}\in\arg\min f.
(ii) For every x∗∈arg⁡min⁡fx^{*}\in\arg\min f with j∈supp−​(x∗−y)j\in{\rm supp}^{-}(x^{*}-y), there exists some k∈supp+​(x∗−y)k\in{\rm supp}^{+}(x^{*}-y) with k≠ik\neq i such that x∗+χj−χk∈arg⁡min⁡fx^{*}+\chi_{j}-\chi_{k}\in\arg\min f.

Proof.

We prove (i) only since (ii) can be proven similarly. We first note that f​(y)<f​(x)f(y)<f(x) holds since xx is not a minimizer [10, Theorem 4.2]. By definition, ff satisfies the condition (SSQM), which, applied to x∗,yx^{*},y and i∈supp+​(x∗−y)i\in{\rm supp}^{+}(x^{*}-y), implies that there exists some h∈supp−​(x∗−y)h\in{\rm supp}^{-}(x^{*}-y) such that at least one of the following conditions holds:

f​(x∗−χi+χh)<f​(x∗),\displaystyle f(x^{*}-\chi_{i}+\chi_{h})<f(x^{*}), (A.1)
f​(y+χi−χh)<f​(y),\displaystyle f(y+\chi_{i}-\chi_{h})<f(y), (A.2)
f​(x∗−χi+χh)=f​(x∗)​ and ​f​(y+χi−χh)=f​(y).\displaystyle f(x^{*}-\chi_{i}+\chi_{h})=f(x^{*})\mbox{ and }f(y+\chi_{i}-\chi_{h})=f(y). (A.3)

Note that h≠ih\neq i holds. We have

f​(x∗−χi+χh)≥f​(x∗)f(x^{*}-\chi_{i}+\chi_{h})\geq f(x^{*}) (A.4)

since x∗∈arg⁡min⁡fx^{*}\in\arg\min f. By the choice of i,j∈Ni,j\in N, we have

f​(y+χi−χh)≥f​(y),f(y+\chi_{i}-\chi_{h})\geq f(y), (A.5)

where y+χi−χh=x−χh+χjy+\chi_{i}-\chi_{h}=x-\chi_{h}+\chi_{j}. The inequalities (A.4) and (A.5) exclude the possibility of (A.1) and (A.2), respectively. Therefore, we have (A.3). The former equation in (A.3) implies that x∗−χi+χhx^{*}-\chi_{i}+\chi_{h} is also a minimizer of ff. We also have h≠jh\neq j, which follows from the latter equation in (A.3) and the inequality f​(y)<f​(x)f(y)<f(x) since y+χi−χh=x−χh+χjy+\chi_{i}-\chi_{h}=x-\chi_{h}+\chi_{j}. ∎

Proof of Theorem A.5 (i).

Putting y=x−χi+χjy=x-\chi_{i}+\chi_{j}, we have f​(y)<f​(x)f(y)<f(x). We first show that there exists some y∗∈M​(x)y^{*}\in M(x) such that y∗​(i)≤x​(i)−1y^{*}(i)\leq x(i)-1. Assume, to the contrary, that y∗​(i)>x​(i)−1=y​(i)y^{*}(i)>x(i)-1=y(i) holds for every y∗∈M​(x)y^{*}\in M(x). Let y∗∈M​(x)y^{*}\in M(x) be a vector minimizing the value y∗​(i)y^{*}(i) among all such vectors. By Lemma A.6 (i), there exists some h∈supp−​(y∗−y)h\in{\rm supp}^{-}(y^{*}-y) with h≠jh\neq j such that y∗−χi+χh∈arg⁡min⁡fy^{*}-\chi_{i}+\chi_{h}\in\arg\min f. Since y∗​(h)<y​(h)=x​(h)y^{*}(h)<y(h)=x(h), we have ∥(y∗−χi+χh)−x∥1≤∥y∗−x∥1\lVert(y^{*}-\chi_{i}+\chi_{h})-x\rVert_{1}\leq\lVert y^{*}-x\rVert_{1}. Since y∗∈M​(x)y^{*}\in M(x) and y∗−χi+χh∈arg⁡min⁡fy^{*}-\chi_{i}+\chi_{h}\in\arg\min f, it follows that y∗−χi+χh∈M​(x)y^{*}-\chi_{i}+\chi_{h}\in M(x). This, however, is a contradiction to the choice of y∗y^{*} since (y∗−χi+χh)​(i)=y∗​(i)−1<y∗​(i)(y^{*}-\chi_{i}+\chi_{h})(i)=y^{*}(i)-1<y^{*}(i).

We then show that there exists some x∗∈M​(x)x^{*}\in M(x) satisfying both of x∗​(i)≤x​(i)−1x^{*}(i)\leq x(i)-1 and x∗​(j)≥x​(j)+1x^{*}(j)\geq x(j)+1. Let x∗∈M​(x)x^{*}\in M(x) be a vector with x∗​(i)≤x​(i)−1x^{*}(i)\leq x(i)-1. If there exists such x∗x^{*} with x∗​(j)≥x​(j)+1x^{*}(j)\geq x(j)+1, then we are done. Hence, we assume, to the contrary, that x∗​(j)<x​(j)+1=y​(j)x^{*}(j)<x(j)+1=y(j) for every x∗∈M​(x)x^{*}\in M(x) with x∗​(i)≤x​(i)−1x^{*}(i)\leq x(i)-1, and suppose that x∗x^{*} maximizes the value x∗​(j)x^{*}(j) among all such x∗x^{*}. By Lemma A.6 (ii), there exists some k∈supp+​(x∗−y)k\in{\rm supp}^{+}(x^{*}-y) with k≠ik\neq i such that x∗+χj−χk∈arg⁡min⁡fx^{*}+\chi_{j}-\chi_{k}\in\arg\min f. We show that x∗+χj−χk∈M​(x)x^{*}+\chi_{j}-\chi_{k}\in M(x) holds. Since x∗​(k)>y​(k)=x​(k)x^{*}(k)>y(k)=x(k), we have ∥(x∗+χj−χk)−x∥1≤∥x∗−x∥1\lVert(x^{*}+\chi_{j}-\chi_{k})-x\rVert_{1}\leq\lVert x^{*}-x\rVert_{1}. We also have (x∗+χj−χk)​(i)=x∗​(i)≤x​(i)−1(x^{*}+\chi_{j}-\chi_{k})(i)=x^{*}(i)\leq x(i)-1 since i∉{j,k}i\notin\{j,k\}. This, however, is a contradiction to the choice of x∗x^{*} since (x∗+χj−χk)​(j)=x∗​(j)+1>x∗​(j)(x^{*}+\chi_{j}-\chi_{k})(j)=x^{*}(j)+1>x^{*}(j). Hence, we have x∗​(j)≥x​(j)+1x^{*}(j)\geq x(j)+1.

This concludes the proof of Theorem A.5 (i). ∎

Proof of Theorem A.5 (ii).

We first prove the equation μ​(x−χi+χj)=μ​(x)−2\mu(x-\chi_{i}+\chi_{j})=\mu(x)-2. It holds that

∀y∗∈M(x−χi+χj):μ(x−χi+χj)\displaystyle\forall y^{*}\in M(x-\chi_{i}+\chi_{j}):\quad\mu(x-\chi_{i}+\chi_{j}) =∥y∗−(x−χi+χj)∥1\displaystyle=\lVert y^{*}-(x-\chi_{i}+\chi_{j})\rVert_{1}
≥∥y∗−x∥1−∥χi−χj∥1\displaystyle\geq\lVert y^{*}-x\rVert_{1}-\lVert\chi_{i}-\chi_{j}\rVert_{1}
=∥y∗−x∥1−2≥μ​(x)−2,\displaystyle=\lVert y^{*}-x\rVert_{1}-2\geq\mu(x)-2, (A.6)

where the first inequality is by the triangle inequality. We also have

∀x∗∈M′:μ(x−χi+χj)≤∥x∗−(x−χi+χj)∥1\displaystyle\forall x^{*}\in M^{\prime}:\quad\mu(x-\chi_{i}+\chi_{j})\leq\lVert x^{*}-(x-\chi_{i}+\chi_{j})\rVert_{1} =∥x∗−x∥1−2=μ​(x)−2,\displaystyle=\lVert x^{*}-x\rVert_{1}-2=\mu(x)-2, (A.7)

where the first equality is by the inequalities x∗​(i)≤x​(i)−1,x∗​(j)≥x​(j)+1x^{*}(i)\leq x(i)-1,\ x^{*}(j)\geq x(j)+1 and the second equality is by x∗∈M​(x)x^{*}\in M(x). The equation μ​(x−χi+χj)=μ​(x)−2\mu(x-\chi_{i}+\chi_{j})=\mu(x)-2 follows from (A.6) and (A.7).

We then prove the equation M​(x−χi+χj)=M′M(x-\chi_{i}+\chi_{j})={M}^{\prime}. It follows from μ​(x−χi+χj)=μ​(x)−2\mu(x-\chi_{i}+\chi_{j})=\mu(x)-2, (A.6), and (A.7) that all the inequalities in (A.6) and (A.7) hold with equality; in particular, we have

∀y∗∈M(x−χi+χj):∥y∗−(x−χi+χj)∥1=∥y∗−x∥1−2=μ(x)−2,\displaystyle\forall y^{*}\in M(x-\chi_{i}+\chi_{j}):\quad\lVert y^{*}-(x-\chi_{i}+\chi_{j})\rVert_{1}=\lVert y^{*}-x\rVert_{1}-2=\mu(x)-2, (A.8)
∀x∗∈M′:μ(x−χi+χj)=∥x∗−(x−χi+χj)∥1.\displaystyle\forall x^{*}\in M^{\prime}:\quad\mu(x-\chi_{i}+\chi_{j})=\lVert x^{*}-(x-\chi_{i}+\chi_{j})\rVert_{1}. (A.9)

The equation (A.9) implies that M​(x−χi+χj)⊇M′M(x-\chi_{i}+\chi_{j})\supseteq M^{\prime}. We can also obtain the reverse inclusion M​(x−χi+χj)⊆M′M(x-\chi_{i}+\chi_{j})\subseteq M^{\prime} from (A.8). Indeed, for every y∗∈M​(x−χi+χj)y^{*}\in M(x-\chi_{i}+\chi_{j}), we have y∗∈M​(x)y^{*}\in M(x) by ∥y∗−x∥1=μ​(x)\lVert y^{*}-x\rVert_{1}=\mu(x), and we also have y∗​(i)≤x​(i)−1y^{*}(i)\leq x(i)-1 and y∗​(j)≥x​(j)+1y^{*}(j)\geq x(j)+1 since ∥y∗−(x−χi+χj)∥1=∥y∗−x∥1−2\lVert y^{*}-(x-\chi_{i}+\chi_{j})\rVert_{1}=\lVert y^{*}-x\rVert_{1}-2. Hence, M​(x−χi+χj)⊆M′M(x-\chi_{i}+\chi_{j})\subseteq M^{\prime} holds, implying the equation M​(x−χi+χj)=M′M(x-\chi_{i}+\chi_{j})={M}^{\prime}. ∎

References

  • [1] Chen, X., Li, M.: M♮-convexity and its applications in operations. Operations Research 69, 1396–1408 (2021)
  • [2] Farooq, R., Shioura, A.: A note on the equivalence between substitutability and M♮-convexity. Pacific Journal of Optimization 1, 243–252 (2005)
  • [3] Minamikawa, N., Shioura, A.: Time bounds of basic steepest descent algorithms for M-convex function minimization and related problems. Journal of the Operations Research Society of Japan 64, 45–60 (2021)
  • [4] Moriguchi, S., Murota, K., Shioura, A.: Scaling algorithms for M-convex function minimization. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences E85-A, 922–929 (2002)
  • [5] Murota, K.: Convexity and Steinitz’s exchange property. Advances in Mathematics 124, 272–311 (1996)
  • [6] Murota, K.: Discrete convex analysis. Mathematical Programming 83, 313–371 (1998)
  • [7] Murota, K.: Submodular flow problem with a nonseparable cost function. Combinatorica 19, 87–109 (1999)
  • [8] Murota, K.: Discrete Convex Analysis. Society for Industrial and Applied Mathematics, Philadelphia (2003)
  • [9] Murota, K., Shioura, A.: M-convex function on generalized polymatroid. Mathematics of Operations Research 24, 95–105 (1999)
  • [10] Murota, K., Shioura, A.: Quasi M-convex and L-convex functions: quasi-convexity in discrete optimization. Discrete Applied Mathematics 131, 467–494 (2003)
  • [11] Murota, K., Yokoi, Y.: On the lattice structure of stable allocations in two-sided discrete-concave market. Mathematics of Operations Research 40, 460–473 (2015)
  • [12] Shioura, A.: Minimization of an M-convex function. Discrete Applied Mathematics 84, 215–220 (1998)
  • [13] Shioura, A.: Fast scaling algorithms for M-convex function minimization with application to the resource allocation problem. Discrete Applied Mathematics 134, 303–316 (2004)
  • [14] Shioura, A.: M-convex function minimization under L1-distance constraint and its application to dock re-allocation in bike sharing system. Mathematics of Operations Research 47, 1566–1611 (2022)
  • [15] Tamura, A.: Coordinatewise domain scaling algorithm for M-convex function minimization. Mathematical Programming 102, 339–354 (2005)