Note on approximating the Laplace transform of a Gaussian on a complex disk

Yury Polyanskiy and Yihong Wu Y.P. is with the Department of EECS, MIT, Cambridge, MA, email: [email protected]. Y.W. is with the Department of Statistics and Data Science, Yale University, New Haven, CT, email: [email protected].

Abstract

In this short note we study how well a Gaussian distribution can be approximated by distributions supported on $[-a,a]$ . Perhaps, the natural conjecture is that for large $a$ the almost optimal choice is given by truncating the Gaussian to $[-a,a]$ . Indeed, such approximation achieves the optimal rate of $e^{-\Theta(a^{2})}$ in terms of the $L_{\infty}$ -distance between characteristic functions. However, if we consider the $L_{\infty}$ -distance between Laplace transforms on a complex disk, the optimal rate is $e^{-\Theta(a^{2}\log a)}$ , while truncation still only attains $e^{-\Theta(a^{2})}$ . The optimal rate can be attained by the Gauss-Hermite quadrature. As corollary, we also construct a “super-flat” Gaussian mixture of $\Theta(a^{2})$ components with means in $[-a,a]$ and whose density has all derivatives bounded by $e^{-\Omega(a^{2}\log(a))}$ in the $O(1)$ -neighborhood of the origin.

1 Approximating the Gaussian

We study the best approximation of a Gaussian distribution by compact support measures, in the sense of the uniform approximation of the Laplace transform on a complex disk. Let $L_{\pi}(z)=\int_{\mathbb{R}}d\pi(y)e^{zy}$ be the Laplace transform, $z\in\mathbb{C}$ , of the measure $\pi$ and $\Psi_{\pi}(t)\triangleq L_{\pi}(it)$ be its characteristic function. Denote $L_{0}(z)=e^{z^{2}/2}$ and $\Psi_{0}(t)=e^{-t^{2}/2}$ the Laplace transform and the characteristic function corresponding to the standard Gaussian $\pi_{0}=\mathcal{N}(0,1)$ with density

\phi(x)\triangleq{1\over\sqrt{2\pi}}e^{-x^{2}/2}\,,\quad x\in\mathbb{R}\,.

How well can a measure $\pi_{1}$ with support on $[-a,a]$ approximate $\pi_{0}$ ? Perhaps the most natural choice for $\pi_{1}$ is the truncated $\pi_{0}$ :

\pi_{1}(dx)\triangleq\phi_{a}(x)dx,\qquad\phi_{a}(x)\triangleq{\phi(x)\over 1-2Q(a)}1\{|x|\leq a\}\,,

(1)

where $Q(a)=\mathbb{P}[\mathcal{N}(0,1)>a]$ . Indeed, truncation is asymptotically optimal (as $a\to\infty$ ) in approximating the characteristic function, as made preicse by the following result:

Proposition 1.

There exists some $c>0$ such that for all $a\geq 1$ and any probability measure $\pi_{1}$ supported on $[-a,a]$ we have

\sup_{t\in\mathbb{R}}|\Psi_{\pi_{1}}(t)-e^{-t^{2}/2}|\geq ce^{-ca^{2}}\,.

(2)

Furthermore, truncation (1) satisfies (for $a\geq 1$ )

\sup_{t\in\mathbb{R}}|\Psi_{\pi_{1}}(t)-e^{-t^{2}/2}|\leq 2e^{-a^{2}/2}\,.

(3)

Proof.

Let us define $B(z)\triangleq L_{\pi}(z)-e^{z^{2}/2}$ , a holomorphic (entire) function on $\mathbb{C}$ . Note that if $\Re(z)=r$ then

|L_{\pi}(z)|\leq e^{a|r|},\qquad|e^{z^{2}/2}|\leq e^{r^{2}/2}\,,

and thus for $r\geq 2a$

b(r)\triangleq\sup\{|B(z)|:\Re(z)=r\}\leq e^{ar}+e^{r^{2}/2}\leq 2e^{r^{2}/2}

(4)

On the other hand, for every $r\geq 3a,a\geq 1$ we have

b(r)\geq|B(r)|\geq e^{r^{2}/2}-e^{ar}\geq{1\over 2}e^{r^{2}/2}\,.

(5)

Applying the Hadamard three-lines theorem to $B(z)$ , we conclude that $r\mapsto\log b(r)$ is convex and hence

b(3a)\leq(b(0))^{1/2}(b(6a))^{1/2}\,.

(6)

Since the left-hand side of (2) equals $b(0)$ , (2) then follows from (4)-(6).

For the converse part, in view of (1), the total variation between $\pi_{0}$ and its conditional version $\pi_{1}$ is given by

\int_{\mathbb{R}}|\phi_{a}(x)-\phi(x)|dx=2\|\pi_{0}-\pi_{1}\|_{\rm TV}=2\pi_{0}([-a,a]^{c})=4Q(a)\,

Therefore for the Fourier transform of $\phi_{a}-\phi$ we get

\sup_{t\in\mathbb{R}}|\Psi_{\pi_{1}}(t)-e^{-t^{2}/2}|\leq 4Q(a)\leq{4\over\sqrt{2\pi}a}e^{-a^{2}/2}\leq 2e^{-a^{2}/2}\,.

∎

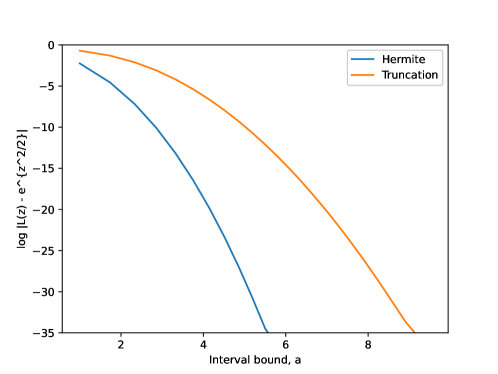
Despite this evidence, it turns out that for the purpose of approximating Laplace transform in a neighborhood of $0$ , there is a much better approximation than (1).

Theorem 2.

There exists some constant $c>0$ such that for any probability measure $\pi$ supported on $[-a,a]$ , $a\geq 1$ , we have

\sup_{|z|\leq 1,z\in\mathbb{C}}|e^{z^{2}/2}-L_{\pi}(z)|\geq ce^{-ca^{2}\log(a)}\,,

(7)

Furthermore, there exists an absolute constant $c_{1}>0$ so that for all $b\geq 1$ and all $a\geq 2c_{1}b$ there exists distribution $\pi$ (the Gauss-Hermite quadrature) supported on $[-a,a]$ such that

\sup_{|z|\leq b,z\in\mathbb{C}}|e^{z^{2}/2}-L_{\pi}(z)|\leq 3(c_{1}b/a)^{a^{2}/4}\,.

Taking $b=1$ implies that the bound (7) is order-optimal.

Remark 1.

When $\pi_{1}$ is given by the truncation (1), then performing explicit calculation for $z\in\mathbb{R}$ we have

L_{\pi_{1}}(z)=e^{z^{2}/2}\frac{\Phi(a+z)+\Phi(a-z)-1}{2\Phi(a)-1}\,.

The same expression (by analytic continuation) holds for arbitrary $z\in\mathbb{C}$ if $\Phi(z)$ is understood as solution of $\Phi^{\prime}(z)=\phi(z),\Phi(0)=1/2$ . For $|z|=O(1)$ , the approximation error is $e^{-\Omega(a^{2})}$ , rather than $e^{-\Omega(a^{2}\log a)}$ . The suboptimality of truncation is demonstrated on Fig. 1.

Refer to caption — Figure 1: Comparison of approximations of $\mathcal{N}(0,1)$ by distributions supported on $[-a,a]$ , as measured by the (log of) $L_{\infty}$ distance between the Laplace transform on the unit disk in $\mathbb{C}$ .

Proof.

As above, denote $B(z)=L_{\pi}(z)-e^{z^{2}/2}$ , and define

M(r)=\sup_{|z|\leq r,z\in\mathbb{C}}|B(z)|\,.

From (5) we have for any $r\geq 3a,a\geq 1$

M(r)\geq{1\over 2}e^{r^{2}/2}

and from $|L_{\pi}(z)|\leq e^{a|z|}$ we also have (for any $r\geq 2a$ ):

M(r)\leq e^{ar}+e^{r^{2}/2}\leq 2e^{r^{2}/2}\,.

Applying the Hadamard three-circles theorem, we have $\log r\mapsto\log M(r)$ is convex, and hence

M(3a)\leq(M(1))^{1-\lambda}(M(5a))^{\lambda}\,,

where $\lambda={\log(5a)\over\log(3a)}$ and $1-\lambda\Theta({1\over\log a})$ . From here we obtain for some constant $c>0$

\log M(1)\geq c(-a^{2}-1)\log(a)\,,

which proves (7).

For the upper bound, take $\pi$ to be the $k$ -point Gauss-Hermite quadrature of $\mathcal{N}(0,1)$ (cf. [SB02, Section 3.6]). This is the unique $k$ -atomic distribution that matches the first $2k-1$ moments of ${\mathcal{N}}(0,1)$ . Specifically, we have:

•

$\pi$ is supported on the roots of the degree- $k$ Hermite polynomial, which lie in $[-\sqrt{4k+2},\sqrt{4k+2}]$ [Sze75, Theorem 6.32];
•

The $i$ -th moment of $\pi$ , denoted by $m_{i}(\pi)$ , satisfies $m_{i}(\pi)=m_{i}(N(0,1))$ for all $i=1,\ldots,2k-1$ .
•

$\pi$ is symmetric so that all odd moments are zero.

We set $k=\lceil a^{2}/8\rceil$ , so that $\pi$ is supported on $[-a,a]$ .

Let us denote $X\sim\pi$ and $G\sim\mathcal{N}(0,1)$ . By Taylor expansion we get

B(z)=\mathbb{E}[e^{zX}]-\mathbb{E}[e^{zG}]=\sum_{m=2k}^{\infty}{1\over m!}z^{m}(\mathbb{E}[X^{m}]-\mathbb{E}[G^{m}])=\sum_{\ell=k}^{\infty}{1\over(2\ell)!}z^{2\ell}(\mathbb{E}[X^{2\ell}]-\mathbb{E}[G^{2\ell}])\,.

Now, we will bound $(2\ell)!\geq(2\ell/e)^{2\ell}$ , $\mathbb{E}[X^{2\ell}]\leq a^{2\ell}$ , $\mathbb{E}[G^{2\ell}]=(2\ell-1)!!\leq(2\ell)^{\ell}$ . This implies that for all $|z|\leq b$ we have

	$\displaystyle\|B(z)\|$	$\displaystyle\leq\sum_{\ell\geq k}\left\{\left(ea\over 2\ell\right)^{2\ell}+\left(e\over\sqrt{2\ell}\right)^{2\ell}\right\}\|z\|^{2\ell}$
		$\displaystyle\leq\sum_{\ell\geq k}\left\{\left(ea\over 2k\right)^{2\ell}+\left(e\over\sqrt{2k}\right)^{2\ell}\right\}\|z\|^{2\ell}$
		$\displaystyle\leq 2\sum_{\ell\geq k}(c_{1}b/a)^{2\ell}\,,$

where in the last step we used ${ea\over 2k},{e\over\sqrt{2k}}\leq{c_{1}\over a}$ for some absolute constant $c_{1}$ . In all, we have that whenever $c_{1}b/a<1/2$ we get

|B(z)|\leq{2\over 1-(c_{1}b/a)^{2}}(c_{1}b/a)^{2k}\leq 3(c_{1}b/a)^{a^{2}/4}\,.

∎

Remark 2.

Note that our proof does not show that for any $\pi$ supported on $[-a,a]$ , its characteristic function restricted on $[-1,1]$ must satisfy:

\sup_{|t|\leq 1}|\Psi_{\pi}(t)-e^{-t^{2}/2}|\geq ce^{-ca^{2}\log a}\,.

It is natural to conjecture that this should hold, though.

Remark 3.

Note also that the Gauss-Hermite quadrature considered in the theorem, while essentially optimal on complex disks, is not uniformly better than the naive truncation. For example, due to its finite support, the Gauss-Hermite quadrature is a very bad approximation in the sense of (2). Indeed, for any finite discrete distribution $\pi_{1}$ we have $\limsup_{t\to\infty}|\Psi_{\pi_{1}}(t)|=1$ , thus only attaining the trivial bound of $1$ in the right-hand side of (2). (To see this, note that $\Psi_{\pi_{1}}(t)=\sum_{j=1}^{k}p_{i}e^{it\omega_{j}}$ . By simultaneous rational approximation (see, e.g., [Cas72, Theorem VI, p. 13]), we have infinitely many values $q$ such that for all $j$ $|q{\omega_{j}\over 2\pi}-p_{j}|<{1\over q^{1/k}}$ for some $p_{j}\in\mathbb{Z}$ . In turn, this implies that $\liminf_{t\to\infty}\max_{j=1,\ldots,m}(t\omega_{j}\mod 2\pi)=0$ , and that $\Psi_{\pi_{1}}(t)\to 1$ along the subsequence of $t$ attaining $\liminf$ .)

2 Super-flat Gaussian mixtures

As a corollary of construction in the previous section we can also derive a curious discrete distribution $\pi_{2}=\sum_{m}w_{m}\delta_{x_{m}}$ supported on $[-a,a]$ such that its convolution with the Gaussian kernel $\pi_{2}*\phi$ is maximally flat near the origin. More precisely, we have the following result.

Corollary 3.

There exist constants $C_{1},C>0$ such that for every $a>0$ there exists $k=\Theta(a^{2})$ , $w_{m}\geq 0$ with $\sum_{m=1}^{k}w_{m}=1$ and $x_{m}\in[-a,a]$ , $m\in\{1,\ldots,k\}$ , such that

\left|\left({d\over dz}\right)^{n}\sum_{m=1}^{k}w_{m}\phi(z-x_{m})\right|\leq n!\cdot C_{1}e^{-Ca^{2}\log(a)}\qquad\forall z\in\mathbb{C},|z|\leq 1,n\in\{1,2,\ldots\}\,.

Proof.

Consider the distribution $\pi=\sum_{m=1}^{k}\widetilde{w}_{m}\delta_{x_{m}}$ claimed by Theorem 2 for $b=2$ . Then (here and below $C$ designates some absolute constant, possibly different in every occurence) we have

\sup_{|z|\leq 2}|L_{\pi}(z)-e^{z^{2}/2}|\leq Ce^{-Ca^{2}\log(a)}\,.

Note that the function $e^{-z^{2}/2}$ is also bounded on $|z|\leq 2$ and thus we have

\sup_{|z|\leq 2}|L_{\pi}(z)e^{-z^{2}/2}-1|\leq Ce^{-Ca^{2}\log(a)}\,.

By Cauchy formula, this also implies that derivatives of the two functions inside $|\cdot|$ must satisfy the same estimate on a smaller disk, i.e.

\sup_{|z|\leq 1}\left|\left({d\over dz}\right)^{n}L_{\pi}(z)e^{-z^{2}/2}\right|\leq n!\cdot Ce^{-Ca^{2}\log(a)}\,.

(8)

Now, define $w_{m}={1\over B}\widetilde{w}_{m}e^{x_{m}^{2}/2}$ , where $B=\sum_{m}\widetilde{w}_{m}e^{x_{m}^{2}/2}$ . We then have an identity:

L_{\pi}(z)e^{-z^{2}/2}=B\sum_{m}w_{m}e^{-(z-x_{m})^{2}/2}

Plugging this into (8) and noticing that $B\geq 1$ we get the result. ∎

Remark 4.

This corollary was in fact the main motivation of this note. More exactly, in the study of the properties of non-parametric maximum-likelihood estimation of Gaussian mixtures, we conjectured that certain mixtures must possess some special $z_{0}$ in the unit disk on $\mathbb{C}$ such that $\left|\sum_{m}w_{m}\phi^{\prime}(z_{0}-x_{m})\right|\geq e^{-O(a^{2})}$ . The stated corollary shows that this is not true for all mixtures. See [PW20, Section 5.3] for more details on why lower-bounding the derivative is important. In particular, one open question is whether the lower bound $e^{-O(a^{2})}$ holds (with high probability) for the case when $a\asymp\sqrt{\log k}$ and $x_{m},m\in\{1,\ldots,k\}$ , are iid samples of $\mathcal{N}(0,1)$ , while $w_{m}$ ’s can be chosen arbitrarily given $x_{m}$ ’s.

References

[Cas72] J. W. S. Cassels. An Introduction to Diophantine Approximation. Cambridge University Press, Cambridge, United Kingdom, 1972.
[PW20] Yury Polyanskiy and Yihong Wu. Self-regularizing property of nonparametric maximum likelihood estimator in mixture models. Arxiv preprint arXiv:2008.08244, Aug 2020.
[SB02] J. Stoer and R. Bulirsch. Introduction to Numerical Analysis. Springer-Verlag, New York, NY, 3rd edition, 2002.
[Sze75] G. Szegö. Orthogonal polynomials. American Mathematical Society, Providence, RI, 4th edition, 1975.

	$\displaystyle\|B(z)\|$	$\displaystyle\leq\sum_{\ell\geq k}\left\{\left(ea\over 2\ell\right)^{2\ell}+\left(e\over\sqrt{2\ell}\right)^{2\ell}\right\}\|z\|^{2\ell}$
		$\displaystyle\leq\sum_{\ell\geq k}\left\{\left(ea\over 2k\right)^{2\ell}+\left(e\over\sqrt{2k}\right)^{2\ell}\right\}\|z\|^{2\ell}$
		$\displaystyle\leq 2\sum_{\ell\geq k}(c_{1}b/a)^{2\ell}\,,$