Not Just Object, But State: Compositional Incremental Learning without Forgetting

For composition-IL, a model sequentially learns $N$ tasks $\mathcal{T}=\left\{\mathcal{T}_{1},\mathcal{T}_{2},\cdots\mathcal{T}_{N}\right\}$ corresponding to a set of composition classes $\mathcal{C}=\left\{\mathcal{C}_{1},\mathcal{C}_{2},\cdots\mathcal{C}_{N}\right\}$. We note that the composition classes between incremental tasks are always disjoint, which means $\mathcal{C}_{i}\cap\mathcal{C}_{j}=\emptyset$ for any $i\neq j$. Different from the composition classes, the primitive classes are allowed to recur in different tasks. That means it allows the tasks to share some primitive concepts of objects and states. Therefore, we can define the set of all state and object classes with $\mathcal{S}=\left\{s_{1},s_{2},\cdots,s_{n}\right\}$ and $\mathcal{O}=\left\{o_{1},o_{2},\cdots,o_{m}\right\}$, respectively. Given each image $x$, it has a composition label $c$ which is constructed with a state label $s$ and an object label $o$, i.e. $c=<s,o>$, where $c\in\mathcal{C}$, $s\in\mathcal{S}$ and $o\in\mathcal{O}$. We take the example of “red shirt”, where “red” is denoted with $s$, “shirt” corresponds to $o$, and “red shirt” is expressed with $c$.

As there are no existing datasets suitable for composition-IL, we re-organize the data in Clothing16K IVR and UT-Zappos50K ut-zappos , and construct two new datasets tailored for composition-IL, namely Split-Clothing and Split-UT-Zappos. To be more specific, we firstly sort the composition classes based on the number of their images, and then select the foremost 35 compositions from Clothing16K and the top 80 from UT-Zappos50K, so as to construct Split-Clothing and Split-UT-Zappos, respectively. In this way, Split-Clothing encompasses 9 states and 8 objects while Split-UT-Zappos consists of 15 states and 12 objects in total. For Split-Clothing, we randomly partition the compositions into 5 tasks. Regarding Split-UT-Zappos, the compositions are sorted by count and are evenly divided into 5 and 10 tasks. The image distribution for each task is shown in Fig. 2. Note that, we elaborate more details on both datasets in the following technical appendix.

The main stumbling block in composition-IL is the ambiguous composition boundary. Although the composition label consists of two primitives (i.e. object and state), we note that the model excessively prioritizes the object primitive while neglecting the state primitive. Consequently, the compositions with the same object but with different states become ambiguous and indistinguishable. To prove that, we apply L2P L2P to composition-IL, whereas it is challenged by significant ambiguities in composition classification. As illustrated in Fig. 3 (a), the t-SNE visualization showcases the entanglement among the compositions like “white dress”, “black dress” and “blue dress”. We conjecture that this ambiguous problem tends to become more severe when more tasks are arriving incrementally. To address it, we propose a new model namely CompILer, which disentangles compositions and primitives via a multi-pool prompt learning. Advantageously, our method promotes the learning on the states and establishes clearer composition boundaries, as shown in Fig. 3 (b).

The learning-to-prompt paradigm L2P ; NotMeetStrongPT , especially suitable for large pre-trained backbones, has opened up a new path for incremental learning. It has proven to incorporate plasticity and stability better through adapting a set of learnable tokens in a prompt pool to a frozen pre-trained backbone. Nevertheless, existing prompt-based approaches are initially designed for class-IL, thereby building a single prompt pool for object classification solely. when dealing with state-object composition classification, they tend to excessively prioritize the object primitive while neglecting the state primitive. To this end, we propose to construct three discrepant and diversified prompt pools $\mathbb{P}_{s}$, $\mathbb{P}_{o}$ and $\mathbb{P}_{c}$, which serve to learn visual information related to states, objects and their compositions, respectively. Besides, each pool is associated with a set of learnable keys $\mathbb{K}_{\omega}$ for query-key prompt selection. The three prompt pools and their keys are defined as:

$$\mathbb{P}_{\omega}=\left\{P_{\omega}^{1},P_{\omega}^{2},\cdots P_{\omega}^{M}\right\},\mathbb{K}_{\omega}=\left\{K_{\omega}^{1},K_{\omega}^{2},\cdots K_{\omega}^{M}\right\},\omega\in\left\{s,o,c\right\},$$

(1)

where $P_{\omega}^{i}\in\mathbb{R}^{L\times D}$ is a single prompt with token length $L$ and embedding dimension $D$. $K_{\omega}^{i}\in\mathbb{R}^{D}$, the key of $P_{\omega}^{i}$, is a learnable token with the same size. $M$ is the number of prompts in each pool.

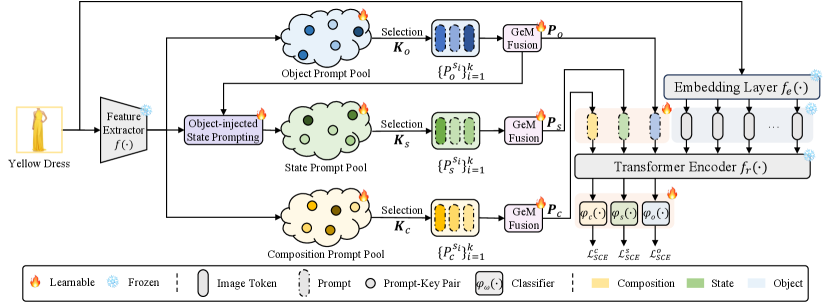
One important concern in such multi-pool prompt learning is how to enrich the prompts with the avoidance of identical pools. To achieve it, we consider integrating inter-pool prompt discrepancy and intra-pool prompt diversity jointly. On the one hand, the inter-pool prompts should be discrepant as the visual information about states, objects, and compositions should be different. One the other hand, within each pool, the intra-pool prompts should be diversified so to capture more comprehensive features from all the classes.

In practice, we formulate a unified objective to regularize both inter-pool discrepancy and intra-pool diversity, by leveraging a simple and effective directional decoupled loss used in PIP . The directional decoupled (dd) loss between any two pools (e.g. $P_{i}$ and $P_{j}$) is formulated as:

$$\mathcal{L}_{dd}^{(i,j)}=\frac{2}{M(M-1)}\sum_{n=1}^{M}\sum_{m=1}^{M}\max\left(0,\theta_{\text{thre}}-\theta_{nm}\right),$$

(2)

$$\theta_{nm}=\cos^{-1}\Big{(}\frac{(P_{i}^{n})^{\mathrm{T}}P_{j}^{m}}{\max(\|P_{i}^{n}\|_{2},\epsilon)\cdot\max(\|P_{j}^{m}\|_{2},\epsilon)}\Big{)},$$

(3)

where $\theta_{nm}$ measures the angle between any two prompts, $n$ and $m$; $\epsilon$ is a scalar to avoid division by zero. Note that, $\mathcal{L}_{dd}^{(i,j)}$ encourages the angles between each prompt to be at least $\theta_{\text{thre}}$ degrees. Since $(i,j)$ is unordered Cartesian product of $\omega$, i.e. $(i,j)\in\left\{(i,j)\mid i\in\omega\wedge j\in\omega\right\}$, the inter-pool prompt discrepancy loss for the three pools can be expressed with $\mathcal{L}_{inter}=\mathcal{L}_{dd}^{(s,o)}+\mathcal{L}_{dd}^{(s,c)}+\mathcal{L}_{dd}^{(o,c)}$, and the intra-pool prompt diversity loss becomes $\mathcal{L}_{intra}=\mathcal{L}_{dd}^{(s,s)}+\mathcal{L}_{dd}^{(o,o)}+\mathcal{L}_{dd}^{(c,c)}$. As opposed to $\mathcal{L}_{inter}$, $\mathcal{L}_{intra}$ computes the angle between any two prompts within the same pool. Thus, it contains the case when $n=m$, for which we set $\theta_{\text{thre}}-\theta_{nm}=0$.

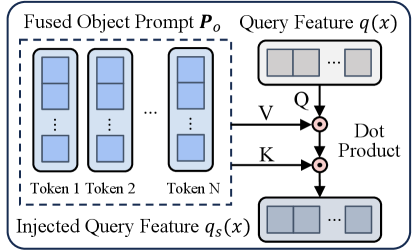
Akin to the query-key matching mechanism in other work L2P ; Dual ; s-prompt , we utilize a fixed feature extractor $f(\cdot)$ to obtain a query feature $q(x)=f(x)[0,:]$, determining which prompts in the pool to be selected. However, pre-trained backbones are typically trained for object classification, thus under-performing for state representation learning. In addition, it is more difficult to predict the state classes due to their more abstract and fine-grained characteristics. To tackle this problem, we strategically inject object prompts to guide the selection of state prompts. Intuitively, once we have learned knowledge about the object class, it may be easier to predict the correct state class and avoid mistaken results. For instance, given an object is “heels”, we can expect that the corresponding state is unlikely to be “canvas” or “plastic”. To summarize, we select object and composition prompts in each pool based on the original query feature, which means $q_{o}(x)=q_{c}(x)=q(x)$; but for the selection of state prompts, we propose object-injected state prompting to ameliorate the query feature as shown in Fig. 5.

Specifically, we employ the fused object prompt $\boldsymbol{P}_{o}$ (see Sec. 4.3) to perform cross attention on the query feature $q(x)$, resulting in object-injected query feature $q_{s}(x)$ for the state prompt selection:

$$q_{s}(x)=\text{CrossAttn}(q(x),\boldsymbol{P}_{o})=\text{Softmax}(\frac{q(x)W^{Q}\cdot\boldsymbol{P}_{o}W^{K}}{\sqrt{D}})\cdot\boldsymbol{P}_{o}W^{V},$$

(4)

where $W^{Q}$, $W^{K}$ and $W^{V}$ are learnable projections. To establish alignment between the query and the selected prompts, we optimize a surrogate loss for state, object and composition prompting jointly:

$$\mathcal{L}_{sur}=\sum_{\omega}\sum_{q_{\omega}}\text{COS}(f_{\omega}(x),K_{\omega}^{s_{i}}),\ \omega\in\left\{s,o,c\right\},$$

(5)

where $\text{COS}(\cdot,\cdot)$ denotes cosine similarity, $\mathbf{K}_{\omega}$ represents the subset of top-k keys selected from $\mathbb{K}_{\omega}$, and ${\left\{s_{i}\right\}_{i=1}^{k}}$ is a subset of top-k indices from $[1,M]$ (prompt number). Despite the simplicity of the object-injected state prompting, it facilitates more judicious prompt selection within the state prompt pool, alleviating the hurdles posed by state learning.

After obtaining the selected top-k prompts ${\left\{P_{\omega}^{s_{i}}\right\}_{i=1}^{k}}$, the next step is fusing these prompts into a single prompt. It is general to utilize a simple mean pooling whereas it overlooks the relative importance of each prompt. Besides, when the prompts contain information that is unrelated or contradictory to current task, it is critical to strengthen useful prompts and eliminate irrelevant ones. To this end, we draw inspiration from generalized-mean pooling GeM and exploit generalized-mean (GeM) prompt fusion which is given by:

$$\boldsymbol{P}_{\omega}=\text{GeM}_{\omega}(P_{\omega}^{s_{1}},P_{\omega}^{s_{2}},\cdots,P_{\omega}^{s_{k}})=\left(\frac{1}{k}\sum_{i=1}^{k}{P_{\omega}^{s_{i}}}^{\eta}\right)^{\frac{1}{\eta}},\omega\in\left\{s,o,c\right\},$$

(6)

where $\eta$ is a learnable parameter. When $\eta=1$, GeM becomes mean pooling; as $\eta$ approaches infinity ($\eta\to\infty$), it converges to max pooling. By taking over mean and max pooling, GeM learns to achieve an optimal fusion, mitigating the influence of irrelevant information present in the prompts.

Classification Objective. We prepend three fused prompts (i.e. $\boldsymbol{P}_{s}$, $\boldsymbol{P}_{o}$ and $\boldsymbol{P}_{c}$) with $x_{e}$, which is the output from a ViT embedding layer $f_{e}(\cdot)$. The extended token sequence is $x_{p}=\left[\boldsymbol{P}_{c};\boldsymbol{P}_{s};\boldsymbol{P}_{o};x_{e}\right]$. Then, we feed $x_{p}$ to a transformer encoder layer $f_{r}(\cdot)$ and achieve $\boldsymbol{P}_{s}^{r}$, $\boldsymbol{P}_{o}^{r}$ and $\boldsymbol{P}_{c}^{r}$ for classifying state, object and composition classes, respectively. We estimate the probability via a classifier $\varphi_{\omega}(\cdot)$: $p(\omega\mid x)=\varphi_{\omega}(\boldsymbol{P}_{\omega}^{r})$. For each image $x$, we denote its ground-truth distribution over labels with $q(\omega\mid x)$. When $\omega$ is consistent with the ground truth, then $q(\omega\mid x)=1$; otherwise, $q(\omega\mid x)=0$. As a result, the cross entropy (CE) loss used for classification objective is:

$$\mathcal{L}_{CE}^{\omega}=-\sum_{\omega=1}^{\Omega}q(\omega\mid x)\log{p(\omega\mid x)},\Omega\in\left[\left|\mathcal{S}\right|,\left|\mathcal{O}\right|,\left|\mathcal{C}\right|\right],$$

(7)

where $\Omega$ represents the number of classes. However, the model optimized with a standard CE loss is easily affected by noisy samples during training. Instead, we advocate using a symmetric cross entropy loss (SCE) SCE , which incorporates an additional term called reverse cross entropy (RCE), to mitigate the impact of noisy data. Contrary to CE, the formula for RCE loss is defined as:

$$\mathcal{L}_{RCE}^{\omega}=-\sum_{\omega=1}^{\Omega}p(\omega\mid x)\log{q(\omega\mid x)},\omega\in\left\{s,o,c\right\}.$$

(8)

Then, the SCE loss combines two loss terms by $\mathcal{L}_{SCE}^{\omega}=\mathcal{L}_{CE}^{\omega}+\alpha\mathcal{L}_{RCE}^{\omega}$, where $\alpha$ is a hyper-parameter that controls the weight of the RCE term. As a result, the whole SCE loss becomes $\mathcal{L}_{SCE}=\mathcal{L}_{SCE}^{c}+\beta(\mathcal{L}_{SCE}^{s}+\mathcal{L}_{SCE}^{o})$, where $\beta$ adjusts the weights between primitives and compositions.

Total Loss. The total loss for training the whole CompILer model is:

$$\mathcal{L}_{total}=\lambda_{1}\mathcal{L}_{inter}+\lambda_{2}\mathcal{L}_{intra}+\lambda_{3}\mathcal{L}_{sur}+\mathcal{L}_{SCE},$$

(9)

where $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$ are hyper-parameters balancing different terms.

Inference. During inference, we incorporate the primitive probabilities to aid the composition probability. Hence, the final probability for composition classification is expressed with:

$$p_{\text{final}}(c\mid x)=p(c\mid x)+\mu(p(s\mid x)+p(o\mid x)),$$

(10)

where $\mu$ adjusts the probabilities.

We conduct experiments on two newly split datasets: Split-Clothing and Split-UT-Zappos as elucidated in Section 3.2. We assess the overall performance on compositions using Average Accuracy (Avg Acc) and Forgetting (FTT). A higher Avg Acc signifies stronger recognition abilities, while a lower FTT indicates improved resilience against forgetting. Additionally, we provide individual Average Accuracy scores on states and objects, denoted as State and Object for simplicity. These metrics imply the ability to recognize fine-grained primitives. Furthermore, we calculate the Harmonic Mean (HM) between State and Object, i.e. $HM=2\times\frac{(State\times Object)}{(State+Object)}$. We provide more emphasis to Avg Acc and HM due to their more comprehensive assessment. Avg Acc encompasses the plasticity and stability CODA ; Consistent_Prompting and HM provides a holistic evaluation on both state and object.

For a fair comparison with previous works L2P ; Dual ; Consistent_Prompting ; CODA , we also employ ViT B/16 ViT_B16 pretrained on the ImageNet 1K dataset as the feature extractor and backbone. For multi-pool prompt learning, the size of each pool is set to $20$, and each prompt has $5$ tokens. We select top-5 prompts from each pool and generate a fused prompt. During training, we utilize the Adam optimizer adam with a batch size of $16$. The whole CompILer undergoes training for $25$ epochs on the Split-Clothing, for $10$ epochs on the 5-task Split-UT-Zappos, and for $3$ epochs on the 10-task Split-UT-Zappos. For the Split-Clothing and the 10-task Split-UT-Zappos, we set the learning rate to $0.03$, while we use a learning rate of $0.02$ for the 5-task Split-UT-Zappos. Note that, for all the methods, their results are averaged over three runs with the corresponding standard deviations reported to mitigate the influence of random factors.

As there are a few hyper-parameters in the model, we conduct a rigorous tuning on them. For instance, we set $\theta_{\text{thre}}$ to $\frac{\pi}{2}$ for all settings. For Split-Clothing, the loss weights $\lambda_{1}$ and $\lambda_{3}$ are set to $0.1$; $\lambda_{2}$ is set to $10^{-7}$; $\alpha$ and $\beta$ for SCE loss are $0.006$ and $0.3$, and the parameter $\mu$ during inference is $0.5$. For 5-task Split-UT-Zappos, $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$, $\alpha$, $\beta$ and $\mu$ are set to $1.0$, $3\times 10^{-6}$, $0.7$, $0.01$, $0.7$ and $0.02$, respectively. For 10-task Split-UT-Zappos, $\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$, $\alpha$, $\beta$ and $\mu$ are set to $0.5$, $10^{-7}$, $0.1$, $0.05$, $0.4$ and $0.03$. We elaborate more details on hyper-parameter analysis in the appendix.

To demonstrate the effectiveness of the proposed method, we compare CompILer with state-of-the-art incremental learning methods, including prompt-free approaches EWC ; LwF ; icarl and prompt-based methods L2P ; Dual ; CODA ; Language_ICCV . All the methods are rehearsal-free except iCaRL icarl . Note that, due to LGCL Language_ICCV relying on CLIP CLIP to achieve language guidance at the task level, it is limited by the length of class names per task. Thereby, LGCL fails to operate on the 5-task Split-UT-Zappos since the total length of class names exceeds the limitation.

To streamline our CompILer, we further implement a simplified version named Sim-CompILer and report its results. Sim-CompILer is optimized using cross entropy loss and is comprised solely of multi-pool prompt learning and generalized-mean prompt fusion. In other words, we exclude the object-injected prompting, directional decoupled loss, and reverse cross entropy loss, resulting in a large reduction of hyperparameters to only $\beta$, $\lambda_{3}$, and $\mu$.

The compared results on Avg Acc and FTT are reported in Table 1. Overall, CompILer consistently outperforms all competitors on Avg Acc by a significant margin. For FTT scores, CompILer excels previous methods with 0.32% on the 5-task Split-Clothing and with 0.14% on the 5-task Split-UT-Zappos, while falling behind Dual-Prompt Dual and LGCL Language_ICCV for the 10-task Split-UT-Zappos. We notice that, the main reason is these methods sacrifice more plasticity for lower forgetting rates. Besides, the number of model parameters in these methods dynamically increases along with more incremental tasks arriving, whereas our CompILer does not rely on imposing task-specific parameters to reduce the forgetting.

We also report the primitives accuracy and their HM in Table 2 and Table 3. Likewise, our method surpasses other methods considerably in terms of State and HM. Interestingly, the prompt-free methods LwF ; EWC ; icarl achieve higher accuracy in state prediction than object prediction for Split-Clothing, which is contrary to other results. This is because the states in Split-Clothing are color-related descriptions, which are easier to capture with the help of parameter fine-tuning. The prompt-based methods do not exhibit this phenomenon because their pre-trained backbones are initially trained for object classification, and are frozen across incremental sessions. As the performance improvements are mainly attributed to the accuracy of state recognition, it suggests that our model enhances the understanding on fine-grained compositionality.

Effect of multi-pool prompt learning. This experiment aims to delineate the contribution of three pools in CompILer. We firstly implement a baseline model with composition prompt pool only. Building upon the baseline, we develop two additional models, which incorporate either object or state prompt pool. As reported in Table 4, the inclusion of primitive prompt pool yields consistent gains over the baseline. Furthermore, the best results are achieved when the model integrates all three pools simultaneously. This experiment signifies the significant necessity of exploiting multiple prompt pools for composition-IL.

Effect of object-injected state prompting. To provide insights into object-injected state prompting, we compare three models: None (vanilla model), S$\rightarrow$O (state-injected object prompting) and O$\rightarrow$S (object-injected state prompting). As shown in Table 5, compared to the None model, the S$\rightarrow$O exhibits a decrease in all metrics, implying that state prompts may interfere with the selection of object prompts. On the contrary, O$\rightarrow$S outperforms the None model as we expect. This phenomenon validates our motivation that state recognition is harder than object recognition, and thereby the former cannot help the latter easily. Yet, it is a promising direction for future research.

Effect of generalized-mean prompt fusion. This study aims to study the impact of prompt fusion on CompILer. As shown in Table 5, GeM performs better than both max and mean pooling across various metrics. It validates the benefit of GeM on mitigating irrelevant information in the selected prompts. as it may hamper the model’s attention on image tokens.

Effect of loss functions. As shown in Table 6, we investigate the influence of loss functions used in our model, including directional decoupled loss ($\mathcal{L}_{inter}$ and $\mathcal{L}_{intra}$) and symmetric cross entropy loss ($\mathcal{L}_{CE}$ and $\mathcal{L}_{RCE}$). The baseline model (the first row) includes all modules but is trained by cross entropy loss only. By adding the RCE loss, the model is equivalent to training with the SCE loss, which help to improve the robustness to noisy labels. The use of either $\mathcal{L}_{inter}$ or $\mathcal{L}_{intra}$ improves the performance on both datasets, and synchronously applying them witnesses all-around improvements compared to the baseline. Eventually, we achieve the best results when combing all the loss terms during training.

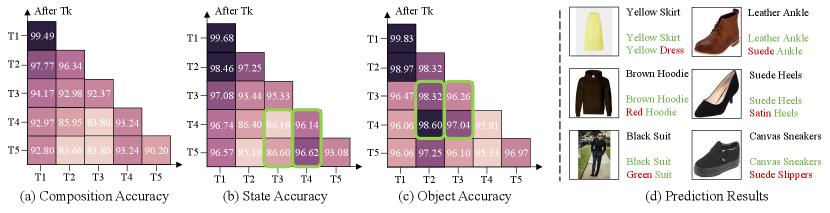
In order to study the repeatability characteristic in composition-IL, we exhibit more results on Split-Clothing in Fig. 6: in (a), it shows a decreasing trend in composition accuracy along with the introduction of new tasks; however, the green rectangles in (b) and (c) showcase that the accuracy occasionally increases as more tasks are learned. We conjecture the reason is mostly attributed to the re-occurrence of primitive concepts. This forward transfer is critical for incremental learners. We compare the composition predictions between CompILer and L2P L2P in Fig. 6 (d). CompILer predicts all the images correctly, while L2P makes some mistakes, particularly for state labels. This limitation arises from an excessive focus on the dominant object primitive, while weakening the attention toward state primitive. Fortunately, CompILer relieves the bias toward object classes, and enhances the perception on state classes.