Not All Heads Matter: A Head-Level KV Cache Compression Method with Integrated Retrieval and Reasoning
Abstract
Key-Value (KV) caching is a common technique to enhance the computational efficiency of Large Language Models (LLMs), but its memory overhead grows rapidly with input length. Prior work has shown that not all tokens are equally important for text generation, proposing layer-level KV cache compression to selectively retain key information. Recognizing the distinct roles of attention heads in generation, we propose HeadKV, a head-level KV cache compression method, and HeadKV-R2, which leverages a novel contextual reasoning ability estimation for compression. Our approach operates at the level of individual heads, estimating their importance for contextual QA tasks that require both retrieval and reasoning capabilities. Extensive experiments across diverse benchmarks (LongBench, LooGLE), model architectures (e.g., Llama-3-8B-Instruct, Mistral-7B-Instruct), and long-context abilities tests demonstrate that our head-level KV cache compression significantly outperforms strong baselines, particularly in low-resource settings (KV size = 64 & 128). Notably, our method retains just 1.5% of the KV cache while achieving 97% of the performance of the full KV cache on the contextual question answering benchmark. 111https://github.com/FYYFU/HeadKV/
1 Introduction
Modern Large Language Models (LLMs) increasingly support extremely long inputs: GPT-4 (Achiam et al., 2023), Llama-3 (Dubey et al., 2024), and Qwen-2 (Yang et al., 2024) handle up to 128K tokens, while Claude (Anthropic, 2024) supports up to 1 million tokens. These extended capacities improve performance on tasks like dialogue generation (Li et al., 2024a; Yi et al., 2024), question answering (Ho et al., 2020; Xu et al., 2023), and summarization (Xiao & Carenini, 2019; Koh et al., 2022). As input lengths increase, memory usage and latency grow significantly due to self-attention in transformers. To improve inference speed and efficiency, most LLM inference consists of two phases: prefilling for input processing and decoding for token generation, with key and value states from attention cached for reuse (KV cache). However, as input length increases, KV cache memory grows rapidly, posing significant challenges for storage and efficiency.
To address this, KV cache compression methods (Xiao et al., 2024; Li et al., 2024d; Cai et al., 2024; Feng et al., 2024) have been proposed, typically using token eviction to optimize retention per layer or head during prefilling, reducing memory without impacting performance. However, none have explored varying KV cache size across individual heads. Inspired by prior observations (Voita et al., 2019; Wu et al., 2024; Zheng et al., 2024) that attention heads vary in importance for generation, we propose HeadKV, a head-level KV cache compression method that allocates KV cache budgets based on head importance distribution using a novel retrieval and reasoning importance estimation. Specifically, heads deemed more important are allocated larger KV cache budgets, while less important ones receive smaller allocations, optimizing memory usage without sacrificing performance.

In addition to allocating KV cache across attention heads rather than layers, a key aspect of our approach is distributing cache budgets based on head importance measures. Prior work (Wu et al., 2024) proposed method to identify retrieval heads, using importance estimation to assess each head’s role in retrieving relevant context. We integrate their measure with our head-level KV cache compression as a baseline, observing improved performance over layer-level cache compression.
However, we argue that allocating larger KV cache budgets solely to retrieval heads is insufficient for tasks like contextual Question Answering (QA), which requires both retrieval and reasoning to handle long input contexts effectively. To address this, we propose an importance-score estimation method that jointly evaluates each head’s retrieval and reasoning capabilities for KV cache allocation. Specifically, as illustrated in the Importance Score Estimation section of Figure 1, we construct questions that require both the retrieval and reasoning abilities of the LLM. For instance, in the provided example, the model must first identify “who is younger between John and Mary” (John) by referencing the context of their ages, and then retrieve John’s favorite thing. We then estimate the importance score of each head based on the attention scores generated by the model while answering the question. Using the estimated importance scores, we allocate the KV cache budget for each individual head, meaning that heads demonstrating greater importance in retrieval and reasoning retain a larger portion of the KV cache, as shown in the Head-Level Allocation section of Figure 1. Within each head, we then retain only the most relevant KV cache entries, following the strategy proposed in Li et al. (2024d).
We conduct experiments on various benchmarks requiring both retrieval and reasoning abilities, including QA tasks from LongBench (Bai et al., 2024) and LooGLE (Li et al., 2024b), using backbone models such as Llama-3-8B-Instruct (Dubey et al., 2024) and Mistral-7B-Instruct (Jiang et al., 2023). Our results demonstrate that the head-level KV cache compression method outperforms previous approaches on nearly all tasks. Furthermore, the allocation strategy based on our estimated importance scores—reflecting both retrieval and reasoning abilities—outperforms allocation strategies based on retrieval ability alone. In challenging scenarios like needle-in-a-Haystack and reasoning-in-a-Haystack tests, our methods effectively preserve the model’s retrieval and reasoning capabilities. Finally, experiments on memory and latency reveal that our approach significantly reduces memory usage and decoding latency, comparing with the original full KV.
2 Related Work
2.1 Attention Heads
Multi-Head Attention, a fundamental component of Transformer architectures (Vaswani et al., 2017), has been extensively analyzed to understand the roles of individual attention heads (Voita et al., 2019; Olsson et al., 2022; Jin et al., 2024; Wu et al., 2024; Zheng et al., 2024), often with goals such as pruning redundant heads(Shim et al., 2021; Kwon et al., 2022) or enhancing interpretability(Olsson et al., 2022; Jin et al., 2024; Zheng et al., 2024). For example, Voita et al. (2019) observed that only a small subset of heads plays a key role in machine translation, typically managing positional information, syntactic parsing, or focusing on rare words. Similarly, Olsson et al. (2022) identified ’induction heads’ that implement a copy-and-paste mechanism, enabling models to replicate previously encountered sequences. Additionally, Zheng et al. (2024) provided a thorough overview of recent efforts to characterize the diverse functions of attention heads, categorizing them into four types: Knowledge Recalling, In-Context Identification, Latent Reasoning, and Expression Preparation. A closely related study by Wu et al. (2024) discovered “retrieval heads” that play a crucial role in knowledge acquisition, using Needle-in-a-Haystack tests. These insights into head-level functionality serve as the foundation for our head-level KV cache compression methods, designed to jointly preserve both retrieval and reasoning capabilities during the compression process.
2.2 KV cache compression
Improving computational efficiency for LLMs, particularly for extremely long inputs, has attracted considerable research interest (Shazeer, 2019; Chen et al., 2023; Dao, 2024; Zhou et al., 2024; Ye et al., 2024), including caching key and value vectors in Multi-Head Attention to improve generation efficiency (Xiao et al., 2024; Zhang et al., 2023; Li et al., 2024d; Cai et al., 2024). One challenge with full KV cache approaches is that the memory usage increases linearly with input length, leading to significant memory management challenges. Various KV cache compression techniques have been proposed to reduce memory usage and improve inference efficiency. For example, Xiao et al. (2024) addressed the ‘attention sink’ issue with StreamingLLM, retaining only the first tokens’ KV cache. Zhang et al. (2023) applied the Heavy Hitter Oracle strategy to select key cache entries, while Li et al. (2024d) used the attention scores of the last tokens to identify relevant entries. Cai et al. (2024) introduced PyramidKV, assigning smaller cache budgets to higher layers based on attention matrix patterns.
While these methods have improved performance and efficiency, they largely depend on rigid layer-level allocation strategies, which may not fully optimize KV cache allocation for downstream tasks. Feng et al. (2024) proposed dynamic head-level allocation using attention scores but still relied on layer-level budgeting. Similarly, Tang et al. (2024) employed Retrieval Heads distribution for head-level allocation but retained a Full KV cache for key heads, limiting true head-level compression. In contrast, our approach allocates KV cache solely based on head-level importance scores, independent of layer constraints, resulting in more effective compression and outperforming baselines without increasing decoding latency or memory usage.
3 Method
This section presents our proposed head-level KV cache compression method, which consists of three key components: (1) identifying important heads and calculating head-level importance score distributions (3.1), (2) using these distributions to efficiently allocate KV cache budgets across heads (3.2), and (3) determining which Key and Value vectors to retain within each head (3.3).
3.1 Head-level Importance Score Estimation
Accurate budget allocation at the head level requires identifying which heads are most and least important for the given task. By leveraging this importance distribution, we can assign larger KV cache budgets to more critical heads and smaller budgets to less significant ones. To achieve this, we propose a novel importance-score estimation method, inspired by Wu et al. (2024), which allows us to effectively estimate the importance of each attention head for optimal KV cache allocation.

Retrieval Heads
Wu et al. (2024) use the Needle-in-a-Haystack test 222https://github.com/gkamradt/LLMTest_NeedleInAHaystack and custom retrieval examples, as shown in Figure 2, to estimate the importance score for each head. In these examples, a question that cannot be answered using the model’s parametric knowledge is paired with an answer (the “Needle”) inserted into a haystack at different positions . The model is required to retrieve the exact answer from the combined input .
During each decoding step , a head earns a fraction of the importance score if (1) the token with the highest attention score matches the generated token, and (2) the token is part of the inserted answer . The final importance score for each head is calculated accordingly:
| (1) |
where is the length of the inserted answer , and is the attention score on the combined input from head . By using various settings of the inserted position , they obtain the head-level Retrieval Heads distribution.
Directly using this distribution poses two issues: (1) it focuses on the retrieval-and-paste mechanism, lacking consideration for the contextual and reasoning skills needed for complex questions; and (2) the distribution is too sparse for effective head-level KV cache allocation, with nearly 70% of heads receiving an importance score of zero due to the strict exact-match requirement (Wu et al., 2024).
Retrieval-Reasoning (R2) Heads
To address these issues, we propose a new importance score estimation method that accounts for both the retrieval and reasoning abilities of the heads, enabling a more accurate assessment of their significance.
First, we construct retrieval-reasoning examples by adding explicit contextual reasoning steps to the retrieval examples from Wu et al. (2024), as shown in the Retrieval-Reasoning Example part of Figure 2. We further modify the inserted needle into three parts: , where is the reasoning step, and and are different answers to the refined question . The model must reason with to retrieve and generate the correct answer , avoiding the wrong answer .
Secondly, we refine the estimation method by focusing on the entire correct answer (Correct Copy in Figure 1), since all tokens are relevant to the question . This approach aligns with Contextual QA, which requires both retrieval and reasoning abilities. By considering the full correct answer, the importance score for each head no longer depends solely on the token with the highest attention score. The importance score for head is calculated as follows:
| (2) |
where represents the -th highest attention score from head , and is the token with the -th highest score. We compute the importance score by considering the entire correct answer and increasing the number of tokens evaluated per head (Importance Score Estimation in Figure 1). Intuitively, heads with higher attention on the correct answer should receive higher importance scores. We further refine the score using attention weights, yielding a more accurate distribution, as shown in Eq. 2.
3.2 Head-Level KV Cache Allocation
With the importance scores estimated for each head, we can identify the key heads and allocate the KV cache budget accordingly. In this section, we explain how to incorporate these distributions into head-level KV cache allocation.
Preliminary
In Multi-Head Attention, for each head in layer , the embedded input is mapped into different subspaces using the query , key , and value matrices:
| (3) |
To optimize memory and enhance efficiency, KV cache compression methods (Xiao et al., 2024; Li et al., 2024d; Cai et al., 2024) are employed to discard unimportant KV cache entries while preserving performance. For each head , the compressed KV cache is reduced to and , where , resulting in a significant improvement to computational efficiency.
Head-level Allocation
Previous works on KV cache compression during the prefill phase (Xiao et al., 2024; Li et al., 2024d; Cai et al., 2024; Feng et al., 2024) are limited to layer-level allocation, using either uniform or dynamic budgets per layer, but treating all heads within a layer equally. While Feng et al. (2024) incorporate head-level information, their approach still depends on layer-level allocation as a prerequisite.
Building on the head-level importance distributions, we propose a comprehensive KV cache allocation strategy. Each head is initially assigned a fixed KV cache size with an associated importance score . To allow dynamic allocation, we create a shared budget pool by extracting a portion of the budget from each head, leaving the remainder as the basic budget. This process is illustrated in the Head-Level Allocation section of Figure 1. The budget pool is then distributed among the heads in proportion to their importance scores . The final head-level KV cache allocation is as follows:
| (4) |
where is the initial fix budget for each head, is a hyper-parameter to control the size of the dynamic budget pool, and is the numbers of layers and heads of current LLM respectively.
The last instruct tokens are preserved before forming the dynamic budget pool to guide the selection process, as detailed in Section 3.3. The retained KV cache for each head includes: (1) the basic budget (), (2) the dynamic budget , proportional to its importance score, and (3) the last instruct tokens.
3.3 KV Cache Selection
After determining the number of KV cache entries to retain using the above algorithm, we apply an attention-based selection strategy from prior works (Li et al., 2024d; Cai et al., 2024; Feng et al., 2024) to keep the most relevant entries. Specifically, the last instruction tokens (local windows) guide KV cache selection for each head. Attention scores from these local windows to the remaining tokens are aggregated through a pooling layer, with higher-scoring tokens considered more important and retained in the cache.
4 Experiments And Analysis
This section outlines the experimental setup, including KV cache baselines and implementation details. We also conduct additional experiments that: (1) emphasize the importance of enhancing contextual reasoning in importance score estimation (4.3); (2) use the Needle-in-a-Haystack and Reasoning-in-a-Haystack tests to demonstrate how our head-level KV cache compression improves long-context retrieval and reasoning (4.4); and (3) provide a comprehensive comparison with previous methods, showing our approach delivers superior performance while maintaining computational efficiency (4.5).
4.1 Experiment settings
Models and Datasets
We compare our head-level KV cache compression method against strong baselines using two open-source LLMs: Llama-3-8B-Instruct (Dubey et al., 2024) and Mistral-7B-Instruct (Jiang et al., 2023). The evaluation is based on two benchmarks for long-context understanding: LongBench (Bai et al., 2024) and LooGLE (Li et al., 2024b). For LongBench, we use datasets from the Single-Doc QA and Multi-Doc QA categories to assess contextual reasoning. For LooGLE, we focus on the Long Dependency QA task, which includes four QA-related tasks. Dataset details are in Appendix Table 5.
Baselines and Settings
We evaluate three strong KV cache compression methods as baselines, ensuring all retain the same number of KV cache entries for fair comparison:
-
1)
SnapKV (Li et al., 2024d) uses the last tokens as local windows to guide KV cache selection. Attention scores from these windows to the remaining tokens are pooled to cluster information and guide the selection process.
-
2)
PyramidKV (Cai et al., 2024) follows a pyramid attention pattern, allocating more KV cache to lower layers to retain key information, while reducing the budget for higher layers where information is already aggregated.
-
3)
Ada-KV (Feng et al., 2024) dynamically allocates budgets to heads within each layer based on their concentration degrees, and can be combined with SnapKV or PyramidKV. Ada-SnapKV is used as the baseline due to its superior performance over Ada-PyramidKV.
Our proposed head-level KV cache compression method also requires a strategy to guide KV cache selection after allocating the budget. Therefore, we use the SnapKV method to guide the selection process for each head. We set the size of the local windows for both the baselines and our method. The hyper-parameter , which controls the size of the shared budget pool, was chosen from {1.005, 1.01, 1.1, 1.2, 1.5, 2, 5, 10}, and we report the best performance.
4.2 Main Results
| Method | Single-Doc QA | Multi-Doc QA | Avg. | Long dependency QA | Avg. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NartvQA | Qasper | MF-en | HotpotQA | 2WikiMQA | Musique | Doc.QA | Info. Retrieval | Timeline | Computation | |||
| Llama-3-8B-Instruct, KV Size = Full | ||||||||||||
| FullKV | 25.56 | 32.07 | 39.71 | 43.57 | 35.28 | 21.18 | 32.90 | 8.73 | 11.21 | 0.67 | 7.43 | 7.01 |
| Llama-3-8B-Instruct, KV Size = 128 | ||||||||||||
| SnapKV | 22.11 | 15.79 | 31.01 | 41.12 | 29.20 | 19.35 | 26.43 | 8.36 | 9.46 | 0.79 | 6.56 | 6.29 |
| PyramidKV | 22.01 | 17.05 | 31.52 | 39.27 | 28.99 | 18.34 | 26.20 | 8.89 | 9.63 | 0.61 | 6.72 | 6.46 |
| Ada-SnapKV | 22.99 | 19.95 | 34.22 | 42.97 | 30.82 | 20.15 | 28.52 | 9.07 | 10.3 | 0.54 | 6.59 | 6.63 |
| HeadKV-R | 23.49 | 25.39 | 38.15 | 42.45 | 32.84 | 19.95 | 30.38 | 8.87 | 10.35 | 0.78 | 7.52 | 6.88 |
| HeadKV-R2 | 21.80 | 29.19 | 41.89 | 43.73 | 35.01 | 20.40 | 32.00 | 9.60 | 11.13 | 0.67 | 7.22 | 7.16 |
| Llama-3-8B-Instruct, KV Size = 1024 | ||||||||||||
| SnapKV | 25.76 | 27.50 | 38.38 | 43.40 | 34.81 | 20.07 | 31.65 | 9.61 | 11.34 | 0.53 | 7.22 | 7.18 |
| PyramidKV | 25.38 | 26.83 | 36.90 | 44.09 | 34.24 | 21.49 | 31.49 | 8.98 | 11.41 | 0.53 | 6.96 | 6.97 |
| Ada-SnapKV | 25.79 | 29.24 | 38.74 | 43.93 | 36.34 | 19.79 | 32.31 | 8.65 | 11.41 | 0.53 | 7.71 | 7.08 |
| HeadKV-R | 24.85 | 30.94 | 39.82 | 43.52 | 36.58 | 20.37 | 32.68 | 9.20 | 11.67 | 0.55 | 7.71 | 7.28 |
| HeadKV-R2 | 24.66 | 30.82 | 39.56 | 43.97 | 36.47 | 22.24 | 32.95 | 9.02 | 11.51 | 0.47 | 7.85 | 7.21 |
| Mistral-7B-Instruct, KV Size = Full | ||||||||||||
| FullKV | 26.63 | 32.99 | 49.34 | 42.77 | 27.35 | 18.78 | 32.98 | 12.17 | 15.52 | 0.49 | 10.03 | 9.55 |
| Mistral-7B-Instruct, KV Size = 128 | ||||||||||||
| SnapKV | 21.47 | 21.95 | 45.24 | 33.88 | 21.83 | 15.53 | 26.65 | 10.86 | 12.24 | 0.57 | 8.81 | 8.12 |
| PyramidKV | 21.76 | 21.98 | 43.72 | 32.76 | 22.73 | 15.59 | 26.42 | 10.64 | 11.9 | 0.47 | 8.69 | 7.93 |
| Ada-SnapKV | 21.57 | 24.59 | 46.70 | 35.74 | 25.57 | 14.37 | 28.09 | 11.14 | 12.37 | 0.45 | 9.57 | 8.38 |
| HeadKV-R | 23.97 | 29.60 | 48.40 | 39.66 | 26.31 | 18.13 | 31.01 | 11.43 | 13.04 | 0.53 | 10.26 | 8.82 |
| HeadKV-R2 | 25.04 | 27.95 | 48.48 | 41.28 | 27.65 | 18.05 | 31.41 | 11.44 | 13.08 | 0.63 | 10.20 | 8.84 |
| Mistral-7B-Instruct, KV Size = 1024 | ||||||||||||
| SnapKV | 25.38 | 30.22 | 49.29 | 41.84 | 26.60 | 18.08 | 31.90 | 11.69 | 13.89 | 0.52 | 10.54 | 9.16 |
| PyramidKV | 24.28 | 30.05 | 49.17 | 40.49 | 26.43 | 18.80 | 31.54 | 11.77 | 14.51 | 0.51 | 10.19 | 9.25 |
| Ada-SnapKV | 24.82 | 31.49 | 48.80 | 41.18 | 27.38 | 18.22 | 31.98 | 11.96 | 13.82 | 0.53 | 9.92 | 9.06 |
| HeadKV-R | 25.87 | 31.44 | 49.55 | 41.95 | 27.09 | 19.88 | 32.63 | 12.21 | 14.17 | 0.50 | 10.58 | 9.37 |
| HeadKV-R2 | 25.64 | 32.54 | 50.49 | 41.80 | 27.88 | 18.89 | 32.87 | 11.94 | 14.93 | 0.50 | 10.49 | 9.47 |
Table 1 lists the evaluation results for contextual tasks from the LongBench and LooGLE benchmarks. Our head-level KV cache compression method consistently outperforms strong baselines, especially with 64 and 128 KV cache configurations. In resource-constrained settings, precise KV cache allocation is crucial. Layer-level methods allocate a fixed cache size to all heads within a layer, making it difficult to retain essential information. Ada-SnapKV improves this by allowing dynamic allocation within layers, but still relies on fixed layer-level budgets. In contrast, our head-level strategy allocates dynamically across individual heads, retaining critical information by adjusting the budget based on each head’s importance.
We perform head-level allocation using both the standard Retrieval Heads distribution (HeadKV-R) and our Retrieval-Reasoning Heads distribution (HeadKV-R2) for global KV cache allocation. This combination leads to superior performance across benchmarks. Notably, integrating the Retrieval-Reasoning Heads distribution significantly improves results over the standard Retrieval Heads distribution, highlighting the impact of our approach. Our Retrieval-Reasoning distribution even surpasses the Full-KV cache average (32.90), achieving 32.95 with a 1024 KV cache. Overall, both the head-level allocation strategy and Retrieval-Reasoning distribution are key to these performance gains.
In addition, we present the results for various retained KV cache sizes (64, 128, 256, 512, 1024) in Figure 3, , with detailed results available in Appendix Table 4.

4.3 Retrieval-Reasoning Heads
As detailed in Section 3.1, we propose to improve the standard Retrieval Heads distribution by incorporating retrieval-reasoning examples and refining importance score estimation to better capture contextual reasoning and identify relevant heads. We also conduct an ablation study to evaluate the impact of these modifications.

| Method | Single-Doc QA | Multi-Doc QA | Avg. | ||||
|---|---|---|---|---|---|---|---|
| NartvQA | Qasper | MF-en | HotpotQA | 2WikiMQA | Musique | ||
| Llama-3-8B-Instruct, KV Size=128 | |||||||
| HeadKV-R | 23.49 | 25.39 | 38.15 | 42.45 | 32.84 | 19.95 | 30.38 |
| HeadKV-ER | 23.33 | 25.86 | 40.28 | 43.25 | 33.23 | 20.28 | 31.04 |
| HeadKV-R2 | 21.80 | 29.19 | 41.89 | 43.73 | 35.01 | 20.40 | 32.00 |
| Mistral-7B-Instruct, KV Size=128 | |||||||
| HeadKV-R | 23.97 | 29.60 | 48.40 | 39.66 | 26.31 | 18.13 | 31.01 |
| HeadKV-ER | 23.23 | 28.70 | 48.10 | 41.39 | 27.31 | 17.39 | 31.02 |
| HeadKV-R2 | 25.04 | 27.95 | 48.48 | 41.28 | 27.65 | 18.05 | 31.41 |
Table 2 presents the ablation study results, while Figure 4 provides visualizations for each distribution. Alongside the standard Retrieval Heads and Retrieval-Reasoning Heads distributions, we introduce the Enhanced-Retrieval Heads distribution, using retrieval examples with our modified importance score estimation method. Comparing Retrieval Heads (HeadKV-R) and Enhanced-Retrieval Heads (HeadKV-ER) reveals that focusing on the entire needle, rather than specific tokens, improves performance. Figure 4 shows that the Retrieval Heads distribution is sparse, while the Enhanced-Retrieval and Retrieval-Reasoning distributions are much denser. The strict constraints on the Retrieval Heads distribution result in most heads receiving a score of zero, leading to a worse results when incorporating Retrieval Heads distributions.
While the Enhanced-Retrieval Heads distribution improves performance slightly, it remains rely on retrieval examples and lacks full consideration of contextual reasoning. In contrast, the Retrieval-Reasoning Heads distribution, reflecting both retrieval and reasoning abilities, consistently outperforms other methods, underscoring the value of incorporating retrieval-reasoning examples.
4.4 Long-Context Retrieval and Reasoning

We conduct the Needle-in-a-Haystack test to assess the long-context retrieval ability of different KV cache compression methods. As illustrated in Figure 5, we set the KV size to 128 for all methods and keep the other hyperparameters consistent with previous experiments. Results from the Llama-3-8B-Instruct demonstrate that our head-level KV cache compression method effectively retain important information compared with other strong baselines, verifying the superior long-context retrieval ability of our proposed method. However, these tests only retrieve the inserted needle from the haystack and paste it into the generation, lacking an assessment of contextual reasoning ability in long-context scenarios. This long-context contextual reasoning ability is crucial for many tasks, such as question answering (QA), summarization (Kuratov et al., 2024; Li et al., 2024c). Therefore, we conduct the Reasoning-in-a-Haystack test to evaluate the long-context reasoning ability of each KV cache compression method across different scenarios.
We follow the setup from Kuratov et al. (2024) to conduct the Reasoning-in-a-Haystack test. This test enhances the bAbI benchmark (Weston et al., 2015), designed for reasoning evaluation, by using text from the PG19 dataset (Rae et al., 2020) as the haystack. Reasoning needles from bAbI are inserted into the haystack, and the model must retrieve and reason through them to generate the correct answer. We use the dataset from Kuratov et al. (2024), averaging results across QA1-QA5 tasks for evaluation. Examples of tasks are shown in Figure 9.
As shown in Table 3, our head-level KV cache compression method significantly outperforms strong baselines, demonstrating its superior long-context reasoning. By incorporating retrieval-reasoning examples, our method achieves even better accuracy, particularly with the Llama-3-8B-Instruct model. Notably, combining head-level KV cache allocation with the standard Retrieval Heads distribution also yields improved results over other baselines. This is due to two factors: first, as shown in Figure 4, there is overlap between Retrieval and Retrieval-Reasoning Heads, indicating heads may serve multiple roles. Second, since the bAbI benchmark contains the answer within the inserted needle (see Figure 9), emphasizing retrieval alone helps our method locate the needle.
| Method | 0k | 1k | 2k | 4k | 8k | Avg. | 0k | 1k | 2k | 4k | 8k | 16k | 32k | Avg. |
| FullKV | 63.00 | 59.40 | 55.80 | 56.60 | 50.40 | 57.04 | 61.40 | 55.20 | 52.40 | 40.80 | 40.40 | 35.00 | 31.80 | 45.29 |
| Llama-3-8B-Instruct, KV Size=128 | Mistral-7B-Instruct, KV Size=128 | |||||||||||||
| SnapKV | 60.80 | 57.00 | 54.80 | 52.60 | 45.60 | 54.16 | 56.60 | 50.60 | 46.60 | 34.40 | 35.40 | 33.20 | 29.00 | 40.83 |
| PyramidKV | 61.20 | 58.00 | 52.80 | 52.60 | 47.60 | 54.44 | 58.40 | 50.60 | 46.80 | 36.00 | 36.20 | 31.20 | 28.40 | 41.09 |
| Ada-SnapKV | 61.80 | 59.20 | 53.80 | 53.60 | 46.60 | 55.00 | 58.00 | 51.20 | 46.20 | 35.40 | 36.40 | 31.60 | 28.80 | 41.09 |
| HeadKV-R | 61.60 | 57.00 | 52.60 | 55.00 | 49.60 | 55.16 | 58.40 | 54.00 | 50.80 | 38.00 | 37.40 | 31.80 | 30.20 | 42.94 |
| HeadKV-R2 | 62.60 | 60.40 | 55.00 | 55.80 | 50.40 | 56.84 | 60.20 | 54.20 | 51.20 | 37.20 | 37.40 | 32.60 | 28.80 | 43.09 |
4.5 Memory & Latency
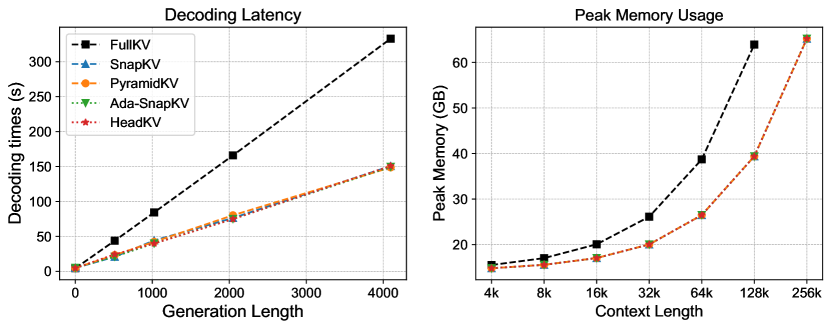
In this section, we evaluate the computational efficiency of our head-level KV cache compression method using the Mistral-7B-Instruct model with a maximum sequence length of 32K, and FlashAttention (Dao, 2024) as the default setting.
To assess the decoding latency of each method, we use 32K-length data from the Reasoning-in-a-Haystack test as input and set various generation lengths (1, 512, 1024, 2048, 4096) for comparison. As shown in the Decoding Latency of Figure 6, our proposed method achieves the same decoding latency as other KV cache compression methods while maintaining performance closest to the Full KV cache. Notably, the decoding time includes both the pre-filling time and the decoding time. Therefore, we can conclude that the pre-filling time for our method and other baselines (such as PyramidKV, Ada-SnapKV) is almost negligible, as shown at the starting point (generation length = 1) of Decoding Latency in Figure 6.
In addition to decoding latency, KV cache compression methods also aim to reduce memory usage during the decoding phase. Therefore, we provide the Peak Memory Usage results, as shown in the Peak Memory Usage of Figure 6. All results for Peak Memory Usage are averaged over three trials. Our proposed methods achieve performance comparable to other KV cache compression baselines, significantly reducing memory usage compared to the Full KV cache.
5 Conclusion and Future Work
In this paper, we introduce HeadKV-R2, a head-level KV cache compression method with two key components. We propose a strategy for allocating KV cache budgets across attention heads based on their importance scores and develop a novel approach to estimate these scores by constructing examples that account for both retrieval and reasoning abilities. By allocating larger KV cache budgets to more important heads and smaller budgets to less important ones, our approach efficiently retain important KV cache than layer-level KV cache compression methods. We thoroughly evaluate HeadKV across multiple benchmarks, models, and long-context ability tests, with comprehensive results demonstrating that our method achieves superior performance while maintaining computational efficiency.
For future work, further exploration of various types of attention heads could offer valuable insights, such as those involved in in-context learning (Olsson et al., 2022) and truthfulness (Li et al., 2023). For example, placing greater emphasis on truthfulness heads could help mitigate issues like hallucination, thereby improving the factual accuracy of model outputs. Additionally, it would be worthwhile to investigate the development of a general task-specific score estimation algorithm. One potential direction is to leverage gradients from specific tasks to allocate KV cache budgets more effectively, enabling tailored compression to enhance model performance across diverse applications.
References
- Achiam et al. (2023) Josh Achiam, Steven Adler, Sandhini Agarwal, Lama Ahmad, Ilge Akkaya, Florencia Leoni Aleman, Diogo Almeida, Janko Altenschmidt, Sam Altman, Shyamal Anadkat, et al. Gpt-4 technical report. arXiv preprint arXiv:2303.08774, 2023.
- Anthropic (2024) Anthropic. The claude 3 model family: Opus, sonnet, haiku, March 2024. URL https://www-cdn.anthropic.com/de8ba9b01c9ab7cbabf5c33b80b7bbc618857627/Model_Card_Claude_3.pdf. Accessed: 2024-07-09.
- Bai et al. (2024) Yushi Bai, Xin Lv, Jiajie Zhang, Hongchang Lyu, Jiankai Tang, Zhidian Huang, Zhengxiao Du, Xiao Liu, Aohan Zeng, Lei Hou, Yuxiao Dong, Jie Tang, and Juanzi Li. LongBench: A bilingual, multitask benchmark for long context understanding. In Lun-Wei Ku, Andre Martins, and Vivek Srikumar (eds.), Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pp. 3119–3137, Bangkok, Thailand, August 2024. Association for Computational Linguistics. doi: 10.18653/v1/2024.acl-long.172. URL https://aclanthology.org/2024.acl-long.172.
- Cai et al. (2024) Zefan Cai, Yichi Zhang, Bofei Gao, Yuliang Liu, Tianyu Liu, Keming Lu, Wayne Xiong, Yue Dong, Baobao Chang, Junjie Hu, and Wen Xiao. Pyramidkv: Dynamic kv cache compression based on pyramidal information funneling, 2024. URL https://arxiv.org/abs/2406.02069.
- Chen et al. (2023) Charlie Chen, Sebastian Borgeaud, Geoffrey Irving, Jean-Baptiste Lespiau, Laurent Sifre, and John Jumper. Accelerating large language model decoding with speculative sampling, 2023. URL https://arxiv.org/abs/2302.01318.
- Dao (2024) Tri Dao. FlashAttention-2: Faster attention with better parallelism and work partitioning. In International Conference on Learning Representations (ICLR), 2024.
- Dubey et al. (2024) Abhimanyu Dubey, Abhinav Jauhri, Abhinav Pandey, Abhishek Kadian, Ahmad Al-Dahle, Aiesha Letman, Akhil Mathur, Alan Schelten, Amy Yang, Angela Fan, et al. The llama 3 herd of models. arXiv preprint arXiv:2407.21783, 2024.
- Feng et al. (2024) Yuan Feng, Junlin Lv, Yukun Cao, Xike Xie, and S. Kevin Zhou. Ada-kv: Optimizing kv cache eviction by adaptive budget allocation for efficient llm inference, 2024. URL https://arxiv.org/abs/2407.11550.
- Ho et al. (2020) Xanh Ho, Anh-Khoa Duong Nguyen, Saku Sugawara, and Akiko Aizawa. Constructing a multi-hop QA dataset for comprehensive evaluation of reasoning steps. In Donia Scott, Nuria Bel, and Chengqing Zong (eds.), Proceedings of the 28th International Conference on Computational Linguistics, pp. 6609–6625, Barcelona, Spain (Online), December 2020. International Committee on Computational Linguistics. doi: 10.18653/v1/2020.coling-main.580. URL https://aclanthology.org/2020.coling-main.580.
- Jiang et al. (2023) Albert Q. Jiang, Alexandre Sablayrolles, Arthur Mensch, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Florian Bressand, Gianna Lengyel, Guillaume Lample, Lucile Saulnier, Lélio Renard Lavaud, Marie-Anne Lachaux, Pierre Stock, Teven Le Scao, Thibaut Lavril, Thomas Wang, Timothée Lacroix, and William El Sayed. Mistral 7b, 2023. URL https://arxiv.org/abs/2310.06825.
- Jin et al. (2024) Zhuoran Jin, Pengfei Cao, Hongbang Yuan, Yubo Chen, Jiexin Xu, Huaijun Li, Xiaojian Jiang, Kang Liu, and Jun Zhao. Cutting off the head ends the conflict: A mechanism for interpreting and mitigating knowledge conflicts in language models, 2024. URL https://arxiv.org/abs/2402.18154.
- Koh et al. (2022) Huan Yee Koh, Jiaxin Ju, Ming Liu, and Shirui Pan. An empirical survey on long document summarization: Datasets, models, and metrics. ACM Computing Surveys, 55(8):1–35, December 2022. ISSN 1557-7341. doi: 10.1145/3545176. URL http://dx.doi.org/10.1145/3545176.
- Kuratov et al. (2024) Yuri Kuratov, Aydar Bulatov, Petr Anokhin, Ivan Rodkin, Dmitry Sorokin, Artyom Sorokin, and Mikhail Burtsev. Babilong: Testing the limits of llms with long context reasoning-in-a-haystack, 2024. URL https://arxiv.org/abs/2406.10149.
- Kwon et al. (2022) Woosuk Kwon, Sehoon Kim, Michael W. Mahoney, Joseph Hassoun, Kurt Keutzer, and Amir Gholami. A fast post-training pruning framework for transformers. In Alice H. Oh, Alekh Agarwal, Danielle Belgrave, and Kyunghyun Cho (eds.), Advances in Neural Information Processing Systems, 2022. URL https://openreview.net/forum?id=0GRBKLBjJE.
- Li et al. (2024a) Jia-Nan Li, Quan Tu, Cunli Mao, Zhengtao Yu, Ji-Rong Wen, and Rui Yan. Streamingdialogue: Prolonged dialogue learning via long context compression with minimal losses, 2024a. URL https://arxiv.org/abs/2403.08312.
- Li et al. (2024b) Jiaqi Li, Mengmeng Wang, Zilong Zheng, and Muhan Zhang. Loogle: Can long-context language models understand long contexts?, 2024b. URL https://arxiv.org/abs/2311.04939.
- Li et al. (2023) Kenneth Li, Oam Patel, Fernanda Viégas, Hanspeter Pfister, and Martin Wattenberg. Inference-time intervention: Eliciting truthful answers from a language model. In Thirty-seventh Conference on Neural Information Processing Systems, 2023. URL https://openreview.net/forum?id=aLLuYpn83y.
- Li et al. (2024c) Mo Li, Songyang Zhang, Yunxin Liu, and Kai Chen. Needlebench: Can llms do retrieval and reasoning in 1 million context window?, 2024c. URL https://arxiv.org/abs/2407.11963.
- Li et al. (2024d) Yuhong Li, Yingbing Huang, Bowen Yang, Bharat Venkitesh, Acyr Locatelli, Hanchen Ye, Tianle Cai, Patrick Lewis, and Deming Chen. Snapkv: Llm knows what you are looking for before generation, 2024d. URL https://arxiv.org/abs/2404.14469.
- Olsson et al. (2022) Catherine Olsson, Nelson Elhage, Neel Nanda, Nicholas Joseph, Nova DasSarma, Tom Henighan, Ben Mann, Amanda Askell, Yuntao Bai, Anna Chen, Tom Conerly, Dawn Drain, Deep Ganguli, Zac Hatfield-Dodds, Danny Hernandez, Scott Johnston, Andy Jones, Jackson Kernion, Liane Lovitt, Kamal Ndousse, Dario Amodei, Tom Brown, Jack Clark, Jared Kaplan, Sam McCandlish, and Chris Olah. In-context learning and induction heads, 2022. URL https://arxiv.org/abs/2209.11895.
- Rae et al. (2020) Jack W. Rae, Anna Potapenko, Siddhant M. Jayakumar, Chloe Hillier, and Timothy P. Lillicrap. Compressive transformers for long-range sequence modelling. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=SylKikSYDH.
- Shazeer (2019) Noam Shazeer. Fast transformer decoding: One write-head is all you need, 2019. URL https://arxiv.org/abs/1911.02150.
- Shim et al. (2021) Kyuhong Shim, Iksoo Choi, Wonyong Sung, and Jungwook Choi. Layer-wise pruning of transformer attention heads for efficient language modeling, 2021. URL https://arxiv.org/abs/2110.03252.
- Tang et al. (2024) Hanlin Tang, Yang Lin, Jing Lin, Qingsen Han, Shikuan Hong, Yiwu Yao, and Gongyi Wang. Razorattention: Efficient kv cache compression through retrieval heads, 2024. URL https://arxiv.org/abs/2407.15891.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Ł ukasz Kaiser, and Illia Polosukhin. Attention is all you need. In I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett (eds.), Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017. URL https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf.
- Voita et al. (2019) Elena Voita, David Talbot, Fedor Moiseev, Rico Sennrich, and Ivan Titov. Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned. In Anna Korhonen, David Traum, and Lluís Màrquez (eds.), Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pp. 5797–5808, Florence, Italy, July 2019. Association for Computational Linguistics. doi: 10.18653/v1/P19-1580. URL https://aclanthology.org/P19-1580.
- Weston et al. (2015) Jason Weston, Antoine Bordes, Sumit Chopra, Alexander M. Rush, Bart van Merriënboer, Armand Joulin, and Tomas Mikolov. Towards ai-complete question answering: A set of prerequisite toy tasks, 2015. URL https://arxiv.org/abs/1502.05698.
- Wu et al. (2024) Wenhao Wu, Yizhong Wang, Guangxuan Xiao, Hao Peng, and Yao Fu. Retrieval head mechanistically explains long-context factuality, 2024. URL https://arxiv.org/abs/2404.15574.
- Xiao et al. (2024) Guangxuan Xiao, Yuandong Tian, Beidi Chen, Song Han, and Mike Lewis. Efficient streaming language models with attention sinks. In The Twelfth International Conference on Learning Representations, 2024. URL https://openreview.net/forum?id=NG7sS51zVF.
- Xiao & Carenini (2019) Wen Xiao and Giuseppe Carenini. Extractive summarization of long documents by combining global and local context. In Kentaro Inui, Jing Jiang, Vincent Ng, and Xiaojun Wan (eds.), Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 3011–3021, Hong Kong, China, November 2019. Association for Computational Linguistics. doi: 10.18653/v1/D19-1298. URL https://aclanthology.org/D19-1298.
- Xu et al. (2023) Fangyuan Xu, Yixiao Song, Mohit Iyyer, and Eunsol Choi. A critical evaluation of evaluations for long-form question answering, 2023. URL https://arxiv.org/abs/2305.18201.
- Yang et al. (2024) An Yang, Baosong Yang, Binyuan Hui, Bo Zheng, Bowen Yu, Chang Zhou, Chengpeng Li, Chengyuan Li, Dayiheng Liu, Fei Huang, et al. Qwen2 technical report. arXiv preprint arXiv:2407.10671, 2024.
- Ye et al. (2024) Lu Ye, Ze Tao, Yong Huang, and Yang Li. Chunkattention: Efficient self-attention with prefix-aware kv cache and two-phase partition, 2024. URL https://arxiv.org/abs/2402.15220.
- Yi et al. (2024) Zihao Yi, Jiarui Ouyang, Yuwen Liu, Tianhao Liao, Zhe Xu, and Ying Shen. A survey on recent advances in llm-based multi-turn dialogue systems, 2024. URL https://arxiv.org/abs/2402.18013.
- Zhang et al. (2023) Zhenyu Zhang, Ying Sheng, Tianyi Zhou, Tianlong Chen, Lianmin Zheng, Ruisi Cai, Zhao Song, Yuandong Tian, Christopher Re, Clark Barrett, Zhangyang Wang, and Beidi Chen. H2o: Heavy-hitter oracle for efficient generative inference of large language models. In Thirty-seventh Conference on Neural Information Processing Systems, 2023. URL https://openreview.net/forum?id=RkRrPp7GKO.
- Zheng et al. (2024) Zifan Zheng, Yezhaohui Wang, Yuxin Huang, Shichao Song, Mingchuan Yang, Bo Tang, Feiyu Xiong, and Zhiyu Li. Attention heads of large language models: A survey, 2024. URL https://arxiv.org/abs/2409.03752.
- Zhou et al. (2024) Zixuan Zhou, Xuefei Ning, Ke Hong, Tianyu Fu, Jiaming Xu, Shiyao Li, Yuming Lou, Luning Wang, Zhihang Yuan, Xiuhong Li, Shengen Yan, Guohao Dai, Xiao-Ping Zhang, Yuhan Dong, and Yu Wang. A survey on efficient inference for large language models, 2024. URL https://arxiv.org/abs/2404.14294.
Appendix A Detaile Results
| Method | Single-Doc QA | Multi-Doc QA | Avg. | Long dependency QA | Avg. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NartvQA | Qasper | MF-en | HotpotQA | 2WikiMQA | Musique | Doc.QA | Info. Retrieval | Timeline | Computation | |||
| Llama-3-8B-Instruct, KV Size=Full | ||||||||||||
| FKV | 25.56 | 32.07 | 39.71 | 43.57 | 35.28 | 21.18 | 32.90 | 8.73 | 11.21 | 0.67 | 7.43 | 7.01 |
| Llama-3-8B-Instruct, KV Size=64 | ||||||||||||
| SKV | 20.51 | 12.80 | 31.69 | 37.02 | 25.91 | 17.02 | 24.16 | 8.84 | 9.43 | 0.66 | 6.18 | 6.28 |
| PyramidKV | 21.17 | 13.66 | 29.34 | 34.86 | 23.46 | 15.88 | 23.06 | 8.27 | 9.31 | 0.63 | 6.86 | 6.27 |
| Ada-SKV | 22.26 | 17.30 | 33.37 | 39.82 | 27.86 | 17.85 | 26.41 | 9.08 | 9.86 | 0.55 | 6.82 | 6.58 |
| Ours. Copy | 22.67 | 23.54 | 37.51 | 37.45 | 29.76 | 19.01 | 28.32 | 8.80 | 10.51 | 0.58 | 6.68 | 6.64 |
| Ours. Mix | 23.21 | 25.33 | 38.71 | 40.64 | 31.33 | 19.35 | 29.76 | 9.46 | 10.66 | 0.61 | 6.92 | 6.91 |
| Llama-3-8B-Instruct, KV Size=128 | ||||||||||||
| SKV | 22.11 | 15.79 | 31.01 | 41.12 | 29.20 | 19.35 | 26.43 | 8.36 | 9.46 | 0.79 | 6.56 | 6.29 |
| PyramidKV | 22.01 | 17.05 | 31.52 | 39.27 | 28.99 | 18.34 | 26.20 | 8.89 | 9.63 | 0.61 | 6.72 | 6.46 |
| Ada-SKV | 22.99 | 19.95 | 34.22 | 42.97 | 30.82 | 20.15 | 28.52 | 9.07 | 10.3 | 0.54 | 6.59 | 6.63 |
| Ours. Copy | 23.49 | 25.39 | 38.15 | 42.45 | 32.84 | 19.95 | 30.38 | 8.87 | 10.35 | 0.78 | 7.52 | 6.88 |
| Ours. Mix | 21.80 | 29.19 | 41.89 | 43.73 | 35.01 | 20.40 | 32.00 | 9.60 | 11.13 | 0.67 | 7.22 | 7.16 |
| Llama-3-8B-Instruct, KV Size=256 | ||||||||||||
| SKV | 23.38 | 20.18 | 37.65 | 42.80 | 33.23 | 20.01 | 29.54 | 9.04 | 10.59 | 0.53 | 7.53 | 6.92 |
| PyramidKV | 23.94 | 20.27 | 36.27 | 42.51 | 31.44 | 19.99 | 29.07 | 8.66 | 10.61 | 0.53 | 6.98 | 6.70 |
| Ada-SKV | 24.20 | 24.63 | 37.95 | 43.64 | 33.27 | 20.03 | 30.62 | 9.29 | 11.23 | 0.62 | 7.10 | 7.06 |
| Ours. Copy | 23.83 | 29.04 | 39.90 | 42.36 | 33.58 | 20.57 | 31.54 | 9.05 | 11.15 | 0.52 | 7.22 | 6.99 |
| Ours. Mix | 24.68 | 30.49 | 38.59 | 44.32 | 36.41 | 20.54 | 32.51 | 9.47 | 11.56 | 0.54 | 7.65 | 7.31 |
| Llama-3-8B-Instruct, KV Size=512 | ||||||||||||
| SKV | 25.47 | 23.75 | 38.64 | 43.66 | 33.98 | 19.83 | 30.89 | 9.00 | 11.07 | 0.63 | 7.34 | 7.01 |
| PyramidKV | 24.69 | 23.65 | 35.10 | 43.25 | 31.16 | 20.06 | 29.65 | 8.90 | 10.62 | 0.74 | 7.57 | 6.96 |
| Ada-SKV | 25.73 | 25.44 | 37.84 | 43.78 | 33.95 | 19.83 | 31.09 | 9.22 | 11.18 | 0.53 | 7.42 | 7.09 |
| Ours. Copy | 23.84 | 29.21 | 39.79 | 44.41 | 36.09 | 20.59 | 32.32 | 9.13 | 11.61 | 0.56 | 7.12 | 7.11 |
| Ours. Mix | 24.75 | 29.75 | 38.03 | 44.43 | 36.45 | 21.67 | 32.51 | 9.34 | 11.26 | 0.56 | 7.54 | 7.18 |
| Llama-3-8B-Instruct, KV Size=1024 | ||||||||||||
| SKV | 25.76 | 27.50 | 38.38 | 43.40 | 34.81 | 20.07 | 31.65 | 9.61 | 11.34 | 0.53 | 7.22 | 7.18 |
| PyramidKV | 25.38 | 26.83 | 36.90 | 44.09 | 34.24 | 21.49 | 31.49 | 8.98 | 11.41 | 0.53 | 6.96 | 6.97 |
| Ada-SKV | 25.79 | 29.24 | 38.74 | 43.93 | 36.34 | 19.79 | 32.31 | 8.65 | 11.41 | 0.53 | 7.71 | 7.08 |
| Ours. Copy | 24.85 | 30.94 | 39.82 | 43.52 | 36.58 | 20.37 | 32.68 | 9.20 | 11.67 | 0.55 | 7.71 | 7.28 |
| Ours. Mix | 24.66 | 30.82 | 39.56 | 43.97 | 36.47 | 22.24 | 32.95 | 9.02 | 11.51 | 0.47 | 7.85 | 7.21 |
| Mistral-7B-Instruct, KV Size=Full | ||||||||||||
| FKV | 26.63 | 32.99 | 49.34 | 42.77 | 27.35 | 18.78 | 32.98 | 12.17 | 15.52 | 0.49 | 10.03 | 9.55 |
| Mistral-7B-Instruct, KV Size=64 | ||||||||||||
| SKV | 19.95 | 18.63 | 38.16 | 31.24 | 21.39 | 13.81 | 23.86 | 10.41 | 11.49 | 0.46 | 9.38 | 7.94 |
| PyramidKV | 20.91 | 19.61 | 38.05 | 32.18 | 22.87 | 15.26 | 24.81 | 10.64 | 11.69 | 0.56 | 9.06 | 7.99 |
| Ada-SKV | 22.70 | 21.28 | 42.39 | 34.35 | 22.40 | 14.85 | 26.33 | 10.56 | 11.50 | 0.45 | 8.72 | 7.81 |
| Ours. Copy | 24.23 | 25.22 | 46.02 | 38.82 | 26.05 | 17.41 | 29.63 | 10.94 | 13.14 | 0.63 | 9.11 | 8.46 |
| Ours. Mix | 21.77 | 26.57 | 48.39 | 40.12 | 26.76 | 16.21 | 29.97 | 11.19 | 13.94 | 0.48 | 9.87 | 8.87 |
| Mistral-7B-Instruct, KV Size=128 | ||||||||||||
| SKV | 21.47 | 21.95 | 45.24 | 33.88 | 21.83 | 15.53 | 26.65 | 10.86 | 12.24 | 0.57 | 8.81 | 8.12 |
| PyramidKV | 21.76 | 21.98 | 43.72 | 32.76 | 22.73 | 15.59 | 26.42 | 10.64 | 11.9 | 0.47 | 8.69 | 7.93 |
| Ada-SKV | 21.57 | 24.59 | 46.70 | 35.74 | 25.57 | 14.37 | 28.09 | 11.14 | 12.37 | 0.45 | 9.57 | 8.38 |
| Ours. Copy | 23.97 | 29.60 | 48.40 | 39.66 | 26.31 | 18.13 | 31.01 | 11.43 | 13.04 | 0.53 | 10.26 | 8.82 |
| Ours. Mix | 25.04 | 27.95 | 48.48 | 41.28 | 27.65 | 18.05 | 31.41 | 11.44 | 13.08 | 0.63 | 10.20 | 8.84 |
| Mistral-7B-Instruct, KV Size=256 | ||||||||||||
| SKV | 22.26 | 24.94 | 48.30 | 36.76 | 25.16 | 14.93 | 28.72 | 11.07 | 12.39 | 0.53 | 9.13 | 8.28 |
| PyramidKV | 21.42 | 25.36 | 47.94 | 38.75 | 25.82 | 15.30 | 29.10 | 11.57 | 12.35 | 0.56 | 9.51 | 8.50 |
| Ada-SKV | 23.81 | 27.04 | 48.56 | 38.32 | 25.34 | 16.42 | 29.91 | 11.67 | 13.57 | 0.52 | 10.53 | 9.07 |
| Ours. Copy | 24.98 | 29.31 | 49.01 | 41.36 | 27.16 | 17.34 | 31.53 | 11.94 | 13.30 | 0.63 | 10.95 | 9.21 |
| Ours. Mix | 24.94 | 31.02 | 50.76 | 42.11 | 26.14 | 18.47 | 32.24 | 12.37 | 13.88 | 0.48 | 9.86 | 9.15 |
| Mistral-7B-Instruct, KV Size=512 | ||||||||||||
| SKV | 24.18 | 28.87 | 48.74 | 38.84 | 25.48 | 15.04 | 30.19 | 11.96 | 13.47 | 0.52 | 10.50 | 9.11 |
| PyramidKV | 23.07 | 28.97 | 48.37 | 39.54 | 25.63 | 16.59 | 30.36 | 11.34 | 13.32 | 0.65 | 10.81 | 9.03 |
| Ada-SKV | 24.22 | 29.92 | 48.96 | 40.08 | 25.55 | 17.45 | 31.03 | 12.12 | 14.53 | 0.52 | 10.57 | 9.44 |
| Ours. Copy | 24.97 | 30.94 | 49.45 | 42.25 | 26.34 | 18.54 | 32.08 | 12.09 | 13.88 | 0.62 | 10.94 | 9.38 |
| Ours. Mix | 25.59 | 31.33 | 50.26 | 42.66 | 27.20 | 19.37 | 32.74 | 11.62 | 15.61 | 0.50 | 9.97 | 9.43 |
| Mistral-7B-Instruct, KV Size=1024 | ||||||||||||
| SKV | 25.38 | 30.22 | 49.29 | 41.84 | 26.60 | 18.08 | 31.90 | 11.69 | 13.89 | 0.52 | 10.54 | 9.16 |
| PyramidKV | 24.28 | 30.05 | 49.17 | 40.49 | 26.43 | 18.80 | 31.54 | 11.77 | 14.51 | 0.51 | 10.19 | 9.25 |
| Ada-SKV | 24.82 | 31.49 | 48.80 | 41.18 | 27.38 | 18.22 | 31.98 | 11.96 | 13.82 | 0.53 | 9.92 | 9.06 |
| Ours. Copy | 25.87 | 31.44 | 49.55 | 41.95 | 27.09 | 19.88 | 32.63 | 12.21 | 14.17 | 0.50 | 10.58 | 9.37 |
| Ours. Mix | 25.64 | 32.54 | 50.49 | 41.80 | 27.88 | 18.89 | 32.87 | 11.94 | 14.93 | 0.50 | 10.49 | 9.47 |
Appendix B Dataset Details
Table 5 provides details of the datasets used in our experiments. To evaluate the retrieval and contextual reasoning abilities of different KV cache compression methods, we use six question-answering datasets from LongBench (Bai et al., 2024) and four additional question-answering datasets from LooGLE (Li et al., 2024b) as benchmarks. For the LooGLE datasets, we randomly selected 100 examples to form the datasets used in this study.
| Source | Label | Task | Task Type | Eval metric | Avg Len | Language | Nums |
|---|---|---|---|---|---|---|---|
| LongBench | NrtvQA | NarrativeQA | Single-Doc. QA | F1 | 18,409 | EN | 200 |
| LongBench | Qasper | Qasper | Single-Doc. QA | F1 | 3,619 | EN | 200 |
| LongBench | MF-en | MultiFieldQA-en | Single-Doc. QA | F1 | 4,559 | EN | 150 |
| LongBench | HotpotQA | HotpotQA | Multi-Doc. QA | F1 | 9,151 | EN | 200 |
| LongBench | 2WikiMQA | 2WikiMultihopQA | Multi-Doc. QA | F1 | 4,887 | EN | 200 |
| LongBench | Musique | Musique | Multi-Doc. QA | F1 | 11,214 | EN | 200 |
| LooGLE | Doc.QA | Comprehension&reasoning | Long Dependency QA | F1 | 15,498 | EN | 100 |
| LooGLE | Info.Retrieval | Multiple information retrieval | Long Dependency QA | F1 | 14,808 | EN | 100 |
| LooGLE | Timeline | Timeline reorder | Long Dependency QA | F1 | 15,425 | EN | 100 |
| LooGLE | Computation | Computation | Long Dependency QA | F1 | 17,001 | EN | 100 |
Appendix C LongBench Results
We list the evaluation results on the remaining datasets from LongBench (Bai et al., 2024) in Table 6. Our head-level KV cache compression method also outperforms the other baselines, particularly on summarization and Code datasets across Llama-3-8B-Instruct and Mistral-7B-Instruct.
| Method | Summarization | Few-Shot Learning | Synthetic | Code | Avg. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GovReport | QMSum | MultiNews | TREC | TriviaQA | SAMSum | PCount | PRe | LCC | RB-P | ||
| Llama-3-8B-Instruct, KV Size=Full | |||||||||||
| FullKV | 28.71 | 23.26 | 26.64 | 73.5 | 90.48 | 42.33 | 4.80 | 69.25 | 59.29 | 54.05 | 47.23 |
| Llama-3-8B-Instruct, KV Size=128 | |||||||||||
| SnapKV | 19.83 | 21.80 | 21.41 | 65.50 | 89.72 | 38.71 | 5.75 | 69.00 | 58.74 | 54.57 | 44.50 |
| Ada-SnapKV | 20.89 | 22.11 | 21.68 | 70.50 | 90.82 | 39.20 | 5.91 | 69.50 | 59.75 | 54.86 | 45.52 |
| HeadKV-R | 21.08 | 22.35 | 22.50 | 71.50 | 89.45 | 38.40 | 5.00 | 69.50 | 60.89 | 59.92 | 46.06 |
| HeadKV-R2 | 21.76 | 22.16 | 23.94 | 71.50 | 90.19 | 38.88 | 6.60 | 69.50 | 61.08 | 60.21 | 46.58 |
| Mistral-7B-Instruct, KV Size=Full | |||||||||||
| FullKV | 32.87 | 24.24 | 27.10 | 71.00 | 86.23 | 42.79 | 2.75 | 86.98 | 56.93 | 54.49 | 48.54 |
| Mistral-7B-Instruct, KV Size=128 | |||||||||||
| SnapKV | 20.76 | 22.72 | 21.38 | 67.00 | 85.06 | 40.22 | 3.51 | 65.06 | 52.20 | 47.01 | 42.49 |
| Ada-SnapKV | 21.13 | 22.76 | 22.25 | 68.50 | 85.60 | 41.05 | 3.33 | 62.54 | 52.88 | 49.25 | 42.93 |
| HeadKV-R | 22.19 | 22.86 | 22.57 | 69.50 | 85.46 | 41.16 | 3.56 | 74.49 | 54.60 | 50.89 | 44.73 |
| HeadKV-R2 | 24.30 | 23.48 | 24.18 | 70.50 | 85.54 | 40.72 | 4.83 | 72.63 | 55.49 | 51.39 | 45.31 |


Appendix D Reasoning-in-a-Haystack details
As shown in Figure 9, we provide examples for each task used in the Reasoning-in-a-Haystack test333https://huggingface.co/datasets/RMT-team/babilong. We use the dataset curated by Kuratov et al. (2024) for the Reason-in-a-Haystack test. Specifically, they use the “Input” listed in Figure 9 as the needle and split it into different sentences using dot. These sentences are then inserted into various positions within the haystack to form the final Reason-in-a-Haystack test examples.
As shown in Figure 10, we provide detailed results across different context lengths and tasks. Our proposed head-level KV cache compression method achieves the best average score among all methods. Notably, on the Llama-3-8B-Instruct model, our method surpasses the Full KV cache on the QA3 task, the most challenging task among the five, as indicated in Kuratov et al. (2024). This suggests that our Retrieval-Reasoning Heads distributions are better at capturing semantically relevant and important content, leading to generating the correct answers.

