Nonwandering sets and Special -limit sets
of Monotone maps on Regular Curves
Abstract.
Let be a regular curve and let be a monotone map. In this paper, nonwandering set of and the structure of special -limit sets for are investigated. We show that AP, where AP, and are the sets of almost periodic points, recurrent points and nonwandering of , respectively. This result extends that of Naghmouchi established, whenever is a homeomorphism on a regular curve [J. Difference Equ. Appl., 23 (2017), 1485–1490] and [Colloquium Math., 162 (2020), 263–277], and that of Abdelli and Abdelli, Abouda and Marzougui, whenever is a monotone map on a local dendrite [Chaos, Solitons Fractals, 71 (2015), 66–72] and [Topology Appl., 250 (2018), 61–73], respectively. On the other hand, we show that for every , the special -limit set is a minimal set, where P is the set of periodic points of and that is always closed, for every . In addition, we prove that , where denotes the union of all special -limit sets of ; these results extend, for monotone case, recent results on interval and graph maps obtained respectively by Hantáková and Roth in [Preprint: arXiv 2007.10883.] and Foryś-Krawiec, Hantáková and Oprocha in [Preprint: arXiv:2106.05539.]. Further results related to the continuity of the limit maps are also obtained, we prove that the map (resp. , resp. s) is continuous on (resp. ).
Key words and phrases:
Minimal set, regular curve, -limit set, local dendrite, monotone map2010 Mathematics Subject Classification:
37B20, 37B45, 54H201. Introduction
In the last two decades, a wide literature on the dynamical properties of maps on some one-dimensional continua has developed. Examples of continua become increasingly studied include, graphs, dendrites and local dendrites (see for instance [1], [2], [3], [30]).
Recently a large class of continua called regular curves has given a special attention (see for example, [5], [12], [13], [14], [20], [21], [28], [29], [31]). These form a large class of continua which includes local dendrites. The Sierpiński triangle is a well known example of a regular curve which is not a local dendrite. Regular curves appear in continuum theory and also in other branches of Mathematics such as complex dynamics; for instance, the Sierpiński triangle can be realized as the Julia set of the complex polynomial (see [9]). Recall that the Julia set of is . Seidler [31] proved that every homeomorphism of a regular curve has zero topological entropy (later, this result was extended by Kato in [20] to monotone maps). In [28], [29], Naghmouchi proved that any -limit set (resp. -limit set) of a homeomorphism on a regular curve is a minimal set. Moreover he established the equality between the set of nonwandering points and the set of almost periodic points. In [12], the first author gave a full characterization of minimal sets for homeomorphisms without periodic points on regular curves. In [15] it was shown that the set of periodic points is either empty or dense in the set of non-wandering points, for homeomorphisms on regular curves. In the present paper, we deal with several questions/problems.
First, we address the question of the equality between the set of nonwandering points and the set of almost periodic points. This was proved in two cases:
for homeomorphisms on regular curves (Naghmouchi [29])
for monotone maps on local dendrites (Abdelli et al. [3])
In Theorem 3.1, we prove a more general result by showing that this is true for monotone maps on regular curves.
Nevertheless, the later result is false in general for monotone maps on dendroids as it is shown in Example 3.5. Moreover, we show in Theorem 3.3 that the set of nonwandering points coincides with the set of points belonging to their special -limit sets (Proposition 6.8).
Second, beside the usual limits sets -limit and -limit, we are interested in the study of another kind of limit sets, called special -limit set (see Section 6). We ask the question whether every special -limit set is a minimal set? We show that for a monotone map on a regular curve, every special -limit set of a non periodic point is a minimal set. However, we built an example of a monotone map on an infinite star for which is not a minimal set for some periodic point . Moreover we show that the inclusion is strict. In addition, we prove that , where respectively denotes the union of all special -limit sets and the set of recurrent points of . Notice that it is shown recently that, for mixing graph maps , every special -limit set is the -limit set of some point from and moreover, for graph maps with zero topological entropy, every special -limit set is a minimal set (cf. [24, Theorem 3.8]). On the other hand, Kolyada et al. showed in ([22, Theorem 3.3 and Corollary 3.11]), that is closed whenever is either an interval map for which the set of all periodic points is closed or is transitive. Recently, Hantáková and Roth [16] showed that a special -limit set is closed for a piecewise monotone interval map. It is previously known that is closed for homeomorphisms on any compact metric space. In Corollary 6.7, we extend the later result to monotone maps on regular curves by showing that for any , is closed. In fact we show more precisely that for every , (cf. Theorem 6.2).
2. Preliminaries
Let be a compact metric space with metric and let be a continuous map. The pair is called a dynamical system. Let and be the sets of integers, non-negative integers and positive integers, respectively. For , denote by the -th iterate of ; that is, and if . For any , the subset is called the orbit of (under ). A subset is called invariant (resp. strongly invariant) if (resp., ); it is further called a minimal set (under ) if it is closed, non-empty and does not contain any invariant, closed proper non-empty subset of . We define the -limit set of a point to be the set:
The set is called the -limit set of . Equivalently a point if and only if there exist an increasing sequence of positive integers and a sequence of points such that and It is much harder to deal with -limit sets since there are many choices for points in a backward orbit. When is a homeomorphism, .
Balibrea et al. [6] considered exactly one branch of the backward orbit as follows.
Definition 2.1.
Let . A negative orbit of is a sequence of points in such that and , for every . The -limit set of denoted by is the set of all limit points of .
It is clear that . The inclusion can be strict; even for onto monotone maps on regular curves (see Example 6.10). Notice that we have the following equivalence:
(i) , (ii) . In particular, if is onto, then for every .
Proposition 2.2.
[14, Corollary 2.2] Let be a continuous self mapping of a compact space . Let . Then:
-
(i)
is non-empty, closed and -invariant. In addition, it is strongly -invariant whenever .
-
(ii)
is non-empty, closed and strongly -invariant, for any negative orbit of .
A point is called:
Periodic of period if and for ; if , is called a fixed point of i.e. ;
Almost periodic if for any neighborhood of there is such that , for all .
Recurrent if .
Nonwandering if for any neighborhood of there is such that .
We denote by P, AP, R, and the sets of periodic points, almost periodic points, recurrent points, nonwandering points and the union of all -limit sets of , respectively. Define the space
. From the definition, we have the following inclusions:
Definition 2.3.
[23, page 131] Let be two topological spaces. A continuous map is said to be monotone if for any connected subset of , is connected.
When is closed and onto, Definition 2.3 is equivalent to that the preimage of any point by is connected (cf. [23, page 131]). In particular, this holds if is compact and is onto. Notice that is monotone for every when itself is monotone.
A continuum is a compact connected metric space. An arc (resp. a circle) is any space homeomorphic to the compact interval (resp. to the unit circle ). A space is called degenerate if it is a single point, otherwise; it is non-degenerate. By a graph , we mean a continuum which can be written as the union of finitely many arcs such that any two of them are either disjoint or intersect only in one or both of their endpoints.
A dendrite is a locally connected continuum which contains no circle. Every subcontinuum of a dendrite is a dendrite ([27, Theorem 10.10]) and every connected subset of is arcwise connected. A local dendrite is a continuum every point of which has a dendrite neighborhood. By ([23, Theorem 4, page 303]), a local dendrite is a locally connected continuum containing only a finite number of circles. As a consequence every subcontinuum of a local dendrite is a local dendrite ([23, Theorems 1 and 4, page 303]). Every graph and every dendrite is a local dendrite.
A regular curve is a continuum with the property that for each point and each open neighborhood of in , there exists an open neighborhood of in such that the boundary set of is finite. Each regular curve is a -dimensional locally connected continuum. It follows that each regular curve is locally arcwise connected (see [23] and [27], for more details). In particular every local dendrite is a regular curve (cf. [23, page 303]).
A continuum is said to be finitely suslinean continuum provided that each infinite family of pairwise disjoint continua is null (i.e. for any disjoint open sets , only a finite number of elements of the family meet both and ). Note that each regular curve is finitely suslinean (see [25]). A continuum is called hereditarily locally connected continuum, written hlc, provided that every subcontinuum of is locally connected. In particular, finitely suslinean continua and (hence regular curves) are hlc (see [23]). A continuum is said to be rational curve provided that each point of and each open neighborhood of in , there exists an open neighborhood of in such that the boundary set of is at most countable. Clearly, regular curve are rational.
Let be a compact metric space. We denote by (resp. ) the set of all non-empty compact subsets (resp. compact connected subsets) of . The Hausdorff metric on (respectively ) is defined as follows: , where (resp. ). For and , . With this distance, and are compact metric spaces. Moreover if is a continuum, then so are and (see [27], for more details). Let be a continuous map of . We denote by , called the induced map. Then is also a continuous self mapping of (cf. [27]). For a subset of , we denote by diam and the cardinality of . For any , we denote by
A family of subsets of is called a null family if for any infinite sequence of . It is well known that each pairwise disjoint family of subcontinua of a regular curve is null (see [25]).
We recall some results which are needed for the sequel.
Proposition 2.4.
Let be a regular curve. Then for any and for any family of pairwise disjoint subcontinua of , the set
is finite. In particular if is a sequence of pairwise disjoint continua, then is a null family.
Definition 2.5.
Weak incompressibility A set is said to have the weak incompressibility property if for any proper closed subset (i.e. is nonempty and distinct from ), we have that .
Notice that the term weak incompressibility seems to have appeared first in [7].
Lemma 2.6.
[10, Lemma 3, page 71] For any , has the weak incompressibility property.
Lemma 2.7.
Let be a closed invariant subset of with the weak incompressibility property. If some is an isolated point of , then .
Proof.
Assume that for some is an open subset of and . Since is an homeomorphism, is a finite open subset of , thus also a proper closed subset of . has the weak incompressibility property and is a closed subset of , we get . Therefore , which contradict the fact that is one to one on . ∎
Let be a monotone map on a regular curve . If is an infinite minimal set of , we call the basin of attraction of .
Theorem 2.8.
[14] Let be a regular curve monotone map. Then the following assertions hold:
-
(1)
is a minimal set, for all .
-
(2)
is a minimal set any negative orbit of . Moreover if , then is a minimal set and , for any negative orbit of .
-
(3)
For every infinite minimal set , is a closed subset of .
-
(4)
For every , if is infinite, then .
-
(5)
.
3. Nonwandering sets of monotone maps on regular curves
The aim of this section is to prove the following theorem which extends [3, Theorem 1.1] and [29, Theorem 2.1].
Theorem 3.1.
Let be a regular curve and a monotone self mapping of . Then .
Proof.
Following Theorem 2.8, (5), it suffices to prove that . Assume that there exists . We distinguish two cases:
Case 1: . In this case, we follow similarly the proof given in ([29, Theorem 2.1]). Let be an open neighborhood of such that . As , there is a sequence in converging to and a sequence of positive integers such that converges to . Since , . Then we can find an open neighborhood of with finite boundary and an open neighborhood of such that .
Since is locally connected, so by ([23, Theorem 4, page 257]), for large enough, we can find a sequence of arcs joining and such that (with respect to the Hausdorff metric). Thus will meets and , for large enough and so it meets the boundary in a point , for large enough. As is finite, one can assume that for infinitely many . Therefore , for infinitely many . It follows that . As , then is a minimal set of (Theorem 2.8). So and hence . A contradiction.
Case 2: . Let be a sequence converging to and set the period of , . Then in unbounded: otherwise, , a contradiction. So we can assume that goes to infinity. Since is a minimal set, (because otherwise, , a contradiction). Now as in Case 1, let be an open neighborhood of and an open neighborhood of with finite boundary and disjoint from . Let be a sequence of arcs joining and such that (with respect to the Hausdorff metric). Thus meets infinitely many times and thus there exists such that . This implies that . As is a minimal, so . A contradiction. ∎
Corollary 3.2.
If is finite or countable, then .
Proof.
In [11], Coven and Nitecki have shown that for continuous maps of the closed interval , Later, it is extended to graph maps in [26, Corollary 1]. However, for dendrite maps, it does not holds (see [32]). The following theorem extend the above result to monotone maps on regular curves.
Theorem 3.3.
Let be a regular curve and a self monotone mapping of . Then .
Proof.
Corollary 3.4.
Let be a regular curve and a self monotone mapping of . If , then :
(i) .
(ii) If , then , for any negative orbit of .
Proof.
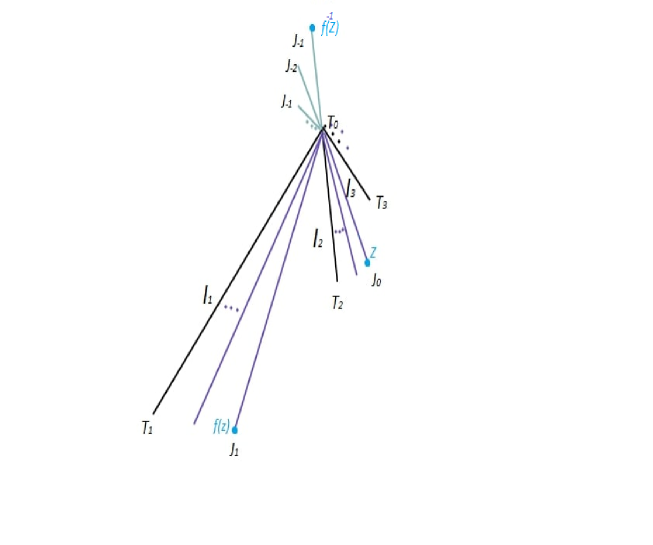
In the following example, we show that Theorem 3.1 cannot be extended to rational curves; we construct a self monotone map on a rational curve (it is in fact a dendroid) such that the inclusion is strict: .
Notice also that Theorem 3.1 does not hold even for continuous maps on intervals; for instance; we may extend the map (defined in Example 3.5) into a continuous map of so that but .
Example 3.5.
The idea of the construction consists to define a continuous map on a countable compact set satisfying and then extends it to a monotone map defined on a dendroid .
Let be the shift map on the Cantor set endowed with the metric defined as follows: For , , where with . We denote by:
We let and . Set
,
,
.
Observe that converges to . Let us show that .
For each , we let . It is clear that is an increasing sequence. Observe that gives the first apparition of the number one after zeros. Then for each , and so . Let and suppose that . Then gives zero before the first apparition of one. Then , so . For , we have . In result, . Conversely, let and suppose that there exist such that and , let be an increasing sequence of integer be such that . Then there exists such that , we have , so ( we have only a single one in the first block with length in but, we have two ones in the first block with length in ). So every point of contains at most only one. Consequently, .
We conclude that is a countable compact set. We let . Then , for any . Pick a homeomorphic copy of in . For , let be an arc joining and so that is an infinite star centered at . in particular .
For each , let such that and let be an arc joining and which is included in the closed ball of the plan. We may assume that for any , and for any . Let . Clearly is a countable union of arcs, so by ([23, Theorem 6, page 286]) is a rational curve which is a dendroid.
We extend into a map on so that and is affine, for each and for . Then and . It is clear that is a pointwise monotone map on and onto, thus monotone. Moreover , since for instance but .
4. The space of minimal sets with respect to the Hausdorff metric
The main result of this section is to prove the following theorem.
Theorem 4.1.
Let be a regular curve and a monotone self mapping of . Then any limit (with respect to the Hausdorff metric) of a sequence of minimal sets is a minimal set.
Proof.
Let be a sequence a sequence of minimal sets converging to some . Then . Since each , so by Theorem 3.1, . Therefore , where is a minimal set for any . Assume that is not a minimal set. Then .
Claim: . Suppose that , so there exists such that is infinite. Set and , where . Then and are disjoint minimal sets and so does and . By Theorem 2.8, is a closed set. So let an open set with finite boundary of cardinality such that and .
Recall that , so fix some and let such that (resp. ) converges to (resp. ). Let be a sequence of arcs joining and so that .
Since is a minimal set, we can find such that , for every . Hence for large enough, and . On the other hand, meets at some point of . As is monotone, thus for large enough, . As is finite, then there exists such that , for infinitely many . Hence (since ). By minimality of (see Theorem 2.8), we get . Hence . A contradiction with . The proof is complete.
Proof of Theorem 4.1. As proven by the claim above, we have . Since any minimal set has the weakly incompressibility property (Lemma 2.6), so does its limit by [4, Proposition 3.1]. Since , it is uncountable, otherwise, will have an isolated point , so by Lemma 2.7, is a periodic orbit. A contradiction. From , there exist and an infinite sequence in Fix with disjoint orbits converging to some . As , there exists an open set with finite boundary such that and . Since converges to , there is some such that for any . For each , let be a sequence of arcs joining and so that converges to as done in the proof of the claim above. As is minimal and , we can find such that . Recall that , so , for any . By the same argument as in the proof of the claim above, we can find, for each , such that . This leads to a contradiction since is an infinite family of disjoint periodic orbits. ∎
5. On the continuity of limit maps and
In this section, we shall investigate the continuity of the limit maps:
and .
Theorem 5.1.
The maps and are continuous everywhere except may be at the periodic points of .
We use the following lemmas.
Lemma 5.2.
[13, Lemma 4.2] Let be a hereditarily locally connected continuum, a closed subset and a sequence of open subsets of such that . Then .
Lemma 5.3.
The restriction map is continuous.
Proof.
Let a sequence of converging to some . By Theorem 3.1, and by Theorem 2.8, is a sequence of minimal set, thus by Theorem 4.1, any limit point of that sequence should be a minimal set. Observe that belongs to any limit point of the sequence , therefore any limit point of the sequence is a minimal set that contains , therefore it has to be .
∎
Let be a dynamical system. For , we denote by
.
Lemma 5.4.
Let such that and are two disjoint orbits. Then and are disjoint.
Proof.
Assume that . Then we can find two positive integers and some . Therefore , which will leads to a contradiction. ∎
Lemma 5.5.
Let be a regular curve and a monotone self mapping of . The limit maps and are continuous at any point of .
Proof.
First note that is a open set disjoint from . Thus for any point , and are minimal sets. Let :
Continuity of :
Assume that is not continuous at and set , then we can find a sequence that converges to such that converges to . By Theorem 4.1, is a minimal set, thus . Let and be an open set with finite boundary such that . Let be a sequence of arcs joining and , where converge to with respect to the Hausdorff metric. Recall that , so for large enough we can find some such that and . Then will meets and so for some . Since , we conclude that is not a minimal set, thus By Theorem 2.8, .
Claim: The sequence satisfies the follow properties:
(i) For any and .
(ii) The sequence converges to .
(iii) By passing to a subsequence if needed, the family is pairwise disjoint.
Proof of the claim:
(i) is already proven above, for the prove of (ii) observe that any limit point of is a point of and since , so by Lemma 5.3 ends the proof of (ii).
(iii) Clearly for any , . Let and be an open neighborhood of such that . As converges to we can find such that . Thus and are disjoint.
For is defined and pairwise disjoint. Let an open neighborhood of such that
. We can find such that and then is pairwise disjoint. We have defined by indication the subsequence so that are pairwise disjoint. This ends the proof of the claim.
Now , so . Let be an open neighborhood of such that and set . By (iii) there exist such that for any . By (i), we may find for each some such that . Fix . By Lemma 5.4 and monotonicity of , the family is a pairwise disjoint family of connected subset of . Observe that for each and meets at some point of . Therefore for each meets . This leads to a contradiction.
Continuity of .
Set . By Theorem 2.8, is a minimal set, assume that converges to , then , so let .
Let be an open neighborhood of with finite boundary such that and a sequence of arcs joining and converging to with respect to the Hausdorff metric. Since , for large enough, we can find some such that and . Then by monotonicity of will meets and thus for some . By Theorem 3.1, , hence . A contradiction.
∎
Proof of Theorem 5.1. Let . If , then by Lemma 5.5, is continuous at . So assume that and set . Then and is an infinite minimal set.
Continuity of on :
By Theorem 2.8, . Assume that there is some sequence of converging to such that converges to and . By minimality of , . Assume that there exists . We distinguish two cases:
Case 1: For infinitely many , . Since in non periodic point, so per( is unbounded. By choosing with pairwise distinct periods per(, one can assume that is pairwise disjoint. Therefore by Lemma 5.4, the family is pairwise disjoint. Let now be two disjoint open neighborhoods of with finite boundary. By Lemma 5.3, the restriction map is continuous. Therefore as , we conclude that the sequence converges to . So one can assume that for any , we have . As , then for each , one can find such that . So let be the connected component of containing . Hence is a family of pairwise disjoint connected sets each of which meets and (since is a periodic point such that ). This leads to a contradiction since is finite.
Case 2: For large enough, . In this case, by Theorem 2.8, is a minimal set. Thus by Theorem 4.1, is also a minimal set and then . So let and be two disjoint neighborhoods of with finite boundary and set . As converges to , then we can find pairwise disjoint arcs , each joins and , for some large enough and satisfying . Then we can find such that for any , . Consider the family , which is a family of pairwise disjoint connected sets, each of which meets at and meets at some point of , this will lead to a nonempty intersection with for each . A contradiction.
This ends the proof of the continuity of .
Continuity of . Assume that there is some sequence of converging to such that converges to and . As is a minimal set, for any , thus by Theorem 4.1, is also a minimal set and then .
Claim 1. For any neighborhood of , there exists such that .
Proof. Fix some neighborhood of . Let and be two disjoint neighborhoods of with finite boundary such that . Set . As converges to and is infinite, then for each , we can find a sequence of arcs joining and converging to such that for any and for any , . Let . Clearly and we may assume that .
We can assume that for any . Thus for each , we can find such that . Therefore for each . Then for each , there exists and such that . Hence , for . Recall that which is finite and . Hence there exists and such that , for infinitely many , . Therefore for infinitely many , we have that . Hence . Moreover as , then and hence . This ends the proof of Claim 1.
Now by Claim 1, we may find a sequence of periodic points with disjoint orbits converging to some point such that . By Lemma 5.3, converges to . Moreover for each , we can find such that . As , then . Therefore we can find such that for any , we have . Recall that is a sequence of periodic points with disjoint orbits, hence is a non null family of pairwise disjoint subcontinua. A contradiction with the fact that is a regular curve and hence finitely Suslinean. This ends the proof of the continuity of . ∎
6. On special -limit sets
In [18], Hero introduced another kind of limit sets, called the special -limit sets. He considered the union of the -limit sets over all backward orbits of .
Definition 6.1.
Let be a metric compact space, a continuous map and . The special -limit set of , denoted , is the union taken over all negative orbits of .
Notice that we have the following equivalence:
(i) , (ii) , (iii) .
In particular, if is onto, then for every .
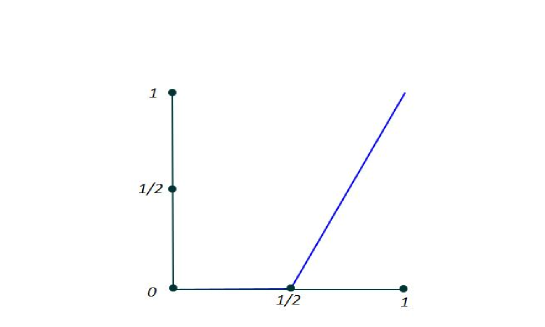
It is clear that . The inclusion can be strict. Hero [18] provided an example of a continuous map on the interval for which the inclusion is strict. Even, one can provide an onto monotone interval map. Indeed, consider the monotone map . We see that .
In ([22, Theorem 3.3 and Corollary 3.11]), Kolyada et al. provided an example of a map on a subset of where a special -limit set is not closed. Recently, Hantáková and Roth proved in ([16], Theorem 37) that a special -limit set for interval map is always Borel, and in fact both and . Furthermore, they provided a counterexample of an interval map with a special -limit set which is not closed, this disproves the conjecture 1 in [22]. However they showed that a special -limit set is closed for a piecewise monotone interval map. Jackson et al. ([19]) proved that a special -limit set is always analytic (i.e. a continuous image of a Polish space) and provide an example of a map of the unit square with special -limit set not a Borel set. Here we show that, for a monotone map on a regular curve, the special -limit set is always closed.
6.1. Relation between Nonwandering sets, -limit and Special -limit sets
The aim of this paragraph is to prove the following theorem.
Theorem 6.2.
Let be a regular curve and a monotone self mapping of . Then for every , we have that .
First, we derive from Theorem 2.8 the following corollary.
Corollary 6.3.
Let be a regular curve and a monotone self mapping of . Then or any :
(i) ,
(ii) is a union of minimal sets.
(iii) if , then is a minimal set.
Proof.
The proof of Theorem 6.2 needs the following lemma.
Lemma 6.4.
Let be a regular curve and a monotone self mapping of . If , then every minimal set is a periodic orbit.
Proof.
Let and an infinite minimal set such that . Fix some , we can find an increasing sequence of integers and such that converges to . Clearly for any , we have . By Theorem 5.1, is continuous at , therefore we get , which is finite. A contradiction. ∎
Recall that given a subset of a topological space , the arc connected component of is defined as
Lemma 6.5.
Let be a regular curve and a subset of . Then the following hold:
(i) Every arc connected component of is closed in .
(ii) If is arcwise connected, then it is locally arcwise connected.
Proof.
Lemma 6.6.
Let be a regular curve and a monotone self mapping of . If and , then .
Proof.
Assume that , by Theorem 3.1, , thus . Observe that for some , if not . So let and such that , then and . This will lead to a contradiction since . ∎
Proof of Theorem 6.2.
If , then by Corollary 6.3, and so . Now assume that . The inclusion follows from Corollary 6.3. Now let . By Lemma 6.4, is a periodic orbit and so . If , then . Now assume that , then and . Therefore by Lemma 6.6, . By Lemma 5.2, we can find an open set such that and Mesh. Denote by , observe that .
Claim: has a finite number of arc connected components.
Denote by the period of . We have
Since is monotone then for each is a subcontinuum of the regular curve , thus arcwise connected, moreover it contains . We conclude that is an arcwise connected subset of . Again since is monotone and is arcwise connected then for each is also arcwise connected. Indeed for , we can find an arc joining and in , thus we can find some arc in joining and . We conclude that can be written as a finite union of arcwise connected subset of , this end the proof of the claim. Recall that then we can find an increasing sequence of integer and so that converges to . For each which has a finite number of arc connected component by the claim above, namely , so we may find such that for each so that . By Lemma 6.5, (i), is arcwise connected. Therefore by Lemma 6.5, (ii), locally arcwise connected. Let then be an arc in joining and so that converges to . We have for each . Therefore for each is an arcwise connected set of meeting only at . Therefore . Thus for each , there exists . As is finite there exists such that , for infinitely many . Hence for infinitely many . Since , so by Theorem 2.8, is a minimal set containing . Thus and . Recall that for each , and hence . Then for some , we have , therefore any negative orbit of can be completed into a negative orbit of hence . By Theorem 2.8, we have and so . ∎
Corollary 6.7.
Let be a regular curve and a monotone self mapping of . Then for every , is a closed set.
Proof.
The proof follows from Theorem 6.2 (since and are closed). ∎
The following proposition improves Theorem 3.3.
Proposition 6.8.
Let be a regular curve and a monotone self mapping of . Then .
6.2. Further results on special -limit sets
Theorem 6.9 (Continuity of special -limit maps).
Let be a regular curve and a monotone self mapping of . Then the special -limit map is continuous everywhere except may be at the periodic points of .
Proof.
Let and be a sequence of converging to . By Theorem 5.1, the sequence converges to . Let be any limit point of with respect to the Hausdorff metric. Clearly , moreover by Corollary 6.7, is an invariant closed subset of . By Theorem 2.8, (2), is a minimal set, therefore . It turn out that is the unique limit point of the sequence . We conclude that the sequence converges to (since is compact). Again by Theorem 2.8, (2), and the result follows. ∎
Note that it may happened that the maps and are discontinuous at some periodic point: For example consider the map given in [14, Example 5.10].
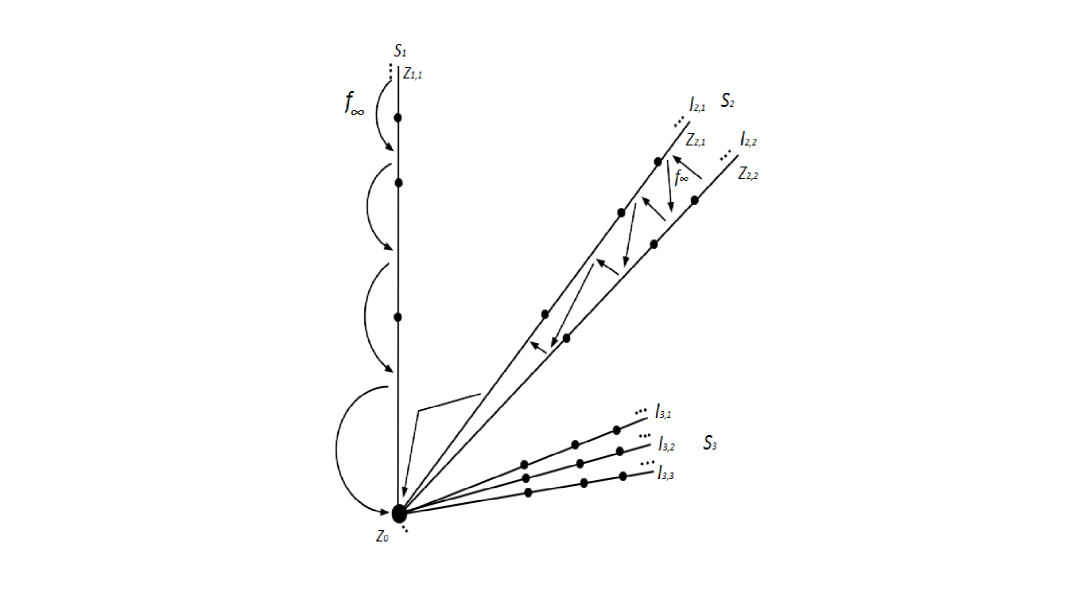
Example 6.10.
[14, Example 5.10] There exists a monotone map on an infinite star centered at a point and beam with endpoints and satisfying the following properties.
-
(i)
For any we have and , where such that .
-
(ii)
For any we have .
-
(iii)
.
We have
is discontinuous at , for every and (resp. ) is discontinuous at .
Denote by (respectively ) the union of all special -limit sets (respectively, all -limit sets) of a map . In [24, Corollary 2.2], it was shown that holds for general dynamical system . For continuous map on graphs, it was shown that (see [33], cf. [8], [18]) and that there are continuous maps on dendrites with (cf. [34]). In the following theorem, we extend the above results to regular curves when we restricted to monotone maps.
Theorem 6.11.
Let be a regular curve and a monotone self mapping of , the following hold:
(i) .
(ii) and are closed.
(iii) If , then .
Proof.
Recall that by Theorem 3.1, . Assertion (i) follows immediately from Corollary 6.3 and Proposition 6.8.
(iii): Assume now that . Then by Corollary 6.3, is a minimal set, for any , so assertion (iii) follows.
(ii): By (i), and so is closed. Let us show that is closed. Let be a sequence of converging to some . We can assume that since otherwise and we are done. For each , let such that . Suppose that , then by passing to a subsequence if needed, one can assume that the sequence is infinite (since otherwise ).
Since , so for large enough, and therefore is not a minimal set. Therefore by Theorem 2.8, . So by passing to a subsequence if needed, the family is pairwise disjoint. Let be an open neighborhood of with finite boundary such that . As and the sequence converges to , there exists such that for any , we can find such that . Since , we have . Since is monotone, it follows that , for any . By Lemma 5.4 the family is pairwise disjoint and as proven above , for each , this will lead to a contradiction since is finite. ∎
Remark 6.12.
If , we have the inclusion which can be strict for monotone maps on regular curves. Indeed, consider the map of Example 6.18. We have that
.
Theorem 6.13.
Let be a regular curve and a monotone self mapping of . Then for any is either a finite union of periodic orbits or an infinite sequence of periodic orbits converging to .
Proof.
Assume that is infinite and that there is an accumulation point of such that . We can find an infinite sequence of converging to . By Theorem 4.1, converges to a minimal set . As , then and hence . Then for large enough, say ,
Since (Lemma 6.6), so by Lemma 5.2, there is an open set such that and
As done in the proof of Theorem 6.2, the set
is -invariant and has a finite number of arc connected components. For each , let be the arc connected component of containing . Since , for each , we can find an increasing sequence of integers and a sequence which converges to , where . By the same arguments as in the proof of Theorem 6.2, we can assume that for infinitely many . Now as the are pairwise distinct and the are locally arcwise connected, , so for large enough, we may find a sequence of pairwise disjoint arcs in joining and which converges to . Choose large enough and set , . So is a family of pairwise disjoint arcs in joining and . Set
and
Since is -invariant, . Moreover is a subcontinuum of which meets the orbits of and . As
then we can find an arc joining and such that . Obviously is connected and . Therefore and . Thus and therefore , for each . It follows that there exists such that , for some . Hence . As is finite, there exists such that for infinitely many , thus . This implies that the family is not pairwise disjoint (otherwise it will be a null family), and hence for some , we have . Thus and so . As and , then . A contradiction.
We conclude that any accumulation point of is a point of . It turns out that is a compact space having a finite set of accumulation points, hence it is countable. ∎
The following corollary is in contrast to the properties of -limit sets.
Corollary 6.14.
Let be a regular curve and a monotone self mapping of and . If contains an isolated point, then .
Proof.
If , then is a minimal set and hence it is a periodic orbit since it contains which is an isolated point in it. If , then from Lemma 6.4, we have . ∎
Corollary 6.15.
A countable -limit set for a monotone map on a regular curve is a union of periodic orbits.
Proof.
Remark 6.16.
Remark 6.17.
- (1)
- (2)
Example 6.18.
The idea is to slightly change the map in Example 6.10 so that is infinite and composed of periodic orbits with unbounded period. Let some point of the plan , and denote by , the -star centered at . For , we define identified as the map , where and play the role of and , respectively. Let now , each is an arc of , where is one of its endpoints, we denote by the other endpoint of distinct from . Let be the homeomorphism of defined as and in an affine way. We let . Clearly is monotone and continuous. Observe that is a periodic orbit of period , and . We may pick in such a way that is an infinite star centered at . Define the map given by its restriction . Clearly is monotone and continuous. Moreover and is totally periodic which contains periodic orbits of period , for any .
Acknowledgements. This work was supported by the research unit: “Dynamical systems and their applications”, (UR17ES21), Ministry of Higher Education and Scientific Research, Faculty of Science of Bizerte, Bizerte, Tunisia.
References
- [1] H. Abdelli, -limit sets for monotone local dendrite maps, Chaos Solitons Fractals, 71 (2015), 66–72.
- [2] H. Abdelli, H. Marzougui, Invariant sets for monotone local dendrites, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 26 (2016), 1650150.
- [3] H. Abdelli, H. Abouda and H. Marzougui, Nonwandering points of monotone local dendrite maps revisited, Topology Appl., 250 (2018), 61–73.
- [4] E.D. Anielloa, T.H. Steele, The persistence of -limit sets defined on compact spaces, J. Math. Anal. Appl. 413 (2014), 789–799.
- [5] G. Askri and I. Naghmouchi, On totally periodic -limit sets in regular continua, Chaos Solitons Fractals 75 (2015), 91–95.
- [6] F. Balibrea, J.L. Guirao and M. Lampart, A note on the definition of -limit set, Appl. Math. Inf. Sci. 7 (2013), 1929–1932.
- [7] F. Balibrea and C. La Paz, A characterization of the -limit sets of interval maps. Acta Math. Hungar., 88(4):291–300, 2000.
- [8] F. Balibrea, G. Dvorníková, M. Lampart, P. Oprocha, On negative limit sets for one-dimensional dynamics, Nonlinear Anal. 75 (2012), 3262–3267.
- [9] P. Blanchard, R.L. Devaney, D. Look, M. Moreno Rocha, P. Seal, S. Siegmund, and D. Uminsky, Sierpinski carpets and gaskets as Julia sets of rational maps, In Dynamics on the Riemann Sphere, European Mathematical Society, Zürich, 2006, pp. 97–119.
- [10] L.S. Block and W. A. Coppel, Dynamics in one dimension, Lecture Notes in Mathematics, 1513, Springer-Verlag, Berlin, 1992.
- [11] E. Coven and Z. Nitecki, Non-wandering sets of the powers of maps of the interval, Ergodic Theory Dyn. Syst. 1 (1981), 9–31.
- [12] A. Daghar (2021): On regular curve homeomorphisms without periodic points, J. Difference Equ. Appl., DOI: 10.1080/10236198.2021.1912030.
- [13] A. Daghar, Homeomorphisms of hereditarily locally connected continua. 2021. ⟨hal-03223435v2⟩
- [14] A. Daghar and H. Marzougui. Limit sets of monotone maps on regular curves. 2021. arXiv: 2106.12418v1
- [15] A. Daghar, I. Naghmouchi and M. Riahi, Periodic Points of Regular Curve Homeomorphisms, Qual. Theory Dyn. Syst. 20 (2) (2021).
- [16] J. Hantáková and S. Roth, On backward attractors of interval maps. 2020. arXiv: 2007.10883v2
- [17] J. Grispolakis, E.D. Tymchatyn, - connectedness in hereditarily locally connected spaces, Trans. Amer. Math. Soc., 253 (1979), 303–315.
- [18] M.W. Hero, Special -limit points for maps of the interval, Proc. Amer. Math. Soc. 116 (1992), 1015–1022.
- [19] S. Jackson, B. Mance and S. Roth, A non Borel special -limit set in the square. 2020. arXiv: 2011.05509v1.
- [20] H. Kato, Topological entropy of monotone maps and confluent maps on regular curves, Topol. Proc. 28 (2004), 587–593.
- [21] H. Kato, Topological entropy of piecewise embedding maps on regular curues, Ergodic Theory Dyn. Syst. 26 (2006), 1115–1125.
- [22] S. Kolyada, M. Misiurewicz and L. Snoha, Special -limit sets, In Dynamics: topology and numbers, 157–173, Contemp. Math., 744, Amer. Math. Soc., Providence, RI, (2020).
- [23] K. Kuratowski, Topology, vol.2, Academic Press, New-York, 1968.
- [24] M. Foryś-Krawiec, M.J. Hantáková, P. Oprocha, On the structure of -limit sets of backward trajectories for graph maps. 2021. arXiv:2106.05539v1.
- [25] A. Lelek, On the topology of curves. II, Fund. Math. 70 (1971), 131–138.
- [26] J. Mai, T. Sun, The -limit set of a graph map, Topology Appl. 154 (2007) 2306–2311.
- [27] S.B. Nadler, Continuum Theory: An Introduction, (Monographs and Textbooks in Pure and Applied Mathematics, 158). Marcel Dekker, Inc., New York, 1992.
- [28] I. Naghmouchi, Homeomorphisms of regular curves, J. Difference Equ. Appl., 23 (2017), 1485–1490.
- [29] I. Naghmouchi, Dynamics of Homeomorphisms of regular curves, Colloquium Math., 162 (2020), 263–277.
- [30] I. Naghmouchi. Dynamics of monotone graph, dendrite and dendroid maps. Internat. J. Bifur. Chaos Appl. Sci. Engrg., 21 (2011), 3205–3215.
- [31] G.T. Seidler, The topological entropy of homeomorphisms on one-dimensional continua, Proc. Amer. Math. Soc., 108 (1990), 1025–1030.
- [32] T. Sun, Q. He, J. Liu, C. Tao, H. Xi, Non-wandering sets for dendrite maps, Qual. Theory Dyn. Syst. 14 (2015), 101–108.
- [33] T. Sun, H. Xi, H. Liang, Special -limit points and unilateral limit points for graph maps, Sci China Math., 54 (2011), 2013–2018.
- [34] T. Sun, Y. Tang, G. Su, H. Xi, B. Qin, Special -limit points and -limit points of a dendrite map, Qual. Theory Dyn. Syst. 17 (2018), 245–257.
- [35] E.D. Tymchatyn, Characterizations of continua in which connected subsets are arcwise connected, Trans. Amer. Math. Soc., 222 (1976), 377–388.