Nonlinear coupling of reversed shear Alfvén eigenmode and toroidal Alfvén eigenmode during current ramp

In next generation magnetically confined fusion devices such as ITER Tomabechi et al. (1991), energetic particles (EPs), e.g., fusion alpha particles, are expected to play important roles as they contribute significantly to the total power density and drive symmetry breaking collective modes including shear Alfvén wave (SAW) instabilities Fasoli et al. (2007); Chen and Zonca (2016); Chen and Wang (2020). SAW can lead to EP anomalous transport loss, degradation of burning plasma performance and possible damage of plasma facing components Ding et al. (2015). So for understanding of EP confinement and thus fusion plasma performance, the in-depth research of SAW instability dynamics including nonlinear evolution is needed. Due to plasma nonuniformities and equilibrium magnetic field geometry, SAW instabilities can be excited as EP modes (EPMs) in the continuum Chen (1994), or various discrete Alfvén eigenmodes (AEs) inside forbidden gaps of SAW continuum such as toroidal AE (TAE) Cheng et al. (1985); Chen (1988); Fu and Van Dam (1989), reversed shear AE (RSAE) Berk et al. (2001); Zonca et al. (2002); Kramer et al. (2004), beta-induced AE (BAE) Heidbrink et al. (1993), etc. The nonlinear mode coupling of SAW instabilities, providing an effective channel for the mode saturation, has been observed in experiments Buratti et al. (2005), and investigated analytically Hahm and Chen (1995); Zonca et al. (1995); Todo et al. (2010); Biancalani et al. (2010); Chen and Zonca (2012) as well as in large scale simulations Todo et al. (2010); Zhang and Lin (2013); Biancalani et al. (2018). In this work, two possible channels for RSAE saturation as the result of the nonlinear coupling to TAE during current ramp are proposed and investigated, which are of relevance for burning plasmas in future reactors due to their typically reversed shear advanced scenarios where RSAEs can be strongly driven unstable by core localized fusion alpha particles Tomabechi et al. (1991); Gong et al. (2019); Huang et al. (2020); Wang et al. (2018); Ren et al. (2020).

TAE is one of the most well-known SAW eigenmodes and widely exists in present-day and future magnetically confined plasmas. It can be resonantly excited by EPs in the SAW continuum gap induced by torodicity Cheng et al. (1985); Fu and Van Dam (1989), as the result of the coupling of neighbouring poloidal harmonics of SAW continuum, and is typically localized near the center of two mode rational surfaces, where $q\left(r\right)\simeq\left(2m+1\right)/\left(2n\right)$, with the parallel wavenumbers of the two dominant poloidal harmonics both being $\left|k_{\parallel}\right|\simeq 1/\left(2qR_{0}\right)$. Here, $m/n$ are the poloidal/toroidal mode number and $q$ is the safety factor of the torus. Furthermore, TAE is considered as an important player in transporting EPs due to its low excitation threshold and suitable resonance condition with fusion alpha particles with $v_{\alpha}\gtrsim v_{A}$ in ITER Fasoli et al. (2007). Here, $v_{\alpha}$ is the birth velocity of the fusion alpha particle, and $v_{A}$ is the Alfvén speed.

RSAE, also called Alfvén cascade in literatures, is excited near the minima of the safety factor ($q_{min}$), and is often composed by one dominant poloidal harmonic Berk et al. (2001); Zonca et al. (2002). With the parallel wave number $k_{\parallel}\simeq\left|n-m/q_{min}\right|/R$ and thus its frequency $\omega\simeq k_{\parallel}v_{A}$ determined by the value of $q_{min}$, RSAE related physics is thus, sensitive to the $q$-profile. One thus expects that, with the change of $q$-profile during, e.g., current ramp, the RSAE frequency can sweep from BAE (as $\left|nq_{min}-m\right|\simeq 0$) to TAE (as $\left|nq_{min}-m\right|\simeq 1/2$) frequency range, which has been shown in many experiments Van Zeeland et al. (2007) as well as simulations Wang et al. (2020). Furthermore, it is shown in Ref. Van Zeeland et al. (2007) that, as the core-localized RSAE frequency sweeps up, RSAE can temporally couple to TAE and generate a global mode, creating an effective channel for particle global transport from Tokamak core to edge. This channel was also predicted and investigated theoretically in Ref. Zonca et al. (2002). The coupling of RSAE and TAE with different mode numbers and generating a low frequency mode during the RSAE frequency sweeping process has also been observed in HL-2A experiments Shi (2019).

In this work, we show that, as the RSAE frequency sweeps up during current ramp, two important potential nonlinear mode coupling processes may happen. In the first process, a RSAE $\Omega_{R}\equiv\Omega_{R}\left(\omega_{R},\mathbf{k_{R}}\right)$ couples to a TAE $\Omega_{T}\equiv\Omega_{T}\left(\omega_{T},\mathbf{k_{T}}\right)$ with same poloidal and toroidal mode numbers and generates a geodesic acoustic mode (GAM) $\Omega_{G}\equiv\Omega_{G}\left(\omega_{G},\mathbf{k_{G}}\right)$ with toroidally symmetric and poloidally near symmetric mode structure Winsor et al. (1968); Zonca and Chen (2008). Here, subscripts “R”, “T” and “G” represent RSAE, TAE and GAM, respectively. In the second channel, a RSAE couples to a counter-propagating TAE and generates an ion acoustic wave (IAW) $\Omega_{S}\equiv\Omega_{S}\left(\omega_{S},\mathbf{k_{S}}\right)$, and this process can occur even if RSAE has different poloidal/toroidal mode numbers with TAE. Therefore, generally speaking, the condition for the latter process to occur, including radial mode structure overlapping, is more easily satisfied, as we show later. It is worthwhile noting that, in both channels, the low frequency secondary modes, i.e., GAM and IAW, can both be Landau damped due to resonance with thermal ions, and thus heat fuel deuterium and tritium ions, proving a new alpha channelling mechanism that indirectly transfer fusion alpha particle energy to fuel ions Fisch and Rax (1992); Hahm (2015); Qiu et al. (2018).

We use the standard nonlinear perturbation theory to study the nonlinear interactions between RSAE and TAE during current ramp. For typical low-$\beta$ discharges, magnetic compression can be neglected, and the electrostatic potential $\delta\phi$ and the parallel component of vector potential $\delta A_{\parallel}$ are used as perturbed field variables. Here, $\beta$ is the ratio of thermal to magnetic pressure. Furthermore, we use $\delta\psi\equiv\omega\delta A_{\parallel}/\left(ck_{\parallel}\right)$ as an alternative field variable replacing $\delta A_{\parallel}$ for convenience, and one can have $\delta\phi=\delta\psi$ in the ideal MHD limit.

For RSAE and TAE with $nq\gg 1$ in reactor relevant parameter regime Fasoli et al. (2007); Chen and Zonca (2016); Wang et al. (2018); Ren et al. (2020), we adopt the following ballooning mode representation in the $\left(r,\theta,\varphi\right)$ field-aligned flux coordinates Connor et al. (1978)

$\displaystyle\delta\phi$

$\displaystyle=$

$\displaystyle Ae^{i\left(n\phi-\hat{m}\theta-\omega t\right)}\underset{j}{\sum}e^{-ij\theta}\Phi\left(x-j\right)+c.c.{\color[rgb]{1,0,0},}{\color[rgb]{0,0,1}.}$

Here, $m=\hat{m}+j$ with $\hat{m}$ being the reference poloidal number, $x\equiv nq-m$, $\Phi$ is the parallel mode structure with the typical radial extension comparable to distance between neighboring mode rational surfaces, and $A$ is the mode envelope amplitude. Furthermore, $\Omega_{G}$ and $\Omega_{S}$ can be shown as

	$\displaystyle\delta\phi_{G}$	$\displaystyle=$	$\displaystyle A_{G}e^{i\left(\int k_{G}dr-\omega_{G}t\right)}+c.c.,$
	$\displaystyle\delta\phi_{S}$	$\displaystyle=$	$\displaystyle A_{S}e^{i\left(n_{S}\phi-m_{S}\theta-\omega_{S}t\right)}\Phi_{S}+c.c..$

The IAW is a secondary mode and its parallel mode structure $\Phi_{S}$ is determined by $\Phi_{R}$ and $\Phi_{T}$ Qiu et al. (2016). Different from previous works on spontaneously decay of a pump wave into two sidebands, e.g., as in the case of zonal flow excited by SAW Chen and Zonca (2012); Qiu et al. (2017), the RSAE and TAE investigated here are simultaneously driven unstable by EPs Wang et al. (2018), and thus, the radial mode structure of RSAE and TAE may not overlap completely.

The nonlinear interaction of $\Omega_{R}$ and $\Omega_{T}$ can be described by quasi-neutrality condition

$\displaystyle\dfrac{n_{0}e^{2}}{T_{i}}\left(1+\dfrac{T_{i}}{T_{e}}\right)\delta\phi_{k}$

$\displaystyle=$

$\displaystyle\underset{s}{\sum}\left\langle qJ_{k}\delta H_{k}\right\rangle_{s},$

(1)

and nonlinear gyrokinetic vorticity equation derived from parallel Ampére’s law Chen and Zonca (2016)

	$\displaystyle\dfrac{c^{2}}{4\pi\omega_{k}^{2}}B\dfrac{\partial}{\partial l}\dfrac{k_{\perp}^{2}}{B}\dfrac{\partial}{\partial l}\delta\psi_{k}+\dfrac{e^{2}}{T_{i}}\left\langle\left(1-J_{k}^{2}\right)F_{0}\right\rangle\delta\phi_{k}$
	$\displaystyle-\underset{s}{\sum}\left\langle\dfrac{q}{\omega_{k}}J_{k}\omega_{d}\delta H_{k}\right\rangle$
	$\displaystyle=-i\dfrac{c}{B_{0}\omega_{k}}\underset{\mathbf{k}=\mathbf{k^{\prime}}+\mathbf{k^{\prime\prime}}}{\sum}\mathbf{\hat{b}}\cdot\mathbf{k^{\prime\prime}}\times\mathbf{k^{\prime}}\left[\dfrac{c^{2}}{4\pi}k_{\perp}^{\prime\prime 2}\dfrac{\partial_{l}\delta\psi_{k^{\prime}}\partial_{l}\delta\psi_{k^{\prime\prime}}}{\omega_{k^{\prime}}\omega_{k^{\prime\prime}}}\right.$
	$\displaystyle\left.+\left\langle e\left(J_{k}J_{k^{\prime}}-J_{k^{\prime\prime}}\right)\delta L_{k^{\prime}}\delta H_{k^{\prime\prime}}\right\rangle\right].$		(2)

Here, $J_{k}\equiv J_{0}\left(k_{\perp}\rho\right)$ with $J_{0}$ being the Bessel function of zero index, $\rho=v_{\perp}/\Omega_{c}$ is the Larmor radius with $\Omega_{c}$ being the cyclotron frequency, $F_{0}$ is the equilibrium particle distribution function, $\omega_{d}=\left(v_{\perp}^{2}+2v_{\parallel}^{2}\right)/\left(2\Omega_{c}R_{0}\right)\left(k_{r}\sin\theta+k_{\theta}\cos\theta\right)$ is the magnetic drift frequency, $l$ is the length along the equilibrium magnetic field line, $\left\langle\cdots\right\rangle$ means velocity space integration, $\sum_{s}$ is the summation of different particle species with $s=i,e$ representing ion and electron, and $\delta L_{k}\equiv\delta\phi_{k}-k_{\parallel}v_{\parallel}\delta\psi_{k}/\omega_{k}$. The three terms on the left hand side of equation (2) are respectively the field line bending, inertial and curvature coupling terms, dominating the linear SAW physics. The two terms on the right hand side of equation (2) correspond to Maxwell (MX) and Reynolds stresses (RS) that contribute to nonlinear mode couplings as MX and RS doesn’t cancel each other Chen and Zonca (2013), with their contribution dominating in the radially fast varying inertial layer, and $\sum_{\mathbf{k}=\mathbf{k^{\prime}}+\mathbf{k^{\prime\prime}}}$ indicates the wavenumber and frequency matching condition required for nonlinear mode coupling. $\delta H_{k}$ is the nonadiabatic particle response, which can be derived from nonlinear gyrokinetic equation Frieman and Chen (1982):

	$\displaystyle\left(-i\omega_{k}+v_{\parallel}\partial_{l}+i\omega_{d}\right)\delta H_{k}=-i\omega_{k}\dfrac{q}{T}F_{0}J_{k}\delta L_{k}$
	$\displaystyle-\dfrac{c}{B_{0}}\underset{\mathbf{k}=\mathbf{k^{\prime}}+\mathbf{k^{\prime\prime}}}{\sum}\mathbf{\hat{b}}\cdot\mathbf{k^{\prime\prime}}\times\mathbf{k^{\prime}}J_{k^{\prime}}\delta L_{k^{\prime}}\delta H_{k^{\prime\prime}}.$		(3)

Here, with the diamagnetic drift related term neglected in the first term on the right hand side of equation (3), we assume that thermal plasma - dominating the nonlinear coupling process - contribution to RSAE/TAE linear destabilization is negligible, and RSAE/TAE are excited by EPs. Inclusion of thermal ion diamagnetic drift effect is straightforward, and will not change the main physics picture here. For TAE/RSAE with $\left|k_{\parallel}v_{e}\right|\gg\left|\omega_{k}\right|\gg\left|k_{\parallel}v_{i}\right|,\>\left|\omega_{d}\right|$, the linear ion/electron responses can be derived to the leading order as $\delta H^{L}_{k,i}=eF_{0}J_{k}\delta\phi_{k}/T_{i}$ and $\delta H^{L}_{k,e}=-eF_{0}\delta\psi_{k}/T_{e}$. Furthermore, one can have, to the leading order, ideal MHD constraint is satisfied, i.e., $\delta\phi_{T}=\delta\psi_{T}$, $\delta\phi_{R}=\delta\psi_{R}$, by substituting these ion/electron responses of TAE and RSAE into quasi-neutrality condition.

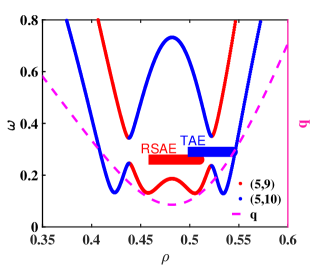
The nonlinear coupling and generation of GAM as the RSAE couples to the TAE can be illustrated in Fig. 1, where a general $n=5$ SAW continuum in a typical reversed shear configuration is given Bao et al. (2020). The $m=9$ and $m=10$ continuum are marked in red and blue, respectively, and they coupled at the vicinity of $q=1.9$. A RSAE can be generated at the local maximum of the continuum, while a TAE can be excited within the continuum gap, with their radial localization determined by $q_{min}$ and $q=(2m+1)/(2n)$, respectively. As $|nq_{min}-m|$ approaches $1/2$ during current ramp, the localization of the RSAE gets closer to that of the TAE, and the frequency difference of RSAE and TAE decreases. As a result, RSAE and TAE may couple, and generate a GAM. Noting that GAM is characterized by the toroidal/poloidal mode numbers being $n/m=0/0$ and a frequency much lower than those of RSAE/TAE, i.e., $|\omega_{G}|\ll|\omega_{R}|,|\omega_{T}|$, one can have that TAE and RSAE have opposite poloidal and toroidal mode numbers as well as opposite frequencies $\left(\omega_{R}\omega_{T}<0\right)$. Thus, the two modes propagate in the same direction, i.e., their parallel phase velocities $V_{P}\equiv\omega/k_{\parallel}$ have the same sign. For GAM with predominantly electrostatic perturbation, its nonlinear generation can be determined by the vorticity equation, while the quasi-neutrality condition is used in determining the linear polarization of GAM and both AEs Qiu et al. (2009); Cheng et al. (1985). The linear ion/electron responses to GAM can be derived considering the $\left|\omega_{tr,e}\right|\gg\left|\omega_{G}\right|\gg\left|\omega_{d,e}\right|$ and $\left|\omega_{G}\right|\gg\left|\omega_{tr,i}\right|,\left|\omega_{d,i}\right|$ orderings, respectively, and one derives, to the leading order, $\delta H_{G,i}^{L}=eF_{0}J_{G}\delta\phi_{G}/T_{i}$ and $\delta H_{G,e}^{L}=-eF_{0}\overline{\delta\phi_{G}}/T_{e}$. Here, $\omega_{tr}\equiv v_{\parallel}/(qR_{0})$ is the transit frequency, and $\overline{(\cdots)}\equiv\int^{2\pi}_{0}(\cdots)d\theta/(2\pi)$ denotes flux surface average. The nonlinear equation describing GAM generation can then be derived from nonlinear vorticity equation as

	$\displaystyle\dfrac{e^{2}}{T_{i}}\left\langle\left(1-J_{G}^{2}\right)F_{0}\right\rangle\delta\phi_{G}-\underset{s}{\sum}\left\langle\dfrac{q}{\omega}J_{G}\omega_{d}\delta H^{L}_{G}\right\rangle$
	$\displaystyle\simeq-i\dfrac{c}{B_{0}\omega}\mathbf{\hat{b}}\cdot\mathbf{k_{R}}\times\mathbf{k_{T}}$
	$\displaystyle\times\left[\dfrac{c^{2}}{4\pi}\left(k_{T\perp}^{2}-k_{R\perp}^{2}\right)\dfrac{k_{T,\parallel}k_{R,\parallel}}{\omega_{T}\omega_{R}}\delta\psi_{T}\delta\psi_{R}\right.$
	$\displaystyle\left.+\left\langle e\left(J_{T}-J_{R}\right)\left(\delta\phi_{T}\delta H_{R}+\delta\phi_{R}\delta H_{T}\right)\right\rangle\right].$		(4)

In deriving equation (4), the linear field line bending term associated with the GAM electromagnetic effects is neglected because GAM is predominantly an electrostatic mode. The last term of equation (4) is the RS evaluated using the linear ion responses to RSAE/TAE and the $k^{2}_{\perp}\rho^{2}_{i}\ll 1$ ordering. Noting that $k_{G}=k_{T,r}+k_{R,r}$, $k_{r}\gg k_{\theta}$ for inertial layer responses of TAE and RSAE that dominates the nonlinear mode coupling Chen and Zonca (2013), one obtains

	$\displaystyle\delta\phi_{G}$	$\displaystyle=$	$\displaystyle\dfrac{c\omega}{B_{0}\left(\omega^{2}-\omega_{G}^{2}\right)}k_{T,\theta}\left(1-\dfrac{k_{T,\parallel}k_{R,\parallel}}{\omega_{T}\omega_{R}}v_{A}^{2}\right)$		(5)
		$\displaystyle\times$	$\displaystyle\left(\delta\phi_{R}\partial_{r}\delta\phi_{T}-\delta\phi_{T}\partial_{r}\delta\phi_{R}\right).$

Here, $\omega_{G}$ is the eigenfrequency of GAM and is given as $\omega^{2}_{G}=\left(7/4+T_{e}/T_{i}\right)v_{ti}^{2}/R_{0}^{2}$ Qiu et al. (2009), $\omega=\omega_{T}+\omega_{R}$ from balancing the temporal evolution of both sides of equation (4), which is not necessarily exactly the same as $\omega_{G}$. Equation (5) describes the nonlinear drive of GAM by the beating of co-existing TAE and RSAE simultaneously driven unstable by e.g., EPs. The effective coupling and GAM generation, requires that $1-k_{T,\parallel}k_{R,\parallel}v^{2}_{A}/(\omega_{T}\omega_{R})\neq 0$, i.e., breaking of pure Alfvénic state Chen and Zonca (2013). This condition is satisfied by the deviation of both RSAE and TAE from ideal SAW dispersion relation, due to the effects of reversed shear profile and toroidicity Zonca et al. (2002); Zonca and Chen (1996), respectively, and one has $1-k_{T,\parallel}k_{R,\parallel}v^{2}_{A}/(\omega_{T}\omega_{R})\simeq O(\epsilon)$ with $\epsilon\equiv r/R_{0}$ being the inverse aspect ratio. Noting that, this forced driven process is thresholdless, but only when $\omega_{T}+\omega_{R}$ gets sufficiently close to $\omega_{G}$ during RSAE frequency sweeping as a result of current ramp, GAM will be strongly excited, and the process can be observed experimentally and play an important role in the RSAE/TAE saturation.

In Ref. Van Zeeland et al. (2007), a central localized RSAE coupling to TAE and generate a global TAE is investigated, where a continuum similar to Fig. 1 is used for the illustration of the mechanism. However, the process discussed in Ref. Van Zeeland et al. (2007) is a linear process, where the RSAE has the same toroidal mode number with the TAE while neighboring poloidal mode number is coupled through toroidicity, and is thus completely different from the present work.

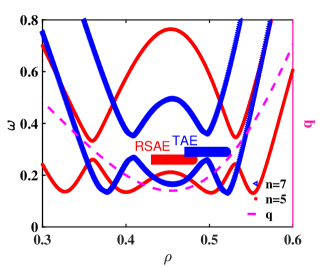
Considering the other case of RSAE coupling to TAE and generating an IAW with finite $k_{S,\parallel}$ and $|\omega_{S}|\ll|\omega_{T}|,|\omega_{R}|$, one can have TAE and RSAE have opposite frequencies while their parallel wavenumbers have the same sign, and thus are counter-propagating with opposite $V_{p}$. This process is illustrated in Fig. 2 using the nonlinear coupling of an $n=5$ RSAE and an $n=7$ TAE as example, where the red and blue curve represent the $n=5$ and $n=7$ SAW continua, and the corresponding RSAE and TAE are radially overlapped, leading to potential nonlinear coupling. Note that, the RSAE and TAE can have different toroidal mode numbers, unlike the case of GAM generation limited by the $n_{R}+n_{T}=0$ constraint. Thus, it is expected the condition for IAW generation can be more easily satisfied (as shown clearly in Fig. 2), in future burning plasmas where multiple-$n$ SAW instabilities can be driven unstable simultaneously.

Separating the linear to nonlinear particle responses to IAW as $\delta H_{S}=\delta H_{S}^{L}+\delta H_{S}^{NL}$, the leading order linear ion/electron responses to IAW can be derived from gyrokinetic equation as $\delta H_{S,i}^{L}=\left(eF_{0}J_{S}\omega_{S}\delta\phi_{S}\right)/\left[T_{i}\left(\omega_{S}-k_{S,\parallel}v_{\parallel}\right)\right]$ and $\delta H_{S,e}^{L}=0$, considering the $\left|\omega_{tr,e}\right|\gg\left|\omega_{S}\right|\simeq\left|\omega_{tr,i}\right|\gg\left|\omega_{d,i}\right|,\left|\omega_{d,e}\right|$ ordering. Furthermore, the nonlinear particle responses to IAW can be derived as

	$\displaystyle\delta H_{S,e}^{NL}$	$\displaystyle=$	$\displaystyle-i\dfrac{\hat{\Lambda}}{\omega_{T}}\dfrac{e}{T_{e}}F_{0}\delta\psi_{T}\delta\psi_{R},$		(6)
	$\displaystyle\delta H_{S,i}^{NL}$	$\displaystyle=$	$\displaystyle-i\dfrac{\hat{\Lambda}}{\omega_{T}}\dfrac{e}{T_{i}}F_{0}J_{T}J_{R}\delta\psi_{T}\delta\psi_{R},$		(7)

with $\hat{\Lambda}=\left(c/B_{0}\right)\mathbf{\hat{b}}\cdot\mathbf{k_{R}}\times\mathbf{k_{T}}$. Here, $\omega_{S}\simeq-\omega_{T}$ is used. Assuming ideal MHD condition ($\delta\psi=\delta\phi$) for RSAE and TAE in the radially fast varying inertial layer where nonlinear coupling dominates, the excitation of electrostatic IAW by TAE and RSAE can be derived from quasi-neutrality condition, by substituting the particle responses into quasi-neutrality condition, and one obtains

$\displaystyle\mathscr{E}_{S}\delta\phi_{S}$

$\displaystyle=$

$\displaystyle i\dfrac{\hat{\Lambda}}{\omega_{T}}\beta_{S}\delta\phi_{T}\delta\phi_{R}.$

(8)

Here, $\mathscr{E}_{S}\equiv 1+\tau+\tau\left\langle F_{0}J_{S}^{2}/n_{0}\right\rangle\zeta_{S}Z\left(\zeta_{S}\right)$ is the linear dispersion function of $\Omega_{S}$, with $\tau\equiv T_{e}/T_{i}$, $\zeta_{S}\equiv\omega_{S}/\left(k_{S,\parallel}v_{i}\right)$ and $Z\left(\zeta_{S}\right)$ being the plasma dispersion function defined as

$\displaystyle Z\left(\zeta_{S}\right)$

$\displaystyle\equiv\frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty}\frac{e^{-y^{2}}}{y-\zeta_{S}}dy.$

In addition, $\beta_{S}\equiv 1+\tau\left\langle F_{0}J_{S}J_{T}J_{R}/n_{0}\right\rangle\left(1+\zeta Z\left(\zeta\right)\right)$ is related to the cross-section of the coupling, and in the case of counter-propagating RSAE/TAE of interest here, the RS and MX have the same sign, and $\beta_{S}\simeq 2$ in the long wavelength limit. Similarly with the case discussed before, equation (8) describes the nonlinear generation of IAW by the coupling of TAE and RSAE, showing that this coupling process is thresholdless, but only significantly affect the nonlinear dynamics as $|\omega_{R}+\omega_{T}|\lesssim O(v_{i}/(qR_{0}))$ (i.e., $\zeta_{S}\lesssim O(1)$). In this parameter regime, RSAE and TAE strongly couples as $|\mathscr{E}_{S}|\ll 1$, as shown by equation (8). On the other hand, as $\zeta_{S}\lesssim O(1)$, the nonlinearly generated IAW is a heavily Landau damped quasi-mode that effectively gives energy to thermal ions, leading to effective dissipation of RSAE/TAE wave energy.

In conclusion, two novel nonlinear coupling channels for RSAE saturation are proposed and investigated. In the first channel, the RSAE couples to a co-propagating TAE with the same toroidal and poloidal mode numbers, and generates a GAM. In the second channel, the RSAE couples to a counter-propagating TAE and generates an IAW. In the latter case, the RSAE and TAE toroidal/poloidal mode numbers are not necessarily the same. The frequency matching condition is more easily satisfied as the RSAE frequency is slightly lower than that of TAE, and is more easily satisfied during current ramp. Our results show that, the IAW generation can be more efficient in that 1. the RSAE and TAE don’t have to have the same toroidal/poloidal mode numbers, and thus, the condition for mode structure radial overlapping can be more easily satisfied, and 2. the RSAE and TAE are counter-propagating, so the RS and MX will not cancel each other, and thus, the nonlinear coupling cross-section is much larger. In burning plasmas, the RSAE and TAE are linearly excited by EPs simultaneously, and as a result, both processes are thresholdless. In both processes, the nonlinearly generated secondary mode, i.e., GAM and IAW, can be Landau damped due to resonance with thermal ions, and heat thermal ions, and thus provides an effectively channel for nonlinearly transfer fusion alpha particles to fuel ions for the sustained burning of fusion plasmas. The saturation level of the low frequency sideband in the two processes, can be estimated from equation(5) or (8), by expanding the GAM or IAW linear dispersion function along the characteristics Qiu et al. (2018) and balancing the nonlinear drive by RSAE&TAE nonlinear coupling, and the GAM/IAW Landau damping. The corresponding fuel ion anomalous heating rate can also be obtained, and will be investigated in a future publication.

This work is supported by the National Key R&D Program of China under Grant No. 2017YFE0301900, the National Science Foundation of China under grant No. 11875233, and China Postdoctoral Science Foundation under grant No. 2020M670756. The authors are grateful to Dr. Jian Bao (Institute of physics, Chinese Academy of Science) for his help with the SAW continua.