Nonlinear Bloch-Zener oscillations for Bose-Einstein condensates in a Lieb optical lattice
Abstract
We investigate Bloch-Zener oscillations and mean-field Bloch bands of a Bose-Einstein condensate (BEC) in a Lieb optical lattice. We find that the atomic interaction will break the point group symmetry of the system, leading to the destruction of the Dirac cone structure, while the flat band is preserved on the highly symmetric lines. Due to the nonlinear effect, a tubular band structure with a flat band will appear in the system. Furthermore, comparing with that the tight-binding (TB) model fails to describe the interacting bosonic systems in the honeycomb lattice, we show that the TB model is applicable to study the nonlinear energy band structures for the Lieb lattice. In addition, we show that the loop structure can be determined by the observation of the chaos of the state in the Bloch-Zener oscillations.
pacs:
Valid PACS appear hereI Introduction
Two-dimensional condensed matter such as graphene and similar materials Liu2011 ; Mal2012 ; Zhou2014 with Dirac cones at Fermi energy, in which low-energy excitations at high symmetry points can be described by the Dirac equation, are of great theoretical and experimental interests due to their unique electronic properties. Recent advances in exploring spin-orbit coupling and artificial gauge fields for neutral atoms DWZhang2018AIP ; Dali2011 ; Glodman2014 ; Galtski2013 ; SLZhu2006 ; SLZhu2011 make possible the creation and manipulation of Dirac cones in optical lattices Tarr2012 ; Monta2009 ; SLZhu2007 ; DWZhang2012 . Different lattice geometries of one or two dimensions in ultracold atomic gases Sol2011 ; Sol2012 ; Tarr2012 have been realized experimentally, such as honeycomb lattice with Dirac points at the corner of Brillouin zone (BZ) Wun2008 , the Lieb lattice with a flat band Taie2015 , and the kagome lattice Jo2012 ; SZhang2019 , etc. Furthermore, some well-known models in condensed matter physics such as Harper-Hofstadter model and Haldane model Miv2013 ; Aidelsburger2013 ; Aidelsburger2015 ; Jotzu2014 ; DWZhang2017 ; LBShao2008 have been theoretically investigated and experimentally realized in optical lattices with promising controllability. The band structure of the cold atom systems can be reconstructed by combining techniques of Bloch-Zenor oscillations with adiabatic mapping of cold atoms, and the existence of Dirac points can be revealed by the momentum-resolved inter-band transitions Mor2006 ; Sal2007 ; Kling2010 ; Lim2012 ; Lim2015 ; DWZhang2016 ; FMei2012 ; YQZhu2017 .
On the other hand, with high purity and tunability, the ultracold atomic system is one of the best quantum simulators Lewe2007 ; DWZhang2018AIP ; Bloch2008 to study nonlinear dynamics for a BEC with weak interaction. For instance, the lattice structure can be changed by adjusting the laser intensity, while the interaction can be manipulated by tuning s-wave scattering length Bloch2008 . In this paper, a nonlinear Gross-Pitaevskii (GP) theory is derived by applying the mean-field approximation to a weakly coupling system. Besides the atomic systems, GP equation can also be used to study other nonlinear systems such as photonic systems with Kerr nonlinearity, exciton-polariton condensates, acoustic cavities, and circuit resonators Hennig1999 ; Lagoudakis2008 ; Ley2012 ; Ley2016 ; Hadad2016 ; Whittaker2018 ; Nejad2019 . Previous studies have shown that the mean-field Bloch bands for a BEC in an optical lattice possess unique loop structures Dia2002 ; Wu2002 ; Wang2006 ; Bona2017 . As predicted in Ref. Chen2011 , while Dirac points in a honeycomb lattice are broken by the nonlinearity and an intersecting tubular structure appears around the K point, the TB model, however, fails to describe the nonlinear dynamics in this system Chen2011 . In this article, we study BEC in an optical Lieb lattice. The Lieb lattice features a diabolic single dirac cone with a flat band, distinguishing from most systems in which the Dirac points come up in pairs (the so-called Fermion doubling) Shen2010 ; GSilva2014 ; JWei2019 ; Mukherjee2015 ; Poli2017 . The flat band is attributed to the bipatite nature of the lattice Mielke1991 ; ZLiu2014 , leading to exotic physics which is entirely determined by the interaction and topology due to constant dispersion caused by destructive interference Kopnin2011 ; JUlku2016 . Thus the nonlinear Lieb lattice may serve as a natural, and possibly indispensable extension of the honeycomb lattice considered in Ref. Chen2011 . Our results show that the nonlinear Dirac cone for the Lied lattice has a similar tubular structure to that of Ref. Chen2011 . Furthermore, the Dirac points in our model are protected by a plane point group symmetry. Any small interatomic interaction will break the symmetry, then the Dirac points will be lifted. And more importantly, the TB model works well in the vicinity of the M point for our system unexpectedly, which is sharply different with the results in the honeycomb lattice explored in Ref. Chen2011 .
The interplay of nonlinear superfluidity and relativistic Dirac dynamics leads to many novel effects, such as adiabatic failure, chaos Wu2000 ; Wang2006 and dynamic instability Bro2001 , which can be utilized to reveal information on the nonlinear energy bands. In this article we prove that the Bloch-Zener oscillations for the BEC in an optical lattice can be used as an efficient tool to study the structure of the nonlinear energy bands. The regime of fold bands can be determined by detecting the time evolution of the population of sublattices during Bloch oscillations, while the nonlinearity strength could be measured by the interband transition probability of specific tunneling process.
The paper is organized as follows. In Sec. II, we numerically calculate the energy spectra from both the GP Hamiltonian and the Bloch Hamiltonian of the TB model. And we discuss how the nonlinearity breaks the Dirac cone from the perspectives of symmetry. In Sec. III, we consider atoms performing Bloch-Zener oscillations. The transition probabilities for different tunneling process are given both in the adiabatic limit and sudden limit. Finally, a short conclusion is given in Sec. IV.
II Superfluid in Lieb lattice

The mean-filed description of a condensate in superfluid phase leads to the Gross-Pitaevskii (GP) equation,
| (1) |
where is the mass of particle, is the scattering length and is the optical lattice potential of configurations of Lieb lattice (see Fig. 1). The nonlinear strength is denoted as in following discussions. The lattice could be experimentally realized by superimposing three pairs of laser beams with the following formation Taie2015 ; Shen2010 ; Weeks2010 ,
| (2) |
where is the wave number of the lattice and the wavelength of the lasers. The potential amplitudes , and could be tuned by adjusting the laser intensities, and are the phase of laser beams. For simplicity we choose and .
The Landau instability of the BEC superfluid is not much affected by the lattice strength ZChen2010 . As the lattice strength increases, the system goes into the tight binding regime. Following the methods outlined in Ref. Smerzi2002 ; Trombettoni2001 ; Hu2015 , we map the GP equation (1) onto a discrete nonlinear Scrdinger equation to contruct an effective tight-binding Hamiltonian. We write the bosonic field as a sum over the three sub-lattices , where is the Wannier function and () are lattice vectors in the three sub-lattices of the -th cell. Then the tight-binding Hamiltonian for our BEC system reads
| (3) |
where runs over all nearest-neighboring sites, includes the sublattices in one unit cell, is the hopping constant and is the nonlinear strength, for simplicity we take and do not consider the next-nearest hopping in the main text. In experiments, one may upload atoms which weigh into the optical lattice. The lattice can be created by a laser of wavelength . Thus the recoil energy is estimated by . And the tunneling rate for a lattice depth in the absence of nonlinearity Miyake2013 .
In momentum space, with , and
| (4) |
where denotes the Bloch vector with and , and are spin-one matrices with , from the Gell-Mann matrices (for explicit form, see Appendix A), together with which consist the Lie algebra . is the nonlinear term. The Bloch Hamiltonian in absence of nonlinear term has energy dispersions,
| (5) |
as illustrated in Fig. 1 (c), which are in good agreement with Bloch bands of the continuous system Eq. (1), see Appendix B.

Note that the low energy effective Hamiltonian has a rotation symmetry , where and and a sublattice symmetry , where .
In fact the Lieb lattice has a plane point group symmetry. The quasi-momentum is invariant with operations in little group at and at . And the invariant line and are protected by mirror symmetry and respectively, thus indegenerate, while the Dirac point at M is protected by the 4mm symmetry featuring a nontrivial two dimensional irreducible representation. However, in presence of a nonzero nonlinear term , even weak interaction will violate this symmetry, lifting the degeneracy at M and resulting in two more additional crossings, as shown in Fig. 2.
We numerically calculate the Bloch bands of the GP equation Eq. (1) with the Bloch wave solutions which are of the form , here is the reciprocal lattice vector. The results are shown in Fig. 2, which are in good agreement with that of the tight binding model in the vicinity of . As predicted by previous works Chen2011 , the Bloch bands of a nonlinear two dimensional system possess tube structures and the Dirac point is extended into a closed self-crossing loop. The bands of our system have similar structures around the point. As illustrated in Fig. 2 (g), the energy bands consist of three ”tubes”, which intersect at point . They have wedged cross-section with size increasing monotonically from to ( denotes the invariant line cross and parallel to -direction) as shown in Fig. 2 (g), (ii)-(iii), and overlap with each other to produce the structure of Fig. 2 (g), (i/iv). For the Dirac point at accidentally degenerates with the flat band, which produces a triple point. As shown before, the Dirac point at will be lifted to two crossing points and for any as the nonlinearity breaks the symmetry. However, the loop structures at the zone of Brillouin zone, as illustrated in Fig. 2 (c) [or Fig. 2 (f)], only emerges as the nonlinear strength () exceeds a critical value (). Specifically, the nonlinearity does not modify the flat band on the invariant line , as shown in Fig. 2 (a) and (c). Furthermore, the flat bands of the tight binding model for and on share the same eigen-states, only with a uniform shift of the eigen-value from to for any finite .
III Landau-Zener transition
Now we consider atoms performing Bloch oscillations with a constant applied force . As these atoms are accelerated in the vicinity of the triple Dirac point, the tunneling probability to other bands is finite. This is a problem first considered by Landau and Zener, usually referred to as Landau-Zener (LZ) transition LandauZener1932 ; XTan2014 ; Shevchenko2010 ; Oliver2005 ; Car1986 .
The effective Hamiltonian can be obtained from Eq. (4) by performing Peierls substitution ,
| (6) |
where . The Peierls substitution can also be understood in a semiclassical way that the quasimomentums are subjected to a constant force Lim2015 . An initial state in the n-th band evolves as
| (7) |
where . The force linearly increases momentum of atoms and leads to a non-adiabatic transition to other bands near the crossing (or anti-crossing) point. From the finial state the transition probability is defined as
| (8) |
where and is m-th eigen-state of , with at the final time .
III.1 Adiabatic limit



For simplicity, we start with considering atoms performing one Bloch oscillation in directions. We numerically calculate the interband transition probabilities as a function of force (see Fig. 3). The applied force is given by and atoms initially prepared in . The evolution time is set to be . Thus the momentum of atoms increases form to under the influence of the force, along path of which the system has the spectrum shown in Fig. 2 (f).
For g = 0, if the atoms take shorter time to travel across the anti-crossing than the Zener tunneling time , the system will evolve adiabatically, where is the adiabaticity parameter and is the minimal energy splitting Shevchenko2010 . For the parameters adopted in this paper, this corresponds to . In presence of nonlinearity, the adiabaticity only holds for the bands whose structure is not modified by the nonlinearity. As seen in Fig. 3 (a) and (c), the interband transition probabilities are vanishing while the force is weak enough. However, as shown in Fig.3 (b), the adiabaticity breaks down when atoms are initially prepared in the second band, since the nonlinearity changes the topological structure of this band.
Furthermore, the tunneling probability shows an irregular oscillation for atoms initially in the band with a loop structure, as observed in similar nonlinear systems studied in previous works Graefe2006 ; Wang2006 . This irregularity is thought to be associated with the chaotic behavior of the nonlinear system Wang2006 . As shown in Fig. 3 (d), the evolution of state exhibits chaotic features, which could be directly observed in the laboratory by detecting the particle number density of the sublattices by means of hybrid time-of-flight images. For diagonal sweeping, the oscillation of state emerges shortly after the atoms travel across the band loops. Thus we could determine the regime of the fold in the energy bands. In fact, the time evolution of at the loops is unstable, which leads to the chaos in the LZ process. As illustrated in Fig. 4, the norm mode for the evolution of a eigen-state is cyclic. However, the periodicity breakdowns for the states on the fold, which implies the instability of the dynamics. The dynamical instability is attributed to the superfluidity of the BEC, which can be understood by the response of the superflow to a perturbation governed by the Bogoliubov equation WuL2001 , or the semiclassic fixed point theory of the Hamiltonian-Jacobi matrix Wang2006 . We adopt the latter method and give a brief introduction in Appendix C. As suggested by a previous work ZChen2010 , the Landau instability of superfluidity in a two-dimensional lattice is direction independent while the dynamical instability is not. Furthermore, Landau instability occurs beyond a critical wave number , and the superfluidity goes into a more stable phase as the nonlinear interaction increases.
Next we consider tunneling process along the diagonal path , i.e., the applied force is given by , where we set . The spectrum on this sweeping path has the structure shown in Fig. 2 (d). The atoms are still initially prepared in and the evolution time still set to be . Fig. 5 presents the transition probability as a function of the force . Different from the linear transition process, the relation of transition probability (see Appendix D) does not hold for , since the nonlinear term breaks the particle-hole symmetry (or the symmetric structure of the spectrum). And particularly, as shown in Fig. 5 (c) and (f), the results for atoms initially in the middle band remain the same as that of , as the nonlinearity does not change the structure of the flat band. Moreover, atoms prepared in the up or down band do not tunnel into the middle band when they travel across M, just like their behaviors in the absence of nonlinearity (see Appendix. D).
III.2 Sudden limit

We consider the LZ transition acorss a single M point (gapless for ) in sudden limit, i.e., . As the force becomes large, the time that atoms take to travel across M point is much shorter than the Zener tunneling time. Thus the atoms stay in the initial state in most of the evolution time. The transition probability that depends on the nonlinear strength is displayed in Fig. 6. We find that difference between the transition probability for and narrows as the sweeping velocity increases. And such difference is vanishing in the sudden limit, as shown in Fig. 6 (c), since the transition probability does not relate much to the structure of the spectrum. We could determine the nonlinearity of the condensate by fitting the experimental data with the interpolation function of numerically.
IV Conclusions
In conclusion, we have numerically studied the energy band structure of a BEC in an optical Lieb lattice and have provided a useful TB model. It is shown that under nonlinearity, the Dirac points at M point are broken and extended into a closed curve, while the flat band still exists on the high-symmetry line. We have shown that the Bloch-Zener oscillations could be utilized as a useful tool to explore the nonlinear bands: (i) the size of metastable fold bands can be determined by detecting the time evolution of the population of sublattices during Bloch oscillations, (ii) the nonlinearity strength could be measured through the interband transition probability of specific tunneling process. Since the interatomic interaction can be easily manipulated, the observation of the phenomena studied here is expectable in the table-top ultracold atomic experiments.
Acknowledgements.
We thank Profs. Li-Jun Lang, Dan-Wei Zhang, and Shi-Liang Zhu for useful discussions. We also thank Zhu Chen for the help on numerical calculation. This work was supported by the Key-Area Research and Development Program of GuangDong Province (Grant No. 2019B030330001), the National Key Research and Development Program of China (Grant No. 2016YFA0301800), and the Key Project of Science and Technology of Guangzhou (Grant No. 201804020055), National Natural Science Foundation of China (Grants numbers 11704132), China Postdoctral Science Foundation (Grant number 2018M633063), and the Startup Foundation of SCNU.Appendix A Mapping to universal Hamiltonian
The Gell-Mann matrices used in this paper is given by
| (9) |
At , an expansion of for small momentum shift gives rise to an effective Hamiltonian which has the universal form
| (10) |
where denotes deviation of the Bloch wave number away from . And by a simple replacement of with , we obtain the motion equation in real space,
| (11) |
where and is with the replacement ().
Appendix B NUMERICAL BAND STRUCTURE CALCULATION FOR
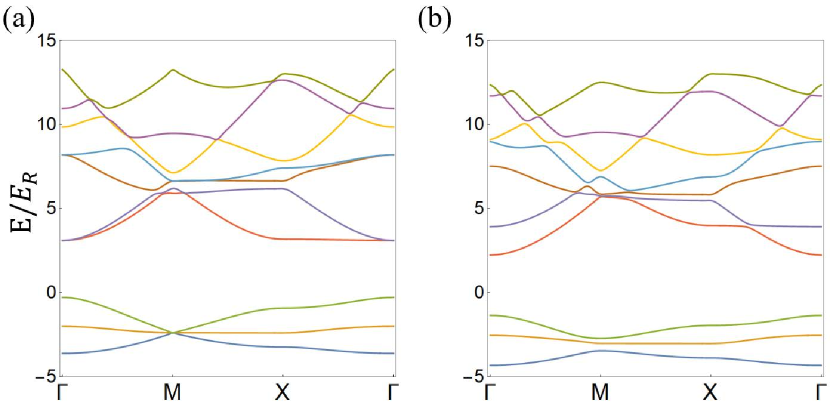
We numerically study the band structure ab initio with the plane wave truncate approximation. We take Fourier transformation and write down the Hamiltonian in momentum space. The eigen-states have the form . And in reciprocal space the potential Eq. (2) is writen as , with components
| (12) |
Then by diagonalizing the Hamiltonian
| (13) |
we obtain the eigen-energies for a specific , where denotes the kinetic energy.
The results are shown in Fig. 7. Here we choose recoil energy as the energy unit. The lowest three bands are quite well approximated by the tight binding model. Bands of Lieb lattice can be gapped for some lattice configurations .
Appendix C Mapping to classical equations

The nonlinear three-level model Eq. 4 can also be described as a classical Hamiltonian system, similar to Ref. Wang2006 ; Graefe2006 . With , , , the nonlinear TB Hamiltonian can be cast into a classical Hamiltonian system,
| (14) | ||||
where , are relative phase, and we treat and as parameters. and are two pairs of canonically conjugate variables which are governed by,
| (15) |
| (16) | ||||
| (17) |
| (18) | ||||
By setting , the eigenenergy is obtained from . And the chaotic nature of the nonlinear system can be revealed by the Hamiltonian-Jacobi matrix, which is obtained by linearizing the above motion equations at the fixed points (corresponding to the eigenstates),
| (19) |
We numerically solve the eigenvalues of along the invariant line . The results are shown in Fig. 8. In general, the eigenvalues are a complex number and only solutions with pure imaginary values are stable. We can see that near point the real parts of the eigenvalue become nonzero, which implies the emergency of the unstable fold structure.
Appendix D Landau-Zener transition for

We consider the tight binding Hamiltonian Eq. (3) with and which possess a finite gap in the system . In momentum space,
| (20) |
And the energy spectrum is given by
| (21) |
Without loss of generality, we consider the motion along the direction. The constant force is given by , and the evolution time is chosen to be . Following the calculations outlined in Ref.Car1986 ; Wang2006 , we can obtain the transition probability for ,
| (22) |
| (23) |
| (24) |
| (25) |
where is the occupation probability on the band at for the state initially on the n band at , and . And we have due to the symmetry of the levels.
We calculate the transition probabilities for with atoms performing a single Bloch oscillation in directions. The results are shown in Fig. 9. Since the parallel momentum is conserved, the term can be seen as an effective mass term. Thus is modified with different initial momentum . In particular, for system in gappless phase, i.e., , and atoms prepared in initial momentum , the travel across the triple Dirac point leads to a unit transferred probability () as shown in Fig. 9 (d).
References
- (1) C. C. Liu, W. Feng, and Y. Yao, Quantum spin Hall effect in silicene and two-dimensional germanium, Phys. Rev. Lett. 107, 076802 (2011).
- (2) D. Malko, C. Neiss, F. Vines, and A. Grling, Competition for graphene: graphynes with direction-dependent dirac cones, Phys. Rev. Lett. 108, 086804 (2012).
- (3) X. F. Zhou et al., Phys. Rev. Lett. 112, 085502 (2014).
- (4) D.-W. Zhang et al., Topological quantum matter with cold atoms, Adv. Phys. 67, 253 (2018).
- (5) J. Dalibard, F. Gerbier, G. Juzeliunas, and P. Öhberg, Colloquium: Artificial gauge potentials for neutral atoms, Rev. Mod. Phys. 83, 1523 (2011).
- (6) N. Goldman, G. Juzelinas, P. Öhberg, and I. B. Spielman, Light-induced gauge fields for ultracold atoms, Rep. Prog. Phys. 77, 126401 (2014).
- (7) S. L. Zhu, H. Fu, C. J. Wu, S. C. Zhang, and L. M. Duan, Spin Hall effects for cold atoms in a light-induced gauge potential, Phys. Rev. Lett. 97, 240401 (2006).
- (8) S. L. Zhu, L. B. Shao, Z. D. Wang, and L.M.Duan, Probing non-Abelian statistics of Majorana fermions in ultracold atomic superfluid, Phys. Rev. Lett. 106, 100404 (2011).
- (9) V. Galitski and I. B. Spielman, Spin-orbit coupling in quantum gases, Nature (London) 494, 49 (2013).
- (10) L. Tarruell et al. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice, Nature 483, 302 (2012).
- (11) G. Montambaux et al., Merging of Dirac points in a two-dimensional crystal, Phys. Rev. B 80, 153412 (2009).
- (12) S. L. Zhu, B. G. Wang, and L. M. Duan, Simulation and detection of Dirac fermions with cold atoms in an optical lattice, Phys. Rev. Lett. 98, 260402 (2007).
- (13) D. W. Zhang et al., Relativistic quantum effects of Dirac particles simulated by ultracold atoms, Frontiers of Physics, 7, 31 (2012).
- (14) P. Soltan-Panahi, et al., Multi-component quantum gases in spin-dependent hexagonal lattices, Nature Phys. 7,434 (2011).
- (15) P. Soltan-Panahi, D. S. Lühmann, J. Struck, P. Windpassinger, K. Sengstock, Quantum phase transition to unconventional multi-orbital superfluidity in optical lattices, Nature Phys. 8,71 (2012).
- (16) B. Wunsch, F. Guinea, and F. Sols, Dirac-point engineering and topological phase transitions in honeycomb optical lattices, New J. Phys. 10, 103027 (2008).
- (17) S. Taie et al., Coherent driving and freezing of bosonic matter wave in an optical Lieb lattice, Sci. Adv. 1, 1500854 (2015).
- (18) G. B. Jo et al., Ultracold atoms in a tunable optical kagome lattice, Phys. Rev. Lett., 108, 045305 (2012).
- (19) S. Zhang, et al., Kagome bands disguised in a coloring-triangle lattice, Phys. Rev. B 99, 100404 (2019).
- (20) H. Miyake, G. A. Siviloglou, C. J. Kennedy, W. C. Burton, and W. Ketterle, Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices, Phys. Rev. Lett. 111, 185302 (2013).
- (21) M. Aidelsburger et al., Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices, Phys. Rev. Lett. 111, 185301 (2013).
- (22) M. Aidelsburger et al., Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms, Nat. Phys. 11, 162 (2015).
- (23) G. Jotzu et al., Experimental Realization of the Topological Haldane Model with Ultracold Fermions, Nature (London) 515, 237 (2014).
- (24) L. B. Shao et al., Realizing and detecting the quantum Hall effect without Landau levels by using ultracold atoms, Phys. Rev. Lett. 101, 246810 (2008).
- (25) D. W. Zhang et al., Generalized Hofstadter model on a cubic optical lattice: From nodal bands to the three-dimensional quantum Hall effect, Phys. Rev. A 95, 043619 (2017).
- (26) O. Morsch and M. Oberthaler, Dynamics of Bose-Einstein condensates in optical lattices, Rev. Mod. Phys. 78, 179 (2006).
- (27) T. Salger et al., Atomic Landau-Zener tunneling in Fourier-synthesized optical lattices, Phys. Rev. Lett. 99, 190405 (2007).
- (28) S. Kling et al., Atomic Bloch-Zener oscillations and Stuckelberg interferometry in optical lattices, Phys. Rev. Lett. 105, 215301 (2010).
- (29) L. K. Lim, J. N. Fuchs, G. Montambaux, Bloch-Zener oscillations across a merging transition of Dirac points, Phys. Rev. Lett. 108, 175303 (2012).
- (30) L. K. Lim and J. N. Fuchs, G. Montambaux. Geometry of Bloch states probed by Stuckelberg interferometry, Phys. Rev. A, 92 063627 (2015).
- (31) D. W. Zhang et al., Quantum simulation of exotic PT-invariant topological nodal loop bands with ultracold atoms in an optical lattice, Phys. Rev. A 93, 043617 (2016).
- (32) F. Mei et al, Simulating Z2 topological insulators with cold atoms in a one-dimensional optical lattice, Phys. Rev. A 85, 013638 (2012).
- (33) Y. Q. Zhu et al., Emergent pseudospin-1 Maxwell fermions with a threefold degeneracy in optical lattices, Phys. Rev. A 96, 033634 (2017).
- (34) M. Lewenstein, et al., Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond, Adv. Phys. 56, 243 (2007).
- (35) I. Bloch, J. Dalibard, and W. Zwerger, Many-body physics with ultracold gases, Rev. Mod. Phys. 80, 885 (2008).
- (36) D. Hennig and G. P. Tsironis, Wave transmission in nonlinear lattices, Phys. Rep. 307, 333 (1999).
- (37) K. G. Lagoudakis, M. Wouters, M. Richard, et al., Quantized vortices in an exciton–polariton condensate, Nat. Phys. 4, 706 (2008).
- (38) D. Leykam, O. Bahat-Treidel, A. S. Desyatnikov, Pseudospin and nonlinear conical diffraction in Lieb lattices, Phys. Rev. A 86, 031805 (2012).
- (39) D. Leykam and Y. D. Chong, Edge Solitons in Nonlinear Photonic Topological Insulators, Phys. Rev. Lett.117, 143901 (2016).
- (40) Y. Hadad , A. B. Khanikaev, A. Al, Self-induced topological transitions and edge states supported by nonlinear staggered potentials, Phys. Rev. B 93, 155112 (2016).
- (41) C. E. Whittaker, E. Cancellieri, P. M. Walker, et al., Exciton Polaritons in a Two-Dimensional Lieb Lattice with Spin-Orbit Coupling, Phys. Rev. Lett. 120, 097401 (2018).
- (42) F. Zangeneh-Nejad, R. Fleury, Nonlinear Second-Order Topological Insulators, Phys. Rev. Lett. 123, 053902 (2019)
- (43) D. Diakonov et al. Loop structure of the lowest Bloch band for a Bose-Einstein condensate. Phys. Rev. A 66, 013604 (2002).
- (44) B. Wu, R. B. Diener, and Q. Niu, Bloch waves and Bloch bands of Bose-Einstein condensates in optical lattices, Phys. Rev. A 65, 025601 (2002).
- (45) G-F. Wang, et al., Landau-Zener tunneling in a nonlinear three-level system, Phys. Rev. A 74, 033414 (2006).
- (46) R. W. Bomantara et al., Nonlinear Dirac cones, Phys. Rev. B 96, 121406 (2017).
- (47) Z. Chen and B. Wu, Bose-Einstein condensate in a honeycomb optical lattice: fingerprint of superfluidity at the Dirac point, Phys. Rev. Lett. 107, 065301 (2011).
- (48) R. Shen et al., Single Dirac cone with a flat band touching on line-centered-square optical lattices, Phys. Rev. B 81, 041410 (2010).
- (49) C. Weeks and M. Franz. Topological insulators on the Lieb and perovskite lattices. Phys. Rev. B 82, 085310 (2010).
- (50) D. Guzmán-Silva, C. Mejía-Cortés, M. A. Bandres, Experimental observation of bulk and edge transport in photonic Lieb lattices, New J. Phys. 16, 063061 (2014).
- (51) S. Mukherjee, et al., Observation of a localized flat-band state in a photonic Lieb lattice, Phys. Rev. Lett. 114, 245504 (2015).
- (52) C. Poli, et al., Partial chiral symmetry-breaking as a route to spectrally isolated topological defect states in two-dimensional artificial materials, 2D Mater. 4, 025008 (2017)
- (53) J. Wei, et al., Topological band evolution between Lieb and kagome lattices, Phys. Rev. B 99 125131 (2019).
- (54) A. Mielke, Exact ground states for the Hubbard model on the Kagome lattice, J. Phys. A: Math. Theor. 24, L73 (1991).
- (55) Z. Liu , F. Liu, Y. S. Wu, Exotic electronic states in the world of flat bands: From theory to material, Chin. Phys. B 23, 077308 (2014).
- (56) N.B. Kopnin, T.T. Heikkilä, and G.E. Volovik, Hightemperature surface superconductivity in topological flatband systems, Phys. Rev. B 83, 220503(R) (2011).
- (57) A. Julku, Geometric Origin of Superfluidity in the Lieb-Lattice Flat Band, Phys. Rev. Lett., 117, 045303 (2016).
- (58) B. Wu and Q. Niu, Nonlinear landau-zener tunneling, Phys. Rev. A 61 023402 (2000).
- (59) J. C. Bronski et al., Bose-Einstein condensates in standing waves: The cubic nonlinear Schrdinger equation with a periodic potential, Phys. Rev. Lett. 86, 1402 (2001).
- (60) H. Miyake, Probing and Preparing Novel States of Quantum Degenerate Rubidium Atoms in Optical Lattices, Ph.D. thesis, Massachusetts Institute of Technology (2013).
- (61) Z. Chen and B. Wu, Stability of Bose-Einstein condensates in two-dimensional optical lattices, Phys. Rev. A, 81, 043611 (2010).
- (62) A. Smerzi, A. Trombettoni, P. G. Kevrekidis, and A. R. Bishop, Dynamical superfluid-insulator transition in a chain of weakly coupled Bose-Einstein condensates, Phys. Rev. Lett., 89, 170402 (2002).
- (63) A. Trombettoni, A. Smerzi, Discrete solitons and breathers with dilute Bose-Einstein condensates, Phys. Rev. Lett., 86, 2353 (2001).
- (64) D. Hu, L. Niu, B. Yang, et al., Long-time nonlinear dynamical evolution for P-band ultracold atoms in an optical lattice, Phys. Rev. A, 92, 043614 (2015).
- (65) C. E. Carroll and F. T. Hioe, Transition probabilities for the three-level Landau-Zener model, J. Phys. A 19, 2061 (1986).
- (66) L. D. Landau, Zur theorie der energieubertragung ii, Phys. Z. Sow. 2, 46 (1932); C. Zener, Non-adiabatic crossing of energy levels, Proc. R. Soc. London A 137, 696 (1932).
- (67) S. Shevchenko, S. Ashhab, and F. Nori, Landau-Zener-Stuckelberg interferometry, Phys. Rep. 492, 1 (2010).
- (68) W. D. Oliver et al., Mach-Zehnder Interferometry in a Strongly Driven Superconducting Qubit, Science 310, 1653 (2005).
- (69) X. Tan et al., Demonstration of Geometric Landau-Zener Interferometry in a Superconducting Qubit, Phys. Rev. Lett. 112, 027001 (2014).
- (70) B. Wu, Q. Niu, Landau and dynamical instabilities of the superflow of Bose-Einstein condensates in optical lattices, Phys. Rev. A 64, 061603 (2001).
- (71) E. M. Graefe, H. J. Korsch, and D. Witthaut, Mean-field dynamics of a Bose-Einstein condensate in a time-dependent triple-well trap: Nonlinear eigenstates, Landau-Zener models and stimulated Raman adiabatic passage, Phys. Rev. A 73, 013617 (2006).