Nonanalyticity, sign problem and Polyakov line in $Z_{3}$-symmetric heavy quark model at low temperature: Phenomenological model analyses

In this subsection, we briefly summarize the nonanalyticity of the equation of states (EOS) of the free fermion at $T=0$. For the free fermion with finite mass $M$, thermodynamical quantities vanish at $T=0$, when $\mu<M$. When $\mu\geq M$, the pressure $P$ of the free fermion gas at $T=0$ is given by

	$\displaystyle P$	$\displaystyle=$	$\displaystyle{g\mu\over{6\pi^{2}}}(\mu^{2}-M^{2})^{3/2}$		(1)
			$\displaystyle-{g\over{8\pi^{2}}}\left\{\mu\sqrt{\mu^{2}-M^{2}}\left(\mu^{2}-{M^{2}\over{2}}\right)\right.$
			$\displaystyle\left.-{1\over{2}}M^{4}\log{\left({\mu+\sqrt{\mu^{2}-M^{2}}\over{M}}\right)}\right\},$

where $g$ is the fermion degree of freedom including the number of spin states. The fermion number density and its derivative with respect to $\mu$ are given by

$\displaystyle\rho={\partial P\over{\partial\mu}}={g\over{6\pi^{2}}}(\mu^{2}-m^{2})^{3/2},$

(2)

and

$\displaystyle{\partial\rho\over{\partial\mu}}={\partial^{2}P\over{\partial\mu^{2}}}={g\mu\over{4\pi^{2}}}\sqrt{\mu^{2}-m^{2}}.$

(3)

Note that these quantities are continuous at $\mu=M$. However, the third derivative of the pressure

$\displaystyle{\partial^{2}\rho\over{\partial\mu^{2}}}={\partial^{3}P\over{\partial\mu^{3}}}={g\over{4\pi^{2}}}\left(\sqrt{\mu^{2}-m^{2}}+{\mu^{2}\over{\sqrt{\mu^{2}-m^{2}}}}\right),$

(4)

is divergent at $\mu\to M+0$. Hence the pressure is nonanalytic at $\mu=M$.

In this subsection, we consider the free heavy quark model (FHQM) on the lattice with $N_{\rm s}$, $N_{f}=3$ and $N_{c}=3$ where $N_{\rm s}$, $N_{f}$ and $N_{c}$ are the number of the spatial sites, the number of flavor and the number of color , respectively. Quarks in the heavy mass limit have no spatial momentum and the energy of them is always equal to their mass $M_{f}~{}(f=u,d,s)$. Hence, the grand canonical partition function is given by

	$\displaystyle Z(T,\mu)$	$\displaystyle=$	$\displaystyle\prod_{f=u,d,s}(1+e^{\beta(\mu_{f}-M_{f})})^{N}$
	$\displaystyle\times$		$\displaystyle(1+e^{\beta(-\mu_{f}-M_{f})})^{N},$		(5)

where $N=2N_{c}N_{s}$, and $M_{f}$ and $\mu_{f}$ are the mass and the chemical potential for the $f$ quark. In (5), the antiquark contributions are included since they are important for the reality of $Z$ when imaginary chemical potential is introduced, although the contributions vanish in the limit $M_{f},\mu_{f}\to\infty$. If we put $\mu_{f}=M_{f}+i(2k+1)\pi T$ with an integer $k$, we obtain $Z=0$. When $T$ approaches to zero, the location of the zeros of $Z$ approaches a real value $\mu_{f}=M_{f}$. Hence, in the analogy of the famous Lee-Yang theorem Yang:1952be ; Lee:1952ig , the (dimensionless) pressure

$\displaystyle P=\lim_{N_{\rm s}\to\infty}{1\over{\beta N_{s}}}\log{Z}$

(6)

is expected to be non-analytic at $\mu=M_{f}$ when $\beta\to\infty$. (For the application of the Lee-Yang theorem to the QCD phase transitions, e.g., see Nagata:2014fra and references therein. )

Note that, beside the infinite limit of the spatial volume $N_{\rm s}$, here we also take the infinite limit of the imaginary time ($\tau$) length $\beta$. It is known that, by the redefinition of the quark filed

$\displaystyle q_{f}\to e^{i\theta T\tau}q_{f},$

(7)

the imaginary chemical potential $\mu_{\rm I}=i\theta T$ can be transformed into the twisted temporal boundary condition

$\displaystyle q_{f}(\tau=\beta)=-e^{-i\theta}q_{f}(\tau=0).$

(8)

Hence, if $\theta=(2k+1)\pi$, the quark boundary condition is a periodic boundary condition. It should be noted that, except for the singular point $\mu=M_{f}+i(2k+1)\pi$, the twisted model approaches to the original model in the limit $\beta\to\infty$, since the boundary condition becomes irrelevant in this limit. (Since $\theta$ has a trivial periodicity $2\pi$, in this paper, we restrict $\theta$ in the region $(-\pi,\pi]$ for simplicity. )

Hereafter, we consider the flavor symmetric case, namely, $M_{u}=M_{d}=M_{s}=M$, unless otherwise mentioned. The derivative of $P$ with respect to $\mu$, namely, the (dimensionless) number density is given by

	$\displaystyle n_{\rm q}$	$\displaystyle=$	$\displaystyle\lim_{N_{\rm s}\to\infty}{1\over{\beta N_{\rm s}}}{\partial\log{Z}\over{\partial\mu}}$		(12)
		$\displaystyle=$	$\displaystyle 2N_{f}N_{c}\left\{{1\over{e^{\beta(M-\mu)}+1}}+{1\over{e^{\beta(M+\mu)}+1}}\right\}$
		$\displaystyle=$	$\displaystyle\left\{\begin{array}[]{cc}0&(\mu<M,~{}~{}~{}\beta\to\infty)\\ N_{f}N_{c}&(\mu=M,~{}~{}~{}\beta\to\infty)\\ 2N_{f}N_{c}&(\mu>M,~{}~{}~{}\beta\to\infty)\end{array}\right.,$

and it is clear that $n_{\rm q}$ is nonanalytic at $\mu=M$ and $T=0$.

However, in the actual numerical simulations such as EPLM, we can not put ${\beta}=\infty$. Hence, $n_{\rm q}$ and its derivatives are continuous functions of $\mu$ as seen in Figs. 2 and 3. Near the point $\mu=M$, the quark number density $n_{\rm q}$ increases monotonically. The second derivative $n_{\rm q}^{\prime\prime}={\partial^{2}n_{\rm q}\over{\partial\mu^{2}}}$ has maximum and minimum around the point $\mu=M$. When $M/T$ becomes larger, $n_{\rm q}$ increases more rapidly and the absolute values of the maximum and minimum of $n^{\prime\prime}$ becomes larger, while the width of the peaks becomes narrower.

Figs. 4 and 5 are the same as Figs. 2 and 3, respectively, but for $\theta=\pi$. As ${\rm Re}(\mu)$ approaches to $M$, $n_{\rm q}$ and $n_{\rm q}^{\prime\prime}$ diverge. The region of the divergent behavior be narrower as $M/T$ be larger. Hence, it is expected that the results with $\theta=\pi$ approach to those with $\theta=0$ except for the point of ${\rm Re}(\mu)=M$. Here, we only show the results of the odd derivatives of the pressure $P$ with respect to the chemical potential $\mu$. As is seen in the next section, in EPLM, these odd derivatives are related to the sign problem around $\mu=M$.

As is seen in the previous subsection, in the case of the free fermion with smaller mass and spatial momentum, the number density itself is continuous at $\mu=M$. It seems that the effects of the spatial momentum make the transition smoother. At finite temperature, the pressure of the free fermion gas is given by

	$\displaystyle P$	$\displaystyle=$	$\displaystyle{g\over{4\pi^{2}}}\left(\int_{0}^{\infty}~{}dp~{}p^{2}~{}T\log{(1+e^{-\beta(E-\mu)})}\right.$		(13)
			$\displaystyle\left.+\int_{0}^{\infty}~{}dp~{}p^{2}~{}T\log{(1+e^{-\beta(E+\mu)})}\right).$

Then, the grand canonical partition function is given by

	$\displaystyle Z$	$\displaystyle=$	$\displaystyle\lim_{\Lambda\to\infty}\lim_{N\to\infty}\prod_{n=0}^{N}(1+e^{-\beta(\sqrt{(n\Delta p)^{2}+M^{2}}-\mu)})^{gn^{2}\Delta p^{3}\over{4\pi^{2}}}$		(14)
			$\displaystyle\times(1+e^{-\beta(\sqrt{(n\Delta p)^{2}+M^{2}}+\mu)})^{gn^{2}\Delta p^{3}\over{4\pi^{2}}},$

where $\Delta p={\Lambda\over{N}}$. The function $(1+e^{-\beta(\sqrt{(n\Delta p)^{2}+M^{2}}-\mu)})$ is zero at $\mu=\sqrt{(n\Delta p)^{2}+M^{2}}+i\pi$. Zeros of $(1+e^{-\beta(\sqrt{(n\Delta p)^{2}+M^{2}}-\mu)})$ depend on the absolute value $p=n\Delta p$ of the spatial momentum of fermions. The set of zeros of $Z$ forms a continuous structure. This structure of zeros of $Z$ may smoothen the transition. In Fig. 2, the quark number density $n_{\rm q}$ in FHQM with $M_{u}=0.5M$, $M_{d}=M$ and $M_{s}=1.5M$ is shown for $M/T=10$. We see that $n_{\rm q}$ increases slowly as $\mu$ increases. For the infinite flavor quarks with mass $\sqrt{(n\Delta p)^{2}+M^{2}}$ with infinitesimal degree of freedom, ${gn^{2}\Delta p^{3}\over{4\pi^{2}}}$, it can be expected that $n_{\rm q}$ increases slowly, even if the limit $M/T\to\infty$ is taken. In this meaning, the result in FHQM with nonsymmetric flavors mimics the free quark model with lighter mass and the spatial momentum.

In the symmetric three flavor quark model, we consider the case where

$\displaystyle\mu_{f}=\mu+i\theta_{f}T~{}~{}~{}~{}~{}(f=u,d,s)$

(15)

with $\theta_{u}=i{2\pi\over{3}}$, $\theta_{d}=-i{2\pi\over{3}}$, $\theta_{s}=0$. In this paper, we call this setting ”$Z_{3}$-symmetrization” and $Z_{3}$-symmetric FHQM ”$Z_{3}$-FHQM”. Since the additional imaginary chemical potential $i\theta_{f}T$ is the isospin chemical potential rather than the quark chemical potential, it can not be included in the definition of $\mu$. It should be noted that $Z$ is real at $\mu_{f}=\mu+i\theta_{f}T$ for real $\mu$ and is not zero at $\mu_{f}=M+i\theta_{f}$.

The setting (15) of chemical potential is related to the so-called $Z_{3}$ symmetry. In fact, by the redefinition of the quark field $q_{f}$, the imaginary part of the chemical potential $\mu_{f}$ can be transformed into the temporal ($\tau$) boundary condition

$\displaystyle q_{f}(\tau=\beta)=-e^{-i\theta_{f}}~{}q_{f}(\tau=0)~{}~{}~{}~{}~{}(f=u,d,s),$

(16)

where $e^{-i\theta_{f}}$ is an element of the $Z_{3}$ group. In QCD, the $Z_{3}$-transformation changes the boundary condition of quark field by the factor of the $Z_{3}$ group element. Hence, the $Z_{3}$ symmetry which exists in the pure gluon theory and related to the quark confinement is explicitly broken. However, in the symmetric three flavor QCD, the $Z_{3}$ symmetry is restored by use of the $Z_{3}$-symmetrization (15) Kouno:2012dn_2 . It should be noted that the $Z_{3}$-symmetric theory is expected to approach to the original one in the limit $\beta\to\infty$, since the boundary condition is not relevant in the limit.

In $Z_{3}$-FHQM, the partition function $Z$ becomes zero at following three points,

$\displaystyle\mu=M-i{\pi\over{3}}T,~{}~{}~{}~{}~{}M+i{\pi\over{3}}T,~{}~{}~{}~{}~{}M+i\pi T.$

(17)

Hence there are three zeros of $Z$ in the complex $\mu$ plane. However, these zeros correspond to the same nonanalyticity at $\mu=M$ when the zero temperature limit is taken. Therefore, $Z_{3}$-symmetric FHQM has the same information of the nonanalyticity of the original FHQM at zero temperature, although the two models are different each other at finite temperature.

It is known that the $Z_{3}$-symmetrization enhances the confinement-like structure and a quark behaves as the particle with the mass $3M$ rather than that with $M$. Hence, the effects of the $Z_{3}$-symmetrization resembles the ones of the increases of $M/T$. In fact, the partition function of $Z_{3}$-FHQM is given by

	$\displaystyle Z_{Z_{3}}(T,\mu)$	$\displaystyle=$	$\displaystyle(1+e^{(3\mu-3M)/T})^{N}(1+e^{(-3\mu-3M)/T})^{N}$		(18)
		$\displaystyle=$	$\displaystyle Z(T,3\mu;3M,N_{f}=1).$

Hence, $Z_{3}$-FHQM has the same properties as the ordinary FHQM with one flavor, threefold mass and threefold chemical potential. If we define the baryonic chemical potential $\mu_{\rm B}=3\mu$, the zero of $Z$ locates only at $\mu_{\rm B}=3M+i\pi$. The quark number density is given by

	$\displaystyle n_{{\rm q},Z_{3}}(T,\mu)$	$\displaystyle=$	$\displaystyle{3\over{N_{\rm s}}}{\partial\log{Z(T,\mu_{\rm B};3M,N_{f}=1)}\over{\partial\mu_{\rm B}}}$		(19)
			$\displaystyle=n_{\rm q}(T,3\mu;3M,N_{f}=3).$

The factor 3 complements the flavor decreasing from 3 to 1 in Eq. (18). Hence, the number density in $Z_{3}$-FHQM coincides the one in the ordinary FHQM with three flavor, threefold mass and threefold chemical potential. The similar correspondence is seen in $n^{\prime\prime}M^{2}={\partial^{2}n_{\rm q}\over{\partial(\mu/M)^{2}}}$. In Figs. 2$\sim$5, the ${\rm Re}(\mu)$-dependence of $n_{\rm q}$ and $n_{\rm q}^{\prime\prime}$ of the $Z_{3}$-FHQM are shown for $\theta=0$ and $\pi$. In all case, the perfect coincidence between $Z_{3}$-FHQM with $M/T=10$ and FHQM with $M/T=30$ is seen. When $M/T$ is fixed and $\theta=0$, $n_{\rm q}$ increases more rapidly and the absolute values of the maximum and minimum of $n^{\prime\prime}$ becomes larger in $Z_{3}$ FHQM than in FHQM, while the width of finite $n^{\prime\prime}$ becomes narrower. The localization of the peaks of the odd derivatives makes the sign problem weaker than that in EPLM.

The grand canonical partition function of EPLM in temporal gauge is given by Aarts_James ; Greensite:2014cxa ; Hirakida:2017bye

	$\displaystyle Z$	$\displaystyle=$	$\displaystyle\int{\cal D}\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}{\cal D}\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}\exp{\left(-S_{\rm H}-S_{\rm G}-S_{\rm F}\right)};$		(20)
	$\displaystyle S_{\rm G}$	$\displaystyle=$	$\displaystyle-\kappa\sum_{{\mbox{\boldmath${\scriptstyle x}$}}}\sum_{i=1}^{3}\left({\rm Tr}[U_{{\mbox{\boldmath${\scriptstyle x}$}}}]{\rm Tr}[U_{{\mbox{\boldmath${\scriptstyle x}$}}+{\mbox{\boldmath${\scriptstyle i}$}}}^{\dagger}]+{\rm Tr}[U_{{\mbox{\boldmath${\scriptstyle x}$}}}^{\dagger}]{\rm Tr}[U_{{\mbox{\boldmath${\scriptstyle x}$}}+{\mbox{\boldmath${\scriptstyle i}$}}}]\right),$
					(21)
	$\displaystyle S_{\rm F}$	$\displaystyle=$	$\displaystyle\sum_{{\mbox{\boldmath${\scriptstyle x}$}}}{\cal L}_{\rm F}({\bf x}),$		(22)

where $U_{\mbox{\boldmath${\scriptstyle x}$}}$ is the Polyakov line (loop) holonomy, the symbol $\mathbf{i}$ is an unit vector for $i$-th direction and ${\cal L}_{\rm F}$ is the fermionic Lagrangian density the concrete form of which will be shown later. The site index ${\bf x}$ runs over a 3-dimensional lattice. Large (small) $\kappa$ in EPLM corresponds to high (low) temperature DeGrand and DeTar (1983) in QCD. Although the relation between $\kappa$ and $T$ is not simple, we regard the case with $\kappa\to 0$ and $M/T\to\infty$ as the zero-temperature limit in this paper.

The Polyakov line holonomy $U_{\mbox{\boldmath${\scriptstyle x}$}}$ is parameterized as  Greensite:2014cxa

	$\displaystyle U_{\mbox{\boldmath${\scriptstyle x}$}}$	$\displaystyle=$	$\displaystyle{\rm diag}\left(e^{i\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}},e^{i\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}},e^{i\varphi_{b,{\mbox{\boldmath${\scriptstyle x}$}}}}\right),$		(23)
	$\displaystyle U_{\mbox{\boldmath${\scriptstyle x}$}}^{\dagger}$	$\displaystyle=$	$\displaystyle{\rm diag}\left(e^{-i\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}},e^{-i\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}},e^{-i\varphi_{b,{\mbox{\boldmath${\scriptstyle x}$}}}}\right),$		(24)

with the condition $\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}+\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}+\varphi_{b,{\mbox{\boldmath${\scriptstyle x}$}}}=0$. Instead of $U_{\mbox{\boldmath${\scriptstyle x}$}}$ and $U_{\mbox{\boldmath${\scriptstyle x}$}}^{\dagger}$, here the phase variables $\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}$ and $\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}$ are treated as dynamical variables. The Haar measure part ${\cal L}_{\rm H}$ is given by Greensite:2014cxa

	$\displaystyle S_{\rm H}=\sum_{{\mbox{\boldmath${\scriptstyle x}$}}}{\cal L}_{\rm H}({\bf x}),$		(25)
	$\displaystyle{\cal L}_{\rm H}({\bf x})=-\log{}\Bigl{\{}\sin^{2}{\left({\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}-\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}\over{2}}\right)}$
	$\displaystyle\times\sin^{2}{\left({2\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}+\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}\over{2}}\right)}\sin^{2}{\left({\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}+2\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}\over{2}}\right)\Bigr{\}}}.$		(26)

The (traced) Polyakov line (loop) $P_{\mbox{\boldmath${\scriptstyle x}$}}$ and its conjugate $P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}$ are defined as

	$\displaystyle P_{\mbox{\boldmath${\scriptstyle x}$}}={1\over{3}}{\rm Tr}\left[U_{\mbox{\boldmath${\scriptstyle x}$}}\right]$	$\displaystyle=$	$\displaystyle{1\over{3}}\left(e^{i\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}}+e^{i\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}}+e^{i\varphi_{b,{\mbox{\boldmath${\scriptstyle x}$}}}}\right),$		(27)
	$\displaystyle P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}={1\over{3}}{\rm Tr}\left[U_{\mbox{\boldmath${\scriptstyle x}$}}^{\dagger}\right]$	$\displaystyle=$	$\displaystyle{1\over{3}}\left(e^{-i\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}}+e^{-i\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}}+e^{-i\varphi_{b,{\mbox{\boldmath${\scriptstyle x}$}}}}\right).$

For the fermionic Lagrangian density with the flavor dependent quark chemical potential $\mu_{f}$ and temperature $T$, we consider a logarithmic one of Ref. Greensite:2014cxa ; Hirakida:2017bye :

	$\displaystyle{\cal L}_{\rm F}$	$\displaystyle=$	$\displaystyle-2\sum_{f=u,d,s}\sum_{c=r,g,b}\Big{\{}\log{\Bigl{(}1+e^{\beta(\mu_{f}-M_{f})+i\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}}\Big{)}}$		(29)
			$\displaystyle+\log{\Bigl{(}1+e^{-\beta(\mu_{f}+M_{f})-i\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}}\Big{)}}\Big{\}}$
		$\displaystyle=$	$\displaystyle-2\sum_{f=u,d,s}\Bigl{\{}\log{\Bigl{(}1+3e^{\beta(\mu_{f}-M_{f})}P_{\mbox{\boldmath${\scriptstyle x}$}}}$
			$\displaystyle+3e^{2\beta(\mu_{f}-M_{f})}P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}+e^{3\beta(\mu_{f}-M_{f})}\Bigr{)}$
			$\displaystyle+\log{\Bigl{(}1+3e^{-\beta(\mu_{f}+M_{f})}P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}}$
			$\displaystyle+3e^{-2\beta(\mu_{f}+M_{f})}P_{\mbox{\boldmath${\scriptstyle x}$}}+e^{-3\beta(\mu_{f}+M_{f})}\Bigr{)}\Bigr{\}},$

where $M_{f}$ is the quark mass. In the limit $M_{f}\to\infty$, ${\cal L}_{\rm F}$ becomes real at $\mu=M_{f}$, since $e^{\beta(\mu-M_{f})}=e^{2\beta(\mu-M_{f})}=1$ and $e^{-\beta(\mu+M)}=e^{-2\beta(\mu+M_{f})}=0$. The reality of ${\cal L_{\rm F}}$ at $\mu=M_{f}$ is related to the particle-hole symmetry Rindlisbacher and Forcrand (2016); Hirakida:2017bye . In the zero-temperature limit, the antiparticle part of (29) vanishes.

It should be also noted that, at $\mu=M_{f}$, there is no dependence on $M_{f}/T$ in EPLM with symmetric flavors, if the antiquark contributions can be neglected. Hence, the point $\mu=M$ is the fixed point where physical quantities are not changed when $M_{f}/T$ varies. Breaking of the flavor symmetry also breaks this invariance.

The (dimensionless) quark-number density $n_{q}$ is obtained by

$\displaystyle n_{q}$

$\displaystyle=$

$\displaystyle{1\over{\beta N_{\rm s}}}{\partial(\log{Z})\over{\partial\mu}},$

(30)

where $N_{\rm s}$ is the number of the lattice spatial sites.

As in the case of FHQM, $Z_{3}$-symmetrization (15) can be done for EPLM with three symmetric flavors. In this paper, we call the $Z_{3}$-symmetric EPLM ”$Z_{3}$-EPLM”. The fermionic Lagrangian density of $Z_{3}$ EPLM is given by

	$\displaystyle{\cal L}_{\rm F}$	$\displaystyle=$	$\displaystyle-2\sum_{c=r,g,b}\Big{\{}\log{\Bigl{(}1+e^{\beta(3\mu-3M)+i3\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}}\Big{)}}$		(31)
			$\displaystyle+\log{\Bigl{(}1+e^{-\beta(3\mu+3M)-i3\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}}\Big{)}}\Big{\}}.$

In the case of EPLM, the internal dynamical variables $\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}$ are also threefold. Hence, this breaks the equivalence between $Z_{3}$-EPLM and the ordinary EPLM with threefold mass and threefold chemical potential.

For $\kappa=0$, the partition function becomes simple, since the $S_{\rm G}$ term vanishes. For large $N_{\rm s}$ in which the periodic boundary condition is negligible, the integration over $\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}$ and $\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}$ can be performed independently for each site ${\bf x}$. The partition function turns out to be

	$\displaystyle Z$	$\displaystyle=$	$\displaystyle\prod_{{\mbox{\boldmath${\scriptstyle x}$}}}\left[\int_{-\pi}^{\pi}d\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}}\int_{-\pi}^{\pi}d\varphi_{g,{\mbox{\boldmath${\scriptstyle x}$}}}e^{-{\cal L}(\varphi_{r,{\mbox{\boldmath${\scriptstyle x}$}}},\varphi_{g{\mbox{\boldmath${\scriptstyle x}$}}})}\right]$		(32)
		$\displaystyle=$	$\displaystyle\left[\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dve^{-{\cal L}(u,v)}\right]^{N_{\rm s}}=z^{N_{\rm s}},$

where ${\cal L}={\cal L}_{\rm H}+{\cal L}_{\rm F}$, $N_{\rm s}$ is the number of the spatial lattice sites, and $z$ is the local partition function at one lattice site. It is known that the integral such as (32) can be evaluated analytically Rindlisbacher and Forcrand (2016). Hence, we call the equation ”analytical” in this paper. However, the integral form is useful here, since we are interested in the mechanism of the sign problem.

When ${\cal L}$ is not real, instead of ${\cal L}$, we may use an approximate real Lagrangian ${\cal L}^{\prime}$ for constructing the probability density function. Then, the approximate partition function reads

$\displaystyle Z^{\prime}$

$\displaystyle=$

$\displaystyle\left[\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dve^{-{\cal L}^{\prime}(u,v)}\right]^{N_{\rm s}}={z^{\prime}}^{N_{\rm s}},$

(33)

and the reweighting factor is $W=Z/Z^{\prime}=(z/z^{\prime})^{N_{\rm s}}$. When we put ${\cal L}^{\prime}={\rm Re}({\cal L})$, we obtain the reweighting (phase) factor in the phase quenched (PQ) approximation. In this paper, we call the reweighting method with PQ approximation ”PQRW”. We examine how PQRW works in EPLM. For the brief review of PQRW, see appendix A.

Using Eq. (32), the pressure $P$, the quark number density $n_{q}$, the scalar density $n_{\rm s}$, the averaged value of the Polyakov line $P_{\mbox{\boldmath${\scriptstyle x}$}}$ and its conjugate $P_{\mbox{\boldmath${\scriptstyle x}$}}$ are given by

$\displaystyle{P}={T\over{N_{\rm s}}}\log{Z}=T\log{z},$

(34)

$\displaystyle n_{q}={\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dv\left(-T{\partial L\over{\partial\mu}}\right)e^{-{\cal L}(u,v)}\over{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dve^{-{\cal L}(u,v)}}},$

(35)

$\displaystyle n_{\rm s}=\sum_{f=u,d,s}{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dv\left(T{\partial L\over{\partial M_{f}}}\right)e^{-{\cal L}(u,v)}\over{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dve^{-{\cal L}(u,v)}}},$

(36)

$\displaystyle\langle P_{\mbox{\boldmath${\scriptstyle x}$}}\rangle$

$\displaystyle=$

$\displaystyle{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dvP_{\mbox{\boldmath${\scriptstyle x}$}}(u,v)e^{-{\cal L}(u,v)}\over{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dve^{-{\cal L}(u,v)}}},$

(37)

$\displaystyle\langle P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}\rangle$

$\displaystyle=$

$\displaystyle{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dvP_{\mbox{\boldmath${\scriptstyle x}$}}^{*}(u,v)e^{-{\cal L}(u,v)}\over{\int_{-\pi}^{\pi}du\int_{-\pi}^{\pi}dve^{-{\cal L}(u,v)}}},$

(38)

respectively. These physical quantities are independent of $N_{\rm s}$, although $Z$ depends on $N_{\rm s}$. The analytical form of these quantities are modified when we consider the boundary condition. See Appendix B for detail. (It is easily seen that the modified results coincides with the equations above in the thermodynamical limit $N_{\rm s}\to\infty$. )

In Ref. Hirakida:2017bye , it was found that the phase factor and physical quantities at small $\kappa$ is very close to the ones at $\kappa=0$. Hence, we use Eqs. (32)$\sim$(38) as a phenomenological model for QCD with heavy quarks at low temperature. By use of these equations, we can discuss the sign problem from the results which are free from the sign problem. In the numerical calculations, we put $M_{u}=M_{d}=M_{s}=M$ unless otherwise mentioned. Figure 6 shows the $\mu$-dependence of the phase factor $W$ in PQRW. Since $W$ depends on $N_{\rm s}$, we set $N_{\rm s}=10^{3},20^{3}$ and $30^{3}$. Around $\mu=M$, $W$ is small and the sign problem is serious in that region. However, due to the particle-hole symmetry, $S_{\rm F}$ is real and $W=1$ is always hold at $\mu=M$. The small $W$ indicates that the sign problem is serious when PQRW is used in simulations. When $N_{\rm s}$ increases, the sign problem be more serious. However, the $N_{\rm s}$-dependence becomes small when $N_{s}$ is large. Hence, we set $N_{\rm s}=30^{3}$ hereafter.

Figures 7 shows the similar as Fig. 6 but the one with fixed $N_{s}$. Roughly speaking, the sign problem is serious when $|\mu-M|<5T$. Hence, when $M/T$ increases, the sign problem be weaker for fixed $\mu/M$. (However, the situation may be different when we compare them for fixed $\mu$. The phase factor $W$ can be larger for lighter quark than for heavier one when we compare them at fixed $\mu$. )

Figures 8 shows the result in EPLM without three flavor symmetry. When the strange quark mass $M_{s}$ is larger than the light quark mass $M_{l}$, the sign problem becomes weaker, but the change is not so large. This indicates that the lighter quark dominates the sign problem. In Fig. 8, the results in $Z_{3}$-EPLM are also shown. It can be seen that the $Z_{3}$-symmetrization makes the sign problem weak drastically. In the case of $Z_{3}$-EPLM with $M/T=100$, the sign problem almost vanishes except for the vicinity of $\mu=M$. In this case, from $W$ itself, we see that nonanalyticity certainly happens just at $\mu=M$.

Comparing Fig. 8 with Fig. 7, we see that the sign problem is somewhat weaker in $Z_{3}$-EPLM with $M/T=10$ than EPLM with $M/T=30$. This is because, different from the number density, the partition function in $Z_{3}$-EPLM is close to the one in EPLM with threefold mass and three fold chemical potential but one flavor. As well as the decrease of $N_{\rm s}$, the decreases of $N_{f}$ make the sign problem weaker.

Figures 9 shows the $\mu$-dependence of the quark number density $n_{q}$. It is seen that $n_{q}$ abruptly increases at $\mu=M$, when $M/T$ is large. The results are antisymmetric with respect the point $\mu=M$. This property is the consequence of the particle-hole symmetry. Due to the effect of the gauge field $\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}$, the equivalence between $Z_{3}$-EPLM and EPLM with threefold mass and threefold chemical potential is slightly broken, but the difference be smaller when $M/T$ becomes larger.

In the heavy quark model, the scalar density $n_{\rm s}$ is almost the same as $n_{\rm q}$, since the effects of the spatial momentum and the vacuum fluctuations are absent and the antiquark contribution is negligible. If it couples to the quark field, it can make the quark mass smaller. In Fig. 10, the results in EPLM and $Z_{3}$-EPLM in which quark mass changes from large mass $M(=10T)$ to small one $m(=T)$ at $\mu/M=1.1$. Remember that $W$ can be larger for lighter quark than the one for heavier quark when we compare them at fixed $\mu$. Due to the change of the quark mass, the symmetry with respect to the line $\mu/M=1$ is broken. In EPLM and $Z_{3}$-EPLM, the breaking of symmetry around $\mu=M$ may indicate a nontrivial change of the system. However, in QCD, such symmetry is not expected at the beginning. Hence, we should control the trivial sign problem caused by the formation of Fermi sphere anyway.

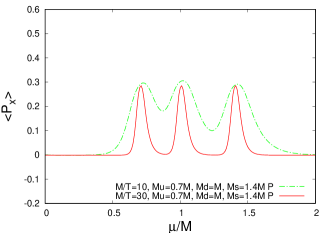
Figures 11 shows the $\mu$-dependence of the averaged value $\langle P_{{\mbox{\boldmath${\scriptstyle x}$}}}\rangle$ and $\langle P_{{\mbox{\boldmath${\scriptstyle x}$}}}^{*}\rangle$ in EPLM. It is seen that the both quantities somewhat large in the vicinity of $\mu=M$. $\langle P_{{\mbox{\boldmath${\scriptstyle x}$}}}\rangle$ has a maximum in the region $\mu>M$, while $\langle P_{{\mbox{\boldmath${\scriptstyle x}$}}}^{*}\rangle$ does in the region $\mu<M$. This property is also a consequence of the particle-hole symmetry. In $Z_{3}$-EPLM, the expectation value of the Polyakov-loop vanishes due to the exact $Z_{3}$-symmetry.

When all $\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}$ vanish, $\langle P_{\mbox{\boldmath${\scriptstyle x}$}}\rangle$ and $\langle P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}\rangle$ becomes 1. The case corresponds to the ordered phase and the sign problem does not happen since all $\varphi_{c.{\mbox{\boldmath${\scriptstyle x}$}}}$ vanish. However, the absolute values of the Polyakov line is far from 1 and the $\varphi_{c,{\mbox{\boldmath${\scriptstyle x}$}}}$ fluctuates almost randomly. This causes the serious sign problem around $\mu=M$.

In Fig. 11, when $M/T$ increases, $\langle P_{\mbox{\boldmath${\scriptstyle x}$}}\rangle$ and $\langle P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}\rangle$ becomes smaller at $\mu\neq M$, but they do not change at $\mu=M$ since the point $\mu=M$ is the fixed point. Hence, in the limit $M/T\to\infty$, the Polyakov line (and its conjugate) at $\mu\neq M$ and all the other quantities at any $\mu$ approach to the ones in $Z_{3}$-EPLM, however, the Polyakov line (and its conjugate) at $\mu=M$ has different value in two models. It seems that the Polyakov line on the nonanalytical point can detect the difference of the boundary condition even in the zero-temperature limit.

It should be remarked that the existence of the fixed point at $\mu=M$ has an important role in the anomalous phenomena mentioned above. When the flavor symmetry is broken, the exact fixed point disappears. Figure 12 shows the $\mu$-dependence of $\langle P_{\mbox{\boldmath${\scriptstyle x}$}}\rangle$ in EPLM with nonsymmetric flavors. In this case, the absolute values of these quantities are smaller than those in the symmetric flavor case. Furthermore, since $\mu=M_{f}~{}(f=u,d,s)$ is an approximate fixed point but not an exact one, the maximum values of these quantities decrease as $M_{f}/T$ increases. Hence, if we take the effect of the spatial momentum of quarks into account and take the zero temperature limit, the expectation value of the Polyakov line may vanish. (Althouh we do not show the result, the $\mu$-dependence of $\langle P_{\mbox{\boldmath${\scriptstyle x}$}}^{*}\rangle$ shows the similar tendency. )

The local partition function $z$ can be written as

$\displaystyle z=\int_{-\pi}^{\pi}d\varphi_{r}\int_{-\pi}^{\pi}d\varphi_{g}e^{-{\cal L}_{\rm H}}e^{-{\cal L}_{\rm F}},$

(39)

where the spatial index ${\scriptstyle x}$ is ommited for simplicity of the notation. The factor $f=e^{-{\cal L}_{\rm F}}$ is given by

$\displaystyle f(\varphi_{r},\varphi_{g})$

$\displaystyle=$

$\displaystyle\exp{\left(2\sum_{f,c}\log{(1+e^{(\mu_{f,c}-M)/T})}\right)},$

(40)

where $\mu_{f,c}=\mu+i\varphi_{c}T$ in EPLM and $\mu_{f,c}=\mu+i(\theta_{f}+i\varphi_{c})T$ in $Z_{3}$-EPLM. This factor can be used as a microscopic probability density function in numerical simulation if the sign problem is absent. Figure 13 shows $f/(|f|+\epsilon)$ at $\mu=M$ in EPLM with $M/T=100$, where $\epsilon$ is a positive infinitesimal constant. Note that, due to the particle-hole symmetry, $f$ is real and is nonnegative at $\mu=M$. Hence $f/(|f|+\epsilon)$ is 1 unless $f=0$. The set of zeros forms a line structure. If one of ${\rm Im}(\mu_{f,c})$ is equal to $(2k+1)\pi$, where $k$ is an integer, $f$ becomes zero at $\mu=M$. This condition corresponds to the horizontal and vertical black lines at the edges in the figure. Furthermore, $f$ is also zero when $\varphi_{g}=(2k+1)\pi-\varphi_{r}$ is satisfied. This condition corresponds to the black oblique lines in the figure.

Figure 14 shows the same as Fig. 13 but $Z_{3}$-EPLM with $M/T=33.3$ is used. Due to the $Z_{3}$-symmetry, the zero-structure in the region where $\varphi_{g}={2k-1\over{3}}\pi\sim{2k+1\over{3}}\pi$ and ${2l-1\over{3}}\pi\sim{2l+1\over{3}}\pi$ with $k,l=-1,0,1$ is similar to the one of the EPLM result in the region where $\varphi_{r}=-\pi\sim\pi$ and $\varphi_{g}=-\pi\sim\pi$.

The structure of zeros of $f$ in Fig. 14 is $Z_{3}$-symmetric but is not in Fig. 13. Hence, it can be said that the Polyako-line and its conjugate can detect the microscopic structure of zeros of $f$ at $\mu=M$ and decide to be or not to be finite in the limit of $M/T\to\infty$, although the other quantities are not sensible to the structure.

It should be noted that the zeros of $f$ at $\mu=M$ themselves do not induce the sign problem. However, in the vicinity of $\mu=M$, the situation is changed drastically. Suppose $f=0$ at $\varphi_{r}=\varphi_{r0}$ and $\varphi_{g0}$ when $\mu=M$. Then, the absolute value of ${\rm Im}[{\cal{L}_{\rm F}}(\varphi_{r,0},\varphi_{g,0})]$ may be still small at $\mu=M+\Delta\mu$ when $|\Delta\mu|$ is small enough. However, expanding ${\cal L}_{\rm F}(\varphi_{r},\varphi_{g})$ at $\mu=M+\Delta\mu$ in term of $\Delta\varphi_{r}=\varphi_{r}-\varphi_{r,0}$ and $\Delta\varphi_{g}=\varphi_{g}-\varphi_{g,0}$, we obtain

	$\displaystyle{\cal L}_{\rm F}(\varphi_{r},\varphi_{g})={\cal L}(\varphi_{r,0},\varphi_{g,0})$
	$\displaystyle+i{\cal L}_{\rm F}^{\prime}(\varphi_{r,0}\varphi_{g,0})(\Delta\varphi_{r}+\Delta\varphi_{g})$
	$\displaystyle-{1\over{2}}{\cal L}_{\rm F}^{\prime\prime}(\varphi_{r,0}\varphi_{g,0})(\Delta\varphi_{r,0}+\Delta\varphi_{g,0})^{2}$
	$\displaystyle-i{1\over{6}}{\cal L}_{\rm F}^{\prime\prime\prime}(\varphi_{r,0}\varphi_{g,0})(\Delta\varphi_{r,0}+\Delta\varphi_{g,0})^{3}+\cdots,$		(41)

where $\prime$ denotes the differentiation with respect to $\mu$. Since structure of the fermionic Lagrangian ${\cal L}_{\rm F}$ in EPLM is similar to the pressure of FHQM discussed in Sec. II, the odd coefficients in the expansion (41) have divergent behavior and ${\rm Im}({\cal L}_{\rm F})$ can be large at $\mu=M+\Delta\mu$. This makes the sign problem serious in the vicinity of $\mu=M$. Figure 15 shows ${\rm Re}(f)/(|f|+\epsilon)$ at $\mu=0.98M$ in EPLM with $M/T=100$. There are area-like regions where ${\rm Re}(f)$ is negative. These regions make $|z|$ smaller than the quenched one $z^{\prime}$ and induce a serious sign problem. (Note that $W$ will be almost zero in the large $N_{\rm s}$ limit, even if $|z|$ is slightly smaller than $z^{\prime}$. )

Figure 16 shows the same as Fig. 15 but $Z_{3}$-EPLM with $M/T=33.3$ is used. As is the same as in Fig. 14, $Z_{3}$-symmetric structure is seen also in this figure. The minimum value of ${\rm Re}(f)/(|f|+\epsilon)$ is much larger than that in Fig. 15 and is not negative. Hence, the sign problem is not so strong in this case. When we set $M/T=100$ in $Z_{3}$-EPLM, ${\rm Re}(f)/|f|=1$ is realized anywhere, almost perfectly, the sign problem almost vanishes at $\mu=0.98M$.

When the imaginary quark chemical potential $i\theta T$ is introduced, the reality of the grand canonical partition function $Z$ and physical quantities is not ensured in general. Figure 17 shows the complex chemical potential dependence of ${\rm Re}(n_{q})$ in EPLM with $M/T=100$. Except in the neighbor of ${\rm Re}(\mu)=M$, the results for finite $\theta$ coincide with that for $\theta=0$. This is because the imaginary chemical potential, which is equivalent to the change of the boundary condition, is irrelevant in the zero temperature limit. In the neighborhood of ${\rm Re}(\mu)=M$ the result for $\theta=\pi$ vibrates violently. The maximum value of $|{\rm Re}(n_{\rm q})|$ is much larger than the degree of freedom of quarks, namely, $2N_{f}N_{c}=18$. In this figure, we show the result at $0.001$ intervals in the horizontal axis. The singular behavior for $\theta=\pi$ depends strongly on the interval we use. When the interval is smaller, the maximum value of $|{\rm Re}(n_{\rm q})|$ is larger. For $\theta=\pi$, large quark number density can be induced at the singular point. This phenomenon happens also at ${\rm Re}(\mu)=-M$.

Figure 18 shows the complex chemical potential dependence of ${\rm Im}(n_{q})$ in EPLM with $M/T=100$. When $\theta=0$ or $\pi$, ${\rm Im}(n_{\rm q})=0$. For $\theta={5\over{6}}\pi$, ${\rm Im}(n_{q})$ is finite only in the vicinity of ${\rm Re}(\mu)=M$. This is also because the imaginary chemical potential which induces the imaginary part of ${\rm Im}(n_{q})$ is irrelevant in the zero temperature limit.