Università di Roma “La Sapienza”, Via Antonio Scarpa 16, 00161 Rome, Italy,
&
I.N.F.N. - Sezione Roma1, Gr. IV - M.M.N.L.P., Rome, Italy
11email: [email protected],22institutetext: DICATAM, Università degli Studi di Brescia, Via Valotti 9, Brescia, Italy
22email: [email protected], 22email: [email protected], 22email: [email protected]
Non rectification of heat in graded Si-Ge alloys
Abstract
We investigate the possibility to obtain a thermal diode with functionally graded Si-Ge alloys. A wire with variable section is considered. After the introduction of a formula giving the thermal conductivity of the wire as a function of the species content and of the diameter of the wire, numerical and analytical results are presented supporting the impracticability to get a thermal diode with the characteristics here considered.However, the present study opens the way to further generalisations amenable to give applicative promising results.
keywords:
Thermal rectification, graded materials, Fourier law,silicon germanium alloys
1 Introduction
The thermal phenomenon that allows the heat to be transferred in a suitable direction in a given material, while the flow is impeded in the opposite direction, is called thermal rectification [1, 2]. This is the analogue of the current rectification of the electronic diodes and for this reason any device showing some thermal rectifying feature is called thermal diode. An homogeneous material possessing a constant thermal conductivity is known to not possess any rectifying property [3]: the heat flows, under the same thermal gradient applied, equally in all the directions. It follows that, if a material possesses a rectifying effect, then the thermal conductivity is a non-homogeneous function of the temperature. With non-homogeneous we mean that the thermal conductivity also depends on the space variable x. Despite to be necessary, this condition is however far from being sufficient: indeed, it has been shown [3] that, if the thermal conductivity is a separable function, i.e. if there exist two functions and such that , then no rectifying effect can be observed in the material.
A practicable process to obtain non-homogeneous values of macroscopic properties, such as the thermal conductivity, is the manufacturing of functionally graded materials, i.e. materials with a specific gradation in the composition in order to achieve particular performances or functions [4, 5]. One of the most common example of graded materials are materials made of binary alloys , where and are two different atomic species and is the content of the specie (so that ). In this work we present a detailed analysis of the possibility to get a thermal diode with graded Si-Ge alloys. The investigation is mainly based on the results given in [1], where a systematic approach has been introduced to find the optimal gradation of the species in order to maximize the efficiency of the fin. Our main assumptions are the following ones:
-
•
the device is a wire of variable diameter , hence the problem can be considered one-dimensional;
-
•
the Fourier law describes with enough accuracy the distribution of temperature along the device;
-
•
the anharmonic, alloy and boundary scattering of the phonons all give contributions to the value of the thermal conductivity;
-
•
the concentration and the diameter are unknown variables and must be determined in order to optimize the rectifying effect.
The paper is organized as follows: in Section 2 we introduce the main equations and the rectification coefficient . Also, for the sake of clearness and completeness we briefly describe the approach given in [1] to maximize this coefficient. In Section 3 we apply the formulae to a Si-Ge graded wire with variable diameter. An analytical formula for the thermal conductivity, mainly based on [6] (see also [7, 8, 9]), is presented and discusses. In Section 4 we apply the results given in Section 2 to the formula for the thermal conductivity obtained. Finally, in the conclusions, the main aspects of this work are emphasized, under a constructive point of view. Indeed, even if it is true that our analysis seems to preclude the possibility to get significant values of the rectification coefficient, different perspectives which may indicate the methodology to achieve applicable results.
2 The rectification coefficient and its maximization
This section is mostly based on a work of Peyrard [2] and on a previous work of some of the co-authors [1] and introduces the main findings described in Section 3. It has been shown in [2] that it is possible to get a rectifying effect from a device composed of two materials with at least one of them with a temperature dependent thermal conductivity. When the temperature range considered is large, almost every metallic or semiconductor material has a temperature dependent thermal conductivity. Furthermore, for graded materials, the thermal conductivity may be also a function of the gradation in composition: for example, for binary alloys , is a function of and of the species content (see e.g. [10]). If the species content is variable inside the material, i.e. , then the thermal conductivity becomes dependent on and x, . In [1] a systematic way to choose the spatial distribution of the composition and the geometry of the device presenting the more interesting rectification performances has been introduced. Here we will recall the main findings for completeness and easy of readability of Section 3. By assuming that the Fourier law holds, the steady state distribution of the temperature is described by the solution of the following equation:
| (1) |
In a steady state situation, like the one we are considering, the heat flux across the device is a constant (since it solves ). Then, the implicit solution of equation (1) is given by
| (2) |
giving
| (3) |
The efficiency of a thermal rectifier can be evaluated through the rectification coefficient, defined by the ratio of the heat flux in two opposite configurations, the “direct” and the “inverse”. To fix ideas, we take the two boundaries of the device at and at the temperatures and , where . In the direct configuration the end is at the temperature and the end at the higher temperature . In the reverse configuration the boundary is at the higher temperature whereas the end at is at the lower temperature . From equation (2), if and are respectively the direct and reverse heat fluxes, the rectification coefficient is defined as:
| (4) |
where and are the solutions of the steady Fourier equation (1) in the reverse and direct configurations respectively [1]. From (4) it is clear that if was a constant, the rectification constant would be equal to 1, i.e. the heat fluxes in the direct and inverse configurations are equal and no rectifying effect is observed. Notice that, if is constant, then the distribution of the temperatures in the two configurations is represented by the distributions of the temperatures and in the direct and reverse configurations, given, respectively, by
| (5) |
If we look at the plane , these temperatures lie exactly on the diagonals of the rectangle with vertices in , , and . According to [1], if is a regular continuous function of and , at steady state the temperature profiles roughly will follow the same diagonals. Then, if the value that the thermal conductivity assumes on one of these diagonals is much greater then the value it assumes on the other diagonal, a considerable rectifying effect should be observed. Based on this reasoning, in [1] the following methodology has been proposed to maximize the rectification coefficient (4):
-
1.
Among the various possible geometries and distributions , look for the particular geometry and distribution giving a saddle point to the function in the middle of the domain of interest. In the plane , the saddle must present a maximum on one diagonal and a minimum on the other diagonal.
-
2.
Among the various possible geometries and distributions , look for the particular geometry and the particular distribution which maximizes the difference between the values that assumes on the vertices of the rectangle whose diagonals are given by (5). More precisely, if denotes the values on one of the two diagonals and the values on the other, maximize the differences and .
In the next section, in order to apply the above line of reasoning to graded Si-Ge devices, we will describe the dependence of the thermal conductivity on the temperature, gradation and dimension of the section of the wire.
3 Si-Ge alloys with variable section
The thermal conductivity of silicon germanium alloys is in general lower than the corresponding thermal conductivities of the bulk materials. From a microscopic point of view, this is due to an additional scattering mechanism of the phonons inside the material, the so-called alloy scattering. The geometry of the material may play also a role in the determination of the thermal conductivity. Indeed, if the dimensions are small enough, the scattering of the phonons with the boundaries of the material may become strong enough and contribute to a further lowering of the thermal conductivity. The properties of the Si-Ge alloys can be computed by using first-principles approaches, like the density-functional perturbation theory (see e.g. [11] for bulk materials with diffusive boundary conditions or [12] for disordered silicon-germanium alloys). As for the case of porous silicon, we need an analytical formulation of the thermal conductivity accurate enough and simple enough to be manipulated. In [6] the authors presented a theoretical, phenomenological formulation of the thermal conductivity of nanowire alloys, with the section of the wire explicitly taken into account. This formulation has been compared with experimental results: between a temperature range of K, the agreement seems to be good enough in order to be utilized here [7], [8], [6]. The thermal conductivity of a nanowire is then given by [6]
| (6) |
where and are the Boltzmann’s and reduced Planck’s constants, the inverse scattering rate is given, by the Mathiessen’s rule, by the sum of three terms, i.e.
where , and are respectively the contributions due to anharmonic, alloy and boundary scattering. The anharmonic contribution is described by the weighted average between the Si and Ge terms, with proportional to and proportional to ( and are constants, is the frequency of the phonons). The alloy scattering term is approximated by a quadratic function of , that must be zero for and , giving (see also [9] for the proportionality to the term). The boundary term is taken in [6] to be equal to , where is the diameter of the wire and is the average speed of sound, given by ( and are the average speeds of sound in silicon and germanium). The overall cutoff frequency is given by , where THz [6].
Putting all together and taking the constants of proportionality from [6], we get
| (7) |
where , , , and . The three constants are given by , , .
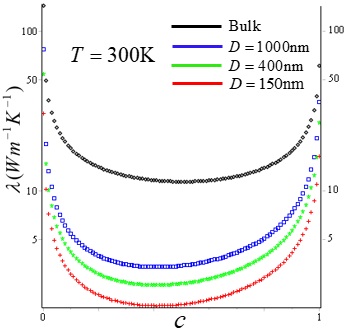
In Figure (1) the plots of the value of the thermal conductivity for and for different values of are reported. In the next subsection we apply our methodology to the thermal conductivity (7): as we will see, in this case we find that it is not possible to obtain high values of the rectification coefficient (4) following our approach.
4 Analysis of the thermal conductivity (7) and the corresponding rectification coefficient
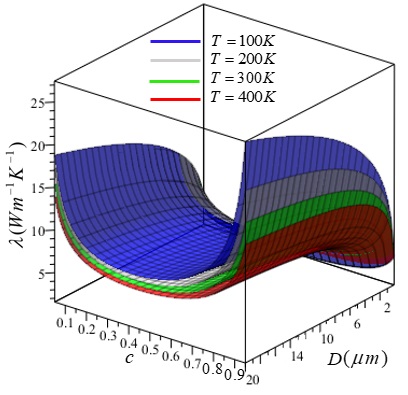
In the approach explained in Section 2 to obtain sufficiently large values of the rectification coefficient it is crucial, for both the steps 1) and 2), to have large values for the differences and , where defines the values of the temperatures on one of the two diagonals and the values on the other.
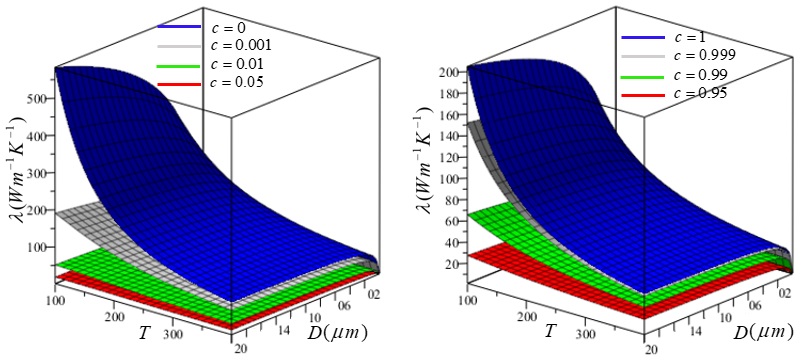
It is clear however that, in order to satisfy these conditions, the function , as a function of in the domain , is required to be increasing at least in some interval of the domain, whereas the function is required to be decreasing at least in some interval of the same domain. Since in formula (7) we assume that both the concentration and the diameter are function of , the values and pick out some values , , and . If the function would be increasing, as a function of , in some region of the variables and , and decreasing in some other regions, then it would be possible, by tuning the dependence of and on , to give a thermal conductivity presenting an interesting rectification coefficient. But, in the range of temperatures K, the function does not satisfy the requested properties. Indeed, in the region is almost flat for all values of and for all the reasonable values of , i.e. from nm to nm. In this range of , the values of are bounded in the interval , as shown in (2), whereas in the full range of variation of (i.e. ), the values of can reach values as large as . This suggests to look at values of giving almost pure silicon () or almost pure germanium (). However, in these ranges the thermal conductivity is always a decreasing function of the temperature, independently on the value the concentration assumes, apart very flat maxima for fixed and small values of (see the plots (3) for the dilute zones). This seems to preclude the possibility to tune the dependence of and on in such a way to get an interesting value of the rectification coefficient. The above result could explain the small values of found in literature for devices (see, e.g., [13]).
5 Conclusions
In this work we systematically analyzed the possibility to obtain a thermal diode for functionally graded Si-Ge alloys. We tried to get the particular spatial distribution of the species content and the geometry of the wire giving reasonably high values of the rectification coefficient. This same methodology is applied to porous silicon materials in [1] showing the possibility to obtain a rectification coefficient equal to 3.15. The same approach applied to Si-Ge materials shows that a thermal diode with the characteristics here described has instead few chances to become a good heat rectifier. Clearly, this negative result only implies the impracticability to get a thermal diode with the above characteristics. The model here presented, although to be physical consistent and accurate, can be regarded as a first approximation to more complex approaches and if new variables or different heat transfer laws are embedded in the model here considered, more satisfactory results could be achieved.
6 Acknowledgments
Work performed under the auspices of the Gruppo Nazionale per la Fisica Matematica (GNFM-INdAM).
M.G.N., E.V., and F.Z. would like to acknowledge the financial support of the Università degli Studi di Brescia.
S.C. acknowledges the partial financial support of Università di Roma “La Sapienza”.
S.C. and F.Z. would like to acknowledge the financial support of INFN.
References
-
[1]
M. G. Naso, E. Vuk, F. Zullo,
On
the optimization of heat rectification in graded materials, Int. J. Heat
Mass Transf. 143 (2019) 118520.
doi:10.1016/j.ijheatmasstransfer.2019.118520.
URL http://www.sciencedirect.com/science/article/pii/S0017931019313080 -
[2]
M. Peyrard, The design of a
thermal rectifier, EPL 76 (1) (2006) 49–55.
doi:10.1209/epl/i2006-10223-5.
URL https://doi.org/10.1209/epl/i2006-10223-5 -
[3]
D. B. Go, M. Sen, On the Condition
for Thermal Rectification Using Bulk Materials, Journal of Heat Transfer
132 (12).
doi:10.1115/1.4002286.
URL https://doi.org/10.1115/1.4002286 -
[4]
E. Müller, Č. Drašar, J. Schilz, W. A. Kaysser,
Functionally
graded materials for sensor and energy applications, Mater. Sci. Eng. A
362 (1) (2003) 17–39.
doi:10.1016/S0921-5093(03)00581-1.
URL http://www.sciencedirect.com/science/article/pii/S0921509303005811 -
[5]
M. Naebe, K. Shirvanimoghaddam,
Functionally
graded materials: A review of fabrication and properties, Appl. Mater. Today
5 (2016) 223–245.
doi:10.1016/j.apmt.2016.10.001.
URL http://www.sciencedirect.com/science/article/pii/S2352940716301214 -
[6]
Z. Wang, N. Mingo, Diameter dependence
of sige nanowire thermal conductivity, Appl. Phys. Lett. 97 (10) (2010)
101903.
doi:10.1063/1.3486171.
URL https://doi.org/10.1063/1.3486171 - [7] R. Cheaito, J. C. Duda, T. E. Beechem, K. Hattar, J. F. Ihlefeld, D. L. Medlin, M. A. Rodriguez, M. J. Campion, E. S. Piekos, P. E. Hopkins, Experimental Investigation of Size Effects on the Thermal Conductivity of Silicon-Germanium Alloy Thin Films, Phys. Rev. Lett. 109 (19) (2012) 195901. doi:10.1103/PhysRevLett.109.195901.
-
[8]
J. Kim, E. Ou, D. P. Sellan, L. Shi, A
four-probe thermal transport measurement method for nanostructures, Rev.
Sci. Instrum. 86 (4) (2015) 044901.
doi:10.1063/1.4916547.
URL https://doi.org/10.1063/1.4916547 -
[9]
P. G. Klemens, The
scattering of low-frequency lattice waves by static imperfections, Proc.
Math. Phys. Eng. Sci. 68 (12) (1955) 1113–1128.
doi:10.1088/0370-1298/68/12/303.
URL https://doi.org/10.1088/0370-1298/68/12/303 - [10] F. Schaffler, Silicon-Germanium (Si-1-xGe-x), in: M. Levinshtein, S. Rumyantsev, M. Shur (Eds.), Properties of advanced semiconductor materials : GaN, AlN, InN, BN, SiC, SiGe, Wiley & Sons, Inc., New York, 2001, pp. 149–188.
-
[11]
J. Carrete, B. Vermeersch, A. Katre, A. van Roekeghem, T. Wang, G. K. H.
Madsen, N. Mingo,
almaBTE: a solver of the space-time dependent Boltzmann transport
equation for phonons in structured materials, Comput. Phys. Commun. 220
(2017) 351–362.
doi:10.1016/j.cpc.2017.06.023.
URL https://doi-org.proxy.unibs.it/10.1016/j.cpc.2017.06.023 - [12] J. Garg, N. Bonini, B. Kozinsky, N. Marzari, Role of disorder and anharmonicity in the thermal conductivity of silicon-germanium alloys: A first-principles study, Phys. Rev. Lett. 106 (4). doi:10.1103/physrevlett.106.045901.
-
[13]
I. Carlomagno, V. A. Cimmelli, D. Jou,
Heat
flux rectification in graded : Longitudinal
and radial heat flows, Physica E Low Dimens. Syst. Nanostruct. 90 (2017)
149–157.
doi:https://doi.org/10.1016/j.physe.2017.03.012.
URL http://www.sciencedirect.com/science/article/pii/S1386947716315806