Non-minimal bridge position of -cable links
Abstract.
Suppose that every non-minimal bridge position of a knot is perturbed. We show that if is a -cable link of , then every non-minimal bridge position of is also perturbed.
Key words and phrases:
2010 Mathematics Subject Classification:
Primary: 57M251. Introduction
A knot in is said to be in bridge position with respect to a bridge sphere, the original notion introduced by Schubert [12], if the knot intersects each of the -balls bounded by the bridge sphere in a collection of -parallel arcs. It is generalized to knots (and links) in -manifolds with the development of Heegaard splitting theory, and is related to many interesting problems concerning, e.g. bridge number, (Hempel) distance, and incompressible surfaces in -manifolds.
From any -bridge position, we can always get an -bridge position by creating a new local minimum point and a nearby local maximum point of the knot. A bridge position isotopic to one obtained in this way is said to be perturbed. (It is said to be stabilized in some context.) A bridge position of the unknot is unique in the sense that any -bridge () position of the unknot is perturbed [7]. The uniqueness also holds for -bridge knots [8]. See also [11], where all bridge surfaces for -bridge knots are considered. Ozawa [9] showed that non-minimal bridge positions of torus knots are perturbed. Zupan [14] showed such property for iterated torus knots and iterated cables of -bridge knots. More generally, he showed that if is an mp-small knot and every non-minimal bridge position of is perturbed, then every non-minimal bridge position of a -cable of is also perturbed [14]. (Here, a knot is mp-small if its exterior contains no essential meridional planar surface.) We remark that there exist examples of a knot with a non-minimal bridge position that is not perturbed [10] and furthermore, knots with arbitrarily high index bridge positions that are not perturbed [5].
In this paper, we consider non-minimal bridge position of -cable links of a knot without the assumption of mp-smallness of .
Theorem 1.1.
Suppose that is a knot in such that every non-minimal bridge position of is perturbed. Let be a -cable link of . Then every non-minimal bridge position of is also perturbed.
For the proof, we use the notion of t-incompressibility and t--incompressibility of [3]. We isotope an annuls whose boundary is to a good position so that it is t-incompressible and t--incompressible in one side, say , of the bridge sphere. Then consists of bridge disks and (possibly) properly embedded disks. By using the idea of changing the order of t--compressions in [2] or [3], we show that in fact consists of bridge disks only. Then by a further argument, we find a cancelling pair of disks for the bridge position.
2. T-incompressible and t--incompressible surfaces in a -ball
A trivial tangle is a union of properly embedded arcs in a -ball such that each cobounds a disk with an arc in , and . By standard argument, ’s can be taken to be pairwise disjoint.
Let denote a surface in satisfying . A t-compressing disk for is a disk in such that and is essential in , i.e. does not bound a disk in . A surface is t-compressible if there is a t-compressing disk for , and is t-incompressible if it is not t-compressible.
An arc properly embedded in with its endpoints on , is t-essential if does not cobound a disk in with a subarc of . In particular, an arc in parallel to a component of can be t-essential. See Figure 1. (Such an arc will be called bridge-parallel in Section 3.) A t--compressing disk for is a disk in such that is an endpoint union of two arcs and , and is t-essential, and . A surface is t--compressible if there is a t--compressing disk for , and is t--incompressible if it is not t--compressible.
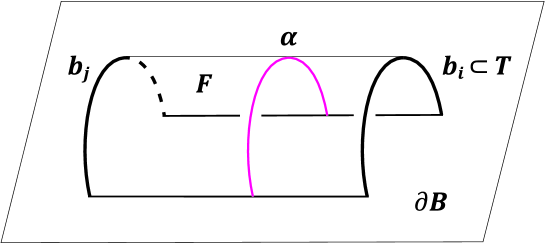
Hayashi and Shimokawa [3] classified t-incompressible and t--incompressible surfaces in a compression body in more general setting. Here we give a simplified version of the theorem.
Lemma 2.1 ([3]).
Let be a pair of a -ball and a trivial tangle in , and let be a surface satisfying . Suppose that is both t-incompressible and t--incompressible. Then each component of is either
-
(1)
a disk cobounded by an arc of and an arc in with , or
-
(2)
a disk properly embedded in with .
3. Bridge position
Let be a -sphere decomposing into two -balls and . Let denote a knot (or link) in . Then is said to be in bridge position with respect to if is a trivial tangle. Each arc of is called a bridge. If the number of bridges of is , we say that is in -bridge position. The minimum such number among all bridge positions of is called the bridge number of . A bridge cobounds a bridge disk with an arc in , whose interior is disjoint from . We can take a collection of pairwise disjoint bridge disks by standard argument, and it is called a complete bridge disk system. For a bridge disk in, say , if there exists a bridge disk in such that is a single point of , then is called a cancelling disk. We call a cancelling pair.
A perturbation is an operation on an -bridge position of that creates a new local minimum and local maximum in a small neighborhood of a point of , resulting in an -bridge position of . A bridge position obtained by a perturbation admits a cancelling pair by the construction. Conversely, it is known that a bridge position admitting a cancelling pair is isotopic to one obtained from a lower index bridge position by a perturbation. (See e.g. [11, Lemma 3.1]). Hence, as a definition, we say that a bridge position is perturbed if it admits a cancelling pair.
Let be a standard solid torus in with core , and be a solid torus in whose core is a knot . A meridian of is uniquely determined up to isotopy. Let be a longitude of such that the linking number , called the preferred longitude. Similarly, let and be a meridian and a longitude of respectively such that . Take a -torus knot (or link) in that wraps longitudinally times; more precisely, and . Let be a homeomorphism sending to and to . Then is called a -cable of . Concerning the bridge number, it is known that [12], [13].
Let be a knot (or link) in -bridge position with respect to a decomposition , so is a union of bridges . Let be a complete bridge disk system for , where is a bridge disk for . Let be a surface bounded by and . When we move to an isotopic bridge position, moves together. We consider . By isotopy we assume that in a small neighborhood of , .
An arc in is bridge-parallel (b-parallel briefly) if is parallel, in , to some and cuts off a rectangle from whose four edges are , , and two arcs in . Let () denote an arc of which is outermost in some and cuts off the corresponding outermost disk disjoint from . The following lemma will be used in Section 6.
Lemma 3.1.
After possibly changing to an isotopic bridge position, there is no that is b-parallel.
Proof.
We isotope and and take so that the minimal number of is realized. Suppose that there is such an arc which is parallel in to (same or not with ). Isotope along to an arc parallel to so that the changed surface is disjoint from . See Figure 2. Take a new bridge disk for to be a parallel copy of . Other bridge disks () remain unaltered. They are all mutually disjoint. Hence is a new complete bridge disk system. We see that since at least no longer belongs to the intersection . This contradicts the minimality of . ∎
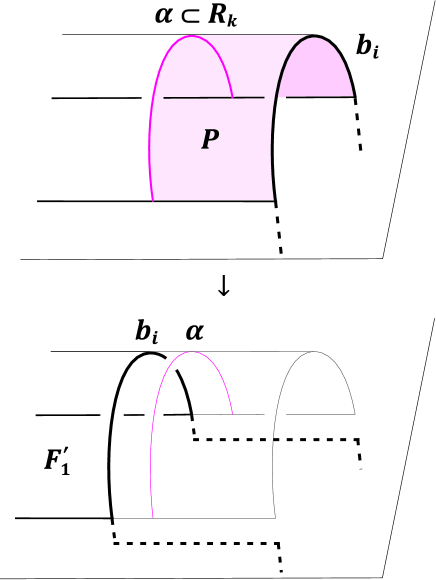
Now we consider a sufficient condition for a bridge position to be perturbed.
Lemma 3.2.
Suppose a separating arc of cuts off a disk from such that
-
(1)
is a single disk , and
-
(2)
() consists of bridge disks .
Then the bridge position of is perturbed.
Proof.
Let () denote the bridge for and . Let denote the bridges contained in . We assume that is adjacent to and . See Figure 3. Let be a union of disjoint bridge disks, where is a bridge disk for . In the following argument, we consider except for .
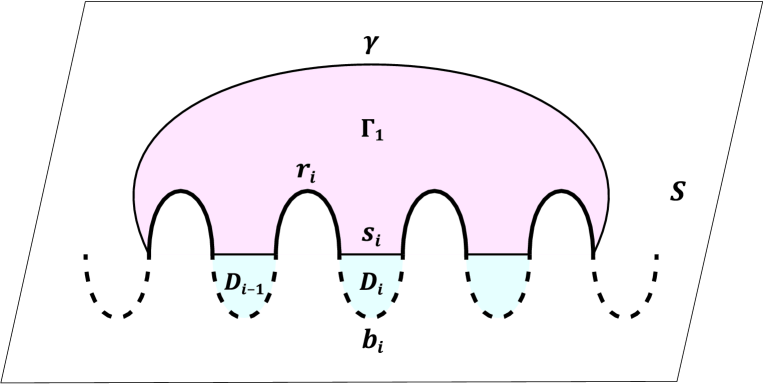
Suppose there is a circle component of . Let () be one which is innermost in and be the innermost disk that bounds. Let be the disk that bounds in . Then by replacing with , we can reduce . So we assume that there is no circle component of .
Suppose there is an arc component of with both endpoints on the same arc of . Let () be one which is outermost in and be the corresponding outermost disk in cut off by . The arc cuts into two disks and let be one of the two disks that does not contain . By replacing with , we can reduce . So we assume that there is no arc component of with both endpoints on the same arc of .
If , then is a desired cancelling pair and the bridge position of is perturbed. So we assume that .
Case . Every arc of is b-parallel.
Let be an arc of which is outermost in some and be the outermost disk that cuts off from . In addition, let be b-parallel to via a rectangle . Then is a new bridge disk for , and or is a cancelling pair.
Case . There is a non-b-parallel arc of .
Consider only non-b-parallel arcs of . Let denote one which is outermost in among them and denote the outermost disk cut off by . Because there are at least two outermost disks, we take such that contains some . Let be the bridges contained in and . In the following, we consider except for and . If , then there exists a cancelling pair . Otherwise, every arc of is b-parallel. Let be an arc of which is outermost in some and be the outermost disk that cuts off from . In addition, let be b-parallel to via a rectangle . Then is a new bridge disk for , and or is a cancelling pair. ∎
Remark 3.3.
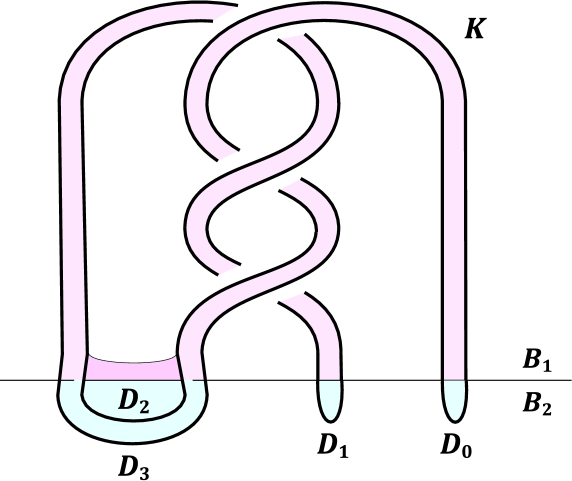
Let be an unknot in -bridge position, with and . We assume that the bridge () is adjacent to and , where we consider the index modulo . Let and denote bridge disks for and respectively. Then is called a complete cancelling disk system if each and each is a cancelling pair.
Let denote a disk bounded by . By following the argument of the proof of Theorem 1.1, we can assume that consists of bridge disks and is a single disk, as in [3]. Then if , the bridge position of admits a cancelling pair by Lemma 3.2, giving a proof of the uniqueness of bridge position of the unknot. One may hope that extends to a complete cancelling disk system. But when , there exists an example such that does not extend to a complete cancelling disk system, as expected in [3, Remark 1.2]. Some is even not a cancelling disk. This issue was related to one of the motivations for the present work. In Figure 4, is an unknot in -bridge position bounding a disk and . Each of the disks and is a cancelling disk. However, and are not cancelling disks because, say for , an isotopy of along and then slightly into does not give a -bridge position of (see [11], [6]).
4. Proof of Theorem 1.1: First step
Let be a knot such that every non-minimal bridge position of is perturbed. Let be a -cable link of , with components and . Suppose that is in non-minimal bridge position with respect to a bridge sphere bounding -balls and . Each is a trivial tangle. Since is a -cable link, bounds an annulus, denoted by . We take so that is minimal.
Claim 1.
One of the following holds.
-
•
is the unlink in a non-minimal bridge position, hence perturbed.
-
•
is t-incompressible in .
Proof.
Suppose that is t-compressible. Let be a t-compressing disk for and let . Let be the component of containing .
Case . is essential in .
A t-compression of along gives two disjoint disks bounded by and respectively. Then is an unlink. Since the complement of an unlink has a reducing sphere, by [1] a bridge position of an unlink is a split union of bridge positions of unknot components. Since a non-minimal bridge position of the unknot is perturbed, we see that is perturbed.
Case . is inessential in .
Let be the disk that bounds in . Then , since otherwise is inessential in . By replacing of with , we get a new annulus bounded by such that , contrary to the minimality of . ∎
Since our goal is to show that the bridge position of is perturbed, from now on we assume that is not the unlink. By Claim 1, is t-incompressible in . If is t--compressible in , we do a t--compression.
Claim 2.
A t--compression preserves the t-incompressibility of .
Proof.
Let be a t--compressing disk for . Suppose that the surface after the t--compression along is t-compressible. A t-compressing disk can be isotoped to be disjoint from two copies of and the product region . Then would be a t-compressing disk for before the t--compression, a contradiction. ∎
A t--compression simplifies a surface because it cuts the surface along a t-essential arc. So if we maximally t--compress , we obtain a t--incompressible . Note that the effect on of a t--compression of is just pushing a neighborhood of an arc in into , which is called an isotopy of Type in [4]. After a maximal sequence of t--compressions, is both t-incompressible and t--incompressible by Claim 2. Then by applying Lemma 2.1,
-
()
consists of bridge disks ’s and properly embedded disks ’s.
5. Proof of Theorem 1.1: T--compression and its dual operation
Take an annulus bounded by so that holds and the number of properly embedded disks is minimal. In this section, we will show that , i.e. consists of bridge disks only.
Suppose that . Then is homeomorphic to an -punctured annulus. A similar argument as in the proof of Claim 1 leads to that is t-incompressible. By Lemma 2.1 again, is t--compressible. We can do a sequence of t--compressions on until it becomes t--incompressible. Note that the t-incompressibility of is preserved.
Now we are going to define a t--compressing disk ( for some ) and its dual disk inductively. Let . Let be a t--compressing disk for and and . By a t--compression along , a neighborhood of is pushed along into and thus a band is created in . Let denote the resulting annulus bounded by . Let be a dual disk for , that is, a disk such that an isotopy of Type A along recovers a surface isotopic to . For the next step, let .
Let be a t--compressing disk for and and . After a t--compression along , a band is created in . Let denote the resulting annulus bounded by . There are three cases to consider.
Case . intersects the arc more than once.
The band cuts off small disks from , which are mutually parallel along the band. We designate any one among the small disks, say , as the dual disk . Let be the union of others.
Case . intersects once.
We take the subdisk that cuts off from as the dual disk , and let in this case.
Case . does not intersect .
We take a dual disk freely, and let in this case.
In any case, let .
In general, assume that and are defined. Let be a t--compressing disk for and and . After a t--compression along , a band is created in . Let denote the resulting annulus bounded by .
Case a. intersects the collection of arcs more than once.
The band cuts off small disks from , which are mutually parallel along the band. We designate any one among the small disks, say , as the dual disk . Let be the union of others.
Case b. intersects once.
We take the subdisk that cuts off from as the dual disk , and let in this case.
Case c. does not intersect .
We take a dual disk freely, and let in this case.
In any case, let .
Later, we do isotopy of Type A, dual to the t--compression, in reverse order along . Let us call it dual operation for our convenience.. Let be the band mentioned above, cutting off from (in Case a). When the dual operation along is done, we modify every and () containing any ( of , by replacing each () with the union of a subband of between and () and a copy of , and doing a slight isotopy. We remark that, although it is not illustrated in Figure 5, some ’s and ’s temporarily become immersed when the subband passes through some removed region, say (). But the () is also modified as we proceed the dual operations, and the ’s and ’s again become embedded. (In Figure 5 and Figure 6, the dual operation along is done, and the dual operation along is not done yet.) Actually, before the sequence of dual operations, ’s and ’s () are modified in advance so that is disjoint from the union of certain band and a disk (which will be explained later). See Figure 6.
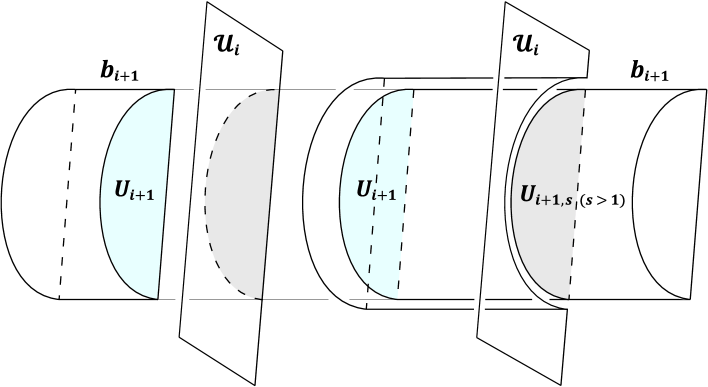
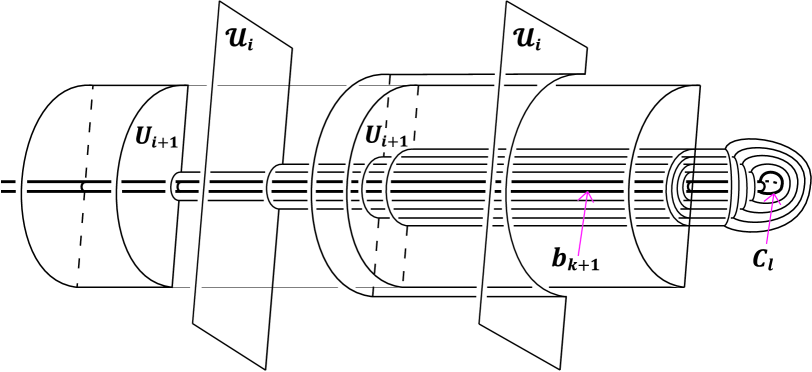
The t--compressing disk is taken to be disjoint from two copies of (). Moreover, for every we can draw on (). Since the t--compression along is equivalent to cutting along and the sequence is maximal, every is incident to some .
Claim 3.
For each , there exists an such that connects to other component of .
Proof.
Suppose that there exists a which is not connected to other component of . That is, for such , every incident to connects to itself. Then after a maximal sequence of t--compressions on , some non-disk components will remain. This contradicts Lemma 2.1. ∎
Let be the smallest index such that connects some , say , to other component (other or ). If , then by a t--compression along , either and other are merged into one properly embedded disk, or and a bridge disk are merged into a new bridge disk. This contradicts the minimality of . So we assume that .
Suppose that we performed t--compressions along . Consider the small disks that the band cuts off from . They are parallel along . We replace the small disks one by one, the nearest one to first, so that is disjoint from . Let be the small disk nearest to . Let be the union of a subband of and that cuts off from . For every and () containing , we replace with . Then again let be the (next) small disk nearest to and we repeat the above operation until is disjoint from .
Now we do the dual operation on in reverse order along . Let () be the resulting annulus after the dual operation along . The shape of the dual disk is possibly changed but the number of circle components and arc components of is same with those of . After the dual operation along , it is necessary to modify some ’s and ’s () further as in Figure 6 so that is disjoint from . In this way, we do the sequence of dual operations, and the number of circle components of is also . Then because is disjoint from , we can do the t--compression of along first and the number of properly embedded disks is reduced, contrary to our assumption.
We have shown the following claim.
Claim 4.
consists of bridge disks.
6. Proof of Theorem 1.1: Finding a cancelling pair
By Claim 4, consists of bridge disks. Let and be bridges of and respectively that are indexed consecutively along each component. Let () be the bridge disk for and , and let () be the bridge disk for and . Let be a complete bridge disk system for and let . We consider except for the bridges .
If there is an inessential circle component of in , it can be removed by standard innermost disk argument. If there is an essential circle component of in , then would be the unlink as in Case of the proof of Claim 1. So we assume that there is no circle component of . If there is an inessential arc component of in with both endpoints on the same (or ), then the arc can be removed by standard outermost disk argument. So we assume that there is no arc component of with both endpoints on the same (or ).
If , we easily get a cancelling pair, say or , so we assume that . Let denote an arc of which is outermost in some and let denote the outermost disk that cuts off from . Applying Lemma 3.1, is not b-parallel. Suppose that one endpoint of is in, say , and the other is in with the cyclic distance greater than . Then after the t--compression along , we get a subdisk of satisfying the assumption of Lemma 3.2, hence is perturbed. So without loss of generality, we assume that one endpoint of is in and the other is in .
Let be the annulus obtained from by the t--compression along and . The bridge disks and are connected by a band, and let be the resulting rectangle with four edges , and two arcs in , say . Let denote an arc of which is outermost in some and let denote the outermost disk cut off by . If at least one endpoint of is contained in or , or one endpoint of is in ( respectively) and the other is in ( respectively), then similarly as above,
-
•
either is inessential with both endpoints on the same component of , or
-
•
is b-parallel, or
-
•
Lemma 3.2 can be applied.
Hence we may assume that one endpoint of is in () and the other is in (). After the t--compression along , and are merged into a rectangle. Arguing in this way, each () is merged with some because of the fact that gives us a cancelling pair. Moreover, we see that . After successive t--compressions on , the new annulus intersects and alternately, in rectangles.
Note that and is in -bridge position. Since is in non-minimal bridge position, . So by the assumption of the theorem, the bridge position of () is perturbed. Let be a cancelling pair for with and . However, and may intersect . Let and be any adjacent rectangles of in and respectively. We remove any unnecessary intersection of and , the nearest one to first, by isotopies along subdisks of and respectively. See Figure for an example. Then becomes a cancelling pair for the bridge position of as desired.
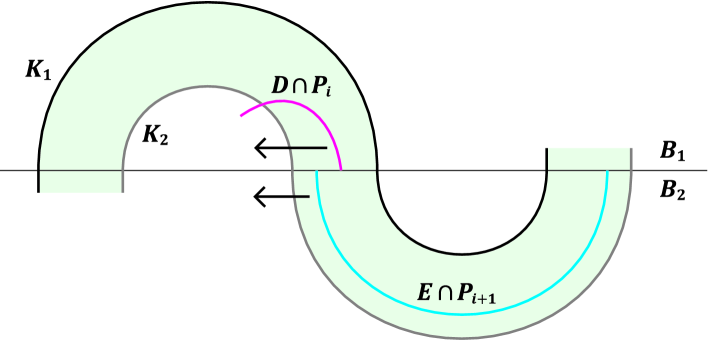
Acknowledgments.
The author was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2018R1D1A1A09081849).
References
- [1] D. Bachman and S. Schleimer, Distance and bridge position, Pacific J. Math. 219 (2005), no. 2, 221–235.
- [2] H. Doll, A generalized bridge number for links in -manifolds, Math. Ann. 294 (1992), no. 4, 701–717.
- [3] C. Hayashi and K. Shimokawa, Heegaard splittings of the trivial knot, J. Knot Theory Ramifications 7 (1998), no. 8, 1073–1085.
- [4] W. Jaco, Lectures on three-manifold topology, CBMS Regional Conference Series in Mathematics, 43. American Mathematical Society, Providence, R.I., 1980.
- [5] Y. Jang, T. Kobayashi, M. Ozawa, and K. Takao, A knot with destabilized bridge spheres of arbitrarily high bridge number, J. Lond. Math. Soc. (2) 93 (2016), no. 2, 379–396.
- [6] J. H. Lee, Reduction of bridge positions along bridge disks, Topology Appl. 223 (2017), 50–59.
- [7] J. -P. Otal, Présentations en ponts du nœud trivial, C. R. Acad. Sci. Paris Sér. I Math. 294 (1982), no. 16, 553–556.
- [8] J. -P. Otal, Présentations en ponts des nœuds rationnels, Low-dimensional topology (Chelwood Gate, 1982), 143–160, London Math. Soc. Lecture Note Ser., 95, Cambridge Univ. Press, Cambridge, 1985.
- [9] M. Ozawa, Nonminimal bridge positions of torus knots are stabilized, Math. Proc. Cambridge Philos. Soc. 151 (2011), no. 2, 307–317.
- [10] M. Ozawa and K. Takao, A locally minimal, but not globally minimal, bridge position of a knot, Math. Proc. Cambridge Philos. Soc. 155 (2013), no. 1, 181–190.
- [11] M. Scharlemann and M. Tomova, Uniqueness of bridge surfaces for -bridge knots, Math. Proc. Cambridge Philos. Soc. 144 (2008), no. 3, 639–650.
- [12] H. Schubert, Über eine numerische Knoteninvariante, Math. Z. 61 (1954), 245–288.
- [13] J. Schultens, Additivity of bridge numbers of knots, Math. Proc. Cambridge Philos. Soc. 135 (2003), no. 3, 539–544.
- [14] A. Zupan, Properties of knots preserved by cabling, Comm. Anal. Geom. 19 (2011), no. 3, 541–562.