Non-Hermitian Pseudo-Gaps

Linhu Li [email protected] Guangdong Provincial Key Laboratory of Quantum Metrology and Sensing

\&

School of Physics and Astronomy, Sun Yat-Sen University (Zhuhai Campus), Zhuhai 519082, China Ching Hua Lee [email protected] Department of Physics, National University of Singapore, Singapore 117551, Republic of Singapore

Abstract

The notion of a band gap is ubiquitous in the characterization of matter. Particularly interesting are pseudo-gaps, which are enigmatic regions of very low density of states that have been linked to novel phenomena like high temperature superconductivity. In this work, we discover a new non-Hermitian mechanism that induces pseudo-gaps when boundaries are introduced in a lattice. It generically occurs due to the interference between two or more asymmetric pumping channels, and possess no analog in Hermitian systems. Mathematically, it can be visualized as being created by divergences of spectral flow in the complex energy plane, analogous to how sharp edges creates divergent electric fields near an electrical conductor. A non-Hermitian pseudo-gap can host symmetry-protected mid-gap modes like ordinary topological gaps, but the mid-gap modes are extended instead of edge-localized, and exhibit extreme sensitivity to symmetry-breaking perturbations. Surprisingly, pseudo-gaps can also host an integer number of edge modes even though the pseudo-bands possess fractional topological windings, or even no well-defined Chern number at all, in the marginal case of a phase transition point. Challenging conventional notions of topological bulk-boundary correspondences and even the very concept of a band, pseudo-gaps post profound implications that extend to many-body settings, such as fractional Chern insulators.

Introduction.– Band gaps play a central role in intriguing condensed matter phenomena, from metal-insulator transitions to superconductivity to topological phases. These phenomena are typically protected by band gaps or quasiparticle excitation gaps, which are induced through physical mechanisms such as cooper paring for superconductors Bardeen et al. (1957); Schrieffer (2018) and spin-orbit couplings for topological insulators Kane and Mele (2005); Bernevig and Hughes (2013). However, band gaps are not always cleanly defined, such as the case of pseudo-gaps, which resemble band gaps but are in reality regions of very low density of states (DOS). Possessing vestiges of both gapped and gapless scenarios, the enigmatic role of pseudogaps in high-temperature superconducting cuprates and non-Fermi liquids have mystified physicists for decades Emery and Kivelson (1995); Kaminski et al. (2002); Lee et al. (2006); Fauqué et al. (2006); Xia et al. (2008); Vojta (2009); Varma (2010); Tahir-Kheli and Goddard III (2011); Yamaji and Imada (2011); Mei et al. (2012); she ; Mishra et al. (2014); Keimer et al. (2015); Proust et al. (2016); Battisti et al. (2017); Zhang and Sachdev (2020).

In this work, we introduce a new type of pseudo-gap arising from a novel non-Hermitian (NH) mechanism. It exists because NH systems are special in at least two fundamental ways. Firstly, their spectrum is not constrained to be real, and can thus acquire geometric and topological features in the complex energy plane, such as point-gapped loops without Hermitian analog Xiong (2018); Gong et al. (2018); Zhang et al. (2020); Okuma et al. (2020); Li et al. ; Su et al. (2020); Wang et al. (2021). Secondly, with point gaps, NH lattices also experience the non-Hermitian skin effect (NHSE) marked by dramatic boundary mode accumulation with universal spectral flow in the complex energy plane Yao and Wang (2018); Yokomizo and Murakami (2019); Lee and Thomale (2019); Yang et al. (2020); Lee et al. (2020).

Our work shows how the combination of these two fundamental features create pseudo-gaps with arbitrarily low DOS, going beyond previous theoretical Xiong (2018); Shen et al. (2018); Gong et al. (2018); Li et al. ; Kawabata et al. (2019a); Yao and Wang (2018); Yokomizo and Murakami (2019); Lee and Thomale (2019); Kunst et al. (2018); Yao et al. (2018); Yin et al. (2018); Jiang et al. (2018); Li et al. (2019); Song et al. (2019a, b); Okuma and Sato (2019); Mu et al. (2020); Jiang et al. (2019); Longhi (2019); Kunst and Dwivedi (2019); Jin and Song (2019); Borgnia et al. (2020); Lee et al. (2019); Li et al. (2020a); Okuma et al. (2020); Zhang et al. (2020); Wang et al. (2020); Lee et al. (2020); Chang et al. (2020); Li et al. (2020b); Budich and Bergholtz (2020); Lee and Longhi (2020); Yang et al. (2020); Yi and Yang (2020); Lee (2020a, b); Mandal et al. (2020); Teo et al. (2020); Okuma and Sato (2021a); Li et al. (2021); Zhang et al. (2021a, b); Yang et al. (2021); Song et al. (2021) and experimental Su et al. (2020); Wang et al. (2021); Helbig et al. (2020); Xiao et al. (2020); Ghatak et al. (2020); Weidemann et al. (2020); Zou et al. (2021); Stegmaier et al. (2021) works where adiabatic continuity between the periodic and open boundary condition (PBC and OBC) spectra is generally assumed. As such, besides reformulating major notions like topological bulk-boundary correspondences and criticality Xiong (2018); Yao and Wang (2018); Okuma et al. (2020); Lee (2020a); Li et al. (2020b), the NHSE here also raises fundamental questions on the nature of topological band gaps, with implications like quasi-particle fractionalization.

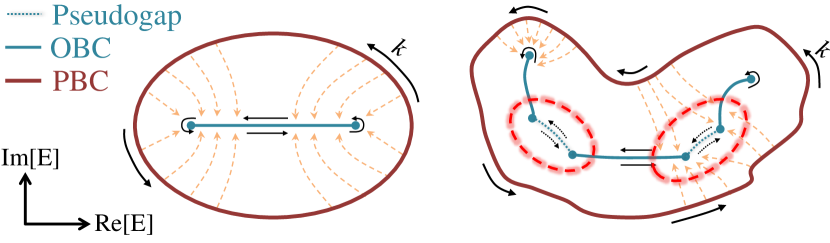
Refer to caption — Figure 1: Emergence of pseudo-gaps in non-Hermitian OBC spectra. In 1D NH Hamiltonians, PBC spectra (brown) generically trace out closed loops in the complex $E$ plane. Their OBC spectra (cyan) are obtained by conformally shrinking PBC loops (dashed orange arrows) until they form lines or curves within their interiors. (Left) Ordinarily, a PBC loop shrinks into one OBC curve, with 1:1 correspondence between OBC and PBC bands. (Right) However, depending on PBC loop curvature, two or more distinct OBC curves (pseudo-bands) can also form, separated by regions of very low DOS (dotted cyan, circled in red) known as NH pseudo-gaps.

Origin of the NH pseudo-gap.– To understand the mechanism behind NH pseudo-gaps, we consider a 1D NH lattice chain ¹¹1The mechanism for NH pseudo-gaps applies in higher-dimensional lattices, but we specialize to 1D for simplicity. with PBC spectrum $E(k)$ , $k\in[0,2\pi)$ tracing out a loop in complex energy space (brown loops in Fig. 1). The loop generically enclose a non-zero area if non-reciprocity exists in the couplings. It is established Xiong (2018); Yao and Wang (2018); Lee and Thomale (2019) that upon the introduction of spatial inhomogeneities such as open boundaries (OBCs) , the PBC spectral loop will shrink into its interior (via orange arrows), such that it collapses into a line, curve or tree-like structure Lee et al. (2020) (cyan). This extensive spectral flow moves the eigenvalues far away from the bulk (PBC) spectrum, implying that all states must accumulate at a physical boundary. Mathematically, the accumulation is represented by the complex deformation $k\rightarrow k+i\kappa(k)$ with $E(k+i\kappa(k))$ being the degenerate OBC spectrum (cyan in Fig. 1), such that an original Bloch state $\psi_{k}(x)\sim e^{ikx}\rightarrow e^{ikx}e^{-\kappa(k)x}$ acquires an exponential decay term. In most cases (Left in Fig. 1), there exists a clear 1-to-1 correspondence between the PBC (outer brown loop) and OBC (internal cyan line) bands. However, it is also possible that the OBC band breaks into multiple pseudo-bands separated by pseudo-gaps (Right, dotted cyan and circled red). These are not true gaps due to adiabatic continuity inherited from the continuous PBC loop. However, they are pseudo-gaps in the sense that their DOS can be made arbitrarily low.

For general insights into when pseudo-gaps occur, we note that as we interpolate from PBCs to OBCs, the shrinking of the spectral loop is controlled by the conformal map $E(k)$ , with both $E$ and $k$ regarded as complex variables. As such, the spectral flow lines traced out as $\text{Im}[k]=\kappa$ are varied (orange in Fig. 1) are perpendicular to the PBC loop with $\text{Im}[k]=0$ (brown), mathematically analogous to the electric field lines emanating from a conductor Schinzinger and Laura (2012). In particular, they diverge/converge if the PBC loop (“conductor”) is convex/concave on the inside. As such, by engineering the geometry i.e. curvature of the PBC spectrum, one can arrange for the divergences to meet at certain segments of the OBC spectrum (Fig. 1 Right). As demonstrated in the model below, a pseudo-gap with very low DOS can already be produced even from a benign-looking model with simple couplings.

Minimal model for a NH pseudo-gap.– For concrete illustration of a NH pseudo-gap, we discuss the minimal model Hamiltonian $H=H_{1}+H_{2}$ with

	$\displaystyle H_{1}$	$\displaystyle=$	$\displaystyle\sum_{x}t_{1}\hat{c}^{\dagger}_{x}\hat{c}_{x+1}+t_{-1}\hat{c}^{\dagger}_{x+1}\hat{c}_{x},$
	$\displaystyle H_{2}$	$\displaystyle=$	$\displaystyle\sum_{x}t_{2}\hat{c}^{\dagger}_{x}\hat{c}_{x+2}+t_{-2}\hat{c}^{\dagger}_{x+2}\hat{c}_{x},$		(1)

which is the juxtaposition of two Hatano-Nelson (HN) chains Hatano and Nelson (1996, 1997); Okuma and Sato (2021b) $H_{1}$ and $H_{2}$ with nearest and next-nearest neighbor couplings [Fig. 2(a)]. The HN chain is the simplest model with exhibiting NHSE due to nontrivial PBC point-gap Zhang et al. (2020); Okuma et al. (2020), with OBC eigenenergies occupying the line segment between $\pm 2\sqrt{t_{j}t_{-j}}$ , $j=1,2$ . We specialize to real $t_{1}=t_{-1}$ and $t_{2}=-t_{-2}$ , such that the two HN chains separately possess pure real and imaginary OBC spectra. In momentum space, $H(k)=H_{1}(k)+H_{2}(k)$ ,

\displaystyle H_{1}(k)=2t_{1}\cos k,\,H_{2}(k)=2it_{2}\sin 2k.

(2)

which also gives the PBC spectrum for $k\in[0,2\pi)$ .

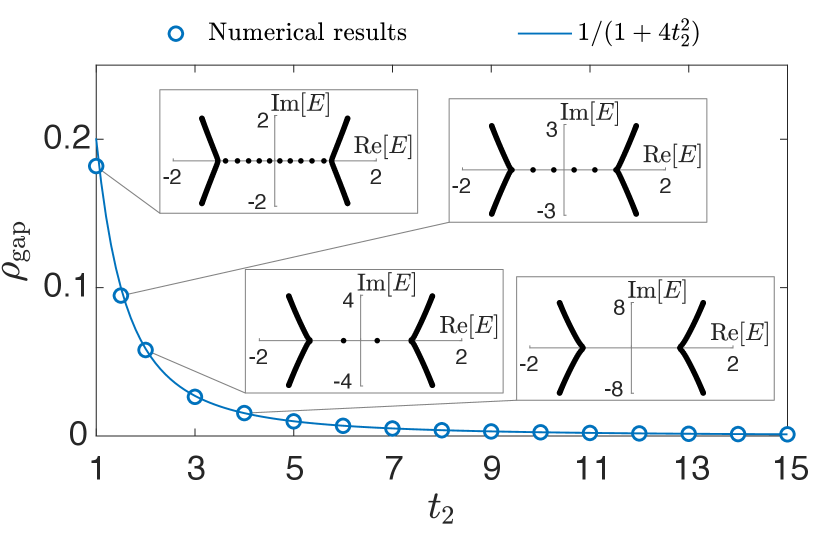
As shown in Fig. 2(b), the OBC spectrum of $H$ consists of two distinct types of segments: (i) blue arcs at positive and negative $\text{Re}[E]$ with high DOS, separated by (ii) a red segment in the middle with much lower DOS. This middle red segment is dubbed as the NH pseudo-gap because its DOS can be made arbitrarily low by tuning $t_{2}/t_{1}$ , as further shown in Fig. 3, unlike the blue arcs which behave like ordinary bands.

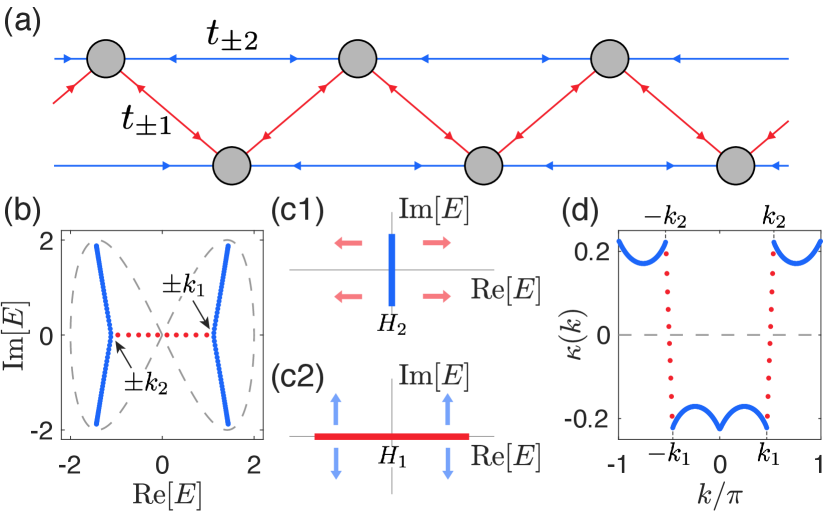
This NH pseudo-gap is real, and originates from the competition between the NHSE channels of $H_{1}$ and $H_{2}$ i.e. their differing tendencies to boundary-localize. For our model, this can be traced to the relative sign between $t_{1}/t_{-1}=1$ and $t_{2}/t_{-2}=-1$ hopping ratios, which leads to an enigmatic form of competitive interference between boundary localized skin eigenstates. This is most transparently seen on the complex energy plane. Under OBCs, $H_{1}$ has a purely real spectrum, while $H_{2}$ has a purely imaginary spectrum. As such, the OBC spectrum of their sum $H=H_{1}+H_{2}$ shall be neither purely real or purely imaginary, but a competitive combination of the two. In terms of PBC-OBC spectral flow sketched in Fig. 1, we have a juxtaposition of two spectral flows (of $H_{1}$ and $H_{2}$ ) resembling the left figure, with one set of PBC ellipse plus OBC line segment relatively rotated by $\pi/2$ . This is analyzed in careful detail in sup . The main idea, as illustrated in Fig. 2(c), is that $H_{1}$ can be understood as “pulling” the vertical OBC spectrum (blue) of $H_{2}$ apart, while $H_{2}$ simultaneously “pulls” the horizontal OBC spectrum (red) of $H_{1}$ vertically. However, due to the dissimilarity between the periodicities of $H_{1}(k)$ and $H_{2}(k)$ [Eq. 2], the net effect is that most of the states are “pulled” away from the real line into almost vertical OBC arcs (blue), resulting in $H=H_{1}+H_{2}$ having a real pseudo-gap of very low DOS [Fig. 2(b)]. More generally, NH pseudo-gap regions are not necessarily real or straight, but they all originate from analogous competitive mechanisms between different NHSE channels.

Since pseudo-gaps contain so few states, they appear as steep jumps of the skin inverse decay length $\kappa(k)$ [Fig. 2(d)]. The values of $\kappa(k)$ before and after the jumps are that of the two pseudo-bands, and can be obtained through the Generalized Brillouin zone (GBZ) Yao and Wang (2018); Yokomizo and Murakami (2019); Lee and Thomale (2019); Lee et al. (2020) (detailed in the Supplemental Materials sup ). The jumps of $\kappa(k)$ occur as an opposite pair that, for this model, crosses $\kappa=0$ twice. In other words, a pseudo-gap between bands that are oppositely localized (with different signs of $\kappa$ ) may contain delocalized states.

The DOS within the pseudo-gap can be estimated via $\rho_{\rm gap}=2\Delta k/E_{\rm gap}$ with $\Delta k=|k_{2}-k_{1}|$ the GBZ momentum jump across the pseudo-gap, and $E_{\rm gap}$ the gap size, as shown in Fig. 3. As further derived in sup ,

\displaystyle\rho_{\rm gap}=\sum_{\pm}\frac{dk}{dE}\approx\frac{t_{1}}{t_{1}^{2}+4t_{2}^{2}}

(3)

with $\pm$ indexing the jump regions, agreeing closely with numerics [Fig. 3]. For $t_{1}=1$ and $t_{2}\sim\mathcal{O}(1)$ , we can easily obtain $\rho_{\rm gap}\sim\mathcal{O}(10^{-1})$ , much smaller than $\rho\sim\mathcal{O}(1)$ within typical bands. Indeed, even for a larger number of sites ( $L=150$ ), the discrete number of in-gap states already falls to zero at $t_{2}\geq 4$ (Fig. 3).

Robust extended mid-pseudogap modes. – Like ordinary topological gaps Shanahan (2006); Hasan and Kane (2010); Essin and Gurarie (2011); Qi et al. (2013); Gu et al. (2016), NH pseudo-gaps can also host symmetry-protected mid-gap zero modes. However, unlike ordinary in-gaps states which by definition are not extended bulk states, states within NH pseudo-gaps can be extended throughout the sample, and may in fact be obliged to be delocalized due to symmetry protection. This scenario represents a “role-reversal” from ordinary settings, with delocalized mid-pseudogap modes accompanied by localized NHSE-deformed bulk skin modes.

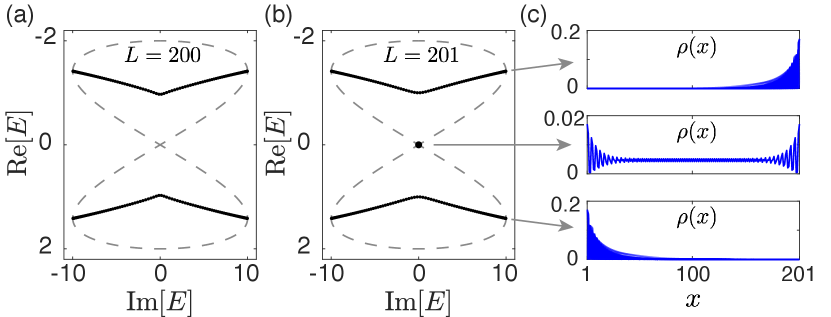
In our model, the DOS within the pseudo-gap decreases rapidly as $t_{2}$ increases [Fig. 3], such that there are no “bulk” eigenmode in the pseudo-gap for a finite system with sufficiently large $t_{2}$ , as in Fig. 4(a) with $L=200$ sites. Nevertheless, a robust in-gap eigenmode emerges at $E=0$ for odd $L$ [Fig. 4(b)]. Unlike conventional topological in-gap modes, this pseudo-gap mode is extended along the 1D chain [ 4(c)], since its eigenenergy lies within the PBC spectrum and is hence free from the NHSE Zhu et al. (2021). Yet it is also symmetry-protected like conventional 1D topological edge modes, since our real-space model Hamiltonian Eq. 1 satisfies $SHS^{-1}=-H^{\dagger}$ with $S={\rm diag}\{1,-1,1,-1,...\}$ , which represents chiral symmetry for non-Hermitian systems Kawabata et al. (2019b); Li et al. (2019). Due to this symmetry, for any $H|\Psi\rangle=E|\Psi\rangle$ , we have

\displaystyle H^{\dagger}S|\Psi\rangle=-ES|\Psi\rangle,

(4)

meaning that $S|\Psi\rangle$ is a left eigenstate of $H$ localized together with the right eigenstate $|\Psi\rangle$ . Hence there must be another right eigenstate $|\Psi^{\prime}\rangle$ at eigenenergy $-E^{*}$ , biorthogonal-paired with the left eigenstate $S|\Psi\rangle$ and localized at the opposite boundary Kunst et al. (2018), forming a chiral pair together with $|\Psi\rangle$ . Therefore, with an odd number of lattice sites, there will be an unpaired eigenmode with balanced distribution in both directions satisfying $|\Psi^{\prime}\rangle=|\Psi\rangle$ and $E^{\prime}=-E^{*}$ , implying purely imaginary eigenenergy and lying within the pseudo-gap of the two symmetric pseudo-bands. Note that chiral symmetry itself does not guarantee zero energy for this in-gap eigenmode: this also requires spinless time-reversal symmetry (TRS) $H=H^{*}$ [or $H(k)=h^{*}(-k)$ ], under which a time-reversal pair of eigenstates shall have eigenenergies with opposite imaginary parts, leading to real energy for the self-paired eigenstate (which is hence pinned to zero in this case, since it must also be pure imaginary). See sup on the consequences of breaking this symmetry.

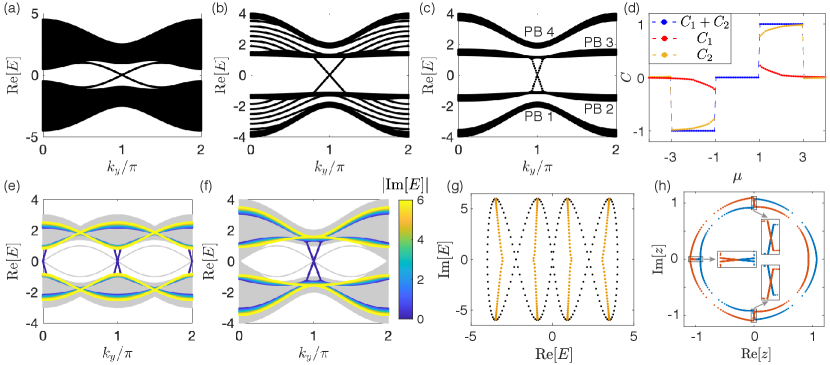
Pseudo-Chern bands and non-quantized Chern numbers. – We next consider pseudo-gaps within bands of nontrivial band topology, and find that notions of band topology i.e. the topological bulk-boundary correspondence become murky: (i) a pseudo-gap splits a band into two or more pseudo-bands with non-integer Chern numbers, yet the pseudo-bands are still connected by integer numbers of edge modes; (ii) a pseudo-gap can remain open when the ordinary gap is closed, allowing in-(pseudo)gap chiral edge modes to exist even at the topological transition point or the trivial regime, in defiance of the total Chern number within “occupied” pseudo-bands.

We consider a non-Hermitian 2D Hamiltonian $h_{\rm 2D}(\mathbf{k})=h_{\rm QWZ}(\mathbf{k})+h_{2}(\mathbf{k})\mathbb{I}$ , with

	$\displaystyle h_{\rm QWZ}(\mathbf{k})$	$\displaystyle=$	$\displaystyle(2t_{x}\cos k_{x}+2t_{y}\cos k_{y}+\mu)\sigma_{z}$		(5)
			$\displaystyle+2t^{ab}_{y}\sin k_{y}\sigma_{y}+2t^{ab}_{x}\sin k_{x}\sigma_{x}$		(5)

the Qi-Wu-Zhang (QWZ) model with nontrivial Chern topology Qi et al. (2006), and $h_{2}(\mathbf{k})=2it_{2}\sin 2k_{x}$ the same anti-Hermitian term as in Eq. 1. Figs. 5(a-c) illustrates the x-OBC spectra of $h_{\rm QWZ}$ as the non-Hermiticity parameter $t_{2}$ is increased from 0 to 1 and then 3, in the topologically non-trivial regime of $\mu=1.5$ . As $t_{2}$ increases, the two ordinary bands split into four pseudo-bands (PB1 to PB4 in Fig. 5(c)). A pair of chiral edge modes initially connects both bands, but eventually connect only two pseudo-bands when $t_{2}=3$ . Even though the pseudo-bands cannot be distinguished from ordinary bands ²²2Under OBCs, band eigenstates are not labeled by momentum, and a pseudo-band represent an isolated cluster of eigenenergies just like an ordinary band., they interestingly possess non-integer Chern numbers despite being connected by integer numbers of Chern edge states. This is presented in Fig. 5(d), where $C_{1}$ and $C_{2}$ are the Chern numbers of PB1 and PB2 computed from the Berry curvature in the GBZ $(k_{x}+i\kappa_{x}(\mathbb{k}),k_{y})$ i.e. of the Surrogate Hamiltonian Lee et al. (2020). The sum $C_{1}+C_{2}$ is quantized as expected of the ordinary Chern band, with transitions at $|\mu|=1$ , independent of $t_{2}$ for this model. In the topologically trivial $|\mu|<1$ phase, the Hermitian QWZ model ( $t_{2}=0$ ) possesses trivial in-gap edge modes with two crossing, shown in gray in Fig. 5(e). With a nonzero $t_{2}$ , the edge modes partially merge into the bulk to become counter-propagating chiral modes Lababidi et al. (2014); Zhou et al. (2014a, b); Ho and Gong (2014); Fulga and Maksymenko (2016); Höckendorf et al. (2019); Umer et al. (2020).

Interestingly, well-defined edge modes can also traverse a pseudo-gap even if the Chern number is not well-defined, such as the $\mu=1$ case at the topological transition. This is because gapless bands can still look gapped with a large pseudo-gap. At $t_{2}=0$ , the OBC spectrum is gapless at $k_{y}=0$ . But at nonzero $t_{2}=3$ , a third pseudo-gap at ${\rm Re}[E]=0$ opens up in the x-OBC spectrum [Fig. 5(g)], in addition to the two pseudo-gaps at nonzero $\text{Re}[E]$ , even though the PBC spectrum remains gapless at $k_{y}=0$ . Notably, this pseudo-gap is traversed by chiral modes which are not immediately canceled by another counter-propagating pair at $k_{y}=0$ after entering the topologically trivial phase (see sup ). To affirm that these three gap-like regions are indeed pseudo-gaps, we examine its GBZ $z=e^{ik_{x}}e^{-\kappa_{x}}$ at $k_{y}=0$ [Fig. 5(h)], which is seen to display three sharp jumps in the radius $|z|$ , reminiscent of the 1D case in Fig. 2(d)], suggesting three pseudogaps with vanishing DOS. Specifically, the two jumps at ${\rm Re}[z]=0$ occur within ordinary bands (continued by the same color), corresponding to the pseudo-gaps with positive and negative real energies respectively. The third pseudo-gap at ${\rm Im}[z]=0$ connects different ordinary bands (continued by different colors), representing the pseudo-gap at $E=0$ .

Chern pseudo-bands harbor interesting implications for both experiment and theory. Despite existing in non-Hermitian systems with complex spectra, they harbor real Chern chiral modes which will be convenient for experimental detection in photonic lattices Ozawa et al. (2019), especially with larger group velocities from more pronounced pseudo-gaps. These chiral edge modes can even be well separated from bulk bands at a topological phase transition, where the system is technically gapless, but appearing gapped due to a pseudo-gap. The lack of integer Chern number quantization of seemingly isolated pseudo-bands will also lead to renewed theoretical discourse on fractional Chern phases. Despite being supposedly lattice analogs of fractional quantum Hall phases Sun et al. (2011); Neupert et al. (2011); Lee and Qi (2014); Anisimovas et al. (2015); Neupert et al. (2015); Lee et al. (2017); Kourtis et al. (2017), the requirement of accordingly fractionally occupied Chern bands have been questioned Kourtis et al. (2014); Huang et al. (2018), and our discovery of isolated pseudo-bands with non-integer Chern numbers brings about an additional avenue of intrigue.

Discussion. – We have uncovered a new mechanism for creating pseudo-gaps. It is based on a unique form of interference between different NHSE channels, and arise generically when the complex PBC spectrum geometrically resembles a conductor surface that gives rise to divergent electric fields. Despite having entanglement entropy with gapless logarithmic scaling sup , NH pseudo-gaps host enigmatic states like delocalized in-gap modes, as well as Chiral edge modes that seem to defy the topological bulk-boundary correspondence.

The notion of NH pseudo-gaps spurs various new fruitful directions. Robust eigenmodes within pseudo-gaps may be exploited for sensing applications since they are extended yet significantly modified by symmetry-breaking terms. Finally, the decomposition of topological bands into isolated pseudo-bands may post profound implications for quasi-particles fractionalization.

Acknowledgements.– L. L. acknowledges funding support by the Guangdong Basic and Applied Basic Research Foundation (No. 2020A1515110773).

Supplementary Materials

I Pseudo-gap from the competition/interference between $H_{1}(k)$ and $H_{2}(k)$ Hatano-Nelson models

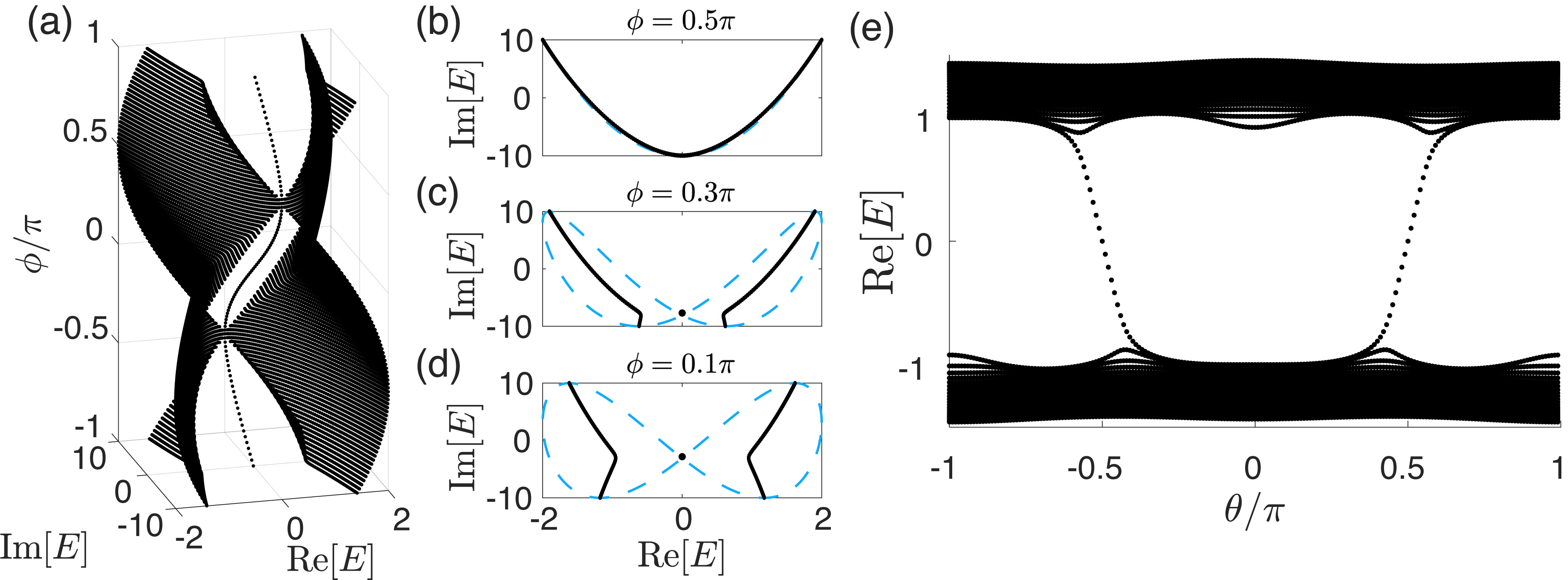
In this section ,we give a detailed discussion about how the pseudo-gap emerge from the competition between $H_{1}(k)=2t_{1}\cos k$ and $H_{2}(k)=2it_{2}\sin 2k$ , for the model of Eq. 1 in the main text. Following the theory of the generalized (non-Bloch) Brillouin zone for systems exhibiting the NHSE Yao and Wang (2018); Lee and Thomale (2019); Lee et al. (2020), the OBC spectrum must form lines or curves enclosing zero area in the complex plane, so that pairs of eigenenergies with different $k$ merge into the same point on the energy plane i.e. are degenerate in energy. Such a condition is satisfied by each of $H_{1}(k)$ and $H_{2}(k)$ , with $H_{1}(k)=H_{1}(-k)$ and $H_{2}(k_{0}-k)=H_{2}(k_{0}+k)$ respectively, where $k_{0}=\pm\pi/4$ or $\pm 3\pi/4$ . However, the overall system does not satisfy either of them, and its fate depends on the competition between these merging effects from $H_{1}(k)$ and $H_{2}(k)$ respectively.

To give a qualitative glance, we first consider a pair of momenta $k_{\pm}=\pi/4\pm\Delta k$ with $\Delta{\color[rgb]{1,0,1}k}\in[0,\pi/4]$ , where the eigenenergies merge into the same point and form a line-spectrum along the imaginary axis in the absence of $H_{1}(k)$ (e.g. see Fig. 2(c1) in the main text). A nonzero $t_{1}$ separates these two points by assigning different real energies $E_{1}(k_{\pm})=2t_{1}\cos k_{\pm}$ to the total energies $E(k_{\pm})$ . To cancel out this separation, a complex deformation of the momentum $k_{\pm}\rightarrow k_{\pm}+i\kappa$ is required, and the eigenenergies of the overall system satisfy

$\displaystyle E$	$\displaystyle(k_{+}+i\kappa)-E(k_{-}+i\kappa)=$	(S1)
	$\displaystyle-\sin\Delta k[\sqrt{2}t_{1}+4t_{2}\cos\Delta k(e^{-\kappa}-e^{\kappa})](e^{-\kappa}+e^{\kappa})$
	$\displaystyle+i\sqrt{2}t_{1}\sin\Delta k(e^{-\kappa}-e^{\kappa}).$

Here a nonzero $\kappa$ also indicates a non-Hemritian skin localization of the corresponding eigenmode under OBC. We can see that the real-energy separation between $E(k_{\pm})$ induced by $t_{1}$ is canceled out by a $\kappa$ with

\displaystyle e^{\kappa}-e^{-\kappa}=\frac{\sqrt{2}t_{1}}{4t_{2}\cos\Delta k}.

(S2)

Note that while $\kappa$ cancels the separation in real energy, it induces another separation in imaginary energy $\delta E_{i}$ at the same time, meaning that the merging of different $k$ modes does not occur exactly for the pair of $k_{\pm}$ . Nevertheless, it suggests that the two merging points are close to $k_{\pm}$ , especially when $\kappa$ is small and hence the strength of the imaginary separation $\delta E_{i}$ is weak. Thus we can obtain some quantitative conclusions from Eq.. S2:

i). the value of $\kappa$ decreases when $\Delta k$ decreases, meaning that the merging effect from $H_{2}(k)$ (i.e. between $k_{\pm}$ ) dominates with smaller $\Delta k$ , i.e. closer to $k=\pi/4$ ;

ii). the value of $\kappa$ also decreases when $t_{2}/t_{1}$ increases, meaning that the system favors the merging effect more for larger $t_{2}$ .

Combining these conclusions, we can see that when $t_{2}$ gets larger, the eigenvalues in a wider range of $\Delta k$ tends to follow the merging effect from $H_{2}(k)$ , or in other words, the skin effect of the corresponding eigenmodes are less affected by the presence of $H_{1}(k)$ . On the other hand, even when $t_{2}\gg t_{1}$ , the real part of $E(k_{\pm}+i\kappa)$ cannot be zero. This is because both of $E(k_{\pm})$ have positive real energies, and $E(k_{\pm}+i\kappa)$ is obtained by erasing the difference between them, i.e.

\displaystyle{\rm Re}[E(k_{\pm}+i\kappa)]\propto{\rm Re}[E(k_{+})+E(k_{-})]/2\neq 0.

(S3)

As a matter of fact, we shall have $\kappa\rightarrow 0$ when $t_{2}\gg t_{1}$ , and ${\rm Re}[E(k_{\pm}+i\kappa)]$ ranges from $t_{1}$ (when $\Delta k=\pi/4$ ) to $\sqrt{2}t_{1}$ (when $\Delta k=0$ ). Finally, similar results can be obtained for pairs of momenta around $k=-\pi/4,3\pi/4,-3\pi/4$ respectively, with the latter two give negative real energies ranging from $-t_{1}$ and $-\sqrt{2}t_{1}$ for them. In short, as sketched in Fig. 2(c1) in the main text, different parts of the imaginary spectrum of $H_{2}(k)$ tend to acquire positive and negative real values due to a nonzero $H_{1}(k)$ , inducing a non-Hemritian pseudo-gap between $t_{1}$ and $-t_{1}$ for the whole system.

Following the same spirit, we may also check another pair of momenta $k^{\prime}_{\pm}=\pm(\pi/2-\Delta k^{\prime})$ , where the eigenenergies merge into the same point and give a real spectrum in the absence of $H_{2}(k)$ (e.g. see Fig. 2(c2) in the main text). Similarly, with a nonzero $t_{2}$ , a separation in their imaginary energies emerges between the eigenmodes of $k^{\prime}_{\pm}$ , which can also be erased through a complex deformation $i\kappa^{\prime}$ of the momenta. Namely we have

	$\displaystyle E(k^{\prime}_{+}+i\kappa^{\prime})-E(k^{\prime}_{-}+i\kappa^{\prime})=$
	$\displaystyle+i\cos\Delta k^{\prime}[t_{1}(e^{-\kappa^{\prime}}-e^{\kappa^{\prime}})+2t_{2}\sin\Delta k^{\prime}(e^{-2\kappa^{\prime}}+e^{2\kappa^{\prime}})],$

and the imaginary separation is erased when

\displaystyle\frac{t_{1}}{2t_{2}\sin\Delta k^{\prime}}=e^{\kappa^{\prime}}-e^{-\kappa^{\prime}}+\frac{2}{e^{\kappa^{\prime}}-e^{-\kappa^{\prime}}}.

(S5)

Thus we obtain the following conclusions: (i) At $\Delta k^{\prime}=0$ , the two points of $k^{\prime}=\pm\pi/2$ always merge into each other at $\kappa^{\prime}=0$ , meaning that they always obey the merging effect from $H_{1}(k)$ and exhibit no skin localization. (ii) For $\Delta k^{\prime}\neq 0$ , a nonzero $\kappa^{\prime}$ is required to erase the imaginary separation of the eigenenergy. The value of $\kappa^{\prime}$ increases with $\Delta_{k}^{\prime}$ before it reaches $e^{\kappa^{\prime}}-e^{-\kappa^{\prime}}=\sqrt{2}$ , where the right-hand side of Eq. S5 reaches its minimum. (iii) The system tends to follow the merging effect from $H_{1}(k)$ when $t_{1}\gg t_{2}$ . Here $E(k^{\prime}_{\pm}+i\kappa^{\prime})$ is obtained by erasing the difference between ${\rm Im}[E(k^{\prime}_{\pm})]$ , leading to

\displaystyle{\rm Im}[E(k^{\prime}_{\pm}+i\kappa^{\prime})]\propto{\rm Im}[E(k^{\prime}_{+})+E(k^{\prime}_{-})]/2=0.

(S6)

Therefore no (imaginary) pseudo-gap emerges in this case, and the eigenenergies are all real when the merging effect of $H_{1}(k)$ dominates.

Combining the above two scenario, the system at a given momentum shall obey the merging effect from either $H_{1}(k)$ or $H_{2}(k)$ , depending on which one comes with a smaller complex deformation ( $\kappa$ or $\kappa^{\prime}$ ) of the momentum of concern. And a real pseudo-gap emerges when $t_{2}$ is large enough, where a majority of the system obeys the merging effect of $H_{2}(k)$ . This can be seen in Fig. 2(b) in the main text, where the pseudo-gap structure is already clear only ten eigenmodes fall with the regime between $E=\pm t_{1}$ in a system with $L=150$ sites.

In more generic models, an analogous analysis that reveals similar asymmetry arising from the competition/interference of the NHSE from different subsystems will result in a pseudo-gap region of low DOS.

II Detailed computation of low density of states

II.1 Formalism

We next explicitly compute the density of states within the pseudo-gap of our 1D model (Eq. 1 of the main text). To do so, we first provide some general results for computing the DOS along an interval with real eigenvalues (which is the case of our pseudo-gap).

Consider a PBC Hamiltonian with dispersion of the form

E(z)=\sum_{j}a_{j}z^{j}

(S7)

where $z=e^{ik}$ and the $a_{j}$ s are all real. When $|a_{j}|\neq|a_{-j}|$ , $H(z)$ generically traces out a PBC loop, and undergoes the the non-Hermitian skin effect (NHSE) under OBCs. Suppose that there exist a certain segment of the OBC spectrum which is real i.e. $\text{Im}[E(e^{i\tilde{k}})]=0$ for $k\in[k_{\text{min}},k_{\text{max}}]$ , where $\tilde{k}=k+i\kappa(k)$ . The objective of this subsection is to solve for the OBC DOS along this real line in energy space. We remind the reader that the results obtained here are only valid if the actual OBC eigenenergies involved are indeed real; the purpose here is not to check whether this assumption is true, but to determine the OBC DOS should the eigenenergies lie on the real line.

We write $z=re^{ik}$ where $r=e^{-\kappa(k)}$ . For $k\in[k_{\text{min}},k_{\text{max}}]$ ,

\text{Im}[E(re^{ik})]=\sum_{j}a_{j}r^{j}\sin jk=0

(S8)

and

\epsilon=\text{Re}[E(re^{ik})]=\sum_{j}a_{j}r^{j}\cos jk

(S9)

where $\epsilon$ refers to the real eigenenergy. The DOS $\rho=\frac{dk}{d\epsilon}$ can be solved in terms of $k$ if $r=e^{-\kappa(k)}$ can be explicitly expressed in terms of $k$ i.e. if $\kappa(k)$ can be explicitly solved. To do, one expresses all the $\sin jk$ in Eq. S8 in terms of polynomials in $\sin k$ , such that Eq. S8 becomes a bivariate polynomial in terms of $r$ and $\sin k$ . If $r$ can be solved for, we will be able to obtain a closed form solution to the DOS.

II.2 Specialization to our 1D example

We consider the 1D model discussed in Eq. 1 of the main text, whose energy dispersion read (with real $t_{1},t_{2}$ )

\displaystyle E(z)=2t_{1}\cos k+4it_{2}\cos k\sin k=t_{1}z+\frac{t_{1}}{z}+t_{2}z^{2}-\frac{t_{2}}{z^{2}}.

(S10)

We have

0=\text{Im}[E(re^{ik})]=t_{1}\left(r-\frac{1}{r}\right)\sin k+t_{2}\left(r^{2}+\frac{1}{r^{2}}\right)\sin 2k

(S11)

\epsilon=\text{Re}[E(re^{ik})]=t_{1}\left(r+\frac{1}{r}\right)\cos k+t_{2}\left(r^{2}-\frac{1}{r^{2}}\right)\cos 2k

(S12)

such that Eq. S11 simplifies to

\cos k=-\frac{t_{1}(r-\frac{1}{r})}{2t_{2}\left(r^{2}+\frac{1}{r^{2}}\right)}=\frac{t_{1}\sinh\kappa}{2t_{2}\cosh 2\kappa}.

(S13)

where $\kappa=\kappa(k)$ . Substituting Eq. S13 into Eq. S12, we obtain

\epsilon=2t_{2}\sinh 2\kappa+\frac{t_{1}^{2}\sinh 2\kappa}{2t_{2}\cosh^{2}2\kappa}.

(S14)

To proceed, we express $\epsilon$ in terms of $k$ by inverting Eq. S13 to obtain $\kappa$ in terms of $k$ :

\sinh\kappa=\frac{1}{8t_{2}\cos k}\left[t_{1}-\sqrt{t_{1}^{2}-32t_{2}^{2}\cos^{2}k}\right].

(S15)

The negative solution branch has been chosen as the smaller $\kappa$ solution dominates the larger $\kappa$ solution viz. $~{}e^{-\kappa x}$ . Substituting it into Eq. S14, we obtain the DOS $\rho$ via

\rho=\sum\left|\frac{d\epsilon}{dk}\right|^{-1}=\sum\left|\sin k\frac{d\epsilon}{d(\cos k)}\right|^{-1}

(S16)

where we have included a sum over all the different $k$ that contribute to each OBC eigenenergy (at least two unique $k$ solutions are required for OBC spectra, which has to satisfy the boundary conditions on both sides ). So far, no approximation has been made.

II.2.1 Smallness of the density of states

If we examine Eq. S13 again, we note that the maximal value of $|(t_{2}/t_{1})\cos k|=\left|\frac{\sinh\kappa}{2\cosh 2\kappa}\right|$ is $\frac{1}{8}\left(\frac{1}{\sqrt{2-\sqrt{3}}}-\sqrt{2-\sqrt{3}}\right)\approx 0.177$ , which is rather small. Note, however, this does not give the window of $k$ that realizes real OBC eigenvalues, because nowhere was the condition $\kappa_{1}=\kappa_{2}$ used. However, what it gives is the drastic simplification $\sinh\kappa\approx 2(t_{2}/t_{1})\cos k$ , $\sinh 2\kappa\approx 4(t_{2}/t_{1})\cos k$ , $\cosh\kappa\approx\cosh 2\kappa\approx 1$ and of course $k\approx\pm\frac{\pi}{2}$ (remember, it is the small window of $k$ that gives the pseudo-gap its small DOS). Putting these into Eq. S16, we obtain the nice simple result in the main text

\rho_{\text{tot}}=\sum\left|\frac{d\epsilon}{dk}\right|^{-1}\approx\sum_{\pm}\left|\frac{d[(2t_{1}+8t_{2}^{2}/t_{1})\cos k]}{dk}\right|^{-1}\approx\frac{t_{1}}{t_{1}^{2}+4t_{2}^{2}}.

(S17)

Even for $t_{2}/t_{1}$ slightly greater than one, we already obtain a rather small DOS. Retaining a few more orders of $\cos k$ in our derivation, we can obtain a more precise expression

\displaystyle\rho_{\text{tot}}\approx\frac{1}{t_{1}}\frac{t_{1}^{4}-6t_{2}^{2}t_{1}^{2}\cos^{2}k-114t_{2}^{4}\cos^{4}k}{t_{1}^{4}+4t_{2}^{2}t_{1}^{2}+(224t_{2}^{4}+6t_{2}^{2}t_{1}^{2}-t_{1}^{4}/2)\cos^{2}k}.

(S18)

III Numerical approach to the inverse decay length $\kappa(k)$

Here we give a short discussion about how we numerically obtain the generalized Brillouin zone (GBZ), i.e. the value of $\kappa(k)$ . First, the PBC Hamiltonian is rewritten as $h(z)$ with $z=e^{ik}$ . Then we solve the characteristic equation $h(z)-E=0$ for $z$ with different complex values of $E$ , and label the solutions as $z_{-r},z_{-r+1},...z_{l}$ (without $z_{0}$ ). Here $r$ and $l$ are the longest hopping ranges toward the right- and left-hand sides respectively. A given $E$ belongs to the OBC spectrum as long as $|z_{1}|=|z_{-1}|$ , and this pair of solutions $z_{\pm 1}$ give two points of the GBZ, denoted as $z_{\rm GBZ}$ . The GBZ is obtained by scanning over different complex energies $E$ and collecting all possible $z_{\rm GMZ}$ , and the inverse decaying length $\kappa(k)$ is given by $z_{\rm GBZ}=e^{ik}e^{-\kappa(k)}$ .

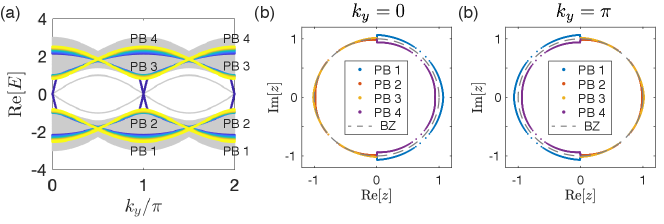
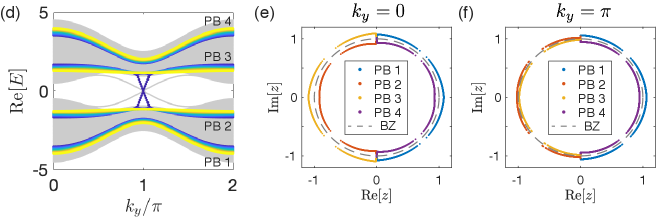
In the 2D cases with nontrivial topology, the Berry curvature is obtained by complex shifting the momentum by $i\kappa(k)$ to obtain the so-called surrogate Hamiltonian Lee et al. (2020) $H(k_{x}+i\kappa(k_{x}),k_{y})$ , from which the Chern numbers $C_{1,2}$ for the pseudo-bands are obtained by integrating the Berry curvature (a discrete sum in numerical approach) only in the associated partial GBZ, i.e. $k_{x}\in[-\pi/2,\pi/2]$ or $k_{x}\in[\pi/2,3\pi/2]$ , with $k_{y}\in[0,2\pi]$ . [Also see Fig. S5(d)-(e) for the correspondence between different parts of the GBZ and the pseudo-bands.]

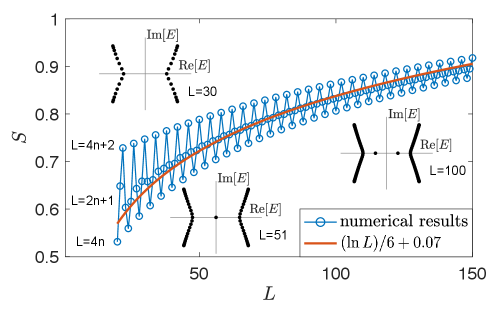
IV Entanglement entropy

In our system, the two parts of the spectrum are separated by a pseudo-gap at finite size, which is filled with sparse eigenmodes when $L$ is large. To see that a pseudo-gap is not a genuine gap, we compute its biorthogonal entanglement entropy (EE) for a chosen entanglement cut, as described in Li et al. (2020b); Chang et al. (2020):

\displaystyle S=-\sum_{j}[\eta_{j}\ln\eta_{j}+(1-\eta_{j})\ln(1-\eta_{j})],

(S19)

where $\eta_{j}$ are the eigenvalues of the correlator matrix

\displaystyle C_{xy}=\langle G_{L}|\hat{c}^{\dagger}_{x}\hat{c}_{y}|G_{R}\rangle.

(S20)

Here $G_{L}$ ( $G_{R}$ ) are the left (right) many-body ground state, and we consider the case of half-filling , i.e. only the single-particle eigenmodes with negative real energies are occupied. The entanglement cut is chosen as the lattice sites with $x,y\in[L/2+1,L]$ (here we consider an even number of sites only). as the eigenmodes with negative real energies accumulate at the right-hand side. It is known that the EE obeys an area law scaling for a gapped system, and has a logarithmic dependence on system size for gapless system. In Fig. S1, we see that the EE obeys a logarithmic scaling $S\approx(\ln L)/6$ , even when the spectrum is seen to be gapped.

Note that EE is obtained solely from the eigenmodes. That is to say, although the eigenenergies of our model give a gapped spectrum, the eigenmodes behave like those of a gapless system.

V In-gap extended eigenmode with symmetry breaking

In the 1D model discussed in the main text, we have shown that the in-gap extended eigenmode is protected by a chiral symmetry, and it is pinned at the zero energy by the spinless time-reversal symmetry (TRS). In this section, we will give more details about how this eigenmode behaves upon symmetry breaking.

V.1 TRS breaking

We first keep the chrial symmetry and break the TRS by adding an extra phase $\phi$ , i.e. $t_{\pm 2}\rightarrow t_{2}e^{\pm i\phi}$ . As shown in Fig. S2, the in-gap eigenmode can move along the imaginary axis with the symmetry unbroken. On the other hand, this eigenmode always coincides with the PBC spectrum at $k=\pi/2$ [e.g. in Fig. S2(b)-(d)], meaning that no complex deformation of $k$ is needed to give raise to it under OBC. Thus the in-gap eigenmode shall has an extended distribution across the system, e.g. as shown Fig. 4(c) in the main text.

V.2 Chiral symmetry breaking

Next we keep the TRS and break the chiral symmetry that protect the in-gap eigenmode by adding the following term,

\displaystyle H_{2}^{\prime}=t_{2}^{\prime}\cos\theta\sum_{x}\hat{c}^{\dagger}_{x}\hat{c}_{x+2}+h.c..

(S21)

The single in-gap eigenmode will acquire a real energy and move into the bulk, as shown in Fig. S2(e) The in-gap eigenmode looks like a chiral edge mode, but behaves differently. It exhibits a skin localization toward one direction when its energy is negative, and the other direction when positive. And if we consider a smaller $t_{2}^{\prime}$ , the in-gap eigenmode does not necessarily goes into the bulk, it may just connect to itself in the pseudo-gap.

VI Pseudo-bands in a topologically nontrivial 1D system

Here we consider a topologically nontrivial 1D model, constructed by two copies of the simple 1D chains discussed in the main text with opposite signs, and some extra inter-chain couplings and on-site potentials. The momentum-space Hamiltonian reads

	$\displaystyle H_{\rm 2-chain}(k)$	$\displaystyle=$	$\displaystyle[H(k)+V]\sigma_{z}+t_{ab}\sin k\sigma_{x},$		(S22)
	$\displaystyle H(k)$	$\displaystyle=$	$\displaystyle 2t_{1}\cos k+2it_{2}\sin 2k$

with $H(k)$ given by Eq. 2, $V$ a chain-depedent on-site potential, and $t_{ab}$ the inter-chain couplings. With $t_{2}=V=0$ , the Hamiltonian vector $\vec{h}(k)=(h_{z}(k),h_{x}(k))$ has a nontrivial winding number $\nu_{\vec{h}}$ across the Brillouin zone, leading to the topological properties of this system. Note that this winding is different from the spectral winding number $\nu_{E}$ that induces the NHSE. A nonzero $V$ will shift the trajectory of $\vec{h}(k)$ , but does not change the topology untill $|V|>|2t_{1}|$ . On the other hand, a nonzero $t_{2}$ introduce non-Hermiticity to the system, and may induce pseudo-gaps in this system.

In Fig. S3 we illustrate the spectra of two typical cases of this model, where the nontrivial topology gives gives raise to two zero edge modes under OBC (the black dots at $E=0$ ). Note that when $V=0$ , there is no NHSE under OBC even the PBC spectrum forms a loop. This is because the Hamiltonian satisfies the symmetry $\sigma_{x}H_{\rm 2-chain}(\pi/2+k)\sigma_{x}=H(\pi/2-k)$ provided $V=0$ , thus the two segments of the spectrum with $k\in(-\pi/2,\pi/2]$ and $k\in(\pi/2,3\pi/2]$ are identical. On the other hand, the eigenenergies of the system satisfy $E(\pi/2)=E(-\pi/2)$ , meaning that each segment is connected to itself head to tail. Therefore the PBC spectrum winds along the same loop twice with opposite directions (clockwise and anticlockwise), resulting in a zero spectral winding number $\nu_{E}=0$ . The OBC spectrum is also seen to be almost identical with the PBC one. However, with a nonzero $V$ , the above mentioned symmetry is broken, thus the degeneracy between the two segments is lifted and the NHSE emerges, leading to a divergence between the PBC and OBC spectra. Furthermore, the OBC spectrum now forms four pseudo-bands, with a few isolated in-gap eigenmodes. Meanwhile, the nontrivial topology at $V=0$ is still preserved and the associated zero modes still survive.

The emergence of pseudo-band structure here is actually a bit different from the previous model. When $V=t_{ab}=0$ , the system has two decoupled chains, each has two pseudo-bands as discussed in the main text, denoted here as $E^{\pm}_{1}$ and $E^{\pm}_{2}$ for the two chains respectively. These two pairs of pseudo-bands are also degenerate to each other, i.e. $E^{\pm}_{1}=E^{\pm}_{2}$ . A nonzero $t_{ab}$ couples each degenerate pair of the pseudo-bands, e.g. $E^{+}_{1}$ and $E^{+}_{2}$ , and turns them into an energy band of the overall 2-band system. That is, the gap at $E=0$ of this system (in both panels of Fig. S3) is a normal gap, not a pseudo-gap. On the other hand, a nonzero $V$ lifts this degeneracy, effectively making it more difficult to couple them. Consequently, a pseudo-gap emerges within each of the two normal band in Fig. S3(a), giving raise to the four pseudo-bands in (b).

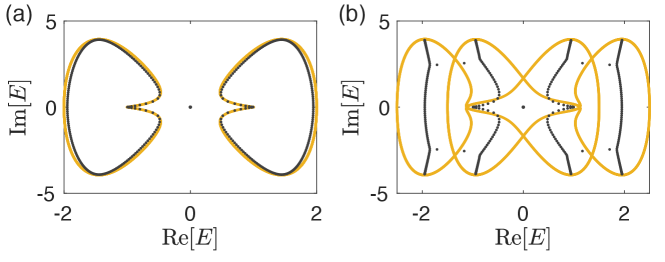
VII Further results of the 2D model

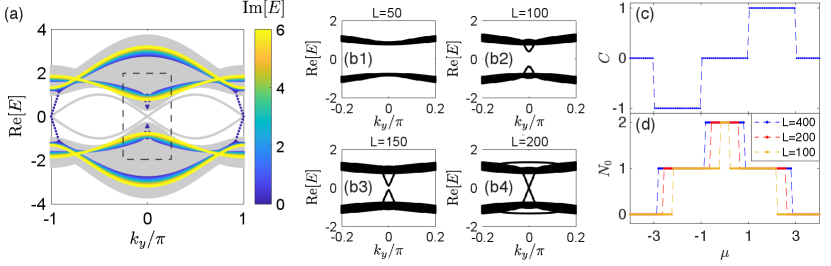
VII.1 Finite-size effect of the topological edge modes

In Fig. 5(f) in the main text, we show that our 2D non-Hermitian system at the topological phase transition point possesses a pseudo-gap, instead of a normal gap closing. Especially, in a finite-size system, the pseudo-gap effectively acts as a normal gap as no eigenmode lies within it, which seems to be contradictory to the notion of gap-protected topology. That is, a pair of chiral edge modes may appear/disappear without different (pseudo-)bands touching each other.

In Fig. S4(a), we illustrate the x-OBC spectrum of the model in a topologically trivial phase with the Chern number $C=0$ , where its Hermitian counterpart has a pair of topologically trivial edge modes with two crossing. Yet when the non-Hermiticity is tuned to $t_{2}=3$ , the crossing at $k_{y}=0$ separates into two gapped branches, while the other one at $k_{y}=\pi$ evolves into a pair of chiral edge modes. This observation seems to suggest a nontrivial topology with $|C|=1$ in such cases.

To resolve this contradiction, we note that the Chern number describes the topological properties in the thermodynamic limit, but non-Hermitian systems usually suffer significantly from finite-size effect (e.g. in Refs. Budich and Bergholtz (2020); Li et al. (2020b)). In Fig. S4(b), we zoom in on the regime around $k_{y}=0$ for the system with different values of $L$ , the number of unit cells along $x$ direction. It is seen that with increasing $L$ , a pair edge modes emerges from the two pseudo-bands, and connects into a chiral edge modes when $L$ gets large enough. Together with the other pair of chiral edge modes at $k_{y}=\pi$ in Fig. S4(a), they form the counter-propagating edge modes and correspond to the zero Chern number.

In Fig. S4(c) and (d), we compare the Chern number $C$ and the number of pairs of zero-energy modes $N_{0}$ for different values of $L$ . Here $N_{0}$ is obtained by numerically counting the zero-energy modes at $k_{y}=0$ and $k_{y}=\pi$ . For example, the in-gap modes in Fig. S4(b4) count as $1$ , and those in Fig. S4(b2 and b3) count as $0$ . It is clearly seen that the transition point of $N_{0}$ matches the topological transition of $C$ better when the size of the system gets larger.

VII.2 Correspondence between the GBZs and the pseudo-bands

In Fig. S5, we further illustrate the correspondence between different parts of the two GBZs and the four pseudo-bands, for two different cases with crossed and fully-separated pseudo-bands, at $k_{y}=0$ and $k_{y}=\pi$ .

References

Bardeen et al. (1957) John Bardeen, Leon N Cooper, and John Robert Schrieffer, “Theory of superconductivity,” Physical review 108, 1175 (1957).
Schrieffer (2018) J Robert Schrieffer, Theory of superconductivity (CRC press, 2018).
Kane and Mele (2005) C. L. Kane and E. J. Mele, “Quantum spin hall effect in graphene,” Phys. Rev. Lett. 95, 226801 (2005).
Bernevig and Hughes (2013) B. Andrei Bernevig and Taylor L. Hughes, Topological insulators and topological superconductors (Princeton university press, 2013).
Emery and Kivelson (1995) VJ Emery and SA Kivelson, “Importance of phase fluctuations in superconductors with small superfluid density,” Nature 374, 434–437 (1995).
Kaminski et al. (2002) A Kaminski, S Rosenkranz, HM Fretwell, JC Campuzano, Z Li, H Raffy, WG Cullen, H You, CG Olson, CM Varma, et al., “Spontaneous breaking of time-reversal symmetry in the pseudogap state of a high-t c superconductor,” Nature 416, 610–613 (2002).
Lee et al. (2006) Patrick A Lee, Naoto Nagaosa, and Xiao-Gang Wen, “Doping a mott insulator: Physics of high-temperature superconductivity,” Reviews of modern physics 78, 17 (2006).
Fauqué et al. (2006) B Fauqué, Y Sidis, V Hinkov, S Pailhes, CT Lin, Xavier Chaud, and Ph Bourges, “Magnetic order in the pseudogap phase of high-t c superconductors,” Physical Review Letters 96, 197001 (2006).
Xia et al. (2008) Jing Xia, Elizabeth Schemm, G Deutscher, SA Kivelson, DA Bonn, WN Hardy, R Liang, W Siemons, Gertjan Koster, MM Fejer, et al., “Polar kerr-effect measurements of the high-temperature yba 2 cu 3 o 6+ x superconductor: evidence for broken symmetry near the pseudogap temperature,” Physical Review Letters 100, 127002 (2008).
Vojta (2009) Matthias Vojta, “Lattice symmetry breaking in cuprate superconductors: stripes, nematics, and superconductivity,” Advances in Physics 58, 699–820 (2009).
Varma (2010) Chandra Varma, “Mind the pseudogap,” Nature 468, 184–185 (2010).
Tahir-Kheli and Goddard III (2011) Jamil Tahir-Kheli and William A Goddard III, “Origin of the pseudogap in high-temperature cuprate superconductors,” The Journal of Physical Chemistry Letters 2, 2326–2330 (2011).
Yamaji and Imada (2011) Youhei Yamaji and Masatoshi Imada, “Composite-fermion theory for pseudogap, fermi arc, hole pocket, and non-fermi liquid of underdoped cuprate superconductors,” Physical review letters 106, 016404 (2011).
Mei et al. (2012) Jia-Wei Mei, Shinji Kawasaki, Guo-Qing Zheng, Zheng-Yu Weng, and Xiao-Gang Wen, “Luttinger-volume violating fermi liquid in the pseudogap phase of the cuprate superconductors,” Physical Review B 85, 134519 (2012).
(15) .
Mishra et al. (2014) Vivek Mishra, U Chatterjee, JC Campuzano, and MR Norman, “Effect of the pseudogap on the transition temperature in the cuprates and implications for its origin,” Nature Physics 10, 357–360 (2014).
Keimer et al. (2015) Bernhard Keimer, Steven A Kivelson, Michael R Norman, Shinichi Uchida, and J Zaanen, “From quantum matter to high-temperature superconductivity in copper oxides,” Nature 518, 179–186 (2015).
Proust et al. (2016) Cyril Proust, Baptiste Vignolle, Julien Levallois, S Adachi, and Nigel E Hussey, “Fermi liquid behavior of the in-plane resistivity in the pseudogap state of yba2cu4o8,” Proceedings of the National Academy of Sciences 113, 13654–13659 (2016).
Battisti et al. (2017) Irene Battisti, Koen M Bastiaans, Vitaly Fedoseev, Alberto De La Torre, Nikos Iliopoulos, Anna Tamai, Emily C Hunter, Robin S Perry, Jan Zaanen, Felix Baumberger, et al., “Universality of pseudogap and emergent order in lightly doped mott insulators,” Nature Physics 13, 21–25 (2017).
Zhang and Sachdev (2020) Ya-Hui Zhang and Subir Sachdev, “From the pseudogap metal to the fermi liquid using ancilla qubits,” Physical Review Research 2, 023172 (2020).
Xiong (2018) Ye Xiong, “Why does bulk boundary correspondence fail in some non-hermitian topological models,” Journal of Physics Communications 2, 035043 (2018).
Gong et al. (2018) Zongping Gong, Yuto Ashida, Kohei Kawabata, Kazuaki Takasan, Sho Higashikawa, and Masahito Ueda, “Topological phases of non-hermitian systems,” Physical Review X 8, 031079 (2018).
Zhang et al. (2020) Kai Zhang, Zhesen Yang, and Chen Fang, “Correspondence between winding numbers and skin modes in non-hermitian systems,” Phys. Rev. Lett. 125, 126402 (2020).
Okuma et al. (2020) Nobuyuki Okuma, Kohei Kawabata, Ken Shiozaki, and Masatoshi Sato, “Topological origin of non-hermitian skin effects,” Phys. Rev. Lett. 124, 086801 (2020).
(25) Linhu Li, Sen Mu, Ching Hua Lee, and Jiangbin Gong, “Quantized classical response from spectral winding topology,” 2012.08799v2 .
Su et al. (2020) Rui Su, Eliezer Estrecho, Dkabrówka Biegańska, Yuqing Huang, Matthias Wurdack, Maciej Pieczarka, Andrew G Truscott, Timothy CH Liew, Elena A Ostrovskaya, and Qihua Xiong, “Direct measurement of a non-hermitian topological invariant in a hybrid light-matter system,” arXiv preprint arXiv:2012.06133 (2020).
Wang et al. (2021) Kai Wang, Avik Dutt, Ki Youl Yang, Casey C Wojcik, Jelena Vučković, and Shanhui Fan, “Generating arbitrary topological windings of a non-hermitian band,” Science 371, 1240–1245 (2021).
Yao and Wang (2018) Shunyu Yao and Zhong Wang, “Edge states and topological invariants of non-hermitian systems,” Phys. Rev. Lett. 121, 086803 (2018).
Yokomizo and Murakami (2019) Kazuki Yokomizo and Shuichi Murakami, “Non-bloch band theory of non-hermitian systems,” Physical review letters 123, 066404 (2019).
Lee and Thomale (2019) Ching Hua Lee and Ronny Thomale, “Anatomy of skin modes and topology in non-hermitian systems,” Phys. Rev. B 99, 201103 (2019).
Yang et al. (2020) Zhesen Yang, Kai Zhang, Chen Fang, and Jiangping Hu, “Non-hermitian bulk-boundary correspondence and auxiliary generalized brillouin zone theory,” Physical Review Letters 125, 226402 (2020).
Lee et al. (2020) Ching Hua Lee, Linhu Li, Ronny Thomale, and Jiangbin Gong, “Unraveling non-hermitian pumping: Emergent spectral singularities and anomalous responses,” Phys. Rev. B 102, 085151 (2020).
Shen et al. (2018) Huitao Shen, Bo Zhen, and Liang Fu, “Topological band theory for non-hermitian hamiltonians,” Phys. Rev. Lett. 120, 146402 (2018).
Kawabata et al. (2019a) Kohei Kawabata, Ken Shiozaki, Masahito Ueda, and Masatoshi Sato, “Symmetry and topology in non-hermitian physics,” Physical Review X 9, 041015 (2019a).
Kunst et al. (2018) Flore K. Kunst, Elisabet Edvardsson, Jan Carl Budich, and Emil J. Bergholtz, “Biorthogonal bulk-boundary correspondence in non-hermitian systems,” Phys. Rev. Lett. 121, 026808 (2018).
Yao et al. (2018) Shunyu Yao, Fei Song, and Zhong Wang, “Non-hermitian chern bands,” Phys. Rev. Lett. 121, 136802 (2018).
Yin et al. (2018) Chuanhao Yin, Hui Jiang, Linhu Li, Rong Lü, and Shu Chen, “Geometrical meaning of winding number and its characterization of topological phases in one-dimensional chiral non-hermitian systems,” Phys. Rev. A 97, 052115 (2018).
Jiang et al. (2018) Hui Jiang, Chao Yang, and Shu Chen, “Topological invariants and phase diagrams for one-dimensional two-band non-hermitian systems without chiral symmetry,” Phys. Rev. A 98, 052116 (2018).
Li et al. (2019) Linhu Li, Ching Hua Lee, and Jiangbin Gong, “Geometric characterization of non-hermitian topological systems through the singularity ring in pseudospin vector space,” Physical Review B 100, 075403 (2019).
Song et al. (2019a) Fei Song, Shunyu Yao, and Zhong Wang, “Non-hermitian topological invariants in real space,” Physical Review Letters 123, 246801 (2019a).
Song et al. (2019b) Fei Song, Shunyu Yao, and Zhong Wang, “Non-hermitian skin effect and chiral damping in open quantum systems,” Physical review letters 123, 170401 (2019b).
Okuma and Sato (2019) Nobuyuki Okuma and Masatoshi Sato, “Topological phase transition driven by infinitesimal instability: Majorana fermions in non-hermitian spintronics,” Physical review letters 123, 097701 (2019).
Mu et al. (2020) Sen Mu, Ching Hua Lee, Linhu Li, and Jiangbin Gong, “Emergent fermi surface in a many-body non-hermitian fermionic chain,” Phys. Rev. B 102, 081115 (2020).
Jiang et al. (2019) Hui Jiang, Li-Jun Lang, Chao Yang, Shi-Liang Zhu, and Shu Chen, “Interplay of non-hermitian skin effects and anderson localization in nonreciprocal quasiperiodic lattices,” Physical Review B 100, 054301 (2019).
Longhi (2019) Stefano Longhi, “Topological phase transition in non-hermitian quasicrystals,” Physical Review Letters 122, 237601 (2019).
Kunst and Dwivedi (2019) Flore K Kunst and Vatsal Dwivedi, “Non-hermitian systems and topology: A transfer-matrix perspective,” Physical Review B 99, 245116 (2019).
Jin and Song (2019) L. Jin and Z. Song, “Bulk-boundary correspondence in a non-hermitian system in one dimension with chiral inversion symmetry,” Phys. Rev. B 99, 081103 (2019).
Borgnia et al. (2020) Dan S. Borgnia, Alex Jura Kruchkov, and Robert-Jan Slager, “Non-hermitian boundary modes and topology,” Phys. Rev. Lett. 124, 056802 (2020).
Lee et al. (2019) Ching Hua Lee, Linhu Li, and Jiangbin Gong, “Hybrid higher-order skin-topological modes in nonreciprocal systems,” Phys. Rev. Lett. 123, 016805 (2019).
Li et al. (2020a) Linhu Li, Ching Hua Lee, and Jiangbin Gong, “Topological switch for non-hermitian skin effect in cold-atom systems with loss,” Physical Review Letters 124, 250402 (2020a).
Wang et al. (2020) Xiao-Ran Wang, Cui-Xian Guo, and Su-Peng Kou, “Defective edge states and number-anomalous bulk-boundary correspondence in non-hermitian topological systems,” Phys. Rev. B 101, 121116 (2020).
Chang et al. (2020) Po-Yao Chang, Jhih-Shih You, Xueda Wen, and Shinsei Ryu, “Entanglement spectrum and entropy in topological non-hermitian systems and nonunitary conformal field theory,” Physical Review Research 2, 033069 (2020).
Li et al. (2020b) Linhu Li, Ching Hua Lee, Sen Mu, and Jiangbin Gong, “Critical non-hermitian skin effect,” Nature communications 11 (2020b).
Budich and Bergholtz (2020) Jan Carl Budich and Emil J. Bergholtz, “Non-hermitian topological sensors,” Phys. Rev. Lett. 125, 180403 (2020).
Lee and Longhi (2020) Ching Hua Lee and Stefano Longhi, “Ultrafast and anharmonic rabi oscillations between non-bloch bands,” Communications Physics 3, 1–9 (2020).
Yi and Yang (2020) Yifei Yi and Zhesen Yang, “Non-hermitian skin modes induced by on-site dissipations and chiral tunneling effect,” Phys. Rev. Lett. 125, 186802 (2020).
Lee (2020a) Ching Hua Lee, “Many-body topological and skin states without open boundaries,” arXiv preprint arXiv:2006.01182 (2020a).
Lee (2020b) Ching Hua Lee, “Exceptional boundary states and negative entanglement entropy,” arXiv preprint arXiv:2011.09505 (2020b).
Mandal et al. (2020) Subhaskar Mandal, Rimi Banerjee, Elena A Ostrovskaya, and Timothy Chi Hin Liew, “Nonreciprocal transport of exciton polaritons in a non-hermitian chain,” Physical Review Letters 125, 123902 (2020).
Teo et al. (2020) Wei Xin Teo Teo, Linhu Li, Xizheng Zhang, and Jiangbin Gong, “Topological characterization of non-hermitian multiband systems using majorana’s stellar representation,” Physical Review B 101, 205309 (2020).
Okuma and Sato (2021a) Nobuyuki Okuma and Masatoshi Sato, “Quantum anomaly, non-hermitian skin effects, and entanglement entropy in open systems,” Physical Review B 103, 085428 (2021a).
Li et al. (2021) Linhu Li, Ching Hua Lee, and Jiangbin Gong, “Impurity induced scale-free localization,” Communications Physics 4, 1–9 (2021).
Zhang et al. (2021a) Xiao Zhang, Guangjie Li, Yuhan Liu, Tommy Tai, Ronny Thomale, and Ching Hua Lee, “Tidal surface states as fingerprints of non-hermitian nodal knot metals,” Communications Physics 4, 1–10 (2021a).
Zhang et al. (2021b) Kai Zhang, Zhesen Yang, and Chen Fang, “Universal non-hermitian skin effect in two and higher dimensions,” arXiv preprint arXiv:2102.05059 (2021b).
Yang et al. (2021) Zhesen Yang, Qinghong Yang, Jiangping Hu, and Dong E Liu, “Dissipative floquet majorana modes in proximity-induced topological superconductors,” Physical Review Letters 126, 086801 (2021).
Song et al. (2021) Fei Song, Hong-Yi Wang, and Zhong Wang, “Non-bloch pt symmetry breaking: Universal threshold and dimensional surprise,” arXiv preprint arXiv:2102.02230 (2021).
Helbig et al. (2020) T Helbig, T Hofmann, S Imhof, M Abdelghany, T Kiessling, LW Molenkamp, CH Lee, A Szameit, M Greiter, and R Thomale, “Generalized bulk–boundary correspondence in non-hermitian topolectrical circuits,” Nature Physics , 1–4 (2020).
Xiao et al. (2020) Lei Xiao, Tianshu Deng, Kunkun Wang, Gaoyan Zhu, Zhong Wang, Wei Yi, and Peng Xue, “Non-hermitian bulk–boundary correspondence in quantum dynamics,” Nature Physics 16, 761 (2020).
Ghatak et al. (2020) Ananya Ghatak, Martin Brandenbourger, Jasper van Wezel, and Corentin Coulais, “Observation of non-hermitian topology and its bulk–edge correspondence in an active mechanical metamaterial,” Proceedings of the National Academy of Sciences 117, 29561–29568 (2020).
Weidemann et al. (2020) Sebastian Weidemann, Mark Kremer, Tobias Helbig, Tobias Hofmann, Alexander Stegmaier, Martin Greiter, Ronny Thomale, and Alexander Szameit, “Efficient light funneling based on the non-hermitian skin effect,” arXiv preprint arXiv:2004.01990 (2020).
Zou et al. (2021) Deyuan Zou, Tian Chen, Wenjing He, Jiacheng Bao, Ching Hua Lee, Houjun Sun, and Xiangdong Zhang, “Observation of hybrid higher-order skin-topological effect in non-hermitian topolectrical circuits,” arXiv preprint arXiv:2104.11260 (2021).
Stegmaier et al. (2021) Alexander Stegmaier, Stefan Imhof, Tobias Helbig, Tobias Hofmann, Ching Hua Lee, Mark Kremer, Alexander Fritzsche, Thorsten Feichtner, Sebastian Klembt, Sven Höfling, et al., “Topological defect engineering and p t symmetry in non-hermitian electrical circuits,” Physical Review Letters 126, 215302 (2021).
Note (1) The mechanism for NH pseudo-gaps applies in higher-dimensional lattices, but we specialize to 1D for simplicity.
Schinzinger and Laura (2012) Roland Schinzinger and Patricio AA Laura, Conformal mapping: methods and applications (Courier Corporation, 2012).
Hatano and Nelson (1996) Naomichi Hatano and David R. Nelson, “Localization transitions in non-hermitian quantum mechanics,” Phys. Rev. Lett. 77, 570–573 (1996).
Hatano and Nelson (1997) Naomichi Hatano and David R. Nelson, “Vortex pinning and non-hermitian quantum mechanics,” Phys. Rev. B 56, 8651–8673 (1997).
Okuma and Sato (2021b) Nobuyuki Okuma and Masatoshi Sato, “Non-hermitian skin effects in hermitian correlated or disordered systems: Quantities sensitive or insensitive to boundary effects and pseudo-quantum-number,” Phys. Rev. Lett. 126, 176601 (2021b).
(78) “Supplemental materials,” Supplemental Materials .
Shanahan (2006) Patrick Shanahan, The Atiyah-Singer index theorem: an introduction, Vol. 638 (Springer, 2006).
Hasan and Kane (2010) M Zahid Hasan and Charles L Kane, “Colloquium: topological insulators,” Rev. Mod. Phys. 82, 3045 (2010).
Essin and Gurarie (2011) Andrew M Essin and Victor Gurarie, “Bulk-boundary correspondence of topological insulators from their respective green’s functions,” Physical Review B 84, 125132 (2011).
Qi et al. (2013) Xiao-Liang Qi, Edward Witten, and Shou-Cheng Zhang, “Axion topological field theory of topological superconductors,” Physical Review B 87, 134519 (2013).
Gu et al. (2016) Yingfei Gu, Ching Hua Lee, Xueda Wen, Gil Young Cho, Shinsei Ryu, and Xiao-Liang Qi, “Holographic duality between (2+ 1)-dimensional quantum anomalous hall state and (3+ 1)-dimensional topological insulators,” Phys. Rev. B 94, 125107 (2016).
Zhu et al. (2021) Weiwei Zhu, Wei Xin Teo, Linhu Li, and Jiangbin Gong, “Delocalization of topological edge states,” Phys. Rev. B 103, 195414 (2021).
Kawabata et al. (2019b) Kohei Kawabata, Ken Shiozaki, Masahito Ueda, and Masatoshi Sato, “Symmetry and topology in non-hermitian physics,” Phys. Rev. X 9, 041015 (2019b).
Qi et al. (2006) Xiao-Liang Qi, Yong-Shi Wu, and Shou-Cheng Zhang, “Topological quantization of the spin hall effect in two-dimensional paramagnetic semiconductors,” Phys. Rev. B 74, 085308 (2006).
Note (2) Under OBCs, band eigenstates are not labeled by momentum, and a pseudo-band represent an isolated cluster of eigenenergies just like an ordinary band.
Lababidi et al. (2014) Mahmoud Lababidi, Indubala I. Satija, and Erhai Zhao, “Counter-propagating edge modes and topological phases of a kicked quantum hall system,” Phys. Rev. Lett. 112, 026805 (2014).
Zhou et al. (2014a) Longwen Zhou, Hailong Wang, Derek YH Ho, and Jiangbin Gong, “Aspects of floquet bands and topological phase transitions in a continuously driven superlattice,” The European Physical Journal B 87, 1–13 (2014a).
Zhou et al. (2014b) Zhenyu Zhou, Indubala I. Satija, and Erhai Zhao, “Floquet edge states in a harmonically driven integer quantum hall system,” Phys. Rev. B 90, 205108 (2014b).
Ho and Gong (2014) Derek Y. H. Ho and Jiangbin Gong, “Topological effects in chiral symmetric driven systems,” Phys. Rev. B 90, 195419 (2014).
Fulga and Maksymenko (2016) I. C. Fulga and M. Maksymenko, “Scattering matrix invariants of floquet topological insulators,” Phys. Rev. B 93, 075405 (2016).
Höckendorf et al. (2019) Bastian Höckendorf, Andreas Alvermann, and Holger Fehske, “Universal driving protocol for symmetry-protected floquet topological phases,” Phys. Rev. B 99, 245102 (2019).
Umer et al. (2020) Muhammad Umer, Raditya Weda Bomantara, and Jiangbin Gong, “Counterpropagating edge states in floquet topological insulating phases,” Phys. Rev. B 101, 235438 (2020).
Ozawa et al. (2019) Tomoki Ozawa, Hannah M Price, Alberto Amo, Nathan Goldman, Mohammad Hafezi, Ling Lu, Mikael C Rechtsman, David Schuster, Jonathan Simon, Oded Zilberberg, et al., “Topological photonics,” Reviews of Modern Physics 91, 015006 (2019).
Sun et al. (2011) Kai Sun, Zhengcheng Gu, Hosho Katsura, and S Das Sarma, “Nearly flatbands with nontrivial topology,” Phys. Rev. Lett. 106, 236803 (2011).
Neupert et al. (2011) Titus Neupert, Luiz Santos, Claudio Chamon, and Christopher Mudry, “Fractional quantum hall states at zero magnetic field,” Phys. Rev. Lett. 106, 236804 (2011).
Lee and Qi (2014) Ching Hua Lee and Xiao-Liang Qi, “Lattice construction of pseudopotential hamiltonians for fractional chern insulators,” Phys. Rev. B 90, 085103 (2014).
Anisimovas et al. (2015) Egidijus Anisimovas, Giedrius Žlabys, Brandon M Anderson, Gediminas Juzeliūnas, and André Eckardt, “Role of real-space micromotion for bosonic and fermionic floquet fractional chern insulators,” Physical Review B 91, 245135 (2015).
Neupert et al. (2015) Titus Neupert, Claudio Chamon, Thomas Iadecola, Luiz H Santos, and Christopher Mudry, “Fractional (chern and topological) insulators,” Physica Scripta 2015, 014005 (2015).
Lee et al. (2017) Ching Hua Lee, Martin Claassen, and Ronny Thomale, “Band structure engineering of ideal fractional chern insulators,” Phys. Rev. B 96, 165150 (2017).
Kourtis et al. (2017) Stefanos Kourtis, Titus Neupert, Christopher Mudry, Manfred Sigrist, and Wei Chen, “Weyl-type topological phase transitions in fractional quantum hall like systems,” Physical Review B 96, 205117 (2017).
Kourtis et al. (2014) Stefanos Kourtis, Titus Neupert, Claudio Chamon, and Christopher Mudry, “Fractional chern insulators with strong interactions that far exceed band gaps,” Physical review letters 112, 126806 (2014).
Huang et al. (2018) Zhoushen Huang, Wei Zhu, Daniel P Arovas, Jian-Xin Zhu, and Alexander V Balatsky, “Invariance of topological indices under hilbert space truncation,” Physical review letters 120, 016403 (2018).