Non-Gaussian state generation with time-gated photon detection
Abstract
Non-Gaussian states of light, which are essential in fault-tolerant and universal optical quantum computation, are typically generated by a heralding scheme using photon detectors. Recently, it is theoretically shown that the large timing jitter of the photon detectors deteriorates the purity of the generated non-Gaussian states [T. Sonoyama, et al., Phys. Rev. A 105, 043714 (2022)]. In this study, we generate non-Gaussian states with Wigner negativity by time-gated photon detection. We use a fast optical switch for time gating to effectively improve the timing jitter of a photon-number-resolving detector based on transition edge sensor from 50 ns to 10 ns. As a result, we generate non-Gaussian states with Wigner negativity of , which cannot be observed without the time-gated photon detection method. These results confirm the effect of the timing jitter on non-Gaussian state generation experimentally for the first time and provide the promising method of high-purity non-Gaussian state generation.
Introduction.-
Non-Gaussian states of light are important resources in various fields such as quantum metrology [1, 2], quantum communication [3, 4], quantum computation [5, 6, 7, 8, 9, 10, 11, 12, 13]. Especially in the field of continuous-variable quantum information processing, quantum computation with Gaussian states and Gaussian operations have already been demonstrated [14, 15, 16, 17], and the remaining issues are quantum computation with Non-Gaussian states and non-Gaussian operations, which are necessary for fault-tolerance and universality.
In the optical systems, non-Gaussian states are typically generated by a heralding scheme using entangled resource and photon detectors [18, 19, 20, 21] as in Fig.1. However, the purity of non-Gaussian states generated experimentally, which is crucial for their applications, is still limited because of the performances of photon detectors such as detection efficiency and photon-number-resolving ability. Recently, it has become theoretically clear that the timing jitter of the photon detector also affects the purity of the generated states when continuous-wave (CW) light is used [22]. In particular, when the magnitude of the timing jitter is large and non-negligible relative to the wave packet width of the generated state, the timing of the state generation is unclear as shown in Fig.1 (a) and the purity is degraded. Most of the previous studies used single-photon detectors [23, 24] with low timing jitter of less than 1 nanosecond to generate states on wave packets of several tens of nanoseconds [25, 26, 27, 28]. Thus, the effect of timing jitter was low enough to ignore. On the other hand, the use of photon-number-resolving detectors (PNRDs) is needed for generating more complex non-Gaussian states. The timing jitter of the typical PNRD based on Transition Edge Sensors (TESs) [29] is about 50 ns, which is non-negligible compared to the typical wave packet width of several tens of nanoseconds. Furthermore, considering its application in quantum computation, the wave packet width is expected to become even shorter for ultrafast quantum computation. This is because the wave packet width is related to the clock frequency when time-domain multiplexing scheme is used, which is one of the promising methods of optical quantum computation [14, 15, 16, 17]. Therefore, the relative magnitude of timing jitter to wave packet width is expected to become larger and it has become necessary to deal with this problem of timing jitter in non-Gaussian state generation.
Here, we introduce time-gated photon detection using a high-speed optical switch to improve the timing jitter in non-Gaussian state preparation. In conventional photon detection, the output signal of the detector is used as a timing reference of the state generation as shown in Fig.1 (a). In this case, the temporal resolution is determined by the detector’s timing jitter . On the other hand, in time-gated photon detection, an optical switch is placed in front of the detector as shown in Fig.1 (b), which operates only for a short time to limit the photon detection time. By using the ON/OFF signal of the optical switch as the reference signal for the state generation time, the temporal resolution is determined by the time window of the optical switch, which becomes the effective timing jitter. Thus, the timing jitter can be improved when the time window of the optical switch is shorter than the original timing jitter of the detector.
In this study, a Pockels cell and a polarizing beam splitter (PBS) are used as an optical switch, and the effective timing jitter of a TES is controlled by the time window of the optical switch. As a result, the timing jitter of the TES is improved from 50 ns to 10 ns, and a Schrödinger cat state, one of non-Gaussian states, with Wigner negativity of is successfully generated. This is in contrast with the case without time-gated photon detection, where the negative value of the Wigner function cannot be confirmed. To our knowledge, this is the first successful generation of Schrödinger cat states using TESs and CW light. These results show the effect of timing jitter on the generated states experimentally and provide a promising method for generating high-purity non-Gaussian states.

Temporal mode functions of optical quantum states.- The optical quantum states we are dealing with exist in a wave packet. By defining the temporal mode function as the function that represents the temporal shape of the wave packet, the complex amplitude of the wave packet is expressed using the amplitude of the electromagnetic field at time as follows,
| (1) |
where satisfies . Here we consider rotating frame so that does not include the oscillation components of the carrier frequency. Since the complex amplitude is not an observable, the quadratures corresponding to the real and imaginary components are used to describe quantum states. The quadratures satisfy the commutation relation , where is set to 1. In this paper, we denote the density matrix and the state vector of the quantum state excited on the temporal mode as and .
Heralded generation of Shrödinger cat states.- In this experiment, a Schrödinger cat state, known as a fundamental element of optical quantum information processing, is chosen as a non-Gaussian state to be generated. This Schrödinger cat state is a superposition of a coherent state, i.e., , where is the relative phase and is a normalization constant. Such a cat state is generated by subtracting a photon from the squeezed light, limiting the frequency region to be measured with a frequency filter and then detecting the photons [21, 20, 26, 27, 28, 30, 31].
Here, we discuss the effect of the timing jitter of photon detection on the generated quantum state quantitatively. The theoretical analysis for the case of single-photon-state generation has been presented in [22], so in this paper we extend it to the case of Schrödinger-cat-state generation as well. First, if the timing jitter is sufficiently low, it is known that the generated quantum state is expressed as follows [27, 28],
| (2) |
where is a normalizing operation, is a time-reversed function of the frequency filter’s impulse response, is the time correlation function of the squeezed light and is a squeezing operator. By defining as , this quantum state can be approximated as . On the other hand, if the timing jitter is poor and its effect cannot be ignored, the quantum state generated is a mixture of cat states excited on wave packets with different times, as shown in Fig.1 (a). Assuming the distribution function of timing jitter as , the generated state can be expressed as follows,
| (3) |
Such a quantum state is a multimode state in multiple wave packets, but what we want to generate is a single-mode Schrödinger cat state that can be used for quantum computation. We consider therefore choosing a temporal mode such that the quantum state on is closest to the cat state. This can be obtained by a principal component analysis (PCA) method [22]. Then, the generated state in the temporal mode can be expressed as follows using the cat state and the squeezed state :
| (4) |
where the parameter and the temporal mode function depend on the ratio of the timing jitter to the time width of the original wave packet . When the timing jitter relative to is low enough, approaches 1 and approaches . On the other hand, when the timing jitter becomes worse, becomes smaller and becomes wider in time. Thus, the generated quantum state becomes a mixture of the cat state (non-Gaussian state), and the squeezed state (Gaussian state).
The timing jitter dependence on the generated quantum states can be confirmed experimentally. First, the optimal time mode can be obtained by PCA method, and the timing jitter’s effect is confirmed by seeing how the shape of changes with the magnitude of the timing jitter. In addition, the purity of the quantum state, which is related to in Eq.4, can be confirmed from the photon number distribution of the generated quantum states and the value of the Wigner function near the origin. This is because the squeezed light has an even-photon nature and the cat state generated by the single-photon subtraction in this experiment has an odd-photon nature [19], and the value at the origin of the Wigner function is for a quantum state with odd-photon nature and for a quantum state with even-photon nature [32, 33]. In this paper, these properties are used to evaluate the generated quantum states.
Experimental setup.-

In this experiment, Schrödinger cat states are generated by photon subtraction both with and without the optical switch for comparison. In particular, five patterns are performed with the optical switch (time window of 10, 30, 50, and 70 ns) and without the optical switch (the original timing jitter of the TES is 58 ns, which is estimated experimentally).
The experimental setup is shown in Fig.2, where the light source is a CW laser at 1545.32 nm and the squeezed light is generated by an Optical Parametric Oscillator (OPO) whose half-width-at-half-maximum (HWHM) is 58 MHz. A small portion (4.7%) of the generated squeezed light is tapped and a single photon is detected by the TES after a frequency filtering whose HWHM is 8 MHz. These parameters determine the wave packet width of the generated state when the timing jitter of photon detection can be neglected. The theoretically expected value is about 22 ns. Here, a Pockels cell and a PBS are used as an optical switch and the minimum time window of this optical switch is 10 ns, which is small compared to the temporal width of the wave packet . The Pockels cell used in this study is , which has the extinction ratio of more than 30 dB and the transmittance of more than 95 %. The Pockels cell driver, which drives the voltage applied to the Pockels cell, has a rise time of about 3.5 ns and a maximum repetition rate of 1.2 MHz.
For verification, quadratures of the generated quantum states at time , are obtained by homodyne measurements, from which the temporal mode functions and Wigner functions of the generated states are reconstructed. The count rates in this experiment are 17 (with the switch, 10 ns), 52 (30 ns), 79 (50 ns), 108 (70 ns) and 3900 (without the switch), respectively.
Evaluation.-

The first step is to check the operation of the optical switch. Classical coherent light is injected into the optical switch, and a fast photodetector is placed immediately after the PBS to check its response. Figure 3 (a) shows the response of the optical switch when the time window is set to 10, 30, 50, and 70 ns, respectively. The actual time widths are and ns, which are consistent with the set values.
Next, the temporal mode functions of the generated quantum states are reconstructed. The temporal mode functions are obtained by PCA of the covariance matrix of the quadratures, taking advantage of the fact that the quadrature’s variance of the generated quantum state is larger than the background quantum state [34, 35]. Figure 3 (b) shows the estimated temporal mode functions of the generated states with and without the optical switch. This corresponds to the first principal component obtained by PCA. Theoretically, as the timing jitter becomes worse, the width of the estimated temporal mode should widen in time and its peak value should become smaller, and such a tendency is confirmed in Fig.3. In addition, Fig.3 (c) compares experimental and numerically calculated theoretical values of the full-width-at-half-maximum (FWHM) of the temporal mode function with respect to the timing jitter. The results with the optical switch are generally consistent with the theoretical line, but the result without the optical switch seems to deviate a little from the theoretical line. This may be due to the fact that the shape of distribution function in Eq.3 is not the same as in the case of using an optical switch, or the output signal of the TES changed during the experiment and the timing jitter may have differed from the estimated one. From these results, we confirm the improvement of the timing jitter and the change of the temporal mode function by time-gated photon detection.
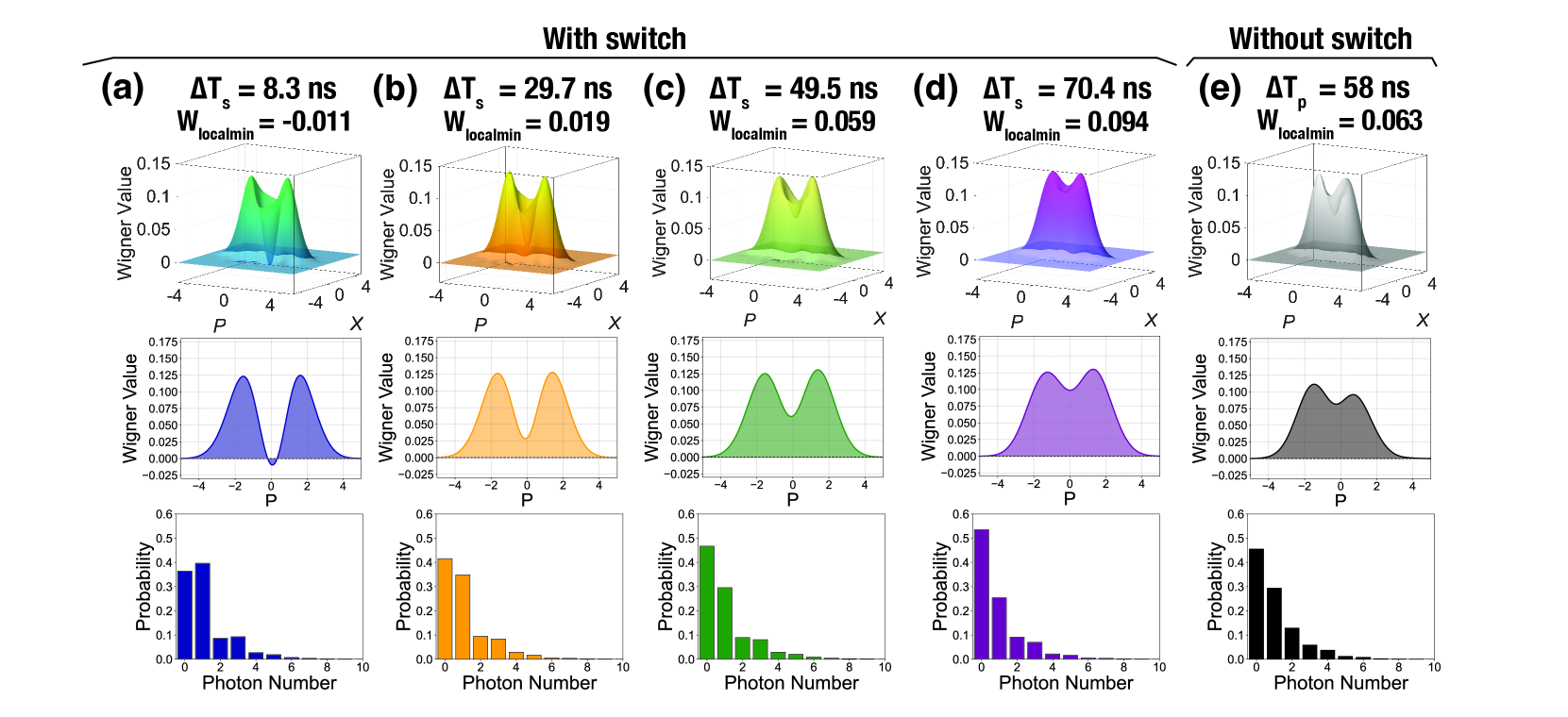
Finally, the quadratures in the temporal mode are calculated numerically as Then, the density matrices and the Wigner functions are reconstructed from the quadrature data by quantum state tomography [36] without any loss correction. The reconstructed Wigner functions, their cross sections at , and the photon number distributions are shown in Fig.4. As shown in Fig.4 (a), the Shrödinger cat state with a negative value of near the origin is successfully generated when the time window of the optical switch is the shortest ( ns). The photon number distribution also confirms the odd-photon nature of the generated state, which is caused by subtracting a single photon from the squeezed state with even-photon nature. This shows that we succeed in generating a Shrödinger cat state. Figure 4 (b)-(d) show that as the optical switch time window becomes wider (29.7 ns, 49.5 ns and 70.4 ns), the value of Wigner function near the origin gradually increases. Furthermore, Fig.4 (e) shows the Wigner function of the generated state without the optical switch ( ns) and the negative value near the origin cannot be observed here. From these results, we confirm that the improvement of timing jitter leads to the improvement of non-Gaussian states generation, as expected theoretically.
Conclusion.- In this study, we introduce time-gated photon detection using a high-speed optical switch for non-Gaussian state generation. As a result, the effect of the timing jitter of the detector on the non-Gaussian state generation is experimentally clarified for the first time, and it is confirmed that the purity deteriorates when the timing jitter is non-negligibly large compared to the wave packet width of the generated state as expected theoretically. In addition, we improve the timing jitter of the PNRD-TES from 50 ns to 10 ns using this method, and succeed in generating a Schrödinger cat state with a negative Wigner function value of . To the best of our knowledge, this is the first successful generation of Schrödinger cat state using TES and a CW light source.
This time-gated photon detection method does not sacrifice the other performances of the detector TES such as detection efficiency and photon-number-resolving capability. Thus, we expect more complex non-Gaussian state generation is possible by using this time-gated scheme in multi-photon detection regime. Furthermore, by using further faster optical switches using non-linear optical effect as in [37, 38], the timing jitter of a photon detector could be further improved to the subpicosecond regime. This means that this scheme can be used to generate high-purity non-Gaussian states in picosecond wave packet. This technology is therefore expected to become the key technology for realizing ultrafast, fault-tolerant and universal optical quantum computation with GHz to THz clock frequency.
The authors acknowledge supports from UTokyo Foundation and donations from Nichia Corporation of Japan. W.A. and M.E. acknowledge supports from Research Foundation for OptoScience and Technology. T.S., K.Takahashi and B.C acknowledge financial supports from The Forefront Physics and Mathematics Program to Drive Transformation (FoPM). The authors would like to thank Mr. Takahiro Mitani for careful proofreading of the manuscript. This work was partly supported by Japan Society for the Promotion of Science KAKENHI (18H05207, 20J10844, 20K15187, 22K20351), Japan Science and Technology Agency Moonshot Research and Development (JPMJMS2064), PRESTO (JPMJPR2254), and CREST(JPMJCR17N4).
References
- Huver et al. [2008] S. D. Huver, C. F. Wildfeuer, and J. P. Dowling, Entangled fock states for robust quantum optical metrology, imaging, and sensing, Phys. Rev. A 78, 063828 (2008).
- Anisimov et al. [2010] P. M. Anisimov, G. M. Raterman, A. Chiruvelli, W. N. Plick, S. D. Huver, H. Lee, and J. P. Dowling, Quantum metrology with two-mode squeezed vacuum: Parity detection beats the heisenberg limit, Phys. Rev. Lett. 104, 103602 (2010).
- Namiki et al. [2014] R. Namiki, O. Gittsovich, S. Guha, and N. Lütkenhaus, Gaussian-only regenerative stations cannot act as quantum repeaters, Phys. Rev. A 90, 062316 (2014).
- Sabapathy and Winter [2017] K. K. Sabapathy and A. Winter, Non-gaussian operations on bosonic modes of light: Photon-added gaussian channels, Phys. Rev. A 95, 062309 (2017).
- Lloyd and Braunstein [1999] S. Lloyd and S. L. Braunstein, Quantum computation over continuous variables, Phys. Rev. Lett. 82, 1784 (1999).
- Andersen et al. [2015] U. L. Andersen, J. S. Neergaard-Nielsen, P. van Loock, and A. Furusawa, Hybrid discrete- and continuous-variable quantum information, Nature Physics 11, 713 (2015).
- Gottesman et al. [2001] D. Gottesman, A. Kitaev, and J. Preskill, Encoding a qubit in an oscillator, Phys. Rev. A 64, 012310 (2001).
- Cochrane et al. [1999] P. T. Cochrane, G. J. Milburn, and W. J. Munro, Macroscopically distinct quantum-superposition states as a bosonic code for amplitude damping, Phys. Rev. A 59, 2631 (1999).
- Leghtas et al. [2013] Z. Leghtas, G. Kirchmair, B. Vlastakis, R. J. Schoelkopf, M. H. Devoret, and M. Mirrahimi, Hardware-efficient autonomous quantum memory protection, Phys. Rev. Lett. 111, 120501 (2013).
- Michael et al. [2016] M. H. Michael, M. Silveri, R. T. Brierley, V. V. Albert, J. Salmilehto, L. Jiang, and S. M. Girvin, New class of quantum error-correcting codes for a bosonic mode, Phys. Rev. X 6, 031006 (2016).
- Bergmann and van Loock [2016] M. Bergmann and P. van Loock, Quantum error correction against photon loss using multicomponent cat states, Phys. Rev. A 94, 042332 (2016).
- Albert et al. [2020] V. V. Albert, J. P. Covey, and J. Preskill, Robust encoding of a qubit in a molecule, Phys. Rev. X 10, 031050 (2020).
- Grimsmo et al. [2020] A. L. Grimsmo, J. Combes, and B. Q. Baragiola, Quantum computing with rotation-symmetric bosonic codes, Phys. Rev. X 10, 011058 (2020).
- Asavanant et al. [2019] W. Asavanant, Y. Shiozawa, S. Yokoyama, B. Charoensombutamon, and A. Furusawa, Generation of time-domain-multiplexed two-dimensional cluster state, Science 366, 373 (2019).
- V. Larsen et al. [2019] M. V. Larsen, X. Guo, C. R. Breum, J. S. Neergaard-nielsen, and U. L.Andersen, Deterministic generation of a two-dimensional cluster state, Science 366, 369 (2019).
- Asavanant et al. [2021] W. Asavanant, B. Charoensombutamon, S. Yokoyama, T. Ebihara, T. Nakamura, R. N. Alexander, M. Endo, J. Yoshikawa, N. C. Menicucci, H. Yonezawa, and A. Furusawa, Time-domain-multiplexed measurement-based quantum operations with 25-MHz clock frequency, Phys. Rev. Applied 16, 034005 (2021).
- Larsen et al. [2021] M. V. Larsen, X. Guo, C. R. Breum, J. S. Neergaard-Nielsen, and U. L. Andersen, Deterministic multi-mode gates on a scalable photonic quantum computing platform, Nature Physics 17, 1018 (2021).
- Hong and Mandel [1986] C. K. Hong and L. Mandel, Experimental realization of a localized one-photon state, Phys. Rev. Lett. 56, 58 (1986).
- Dakna et al. [1997] M. Dakna, T. Anhut, T. Opatrný, L. Knöll, and D.-G. Welsch, Generating schrödinger-cat-like states by means of conditional measurements on a beam splitter, Phys. Rev. A 55, 3184 (1997).
- Alexei et al. [2006] O. Alexei, T.-B. Rosa, L. Julien, and G. Philippe, Generating optical schrdinger kittens for quantum information processing., Science 312, 83 (2006).
- Neergaard-Nielsen et al. [2006] J. S. Neergaard-Nielsen, B. M. Nielsen, C. Hettich, K. Mølmer, and E. S. Polzik, Generation of a superposition of odd photon number states for quantum information networks, Phys. Rev. Lett. 97, 083604 (2006).
- Sonoyama et al. [2022] T. Sonoyama, W. Asavanant, K. Fukui, M. Endo, J.-i. Yoshikawa, and A. Furusawa, Analysis of optical quantum state preparation using photon detectors in the finite-temporal-resolution regime, Phys. Rev. A 105, 043714 (2022).
- Cova et al. [1981] S. Cova, A. Longoni, and A. Andreoni, Towards picosecond resolution with single‐photon avalanche diodes, Review of Scientific Instruments 52, 408 (1981).
- Korzh et al. [2020] B. Korzh, Q.-Y. Zhao, J. P. Allmaras, S. Frasca, T. M. Autry, E. A. Bersin, A. D. Beyer, R. M. Briggs, B. Bumble, M. Colangelo, G. M. Crouch, A. E. Dane, T. Gerrits, A. E. Lita, F. Marsili, G. Moody, C. Peña, E. Ramirez, J. D. Rezac, N. Sinclair, M. J. Stevens, A. E. Velasco, V. B. Verma, E. E. Wollman, S. Xie, D. Zhu, P. D. Hale, M. Spiropulu, K. L. Silverman, R. P. Mirin, S. W. Nam, A. G. Kozorezov, M. D. Shaw, and K. K. Berggren, Demonstration of sub-3 ps temporal resolution with a superconducting nanowire single-photon detector, Nature Photonics 14, 250 (2020).
- Yukawa et al. [2013] M. Yukawa, K. Miyata, T. Mizuta, H. Yonezawa, P. Marek, R. Filip, and A. Furusawa, Generating superposition of up-to three photons for continuous variable quantum information processing, Opt. Express 21, 5529 (2013).
- Wakui et al. [2007] K. Wakui, H. Takahashi, A. Furusawa, and M. Sasaki, Photon subtracted squeezed states generated with periodically poled ktiopo4, Opt. Express 15, 3568 (2007).
- Asavanant et al. [2017] W. Asavanant, K. Nakashima, Y. Shiozawa, J. Yoshikawa, and A. Furusawa, Generation of highly pure schrödinger’s cat states and real-time quadrature measurements via optical filtering, Opt. Express 25, 32227 (2017).
- Takase et al. [2022] K. Takase, A. Kawasaki, B. K. Jeong, M. Endo, T. Kashiwazaki, T. Kazama, K. Enbutsu, K. Watanabe, T. Umeki, S. Miki, H. Terai, M. Yabuno, F. China, W. Asavanant, J. ichi Yoshikawa, and A. Furusawa, Generation of schrödinger cat states with wigner negativity using a continuous-wave low-loss waveguide optical parametric amplifier, Opt. Express 30, 14161 (2022).
- Fukuda et al. [2011] D. Fukuda, G. Fujii, T. Numata, K. Amemiya, A. Yoshizawa, H. Tsuchida, H. Fujino, H. Ishii, T. Itatani, S. Inoue, and T. Zama, Titanium-based transition-edge photon number resolving detector with 98% detection efficiency with index-matched small-gap fiber coupling, Opt. Express 19, 870 (2011).
- Namekata et al. [2010] N. Namekata, Y. Takahashi, G. Fujii, D. Fukuda, S. Kurimura, and S. Inoue, Non-gaussian operation based on photon subtraction using a photon-number-resolving detector at a telecommunications wavelength, Nature Photonics 4, 655 (2010).
- Gerrits et al. [2010] T. Gerrits, S. Glancy, T. S. Clement, B. Calkins, A. E. Lita, A. J. Miller, A. L. Migdall, S. W. Nam, R. P. Mirin, and E. Knill, Generation of optical coherent-state superpositions by number-resolved photon subtraction from the squeezed vacuum, Phys. Rev. A 82, 031802 (2010).
- Royer [1977] A. Royer, Wigner function as the expectation value of a parity operator, Phys. Rev. A 15, 449 (1977).
- Nehra et al. [2019] R. Nehra, A. Win, M. Eaton, R. Shahrokhshahi, N. Sridhar, T. Gerrits, A. Lita, S. W. Nam, and O. Pfister, State-independent quantum state tomography by photon-number-resolving measurements, Optica 6, 1356 (2019).
- MacRae et al. [2012] A. MacRae, T. Brannan, R. Achal, and A. I. Lvovsky, Tomography of a high-purity narrowband photon from a transient atomic collective excitation, Phys. Rev. Lett. 109, 033601 (2012).
- Morin et al. [2013] O. Morin, C. Fabre, and J. Laurat, Experimentally accessing the optimal temporal mode of traveling quantum light states, Phys. Rev. Lett. 111, 213602 (2013).
- Lvovsky and Raymer [2009] A. I. Lvovsky and M. G. Raymer, Continuous-variable optical quantum-state tomography, Rev. Mod. Phys. 81, 299 (2009).
- England et al. [2021] D. England, F. Bouchard, K. Fenwick, K. Bonsma-Fisher, Y. Zhang, P. J. Bustard, and B. J. Sussman, Perspectives on all-optical kerr switching for quantum optical applications, Applied Physics Letters 119, 160501 (2021), https://doi.org/10.1063/5.0065222 .
- Kupchak et al. [2019] C. Kupchak, J. Erskine, D. England, and B. Sussman, Terahertz-bandwidth switching of heralded single photons, Opt. Lett. 44, 1427 (2019).