Non-Equilibrium Structural and Dynamic Behaviors of Polar Active Polymer Controlled by Head Activity
Abstract
Thermodynamic behavior of polymer chains out of equilibrium is a fundamental problem in both polymer physics and biological physics. By using molecular dynamics simulation, we discover a non-equilibrium mechanism that controls the conformation and dynamics of polar active polymer, i.e., head activity commands the overall chain activity, resulting in re-entrant swelling of active chains and non-monotonic variation of Flory exponent . These intriguing phenomena are results of two competing non-equilibrium effects arising from the head-controlled railway motion of the chain, i.e., dynamic chain rigidity and the involution of chain conformation characterized by the negative bond vector correlation. Moreover, we identify several generic dynamic features of polar active polymers, i.e., linear decay of the end-to-end vector correlation function, polymer-size dependent crossover from ballistic to diffusive dynamics, and diffusion coefficient sensitive to head activity. A simple dynamic theory is proposed to faithfully explain these interesting dynamic phenomena. This sensitive structural and dynamical response of active polymer to its head activity provides us a practical way to control active-agents with applications in biomedical engineering.
I i Introduction
The scaling theory of polymer introduced by P. G. de Gennes De Gennes (1979) lays the foundation of polymer physics Doi and Edwards (1988); Rubinstein and Colby (2003). One of its prediction is the universal scaling behavior of polymer’s size, or radius of gyration , on monomer number , i.e., with the well-known Flory exponent Flory (1953). For thermal-equilibrated polymer chain, there are three distinct scaling regimes, i.e., polymer in good solvent (), theta solvent () and bad solvent (). Nevertheless, how the introduction of non-equilibrium effects modifies these classical predictions is an open question relevant to some key biological processes. For examples, bio-polymer like DNA chromatin in nucleus and actin filaments in cellular cytoskeleton are subjected to propelling forces from either DNA helicases or motor proteins Harada et al. (1987); Nédélec et al. (1997); Jülicher et al. (2007); Stano et al. (2005); Kim et al. (2002), metabolic enzymes can form filamentous membraneless organelles termed cytoophidia that are efficiently transported through 3D complex cellular structures with the help of actin filaments Liu (2016); Li et al. (2018), polymerlike worms exhibit distinct conformational and dynamical properties with or without driving activity Deblais et al. (2020a, b); Heeremans et al. (2022). These active polymers exhibit complicated self-organized structures and abnormal dynamics that challenge classical polymer physics theory Surrey et al. (2001); Schaller et al. (2011a); Vliegenthart et al. (2020); Moore et al. (2020); Adkins et al. (2022); Natali et al. (2020); Tanida et al. (2020); Cao et al. (2022). On the other side, many artificial active polymers have also been realized, like motility assays of actin filament Schaller et al. (2010); Sumino et al. (2012), active colloidal polymers Dreyfus et al. (2005); Hill et al. (2014); Biswas et al. (2017); Nishiguchi et al. (2018), actuated mechanical chains/ribbons Massana-Cid et al. (2017); Zhang et al. (2009a, b), which show potential application value in drug-delivery and soft-body robots. Thus, a deep understanding of the non-equilibrium behaviors of active polymer is of great significance for both biological physics and biomedical engineering Winkler et al. (2017).
Active polymers are generally categorized into polar and non-polar. For polar active polymers like actin filaments, active forces are along the backbone of the polymer, thus the total active force has a preferred direction Locatelli et al. (2021); Mokhtari and Zippelius (2019); Prathyusha et al. (2018); Isele-Holder et al. (2015); Shee et al. (2021); Foglino et al. (2019); Shi and Ma (2010). This is different from the non-polar active polymers like active Brownian chains, where the active forces on monomers are uncorrelated Kaiser et al. (2015); Eisenstecken et al. (2017); Kaiser et al. (2015); Anand and Singh (2020). The mobility of the head of polar active polymers can significantly influence the structural and dynamic behaviors of the entire chain. For example, Bourdieu et al. observed in motility assays that the actin filaments rotate like spirals or undulate like flagellums when the head movement is frustrated Bourdieu et al. (1995). This phenomenon has inspired many efforts to study active polymers with constrained head Camalet et al. (1999); De Canio et al. (2017); Ziebert et al. (2015); Zheng et al. (2023); Wang et al. (2022); Martin et al. (2019); Chelakkot et al. (2014, 2021). Furthermore, head effects also affect the conformation and dynamics of unconstrained active polymers Schaller et al. (2011b); Hu et al. (2022). Most recently, Patil et al. revealed that the changes in head chirality of the California blackworm are responsible for the rapidly alternation of their self-assembly state Patil et al. (2023). Nevertheless, a more general mechanism of head activity-induced conformation and dynamics transition of the polar active polymer remains unknown. Systematic investigations of this issue can contribute to a deeper understanding of the conformation and dynamic behaviors of polar active polymers, including the recently discovered activity-induced coil-to-globule transition Bianco et al. (2018); Jain and Thakur (2022).
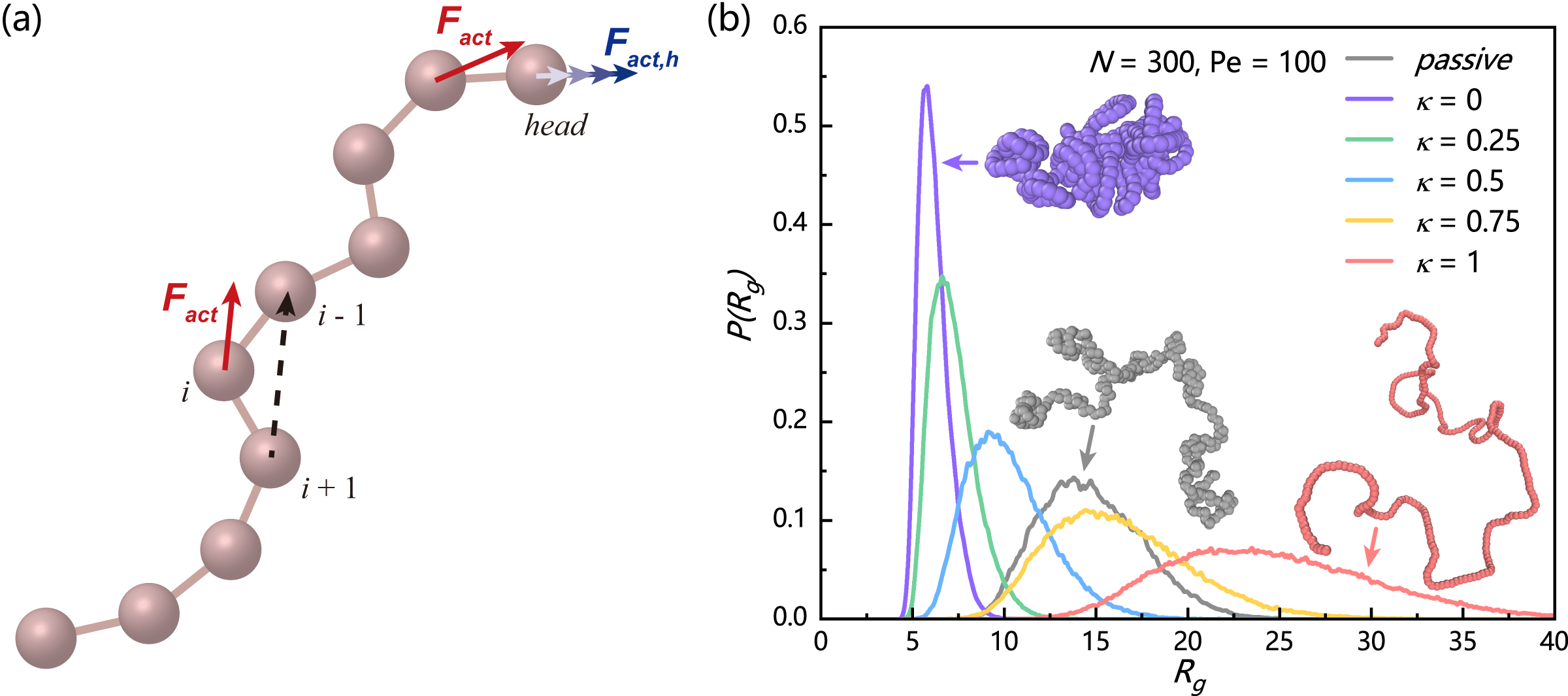
In this study, we systemically study the structures and dynamics of polar active polymers with controllable head activity. We find that the head activity plays a commanding role for the overall chain activity, resulting in re-entrant swelling of active polymer and non-monotonic variation of Flory exponent , as well as head-activity-controlled polymer dynamics. These intriguing behaviours are results of the competition between two non-equilibrium effects (i.e. dynamic chain rigidity and the involution of chain configurations) arising from the head-controlled railway motion of active polymer. Moreover, we also identify several generic dynamic features of polar active polymers, like linear rather than exponential decay of the end-to-end vector correlation function, polymer-size dependent crossover from ballistic to diffusive dynamics, and the head-activity-controlled diffusion coefficient. These dynamic phenomena are explained satisfactorily by a dynamic theory based on the railway motion.
II ii Model and simulations
As shown in FIG. 1(a), we model the active polymer as a bead-spring chain of monomers with bond length . To ensure conformation stability under self-driving conditions, a modified Kremer-Grest model was used, where the excluded volume interactions are modeled by a WCA-like potential:
| (1) |
with and setting the units of length and energy, and as the distance between two monomers. Neighboring beads are connected by finitely extensible nonlinear elastic (FENE) potential:
| (2) |
with . Such a pair of steep potentials severely limits the fluctuations in bond length and can avoid chain crossing in extremely contracted or extended conformations. Based on Bianco et al. (2018), we assume that the active force on backbone monomer has a constant magnitude and its direction polarizes to the head monomer () along the local tangent determined by the nearest two monomers, i.e.,
| (3) |
with . The active force on tail monomer () is set as , while the active force on head monomer is controlled by the dimensionless head activity strength ,
| (4) |
can also be understood as the ratio between the head and backbone activities. Standard Langevin dynamics is used to simulate the active polymer in free 3D space:
| (5) |
with and setting the mass scale and the friction constant Prathyusha et al. (2018); Shee et al. (2021); Locatelli et al. (2021); Isele-Holder et al. (2016). represents the conservative force (including excluded volume interactions Eq. (1) and bonding interactions Eq. (2)), denotes the noise with magnitude of , and is the active force applied on the beads, where and are the Boltzmann constant and temperature, respectively. We have confirmed that Langevin dynamics gives essentially the same results as overdamped Langevin dynamics (Supplemental FIG. S1) but the computational cost is over two orders of magnitude smaller than the latter. In our simulations, and are set to unit, hence controls the thermal energy of the heat bath. The Péclet number
| (6) |
is introduced to quantify the overall activity of the polymer. Without losing generality, we set as the energy unit of the system, and adjust the Péclet number by changing thermal energy Locatelli et al. (2021); Stenhammar et al. (2014). The typical speed of active monomers is with the friction coefficient, and the unit time of the system is chosen as . Velocity-Verlet algorithm with time step of is used to integrate the equations of polymer motions. At least 160 separate simulations with sufficient time (at least ) are performed for each parameter sequences. The control parameters of , and are scanned in the range of , and , respectively. All simulations are peformed by a custom modified version of LAMMPS, and all visualizations are produced by OVITO.
III iii Result and Discussion
III.1 A. Conformation of polar active polymers
The most direct method to investigate the conformation of polymers is the calculation of the gyration radius :
| (7) |
where is the number of monomers, denotes the position of the monomers. FIG. 1(b) shows the probability distribution of radius of gyration for active polymers with various head activity under fixed and , where for passive polymers is also shown for comparison. In the absence of head activity (), we find strong activity-induced collapse of the polymer chain, consistent with previous studies Bianco et al. (2018); Jain and Thakur (2022). However, with increasing head activity, active polymer gradually swells and becomes even more expanded than the passive polymer.
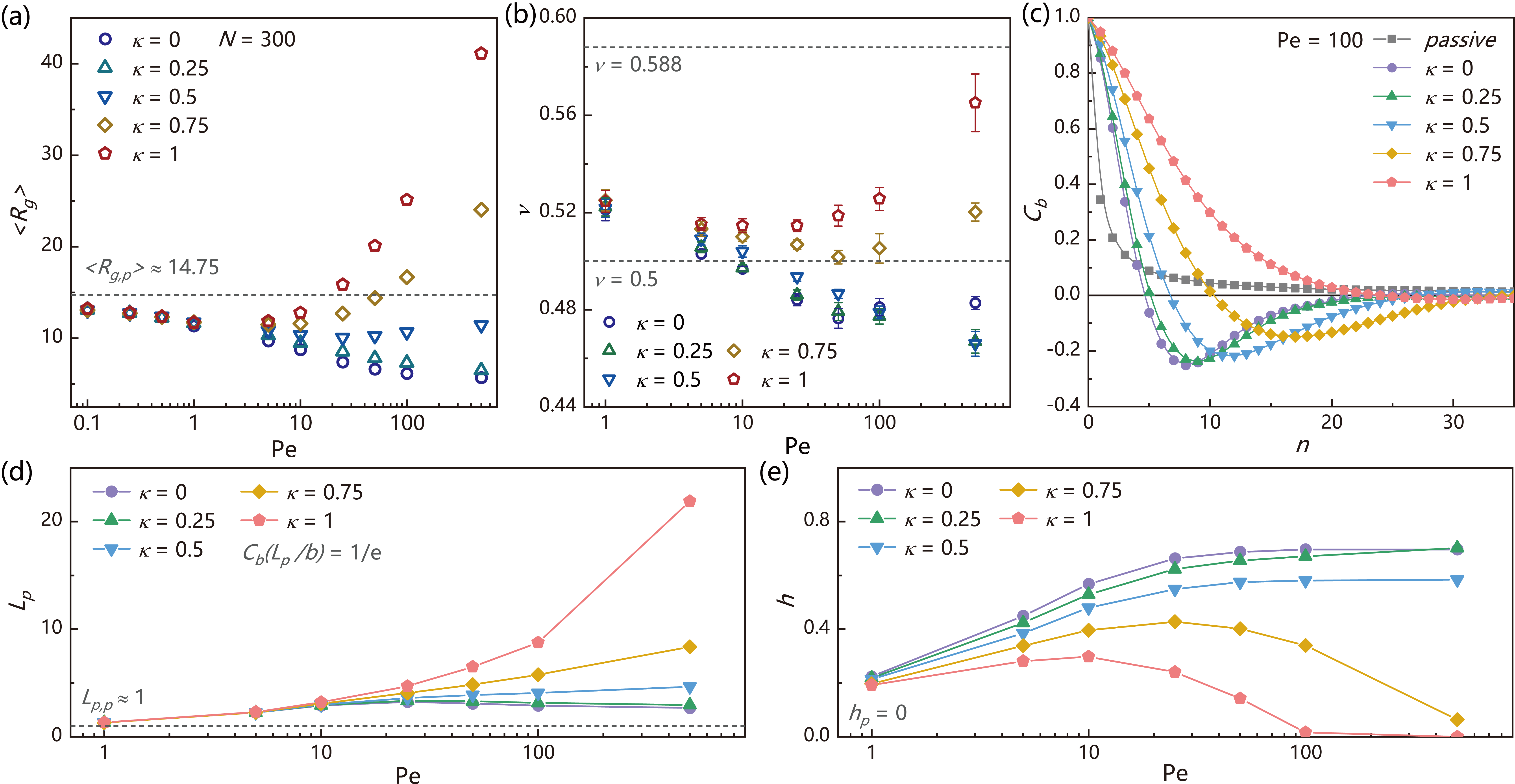
In FIG. 2(a), we plot the average radius of gyration as a function of under different , where for passive polymers is drawn as a dashed line for comparison. For small head activity , we find that shows monotonic decrease with increasing . Nevertheless, for large head activity, an unusual non-monotonic behaviour of is observed with a first-stage shrinkage when and late-state expand at large . Additionally, the Flory exponent is obtained through plotting as a function of (See Supplemental FIG. S2 for more data). In FIG. 2(b), we show as a function of under different where the reference values of the random-walk chain () and self-avoid walks chain () are drawn as dashed lines. We find that under large head activity, also exhibits a non-monotonic variation with increasing , which indicates a fundamental change of the fractal dimension of polymer configurations by head activity.
To explore these phenomena deeper, we calculate the bond-vector correlation function:
| (8) |
where . For typical semi-flexible polymers, decays exponentially. The characteristic correlation length at which decays to defines the persistence length . In FIG. 2(c), we plot for the passive polymer and active polymers with different under fixed . We find that compared with the passive polymer, for active polymers with small show a longer , but with an abnormal negative correlation at intermediate length scale. This negative correlation indicates that the conformation of the active polymer has a strong inward or involution tendency which is associated with the collapsed configuration. Nevertheless, this negative correlation is absent for passive polymers in bad solvent (Supplemental FIG. S3), which suggests a fundamental difference between these two systems, despite their apparent similarity. As grows, the persistence length increases significantly, with the negative correlation strength decrease rapidly to zero. Here, is defined as the area ratio between negative and positive regions in correlation function. Thus, active polymers with large head activity behave similarly to that of passive semi-flexible chains. This emerging “dynamic rigidity” is a pure non-equilibrium effect, since the chain still remains mechanically flexible. Unlike semi-flexible passive chains, this dynamic rigidity alone can not predict the conformation of polymers. For example, FIG. 2(a) shows that even is much larger than that of reference passive polymer, is still smaller than due to a large negative correlation in .
We summarize the behaviors of persistence length and in FIG. 2(d) and 2(e), respectively. One can see that with increasing , remains around the low value and even decreases for polymer with small , but rises significantly for polymer with large , while increases monotonically at small but exhibit strong non-monotonic behavior at large . Therefore, the activity of single head monomer determines the direction of overall active forces acting on the chain: for small head activity, the totally active driving is “inward”, corresponding to a large (small ) and a collapsed polymer state, while for large head activity, the totally active forces is “outward”, corresponding to a large (small ) and an extended polymer state.
III.2 B. Head-controlled railway motion
The above abnormal conformation behaviors have a deep connection with the dynamic motion of active polymer. Since the active propelling forces are along the chain’s contour, the active polymer adopts active reptation motion, which is also referred as “railway motion” Isele-Holder et al. (2015) (see Supplemental Movie S1-S5). To quantify such motion, we define a correlation function of head-tail position:
| (9) |
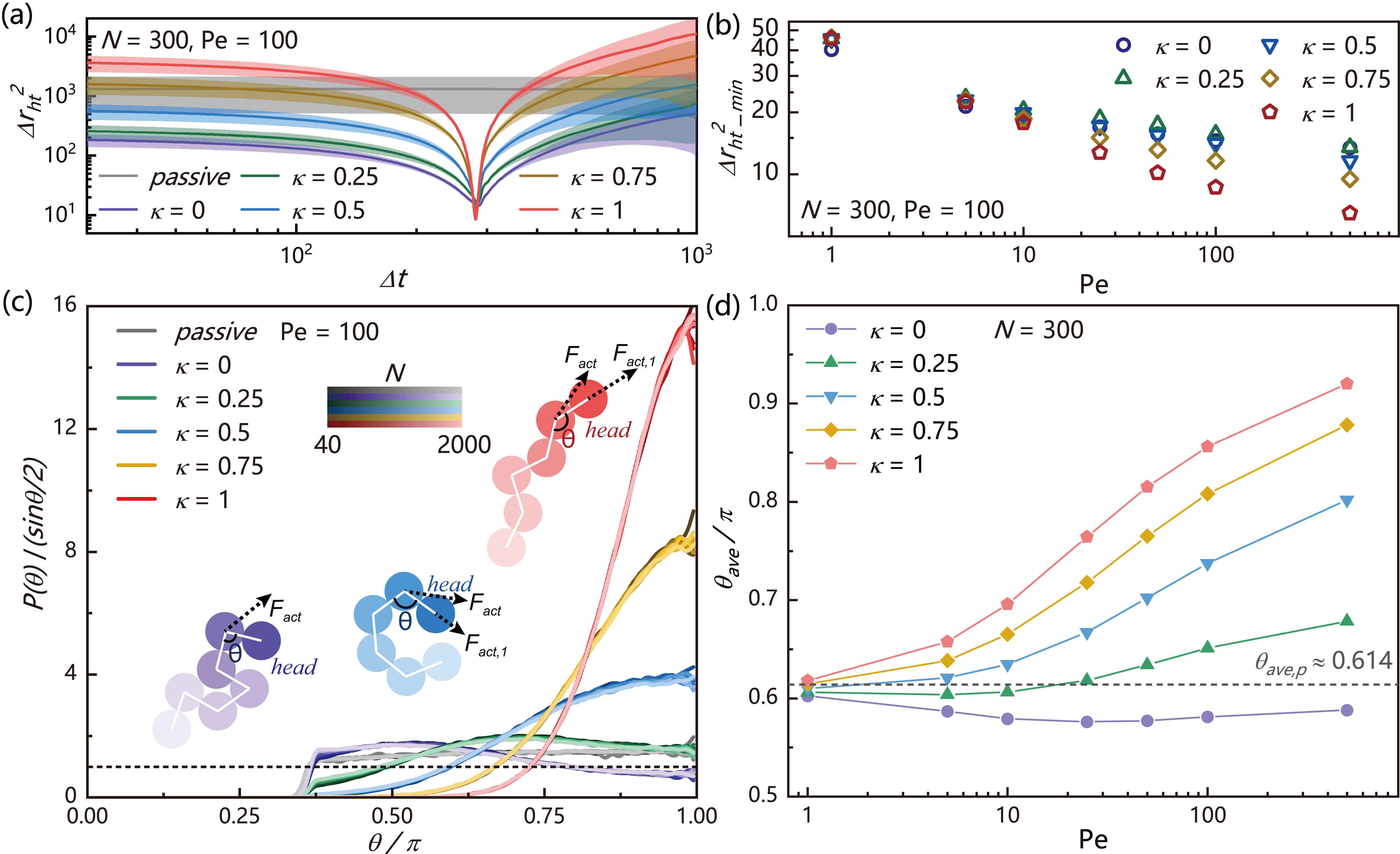
where the angle bracket represents the time and ensemble average. For perfect railway motion, decays to zero at time and bounces back, which is the time for the tail to reach the original position of the head. For pure diffusive dynamics, will be a flat line determined by polymer’s mean squared end-to-end distance . In FIG. 3(a), we plot for active polymers with different under fixed , where we find shows pronounce dips at the same independent of head activity. We further extract the minimal values of the correlation function of head-tail position, , to quantify the deviation from the perfect railway motion, and plot them as a function of in FIG. 3(b). We find that decreases with increasing and , which indicates that polymers with a higher head activity show relatively stronger railway motion.
For perfect railway motion chain, the direction of the head monomer is the only degree of freedom that determines the chain conformation. This direction can be represented by the bond angle between the first three monomers. In FIG. 3(c), we give the angle distribution for active polymers with different along with the passive polymer under varying polymer lengths. We find that for the active polymer without head activity, the peak of locates at a small value around , indicating the averaged bent configuration of polymer head. With increasing , the polymer head takes a more straight configuration. These results are independent of polymer length, indicating a similar way of the head activity affecting the polymer contour. Simple mechanical analysis in the inset of FIG. 3(c) shows that when the propulsion force of the head monomer is smaller than the second monomer, the pushing force from back will induce a “torque” that makes the bond bending inward. One the contrary, when the propulsion force of the head monomer is large enough, the head monomer will pull the three monomers straight. For railway motion chain, determines the bond angle distribution of the whole chain. Thus, an increasing average corresponds to an increasing persistence length and a decreasing involution degree of polymer. In FIG. 3(d), we summarized the average value of , which is qualitatively agreed with the behaviour of and in FIG. 2(d) and 2(e).
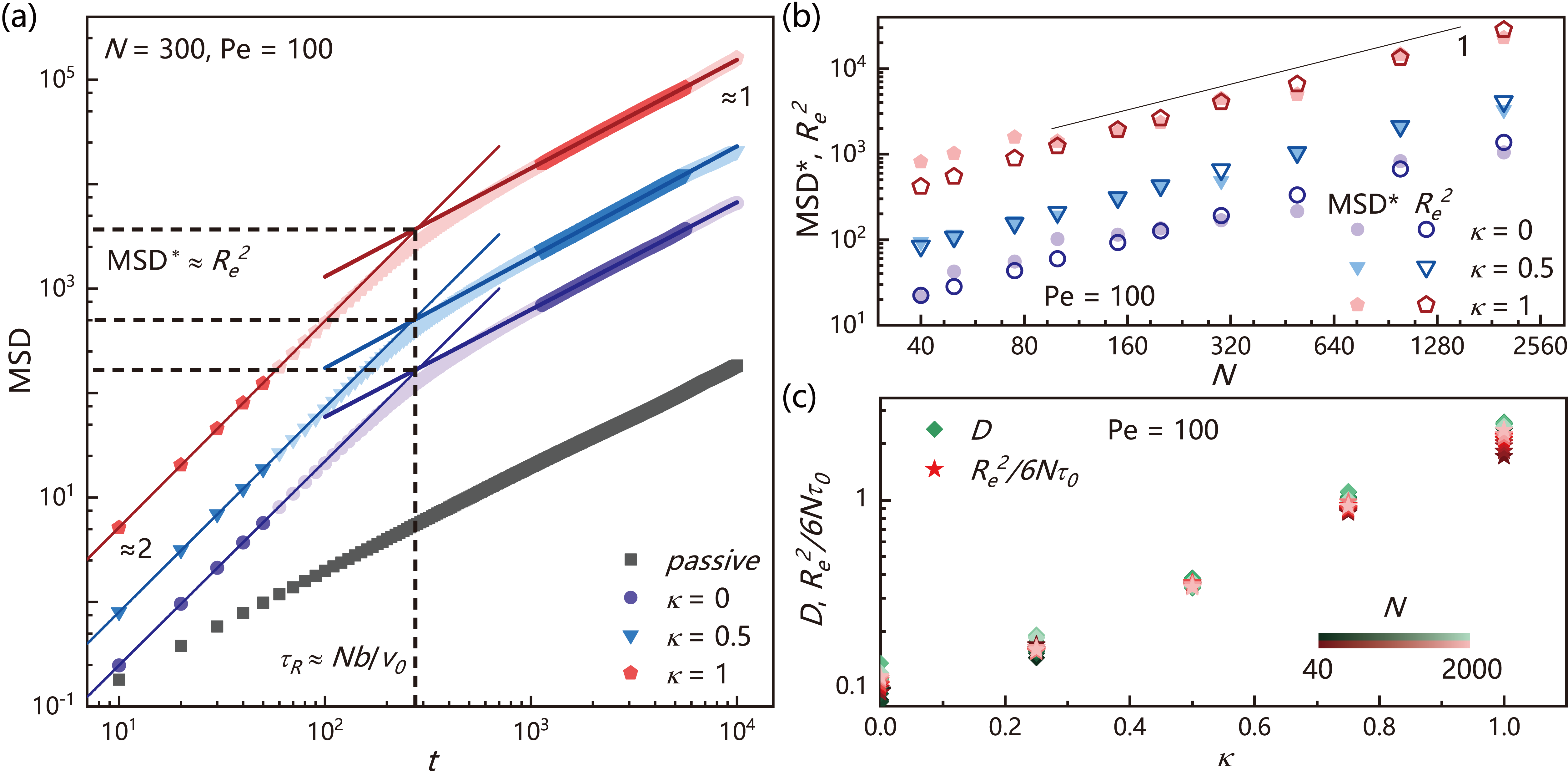
III.3 C. Dynamics of polar active polymers
To further explore the impact of head activity on the dynamics of polar active polymer, we calculate the end-to-end vector correlation function
| (10) |
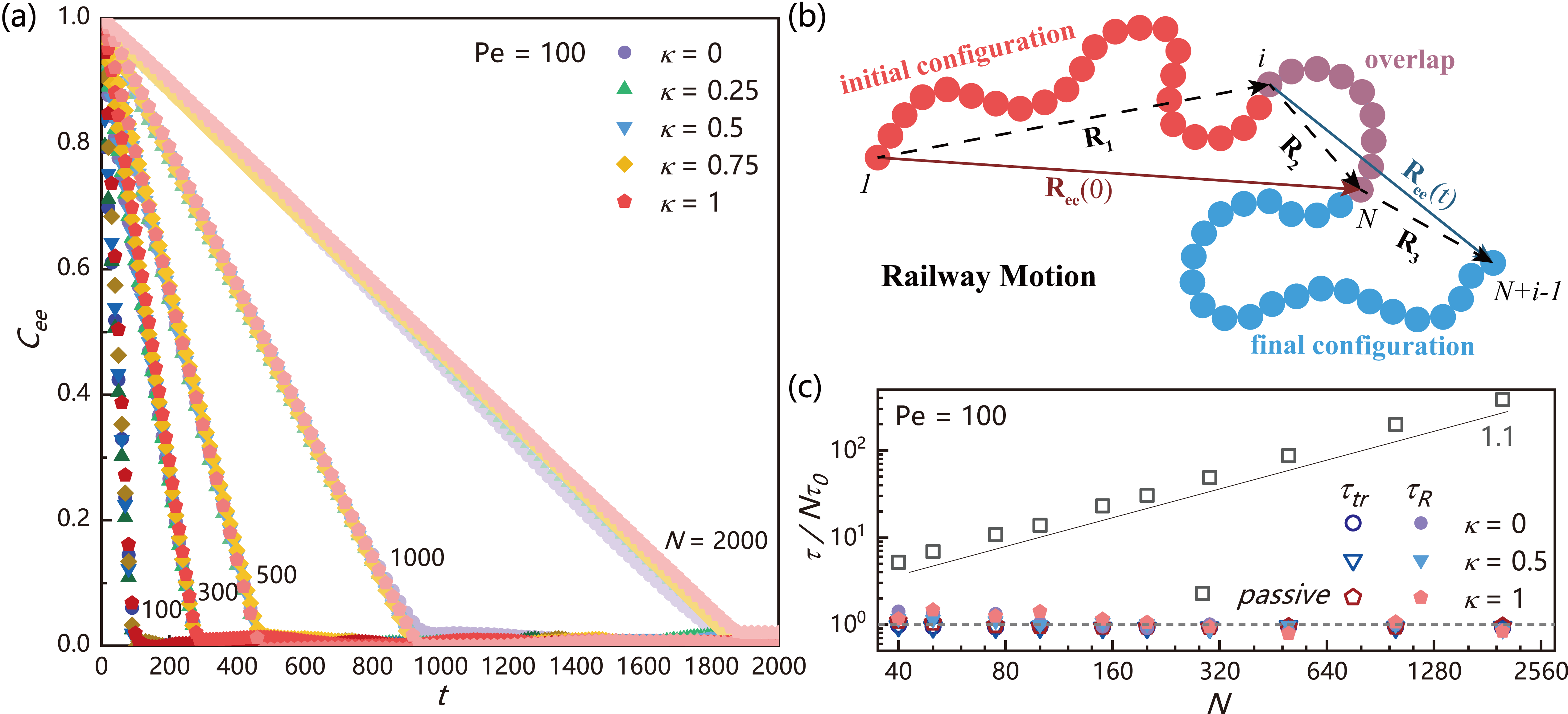
and compare for polymers with different head activity and polymer length in FIG. 4(a). A surprising finding is that all exhibit linear decay rather than exponential decay as for the passive polymer (Supplemental FIG. S4) Azuma and Takayama (1999); Descas et al. (2004). Moreover, we find is insensitive to the head activity and overall activity but only depends on the chain length . In FIG. 4(c), we plot the characteristic decay time of (for active polymers while for passive polymers ) as a function of , we find all data from active polymer falling around the line of . This behavior is also distinct from the passive polymer for which .
Such abnormal dynamics can be explained theoretically based on railway motion of the polymer chain. As shown in FIG. 4(b), assuming the initial and final configurations of the polymer on the same “railway” have an overlap part with end-to-end vector , thus we have and , where and are end-to-end vectors of the two non-overlapped parts. Since , , are statistically independent, we have for . Combining the nearly linear dependence of on shown in FIG. 5(b), one can get
| (11) |
which suggests . Note that this result is independent of the shape of “railway” controlled by head activity.
The railway motion also results in interesting polymer diffusion dynamics. Starting from the railway motion hypothesis in FIG. 4(b), one can get the expression of the center-of-mass of the polymer as
| (12) |
When , the displacement of the center-of-mass could be rewritten as:
| (13) |
Using an approximation of and considering continuous motion, we get
| (14) |
Thus, the mean square displacement (MSD) of polymer center-of-mass has the formation of
| (15) |
when . Combining the linear decay of (Eq. (11)), we get
| (16) |
Considering the long-time limit , the internal integral can be completely computed and has symmetric properties. Hence,
| (17) |
where . During the whole time is randomly fluctuated around the average end-to-end distance , hence the integral could be directly calculated as
| (18) |
So now we have a strict expression for on large time-scale. When the situation is opposite, , the internal integral of Eq. (16) cannot be completely computed. Considering the symmetry of and , we have
| (19) |
When , has little fluctuation and nearly maintains the initial value with averages of , hence MSD has an approximate value of
| (20) |
In summary, the expression of the mean squared displacement of center-of-mass of an active polymer has the formation of
| (21) |
Eq. (21) predicts a ballistic dynamics regime () and a diffusion dynamics regime () separated by the characteristic time and characteristic . In FIG. 5(a) and Supplemental FIG. S5, we plot the for active polymers with different , where the reference of the passive polymer is shown in gray color. We find that the simulation results agree well with our theoretical prediction. Especially match with excellently when varying the head activity and polymer length (see FIG. 5(b)). Furthermore, based on Stokes-Einstein relation and Eq. (21), we can obtain the diffusion coefficient
| (22) |
Since , the diffusion coefficient is independent of chain length, which is in contrast with the behavior of classical Rouse chain Tejedor and Ramírez (2019) and consistent with previous work Bianco et al. (2018). These predictions are also confirmed by the simulation results shown in FIG. 5(c) and Supplemental FIG. S6, at which is independent of and matches with very well under different . Moreover, from FIG. 5(c), one can see that the conformation and dynamics are coupled: the diffusion coefficient of an extended active polymer with large head activity can be an order of magnitude larger than the collapsed active polymer with small head activity. Finally, we emphasize another scaling relation hidden in Eq. (22), . Since is defined as with , we have , which provids a connection between dynamics and activity strength. This correlation has been a subject of continuous debate and contention in literatures Anand and Singh (2018); Bianco et al. (2018); Mokhtari and Zippelius (2019). The dynamic theory developed here is based on railway motion, hence it is valid for all polar active polymers exhibiting railway motion, regardless of the model (Supplemental FIG. S7). This provides us an efficient way to control the conformation and dynamics of active polymer, which may have application values in drug delivery and biomedical engineering Sasaki et al. (2014); Vuijk et al. (2021); Isele-Holder et al. (2016). Recently, Philipps et al. submitted an analytical study on polar active polymers, which reports dynamic equations similar to Eq. (22) Philipps et al. (2022).
IV iii Conclusion
In conclusion, we find a general non-equilibrium mechanism that head activity commands the overall active forces on the polar active polymer performing railway motion, which leads to unusual conformation and dynamics behaviors of the polymer chain. We demonstrate that the low head activity favors a bent head configuration, which causes a strong involution and the collapsing of polymer chain, while the high head activity helps the polymer straighten its head, resulting in an emerging “dynamic rigidity” and more extended chain conformation. The competition between the two non-trivial non-equilibrium effects leads to the re-entrant swelling of polar active polymers and non-monotonic variation of the Flory exponent . We also find many interesting dynamic features for polar active polymers, like a linear-decay of end-to-end vector correlation function , a polymer-size dependent crossover from ballistics to diffusion dynamics, as well as a length-independent diffusion coefficient controlled by the head-activity. All these features are explained well by our dynamic theory. Our findings are not only meaningful for understanding the conformational and dynamical behaviors of complicated active polymer aggregations, but also suggestive for designing efficient polymer-based drug delivery systems. In this work, the hydrodynamic interactions (HI) are not considered because the unique railway motion pattern of polar active polymers allows them to exhibit a qualitatively similar behavior regardless of the presence or absence of HI Jiang and Hou (2014a, b). Notwithstanding, the effects of HI on polar active polymers remain a highly significant research topic that requires further investigations.
V Acknowledgments
We thank Prof. Paolo Malgaretti in Max Planck Institute for helpful discussions. This work is supported by the National Natural Science Foundation of China (No.12104219).
References
- De Gennes (1979) P. G. De Gennes, Scaling Concepts in Polymer Physics (Cornell University Press, 1979).
- Doi and Edwards (1988) M. Doi and S. F. Edwards, The Theory of Polymer Dynamics (Oxford University Press, 1988).
- Rubinstein and Colby (2003) M. Rubinstein and R. H. Colby, Polymer Physics (Oxford University Press, 2003).
- Flory (1953) P. J. Flory, Principles of Polymer Chemistry (Cornell University Press, 1953).
- Harada et al. (1987) Y. Harada, A. Noguchi, A. Kishino, and T. Yanagida, Sliding Movement of Single Actin Filaments on One-Headed Myosin Filaments, Nature 326, 805 (1987).
- Nédélec et al. (1997) F. J. Nédélec, T. Surrey, A. C. Maggs, and S. Leibler, Self-Organization of Microtubules and Motors, Nature 389, 305 (1997).
- Jülicher et al. (2007) F. Jülicher, K. Kruse, J. Prost, and J. F. Joanny, Active Behavior of the Cytoskeleton, Phys. Rep. 449, 3 (2007).
- Stano et al. (2005) N. M. Stano, Y. J. Jeong, I. Donmez, P. Tummalapalli, M. K. Levin, and S. S. Patel, DNA Synthesis Provides the Driving Force to Accelerate DNA Unwinding by a Helicase, Nature 435, 370 (2005).
- Kim et al. (2002) D. E. Kim, M. Narayan, and S. S. Patel, T7 DNA Helicase: A Molecular Motor that Processively and Unidirectionally Translocates along Single-Stranded DNA, J. Mol. Biol. 321, 807 (2002).
- Liu (2016) J. L. Liu, The Cytoophidium and Its Kind: Filamentation and Compartmentation of Metabolic Enzymes, Annu. Rev. Cell Dev. Biol. 32, 349 (2016).
- Li et al. (2018) H. Li, F. Ye, J. Y. Ren, P. Y. Wang, L. L. Du, and J. L. Liu, Active Transport of Cytoophidia in Schizosaccharomyces Pombe, FASEB J. 32, 5891 (2018).
- Deblais et al. (2020a) A. Deblais, A. C. Maggs, D. Bonn, and S. Woutersen, Phase Separation by Entanglement of Active Polymerlike Worms, Phys. Rev. Lett. 124, 208006 (2020a).
- Deblais et al. (2020b) A. Deblais, S. Woutersen, and D. Bonn, Rheology of Entangled Active Polymer-Like T. Tubifex Worms, Phys. Rev. Lett. 124, 188002 (2020b).
- Heeremans et al. (2022) T. Heeremans, A. Deblais, D. Bonn, and S. Woutersen, Chromatographic Separation of Active Polymer–Like Worm Mixtures by Contour Length and Activity, Sci. Adv. 8, eabj7918 (2022).
- Surrey et al. (2001) T. Surrey, F. Nédélec, S. Leibler, and E. Karsenti, Physical Properties Determining Self-Organization of Motors and Microtubules, Science 292, 1167 (2001).
- Schaller et al. (2011a) V. Schaller, C. Weber, E. Frey, and A. R. Bausch, Polar Pattern Formation: Hydrodynamic Coupling of Driven Filaments, Soft Matter 7, 3213 (2011a).
- Vliegenthart et al. (2020) G. A. Vliegenthart, A. Ravichandran, M. Ripoll, T. Auth, and G. Gompper, Filamentous Active Matter: Band Formation, Bending, Buckling, and Defects, Sci. Adv. 6, eaaw9975 (2020).
- Moore et al. (2020) J. M. Moore, T. N. Thompson, M. A. Glaser, and M. D. Betterton, Collective Motion of Driven Semiflexible Filaments Tuned by Soft Repulsion and Stiffness, Soft Matter 16, 9436 (2020).
- Adkins et al. (2022) R. Adkins, I. Kolvin, Z. You, S. Witthaus, M. C. Marchetti, and Z. Dogic, Dynamics of Active Liquid Interfaces, Science 377, 768 (2022).
- Natali et al. (2020) L. Natali, L. Caprini, and F. Cecconi, How a Local Active Force Modifies the Structural Properties of Polymers, Soft Matter 16, 2594 (2020).
- Tanida et al. (2020) S. Tanida, K. Furuta, K. Nishikawa, T. Hiraiwa, H. Kojima, K. Oiwa, and M. Sano, Gliding Filament System Giving both Global Orientational Order and Clusters in Collective Motion, Phys. Rev. E 101, 032607 (2020).
- Cao et al. (2022) X.-Z. Cao, H. Merlitz, C.-X. Wu, and M. G. Forest, Screening Confinement of Entanglements : Role of a Self-Propelling End Inducing Ballistic Chain Reptation, Phys. Rev. E 106 (2022).
- Schaller et al. (2010) V. Schaller, C. Weber, C. Semmrich, E. Frey, and A. R. Bausch, Polar Patterns of Driven Filaments, Nature 467, 73 (2010).
- Sumino et al. (2012) Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté, and K. Oiwa, Large-Scale Vortex Lattice Emerging from Collectively Moving Microtubules, Nature 483, 448 (2012).
- Dreyfus et al. (2005) R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone, and J. Bibette, Microscopic Artificial Swimmers, Nature 437, 862 (2005).
- Hill et al. (2014) L. J. Hill, N. E. Richey, Y. Sung, P. T. Dirlam, J. J. Griebel, E. Lavoie-Higgins, I. B. Shim, N. Pinna, M. G. Willinger, W. Vogel, J. J. Benkoski, K. Char, and J. Pyun, Colloidal Polymers from Dipolar Assembly of Cobalt-Tipped CdSe@CdS Nanorods, ACS Nano 8, 3272 (2014).
- Biswas et al. (2017) B. Biswas, R. K. Manna, A. Laskar, P. B. Kumar, R. Adhikari, and G. Kumaraswamy, Linking Catalyst-Coated Isotropic Colloids into ”Active” Flexible Chains Enhances Their Diffusivity, ACS Nano 11, 10025 (2017).
- Nishiguchi et al. (2018) D. Nishiguchi, J. Iwasawa, H. R. Jiang, and M. Sano, Flagellar Dynamics of Chains of Active Janus Particles Fueled by an AC Electric Field, New J. Phys. 20, 015002 (2018).
- Massana-Cid et al. (2017) H. Massana-Cid, F. Martinez-Pedrero, E. Navarro-Argemí, and I. Pagonabarraga, Propulsion and Hydrodynamic Particle Transport of Magnetically Twisted Colloidal Ribbons, New J. Phys. 19, 103031 (2017).
- Zhang et al. (2009a) L. Zhang, J. J. Abbott, L. Dong, B. E. Kratochvil, D. Bell, and B. J. Nelson, Artificial Bacterial Flagella: Fabrication and Magnetic Control, Appl. Phys. Lett. 94, 064107 (2009a).
- Zhang et al. (2009b) L. Zhang, J. J. Abbott, L. Dong, K. E. Peyer, B. E. Kratochvil, H. Zhang, C. Bergeles, and B. J. Nelson, Characterizing the Swimming Properties of Artificial Bacterial Flagella, Nano Lett. 9, 3663 (2009b).
- Winkler et al. (2017) R. G. Winkler, J. Elgeti, and G. Gompper, Active Polymers — Emergent Conformational and Dynamical Properties: A Brief Review, J. Phys. Soc. Japan 86, 101014 (2017).
- Locatelli et al. (2021) E. Locatelli, V. Bianco, and P. Malgaretti, Activity-Induced Collapse and Arrest of Active Polymer Rings, Phys. Rev. Lett. 126, 097801 (2021).
- Mokhtari and Zippelius (2019) Z. Mokhtari and A. Zippelius, Dynamics of Active Filaments in Porous Media, Phys. Rev. Lett. 123, 028001 (2019).
- Prathyusha et al. (2018) K. R. Prathyusha, S. Henkes, and R. Sknepnek, Dynamically Generated Patterns in Dense Suspensions of Active Filaments, Phys. Rev. E 97, 022606 (2018).
- Isele-Holder et al. (2015) R. E. Isele-Holder, J. Elgeti, and G. Gompper, Self-Propelled Worm-Like Filaments: Spontaneous Spiral Formation, Structure, and Dynamics, Soft Matter 11, 7181 (2015).
- Shee et al. (2021) A. Shee, N. Gupta, A. Chaudhuri, and D. Chaudhuri, A Semiflexible Polymer in a Gliding Assay: Reentrant Transition, Role of Turnover and Activity, Soft Matter 17, 2120 (2021).
- Foglino et al. (2019) M. Foglino, E. Locatelli, C. A. Brackley, D. Michieletto, C. N. Likos, and D. Marenduzzo, Non-Equilibrium Effects of Molecular Motors on Polymers, Soft Matter 15, 5995 (2019).
- Shi and Ma (2010) X. Q. Shi and Y. Q. Ma, Understanding phase behavior of plant cell cortex microtubule organization, Proc. Natl. Acad. Sci. U. S. A. 107, 11709 (2010).
- Kaiser et al. (2015) A. Kaiser, S. Babel, B. Ten Hagen, C. Von Ferber, and H. Löwen, How does a Flexible Chain of Active Particles Swell?, J. Chem. Phys. 142, 124905 (2015).
- Eisenstecken et al. (2017) T. Eisenstecken, G. Gompper, and R. G. Winkler, Internal Dynamics of Semiflexible Polymers with Active Noise, J. Chem. Phys. 146, 154903 (2017).
- Anand and Singh (2020) S. K. Anand and S. P. Singh, Conformation and Dynamics of a Self-Avoiding Active Flexible Polymer, Phys. Rev. E 101, 030501 (2020).
- Bourdieu et al. (1995) L. Bourdieu, T. Duke, M. B. Elowitz, D. A. Winkelmann, S. Leibler, and A. Libchaber, Spiral Defects in Motility Assays: A Measure of Motor Protein Force, Phys. Rev. Lett. 75, 176 (1995).
- Camalet et al. (1999) S. Camalet, F. Jülicher, and J. Prost, Self-Organized Beating and Swimming of Internally Driven Filaments, Phys. Rev. Lett. 82, 1590 (1999).
- De Canio et al. (2017) G. De Canio, E. Lauga, and R. E. Goldstein, Spontaneous Oscillations of Elastic Filaments Induced by Molecular Motors, J. R. Soc. Interface 14, 20170491 (2017).
- Ziebert et al. (2015) F. Ziebert, H. Mohrbach, and I. M. Kulić, Why Microtubules Run in Circles: Mechanical Hysteresis of the Tubulin Lattice, Phys. Rev. Lett. 114, 148101 (2015).
- Zheng et al. (2023) E. Zheng, M. Brandenbourger, L. Robinet, P. Schall, E. Lerner, and C. Coulais, Self-Oscillation and Synchronization Transitions in Elastoactive Structures, Phys. Rev. Lett. 130, 178202 (2023).
- Wang et al. (2022) C. Wang, Y. Zhou, X. Yang, Y. Chen, Y. Shen, and M. Luo, Conformation and Dynamics of a Tethered Active Polymer Chain, Phys. Rev. E 106, 054501 (2022).
- Martin et al. (2019) S. E. Martin, M. E. Brunner, and J. M. Deutsch, Emergence of Metachronal Waves in Active Microtubule Arrays, Phys. Rev. Fluids 4, 103101 (2019).
- Chelakkot et al. (2014) R. Chelakkot, A. Gopinath, L. Mahadevan, and M. F. Hagan, Flagellar Dynamics of a Connected Chain of Active, Polar, Brownian Particles, J. R. Soc. Interface 11, 20130884 (2014).
- Chelakkot et al. (2021) R. Chelakkot, M. F. Hagan, and A. Gopinath, Synchronized Oscillations, Traveling Waves, and Jammed Clusters Induced by Steric Interactions in Active Filament Arrays, Soft Matter 17, 1091 (2021).
- Schaller et al. (2011b) V. Schaller, C. A. Weber, B. Hammerich, E. Frey, and A. R. Bausch, Frozen Steady States in Active Systems, Proc. Natl. Acad. Sci. U.S.A. 108, 19183 (2011b).
- Hu et al. (2022) H.-X. Hu, Y.-F. Shen, C. Wang, and M.-B. Luo, Dynamics of a Two-Dimensional Active Polymer Chain with a Rotation-Restricted Active Head, Soft Matter 18, 8820 (2022).
- Patil et al. (2023) V. P. Patil, H. Tuazon, E. Kaufman, T. Chakrabortty, D. Qin, J. Dunkel, and M. S. Bhamla, Ultrafast Reversible Self-Assembly of Living Tangled Matter, Science 380, 392 (2023).
- Bianco et al. (2018) V. Bianco, E. Locatelli, and P. Malgaretti, Globulelike Conformation and Enhanced Diffusion of Active Polymers, Phys. Rev. Lett. 121, 217802 (2018).
- Jain and Thakur (2022) N. Jain and S. Thakur, Collapse Dynamics of Chemically Active Flexible Polymer, Macromolecules 55, 2375 (2022).
- Isele-Holder et al. (2016) R. E. Isele-Holder, J. Jäger, G. Saggiorato, J. Elgeti, and G. Gompper, Dynamics of Self-Propelled Filaments Pushing a Load, Soft Matter 12, 8495 (2016).
- Stenhammar et al. (2014) J. Stenhammar, D. Marenduzzo, R. J. Allen, and M. E. Cates, Phase Behaviour of Active Brownian Particles: The Role of Dimensionality, Soft Matter 10, 1489 (2014).
- Azuma and Takayama (1999) R. Azuma and H. Takayama, Diffusion of Single Long Polymers in Fixed and Low Density Matrix of Obstacles Confined to Two Dimensions, J. Chem. Phys. 111, 8666 (1999).
- Descas et al. (2004) R. Descas, J. U. Sommer, and A. Blumen, Static and Dynamic Properties of Tethered Chains at Adsorbing Surfaces: A Monte Carlo Study, J. Chem. Phys. 120, 8831 (2004).
- Tejedor and Ramírez (2019) A. R. Tejedor and J. Ramírez, Reptation of Active Entangled Polymers, Macromolecules 52, 8788 (2019).
- Anand and Singh (2018) S. K. Anand and S. P. Singh, Structure and Dynamics of a Self-Propelled Semiflexible Filament, Phys. Rev. E 98, 042501 (2018).
- Sasaki et al. (2014) Y. Sasaki, Y. Takikawa, V. S. Jampani, H. Hoshikawa, T. Seto, C. Bahr, S. Herminghaus, Y. Hidaka, and H. Orihara, Colloidal Caterpillars for Cargo Transportation, Soft Matter 10, 8813 (2014).
- Vuijk et al. (2021) H. D. Vuijk, H. Merlitz, M. Lang, A. Sharma, and J.-U. Sommer, Chemotaxis of Cargo-Carrying Self-Propelled Particles, Phys. Rev. Lett. 126, 208102 (2021).
- Philipps et al. (2022) C. A. Philipps, G. Gompper, and R. G. Winkler, Tangentially Driven Active Polar Linear Polymers - An Analytical Study, J. Chem. Phys. 157, 194904 (2022).
- Jiang and Hou (2014a) H. Jiang and Z. Hou, Motion Transition of Active Filaments: Rotation Without Hydrodynamic Interactions, Soft Matter 10, 1012 (2014a).
- Jiang and Hou (2014b) H. Jiang and Z. Hou, Hydrodynamic Interaction Induced Spontaneous Rotation of Coupled Active Filaments, Soft Matter 10, 9248 (2014b).