Next-to-leading-order relativistic and QCD corrections to prompt $\bm{J/\psi}$ pair photoproduction at future $\bm{e^{+}e^{-}}$ colliders

The production of heavy quarkonia, including the $J/\psi$ meson as the most prominent specimen, provides a perfect laboratory to explore the interplay between perturbative and nonperturbative phenomena in quantum chromodynamics (QCD), since it accommodates the creation of a heavy quark pair $Q\bar{Q}$ at high energy as well as its transition into a heavy meson at low energy. The framework of nonrelativistic-QCD (NRQCD) factorization Bodwin:1994jh has been very successful in explaining the heavy-quarkonium production mechanism. However, the $J/\psi$ polarization puzzle Butenschoen:2012px and other problems in the validation of the predicted universality of the NRQCD long-distance matrix elements (LDMEs) Butenschoen:2014dra ; Butenschoen:2022wld still challenge NRQCD factorization. Shortly after the birth of NRQCD factorization, prompt $J/\psi$ pair hadroproduction was proposed as a showcase for the color-octet (CO) mechanism, a key feature of NRQCD factorization, because the hadronization occurs there twice Barger:1995vx . Later on, the color-singlet (CS) channel was found to contribute predominately in the region of small and moderate $J/\psi$ transverse momentum, $p_{T}^{J/\psi}$ Qiao:2002rh ; Li:2009ug ; Ko:2010xy ; He:2015qya . Meanwhile, prompt $J/\psi$ pair hadroproduction is also viewed as a good probe of the double parton scattering (DPS) mechanism in hadron collisions and as a tool to extract its key parameter $\sigma_{\mathrm{eff}}$ Kom:2011bd . However, fit results of $\sigma_{\mathrm{eff}}$ from experimental D0:2014vql ; LHCb:2016wuo ; ATLAS:2016ydt ; LHCb:2023ybt and theoretical Lansberg:2014swa ; Prokhorov:2020owf analyses exhibit an incoherent picture.

Since the discovery of the Higgs boson at the CERN LHC ATLAS:2012yve ; CMS:2012qbp , to build next-generation $e^{+}e^{-}$ colliders reaching center-of-mass energies of hundreds of GeV or even a few TeV for high-precision studies of the electroweak sector of the standard model has been on the agenda of the high-energy physics community. Possible realizations include the CERN Future Circular Lepton Collider (FCC-ee) FCC:2018evy , the Circular Electron Positron Collider (CEPC) CEPCStudyGroup:2018rmc in China, and the CERN Compact Linear Collider (CLIC) CLICdp:2018cto . As we will argue below, such high-luminosity $e^{+}e^{-}$ colliders will also offer great opportunities to deepen our understanding of the double prompt $J/\psi$ production mechanism. A decisive advantage of $e^{+}e^{-}$ colliders versus hadron colliders resides in the absence of DPS. Historically, inclusive single $J/\psi$ production in two-photon collisions at the CERN Large Electron Positron Collider (LEP) is among the earliest evidences of the CO mechanism Klasen:2001cu ; Butenschoen:2011yh .

In $e^{+}e^{-}$ collisions, there are generally two distinct production modes, $e^{+}e^{-}$ annihilation and two-photon scattering, where the photons originate from both electromagnetic bremsstrahlung and synchrotron radiation off the colliding bunches known as beamstrahlung. The photons can either directly participate in the hard collision as pointlike particles, or as resolved photons via their quark and gluon contents as described by photonic parton density functions (PDFs) DeWitt:1978wn . This results in three production channels: direct, single resolved, and double resolved. $J/\psi$ pair production by $e^{+}e^{-}$ annihilation was investigated by several groups Bodwin:2002fk ; Bodwin:2002kk ; Hagiwara:2003cw ; Bodwin:2006yd ; Braguta:2007ge ; Gong:2008ce ; Fan:2012dy , even through next-to-next-to-leading order in the strong-coupling constant $\alpha_{s}$ Sang:2023liy ; Huang:2023pmn . $J/\psi$ pair production by two-photon scattering was first considered by Qiao in 2002 as a contribution to inclusive $J/\psi$ production Qiao:2001wv . Recently, exclusive $J/\psi$ pair production by two-photon scattering at $e^{+}e^{-}$ colliders was studied through next-to-leading order (NLO) in $\alpha_{s}$, with the result that QCD corrections, of relative order $\mathcal{O}(\alpha_{s})$, can decrease theoretical predictions by almost $80\%$ Yang:2020xkl .

In the charmonium rest frame, the charm quark relative velocity $v$ is not small, with $v^{2}\sim\alpha_{s}(2m_{c})$, which explains why relativistic corrections, being of relative order $\mathcal{O}(v^{2})$, may be comparable to QCD corrections. In fact, in $e^{+}e^{-}$ annihilation at center-of-mass energy $\sqrt{S}=10.6$ GeV, $\mathcal{O}(v^{2})$ corrections largely enhance the LO predictions for exclusive double charmonium He:2007te and inclusive $J/\psi+X_{\mathrm{non-c\bar{c}}}$ He:2009uf ; Jia:2009np production, and they are also considerable in $J/\psi$ photo- and hadroproduction, for both yield Xu:2012am ; He:2014sga and polarization He:2015gla . As for prompt $J/\psi$ pair hadroproduction, the $\mathcal{O}(v^{2})$ corrections to the CS channel were found to reduce the cross section appreciably in the large-$p_{T}$ region Li:2013csa and substantially near threshold He:2024ugx . This suggests that $\mathcal{O}(v^{2})$ corrections may also be important in the case of $J/\psi$ pair production in two-photon scattering, the more so as $\mathcal{O}(\alpha_{s})$ corrections were found to dramatically reduce the cross section Yang:2020xkl , as already mentioned above. This strongly motivates our analysis below. Since an independent cross check of the results of Ref. Yang:2020xkl is still lacking, we also recalculate the $\mathcal{O}(\alpha_{s})$ corrections here.

The rest of this paper is organized as follows. In Sec. II, we describe techniques to calculate the $\mathcal{O}(v^{2})$ and $\mathcal{O}(\alpha_{s})$ corrections to the short-distance coefficients (SDCs) within the NRQCD factorization framework. In Sec. III, we present numerical predictions appropriate for FCC-ee, CEPC, and CLIC experimental conditions as anticipated today. In Sec. IV, we summarize our conclusion.

According to the factorization theorem of the QCD parton model, the differential cross section of inclusive prompt $J/\psi$ pair production by two-photon scattering may be expressed as (see, e.g., Ref. Klasen:2001cu )

	$\displaystyle\mathrm{d}\sigma(e^{+}e^{-}\to e^{+}e^{-}+2J/\psi+X)=\sum_{i,j,H_{1},H_{2}}\int\mathrm{d}x_{1}\mathrm{d}x_{2}f_{\gamma}(x_{1})f_{\gamma}(x_{2})\int dx_{i}dx_{j}f_{i/\gamma}(x_{i})f_{j/\gamma}(x_{j})$
	$\displaystyle{}\times\mathrm{d}\hat{\sigma}(i+j\to H_{1}+H_{2})\mathrm{Br}(H_{1}\rightarrow J/\psi+X)\mathrm{Br}(H_{2}\rightarrow J/\psi+X)\,,$		(1)

where $f_{\gamma}(x)$ is the scaled-energy distribution of the photons from both bremsstrahlung and beamstrahlung off the incoming leptons, $f_{i/\gamma}(x)$ is the PDF in longitudinal-momentum fraction of parton $i$ in the resolved photon, being $f_{\gamma/\gamma}(x)=\delta(1-x)$ for the direct photon, $\mathrm{d}\hat{\sigma}(i+j\to H_{1}+H_{2})$ is the partonic differential cross section for associated production of charmonium states $H_{1},H_{2}=J/\psi,\chi_{cJ},\psi(2S)$, and $\mathrm{Br}(H\rightarrow J/\psi+X)$ is the branching fraction of $H$ decay into $J/\psi$, being 1 for $H=J/\psi$ implying direct production. In Eq. (1), $X$ collectively denotes the undetected particles in the respective final states, reflecting the inclusiveness of the experimental observation mode.

At parton level, the Feynman diagrams of $2J/\psi$ production are the same as those of $J/\psi+c\bar{c}$ production, which was studied for two-photon scattering in Ref. Li:2009zzu , where the single-resolved and double-resolved contributions were found to be greatly suppressed. We recover this finding at LO for direct $2J/\psi$ production in two-photon scattering under FCC-ee experimental conditions, where we find the single-resolved and double-resolved contributions to be more than 3 orders of magnitude smaller than the direct contribution. In the following, we thus concentrate on direct photoproduction. In the latter case, CO contributions are known to be important only at large values of $p_{T}^{J/\psi}$ He:2015qya , where the cross sections are likely to be too small to be measurable in the first few years of running at the above-mentioned future $e^{+}e^{-}$ colliders. In the following, we thus focus on CS contributions, which arise from the partonic subprocesses

	$\displaystyle\gamma+\gamma$	$\displaystyle\to$	$\displaystyle(c\bar{c})_{1}({}^{3}S_{1}^{[1]})+(c\bar{c})_{2}({}^{3}S_{1}^{[1]})\,,$		(2)
	$\displaystyle\gamma+\gamma$	$\displaystyle\to$	$\displaystyle(c\bar{c})_{1}({}^{3}P_{J_{1}}^{[1]})+(c\bar{c})_{2}({}^{3}P_{J_{2}}^{[1]})\,,$		(3)

yielding $2J/\psi$, $J/\psi+\psi(2S)$, $2\psi(2S)$, and $\chi_{c_{J1}}+\chi_{c_{J2}}$ final states. We verified that, under FCC-ee experimental conditions, the production rates of the $\chi_{c_{J1}}+\chi_{c_{J2}}$ channels are about one order of magnitude smaller than those of the other channels, and they are reduced by two additional factors of branching fraction to become negligibly small feed-down contributions. We thus concentrate on partonic subprocess (2) and compute relativistic corrections of $\mathcal{O}(v^{2})$ and QCD corrections of $\mathcal{O}(\alpha_{s})$ to its cross section. By color conservation, the latter are purely virtual.

Through $\mathcal{O}(v^{2})$ in NRQCD, the relevant partonic cross section appearing in Eq. (1) factorizes as

	$\displaystyle\mathrm{d}\hat{\sigma}(\gamma+\gamma\to H_{1}+H_{2})=\sum_{m,n,H_{1},H_{2}}\left(\frac{dF(m,n)}{m_{c}^{d_{\mathcal{O}(m)}-4}m_{c}^{d_{\mathcal{O}(n)}-4}}\langle\mathcal{O}^{H_{1}}(m)\rangle\langle\mathcal{O}^{H_{2}}(n)\rangle\right.$				(4)
			$\displaystyle{}+\left.\frac{dG_{1}(m,n)}{m_{c}^{d_{\mathcal{P}(m)}-4}m_{c}^{d_{\mathcal{O}(n)}-4}}\langle\mathcal{P}^{H_{1}}(m)\rangle\langle\mathcal{O}^{H_{2}}(n)\rangle+\frac{dG_{2}(m,n)}{m_{c}^{d_{\mathcal{O}(m)}-4}m_{c}^{d_{\mathcal{P}(n)}-4}}\langle\mathcal{O}^{H_{1}}(m)\rangle\langle\mathcal{P}^{H_{2}}(n)\rangle\right)\,,$

where $m,n={}^{2S+1}L_{J}^{[a]}$ are quantum numbers in spectroscopic notation, with total spin $S$, orbital angular momentum $L$, total angular momentum $J$, and color configuration $a=1,8$ for CS and CO; $\mathcal{O}^{H}(n)$ and $\mathcal{P}^{H}(n)$ are four-fermion operators of mass dimensions $d_{\mathcal{O}}$ and $d_{\mathcal{P}}$ describing the nonperturbative transition $n\to H$ at LO and $\mathcal{O}(v^{2})$; $\langle\mathcal{O}^{H}(n)\rangle$ and $\langle\mathcal{P}^{H}(n)\rangle$ are the respective LDMEs; and $F(m,n)$ and $G_{i}(m,n)$ are the appropriate SDCs. Definitions of the relevant four-fermion operators, $\mathcal{O}^{H}({}^{3}S_{1}^{[1]})$ and $\mathcal{P}^{H}({}^{3}S_{1}^{[1]})$, may be found, e.g., in Eq. (3) of Ref. He:2024ugx . The calculation of $F({}^{3}S_{1}^{[1]},{}^{3}S_{1}^{[1]})$ and $G_{i}({}^{3}S_{1}^{[1]},{}^{3}S_{1}^{[1]})$ proceeds in a fashion similar to the hadron collider case in Ref. He:2024ugx and references cited therein, and we merely list our final results. Notice that, according to the $p_{T}$ power counting rules of Ref. He:2015qya , we have $\mathrm{d}\hat{\sigma}/\mathrm{d}p_{T}^{2}\propto 1/p_{T}^{8}$ for partonic subprocess (2).

Starting from the Mandelstam variables $s=(k_{1}+k_{2})^{2}$, $t=(k_{1}-P_{1})^{2}$, and $u=(k_{1}-P_{2})^{2}$ of process $\gamma(k_{1})+\gamma(k_{2})\to H_{1}(P_{1})+H_{2}(P_{2})$, we denote the counterparts of $t$ and $u$ in the nonrelativistic limit as $t_{0}$ and $u_{0}$, and define $\hat{t}_{0}=t_{0}+(s-8m_{c}^{2})/2$ and $\hat{u}_{0}=u_{0}+(s-8m_{c}^{2})/2$. The two-body phase space element in the nonrelativistic limit may thus be written as

$$d\Phi_{20}=\frac{\mathrm{d}\hat{t}_{0}\mathrm{d}\hat{u}_{0}}{8\pi s}\delta\left(\hat{t}_{0}+\hat{u}_{0}\right)\,,$$

(5)

and receives the $\mathcal{O}(v^{2})$ correction factor $K=-4/(s-16m_{c}^{2})$. Our final results then read

	$\displaystyle\frac{F({{}^{3}S_{1}^{[1]},^{3}S_{1}^{[1]}})}{m_{c}^{4}}$	$\displaystyle=$	$\displaystyle\frac{1}{2s}\int d\Phi_{20}\left(|M_{0}|^{2}+|M_{1}|^{2}\right)\,,$
	$\displaystyle\frac{G_{1}({{}^{3}S_{1}^{[1]},^{3}S_{1}^{[1]}})}{m_{c}^{6}}$	$\displaystyle=$	$\displaystyle\frac{G_{2}({{}^{3}S_{1}^{[1]},^{3}S_{1}^{[1]}})}{m_{c}^{6}}=\frac{1}{2s}\int d\Phi_{20}\left(K|M_{0}|^{2}+|N|^{2}\right)\,,$		(6)

where $|M_{0}|^{2}$ is the absolute square of the tree-level amplitude, $|M_{1}|^{2}$ stands for its $\mathcal{O}(\alpha_{s})$ correction, and $|N|^{2}$ for its $\mathcal{O}(v^{2})$ correction. The expressions for $|M_{0}|^{2}$, $|M_{1}|^{2}$, and $|N|^{2}$ assume relatively compact forms when they are written in terms of $s$ and $\hat{t}_{0}$.

Below, we list $|M_{0}|^{2}$ for reference and $|N|^{2}$ as a new result:

	$\displaystyle|M_{0}|^{2}$	$\displaystyle=$	$\displaystyle\frac{262144\pi^{4}\alpha^{2}e_{c}^{4}\alpha_{s}^{2}}{729m_{c}^{2}\left(s^{3}-4s\hat{t}_{0}^{2}\right)^{4}}\left[s^{10}+48s^{9}m_{c}^{2}-16s^{8}\left(\hat{t}_{0}^{2}-188m_{c}^{4}\right)-512s^{7}m_{c}^{2}\left(4m_{c}^{4}+\hat{t}_{0}^{2}\right)\right.$		(7)
			$\displaystyle{}+96s^{6}\left(128\hat{t}_{0}^{2}m_{c}^{4}+1024m_{c}^{8}+\hat{t}_{0}^{4}\right)+1536s^{5}\hat{t}_{0}^{2}m_{c}^{2}\left(\hat{t}_{0}^{2}-16m_{c}^{4}\right)$
			$\displaystyle{}-256s^{4}\left(-3072\hat{t}_{0}^{2}m_{c}^{8}-88\hat{t}_{0}^{4}m_{c}^{4}+\hat{t}_{0}^{6}\right)+32768s^{3}\hat{t}_{0}^{4}m_{c}^{6}$
			$\displaystyle{}+\left.256s^{2}\left(128\hat{t}_{0}^{6}m_{c}^{4}+6144\hat{t}_{0}^{4}m_{c}^{8}+\hat{t}_{0}^{8}\right)-4096s\hat{t}_{0}^{6}m_{c}^{2}\left(\hat{t}_{0}^{2}-96m_{c}^{4}\right)+49152\hat{t}_{0}^{8}m_{c}^{4}\right]\,,\quad$
	$\displaystyle|N|^{2}$	$\displaystyle=$	$\displaystyle-\frac{131072\pi^{4}\alpha^{2}e_{c}^{4}\alpha_{s}^{2}}{2187m_{c}^{4}\left(s^{3}-4s\hat{t}_{0}^{2}\right)^{5}\left(s-16m_{c}^{2}\right)}\left[3s^{14}-144s^{13}m_{c}^{2}+s^{12}\left(832m_{c}^{4}-76\hat{t}_{0}^{2}\right)\right.$		(8)
			$\displaystyle{}+64s^{11}\left(55\hat{t}_{0}^{2}m_{c}^{2}-2368m_{c}^{6}\right)+32s^{10}\left(-1192\hat{t}_{0}^{2}m_{c}^{4}+82432m_{c}^{8}+25\hat{t}_{0}^{4}\right)$
			$\displaystyle{}-1024s^{9}m_{c}^{2}\left(-2424\hat{t}_{0}^{2}m_{c}^{4}+14336m_{c}^{8}+27\hat{t}_{0}^{4}\right)$
			$\displaystyle{}-128s^{8}\left(-29184\hat{t}_{0}^{2}m_{c}^{8}-1488\hat{t}_{0}^{4}m_{c}^{4}-1769472m_{c}^{12}+35\hat{t}_{0}^{6}\right)$
			$\displaystyle{}+2048s^{7}\hat{t}_{0}^{2}m_{c}^{2}\left(2656\hat{t}_{0}^{2}m_{c}^{4}+50176m_{c}^{8}+47\hat{t}_{0}^{4}\right)$
			$\displaystyle{}+256s^{6}\left(4325376\hat{t}_{0}^{2}m_{c}^{12}+98304\hat{t}_{0}^{4}m_{c}^{8}-1184\hat{t}_{0}^{6}m_{c}^{4}+55\hat{t}_{0}^{8}\right)$
			$\displaystyle{}-4096s^{5}\hat{t}_{0}^{4}m_{c}^{2}\left(-4352\hat{t}_{0}^{2}m_{c}^{4}-100352m_{c}^{8}+49\hat{t}_{0}^{4}\right)$
			$\displaystyle{}-1024s^{4}\hat{t}_{0}^{4}\left(-204800\hat{t}_{0}^{2}m_{c}^{8}-272\hat{t}_{0}^{4}m_{c}^{4}-2752512m_{c}^{12}+23\hat{t}_{0}^{6}\right)$
			$\displaystyle{}+16384s^{3}\hat{t}_{0}^{6}m_{c}^{2}\left(-384\hat{t}_{0}^{2}m_{c}^{4}-75776m_{c}^{8}+27\hat{t}_{0}^{4}\right)$
			$\displaystyle{}+16384s^{2}\hat{t}_{0}^{6}\left(-4352\hat{t}_{0}^{2}m_{c}^{8}-68\hat{t}_{0}^{4}m_{c}^{4}+491520m_{c}^{12}+\hat{t}_{0}^{6}\right)$
			$\displaystyle{}-\left.131072s\hat{t}_{0}^{8}m_{c}^{2}\left(112\hat{t}_{0}^{2}m_{c}^{4}-15360m_{c}^{8}+5\hat{t}_{0}^{4}\right)+6291456\hat{t}_{0}^{10}m_{c}^{4}\left(40m_{c}^{4}+\hat{t}_{0}^{2}\right)\right]\,,$

where $\alpha$ is Sommerfeld’s fine-structure constant and $e_{c}=2/3$ is the fractional electric charge of the charm quark.

In the computation of $|M_{1}|^{2}$, we encounter both ultraviolet (UV) and infrared (IR) divergences, which are both regularized using dimensional regularization with $D=4-2\epsilon$ space-time dimensions. The UV divergences are removed by renormalizing the parameters and external fields of the tree-level amplitude $M_{0}$. As is usually done in loop computations of heavy-quarkonium production, we adopt the on-mass-shell (OM) scheme for the renormalization of the charm quark wave function ($Z_{2}$) and mass ($Z_{m}$), and the gluon wave function ($Z_{3}$), and the modified minimal-subtraction ($\overline{\mathrm{MS}}$) scheme for the renormalization of the strong-coupling constant ($Z_{g}$). For the reader’s convenience, we list the respective one-loop expressions here:

	$\displaystyle\delta Z_{2}^{\mathrm{OS}}$	$\displaystyle=$	$\displaystyle-C_{F}\frac{\alpha_{s}}{4\pi}N_{\epsilon}\left(\frac{1}{\epsilon_{\mathrm{UV}}}+\frac{2}{\epsilon_{\mathrm{IR}}}+4\right)+\mathcal{O}(\alpha_{s}^{2})\,,$
	$\displaystyle\delta Z_{m}^{\mathrm{OS}}$	$\displaystyle=$	$\displaystyle-3C_{F}\frac{\alpha_{s}}{4\pi}N_{\epsilon}\left(\frac{1}{\epsilon_{\mathrm{UV}}}+\frac{4}{3}\right)+\mathcal{O}(\alpha_{s}^{2})\,,$
	$\displaystyle\delta Z_{3}^{\mathrm{OS}}$	$\displaystyle=$	$\displaystyle\frac{\alpha_{s}}{4\pi}N_{\epsilon}\left[(\beta_{0}^{\prime}-2C_{A})\left(\frac{1}{\epsilon_{\mathrm{UV}}}-\frac{1}{\epsilon_{\mathrm{IR}}}\right)-\frac{4}{3}T_{F}(n_{f}-n_{l})\frac{1}{\epsilon_{\mathrm{UV}}}\right]+\mathcal{O}(\alpha_{s}^{2})\,,$
	$\displaystyle\delta Z_{g}^{\overline{\mathrm{MS}}}$	$\displaystyle=$	$\displaystyle-\frac{\beta_{0}}{2}\,\frac{\alpha_{s}}{4\pi}N_{\epsilon}\left(\frac{1}{\epsilon_{\mathrm{UV}}}+\ln\frac{m_{c}^{2}}{\mu_{r}^{2}}\right)+\mathcal{O}(\alpha_{s}^{2})\,,$		(9)

where $N_{\epsilon}=(4\pi\mu_{r}^{2}/m_{c}^{2})^{\epsilon}/\Gamma(1-\epsilon)$, $\mu_{r}$ is the renormalization scale, $\beta_{0}=11C_{A}/3-4T_{F}n_{f}/3$ is the one-loop coefficient of the QCD beta function, $C_{A}=3$, $T_{F}=1/2$, $n_{f}=4$ is the number of active quark flavors, and $\beta_{0}^{\prime}$ emerges from $\beta_{0}$ by replacing $n_{f}$ with the number of light quark flavors $n_{l}=3$. Thanks to the absence of real gluon radiation, the IR singularities in $|M_{1}|^{2}$ cancel among themselves in combination with the IR divergences from wave function renormalization in Eq. (9). Our result for $|M_{1}|^{2}$ is too lengthy to be listed here. We find numerical agreement with the results for double charmonium photoproduction in Ref. Yang:2020xkl upon adopting the inputs specified there. Looking at the one-loop diagrams in Fig. 2 of Ref. Yang:2020xkl , we note that all of them scale with $e_{c}^{2}$, except for the box diagrams in Fig. 2(l), which scale with $e_{q}^{2}$. Keeping this in mind, our analytic results readily carry over to double bottomonium production.¹¹1We can also reproduce the numerical results for double bottomonium production in Ref. Yang:2020xkl , if we attach the superfluous factor of $e_{b}^{2}/e_{c}^{2}=1/4$ to the contribution due to the box diagrams mentioned above.

We use the program packages FeynArts Kublbeck:1990xc and QGRAF Nogueira:1991ex to generate Feynman diagrams and amplitudes, and FeynCalc Mertig:1990an and FORM Vermaseren:2000nd to handle the Dirac and SU(3)_c algebras. We reduce the one-loop scalar integrals to a small set of master integrals using the Laporta algorithm Laporta:2000dsw of integration by parts Chetyrkin:1981qh as implemented in the program packages Reduze 2 vonManteuffel:2012np and FIRE6 Smirnov:2019qkx . We evaluate the master integrals analytically using the program packages Package-X 2.0 Patel:2016fam and QCDloop Ellis:2007qk .

In the numerical analysis, we evaluate $\alpha_{s}^{(n_{f})}(\mu_{r})$ with $n_{f}=4$ and $\Lambda_{\mathrm{QCD}}^{(4)}=215~{}\mathrm{MeV}$ (326 MeV) at tree level (one loop) Pumplin:2002vw . We set $\mu_{r}=\xi\sqrt{s}$, take $\xi=1$ as default, and vary $\xi$ between 1/2 and 2 to estimate the theoretical uncertainties from unknown higher orders in $\alpha_{s}$. For definiteness, we choose $m_{c}=1.5~{}\mathrm{GeV}$ as is frequently done in similar analyses, so as to facilitate comparisons with the literature. The values $m_{J/\psi}=3.097~{}\mathrm{GeV}$, $m_{\psi(2S)}=3.686~{}\mathrm{GeV}$, $\mathrm{Br}(\psi(2S)\rightarrow J/\psi+X)=61.4\%$ for masses and branching fraction are taken from the latest Review of Particle Physics ParticleDataGroup:2022pth . As for the $J/\psi$ and $\psi(2S)$ CS LDMEs, we use the ones evaluated from the wave functions at the origin for the Buchmüller-Tye potential Eichten:1995ch ,

	$\displaystyle\langle\mathcal{O}^{J/\psi}({}^{3}S_{1}^{[1]})\rangle$	$\displaystyle=$	$\displaystyle 1.16~{}\mathrm{GeV}^{3}\,,$
	$\displaystyle\langle\mathcal{O}^{\psi(2S)}({}^{3}S_{1}^{[1]})\rangle$	$\displaystyle=$	$\displaystyle 0.758~{}\mathrm{GeV}^{3}\,,$		(10)

and estimate the $\mathcal{O}(v^{2})$ ones by the ratio obtained for the $J/\psi$ case in Ref. Bodwin:2006dn ,

$$\frac{\langle\mathcal{P}^{J/\psi}({}^{3}S_{1}^{[1]})\rangle}{\langle\mathcal{O}^{J/\psi}({}^{3}S_{1}^{[1]}\rangle}=0.5~{}\mathrm{GeV}^{2}\approx\frac{\langle\mathcal{P}^{\psi(2S)}({}^{3}S_{1}^{[1]})\rangle}{\langle\mathcal{O}^{\psi(2S)}({}^{3}S_{1}^{[1]})\rangle}\,.$$

(11)

In the evaluation of feed-down contributions to differential cross sections, we approximate the momentum of the $J/\psi$ meson from $\psi(2S)$ decay as

$$p_{J/\psi}=\frac{m_{J/\psi}}{m_{\psi(2S)}}p_{\psi(2S)}\,.$$

(12)

We include both bremsstrahlung and beamstrahlung by superimposing their spectra. The bremsstrahlung distribution is described in the Weizsacker-Williams approximation (WWA) as Frixione:1993yw

$$f^{\mathrm{WWA}}_{\gamma}(x)=\frac{\alpha}{2\pi}\left[\frac{1+(1-x)^{2}}{x}\ln\frac{Q_{\mathrm{max}}^{2}}{Q_{\mathrm{min}}^{2}}+2m_{e}^{2}x\left(\frac{1}{Q_{\mathrm{max}}^{2}}-\frac{1}{Q_{\mathrm{min}}^{2}}\right)\right]\,,$$

(13)

with photon virtuality $Q^{2}$ bounded by

	$\displaystyle Q_{\mathrm{min}}^{2}$	$\displaystyle=$	$\displaystyle\frac{m_{e}^{2}x^{2}}{1-x}\,,$
	$\displaystyle Q_{\mathrm{max}}^{2}$	$\displaystyle=$	$\displaystyle E_{e}^{2}\theta_{c}^{2}(1-x)+Q_{\mathrm{min}}^{2}\,,$		(14)

where $x=E_{\gamma}/E_{e}$, $E_{e}=\sqrt{S}/2$ is incoming-lepton energy, $E_{\gamma}$ is the radiated-photon energy, and $\theta_{c}$ the maximum angle by which the photon is deflected from the flight direction of the emitting lepton in the center-of-mass frame. The $x$ distribution of beamstrahlung is characterized by the effective beamstrahlung parameter $\Upsilon$. If $\Upsilon\lesssim 5$, a useful and convenient approximation is given by Chen:1991wd

	$\displaystyle f^{\mathrm{beam}}_{\gamma}(x)$	$\displaystyle=$	$\displaystyle\frac{1}{\Gamma(1/3)}\left(\frac{2}{3\Upsilon}\right)^{1/3}x^{-2/3}(1-x)^{-1/3}e^{-2x/[3\Upsilon(1-x)]}$
			$\displaystyle{}\times\left\{\frac{1-\sqrt{\Upsilon/24}}{g(x)}\left[1-\frac{1}{g(x)N_{\gamma}}\right]\left(1-e^{-g(x)N_{\gamma}}\right)+\sqrt{\frac{\Upsilon}{24}}\left[1-\frac{1}{N_{\gamma}}\left(1-e^{-N_{\gamma}}\right)\right]\right\}\,,$

where

$$g(x)=1-\frac{1}{2}\left[(1+x)\sqrt{1+\Upsilon^{2/3}}+1-x\right](1-x)^{2/3}\,,$$

(16)

and

$$N_{\gamma}=\frac{5\alpha\sigma_{z}m_{e}^{2}\Upsilon}{2E_{e}\sqrt{1+\Upsilon^{2/3}}}$$

(17)

is the average number of photons emitted by an electron or position during the collision, with $\sigma_{z}$ being the longitudinal bunch length.

As mentioned in Sec. I, we assess here three future realizations of high-energy, high-luminosity $e^{+}e^{-}$ colliders under discussion by the world-wide particle physics community, namely FCC-ee FCC:2018evy , CEPC CEPCStudyGroup:2018rmc , and CLIC CLICdp:2018cto , with regard to their potentials to allow for measurements of prompt $J/\psi$ pair photoproduction. For each of them, the set of parameters relevant for our numerical analysis, including $e^{+}e^{-}$ center-of-mass energy $\sqrt{S}$, upper cut $\theta_{c}$ on bremsstrahlung deflection angle, average beamstrahlung parameter $\Upsilon$, longitudinal bunch length $\sigma_{z}$, and estimated luminosity per experiment $\int\mathrm{d}t\,\mathcal{L}$ integrated over one year of running, as quoted in Ref. ParticleDataGroup:2022pth , are collected in Table 1. Throughout our study, we impose the cut $p_{T}^{J/\psi}\geq 2~{}\mathrm{GeV}$ on the transverse momentum of each $J/\psi$ meson.

We start by considering the total cross section $\sigma(e^{+}e^{-}\to 2J/\psi+X)$ via photoproduction. Starting from the LO NRQCD predictions, we in turn add the $\mathcal{O}(v^{2})$ and $\mathcal{O}(\alpha_{s})$ corrections. Our results for FCC-ee, CEPC, and CLIC are displayed in Table 2, where the central values refer to $\xi=1$ and the theoretical error bands to $\xi=1/2,2$. In all three cases, we observe that the $\mathcal{O}(v^{2})$ corrections induce a reduction by about 12% and the $\mathcal{O}(\alpha_{s})$ corrections a further reduction by about 49%, adding up to a total reduction by about 55%. To judge the phenomenological significance of the $\mathcal{O}(v^{2})$ corrections in view of the status quo, we should rather compare them to the $\mathcal{O}(\alpha_{s})$-corrected results Yang:2020xkl , in which case the reduction is as large as $17^{+39}_{-6}$%. As for theoretical uncertainties, we observe from Table 2 that their absolute sizes are reduced whenever $\mathcal{O}(v^{2})$ or $\mathcal{O}(\alpha_{s})$ corrections are included. Contrary to naïve expectations, the relative uncertainty is slightly increased upon inclusion of the $\mathcal{O}(\alpha_{s})$ corrections. This is because of the abnormally large reductions of the central predictions under the influence of the $\mathcal{O}(v^{2})$ and $\mathcal{O}(\alpha_{s})$ corrections.

Experimentally, $J/\psi$ mesons may be most easily detected and reconstructed through their decays to $e^{+}e^{-}$ and $\mu^{+}\mu^{-}$ pairs, with a combined branching fraction of $\mathrm{Br}(J/\psi\rightarrow l^{+}l^{-})=12\%$ ParticleDataGroup:2022pth . Dressing the final predictions in Table 2 with two factors of $\mathrm{Br}(J/\psi\rightarrow l^{+}l^{-})$ and the respective integrated luminosities $\int\mathrm{d}t\,\mathcal{L}$ per experiment from Table 1, we obtain $649^{+82}_{-488}$, $584^{+75}_{-439}$, and $558^{+64}_{-414}$ signal events per year at FCC-ee, CEPC, and CLIC, respectively.

We now turn our attention to cross section distributions in the $J/\psi$ pair invariant mass $m_{\psi\psi}$ and the transverse momentum $p_{T}^{J/\psi}$ and rapidity $y^{J/\psi}$ of any $J/\psi$ meson. Specifically, we consider the ranges $7~{}\mathrm{GeV}\leq m_{\psi\psi}\leq 14~{}\mathrm{GeV}$, $2~{}\mathrm{GeV}\leq p_{T}^{J\psi}\leq 9~{}\mathrm{GeV}$, and $-4\leq y^{J/\psi}\leq 4$ in bins of unit length, yielding 7, 7, and 8 bins, respectively.

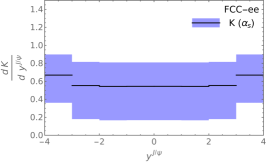
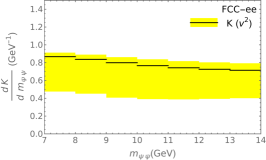
To obtain a more detailed picture of the sizes of corrections and theoretical uncertainties, we study the two consecutive correction factors $K_{\alpha_{s}}=\mathrm{d}\sigma^{\mathcal{O}(\alpha_{s})}/\mathrm{d}\sigma^{\mathrm{LO}}$ and $K_{v^{2}}=\mathrm{d}\sigma^{\mathcal{O}(\alpha_{s},v^{2})}/\mathrm{d}\sigma^{\mathcal{O}(\alpha_{s})}$. For this purpose, we may concentrate on the FCC-ee case because the differences with respect to the CEPC and CLIC cases largely cancel out in the ratios. Our NRQCD predictions for $K_{\alpha_{s}}$ and $K_{v^{2}}$ are presented in Fig. 1. We observe from Fig. 1, that the central values of $K_{\alpha_{s}}$ range between 0.55 and 0.75 in the $m_{\psi\psi}$, $p_{T}^{J/\psi}$, and $y^{J/\psi}$ ranges considered; the $m_{\psi\psi}$ and $|y^{J/\psi}|$ distributions monotonically increase, and so does the $p_{T}^{J/\psi}$ distribution beyond $p_{T}^{J/\psi}=4~{}\mathrm{GeV}$. On the other hand, Fig. 1 shows that $K_{v^{2}}$ ranges from 0.6 to 0.9 and exhibits $m_{\psi\psi}$, $p_{T}^{J/\psi}$, and $y^{J/\psi}$ line shapes that behave inversely to $K_{\alpha_{s}}$. In particular, the relativistic corrections are most important at large values of $m_{\psi\psi}$ and $|y^{J/\psi}|$, and small values of $p_{T}^{J/\psi}$. We conclude that the overall correction factor $K=\mathrm{d}\sigma^{\mathcal{O}(\alpha_{s},v^{2})}/\mathrm{d}\sigma^{\mathrm{LO}}=K_{\alpha_{s}}K_{v^{2}}$ exhibits a strongly reduced variation with $m_{\psi\psi}$, $p_{T}^{J/\psi}$, and $y^{J/\psi}$.

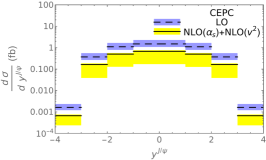
In Fig. 2, we present binned $m_{\psi\psi}$, $p_{T}^{J/\psi}$, and $y^{J/\psi}$ distributions of $e^{+}e^{-}\to 2J/\psi+X$ via photoproduction in NRQCD at LO and full NLO, including both $\mathcal{O}(v^{2})$ and $\mathcal{O}(\alpha_{s})$ corrections, for the FCC-ee, CEPC, and CLIC experimental setups. We observe from Fig. 2 (top row, center column) that the $K$ factors vary only feebly with $m_{\psi\psi}$ and $y^{J/\psi}$ and moderately with $p_{T}^{J/\psi}$, as expected from the above discussion of Fig. 1. In fact, again taking FCC-ee as a representative example, we have $K=045_{-0.37}^{+0.26}$ for the $m_{\psi\psi}$ and $y^{J/\psi}$ distributions, except for bins 1 and 8 of the latter, where $K=0.41_{-0.30}^{+0.23}$. For the $p_{T}^{J/\psi}$ distribution, the $K$ factor ranges from $0.44_{-0.38}^{+0.27}$ in the first bin up to $0.66_{-0.27}^{+0.21}$ in the last bin.

The respective numbers of signal events per year, based on our best predictions, are collected in Table 3. For all three experimental setups, promising yields are expected in the lower $m_{\psi\psi}$ and $p_{T}^{J/\psi}$ ranges and in the central $y^{J/\psi}$ region.

We are faced by considerable theoretical uncertainties in Tables 2 and 3 and Figs. 1 and 2, which manifest themselves in sizable shifts under $\mu_{r}$ variations. While we believe that our default choice $\mu_{r}=\sqrt{s}$ of renormalization scale is most appropriate for the problem at hand, it is instructive to also consider alternatives. In the case of $J/\psi$ single or associated production, the $J/\psi$ transverse mass $m_{T}=\sqrt{p_{T}^{2}+4m_{c}^{2}}$ is often chosen as the default. This motivates us to explore the choice $\mu_{r}=\xi m_{T}$ with $\xi=1/2,1,2$. We do this taking $\mathrm{d}\sigma/\mathrm{d}p_{T}$ at FCC-ee as an example and present our full NLO NRQCD predictions in Table 4. These turn out to be considerably smaller than our default predictions in Fig. 2 and even partly negative, which disqualifies this low scale choice altogether.