New Lower Bounds for Tverberg Partitions with Tolerance in the Plane

Sergey Bereg Department of Computer Science, University of Texas at Dallas. This research is supported in part by NSF award CCF-1718994. Mohammadreza Haghpanah^∗

Abstract

Let $P$ be a set $n$ points in a $d$ -dimensional space. Tverberg’s theorem says that, if $n$ is at least $(k-1)(d+1)+1$ , then $P$ can be partitioned into $k$ sets whose convex hulls intersect. Partitions with this property are called Tverberg partitions. A partition has tolerance $t$ if the partition remains a Tverberg partition after removal of any set of $t$ points from $P$ . Tolerant Tverberg partitions exist in any dimension provided that $n$ is sufficiently large. Let $N(d,k,t)$ be the smallest value of $n$ such that tolerant Tverberg partitions exist for any set of $n$ points in $\mathbb{R}^{d}$ . Only few exact values of $N(d,k,t)$ are known.

In this paper we establish a new tight bound for $N(2,2,2)$ . We also prove many new lower bounds on $N(2,k,t)$ for $k\geq 2$ and $t\geq 1$ .

1 Introduction

The classical Tverberg’s theorem [18] states that a sufficiently large set of points in $\mathbb{R}^{d}$ can be partitioned into subsets such that their convex hulls intersect. For the history and recent advances around Tverberg’s theorem, we refer the reader to [3, 4, 6, 13].

Theorem 1 (Tverberg [18]).

Any set $P$ of at least $(k-1)(d+1)+1$ points in $\mathbb{R}^{d}$ can be partitioned into $k$ sets $P_{1},P_{2},\dots,P_{k}$ whose convex hulls intersect, i.e.

\bigcap_{i=1}^{k}\mathsf{conv}(P_{i})\neq\emptyset.

(1)

In 1972, David Larman proved the first tolerant version of Tverberg’s theorem: any set of $2d+3$ points in $\mathbb{R}^{d}$ can be partitioned into two sets $A$ and $B$ such that their convex hulls intersect with tolerance one, i.e., for any point $x\in\mathbb{R}^{d}$ , $\mathsf{conv}(A\setminus\{x\})\cap\mathsf{conv}(B\setminus\{x\})\neq\emptyset$ . García-Colín [8] generalized it for any tolerance. Soberón and Strausz [17] generalized it further for partitions into many sets. The general problem can be stated as follows.

Problem (Tverberg partitions with tolerance). Given positive integers $d,k,t$ , find the smallest positive integer $N(d,k,t)$ such that any set $P$ of $N(d,k,t)$ points in $\mathbb{R}^{d}$ can be partitioned into $k$ subsets $P_{1},P_{2},\dots,P_{k}$ such that for any set $Y\subset P$ of at most $t$ points

\bigcap_{i=1}^{k}\mathsf{conv}(P_{i}\setminus Y)\neq\emptyset.

(2)

We call a partition of $P$ into $k$ subsets $P_{1},P_{2},\dots,P_{k}$ $t$ -tolerant if condition (2) holds for any set $Y$ of at most $t$ points. Several upper bounds for $N(d,k,t)$ are known [10, 12, 14, 17]. Some lower bounds for $N(d,k,t)$ are known [9, 2, 15].

Theorem 2 (Ramírez-Alfonsín [2]).

For any $d\geq 4$

N(d,2,1)\geq\left\lceil\frac{5d}{3}\right\rceil+3.

(3)

Theorem 3 (García-Colín and Larman [9]).

N(d,2,t)\geq 2d+t+1.

(4)

Theorem 4 (Soberón [15]).

N(d,k,t)\geq k(t+\lfloor d/2\rfloor+1).

(5)

In contrast to Tverberg’s theorem, most bounds are not known to be tight. The only known tight bounds are the following. Larman [12] proved $N(d,2,1)=2d+3$ for $d\leq 3$ . Forge, Las Vergnas and Schuchert [7] proved $N(4,2,1)=11$ . For all $k\geq 2,t\geq 1$ and dimension one, $N(1,k,t)=k(t+2)-1$ by Mulzer and Stein [14]. In this paper we establish a new tight bound for $N(2,2,2)$ .

Theorem 5.

$N(2,2,2)=10$ .

We also improve the bound (5) for the plane.

Theorem 6.

Let $c$ be a positive integer. For any integers $k\geq 2c$ and $t\geq c$

N(2,k,t)\geq k(t+2)+c.

(6)

Remark. The bound of Theorem 6 can be stated without parameter $c$

N(2,k,t)\geq k(t+2)+\min(t,\lfloor k/2\rfloor).

(7)

If $d=2$ and $k=2$ then Equation (6) provides a lower bound $N(2,2,t)\geq 2(t+2)+1$ . We further improve the bound for $k=2$ and $t\geq 3$ .

Theorem 7.

For any $t\geq 3$ , $N(2,2,t)\geq 2t+6$ .

Several upper bounds for $N(d,k,t)$ are known [8, 10, 16]. For example, Soberón [16] proved $N(d,k,t)=kt+O(\sqrt{t})$ for fixed $k$ and $d$ . Therefore, it is interesting to find lower and upper bounds for $P(d,k,t)=N(d,k,t)-kt$ . Theorems 5,6, and 7 provide new lower bounds for $P(d,k,t)$ for $d=2$ .

Remark. Recently, we improved some lower bounds using computer pograms [5]. For example, $N(2,2,t)\geq 2t+7$ for $5\leq t\leq 10$ .

The rest of the paper is organized as follows. Section 2 introduces some observations and lemmas that will be used in our proofs. Theorems 6 and 7 are proven in Section 3. Theorem 5 is proven in Section 4. Finally, we discuss the results and open problems in Section 5.

2 Preliminaries

We start with a simple observation.

Observation 8.

Every part in a $t$ -tolerant partition has size at least $t+1$ .

The following lemma is simple, yet very useful in proving that a partition is not $t$ -tolerant.

Lemma 9.

Let $P_{1},P_{2},\dots,P_{k}$ be a partition of a finite set $P$ in $\mathbb{R}^{d}$ and let $X$ be a subset of a set $P_{i}$ such that

\mathsf{conv}(X)\cap\mathsf{conv}(P\setminus X)=\emptyset

(8)

and $|X|=m,|P_{i}|=t+m$ . Then the partition of $P$ is not $t$ -tolerant.

Proof.

Let $Y=P_{i}\setminus X$ . Then $|Y|=t$ . Therefore

\bigcap_{j=1}^{k}\mathsf{conv}(P_{j}\setminus Y)=\emptyset

(9)

by Equation 8 since one of the sets in the intersection is $X$ and every other set is a subset of $P\setminus X$ . ∎

Two special cases of Lemma 9.

Lemma 10.

A partition $P_{1},P_{2},\dots,P_{k}$ of a finite set $P$ in $\mathbb{R}^{d}$ is not $t$ -tolerant if one of the following conditions holds.

(1)

A set $P_{j}$ contains a vertex of $\mathsf{conv}(P)$ and $|P_{j}|=t+1$ .
(2)

A set $P_{j}$ contains two points $p_{i},p_{i}+1$ such that $p_{i},p_{i}+1$ is an edge of $\mathsf{conv}(P)$ and $|P_{j}|=t+2$ .

Proof.

The first claim follows from Lemma 9 by setting $X=\{p_{i}\}$ where $p_{i}\in P_{j}$ is a vertex of $\mathsf{conv}(P)$ . The second claim follows from Lemma 9 by setting $X=\{p_{i},p_{i+1}\}$ . ∎

3 Proofs of Theorems 6 and 7

First, we prove Theorem 6.

Proof of Theorem 6.

Construct a set $P$ of $k(t+2)+c-1$ points in the plane as follows. Let $Q$ be a regular $(k(t+2)-1)$ -gon with center at the origin $O$ . Place $k(t+2)-1$ points $q_{1},\dots,q_{k(t+2)-1}$ at the vertices of $Q$ and $c$ points $p_{1},\dots,p_{c}$ close to the origin. More specifically, we assume that $|p_{1}|,\dots,|p_{c}|<d$ where $d$ is the distance from the origin to the line $p_{1}p_{k}$ . Let $V=\{q_{1},\dots,q_{k(t+2)-1}\}$ . We assume that the vertices of $Q$ are sorted in clockwise order, see Figure 1.

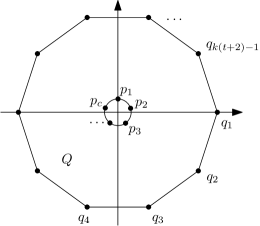
Refer to caption — Figure 1: A point set for Theorem 6.

We show that any partition of $P$ into $P_{1},P_{2},\dots,P_{k}$ is not $t$ -tolerant. By Observation 8, we assume $|P_{i}|\geq t+1$ for all $i$ . If $|P_{i}|=t+1$ for some $i$ , then $P_{i}$ contains a point $q_{j}$ since $t+1>c$ . The partition is not $t$ -tolerant by Lemma 10(1).

It remains to consider the case where all sets in the partition have size at least $t+2$ . At most $c-1$ sets in the partition may have size $\geq t+3$ . Since $k\geq 2c$ there exists a set $P_{i}$ of size $t+2$ such that $P_{i}\subset V$ . Since $|V|=k(t+2)-1$ , there exist two points $q_{a}$ and $q_{a+j}$ with $j\leq k-1$ such that the vertices between $q_{a}$ and $q_{a+j}$ are in $Q\setminus P_{i}$ (we assume here that $q_{x}=q_{y}$ if $x\equiv y\pmod{k(t+2)-1}$ ). There is a set $P_{m},m\neq i$ such that none of these vertices are in $P_{m}$ . Therefore the partition is not $t$ -tolerant since $\mathsf{conv}\{q_{a},q_{b}\}\cap\mathsf{conv}(P_{m})=\emptyset$ . Note that the distance from the origin to any point in $\{p_{1},\dots,p_{c}\}$ is smaller than the distance from the origin to the line $q_{a}q_{b}$ . ∎

Next we prove Theorem 7.

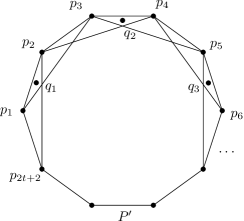
Proof of Theorem 7.

Construct a set $P$ of $2t+5$ points in the plane as follows. First, place $2t+2$ points in convex position $P^{\prime}=\{p_{1},p_{2},\dots,p_{2t+2}\}$ where points are in clockwise order. Then place three points $Q=\{q_{1},q_{2},q_{3}\}$ inside the convex hull of $P^{\prime}$ such that point $q_{i},i=1,2,3$ is close to edge $p_{2i-1}p_{2i}$ (it is required that $q_{i}$ is inside triangles $\bigtriangleup p_{2i-2}p_{2i-1}p_{2i}$ and $\bigtriangleup p_{2i-1}p_{2i}p_{2i+1}$ ), see Figure 2. We show that any partition of $P$ into $P_{1},P_{2}$ is not $t$ -tolerant.

Without loss of generality, we assume $|P_{1}|\leq|P_{2}|$ . Therefore, $|P_{1}|\leq t+2$ . By Observation 8, we assume $|P_{1}|\geq t+1$ . Suppose if $|P_{1}|=t+1$ . Since $t\geq 3$ , $P_{1}$ contains a point of $P^{\prime}$ . The partition is not $t$ -tolerant by Lemma 10(1).

It remains to consider the case where $|P_{1}|=t+2$ . If set $P_{1}$ does not contain a point $q_{i}$ , then $P_{1}\subset P^{\prime}$ and $|P_{1}|\geq|P^{\prime}|/2$ . Then $P_{1}$ contains two consecutive points of $P^{\prime}$ . The partition is not $t$ -tolerant by Lemma 10(2). Therefore $P_{1}\cap Q\neq\emptyset$ .

Suppose $q_{i}\in P_{1}$ for some $i$ . If $p_{2i-1}\in P_{1}$ or $p_{2i}\in P_{1}$ then the partition is not $t$ -tolerant using $X=\{q_{i},p_{2i-1}\}$ or $X=\{q_{i},p_{2i}\}$ , respectively, and Lemma 9. Therefore, we assume that both points $p_{2i-1}$ and $p_{2i}$ are in $P_{2}$ .

Let $m=|P_{1}\cap\{q_{1},q_{2},q_{3}\}|$ . Then $m\in\{1,2,3\}$ . By the previous argument, set $P_{2}$ contains at least $m$ pairs of consecutive points of $P^{\prime}$ (the pair $p_{2i-1},p_{2i}$ for each point $q_{i}\in P_{1}$ ). Note that $|P^{\prime}\cap P_{1}|=t+2-m$ and $|P^{\prime}\cap P_{2}|=t+m$ . We will show that set $P_{1}$ contains a pair of consecutive points of $P^{\prime}$ . Then, the partition is not $t$ -tolerant by Lemma 10(2).

If $m=1$ , then $|P^{\prime}\cap P_{1}|=|P^{\prime}\cap P_{2}|=t+1$ and set $P_{2}$ contains a pair of consecutive points of $P^{\prime}$ . Then set $P_{1}$ contains a pair of consecutive points of $P^{\prime}$ .

Suppose $m=2$ , say $q_{i},q_{j}\in P_{1}$ where $i<j$ . Then set $P_{2}$ contains $p_{2i-1},p_{2i},p_{2j-1}$ , and $p_{2j}$ . There are two intervals $p_{2i+1},\dots,p_{2j-2}$ and $p_{2j+1},\dots,p_{2i-2}$ in $P^{\prime}$ containing points of $P_{1}$ . Note that each interval contains an even number of points. If set $P_{1}$ does not contain a pair of consecutive points of $P^{\prime}$ , then set $P_{1}$ contains at most half of points in each interval. Then $|P^{\prime}\cap P_{1}|<t$ . This contradiction implies that set $P_{1}$ contains a pair of consecutive points of $P^{\prime}$ .

Finally, if $m=3$ , then there exists only one interval $p_{7},p_{8},\dots,p_{2t+2}$ and set $P_{1}$ must contain a pair of consecutive points of $P^{\prime}$ ; otherwise $|P^{\prime}\cap P_{1}|<t+1$ . The theorem follows. ∎

4 Proof of Theorem 5

We found a special configuration of nine points to prove a lower bound for Theorem 5. For this, we checked point configurations of all order types for $n=9$ . Order types, introduced by Goodman and Pollack [11], are useful for characterizing the combinatorial properties of point configurations. An order type of a set of points $p_{1},p_{2},\dots,p_{n}$ in general position in the plane is defined using a mapping that assigns each triple of integers $i,j,k$ with $1\leq i<j<k\leq n$ the orientation (either clockwise or counter-clockwise) of the triple $p_{i},p_{j},p_{k}$ . Two point sets $P_{1}$ and $P_{2}$ have the same order type if there is a bijection $\pi$ from $P_{1}$ to $P_{2}$ preserving this map, i.e., for any three distinct points $a,b,c$ in $P_{1}$ , the orientation of $a,b,c$ and the orientation of $\pi(a),\pi(b),\pi(c)$ are the same. Aichholzer et al. [1] established that there are 158,817 order types for $n=9$ . We developed a program for testing each of these point sets whether it admits a 2-tolerant partition into two sets. The proof of the tolerance of a configuration found by the program turns out to be not simple even using the tools from Section 2.

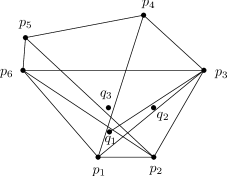
Lemma 11.

There exists a set of nine points in the plane that does not admit a 2-tolerant partition into two sets.

Proof.

Consider a set $S$ of nine points shown in Fig.3 where $S=P\cup Q,P=\{p_{1},\dots,p_{6}\}$ and $Q=\{q_{1},q_{2},q_{3}\}$ . We will prove that any partition of $S=A\cup B$ is not 2-tolerant, i.e. there exists a set $C=\{a,b\}\subseteq S$ such that

\mathsf{conv}(A\setminus C)\cap\mathsf{conv}(B\setminus C)=\emptyset.

We can assume that $|A|<|B|$ . By Observation 8, we assume $|A|\geq 3$ . Suppose that $|A|=3$ . If $A=Q$ , then take $C=\{p_{1},p_{2}\}$ . If $A\neq Q$ , then the partition of $S$ is not 2-tolerant by Lemma 10(1).

It remains to analyze partitions with $|A|=4$ . By Lemma 10(2), we assume that $A$ does not contain two consecutive points $p_{i},p_{i+1}$ (assuming $p_{7}=p_{1}$ ). For example, this implies that $A$ contains at least one point of $Q$ . Consider the following cases depending on $|A\cap P|$ .

Case 1. Set $A$ contains exactly one point of $P$ , say $p_{i}$ . Then $Q\subset A$ . One of the sets $\{p_{1},p_{2},p_{3}\}$ , $\{p_{3},p_{4},p_{5}\}$ , $\{p_{4},p_{5},p_{6}\}$ , say set $X$ , does not contain $p_{i}$ . The partition is not 2-tolerant by Lemma 9 using $X$ .

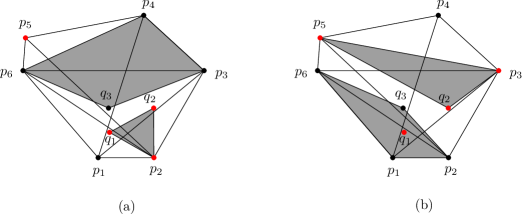
Case 2. Set $A$ contains exactly two points of $P$ , i.e. $A=\{p_{i},p_{j},q_{c},q_{d}\}$ for some $1\leq i<j\leq 6$ and $1\leq c<d\leq 3$ .

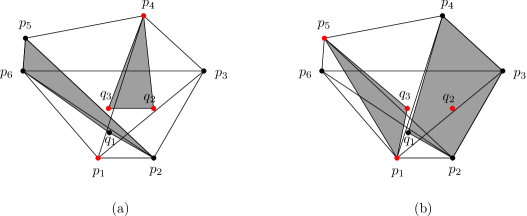
Case 2a. Suppose $i=1$ . By our assumption $j\notin\{2,6\}$ . We can assume that $j\neq 3$ using $X=\{p_{4},p_{5},p_{6}\}$ and Lemma 9. So, $j\in\{4,5\}$ .

We also can assume that $q_{1}\in B$ using $X=\{p_{1},q_{1}\}$ and Lemma 9. Therefore $\{q_{2},q_{3}\}\subset A$ . If $j=4$ (so $A=\{p_{1},p_{4},q_{2},q_{3}\}$ ) then take $C=\{p_{1},p_{3}\}$ , see Fig.4(a). If $j=5$ (so $A=\{p_{1},p_{5},q_{2},q_{3}\}$ ) then take $C=\{p_{6},q_{2}\}$ , see Fig.4(b).

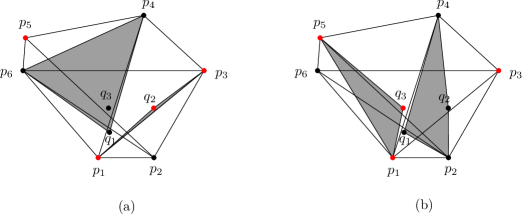
Case 2b. Suppose $i=2$ . Then $j\geq 4$ . We can assume $j\neq 4$ using $X=\{p_{1},p_{5},p_{6}\}$ and Lemma 9. We can assume $j\neq 6$ using $X=\{p_{3},p_{4},p_{5}\}$ and Lemma 9. Thus, $j=5$ . We can assume $q_{1}\in A$ using $X=\{p_{1},p_{6},q_{1}\}$ and Lemma 9.

If $q_{3}\in A$ then $A=\{p_{2},p_{5},q_{1},q_{3}\}$ we can use $X=\{p_{3},p_{4},q_{2}\}$ and Lemma 9. If $q_{2}\in A$ then $A=\{p_{2},p_{5},q_{1},q_{2}\}$ and we can use $C=\{p_{1},p_{5}\}$ , see Fig.5(a).

Case 2c. Suppose $i,j\in\{3,4,5,6\}$ . We can assume $q_{1},q_{2}\in A$ using $X=\{p_{1},p_{2},x\}$ for $x\in\{q_{1},q_{2}\}$ and Lemma 9. Since $p_{i}$ and $p_{i+1}$ cannot be in $A$ together, there are three options. If $p_{3},p_{5}\in A$ , take $C=\{p_{4},q_{1}\}$ , see Fig.5(b). If $p_{4},p_{6}\in A$ then we can use $X=\{p_{1},p_{2},p_{3}\}$ and Lemma 9. If $p_{3},p_{6}\in A$ then we can use $X=\{p_{3},q_{2}\}$ and Lemma 9.

Case 3. Set $A$ contains exactly three points of $P$ , i.e. $\{p_{1},p_{3},p_{5}\}\subset A$ or $\{p_{2},p_{4},p_{6}\}\subset A$ .

Case 3a. Suppose $\{p_{1},p_{3},p_{5}\}\subset A$ . If $q_{1}\in A$ then we can use $X=\{p_{1},q_{1}\}$ and Lemma 9. If $q_{2}\in A$ , take $C=\{p_{2},p_{5}\}$ , see Fig.6(a). If $q_{3}\in A$ , take $C=\{p_{3},p_{6}\}$ , see Fig.6(b).

Case 3b. Suppose $\{p_{2},p_{4},p_{6}\}\subset A$ . If $q_{1}\in A$ , take $C=\{p_{1},p_{4}\}$ , see Fig.7(a). If $q_{2}\in A$ , take $C=\{p_{3},p_{6}\}$ , see Fig.7(b). If $q_{3}\in A$ , take $C=\{p_{2},p_{5}\}$ , see Fig.7(c). The lemma follows. ∎

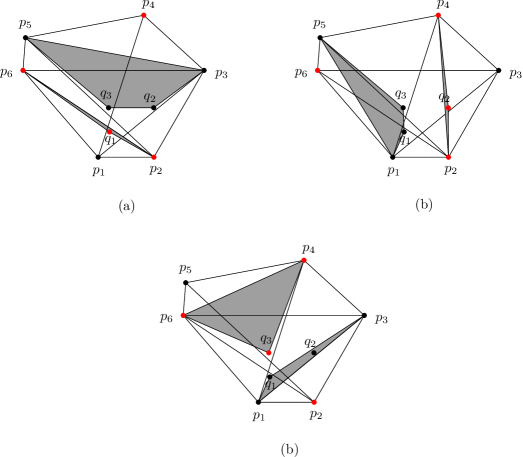
Corollary 12.

$N(2,2,2)\geq 10$ .

Soberón and Strausz [17] proved an upper bound $N(d,k,t)\leq(k-1)(t+1)(d+1)+1$ which implies $N(2,2,2)\leq 10$ . Therefore $N(2,2,2)=10$ .

5 Further Discussion and Open Problems

Improving the bounds for Tverberg partitions with tolerance is an interesting problem. There are many triples $(d,k,t)$ with a gap between known lower and upper bounds. Finding sharp bounds for $N(d,k,t)$ is a challenging problem. For example, Larman [12] conjectured that $N(d,2,1)=2d+3$ for any $d\geq 1$ . The conjecture is open for $d\geq 5$ . For dimension $d=5$ , the best known upper bound is $N(5,2,1)\leq 13$ by Larman [12] and the best known lower bound is $N(5,2,1)\geq 12$ by García-Colín and Larman [9].

Another possibility for a new sharp bound is for $d=2,k=2$ and tolerance $t=3$ . The lower bound is $N(2,2,3)\geq 12$ by Theorem 7. The best upper bound is $N(2,2,3)\leq 13$ by Soberón and Strausz [17]. Based on our computer experiments, we conjecture that $N(2,2,3)=12$ . One way to improve the upper bound for $d=2,k=2$ and $t=3$ is to study the following core lemma in the proof of the upper bound for $N(d,k,t)$ [17].

Lemma 13.

Let $p\geq 1$ and $r\geq 0$ be integers, $S\subset\mathbb{R}^{p}$ be a set of $n=p(r+1)+1$ points $a_{1},a_{2},\dots,a_{n}$ and $G$ be a group with $|G|\leq p$ . If there is an action of $G$ in a set $S^{\prime}\subset\mathbb{R}^{p}$ which is compatible with $S\subset S^{\prime}$ , then for each $a_{i}$ there is a $g_{i}\in G$ such that the set $\{g_{1}a_{1},g_{2}a_{2},\dots,g_{n}a_{n}\}$ captures the origin with tolerance $r$ .

For $d=2,k=2$ and tolerance 3, Lemma 13 uses $n=13$ points since $p=(k-1)(d+1)=3$ . Is this bound for $n$ sharp?

5.1 Order types and tolerant Tverberg partitions

Our proof of Theorem 5 uses the set of nine points shown in Figure 3. It was computed by a program that we developed for testing the tolerance of a given point set. We have applied this program to 158,817 order types for $n=9$ which are provided by Aichholzer et al. [1]. Our program found that 155,115 point sets admit a 2-tolerant partition into two sets. Only 3,702 point sets do not admit a 2-tolerant partition into two sets and therefore, can be used as examples for proving the lower bound $N(2,2,2)\geq 10$ .

We analyzed these 3,702 order types and found that their convex hulls have sizes between three and six. We count the number of different order types for each size of the convex hull, see Table 1. Figures 8, 9, and 10 show some order types with 5, 4, and 3 points on the convex hull, respectively. It follows from our computer experiments that any set of nine points in the plane with at least seven points on the convex hull admits a 2-tolerant partition into two sets. It is interesting to investigate how the size of convex hull of a point set affects lower bounds of $N(d,k,t)$ .

$h$	$h=3$	$h=4$	$h=5$	$h=6$	$h=7$	$h=8$	$h=9$
$N_{h}$	1303	1554	769	76	0	0	0

Table 1: 3,702 order types of nine points that do not admit a 2-tolerant partition into two sets. The point sets are partitioned using the size of the convex hull

h

. The size of each group is

N_{h}

Figure 8: Two point sets of nine points each with five points on the convex hull. The point sets have different order types. Both point sets do not admit a 2-tolerant partition into two sets.

Figure 9: Two point sets of nine points each with four points on the convex hull. The point sets have different order types. Both point sets do not admit a 2-tolerant partition into two sets.

Figure 10: Two point sets of nine points each with three points on the convex hull. The point sets have different order types. Both point sets do not admit a 2-tolerant partition into two sets.

References

[1] O. Aichholzer, F. Aurenhammer, and H. Krasser. Enumerating order types for small point sets with applications. Order, 19:265–281, 2002.
[2] J. L. R. Alfonsín. Lawrence oriented matroids and a problem of mcmullen on projective equivalences of polytopes. Eur. J. Comb., 22(5):723–731, 2001.
[3] I. Bárány, P. V. M. Blagojevic, and G. M. Ziegler. Tverberg’s theorem at 50: extensions and counterexamples. Notices Amer. Math. Soc., 63(7):732–739.
[4] I. Bárány and P. Soberón. Tverberg’s theorem is 50 years old: a survey. Bulletin of the American Mathematical Society, 55(4):459–492, 2018.
[5] S. Bereg and M. Haghpanah. Algorithms for Radon partitions with tolerance. In 6th Internat. Conf. on Algorithms and Discrete Applied Mathematics, pages 476–487, 2020.
[6] J. De Loera, X. Goaoc, F. Meunier, and N. Mustafa. The discrete yet ubiquitous theorems of carathéodory, helly, sperner, tucker, and tverberg. Bulletin of the American Mathematical Society, 56(3):415–511, 2019.
[7] D. Forge, M. Las Vergnas, and P. Schuchert. 10 points in dimension 4 not projectively equivalent to the vertices of a convex polytope. European Journal of Combinatorics, 22(5):705–708, 2001.
[8] N. García-Colín. Applying Tverberg type theorems to geometric problems. PhD thesis, University College of London, 2007.
[9] N. García-Colín and D. G. Larman. Projective equivalences of $k$ -neighbourly polytopes. Graphs and Combinatorics, 31(5):1403–1422, 2015.
[10] N. García-Colín, M. Raggi, and E. Roldán-Pensado. A note on the tolerant Tverberg theorem. Discrete & Computational Geometry, 58(3):746–754, 2017.
[11] J. E. Goodman and R. Pollack. Multidimensional sorting. SIAM J. Comput., 12(3):484–507, Aug. 1983.
[12] D. G. Larman. On sets projectively equivalent to the vertices of a convex polytope. Bulletin of the London Mathematical Society, 4(1):6–12, mar 1972.
[13] J. Matoušek. Lectures on discrete geometry, volume 212. Springer, 2002.
[14] W. Mulzer and Y. Stein. Algorithms for tolerant Tverberg partitions. Int. J. Comput. Geometry Appl., 24(4):261–274, 2014.
[15] P. Soberón. Equal coefficients and tolerance in coloured Tverberg partitions. Combinatorica, 35(2):235–252, 2015.
[16] P. Soberón. Robust Tverberg and colourful Carathéodory results via random choice. Combinatorics, Probability and Computing, 27(3):427–440, 2018.
[17] P. Soberón and R. Strausz. A generalisation of Tverberg’s theorem. Discrete & Computational Geometry, 47(3):455–460, 2012.
[18] H. Tverberg. A generalization of Radon’s theorem. J. London Math. Soc., 41:123–128, 1966.