Neutron-proton differential transverse flow in 132Sn + 124Sn collisions at 270 MeV/nucleon
Abstract
Within a transport model, we study the neutron-proton differential transverse flow and its excitation function in central 132Sn + 124Sn collisions at 270 MeV/nucleon. To more accurately evaluate effects of the high-density behavior of symmetry energy on this observable, we also consider the uncertainties of around the saturation density . It is shown that the neutron-proton differential transverse flow and its excitation function are mainly sensitive to the slope of at . However, the effects of low-density behavior of on this observable should also be considered. Therefore, it is suggested that measurements of the neutron-proton differential transverse flow and its excitation function may provide useful complements to the constraints on extracted from the spectral pion ratio in SRIT experiments.
I introduction
Heavy-ion collisions (HICs) can directly generate high density nuclear matter, and thus provide the opportunity to explore the properties of strong interacting matter at extreme conditions. As an important input in simulations of HICs, the isovector component of nuclear mean field, i.e., symmetry/isovector potential, is rather uncertain because of the extreme challenge of relatively direct detection of isovector potential in experiments. Using the nucleon-nucleus scattering and (,) charge-exchange reactions Hoff72 ; Pat76 ; Kwi78 ; Rap79 ; Jeu91 ; Kon03 , one can only extract limited information of isovector potential at . As a result, the determination of the term of the equation of state (EoS) of asymmetric nuclear matter (ANM) is still unsatisfactory compared to the relatively good determination of the isospin-independent part of the EoS of ANM Dan02 ; Oert17 . Presently, the best knowledge of is around , for which its value is determined to be 25.5 MeV from nuclear masses and isobaric analog states Wang13 ; Brown13 ; Dan14 . At densities greater than , the uncertainties in grow monotonically. For example, the at , that is commonly used as one of the criterion in fitting the parameters of the isovector potential, still has greater uncertainties than that at , e.g., 32 MeV Cozma18 and 32.5 MeV Wang18 . Also, the uncertainties for at suprasaturation densities are rather larger, such as the reported value MeV Bren21 by a calculation of correlated to the improved in the PREX-II experiment PREX-II .
Very recently, the SRIT collaboration reported the results of pion production in Sn + Sn collisions at 270 MeV/nucleon Estee21 ; Jhang21 . Moreover, through comparing the spectral pion ratio with the simulation from a dcQMD model Cozma21 , they deduced that the value of is within the range from 42 to 117 MeV Estee21 . Obviously, this value is consistent with that deduced from the correlated calculation Bren21 . However, the uncertainty for is still rather larger and thus need to be further constrained. We note that the motions of energetic nucleons are directly influenced by the and its value, and thus might provide a more direct detect of the at suprasaturation density. This is because these energetic participants can originate in the regions that are compressed during the violent early stages of HICs and be accelerated by the symmetry potential, resulting in their momenta reflecting the and its value. Naturally, studies on the observables relavant to these nucleons, as an important complement to the pion spectra Tsang17 and/or spectral pion ratio Estee21 , may shed more lights on the at suprasaturation densities. Actually, as one of this kind of observable, elliptic folw is more suitable to probe the at suprasaturation density, and the corresponding studies in Au + Au collisions have already placed constraints on the and its value Cozma18 ; FOPI . As another candidate of this kind of observable, the free neutron-proton differential transverse flow has also been found to be more sensitive to the high-density behavior of LiBA00 ; LiBA02 ; Yong05 ; Yong06 . Therefore, we attempt to predict the sensitivities of this observable to the symmetry energy, and thus to benefit for the upcoming or ongoing measurements in SRIT experiments.
II The Model
This study is carried out within an isospin- and momentum-dependent Boltzmann-Uehling-Uhlenbeck (IBUU) transport model that has incorporated constraints Wei21b on the momentum dependence of isovector potential from the recently reported pion data in SRIT experiments Jhang21 . Specifically, the nuclear interaction is an improved momentum-dependent interaction (IMDI) expressed as
| (1) | |||||
where for neutrons and for protons, and , , and are expressed as
| (2) | |||||
| (3) | |||||
| (4) | |||||
| (5) |
In the framework, the present IBUU model originates from the IBUU04 Das03 ; IBUU and/or IBUU11 CLnote models. However, the present version has been greatly improved to more accurate simulations of HICs as briefly discussed in the following.
First, a separate density-dependent scenario Xu10 ; Chen14 for in-medium nucleon-nucleon interaction has been adopted for a more delicate treatment of the in-medium many-body force effects Chen14 , which also affects significantly the pion production in HICs Wei20 . Therefore, the -terms in Eq. (1) as well in the expressions of and are different from those in Refs. Xu15 ; Xu17 .
Second, a quantity proposed in Ref. CLnote , i.e., the value of symmetry potential at infinitely large nucleon momentum, is used to characterize the momentum dependence of the symmetry potential at as in Refs. Xu15 ; Xu17 . It should be mentioned that this quantity is treated as a free one in Refs. Xu15 ; Xu17 . However, considering that the symmetry potential with different even with the identical can also lead to different pion yields in HICs, we have carried out a study to constrain the through comparing the pion observables of theoretical simulations for reactions 108Sn + 112Sn and 132Sn + 124Sn with the data in SRIT experiments Jhang21 , the central value of is constrained approximately to be MeV, see, Ref. Wei21b for the details.
| Parameters | Case-I | Case-II | L (MeV) |
|---|---|---|---|
| , | , | , | |
| , | , | , | |
| , | , | , | |
| , | , | , |

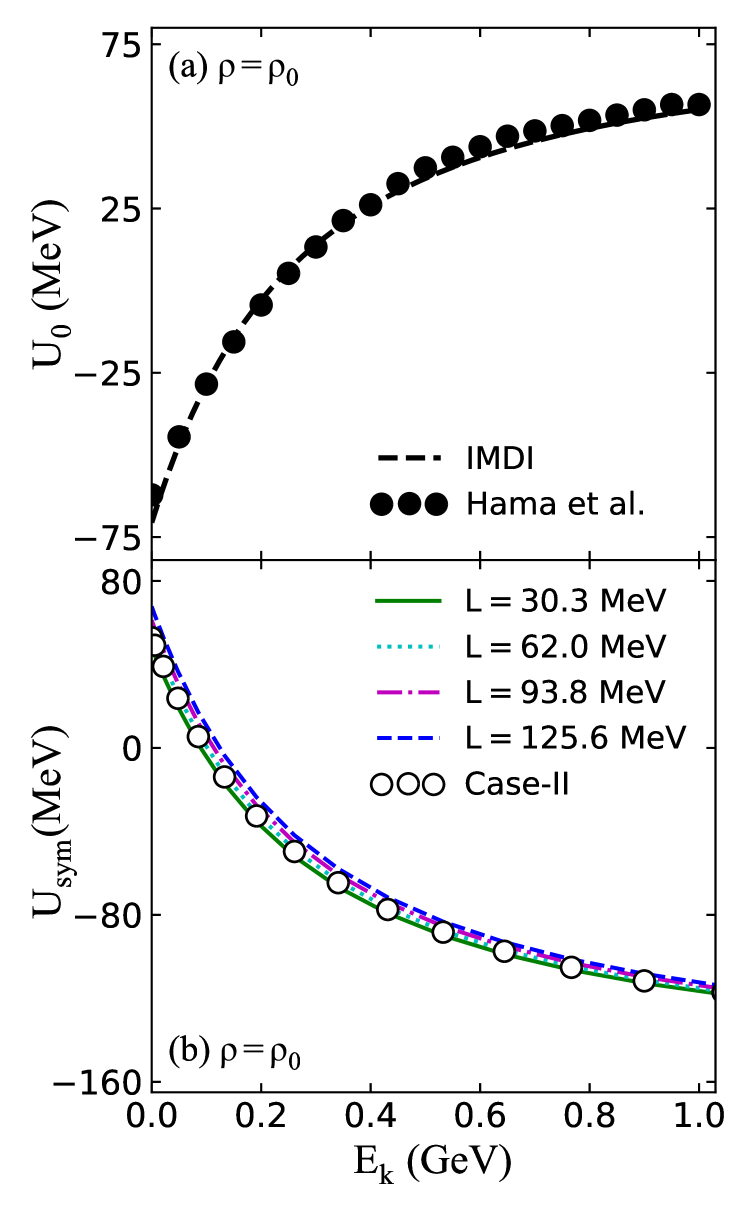
Third, considering that the at still has greater uncertainties than that at , we therefore introduce a parameter for terms in the expressions of and as in Refs. Xu15 ; Xu17 to adjust the at . As the first case, i.e., Case I, we take the value for the parameter to ensure is MeV. For comparison, we also set the value of as zero and take the value for of 32.5 MeV, as commonly used; this case is denoted as Case II. The parameters embedded in IMDI interactions are determined by fitting identical experimental/empirical constraints on properties of nuclear matter at for both Case I and Case II, except the value of 25.5 MeV for used in Case I and 32.5 MeV for used in Case II. Specifically, the values of these parameters are MeV, MeV, MeV, MeV, , and MeV, where is the nucleon Fermi momentum in symmetry nuclear matter (SNM) at . Moreover, to study the effects of high-density behavior of , we adjust the parameter to obtain four different values for both Case I and Case II. The parameters and as well the corresponding values are listed in Table 1. It is seen that except for the value of 6.656 for the parameter being slightly larger than the uncertainties of at , the values are all basically within the allowed uncertain range of at Cozma18 ; Wang18 . This feature can also be seen in the density dependent as shown in Fig. 1. It should be mentioned that except the different symmetry energy criterion the parameters for Case I and Case II can lead to identical properties for nuclear matter at fm-3, i.e., the binding energy MeV, the incompressibility MeV for SNM, the isoscalar effective mass , the isoscalar potential at infinitely large nucleon momentum MeV as well MeV. Shown in Fig. 2 are the isoscalar and isovector potentials at for Case I and Case II. Since the parameters and only affect the isovector properties of ANM, the isoscalar potentials for Case I and Case II are the same and also compatible with the results of Hama et al Hama90 ; Buss12 . Moreover, since the parameter only affects the isovector properties of ANM at nonsaturation densities for both Case I and Case II, as well the identical values used for Case II, we can observe that the isovector potentials at even with different values for Case II are also identical to each other. In contrast, since the parameter is used to ensure to be MeV for Case I by adjusting , it naturally affects isovector potentials at . Therefore, we can see that the isovector potentials at with different for Case I are slightly different due to the different values used for different in Case I. However, the differences of isovector potentials in Case I from those in Case II are very tiny.
III Results and Discussions
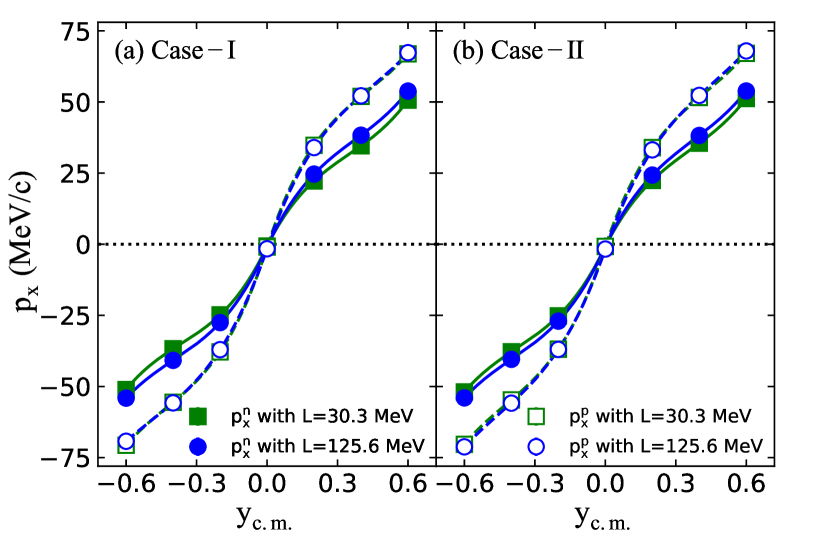
Now, we present the results for the 132Sn + 124Sn reaction at 270 MeV/nucleon with an impact parameter of fm. The free neutron-proton differential transverse flow is measured by LiBA00 ; LiBA02 ; Yong05 ; Yong06
| (6) | |||||
where , and denote, respectively, the number of free neutrons, protons, and total nucleons with local densities less than at rapidities , and is for neutrons and for protons. From this formula, we can see that the isospin fractionation effects are incorporated into the collective flow Dan85 of both neutrons and protons through and . To understand this effect, we show first in Fig. 3 the collective flow of free neutrons and protons as a function of the center-of-mass rapidity. First, it is seen that, consistent with the previous result in Ref. LiBA00 , the proton flow is less sensitive to but higher than the neutron flow due to the Coulomb repulsive effects. Second, with a certain , we can observe that the transverse flows either for neutrons or protons are not changed essentially in the left and righ panels of Fig. 3. This means that the transverse flow is relatively insensitive to the actual value for at any given density, but is mainly sensitive to the slope of , which governs the pressure that the symmetry energy provides in a neutron-rich system as well dense astrophysical environments such as neutron stars. It should be mentioned that this finding is similar to that observed in the ratios/differences of neutron vs proton elliptic flows in Refs. Cozma18 ; Cozma11 as well that observed much earlier in Ref. Dan02 . Nevertheless, the sensitivities of transverse flows to are not obvious either for neutrons or protons. Shown in Fig. 4 are and as a function of the center-of-mass rapidity, respectively. First, since the mass between the target and projectile has a little difference, we thus observe that the shapes of both and are a little asymmetric between the target and projectile rapidities. Second, it is seen that varying from to MeV causes more (less) free neutrons (protons) on the whole for both Case I and Case II. Certainly, we can also find that effects of on either or are reduced somewhat in mid-rapidities for Case II compared to those for Case I. Also, the effects even reverse at the target and/or projectile rapidities. To understand these observations, we show in Fig. 5 the isovector potential of Case I and Case II at both and . First, it is seen that affects the isovector potentials mainly at high densities, and thus the high-density behavior of dominates and . Moreover, varying from to MeV, the neutrons feel stronger repulisve effects while the protons feel stronger attractive effects on the whole for both Case I and Case II. Naturally, we can observe more free neutrons but less free protons with larger values for . Second, we observe that the differences of isovector potentials at between Case I and Case II are negligible, while the differences of isovector potentials at with different are smaller in Case I than those in Case II. This is exactly due to the more accurate criterion, i.e., MeV, used in Case I that reduces the effects of on the isovector potentials and at subsaturation densities. Moreover, since the effects of on the isovector potentials at low densities are opposite to those at high densities, the effects of high-density symmetry energy/potential on observables at compress stages are likely to be smeared out by low density symmetry energy/potential at the expansion stages. In particular, nucleons with target and/or projectile rapidities experience longer time in the expansion stages and emit later compared to those at midrapidities, the effects of low density symmetry energy/potential on observables are naturally considerable. This is the reason we observe in Case II that the isospin fractionation effects are reduced slightly at midrapidities but reversed at target and/or projectile rapidities.




Now, we turn to the free neutron-proton differential transverse flows in the same reaction. Shown in Fig. 6 are the free neutron-proton differential transverse flows as a function of the center-of-mass rapidity. First, it is observed that the free neutron-proton differential transverse flow inherits the asymmetry in shapes from and . Second, it is seen that this observable indeed combines constructively the in-plane transverse momenta generated by the isovector potentials while reducing significantly influences of the isoscalar potentials of both neutrons and protons as indicated in Ref. LiBA02 , and thus it is more sensitive to . Moreover, comparing observations between Case I and Case II, we can find that the sensitivities of this observable to are indeed reduced in Case II. Therefore, to show clearly this observation and facilitate the experimental measurement, we calculate the excitation function of this observable, which is defined as LiBA02b
| (7) |
Shown in Fig. 7 is the excitation function of neutron-proton differential transverse flows as a function of . It is seen that effects of on the excitation function are rather obvious for both Case I or Case II, and thus can be used to further verify the extracted from the spectral pion ratio in SRIT experiments Estee21 . Nevertheless, we can also find that the curve of excitation function in Case I indeed is more steeper compared to that in Case II due to fewer effects of low-density . This feature indicates that the uncertainties of around the should also be considered when using this observable to probe the high-density behavior of . Actually, the authors of Ref. Stone17 have already discussed systematically the effects of uncertainties of low density on the determination of high-density .
Before ending this part, we give two useful remarks. First, the value of MeV used for in this study is more negative than that used in other models, e.g., MeV, used in Refs. Xu15 ; Xu17 . This large and negative appears to have the feature that interactions between two protons or two neutrons with relatively large velocity will be far more attractive than those between a neutron and proton moving at the same relative velocity. The reasons might be due to different isospin states in the former and latter that may originates from the different constituent quarks between neutrons and protons. This issue also deserves serious consideration. Second, we predict the emission of nucleons as free particles and do not consider the clustering effects of nucleons that may change the quantitative results of the present study. Therefore, it will be interesting to see how clusters change the quantitative results of the present study.
IV Summary
In conclusion, we have studied the free neutron-proton differential transverse flow and its excitation function in 132Sn + 124Sn collisions at 270 MeV/nucleon within a transport model. It is found that the sensitivities of free neutron-proton differential transverse flow and its excitation function to are rather obvious, and thus can be used to further verify the extracted from the spectral pion ratio in SRIT experiments. Therefore, we conclude that measurements of the neutron-proton differential transverse flow and its excitation function may provide useful complements to the constraints on extracted from measurements of the spectral pion ratio in SRIT experiments. Moreover, after examining the effects of around on this observable, it is also suggested that the uncertainties of around should also be considered when using the free neutron-proton differential transverse flow to probe the high-density behavior of .
Acknowledgements.
G.-F. Wei would like to thank Profs. Wei Zuo and Bo-Chao Liu for helpful discussions. This work is supported by the National Natural Science Foundation of China under grant Nos.11965008, 11405128, 11865019 and Guizhou Provincial Science and Technology Foundation under Grant No.[2020]1Y034, and the PhD-funded project of Guizhou Normal university (Grant No.GZNUD[2018]11).References
- (1) G. W. Hoffmann, and W. R. Coker, Phys. Rev. Lett. 29, 227 (1972).
- (2) D. M. Patterson et al., Nucl. Phys. A 263, 261 (1976).
- (3) K. Kwiatkowski et al., Nucl. Phys. A 301, 349 (1978).
- (4) J. Rapaport et al., Nucl. Phys. A 330, 15 (1979).
- (5) J. P. Jeukenne, C. Mahaux, and R. Sartor, Phys. Rev. C 43, 2211 (1991).
- (6) A. J. Koning et al., Nucl. Phys. A 713, 231 (2003).
- (7) P. Danielewicz, R. Lacey, and W. G. Lynch, Science 298, 1592 (2002).
- (8) M. Oertel, M. Hempel, T. KIähn, and S. Typel, Rev. Mod. Phys. 89, 015007 (2017).
- (9) N. Wang, L. Ou, and M. Liu, Phys. Rev. C 87, 034327 (2013).
- (10) B. A. Brown, Phys. Rev. Lett. 111, 232502 (2013).
- (11) P. Danielewicz, J. Lee, Nucl. Phys. A 922, 1 (2014).
- (12) M. D. Cozma, Eur. Phys. J. A 54, 40 (2018).
- (13) R. Wang, L. W. Chen, and Y. Zhou, Phys. Rev. C 98, 054618 (2018).
- (14) B. T. Reed, F. J. Fattoyev, C. J. Horowitz, and J. Piekarewicz, Phys. Rev. Lett. 126, 172503 (2021).
- (15) D. Adhikari et al. (PREX Collaboration), Phys. Rev. Lett. 126, 172502 (2021).
- (16) G. Jhang, J. Estee, J. Barney, G. Cerizza, M. Kaneko, J. W. Lee, W. G. Lynch, T. Isobe et al. (SRIT Collaboration), M. Colonna, D. Cozma, P. Danielewicz, H. Elfner, N. Ikeno, C. M. Ko, J. Mohs, D. Oliinychenko et al. (TMEP Collaboration), Phys. Lett. B 813, 136016 (2021).
- (17) J. Estee, W. G. Lynch, C. Y. Tsang, J. Barney, G. Jhang, M. B. Tsang, R. Wang, M. Kaneko et al. (SRIT Collaboration), and M. D. Cozma, Phys. Rev. Lett. 126, 162701 (2021).
- (18) M. D. Cozma, and M. B. Tsang, Eur. Phys. J. A 57, 309 (2021).
- (19) M. B. Tsang, J. Estee, H. Setiawan, W. G. Lynch, J. Barnery, M. B. Chen, G. Cerizza, P. Danielewicz et al., Phys. Rev. C 95, 044614 (2017).
- (20) W. Reisdorf et al. (FOPI Collaboration), Nucl. Phys. A 781, 459 2007; Nucl. Phys. A 848, 366 (2010); Nucl. Phys. A 876, 1 (2012).
- (21) B. A. Li, Phys. Rev. Lett. 85, 4221 (2000).
- (22) B. A. Li, Phys. Rev. Lett. 88, 192701 (2002).
- (23) G. C. Yong, B. A. Li, and W. Zuo, Chin. Phys. Lett. 22, 2226 (2005).
- (24) G. C. Yong, B. A. Li, and L. W. Chen, Phys. Rev. C 74, 064617 (2006).
- (25) G. F. Wei, X. Huang, Q. J. Zhi, A. J. Dong, C. G. Peng, and Z. W. Long, arXiv: 2112.13518.
- (26) C. B. Das, S. Das Gupta, C. Gale, and B. A. Li, Phys. Rev. C 67, 034611 (2003).
- (27) B. A. Li, C. B. Das, S. Das Gupta, and C. Gale, Phys. Rev. C 69, 011603(R) (2004).
- (28) L. W. Chen, B. A. Li, A note of an improved MDI interaction for transport model simulations of heavy ion collisions , Texas A&M University-Commerce, 2010 (Unpublished).
- (29) C. Xu, B. A. Li, Phys. Rev. C 81, 044603 (2010).
- (30) L. W. Chen, C. M. Ko, B. A. Li, C. Xu, and J. Xu, Eur. Phys. J. A 50, 29 (2014).
- (31) G. F. Wei, C. Xu, W. Xie, Q. J. Zhi, S. G. Chen, and Z. W. Long, Phys. Rev. C 102, 024614 (2020).
- (32) J. Xu, L. W. Chen, and B. A. Li, Phys. Rev. C 91, 014611 (2015).
- (33) H. Y. Kong, J. Xu, L. W. Chen, B. A. Li, and Y. G. Ma, Phys. Rev. C 95, 034324 (2017).
- (34) S. Hama, B. C. Clark, E. D. Cooper, H. S. Sherif, and R. L. Mercer, Phys. Rev. C 41, 2737 (1990).
- (35) O. Buss, T. Gaitanos, K. Gallmeister, H. van Hees, M. Kaskulov, O. Lalakulich, A. B. Larionoov, T. Leitner, J. Weil, and U. Mosel, Phys. Rep. 512, 1 (2012).
- (36) G. F. Wei, C. Liu, X. W. Cao, Q. J. Zhi, W. J. Xiao, C. Y. Long, and Z. W. Long, Phys. Rev. C 103, 054607 (2021).
- (37) G. F. Wei, B. A. Li, G. C. Yong, L. Ou, X. W. Cao, and X. Y. Liu, Phys. Rev. C 97, 034620 (2018).
- (38) G. F. Wei, G. C. Yong, L. Ou, Q. J. Zhi, Z. W. Long, and X. H. Zhou, Phys. Rev. C 98, 024618 (2018).
- (39) P. Danielewicz, and G. Odyniec, Phys. Lett. B 157, 146 (1985).
- (40) M. D. Cozma, Phys. Lett. B 700, 139 (2011).
- (41) B. A. Li, Nucl. Phys. A 708, 365 (2002).
- (42) J. R. Stone, P. Danielewicz, and Y. Iwata, Phys. Rev. C 96, 014612 (2017).