Nesting and Degeneracy of Mie Resonances of Dielectric Cavities within Zero-Index Materials

Zero-index materials (ZIMs) Liberal and Engheta (2017a); Engheta (2013), including $\varepsilon$ near zero (ENZ), $\mu$ near zero (MNZ), and both $\varepsilon$ and $\mu$ near zero (EMNZ) materials, have attracted great interest. They have been experimentally realized in natural materials Kim et al. (2016); Naik et al. (2011), engineered dispersion waveguides Edwards et al. (2008); Vesseur et al. (2013); Liberal et al. (2017), photonic crystals Huang et al. (2011), and metamaterials Maas et al. (2013); Moitra et al. (2013); Li et al. (2015); Pollard et al. (2009). Owing to near zero $\varepsilon$ or $\mu$ Liberal and Engheta (2017a); Engheta (2013), the electric field will decouple with the magnetic field in the ZIMs accompanied by constant phase distribution. With many attractive properties, like supercoupling Silveirinha and Engheta (2007, 2006); Marcos et al. (2015); Liberal et al. (2017), directional radiation phase pattern Alu et al. (2007), large optical nonlinearity Alam et al. (2018); lam et al. (2016), random control of reflection and refraction Luo et al. (2018, 2015); Nguyen et al. (2010); Liberal et al. (2018), and resonance “pinning” effect Kim et al. (2016); Schulz et al. (2016), ZIMs have been used in coherent perfect absorption Simin and Klaus (2012), cloaking Chu et al. (2018), waveguide connection Silveirinha and Engheta (2007, 2006), optical antennas Kim et al. (2016); Schulz et al. (2016), and so on. However, these studies only focus on the zero index of bulk material itself rather than the huge index contrast in and out the bulk ZIMs.

Optical cavities are ubiquitous, whose resonances can be used to manipulate light propagation, enhance light-matter interaction, modulate quantum states, and generate quantum sources. With the contrast of indexes ($\varepsilon,\mu$) in and out of the cavities, optical responses such as surface plasmon resonance Kelly et al. (2003); Kreibig and Vollmer (1995); Lian et al. (2015) and dielectric resonance Gastine et al. (1967); Affolter and Eliasson (1973); Richtmyer (1939); Jahani and Jacob (2016); Kuznetsov et al. (2016) occur, characterized as strong local field enhancement. In traditional cavities, once the wavelength is fixed, resonance nesting with different size cavity and resonance degeneracy in nanoscale cavity, though which will provide additional degree of freedom to enhance the performance of photonic devices, have never been reported before. Despite with the highest contrast ratio of $\varepsilon$ or $\mu$ in and out the cavity embedded in the ZIMs, only electric dipole resonance of dielectric cavity has been demonstrated to modify the photon-emitter interaction Liberal et al. (2016); Liberal and Engheta (2017b); Silveirinha (2014); Liberal and Engheta (2016).

Here, we analytically solve Mie resonances of dielectric spherical cavities embedded in ENZ, MNZ, and EMNZ background respectively [Fig. 1]. Unusually, for the same angular mode number $l$, a series of Mie resonances with different radii can be achieved at a fixed wavelength, so called resonance nesting. More interestingly, the $2^{l}$-TM (TE) mode of the dielectric cavity has the same resonant frequency as that of its $2^{l+1}$-TE (TM) mode for the ENZ (MNZ) material; while for EMNZ material, the resonance degeneracy occurs between its $2^{l}$-TM and $2^{l}$-TE modes. The nesting and degeneracy of optical modes originate from the ultrahigh contrast ratio of $\varepsilon$ or $\mu$ in and out the cavities. Therefore, these phenomena also exist in nonspherical dielectric cavities surrounded by ZIMs. We also find that degenerate resonances own different linewidth, in other word, as the order $l$ becomes higher, the linewidth becomes narrower. All above analytical results are confirmed by the numerical finite element method. Owing to the resonance degeneracy of optical modes enabled by ZIMs, the interference or superposition between the modes is expected. Then we used resonance degeneracy to modulate the photon-emitter interaction inside the cavity. The resonance degeneracy and nesting enabled by zero-index materials may have potential application in light manipulation, light-matter interaction, and photonic devices.

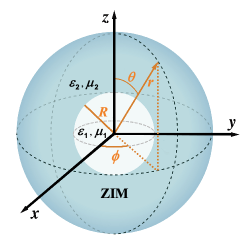
The spherical cavity with ZIM background is shown in Fig. 1. The dielectric sphere (the white part) with the radius of $R$ and dielectric constant $\varepsilon_{1}$ and magnetic permeability $\mu_{1}$ is embedded in the infinite ZIM (the blue part) with $\varepsilon_{2}$ and $\mu_{2}$. In spherical coordinate system, different optical modes of dielectric spherical cavity are usually labeled as TM_lm/TE_lm modes Mie (1908); Debye (1909); Bohren and Huffman (1976); Gastine et al. (1967); Affolter and Eliasson (1973); SM (ials), where TM means transverse magnetic mode and TE means transverse electric mode; $l=1,2,3...$, the angular mode number, decides the polarity of the modes ($2^{l}$-modes), for example, $l=1$ means the dipole mode (2-mode) and $l=2$ means the quadrupole mode (4-mode); $m$ is the azimuthal mode number and satisfies $m\leq l$. As solving the Mie resonances of the cavity modes, we can take $m=0$ as an example because $m$ has no effect on the resonance conditions. On this premise, Mie resonances of cavity modes can be categorized into $2^{l}$-TM and $2^{l}$-TE Mie resonances.

First considering the $2^{l}$-TM modes in the spherical cavity, because the magnetic field of the TM modes has no radial component, so the electromagnetic fields inside and outside the sphere can be written as SM (ials):

where $a$ and $c$ are coefficients to be determined, $\bf M$ and $\bf N$ are two sets of Mie bases Mie (1908); Debye (1909); Bohren and Huffman (1976) on which the electromagnetic field can be expanded. ${\bf M}_{l}^{(j=1,2,3)}=-\dfrac{\partial\mathrm{P}_{l}}{\partial\theta}z_{l}^{(j)}(x)\hat{\mathbf{e}}_{\phi}$, and ${\bf N}_{l}^{(j=1,2,3)}=\dfrac{z_{l}^{(j)}(x)}{x}l(l+1)\mathrm{P}_{l}\hat{\mathbf{e}}_{r}+\dfrac{1}{x}\dfrac{\partial\left[xz_{l}^{(j)}(x)\right]}{\partial x}\dfrac{\partial\mathrm{P}_{l}}{\partial\theta}\hat{\mathbf{e}}_{\theta}$, in which $x=kr$ and $k$ is the wavenumber, labeled as $k_{1}$ in the sphere and $k_{2}$ out the sphere; $z_{l}^{(j)}$ mean different kind of spherical harmonic functions respectively: spherical Bessel function $j_{l}$, spherical Neumann function $n_{l}$, and spherical Hankel function of the first kind $h_{l}^{(1)}$ which is a linear combination of $j_{l}$ and $n_{l}$, i.e. $h_{l}^{(1)}=j_{l}+in_{l}$. For simplicity, we make $\eta_{l}(x)\equiv xj_{l}(x),\zeta_{l}(x)\equiv xn_{l}(x),\xi_{l}(x)\equiv xh_{l}^{(1)}(x)$. $P_{l}$ is the associated Legendre function. More details are shown in Ref. SM (ials).

According to the continuous tangential electric field strength and magnetic field strength on the boundary ($r=R$), for the $2^{l}$-TM modes we get a linear equations with two coefficients $a$ and $c$ SM (ials):

in which $\rho=k_{1}R$, $\tilde{\varepsilon}=\varepsilon_{2}/\varepsilon_{1},\tilde{\mu}=\mu_{2}/\mu_{1},s=k_{2}/k_{1}=\sqrt{\tilde{\varepsilon}\tilde{\mu}}$.

When the spherical cavity is resonant, $a$ and $c$ would go to extrema, which can be satisfied when the denominators of $a$ and $c$ are zero:

This is the limit situation for the resonance, whose premise of real solution can be naturally met by ZIMs with $s\approx 0$. In addition, with $s\approx 0$, $\xi_{l}(s\rho)\approx a_{l}(s\rho)^{-l}$ and $\xi_{l}^{\prime}(s\rho)\approx(-l)a_{l}(s\rho)^{-(l+1)}$ SM (ials), substituting them into Eq. (3), we obtain:

which is the ideal Mie resonance condition for the $2^{l}$-TM modes of spherical cavity embedded in ZIMs. Furthermore, for ENZ and EMNZ media, $\tilde{\varepsilon}\approx 0$, so Eq. (4) can be simplified to $\eta_{l}(\rho)=0$. Ideal resonance conditions only can be achieved when $s=0$ or $s$ is very near zero, but in fact, the small imaginary part of $\varepsilon_{2}$ or $\mu_{2}$ will make a little influence on the $2^{l}$-TM Mie resonances SM (ials).

It is worth mentioning that in addition to ZIMs, $s\approx 0$ can also be satisfied by the situation that $\varepsilon_{1}\gg\varepsilon_{2}$, i.e. the high index cavity embedded in low index material (like air). However, as discussed in Ref. SM (ials), the same resonant conditions as above can be achieved only when $\varepsilon_{1}$ is very high (more than 900).

For the $2^{l}$-TE modes in the spherical cavity, the electromagnetic fields inside and outside the sphere are written as SM (ials):

where $b$ and $d$ are coefficients to be determined,

According to the continuous tangential electric field strength and magnetic field strength on the boundary ($r=R$), for the $2^{l}$-TE modes we can get a linear equations with two unknown numbers $b$ and $d$ SM (ials):

When in resonant, for $s\approx 0$, the determinant of the coefficients of $b$ and $d$ should be zero, i.e.

Take further simplification of $\xi_{l}(s\rho)$, and we can get:

which is the ideal Mie resonance condition for the $2^{l}$-TE modes of spherical cavity embedded in ZIMs. Specially, for MNZ and EMNZ media, $\tilde{\mu}\approx 0$, so Eq. (8) can be simplified to $\eta_{l}(\rho)=0$. Similarly, the small imaginary part of $\varepsilon_{2}$ or $\mu_{2}$ will have effect on the $2^{l}$-TE Mie resonances but different with that on the $2^{l}$-TM Mie resonances SM (ials).

The Mie resonance conditions for $2^{l}$-TM and $2^{l}$-TE modes of dielectric spherical cavity placed in ENZ, MNZ, or EMNZ media are listed in Table. 1B. When the background varies from ENZ to EMNZ, the resonance conditions of the $2^{l}$-TM modes have no change, but that of the $2^{l}$-TE modes are modulated and become the same as the $2^{l}$-TM modes when $\mu_{2}$ is also near zero. For the MNZ background, vice versa SM (ials).

It can be seen that the resonance conditions are related to $\eta_{l}(\rho)$ and its derivative $\eta_{l}^{\prime}(\rho)$. Give the expression of $\eta_{l}(\rho)$ with $l=1,2,3$:

Using the above formula and Table. 1B, we can get the resonance conditions for 2-, 4-, and 8- TE/TM modes, which are listed in Table. 1B. For conciseness, we use A to indicate $\sin\rho-\rho\cos\rho=0$, B to $\sin\rho=0$, C to $(3-\rho^{2})\sin\rho-3\rho\cos\rho=0$ and D to $(15-6\rho^{2})\sin\rho-(15\rho-\rho^{3})\cos\rho=0$. More specially, if the refractive index $n=\sqrt{\varepsilon_{1}\mu_{1}}$ of the sphere is 1, the resonant condition A can be replaced by $R/\lambda=0.7151,1.2295...$, B by $R/\lambda=0.5,1.0...$, C by $R/\lambda=0.9173,1.4475...$, and D by $R/\lambda=1.1122,1.6579...$, where $\lambda$ is the wavelength in the vacuum.All above results are confirmed by the numerical finite element method SM (ials). While when the refractive index $n$ is not 1, the $nR/\lambda$ will be the above values when resonant.

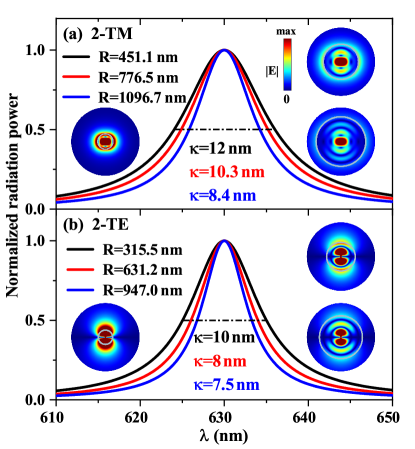
Different to plasmonic particles embedded in non-zero index media that usually have only one resonant $R/\lambda$ value for one mode Kelly et al. (2003); Kreibig and Vollmer (1995); Lian et al. (2015); Duan et al. (2019), in the spherical cavity with ZIM background, there are series of $R/\lambda$ values for each $2^{l}$-TM/TE Mie resonance. Namely, if the optical wavelength is fixed, the same Mie resonance can be achieved in spherical cavities with different radii $R$, which is called as “resonance nesting”. As shown in Fig. 2, when the resonant wavelength is fixed at 630 nm ( take an example, also can be at other wavelengths SM (ials)), the radiation power ($P=\oiint\frac{1}{2}\operatorname{Re}\left(\vec{E}^{*}\times\vec{H}\right)\cdot\mathrm{d}\vec{S}$ ) spectra of 2-TM resonance for ENZ case are analytically obtained at $R=451.1$ nm, 776.5 nm, 1096.7 nm…, and the spectra of 2-TE resonance at $R=315.5$ nm, 631.2 nm, 947.0 nm…. It can be seen from the insets of Fig. 2 (a) (or (b)) that the electric field distributions of the three cavities are consistent in form, which just implies these cavities support the same kind resonance. While the values of cavity loss $\kappa$ are different, and the larger the cavity, the smaller the loss, because of the increase of lossless energy storage space. It is noted that, the resonant $R/\lambda$ values are little bigger than ideal values due to the imaginary part of $\varepsilon_{2}$, and approach ideal values with decreasing the imaginary part SM (ials). Besides, the resonance nesting of 2-/4- modes for different ZIMs background is shown in Ref. SM (ials).

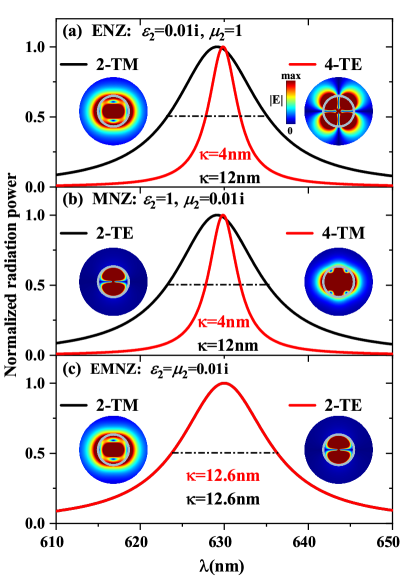
In addition to the nesting of the same polar mode, there is also the degeneracy between different polar modes. From Table. 1B, it can be seen that for the ENZ case when $\mu_{1}=\mu_{2}$, the $2^{l}$-TM and $2^{l+1}$-TE Mie resonances have the same resonance condition, i.e. the same cavity can support both $2^{l}$-TM and $2^{l+1}$-TE modes at the same wavelength. Fig. 3 (a) gives the normalized radiation power spectra of the 2-TM mode and 4-TE mode in the air cavity with $R=450.5$ nm embedded in ENZ background with $\varepsilon_{2}=0.01i$ and $\mu_{2}=1$. The little resonance shifts of the two modes originate from the effect of imaginary part of $\varepsilon_{2}$ SM (ials). Furthermore, the values of $\kappa$ of the two degenerate modes are different, i.e., $\kappa=12$ nm for the 2-TM mode but $\kappa=4$ nm for the 4-TE mode. In a word, the same cavity support two modes with different loss: the higher the $l$, the smaller the loss, due to less radiation. The electric field distribution, for 2-TM mode, is discontinuous on the boundary due to the exist of radial component of $\bf E$ which suddenly changes with the high contrast ratio of $\varepsilon_{2}$ and $\varepsilon_{1}$; but for 4-TE mode, the opposite is true SM (ials).

The resonant degeneracy also happens between the $2^{l}$-TE and $2^{l+1}$-TM Mie resonances for the MNZ case when $\varepsilon_{1}=\varepsilon_{2}$ [Table. 1B]. As shown in Fig. 3 (b), the normalized radiation power spectra of the $2^{l}$-TE (TM) mode for the MNZ case are same with that of the $2^{l}$-TM (TE) mode for the ENZ case, because of the symmetry of electromagnetic field expressions. In the same way, the little difference between the resonant wavelength of the 2-TE and 4-TM modes caused by the influence of imaginary part of $\mu_{2}$ (here $\mu_{2}=0.01i$ and $\varepsilon_{2}=1$). The electric field distribution, no matter for 2-TE or 4-TM mode, is continuous on the boundary because $\varepsilon_{2}=\varepsilon_{1}$; and specially for the 2-TE mode, the electric field is almost zero out the sphere. The magnetic field distribution of the $2^{l}$-TM mode of ENZ case is same with the electric distribution of the $2^{l}$-TE mode of the MNZ case, and vice versa.

For the EMNZ case, the resonant degeneracy occurs between the $2^{l}$-TM and $2^{l}$-TE modes. It can be seen from the Fig. 3 (c) that the normalized radiation power spectra for 2-TM and 2-TE modes overlaps together with the same cavity loss $\kappa=12.6$ nm. The electric field distribution of the 2-TM mode has the same form with that in the ENZ case and the 2-TE mode is similar with that in the MNZ case. Although resonance conditions of $2^{l}$-TM mode for ENZ case, $2^{l}$-TE mode for MNZ case and $2^{l}$-TM mode for EMNZ case have the same form, but they can not be regarded as degenerate because of the different electromagnetic backgrounds.

Next, we used resonance degeneracy to study the photon-emitter interaction. Here, we take the air cavity with radius $R=451.1$ nm embedded in ENZ medium as an example. Choosing the surface where the electric field strength out the cavity is reduced to $1/e$ of that on the boundary, we estimate that the mode volume is about $11R^{3}$, and then the coupling strength $g$ is no more than 1meV when the transition dipole moment is 0.5 enm SM (ials); Ren et al. (2017), much lower than the cavity loss $\kappa$ which is about 37 meV for 2-TM mode and 12.5 meV for 4-TE mode SM (ials). So the interaction between the photon and the dipole emitter is at the weak coupling region in this system, and then we study the Purcell effect Purcell (1946) of the emitter.

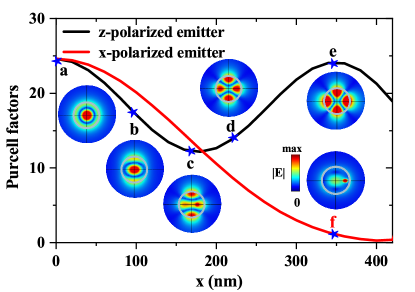
We build spherical module in the COMSOL Multiphysics software to calculate Purcell factors by the the ratio of the radiated power of the emitter in the cavity and that of the emitter in the vacuum SM (ials). When the dipole emitter is at the center of the cavity, only the 2-TM mode can be excited, but the 4-TE mode can be inspired when the emitter moves to the edge [Fig. 4]. For the $z$-polarized emitter, the 2-TM mode (point a ) or 4-TE mode (point e and d) or both of them (points b and c) can be excited and the Purcell factor can keep above 10. It experiences two maximum values due to the interference or superposition between 2-TM mode and 4-TE modes. While for the $x$-polarized emitter, no matter where the emitter is, only the 2-TM mode is excited and the Purcell factor decrease to zero near the boundary. In addition, the Purcell factors will increase greatly if the imaginary part of the background decreases SM (ials).

In summary, we have analytically solved the Mie resonances of dielectric spherical cavities embedded in the ENZ, MNZ, and EMNZ materials. We have theoretically revealed the phenomena of resonance nesting and resonance degeneracy existing in zero-index materials. The nesting and degeneracy originate from the high contrast ratio of $\varepsilon$ or $\mu$ in and out the cavities, thus if the cavities with large $\varepsilon$ or $\mu$ embedded in the low index materials, the same phenomena will occur SM (ials). Owing to possessing the same physical principle, resonance nesting will also exist in other geometrical cavities embedded in ZIMs and resonance degeneracy will occur in spherical symmetrical cavities because of the common spherical harmonics. In contrast to previous mode degeneracy generally occurring between $+l$ and $-l$, the mode degeneracy here with different angular mode number $l$ will provide an additional way to realize quantum entanglement and quantum operation. The resonance degeneracy enabled by ZIMs may have potential application in light manipulation, light-matter interaction, and photonic devices.