Nested Closed Paths in Two-Dimensional Percolation
Abstract
For two-dimensional percolation on a domain with the topology of a disc, we introduce a nested-path operator (NP) and thus a continuous family of one-point functions , where is the number of independent nested closed paths surrounding the center, is a path fugacity, and projects on configurations having a cluster connecting the center to the boundary. At criticality, we observe a power-law scaling , with the linear system size, and we determine the exponent as a function of . On the basis of our numerical results, we conjecture an analytical formula, where , which reproduces the exact results for and agrees with the high-precision estimate of for other values. In addition, we observe that for site percolation on the triangular lattice with any size , and we prove this identity for all self-matching lattices.
Introduction —
Percolation BroadbentHarmmersley57 ; StaufferAharony1994 ; Grimmett1999 ; BollobasRiordan2006 is a paradigmatic model in the field of phase transitions and critical phenomena and a central topic in probability theory. It also finds important applications in various fields such as fluids in porous media hunt2014percolation , gelation stauffer1982gelation and epidemiology Meyers2007 . Bond percolation corresponds to the limiting case in the Fortuin-Kasteleyn cluster representation of the -state Potts model Potts ; FK , and provides a simple illustration of many important concepts for the latter FYWu . In two dimensions (2D), the algebraic use of symmetries—lattice duality KW41 , Yang-Baxter integrability Lieb67 ; Baxter72 and conformal invariance BPZ84 ; FQS84 —has led to a host of exact results. Critical exponents are predicted by Coulomb-gas (CG) arguments Nienhuis1987 , conformal field theory Cardy1987 and Stochastic Loewner Evolutions LawlerSchrammWerner2001 , and have been proven rigorously for e.g. triangular-lattice site percolation Smirnov2001 .
In site percolation, the sites of a lattice are occupied with probability and empty otherwise. A sequence of distinct, occupied sites of which each is nearest neighbor to its predecessor is called a path. Two occupied sites are connected if there is a path from one to the other. Two paths are independent if they do not have a site in common. A closed path has neighboring first and last sites. A maximal set of connected sites is called a cluster.
In bond percolation, the edges or bonds of the lattice are occupied with probability , or vacant (empty). Paths, connectivity and clusters follow the same definitions as in site percolation, with sites replaced by bonds of the lattice, and nearest neighbor by having a site in common. Two paths are independent if they do not have a bond in common, and do not cross, but they may share a site.
Clusters and paths can also be introduced for empty elements. For bond percolation, these paths and clusters typically consist of bonds on the dual lattice. A dual bond is occupied if the (primal) bond it intersects is empty, and vice versa. For this reason, the paths on empty elements are often referred to as dual.
A path between two regions is typically not unique. In contrast, cluster boundaries form trajectories which are uniquely determined by the configuration. Two different cluster boundaries are by nature non-overlapping.
Cluster boundaries define two families of exponents, which have been computed by CG methods. The so-called watermelon exponents BN1984 ; DupSal1987 govern the probability that two (or more) distant regions are connected by a given number, say , of cluster boundaries. The watermelon exponents have the value .
The second, continuous family governs the correlation function of what we here here call the nested-loop operator (see dNijs1983 ; MitNie2004 ). This operator gives a weight, say , to each cluster boundary surrounding the insertion point (multiple such boundaries must be nested, whence the name). Its two-point function gives a weight to those cluster boundaries that surround one, but not both of the insertion points. The corresponding exponent is
| (1) |
Analogous to are the so-called monochromatic -path exponents , governing the decay of probability that between two distant regions there are independent paths, all on clusters (or, equivalently, all on dual clusters). The case means that no cluster boundary separates the two regions, so . But the exponents for (backbone exponent) or higher do not appear amenable to CG analysis, and hence they are known only numerically JacZinn02 ; BefNol2011 ; Xu2014 . As a side-remark we mention that when one or more, but not all, of the paths are on dual clusters, the exponents are different and in fact identical to Aizenman1999 ; BefNol2011 .
In this Letter we propose to similarly consider the path analogue of the nested-loop operator: the nested-path (NP) operator. It gives a weight to each independent closed path surrounding the insertion point. We investigate here the exponent of this operator by numerical means. For simplicity, we simulate its one-point function: 2D percolation with the NP operator placed at the center of a compact domain of linear dimension . We thus estimate the expectation value , where is the indicator function of a path from the center to the boundary of the domain, and the number of independent closed paths surrounding the center. The factor ensures that two consecutive surrounding paths are connected, rather than separated by two cluster boundaries. The configurations with we call percolating.
Results, summary —
We show that, at the percolation threshold, the scaling of obeys a power law with an exponent , that depends continuously on the weight . A high-precision estimate of is obtained as a function of . For , we observe that for site percolation on the triangular lattice with any , and prove this to be true for any self-matching lattice SykesEssam64 . We present an analytical formula (3), analogous to (1), which reproduces some exact values and agrees so well with the numerical results, that we conjecture it to be exact.
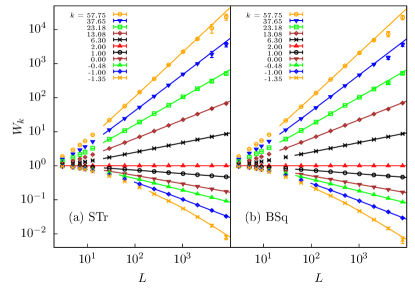
Results, details —
We study site percolation on a triangular lattice (STr) in a hexagonal domain with free boundaries. The scale is the length of the diagonal. Fig. 1a shows a sample configuration, with . The central site is neutral, and the other sites are occupied with probability . For each configuration we calculate the number of independent closed paths that surround the center, and which is 1 (0) if there is (not) a path from the center to the boundary. While is well-defined, the paths are not unique. In Fig. 1a, and .
Analogous procedures are applied to bond percolation on the square lattice (BSq), see Fig. 1b, with a neutral bond placed at the center, and the length of the diagonal, .
We are interested in the scaling behavior of at the percolation threshold . For , represents the probability that the central site is connected to the boundary, which is seen from (1) to decay as . The contributions to are those, which have a path from the center to the boundary, but no closed path surrounding the center. These configurations must have a path of occupied and one of empty elements from the center to the boundary and consequently two cluster boundaries connecting the center to the boundary. These events are selected for the watermelon exponent . Thus, proposing , we already know that and .
We carry out extensive simulations for STr and BSq at the percolation threshold , with geometric shapes as in Fig. 1. The linear size is taken in range . For both models and each , the number of samples is at least for , for , for , and for .
A log-log plot of versus is shown in Fig. 2. The data clearly support asymptotic power-law dependence of on . We fit (by least squares) the data to
| (2) |
We admit only data points with for the fits, and systematically study the effect on the residual value (weighted according to confidence level) when varying . In the best fits, . The results with are given in Tab. 1. The estimates of and agree well with the exact values and , respectively. Table 1 strongly indicates that for .
| -1 | -3/4 | -1/2 | -1/4 | 0 | |
| 23.18 | 15.26 | 9.329 | 5.018 | 2 | |
| conj | -0.8125 | -0.6177 | -0.41964 | -0.21591 | 0 |
| STr | -0.813(5) | -0.619(2) | -0.421(1) | -0.216(1) | -0.0000(2) |
| BSq | -0.810(2) | -0.617(1) | -0.4192(5) | -0.215(2) | 0.0004(5) |
| 1/9 | 1/4 | 1/3 | 3/8 | 4/9 | |
| 1 | 0 | -0.4812 | -0.6915 | -1 | |
| conj | 0.10417 | 0.25 | 0.3542 | 0.4152 | 0.5417 |
| STr | 0.1043(2) | 0.2500(3) | 0.354(2) | 0.414(2) | 0.544(6) |
| BSq | 0.1044(4) | 0.2503(6) | 0.355(1) | 0.416(2) | 0.551(6) |
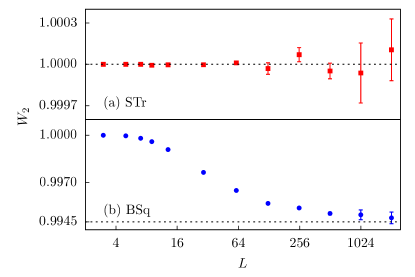
The data for STr and BSq are listed in Tab. 2 and plotted in Fig. 3 versus . For STr we find for by exact enumeration, and for larger within statistical errors, that . For BSq, we find for and for , shown in Tab. 2 together with simulation data for larger . As increases, converges to a value slightly smaller than, and clearly different from 1. A least-squares fit for , gives the asymptotic value as . Thus, we conjecture in general, and, for STr, .
| 3 | 5 | 7 | 9 | |
| STr | 1 | 1 | 1 | 0.999993(4) |
| BSq | 1 | 0.999963283 | 0.999807(5) | 0.999594(6) |
| 13 | 29 | 61 | 125 | |
| STr | 0.999997(6) | 0.999997(7) | 1.000010(9) | 0.99997(4) |
| BSq | 0.999088(5) | 0.99764(1) | 0.99649(1) | 0.99567(5) |
| 253 | 509 | 1021 | 2045 | |
| STr | 1.00007(5) | 0.99995(6) | 0.9999(2) | 1.0001(2) |
| BSq | 0.99538(6) | 0.99503(8) | 0.9949(3) | 0.9948(4) |
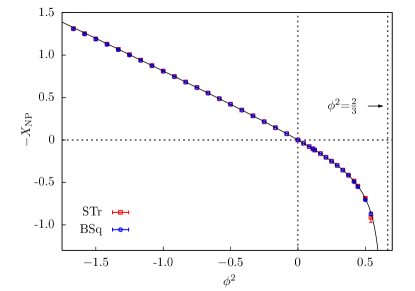
Then, in an attempt to find a formula analogous to (1), we set and plot as a function of , as shown in Fig. 4. Noting (i) , (ii) an apparent pole for some positive , and (iii) an asymptotic slope of 3/4 for negative , just as , (1), it is natural to propose as the simplest rational function that matches these observations. Then the exact results for and fix
| (3) |
in which some well-known exponents of 2D percolation seem to appear. The excellent agreement with the numerical results shown in Fig. 4 and Table 1, leads us to conjecture that (3) is exact. But, in spite of some similarity with (1) we have not found any theoretical basis for (3).
Method —
In simulations, each site (bond) is randomly occupied with probability , a cluster is grown from the center by standard breadth-first search. If the cluster does not reach the boundary, and there is no contribution to . Otherwise, we compute the number of paths surrounding the center. This can be achieved efficiently by the following algorithm.
The -th path surrounding the center acts as the seed of one or more dual (empty) clusters, linked together by the -th surrounding path. By growing the dual clusters from the -th surrounding path, one can locate the -th path as the chain of occupied sites (or bonds) that stops the dual-cluster growth. A caveat is that for BSq the dual cluster consists of bonds of the dual lattice. Algorithm 1 sketches the corresponding procedure, in which is the region that is encircled by the next surrounding path. It is written for STr, but when sites are replaced by bonds, and adjacent sites by bonds sharing a site, it works for BSq too.
Proof of the identity
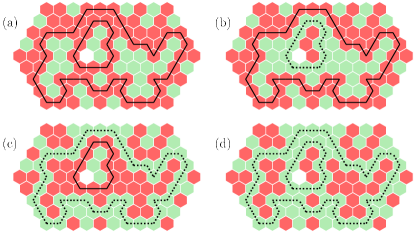
for STr — Take an arbitrary STr configuration on a simply connected piece of the lattice, with a distinguished, ‘central’ site. Consider a maximal set of independent paths surrounding the center, with each path consisting either of only occupied (red) sites or of only empty (green) sites. The innermost such colored paths, given the interior ones, are uniquely defined (and can be constructed by Algorithm 1).
Let be the number of these nested paths. By we denote the map that inverts (red green) the color of path (counted from the center), and of all sites strictly between path and path (or between path 1 and the center). Fig. 5 shows four configurations, related to each other by the maps .
Since , the set generates equiprobable configurations. Within this ensemble, , if and only if all the paths are occupied. The entire ensemble can be generated by the from any of its members. Therefore all configurations are member of precisely one such ensemble, and as a consequence .
An essential property used in the proof is that inverting a path of occupied sites surrounding the center creates a barrier preventing a path of occupied sites to connect the center with the boundary. This is an obstacle against applying the proof to BSq, where a path of occupied bonds can cross a path of empty bonds, see SupMat for more explanation.
The regularity of the lattice and of the domain are not used in the proof, but having is crucial. However, for any self-matching lattice, and in particular for lattices of which all faces are triangles. Hence, the result is also valid for regular or irregular planar triangulation graphs, of any shape and position of the center.
Discussion —
We construct a new family of geometric quantities for critical percolation in two dimensions and determine a continuous set of critical exponents with high precision. An identity , independent of the linear size , is found for triangular-lattice site percolation and proven for any lattice with only triangular faces. This implies an exact exponent . The universality of the critical exponent is well supported by simulations for both bond and site percolation. Apart from the special cases , the exact values of are unknown. We conjecture an analytical function, Eq. (3), which reproduces the known exact results and agrees excellently with numerical estimates of for other values. We note that, though Eq. (3) is somewhat similar to existing results, proving it remains elusive.
Future work will involve the -state Potts model in the Fortuin-Kasteleyn cluster representation, which includes bond percolation as a special case for .
Acknowledgements.
This work was supported by the National Natural Science Foundation of China (under Grant No. 11625522), the Science and Technology Committee of Shanghai (under grant No. 20DZ2210100), the National Key R&D Program of China (under Grant No. 2018YFA0306501), and the European Research Council (under the Advanced Grant NuQFT).References
- (1) S. R. Broadbent and J. M. Hammersley, Percolation Processes, Math. Proc. of the Cambridge Phil. Soc. 53, 629 (1957).
- (2) D. Stauffer and A. Aharony, Introduction to percolation theory (Taylor & Francis, London, 1994), 2nd ed.
- (3) G. R. Grimmett, Percolation (Springer, Berlin, 1999), 2nd ed.
- (4) B. Bollobás and O. Riordan, Percolation (Cambridge University Press, 2006).
- (5) A. Hunt, R. Ewing and B. Ghanbarian, Percolation theory for flow in porous media (Springer, 2014), 3rd ed.
- (6) D. Stauffer, A. Coniglio and M. Adam, Gelation and critical phenomena (Springer, 1982).
- (7) L. Meyers, Contact network epidemiology: Bond percolation applied to infectious disease prediction and control, Bulletin of the American Mathematical Society 44(1), 63-86 (2007).
- (8) P.W. Kasteleyn and C.M. Fortuin, Phase transitions in lattice systems with random local properties, J. Phys. Soc. Jpn. 26 Suppl., 11 (1969).
- (9) R. B. Potts, Some generalized order-disorder transformations, Proc. Cambridge Philos. Soc. 48, 106 (1952).
- (10) F. Y. Wu, The Potts model, Rev. Mod. Phys. 54, 235 (1982).
- (11) H. A. Kramers and G. H. Wannier, Statistics of the two-dimensional ferromagnet. Part I, Phys. Rev. 60, 252 (1941).
- (12) E. H. Lieb, Exact solution of the problem of the entropy of two-dimensional ice, Phys. Rev. Lett. 18, 692 (1967).
- (13) R. J. Baxter, Partition function of the eight-vertex lattice model, Ann. Phys. (NY) 70, 193 (1972).
- (14) A. A. Belavin, A. M. Polyakov and A. B. Zamolodchikov, Infinite conformal symmetry in two-dimensional quantum field theory, Nucl. Phys. B 241, 333 (1984).
- (15) D. Friedan, Z. Qiu and S. Shenker, Conformal invariance, unitarity, and critical exponents in two dimensions, Phys. Rev. Lett. 52, 1575 (1984).
- (16) B. Nienhuis, in Phase transitions and critical phenomena, edited by C. Domb, M. Green and J. L. Lebowitz (Academic Press, London, 1987), Vol. 11.
- (17) J. L. Cardy, in Phase transitions and critical phenomena, edited by C. Domb, M. Green and J. L. Lebowitz (Academic Press, London, 1987), Vol. 11.
- (18) G. F. Lawler, O. Schramm and W. Werner, The dimension of the planar Brownian frontier is 4/3, Math. Res. Lett. 8, 401 (2001).
- (19) S. Smirnov and W. Werner, Critical exponents for two-dimensional percolation, Math. Res. Lett. 8, 729 (2001).
- (20) B. Duplantier and H. Saleur, Exact determination of the percolation hull exponent in two dimensions, Phys. Rev. Lett. 58, 2325 (1987)
- (21) B. Nienhuis, Critical behavior in two dimensions and charge asymmetry of the Coulomb gas, J. Stat. Phys. 34, 731 (1984).
- (22) S. Mitra and B. Nienhuis, Exact conjectured expressions for correlations in the dense O(1) loop model on cylinders, J. Stat. Mech.: Theory Exp., P10006 (2004)
- (23) M. den Nijs, Extended scaling relations for the magnetic critical exponents of the Potts model, Phys. Rev. B 27, 1674 (1983).
- (24) J. L. Jacobsen and P. Zinn-Justin, Monochromatic path crossing exponents and graph connectivity in 2D percolation, Phys. Rev. E 66, 055102(R) (2002).
- (25) V. Beffara and P. Nolin, On monochromatic arm exponents for 2D critical percolation, The Annals of Probability 39, 1286–1304 (2011).
- (26) X. Xu, J. F. Wang, Z. Z. Zhou, T. M. Garoni and Y. J. Deng, Geometric structure of percolation clusters, Phys. Rev. E 89, 012120 (2014).
- (27) M. Aizenman, B. Duplantier and A. Aharony, Path-crossing exponents and the external perimeter in 2D percolation, Phys. Rev. Lett. 83, 1359 (1999).
- (28) M. F. Sykes and J. W. Essam, Exact critical percolation probabilities for site and bond problems in two dimensions, J. Math. Phys. 5, 1117 (1964).
- (29) See Supplemental Material at [URL] for an explanation why the proof for STr does not work for BSq, and an attempt to remedy that situation.
Supplementary material with
Nested Closed Paths in Two-Dimensional Percolation
Y.-F. Song,
X.-J. Tan,
X.-H. Zhang,
J.L. Jacobsen,
B. Nienhuis,
Y. Deng
Applicability of the proof of
The proof that for site-percolation on lattices with only triangular faces fails for bond-percolation on e.g. the square lattice. This note explains why, and discusses some unsuccesful attempts to remedy this.
The first issue is that in the proof we consider paths both on occupied and on empty sites, occupied paths and empty paths, for short. For bond percolation there is a choice how to construct the empty paths; this is between (i) the bonds of the lattice that happen to be empty, or (ii) the bonds of the dual lattice at the positions where the primal bond is empty. The proof uses two properties of the relation between occupied and empty paths: (a) an occupied path becomes an empty path (and v.v.) under inversion, and (b) an empty path and an occupied path cannot cross. With choice (i) we have property (a) but not (b), and with choice (ii) we property (b) but not (a). Fig. 6 below illustrates these facts. As a consequence, a straightforward translation of the proof for BSq is not possible.
One may consider an alternative definition of that would allow to reconstruct the proof. A central concept in the proof is the inversion transformation of a path and (a part of) its interior. Under such transformation a path remains a path but changes color. This seems to make choice (ii) hopeless.
So we concentrate on choice (i), and consider bonds and paths on the primal lattice only. Then we have to deal with the difficulty that paths can cross each other. We rule out crossing paths of the same color by construction, so that it is still possible to define innermost paths. But crossing paths of different colors are difficult to rule out, as in this case one must give precedence to one or the other.
Thus the restriction that the center is connected to the boundary over an occupied path, does not rule out the existence of an empty path surrounding the center. It is tempting to redefine by giving the weight to each occupied path surrounding the center, while demanding there are no empty paths surrounding the center, this condition replacing the one that an occupied path connects the center to the boundary. But for a configuration with occupied and empty paths, both surrounding the center, and crossing each other, we did not succeed to define the transformations appropriately. The difficulties are illustrated in Fig. 7a showing a configuration in which the center (black circle) is surrounded by both an occupied and an empty path. If the empty path is inverted, the resulting configuration has two occupied paths, but with a different structure (b). One may argue that in the original definition, not only the path itself, but also (part of) its interior was inverted. But inverting the empty path with its interior results in an even less hopeful configuration, with only one surrounding path left (Fig. 7c).
In conclusion, we have not found a variant definition of such that we can prove that also for BSq.