Neptune’s ring arcs confined by coorbital satellites: dust orbital evolution through solar radiation
Abstract
Voyager 2 images confirmed the presence of ring arcs around Neptune. These structures need a confinement mechanism to constrain their spreading due to collisions, dissipative forces, and differential keplerian motion. Here we report the results of a set of numerical simulations of the system formed by Neptune, the satellite Galatea, dust ring particles and hypothetical co-orbital satellites. This dynamical system depicts a recent confinement mechanism formed by four co-orbital satellites being responsible for the azimuthal confinement of the arcs, while Galatea responds for their radial confinement. After the numerical simulations, the particles were divided into four groups: particles that stay in the arcs, transient particles, particles that leave the arcs to the Adams ring and particles that collide with the co-orbital satellites. Our results showed that in all arcs the lifetime of the smaller particles is at most 50 years. After 100 years about of the total amount of larger particles is still present in the arcs. From our numerical simulations, the particles should be present in all arcs after 30 years, the period between the discovery of the arcs up to now. Our results can not explain the disappearance of the leading arcs, Liberté and Courage, unless the arcs are formed by different particle sizes. Analysis of the dust production, due to collisions between interplanetary debris onto the surface of the co-orbital satellites, ruled out the hypothesis that small satellites close to or in the arc structure could be its source.
keywords:
planets and satellites: rings, dynamical evolution and stability1 Introduction
The arcs, previously detected by stellar occultation in 1984 (Sicardy et al., 1991), are the densest parts of the tenuous Adams ring (Hubbard et al., 1986). The Liberté, Egalité and Fraternité arcs have azimuthal widths of about 4∘, 4∘ and 10∘, respectively, while the Courage arc has 2∘ of azimuthal width; all of them have about 15km of radial width.
Corotation and Lindblad resonances are essential to the confinement mechanism. The corotation resonance prevents the arc of an azimuthal spreading, while the Lindblad resonance prevents its radial spreading. A previous analysis considered the satellite Galatea as the shepherd satellite of the four arcs (Porco, 1991). The 84:86 corotation inclined resonance and the 42:43 outer Lindblad resonance kept the radial and azimuthal widths of the arcs. The corotation inclined resonance (CIR) induces the formation of 84 equilibrium points, although only five of them are populated by arc particles, the Fraternité arc occupies two sites. Further data on the mean motion of the arcs showed that their semi-major axis is displaced from the corotation resonant semi-major axis (Namouni & Porco, 2002), leaving the arcs without azimuthal confinement.
Foryta & Sicardy (1996) analysed the coupling between three resonances with Galatea ( 84:86 CIR, 84:86 Lindblad inclined resonance (LIR), and 42:43 Lindblad eccentric resonance (LER)) and its effect on the particles motion. They obtained that the eccentricity forced by the LER results in collisions with relative velocities on the order of 1m/s that drive out larger arc particles. These particles are believed to be the source of the dust observed in the arcs. They also noticed that solar radiation pressure removes dust particles from the corotation sites in a few decades.
Recent observations obtained from the Keck II and the Hubble Space Telescope showed that the arcs have changed both in location and brightness since their discovery. All the arcs may have decayed in intensity, and the Liberté and Courage arcs have almost disappeared (de Pater, 2005; Showalter et al., 2013).
A recent confinement model proposes that the Adams ring has a collection of small co-orbital satellites located in specific positions (Renner et al., 2014). These co-orbital satellites would be responsible for maintaining the arc particles in stable azimuthal positions, while Galatea prevents their radial spreading. In detail, this model consists of four small co-orbital satellites (, , and ), where , and are azimuthally placed at longitudes , and , respectively, from (at ). The equilibrium positions of , and are close to the Lagrangian point (or ) of the satellite . Besides their specific positions, to guarantee the nominal location of the arcs in the Adams ring, their masses were accurately calculated to keep them in stable positions (Renner et al., 2014). For a density of 1 g/cm3, the larger co-orbital satellite has a radius of 5.2km and the smallest one has a radius of 1.1km (Renner et al., 2014), all below the detection limit of the Voyager instruments and the recent telescopes’ data.
A recent paper by Hearn et al. (2019) studied the dynamics of multiple massive bodies in corotation resonance through numerical simulations. Their results showed that the bodies exchanged angular momentum and energy during the encounter which changes their orbits. Although it does not mean that if one body moves closer to the resonance the other would move further from the resonance. They explained that this occurs because the timescale of the close encounters is short when compared with the synodic period of the particles and the body. They argued that the exchange in the energy may be similar to a collisional system, although a detailed investigation is necessary.
In the current work is studied the orbital evolution of a set of arc dust particles to estimate their lifetime. Section 2 deals with the gravitational effects on the arc particles, no dissipative force is included in the system. In section 3 we discuss the orbital behaviour of the particles under the solar radiation force, while in section 4 we analyse the dust production rate and its role as a source of the arc particles. In the last section, we discuss our results.
2 Orbital evolution of the arc particles
In this section, we analyse the evolution of the arc particles assuming that Galatea is in a circular and equatorial orbit (case 1) and in an inclined eccentric orbit (case 2).
The dynamical model evokes the presence of four small co-orbital satellites (, , and ), where , and are azimuthally located at longitudes , and , respectively, from (at ) (see Table 1). Their masses are given in Table 1.
The system is formed by Neptune, the satellite Galatea, four hypothetical co-orbital satellites and a sample of ring arc particles. The parameters of Neptune (mass , radius and the gravitational coefficients and ) were taken from Owen et al. (1991). The orbital elements and mass of Galatea are given in Table 2. It is initially in an eccentric ( and inclined orbit () at semi-major axis 61953km.
The co-orbital satellites and the arc system are initially at the same semi-major axis (62932.7km). The eccentricity and inclination of the arcs are and (Table 2).
The longitude of the pericentre () of the co-orbitals satellites and the arc particles is , the same value as adopted by Porco (1991). The true longitude of the Fraternité arc is .
Each arc is formed by a sample of 2000 particles randomly chosen about 1km from the semi-major axis of the co-orbital satellites and of the angular positions , , and .
| Fraternité | Egalité | Liberté | Courage | |||||
|---|---|---|---|---|---|---|---|---|
| (∘) | 0.00 | 48.31 | 59.38 | 72.19 | 40.00 | 50.00 | 66.50 | 84.00 |
| mass ( kg) | 60.00 | 0.54 | 1.17 | 0.66 | – | – | – | – |
| a (km) | e () | I (∘) | (∘) | (∘) | (∘) | m ( kg) | |
|---|---|---|---|---|---|---|---|
| Galatea | 61953.0 | 2.2 | 0.0231 | 225.81 | 196.94 | 351.114 | 1.94 |
| Fraternité arc | 62932.7 | 3.0 | 0.0 | 50.82 | 0.0 | 251.88 | – |
Numerical simulations were performed using the variable timestep Burlish-Stöer algorithm from Mercury package (Chambers, 1999) for a timespan of 1000 years. The algorithm presented in Renner & Sicardy (2006) was used to transform the state vector into geometric orbital elements, in order to avoid the short-period terms caused by and .
With these adopted initial conditions the co-orbital satellites and the arc particles are trapped in the 42:43 Lindblad resonance with Galatea. The resonant angle is , where and are the mean longitude and the longitude of the pericentre of the co-orbital satellites/particles, respectively, and is the mean longitude of Galatea. Figure 1 shows the resonant and azimuthal angles (longitude of the particle in the frame rotating with the mean motion of the co-orbital , ) librating for representative particles of each arc.
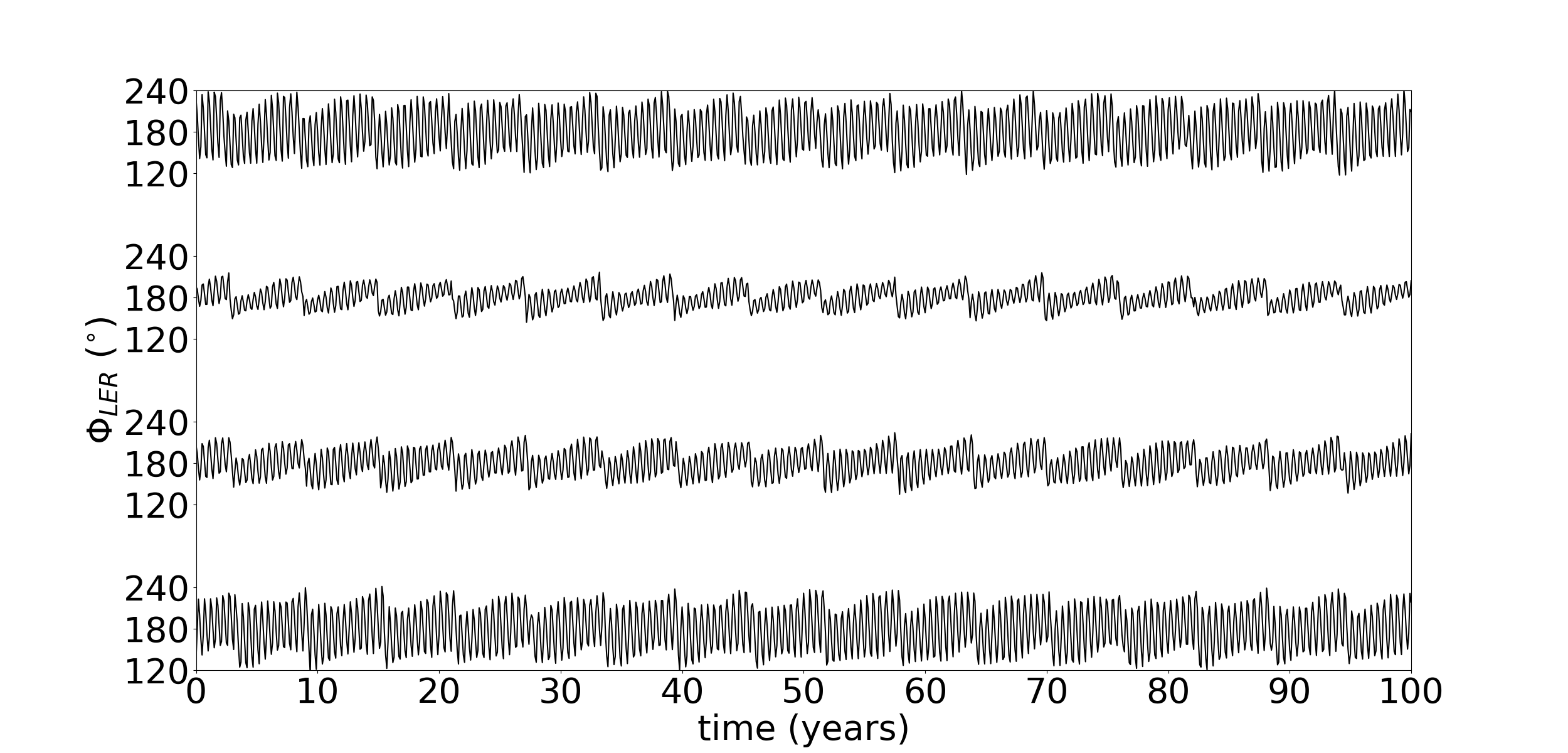
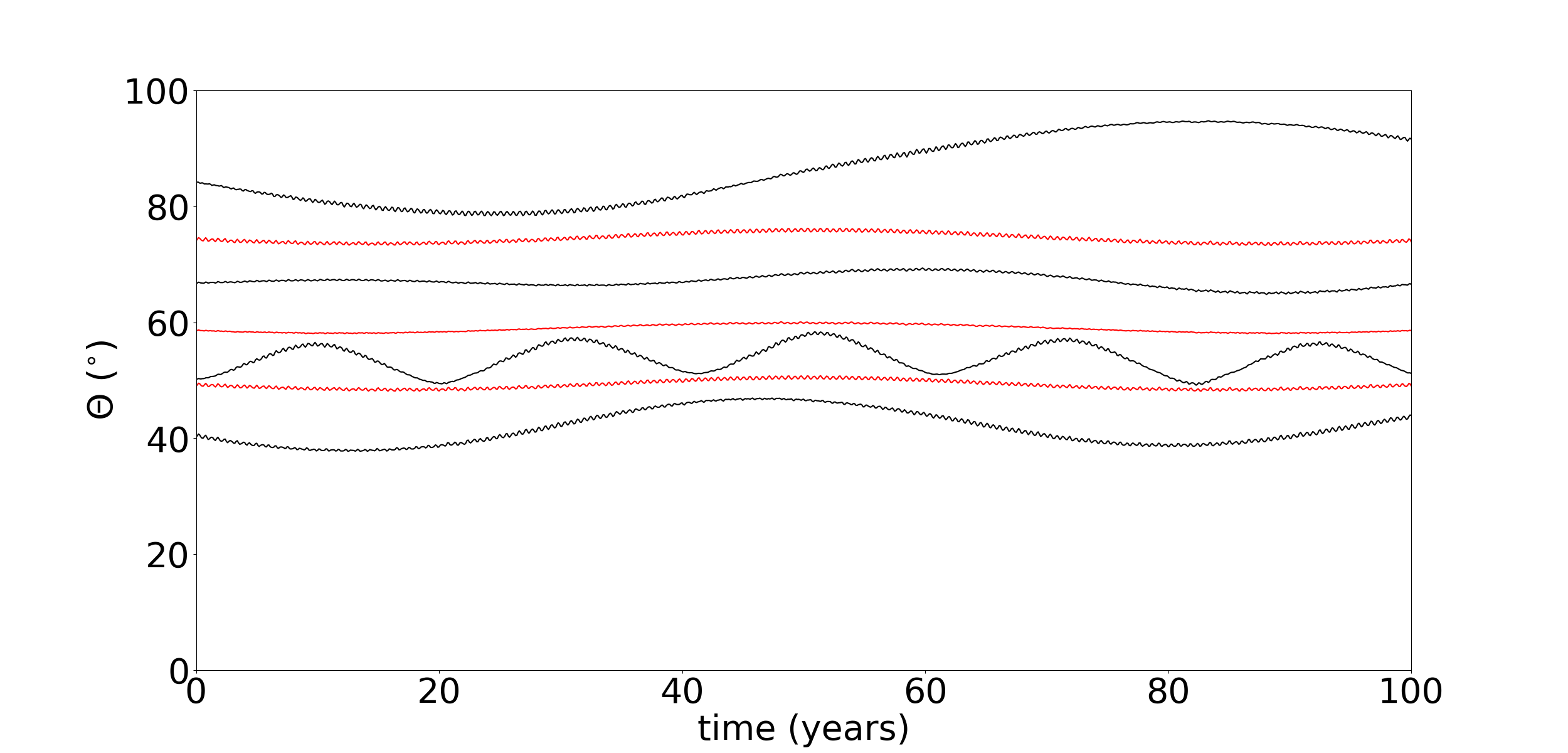
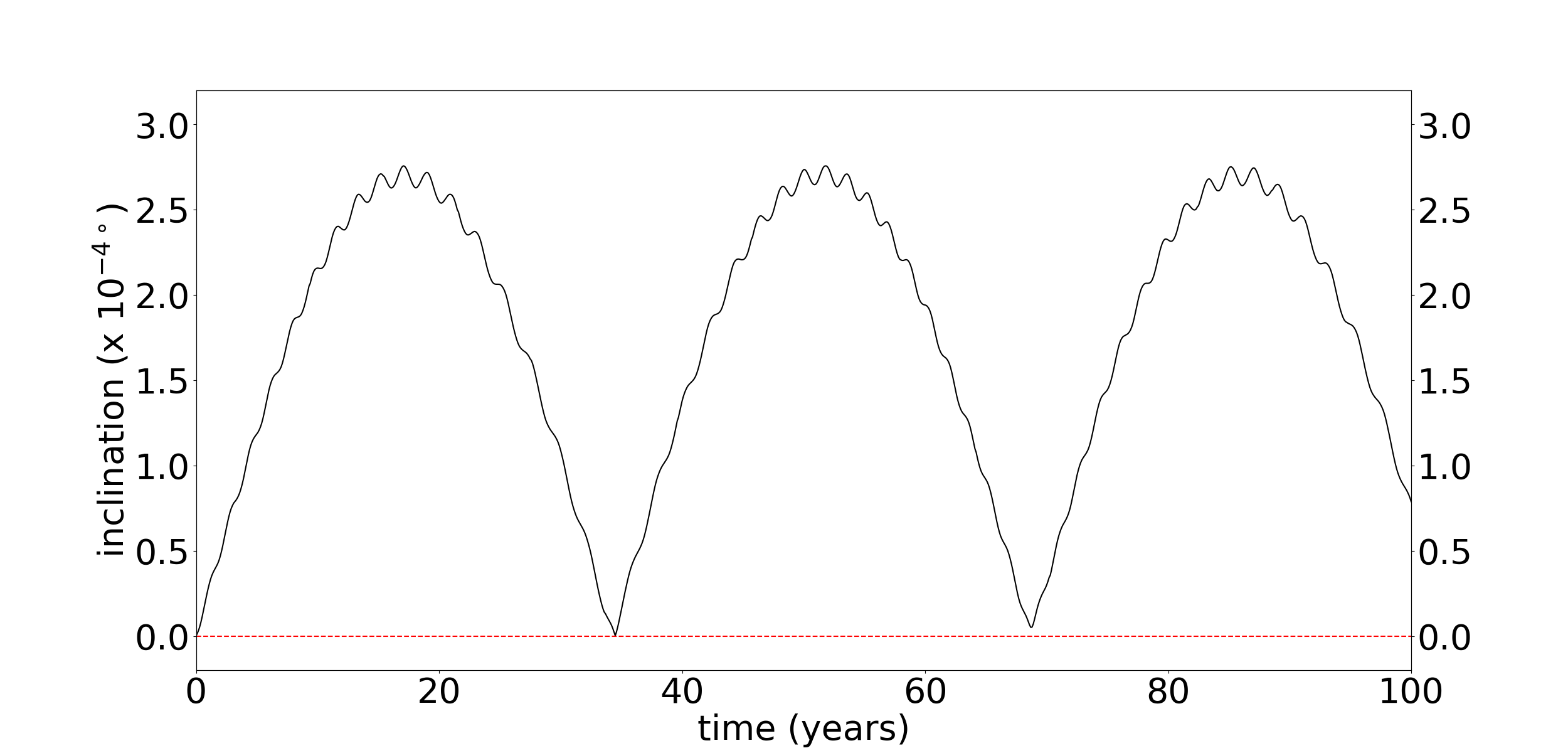
We analyse two cases, cases 1 and 2, as mentioned above. Figure 2 shows the variation of the eccentricity, inclination and the azimuthal angle for a representative particle located in the Fraternité arc in two different dynamical systems. In case 1 Galatea is in equatorial and circular orbit and in case 2 Galatea is in its nominal orbit ( and ). In both cases, 1 and 2, the eccentricity of the particle varies between to . The proximity to the 42:43 corotation inclined resonance due to Galatea affects the inclination of the particle, reaching values up to deg.
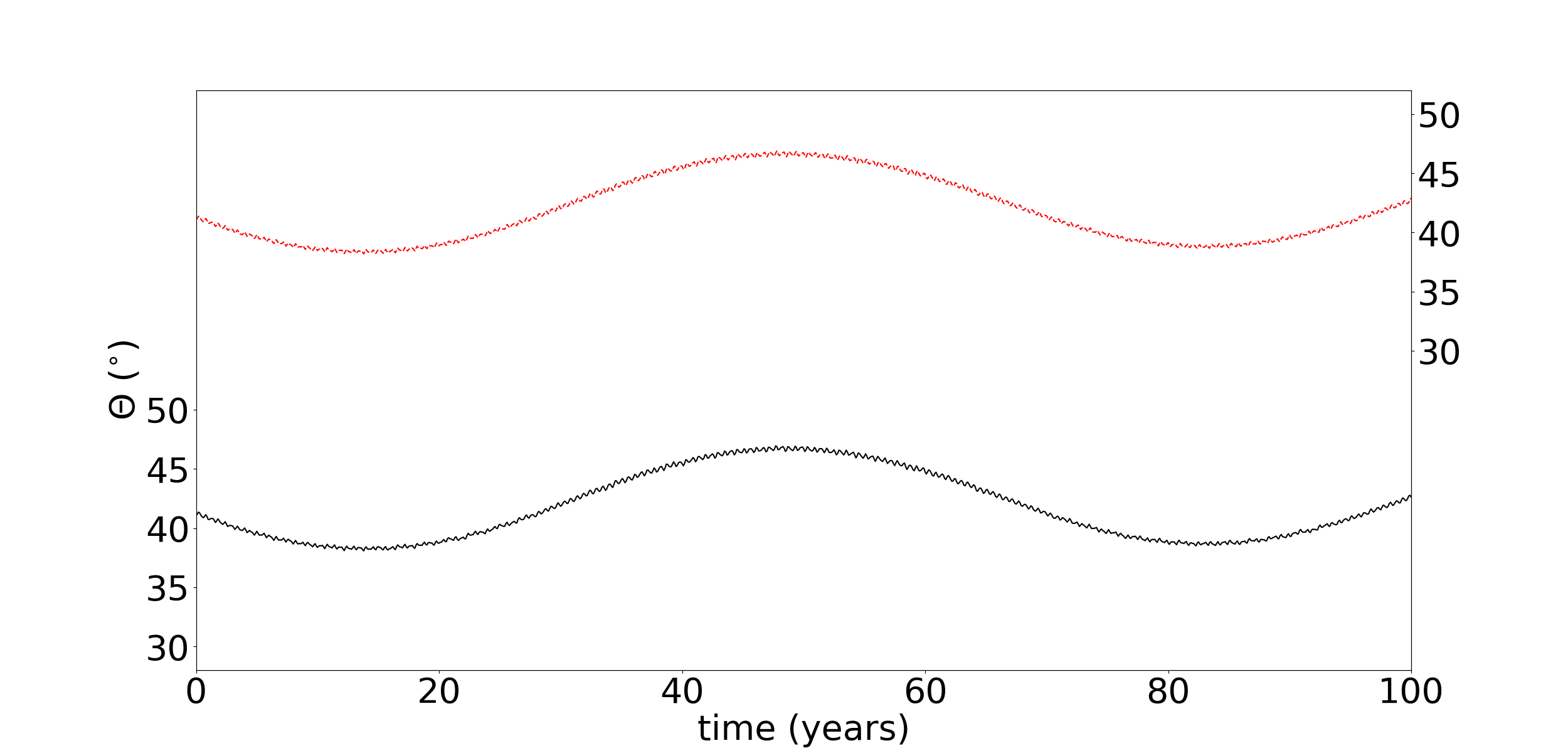
We analyse the outcome of the numerical simulations by separating the particles into four different groups. The first group is composed of confined particles, those particles that stay in the arc under the effects of the Lindblad resonance with Galatea for the whole time of the numerical simulation. Figure 3 shows the variation of the eccentricity, the angle and the azimuthal angle () as a function of time for a particle confined in the arc.
The second group is formed by transient particles, those particles that travel between different arcs. These particles can stay in the Lindblad resonance with Galatea, but they change from one arc to another. Figure 4 shows the temporal variation of the eccentricity, and angles for a transient particle. The third group represents those particles that leave the arc and go to the Adams ring. Figure 5 shows the eccentricity, and angles as a function of time for a particle that leaves the arc. The particle remains, some time, in the Lindblad resonance. The last group is composed of those particles that collide with the co-orbital satellites.
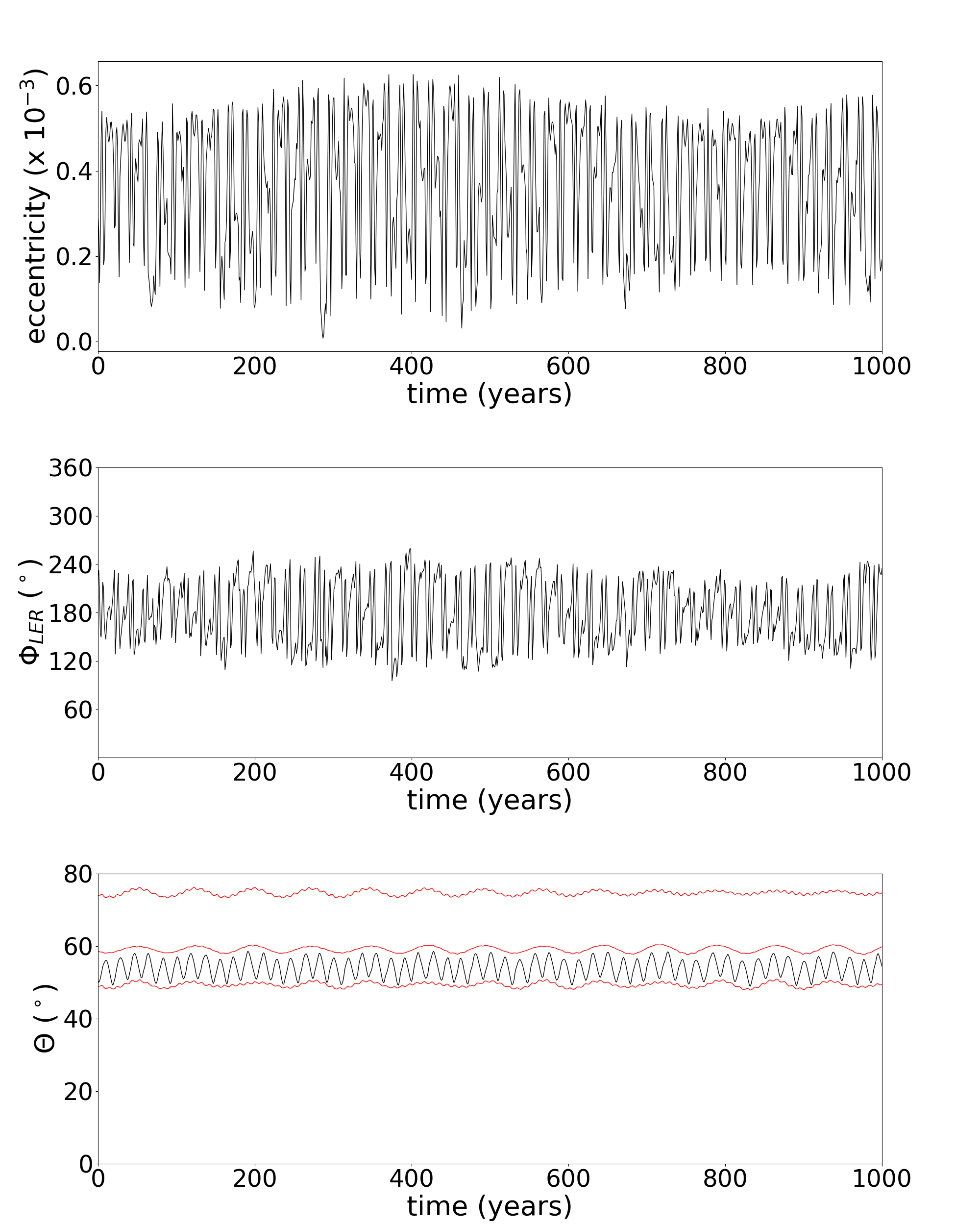
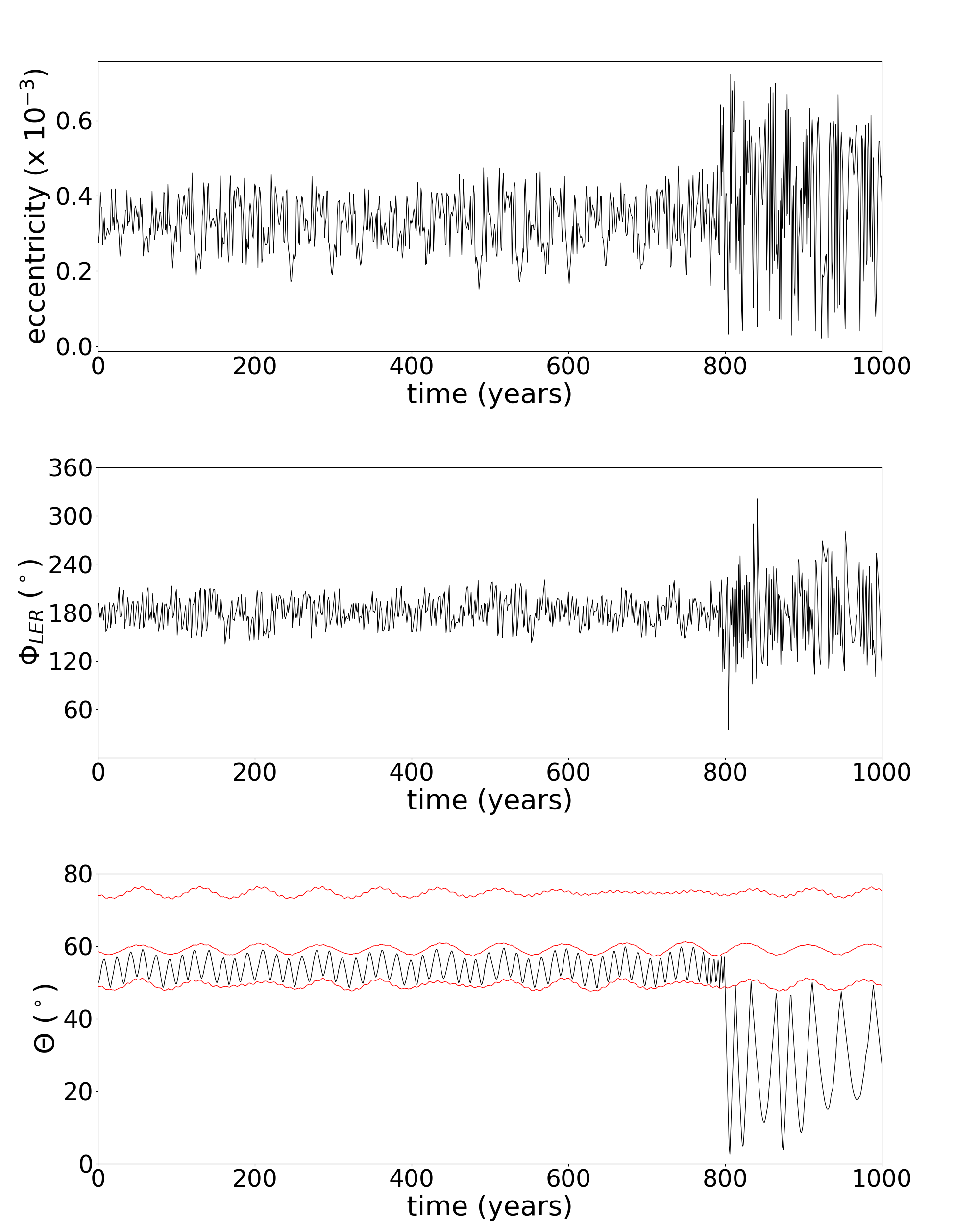
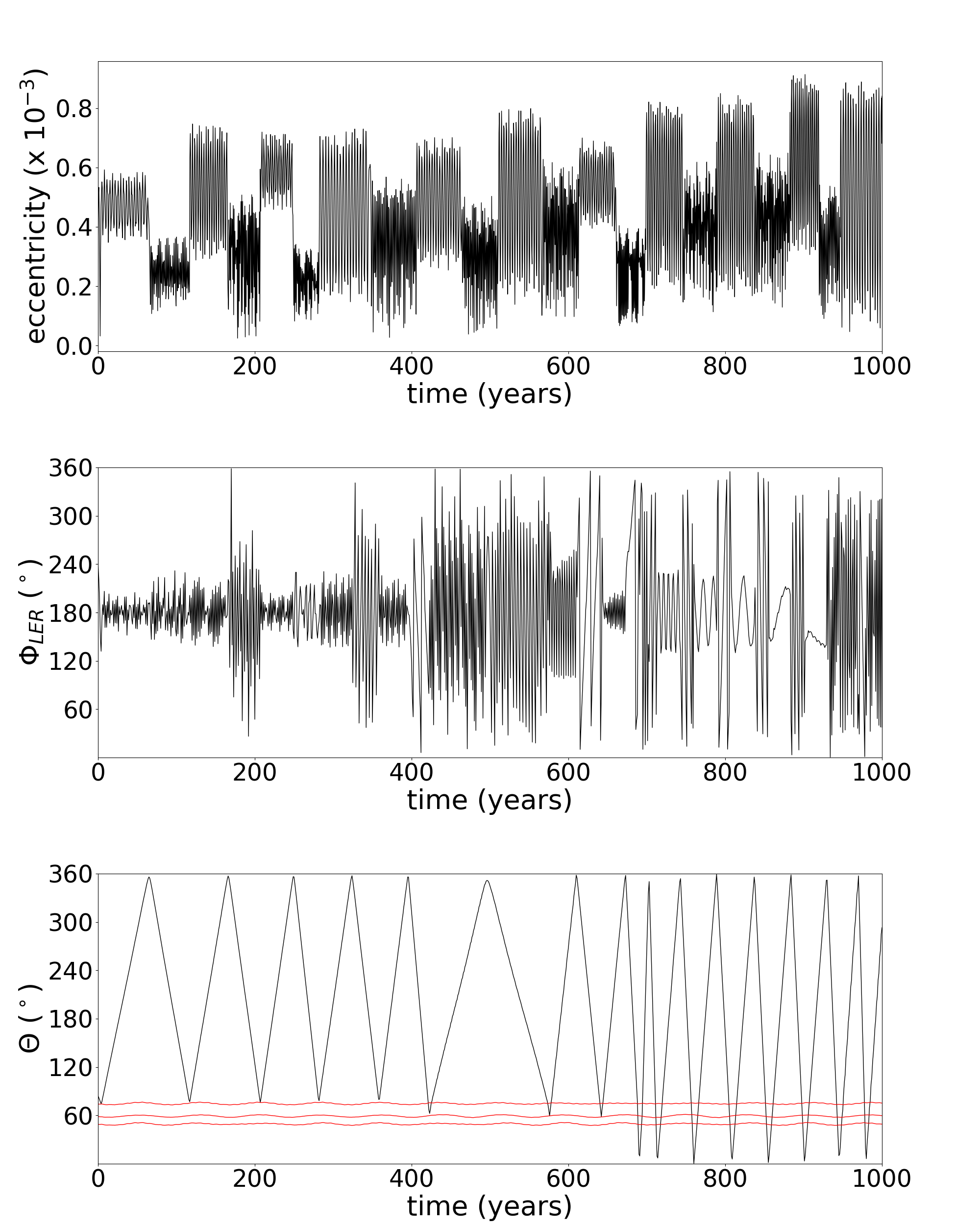
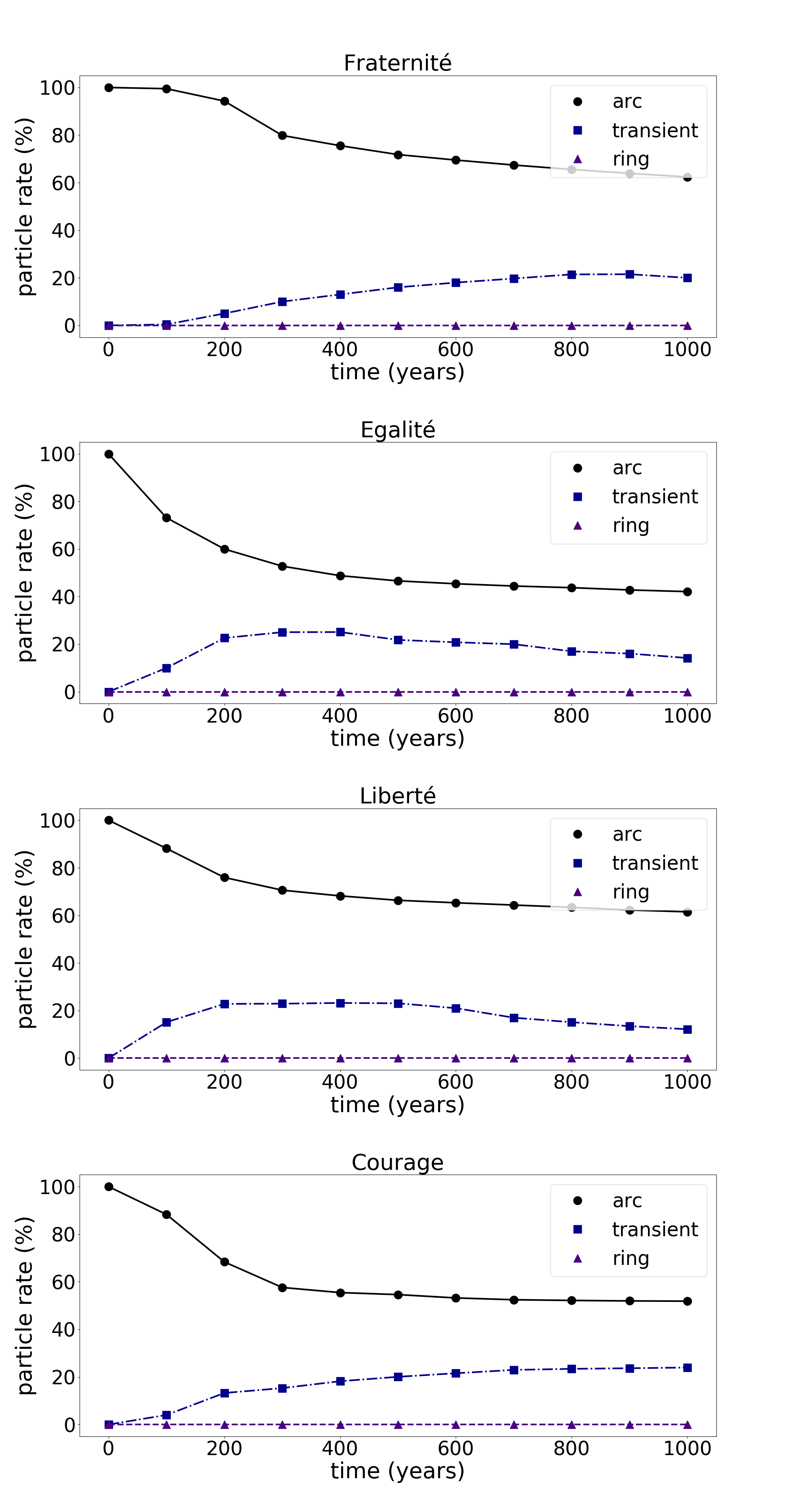
Figure 6 shows the percentage of confined and transient particles and those that leave the arc for case 2. Both cases, 1 and 2, have similar behaviour concerning the orbital evolution of the particles. Although the evolution of each arc (Figure 6) presents small differences, most of the particles stay in the four arcs for the whole time of integration, 1000 years. Some particles became transients, travelling between the arcs, but almost none of them goes to the Adams ring.
The Egalité and Liberté arcs are confined close to two co-orbital satellites, but it does not mean that they are more stable than the Fraternité and Courage arcs. The induced eccentricity caused by Galatea leads to close encounters and collisions between the arc particles and the co-orbital satellites.
3 Orbital Evolution under a Dissipative Force
In this system where the arc particles are confined in the Lindblad resonance due to the satellite Galatea and in the corotation resonance due to hypothetical co-orbital satellites we take a step further by including the effects of the solar radiation force (Madeira et al., 2018).
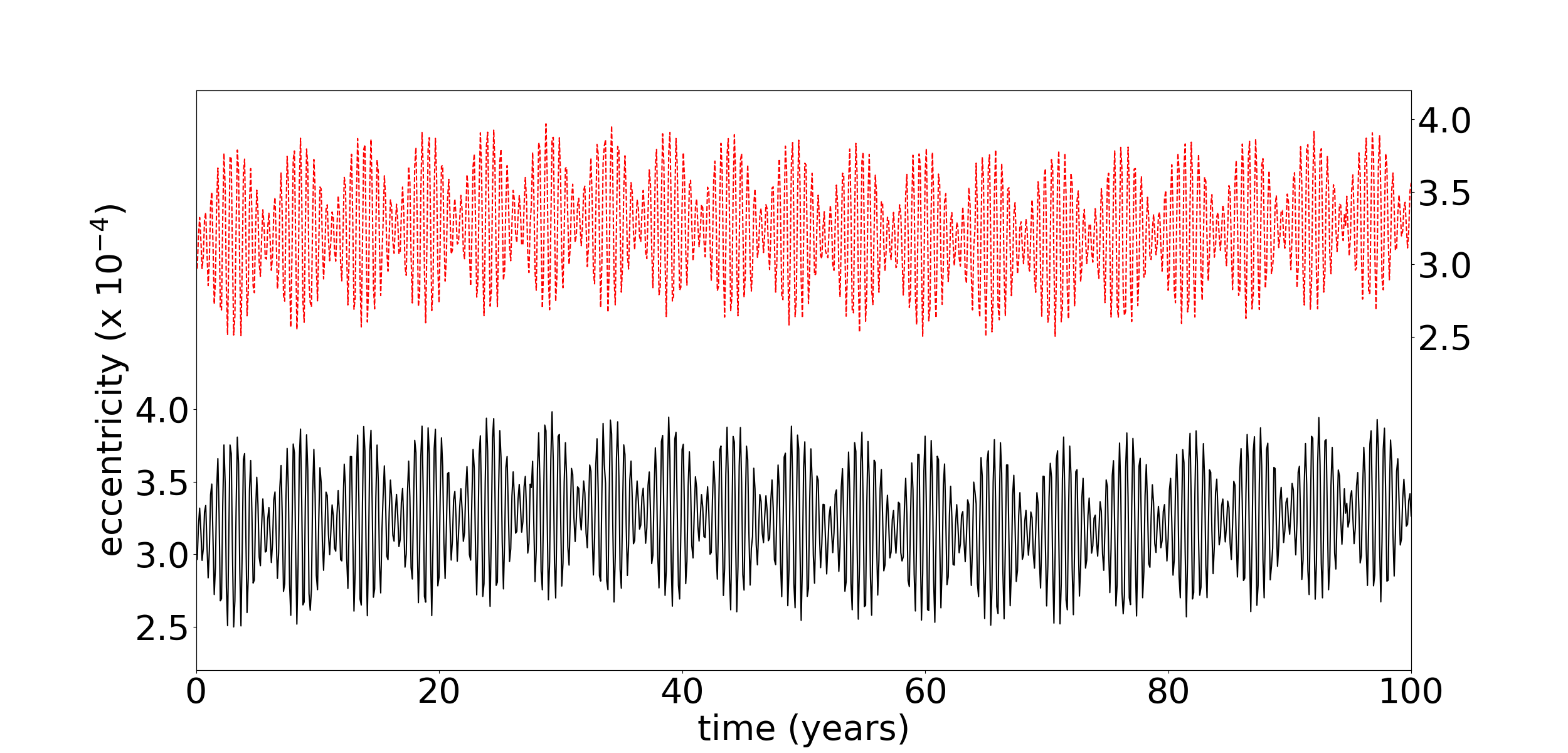
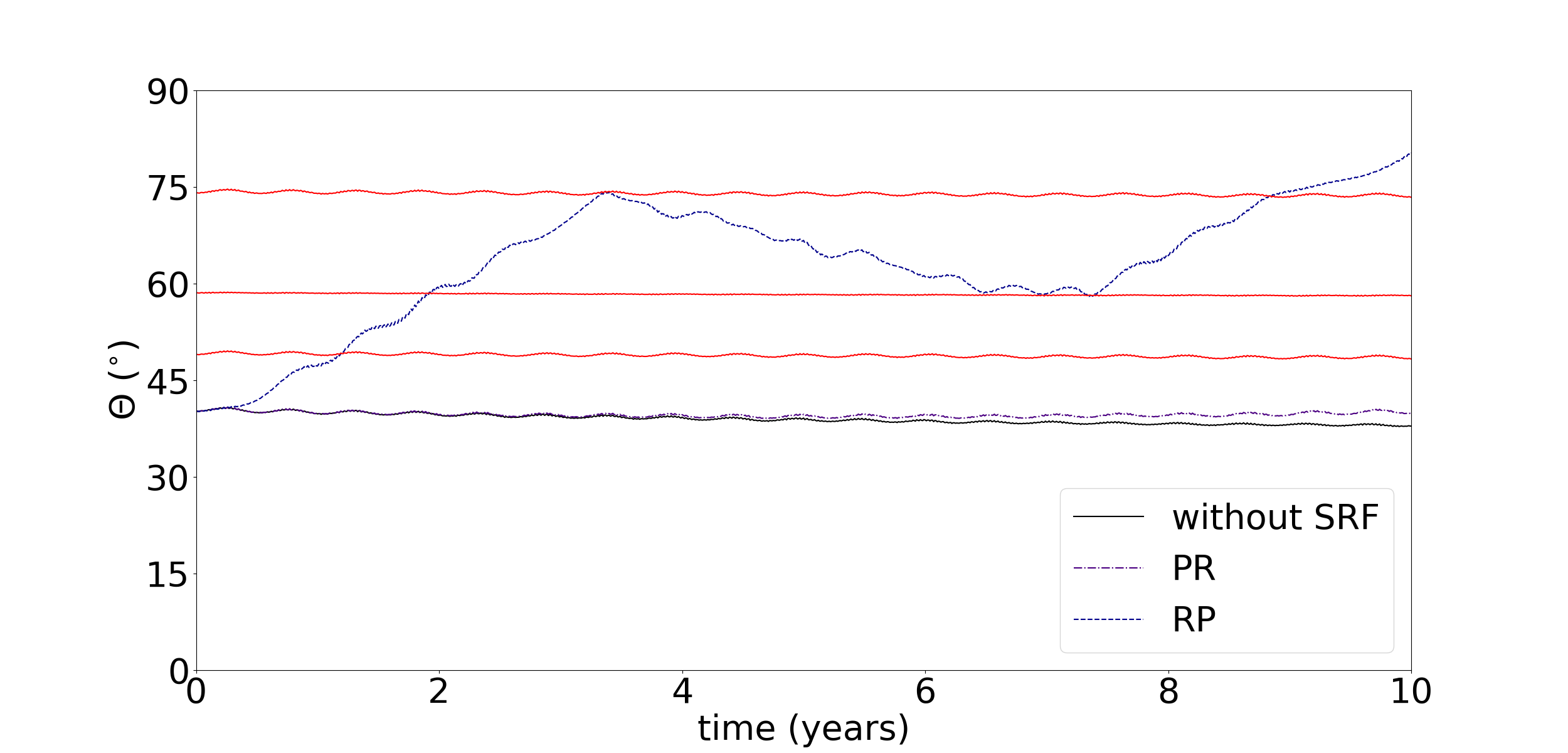
The solar radiation force is composed of two components: the radiation pressure and the Poynting-Robertson components. The Poynting-Robertson component provokes a decrease in the semi-major axis of the particles in a timescale of thousands of years, while the radiation pressure component causes a variation in the eccentricity of the particles in a timescale of few years as shown in Figure 7 for a set of representative particles of different sizes (m, m, m, m and m in radius) at the Fraternité arc.
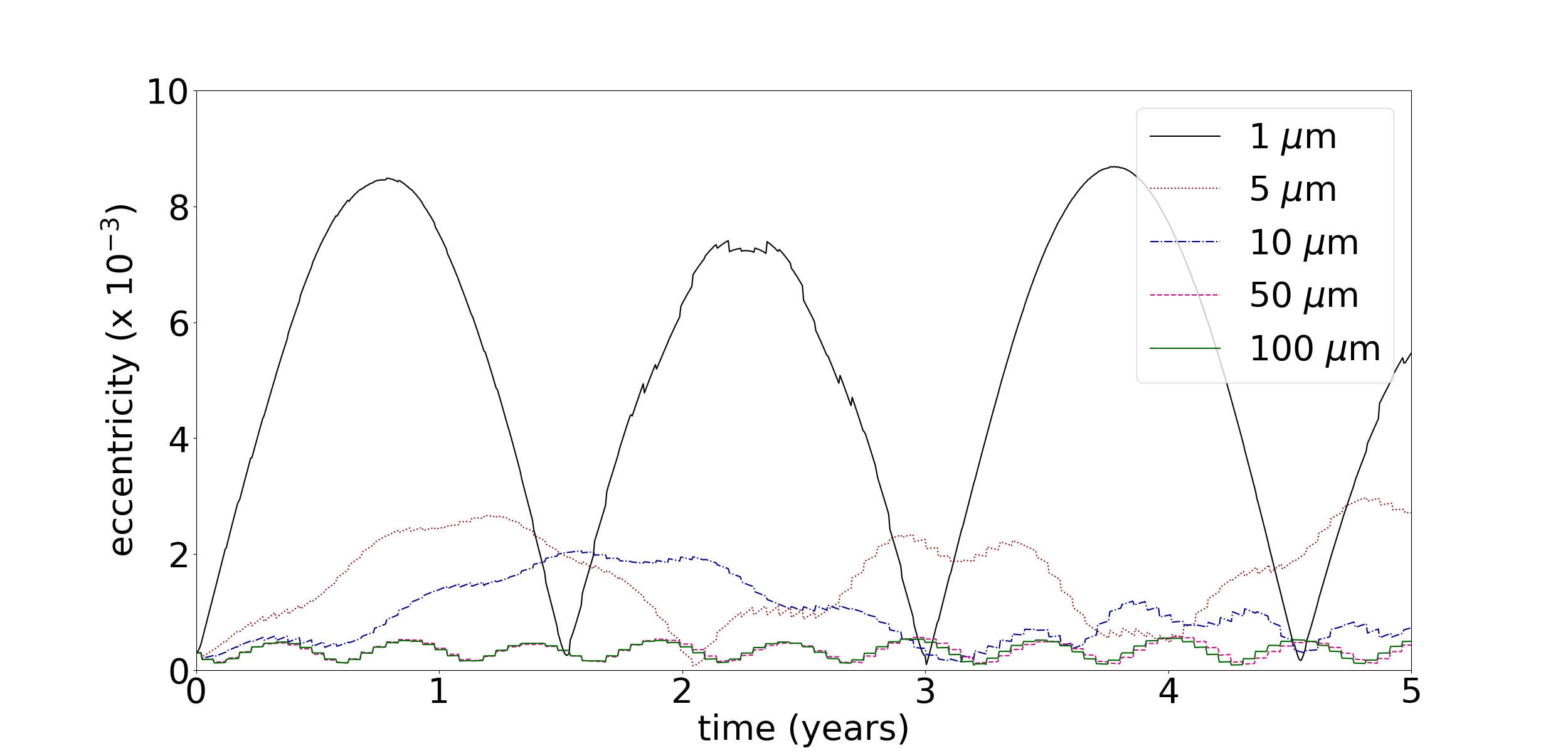
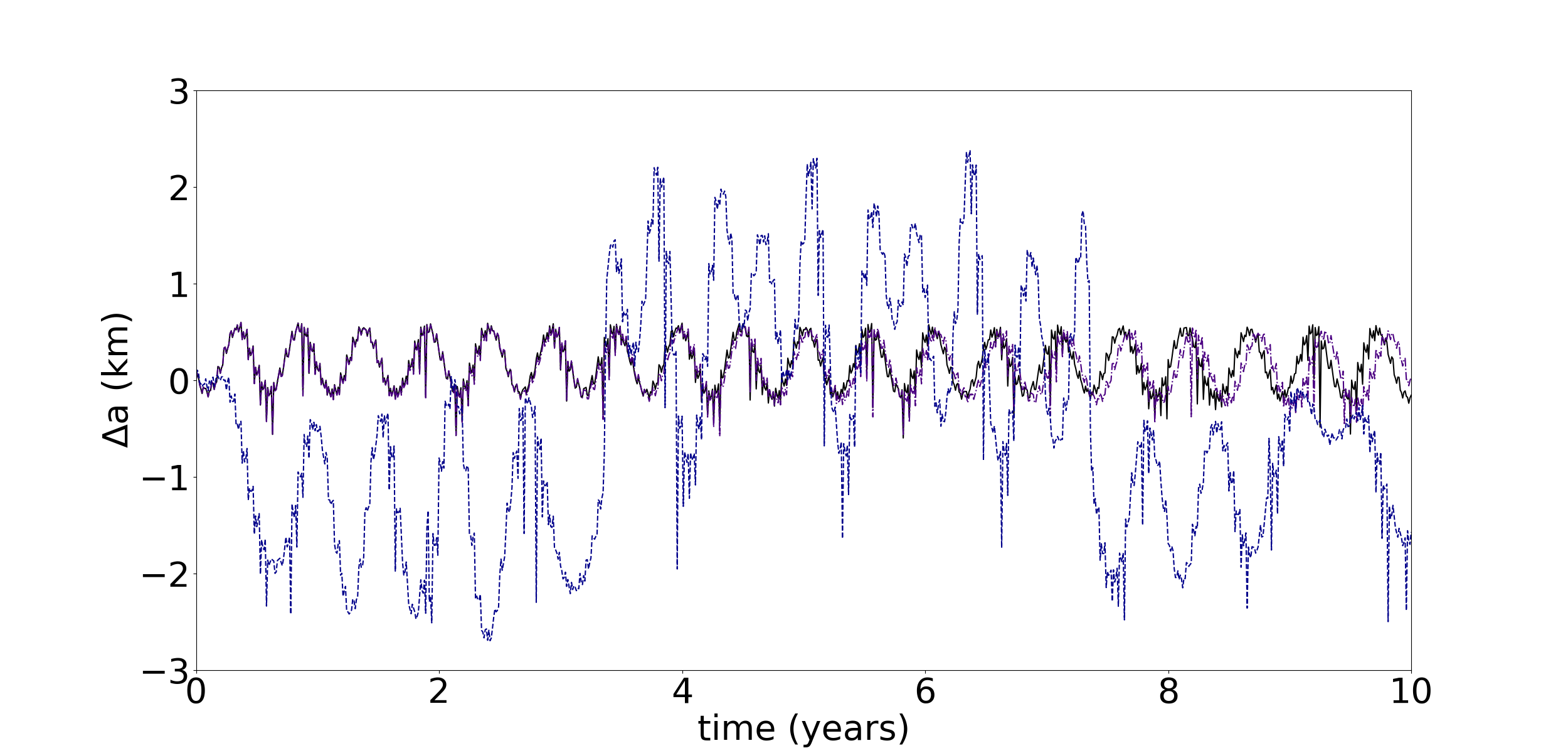
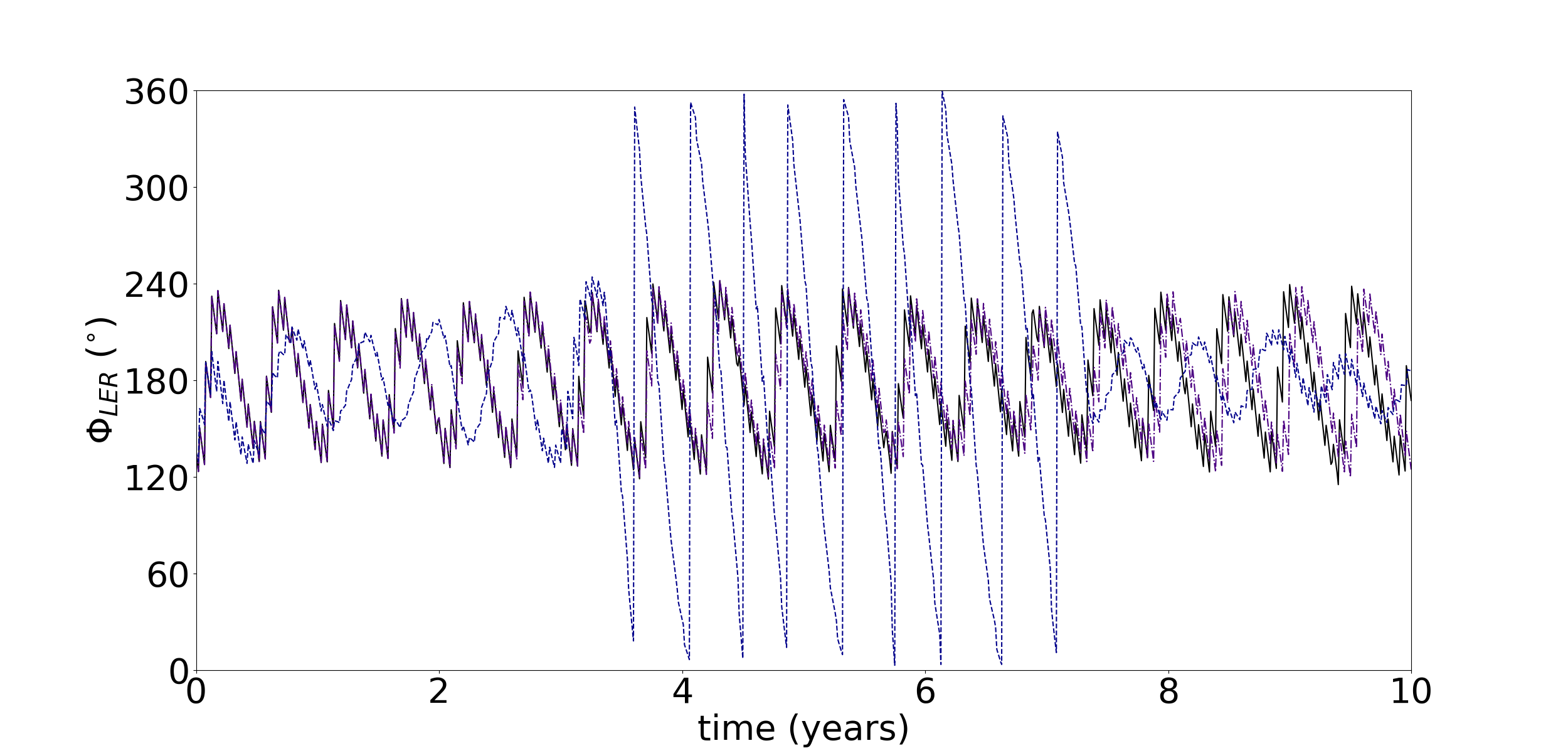
Figure 8 shows the temporal evolution of the semi-major axis (), the resonant angle and the azimuthal angle of a m sized particle in the Fraternité arc under the effects of the Poynting-Robertson component, the radiation pressure component and without any dissipative force. Small variations in the semi-major axis of the particle are due to the proximity to the CIR with Galatea. The Poynting-Robertson component provokes small variations in the and angles. This component does not remove particles from the resonance in 1000 years, the period of the numerical simulation. Variations in the eccentricity change the LER angle due to its constrain with the longitude of the pericentre of the particle. Therefore, the radiation pressure component can remove particles from this resonance, as can be seen in Figure 8. Furthermore, this component also provokes short-period oscillations in the semi-major axis of the particles, as discussed in Madeira et al. (2018), which also affect the angle and remove the particles from the azimuthal confinement.
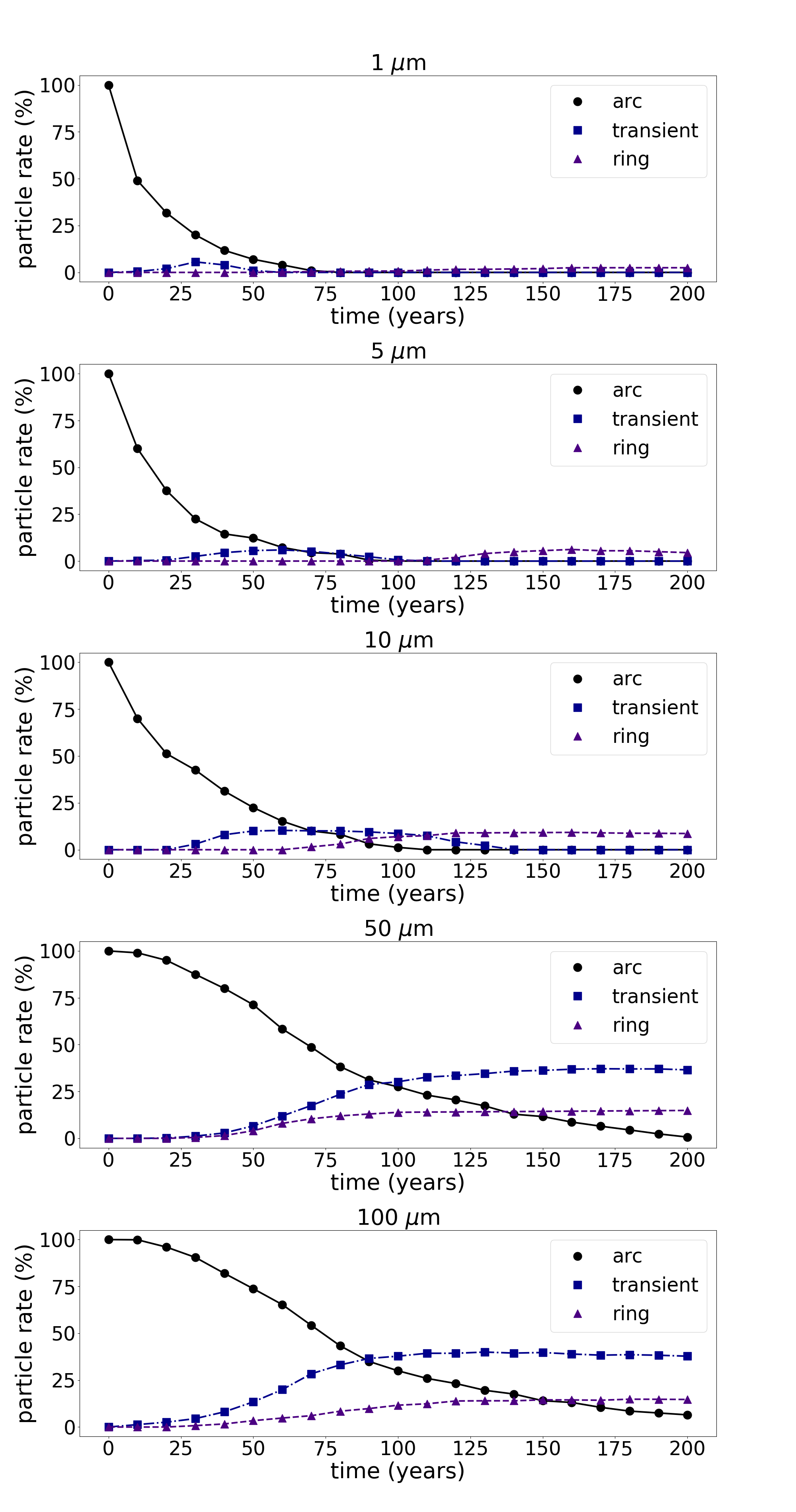
We numerically simulated each arc composed of a sample of 10000 particles, 2000 particles of sizes m, m, m, m and m in radius under the effects of the solar radiation pressure. We analyse the percentage of confined and transient particles and those particles that leave the arcs and go to the Adams ring. Figure 9 shows this percentage for particles of each size located in the Fraternité arc. Particles at the Couragé, Liberté , and Egalité arcs have similar behaviour.
By comparing both systems, with (Fig. 9) and without (Fig. 6) the solar radiation pressure, we concluded that under the effects of this dissipative force larger particles live up to 200 years. Only under the effects of the gravitational force more than of the particles remain in the arc after 200 years. As expected, the solar radiation force decreases the lifetime of the arcs, smaller particles (1m, 5m and m in radius) collide with the co-orbital satellites in a very short period of time. They do not became transient or leave for the Adams ring. The population of larger particles contributes to the other arcs and also to the Adams ring: m and m sized particles can become transient or move to the Adams ring. The lifetime of the smaller arc particles is about 100 years.
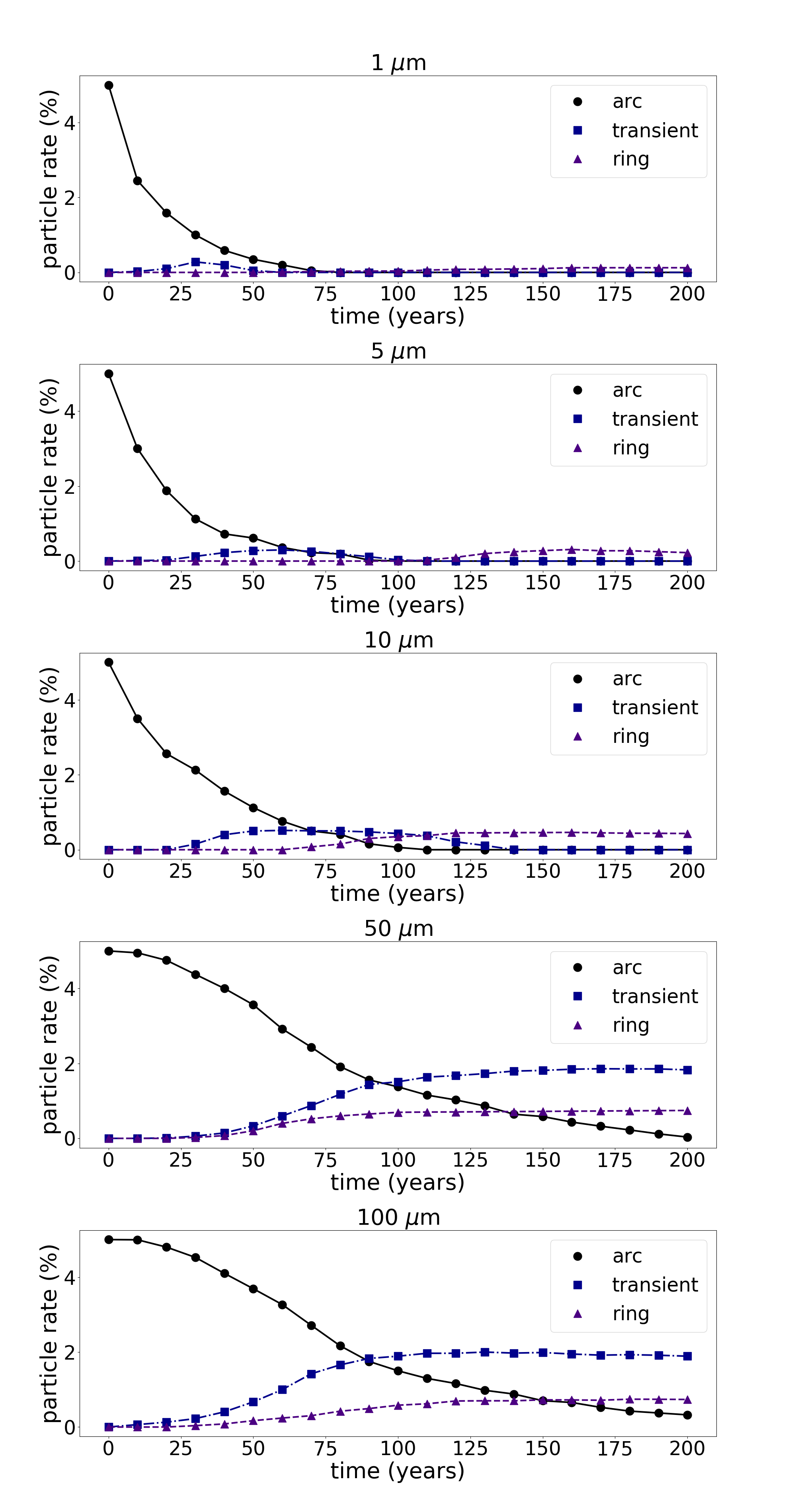
It is worth to point out that without the effects of Galatea the system has a similar behaviour (Fig. 10 ).
30 years ago the arcs were imaged by Voyager 2 spacecraft. Observations by the telescopes showed that the arcs changed in brightness (de Pater, 2005; Showalter et al., 2013). Tables 3 and 4 show the percentage of m-sized particles in each arc and the transient particles after 30 years, respectively. m sized particles are quickly removed from the arcs, only of them can survive for 30 years. The Liberté arc can hold about of the m sized particles while the Courage arc only of them. More than of the larger particles (m and m in radius) can survive in all the arcs after this period (30 years).
Table 3 shows that large particles can stay in all arcs after 30 years. These results can not explain the disappearance of the leading arcs, Liberté and Courage, unless the population of these arcs is formed by particles of different sizes. Although transient particles could explain the variation in the brightness of the arcs, the percentage of transient particles is very small.
From the confinement model, the Fraternité arc is closer to the larger co-orbital satellite (), while the Egalité arc is apart from for only , the Liberté arc is apart from each co-orbital ( and ) for about and the Couragé arc is further from . The arcs are located in different configurations, which may help to explain the small difference in the percentage of confined particles.
| Fraternité | Egalité | Liberté | Courage | |
|---|---|---|---|---|
| m | % | % | % | % |
| m | % | % | % | % |
| m | % | % | % | % |
| m | % | % | % | % |
| m | % | % | % | % |
| Fraternité | Egalité | Liberté | Courage | |
|---|---|---|---|---|
| m | % | % | % | % |
| m | % | % | % | % |
| m | % | % | – | % |
| m | % | % | % | – |
| m | % | % | % | % |
4 Dust Production
The arcs are temporary structures unless a source provides the particles removed from them through collisions or ejections. The co-orbital satellites could be the source (de Pater (2005) suggested that a moonlet immersed in the Fraternité arc can be its source) since they can be hit by interplanetary dust particles (IDPs) that are diverted by the planet. These impacts usually happen at km/s, thus they are energetic enough to eject m-sized particles from the surface of the target body.
The mass rate production () created by this process depends on the flux of the impactors (), the target cross-section (), and the ejecta yield (). With these parameters the amount of dust produced is
Sfair & Giuliatti Winter (2012) present a simple algorithm that allows the computation of the mass rate production of the dust particles by this process. To compute it was assumed an isotropic flux of IDPs at Neptune’s heliocentric distance of (km/m2/s) (Poppe, 2016). However, the satellites are in fact hit by an enhanced flux due to gravitational focusing by the planet, which increases the IDPs velocity and their spatial density. In the region of the arcs, the effective flux is increased by a factor 30.
The yield () is a measurement of the ejecta production efficiency, and it can be estimated using an analytical expression presented in Koschny & Grün (2011) which is a function of the impactor mass, its velocity and the proportion of silicate and ice on the surface of the satellite. For a typical impactor of m hitting a pure ice surface, we obtain .
With all these assumptions, Figure 11 presents the mass production rate for different sizes of satellites. The grey area in Figure 11 comes from different values of the velocities assumed for the projectile: 2.3km/s and 3.0km/s (Sfair & Giuliatti Winter (2012) and Poppe (2016), respectively). The IDPs population in the outer Solar System is poorly constrained. This range covers different models for the unfocused velocity of the projectiles: the value of 2.3km/s comes from the model proposed by Poppe (2016) where it is assumed that the origin of the flux at Neptune comes from the Edgeworth-Kuiper belt, while the higher value comes from a model adjusted with measurements made by New Horizons (Poppe (2016)).
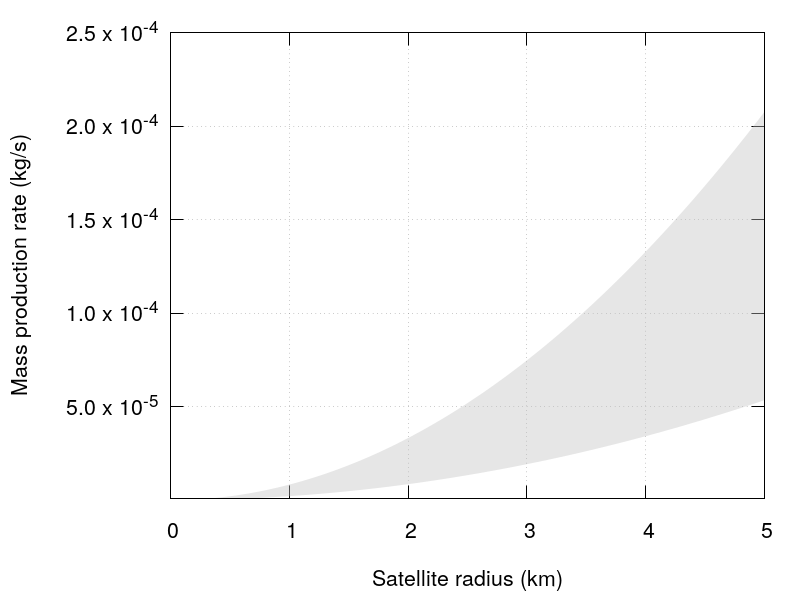
Due to the uncertainty in the parameters, mainly by the IDPs’ flux which is poorly constrained at the heliocentric distance of Neptune, the mass generated by this process must be taken with one order of magnitude of uncertainty. Anyhow, even all particles being ejected with velocities large enough to overcome the escape velocity, the dust produced by the co-orbital satellites does not contribute significantly to the arc population.
In order to analyse how efficient this dust production mechanism is, it was assumed that a small satellite, 5km in radius, produces kg/s of dust (the maximum value derived from Fig. 11). It is also assumed that all particles generated on the surface of the satellite survive for at least 1 year, azimuthally confined in an arc of about . A crude estimative of the optical depth of this arc can be obtained from the mass production ratio (kg/s). Assuming that the arc population is formed by particles with m in radius we can calculate the total number of particles and the area (effective area) covered by them. The optical depth (the ratio between the effective area and the arc area) is , smaller than the value presented in Porco et al. (1995).
Therefore, even considering the best scenario, the larger satellite and the smallest arc, this mechanism of dust production can not be responsible for replenishing the arcs.
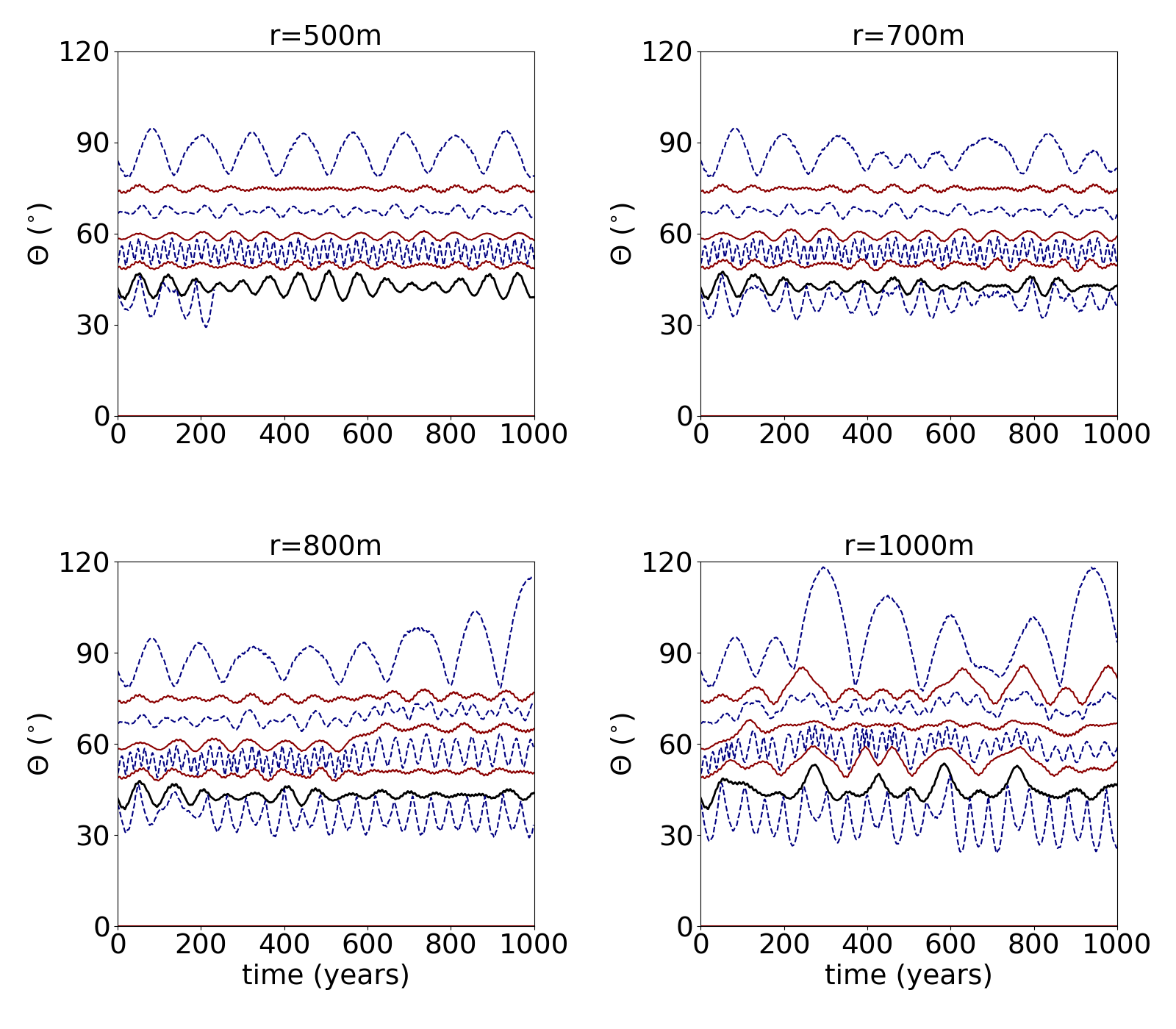
A sample of moonlets located in the arcs can disturb the orbital configuration of the co-orbital satellites, and consequently the arcs. In order to analyse the size of moonlets that can change the configuration of the system we modelled a system formed by four co-orbital satellites, a moonlet located in the Fraternité arc, and a particle located in each arc. Figure 12 shows the temporal variation of as a function of time for the co-orbital satellites, the moonlet and the arc particles. We adopted moonlets with sizes 500m, 700m, 800m and 1000m in radius. For a moonlet of radius 500m and 700m the configuration of the system is preserved, although the Fraternité arc particle collided with the moonlet. For larger moonlets, the arc configuration changes significantly. Therefore, the Fraternité arc can have moonlets smaller than 700m in radius immersed on it.
A secondary population of dust production can be formed by dust produced by collisions between the arc particles onto the surface of the co-orbital satellites or the immersed moonlets. The relative velocities of the dust particles are about 60m/s for a collision between a m sized particle and a co-orbital, while a m sized particle hits the co-orbital satellites at about 6.5m/s. These secondary collisions happen at velocities of a few m/s. Even dust particles could be released from the co-orbital satellites after these collisions, the amount is orders of magnitude smaller than direct impacts (collisions between IDPs and the co-orbital satellites) that happen at km/s.
Close to the Adams ring, an unnamed ring is co-orbital to the satellite Galatea (Porco et al., 1995), at about 61953km. Numerical simulations of the system formed by Neptune, the ring co-orbital particles and Galatea under the effects of the solar radiation force showed that although all small particles remained azimuthally confined (no collision with Galatea was detected), the smaller particles (m sized particles) performed radial oscillation of about 900km, while larger particles (m in radius) oscillated about 120km. The radial oscillations do not cross the inner edge of the Adams ring. Notwithstanding the unnamed ring can influences the internal ring system of Neptune, it does not cause any change in the Adams ring and its arcs. Concerning the dust production, Galatea can produce dust particles at a rate of approximately a hundred times faster than the hypothetical co-orbital satellites. However, most of the grains leave the satellite at a speed that is below the escape velocity. Thus, it is unlikely that Galatea sustains the unnamed ring and helps to replenish the arcs with ejecta dust particles.
5 Discussion
The Adams ring arcs have been a challenger since their discovery in 1989. Confinement mechanisms have been proposed to contain the spreading of the arc particles. Recent data have shown that two arcs changed their intensity, while two others are fading away. In this work we analyse the orbital evolution of the arc particles through the recent model which proposes that co-orbital satellites (or large unseen moonlets) can prevent the azimuthal spreading, while the satellite Galatea keeps their radial spreading.
The dynamical system is formed by an oblate Neptune, Galatea, dust arc particles and four hypothetical small co-orbital satellites. After the numerical simulations, we divided the dust particles into four groups: the first group is formed by confined particles, particles that stay in the same arc trapped in corotation and Lindblad resonances, the second group is composed of transient particles (particles that change from one arc to another), the third group is formed by particles that leave the corotation resonance (the arcs) and go to the Adams ring, and the fourth group is composed of those particles that collide with the co-orbital satellites.
When only the gravitational force is acting in the system, about of the initial population of the arcs is present after 1000 years. However, the solar radiation force changes significantly this scenario. Approximately of the initial set of smaller particles (m and m in radius) can last about 30 years. After 50 years all smaller particles collided with the co-orbital satellites. Larger particles lived longer, but after 100 years only of the initial population is present in the arcs. Apart from the small differences, the four arcs have similar dynamical behaviour. None of them presents a huge discrepancy that can, for example, explain the disappearance of one of them, unless they are formed by particles of different sizes.
The percentage of particles that stay in the arc is similar. From our results the model proposed by Renner et al. (2014) does not explain why the two leading arcs are disappearing. The Courage arc would be fading away only if it is formed by smaller particles. The transient particles could help to explain the difference in the brightness of the arcs. However the percentage of them is small.
Dust production due to inter-particle collisions onto the surface of large moonlets can be the source of dust particles, keeping the arcs in a steady state. By analysing the mass production rate in the best scenario, a large satellite (5km in radius) closes to the smallest arc, our results showed that the satellite can not be the only source of the arcs. Larger moonlets embedded in the arcs can help to replenish the dust particles. However, we found that moonlets larger than 0.7km in radius change the configuration of the co-orbital satellites and the arcs, as proposed in the confinement model.
Collisions may play an important role in the arcs. A recent paper by Hearn et al. (2019) studied the dynamics of multiple massive bodies in a corotation resonance. Their results showed that the bodies exchanged angular momentum and energy during the encounter which change their orbits. They argued that the exchange in the energy may be similar to a collisional system, although a detailed investigation is necessary.
Although no small satellite (less than 10km in radius) was detected in the Adams ring, it is plausible to suppose that small bodies can be part of the ring population. Placed in the right positions, these satellites can trap a number of particles for a short period of time, until the solar radiation force removes them from the arcs. These co-orbital satellites may be the reminiscent of a large parent body that brocke up, and these arcs are temporary features. This work is under investigation.
Acknowledgements
The authors are grateful to the anonymous referee for helping to clarify many questions. The authors thank Fapesp (Procs 2016/24488-0, 2018/23568-6 and 2016/24561-0) and CNPq (Procs 309714/2016-8 and 305737/2015-5) for the financial support. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001.
References
- Burns et al. (1979) Burns, Joseph A and Lamy, Philippe L and Soter, Steven, 1979, Icarus, 40, 48
- Chambers (1999) Chambers J.E., 1999, Monthly Notices of the Royal Astronomical Society, 304, 793
- Dumas et al. (1999) Dumas, Christophe and Terrile, Richard J and Smith, Bradford A and Schneider, Glenn and Becklin, EE, 1999, Nature, 400, 733
- Foryta & Sicardy (1996) Foryta, Dietmar W and Sicardy, Bruno, 1996, Icarus, 123, 123
- Goldreich et al. (1986) Goldreich, Peter and Tremaine, Scott and Borderies, Nicole, 1986, The Astronomical Journal, 92, 490
- Hearn et al. (2019) A’Hearn, Joseph A and Hedman, Matthew M and El Moutamid, Maryame, 2019, The Astrophysical Journal, 882, 66
- Hubbard et al. (1986) Hubbard, William B and Brahic, Andre and Sicardy, B and Elicer, LR and Roques, F and Vilas, F, 1986, Nature, 319, 636
- Koschny & Grün (2011) Koschny, Detlef and Grün, Eberhard, 2011, Icarus, 154, 402
- Lissauer (1985) Lissauer, Jack J, 1985, Nature, 318, 544
- Madeira et al. (2018) Madeira, G and Sfair, R and Mourão, D C and Giuliatti Winter, S M, 2018, Monthly Notices of the Royal Astronomical Society, 475, 5474
- Murray & Dermott (1999) Murray, Carl D and Dermott, Stanley F, 1999. Cambridge university press
- Namouni & Porco (2002) Namouni, Fathi and Porco, Carolyn, 2002, Nature, 417, 45
- Owen et al. (1991) Owen, WM and Vaughan, RM and Synnott, SP, 1991, The Astronomical Journal, 101, 1511
- de Pater (2005) de Pater, Imke and Gibbard, Seran G and Chiang, Eugene and Hammel, Heidi B and Macintosh, Bruce and Marchis, Franck and Martin, Shuleen C and Roe, Henry G and Showalter, Mark, 2005, Icarus, 174, 263
- Poppe (2016) Poppe A. R., 2016, Icarus, 264, 369
- Porco (1991) Porco, Carolyn C, 1991, Science, 253, 995
- Porco et al. (1995) Porco, CC and Nicholson, PD and Cuzzi, JN and Lissauer, JJ and Esposito, LW, 1995, Neptune and Triton
- Renner & Sicardy (2006) Renner, S and Sicardy, B, 2006, Celestial Mechanics and Dynamical Astronomy, 94, 237
- Renner et al. (2014) Renner, S and Sicardy, B and Souami, D and Carry, B and Dumas, C, 2014, Astronomy & Astrophysics, 563, A133
- Sfair & Giuliatti Winter (2012) Sfair, R and Giuliatti Winter, SM, 2012, Astronomy and Astrophysics, 543, 17
- Showalter et al. (2013) Showalter, Mark R and de Pater, I and French, RS and Lissauer, JJ, 2013, AAS/Division for Planetary Sciences Meeting Abstract, 45
- Showalter et al. (2013) Showalter, MR and de Pater, I and Lissauer, JJ and French, RS, 2019, Nature, 566, 7744
- Sicardy et al. (1991) Sicardy, Bruno and Roques, Françoise and Brahic, André, 1991, Icarus, 89, 220
- Sicardy et al. (1999) Sicardy, B and Roddier, F and Roddier, C and Perozzi, E and Graves, JE and Guyon, O and Northcott, MJ, 1999, Nature, 400, 731