Nellie: A Neuro-Symbolic Inference Engine
for Grounded, Compositional, and Explainable Reasoning

Nathaniel Weir¹, Peter Clark², and Benjamin Van Durme¹ ¹Johns Hopkins University, Baltimore, MD, USA
²Allen Institute for AI, Seattle, WA, USA
{nweir, vandurme}@jhu.edu, [email protected]

Abstract

Our goal is to develop a modern approach to answering questions via systematic reasoning where answers are supported by human interpretable proof trees grounded in an NL corpus of facts. Such a system would help alleviate the challenges of interpretability and hallucination with modern LMs, and the lack of grounding of current explanation methods (e.g., Chain-of-Thought). This paper proposes a new take on Prolog-based inference engines, where we replace handcrafted rules with a combination of neural language modeling, guided generation, and semiparametric dense retrieval. Our implementation, Nellie, is the first system to demonstrate fully interpretable, end-to-end grounded QA as entailment tree proof search, going beyond earlier work explaining known-to-be-true facts from text. In experiments, Nellie outperforms a similar-sized state-of-the-art reasoner while producing knowledge-grounded explanations. We also find Nellie can exploit both semi-structured and NL text corpora to guide reasoning. Together these suggest a new way to jointly reap the benefits of both modern neural methods and traditional symbolic reasoning.

1 Introduction

Large language models (LLMs) are impressive at question-answering (QA), but it remains challenging to understand how answers systematically follow from authoritative information. This general opacity is a growing impediment to widespread use of LLMs, e.g., in critical applications such as medicine, law, and hiring decisions, where interpretability and trust are paramount. While there has been rapid progress in having LLMs generate systematic explanations for their answers, e.g., Chain-of-Thought Wei et al. (2022), Entailer Tafjord et al. (2022), or Maieutic Prompting Jung et al. (2022), such explanations are not grounded in external facts and may include hallucinations Ji et al. (2022). Rather, what would be desirable - and what this work pursues - is a system that systematically reasons over authoritative text: to support answers with human interpretable proof trees grounded in the text, while not requiring translation to an entirely symbolic formalism.

Refer to caption — Figure 1: Given a query, Nellie performs a neuro-symbolic backward chaining search for proof trees whose leaves are grounded in a corpus of facts. It generates candidate decomposition rules guided by retrieved facts or templates. Then, it recursively tries to prove rule conditions via entailment from the corpus or further decomposition.

Our approach is to revisit the behavior of expert systems Jackson (1986); Metaxiotis et al. (2002). Expert systems are appealing for their explainable behavior: decisions are made by constructing a well-formed symbolic proof from explicit, formally represented knowledge authored by a knowledge engineer in consultation with a domain expert. However, as expert systems are known to be both expensive and brittle Musen and Van der Lei (1988), the AI community has turned to neuro-symbolic mechanisms that use large language models to reason over natural language (NL). Reasoning over NL does not require a symbolic formalism and allows the use of inferentially powerful LLMs, but also loses the systematic, verifiable proofs that expert systems produced. This motivates our pursuit of a new way to jointly reap the benefits of both modern neural methods and traditional reasoning.

We desire the following expert system-inspired desiderata:

1.

Grounding inferences fully and scalably in a corpus of knowledge from an authoritative human source.
2.

Logical direction, showing how a given hypothesis (and all intermediate inferences leading up to it) follows as the logical consequence of the underlying knowledge source
3.

Competitive end-to-end QA performance in a complex domain requiring diverse forms of reasoning.

As illustrated in Figure 2, various eXplainable QA (XQA) methods accomplish 2 of these criteria, but not all 3. Some methods, like Chain-of-Thought, generate inference chains or logically structured graphs from an LLM without grounding in verified knowledge. Others, like ExplanationLP Thayaparan et al. (2021), compose graphs of grounded facts, but do not show logical direction. LAMBADA Kazemi et al. (2023) achieves both direction and grounding but is limited to simple domains with provided NL Horn rules and sets of 1-2 dozen facts. In contrast, we desire a system that handles a larger corpus (10K statements) and doesn’t need handcrafted rules.

To achieve all three desiderata, we reuse the general inference framework of an expert system, but replace handcrafted rules with a combination of neural language modeling, guided generation, and semiparametric dense retrieval. We demonstrate this in a system called Nellie, the Neuro-Symbolic Large LM Inference Engine. Nellie leverages LLMs as proposal functions in the search of proof trees showing how a conclusion follows via entailment from an external corpus of NL statements. The “symbols” that our neuro-symbolic engine reasons over are free-form NL sentences. Rather than require a knowledge engineer to carefully write hundreds of inference rules as in the classical setting, Nellie employs an LLM as a dynamic rule generator [DRG; Kalyanpur et al. (2021)] to generate (rather than retrieve) candidate rules that decompose a hypothesis into subqueries that, if themselves proved recursively, will prove that hypothesis via composition (Figure 1). In this way, Nellie can answer the question posed by the classical expert system: “Does this statement systematically follow from my knowledge, or not?”.

Nellie is built upon a backward chaining symbolic theorem prover written in Prolog, implemented using a few meta-rules specifying how inference should proceed. These include checking for entailment of a hypothesis against a retrieved fact or decomposing it into a conjunction of subqueries to recursively prove. To treat NL sentences as if they were symbols in a purely symbolic search algorithm, we use a natural language inference-based form of weak unification Sessa (2002); Weber et al. (2019) between the hypothesis and a corpus fact. This produces interpretable proofs similar to the compositional entailment trees of prior work (e.g., EntailmentBank Dalvi et al. (2021)) while tackling the additional challenge of QA.

Nellie is designed to search across hundreds of trees whose leaves come from one of two types of knowledge: (a) a corpus of semi-structured text statements, such as NL renditions of database entries, or (b) a corpus of free-form NL sentences. Many correct proofs might exist for a given hypothesis, but much fewer will be fully groundable in the provided corpus, making the search harder than for ungrounded alternatives like Entailer Tafjord et al. (2022) or COMET-Dynagen Bosselut et al. (2021). To improve grounding, we introduce two guiding methods to boost the likelihood of generating rules whose conditions match against the available text: (1) For applications where a semi-structured corpus is available, Nellie leverages this structure via templates to help steer rule generation towards syntax that is more likely to match corpus entries. (2) For both free-form and semi-structured corpora, Nellie retrieves and conditions on statements to help steer generation towards trees grounded in them. Ablation experiments show these together and individually improve Nellie’s reasoning.

Nellie expands upon methods that ground known-to-be-true hypotheses to provided facts [SCSEARCH; Bostrom et al. (2022)], extending the paradigm to perform QA. This involves searching for and comparing trees for conflicting answer options. Experiments find Nellie outperforms a similar-sized state-of-the-art reasoner, Entailer, while producing compositional trees showing how decisions are grounded in corpus facts. Our contributions are thus:

1.

An architecture for systematic reasoning from a corpus of textual knowledge to answer questions. This can be viewed as a modern approach to expert system inference, but without requiring a formal knowledge representation.
2.

An implementation, Nellie,¹¹1Code found at https://github.com/JHU-CLSP/NELLIE. that outperforms a similar-sized SOTA reasoner (Entailer-3B) while producing grounded trees. To our knowledge, this is the first system to perform grounded XQA as NL entailment tree search.

2 Related Work

Theorem Proving over Language

A long-standing approach to reasoning over NL is to project it into a symbolic form, such as for QA Green et al. (1961); Zelle and Mooney (1996) or entailment Bos and Markert (2005). Provided the translation from NL to symbolic representation is accurate, one can leverage fast and scalable solutions for discrete symbolic inference Riazanov and Voronkov (2002); Kautz et al. (1992); Kautz and Selman (1999). However, reliably translating broad-domain NL into an adequately expressive formalism for reasoning is a challenge Schubert (2015), though some have found success using LLMs to perform this semantic parsing task Wong et al. (2023); Lyu et al. (2023); Olausson et al. (2023); Pan et al. (2023); Ye et al. (2023).

Recent work explores methods of handling NL without parsing it to another formalism. Some use LMs to generate proof steps in mathematical theorem proving Polu and Sutskever (2020); Welleck et al. (2022). Variants of neural theorem provers [NTPs; Rocktäschel and Riedel (2017)] such as NLProlog Weber et al. (2019) reconcile NL facts with symbolic reasoning by learning embeddings for the facts and symbols in a theory, then using weak unification to backward chain. Kalyanpur et al. (2021) inject neural reasoning into a Boxer/Prolog-based symbolic reasoner via a special LM-calling predicate. Arabshahi et al. (2021b) combine handwritten symbolic rules with neural symbol embeddings to classify conversational intents. Other work explores using LMs to emulate stepwise Tafjord et al. (2021); Kazemi et al. (2023) or end-to-end Clark et al. (2021); Picco et al. (2021) logical reasoning over small rulebases converted to NL. These approaches require both user-provided if/then rules to operate, while Nellie requires only facts and is thus applicable to domains in which rules are not available.

Modular Reasoning over NL

Nellie’s systematic reasoning is related to approaches that decompose problems into sequences of modular operations. Gupta et al. (2020) introduce a neural module network [NMN; Andreas et al. (2016)] for QA with modules for span extraction and arithmetic operations. Khot et al. (2021) introduce another NMN that decomposes questions into simpler ones answerable by existing models. These are part of a broader class of work decomposing multi-step reasoning using reasoning modules Khot et al. (2022); Saha et al. (2023a, b).

Systematic Explanation Generation

Recent works have used LMs to generate NL reasoning graphs in support of an answer. “Chain-of-Thought” prompting Wei et al. (2022); Kojima et al. (2022), elicits free-form inference hops from the LM before it generates an answer. Other text graph generation methods connect model-generated statements via common sense relations Bosselut et al. (2021); Arabshahi et al. (2021a) or for/against influence Madaan et al. (2021); Jung et al. (2022), though these are not knowledge-grounded and don’t address entailment (see Figure 2).

The EntailmentBank dataset Dalvi et al. (2021) has driven research towards the construction of explanation trees, challenging models to produce stepwise entailment proofs of a statement using a set of provided support facts. This direction builds upon works on explainable reasoning that build graphs from KB-retrieved sets of support statements, but stop short of showing their role in logical entailment Pan et al. (2019); Jansen and Ustalov (2019); Yadav et al. (2019); Valentino et al. (2022). Components of our framework are related to concurrent approaches for entailment tree construction Bostrom et al. (2022); Hong et al. (2022); Sprague et al. (2022). Ribeiro et al. (2022) also use iterative retrieval-conditioned generation, and Yang et al. (2022) also use entailment classifiers to filter proof steps. None of the above tree generation approaches consider this harder scenario of multiple-choice QA, opting instead to focus on the reconstruction task from support facts. Tafjord et al. (2022) do consider the harder task. They propose a backward chaining QA system, Entailer, that generates entailment trees (not grounded in human-verified facts) using a search grounded to the model’s internal beliefs, complementary to Nellie’s use of guided and retrieval-conditioned generation to obtain knowledge grounding. As with Nellie (§5.2), Entailer benefits from humans adding more useful statements to its available knowledge Dalvi Mishra et al. (2022). The difference between systems is highlighted by the number of generations (i.e. search nodes) considered by the two algorithms: while Entailer considers at most a couple dozen hypothesis decompositions, Nellie must consider hundreds or thousands to find one that is fully grounded.

Faithful Complex LLM Reasoning

Of the growing body of work on LLM-based “Chain-of-X” reasoning methods Xia et al. (2024), a portion considers ways to improve faithfulness to underlying knowledge and reduce LLM hallucinations (see Lyu et al. (2024) for an overview of faithful explanation methods). Nellie contributes to this space by providing a faithful-by-design algorithm that reasons based on logical hypothesis grounding. Other recent methods include Rethinking with Retrieval He et al. (2022), which reranks reasoning chains using a faithfulness score based on retrieved knowledge, and the forward-chaining Faithful Reasoning algorithm Creswell and Shanahan (2022), which follows “a beam search over reasoning traces” to answer a question by iteratively adding deductive inferences to a context of starting facts. Theirs is a different style search to our backward-chaining Nellie, not relying upon NLI for verifying logical connectedness and not scaling to larger knowledge bases.

3 Background

A logical expert system proves a propositional query against a theory comprised of facts and inference rules, generally given in the form of Horn clauses. Upon finding a rule whose head can unify with the query, a depth-first backward chaining algorithm such as those used in Prolog solvers will perform variable substitution and then recursively attempt to prove the terms in the rule’s body. For example, a disease classification system might prove query $\displaystyle\textsc{Contagious}(\textit{flu})$ via facts $\displaystyle\textsc{Contagious}(\textit{influenza})$ and $\displaystyle\textsc{OtherName}(\textit{flu},\textit{influenza})$ , and conjunctive rule $\displaystyle\textsc{Contagious}(X)\Leftarrow\textsc{OtherName}(X,Y)\land$ $\displaystyle\textsc{Contagious}(Y)$ . It does so by unifying $\displaystyle\textsc{Contagious}(\textit{flu})$ with $\displaystyle\textsc{Contagious}(X)$ and then recursively unifying the terms in the rule body with their matching facts. Here, flu is an object symbol, Contagious is a predicate symbol, and $X$ is a variable. See Russell and Norvig (2010) for further details.

Neural Predicates

While most declarative predicates have meaning only in the context of user-defined inference axioms, others can call external neural modules that produce values for their arguments or determine the truth value of the predicate. A popular implementation of this paradigm is DeepProbLog Manhaeve et al. (2018), which we use to define LM-invoking predicates. In the above example, we might train a sequence-to-sequence (seq2seq) model to produce other names for a disease $Y$ , turning $\displaystyle\textsc{OtherName}(Y^{+},X^{-})$ ²²2In Prolog syntax, ‘ $\displaystyle+$ ’ denotes inputs, ‘ $\displaystyle-$ ’ outputs. into a neural predicate. This mechanism creates the ability to introduce externally defined object symbols, e.g. seq2seq-generated NL, into the engine’s vocabulary.

Weak Unification

In classical backward chaining, a unification operator assigns equivalence to two logical atoms; this requires atoms to have the same arity and have no unequal ground literals in the same argument position. Issues arise when literals are NL sentences, which can be syntactically distinct but semantically equivalent. To handle this, Weber et al. (2019) propose a weak unification operator, which allows for the unification of any same-arity atoms regardless of conflicting symbols.³³3Introducing weak unification greatly increases the search runtime, as one might try to unify any two symbols in the vocabulary at every recursive step. This poses a substantial challenge when applying the query grounding algorithm to a search space over NL. They estimate a unification score as the aggregation of pairwise similarity scores using a similarity function $\theta(s_{1},s_{2})\in[0,1]$ . The score of the full proof is taken as the minimum of scores across all steps. In this work, we apply a similar aggregation; we say that a query fact $s_{1}$ “weakly unifies” with provenance fact $s_{2}$ with a unification score equal to the confidence of an NLI model taking $s_{2}$ as the premise and $s_{1}$ as the hypothesis.

4 Overview of Approach

Depicted in Figure 3, our framework is comprised of: an external corpus of facts (some $\{f_{1},\dots f_{n}\}$ ); a module that converts a QA pair to a hypothesis; an off-the-shelf theorem prover; and a suite of meta-axioms that use neural fact retrieval and dynamic rule generation modules to propose, verify, and score inferences. In our experiments, we consider one implementation of this framework that uses the corpus WorldTree Xie et al. (2020), a set of 9K NL science facts that can interchangeably be considered as rows in 81 $n$ -ary relational tables.

Question Conversion

Given a multiple-choice question, the system converts each candidate answer into a hypothesis $h$ using a Question to Declarative Sentence model [QA2D; Demszky et al. (2018)] (See §C). It then searches for a proof of $h$ against its knowledge base. For each alternative, we enumerate $p$ proofs using a time-capped backward chaining search and then take as the system’s answer the candidate with the overall highest-scoring proof.

4.1 Inference Rule Structure

Our approach uses LMs to dynamically generate inference rules given a hypothesis. The rule structure is strikingly simple, instantiating one of the following meta-level templates:

I.

Hypothesis $\Leftarrow$ Fact
II.

Hypothesis $\Leftarrow$ Fact1 $\land$ Fact2

Via template I, the system proves the hypothesis by finding a provenance Fact stored in its knowledge store that entails the hypothesis. Via template II, it enumerates a pair, Fact1 and Fact2, both either stored in the knowledge store or themselves recursively proved, such that the pair in conjunction entails the hypothesis.⁴⁴4We find that two-premise decomposition is sufficiently powerful and expressive for our purposes. For example, to prove a hypothesis such as those in EntailmentBank Dalvi et al. (2021) that requires a three-premise conjunction $h\Leftarrow f_{1}\land f_{2}\land f_{3}$ , Nellie produces instead a recursive set of decompositions $H\Leftarrow f_{1}\land f_{i};f_{i}\Leftarrow f_{2}\land f_{3}$ . Template I is given higher search precedence than II, yielding an intuitive high-level procedure: we first look up the hypothesis against the factbase, searching for an entailing fact. If we do not find one, we decomposes the hypothesis into a pair of statements to be proved. Concretely, for an input hypothesis $h$ , we define the predicate $\textsc{Prove}(h)$ that serves as the primary goal term. We define the following core meta-rules, which use the neural predicates Retrieve, Entails, and RuleGen. At each step in the backward-chaining search, Nellie’s Prolog engine attempts to unify a query with the head of one of these three rules:

1.

Fact Unification
$\displaystyle\textsc{Prove}(h)\Leftarrow\textsc{Retrieve}(h^{+},f^{-})\land\textsc{Entails}(f,h)$
2.

Two Premise Rule Generation
$\displaystyle\textsc{Prove}(h)\Leftarrow\textsc{RuleGen}(h^{+},f_{1}^{-},f_{2}^{-})\ \land$ $\displaystyle\textsc{Entails}([f_{1},f_{2}],h)$
$\displaystyle\quad\land\ \textsc{Prove}(f_{1})\land\textsc{Prove}(f_{2})$
3.

Retrieved First Premise Rule Generation
$\displaystyle\textsc{Prove}(h)\Leftarrow\textsc{Retrieve}(h^{+},f_{1}^{-})\ \land\ \textsc{RuleGen}(h^{+},f_{1}^{+},f_{2}^{-})$
$\displaystyle\quad\land\textsc{Entails}([f_{1},f_{2}],h)\ \land\$ $\displaystyle\textsc{Prove}(f_{2})$

4.2 Unification with Retrieved Facts

For factbase fact $f$ , $\textsc{Prove}(f)$ is vacuously true. Rule 1 shows how we prove $\textsc{Prove}(h)$ using retrieval. The predicate Retrieve proposes candidate $f_{i}$ ’s given $h$ using a FAISS Johnson et al. (2019)-based nearest neighbor dense retrieval index. We train the retrieval encoder via ranking loss such that the embedding for a hypothesis is maximally similar to its supporting facts. To promote logical coherence and improve the precision of the system, we apply a set of neural models for recognizing textual entailment (RTE) as filters $\textsc{Entails}_{j}(\cdot)$ that iteratively rule out $f_{i}$ candidates that are not classified as entailing $h$ .

$\textsc{Entails}(f_{i},h)\Leftarrow\bigwedge_{j=1\dots n}\textsc{Entails}_{j}(f_{i},h)$

Implicit in rule 1 is that $\textsc{Prove}(h)$ weakly unifies with some $\textsc{Prove}(f_{i})$ ; we assign the unification score $\theta(h,f_{i})$ equal to the confidence of one RTE model.

For some questions such as the one depicted in Figure 4, it is necessary to ground a subquery in evidence from the problem. To handle this, we add the question setup (defined as all but its last sentence) as a “fact” always proposed by Retrieve.

4.3 Dynamic Rule Generator (DRG)

If we do not find an entailing fact for hypothesis $h$ , we decompose $h$ into a pair of entailing premises; we propose candidates using nucleus sampling Holtzman et al. (2019) from a seq2seq model. The predicate $\textsc{RuleGen}(h,f_{1},f_{2})$ prompts a model trained to generate $h\rightarrow f_{1},f_{2}$ pairs. The space of potential decompositions is very large; there are many deductively valid ways to prove a hypothesis in natural language, though only a fraction of them are ultimately groundable in the provided factbase. To bias the proof search towards those more likely to be grounded in the corpus, we adopt a two-pronged approach, illustrated in inference rules 2 and 3, that proposes a heterogeneous search frontier using different biasing strategies in addition to straightforward LM sampling.

Template Conditioned Generation (TCG)

One way in which we improve our LM-based proposal function is to leverage the high-level structure that supports reasoning in a given domain: we propose template-guided generation to bias search towards the semi-structure of WorldTree.⁵⁵5While our approach is applicable to a wide array of reasoning problems, the use of WorldTree-specific templates illustrates one way by which we can infuse domain-specific structure into the neural search algorithm. This is a strict departure from the burdensome process of symbolic knowledge engineering. As our experiments show, this guidance method improves Nellie’s QA accuracy by a few points, though ablating it yields a similarly strong performance. WorldTree tables correspond to types of facts with similar syntax and semantics that support scientific reasoning. WorldTree questions are annotated with the fact rows that support their answers. Each table can be viewed as an n-ary relation of columns whose values are text spans. E.g., the Taxonomic relation has columns <A>, [HYPONYM], <is a / a kind of>, <SCOPE1>, [HYPERNYM], <for>, [PURPOSE]. Rows include ‘a bird is an animal’ and ‘a seed is a kind of food for birds.’

Thus, for the RuleGen predicate in rule 2, half of the $f_{1},f_{2}$ candidates are sampled from the DRG conditioned on $h$ plus a template that cues the model to reflect the syntax of a WorldTree table. We train the DRG to accept any masked infilling template (e.g. <mask>is a kind of <mask>, akin to those used to pretrain LMs Lewis et al. (2019); Raffel et al. (2020)), and propose decompositions whose first fact reflects the template’s syntax. We thus create a $h,t_{1}\rightarrow f_{1},f_{2}$ model. We feed the model templates drawn from WorldTree’s tables, guiding it towards proof steps more likely to be grounded in the factbase. A sample of the 150 templates can be found in Figure 5 (a larger list is shown in §D). We reuse the same model for non-template-conditioned generation by feeding it an empty template. In practice, we make two generation calls: one samples $m$ free-generated candidates, and a second samples $n$ candidates for each of $n_{t}$ templates.

WorldTree Relation	Template
KINDOF	<mask>is a kind of <mask>
IFTHEN	if <mask>then <mask>
PROP-THINGS	<mask>has <mask>
CAUSE	<mask>causes <mask>
MADEOF	<mask>made of <mask>
REQUIRES	<mask>requires <mask>
ACTION	<mask>is when <mask>
USEDFOR	<mask>used to <mask>
PARTOF	<mask>a part of <mask>
CHANGE	<mask>changes <mask>
USEDFOR	<mask>used for <mask>
AFFECT	<mask>has <mask>impact on <mask>
PROP-ANIMAL-ATTRIB	<mask>is a <mask>animal
SOURCEOF	<mask>is a source of <mask>
COMPARISON	<mask>than <mask>
EXAMPLES	an example of <mask>is <mask>
COUPLEDRELATIONSHIP	as <mask>decreases <mask>will <mask>
PROP-CONDUCTIVITY	<mask>is <mask>conductor
PROP-GENERIC	<mask>is a property of <mask>
HABITAT	<mask>live in <mask>
MEASUREMENTS	<mask>is a measure of <mask>

Figure 5: Sample of WorldTree templates used for guided generation.

Template Selection

WorldTree is a diverse corpus, containing tables that are specific to a particular subset of science problems (e.g. the “Predator-Prey” table). As conditioning on dozens of templates can be computationally expensive, we introduce a case-based reasoning Schank (1983); Das et al. (2021) approach that selects relevant templates for a given hypothesis. We construct an Okapi-BM25 Jones et al. (2000) retrieval index over questions from the WorldTree QA training set to obtain the most lexically similar items to a query. At inference time, we select the top- $k$ most similar questions to the query and take as our template subset the tables of the questions’ annotated facts.

Retrieval Conditioned Generation (RCG)

In rule 3, rather than generate a pair of subqueries, we immediately ground half of the antecedent by choosing as $f_{1}$ a fact retrieved directly from the corpus. We have the DRG force decode $f_{1}$ before generating $f_{2}$ as normal, then recur only on $f_{2}$ .

Filters

As stochastic sampling from LMs can be noisy, some fraction of the generated candidate set may be invalid: premises may be incoherent, or the decomposition might not properly entail $h$ . Accordingly, we introduce a set of compositional entailment verifiers Khot et al. (2020); Jhamtani and Clark (2020) trained on two-premise compositional entailment. We also add a “self-ask” filter, which following Tafjord et al. (2022) is an LM fine-tuned to assign a statement a truth value. If the confidence is below 0.5 for either an entailment judgment or the ‘self-ask’ belief in $f_{1}$ or $f_{2}$ , then we filter the pair. All filters condition on the question text as context. When Nellie uses these rules, the unification score equals the lowest of the scores for $\textsc{Prove}(f_{1})$ , for $\textsc{Prove}(f_{2})$ , and the confidence of entailment filters $s_{e}([f_{1},f_{2}]\Rightarrow H)$ .

4.4 Proof Search

Given a query, Nellie searches for $t$ seconds to find up to $p$ proofs of depth $d$ or less. We follow Weber et al. (2019) in pruning search branches whose unification score is guaranteed to fall below the current best, given our monotonic aggregation function $\min(\cdot)$ . Found proofs that score under the current best do not count towards $p$ . Full pseudocode for the algorithm, which follows a depth-first search with a breadth-first lookahead Stern et al. (2010) to check for the unification of generated subgoals, can be found in §E. It is parameterized by

1.

A maximum number of proofs $m$ at which to cut off searching. In experiments, we set this to $10$ for top-level queries and $2$ for recursive subqueries.
2.

A number of support facts $n_{f}$ to retrieve at each call to $\textsc{Retrieve}_{K}$ , which we set to 15.
3.

Candidate generation rates $n_{v}$ for vanilla nucleus-sampled decompositions, $n_{t}$ for template-conditioned decompositions, and $n_{r}$ for retrieval-conditioned generations. We set these each to $40$ .⁶⁶6Due to batching, these correspond to 3 total calls to the HuggingFace library’s generate function for the T5-3B model. Upon removing exact match duplicates, a call to RuleGen produces about $100$ candidates.
4.

Entailment scoring module $\textsc{Score}_{e}(\cdot)$ , which is a separate RTE cross-encoder model for single- and double-premise entailments.

5 Experiments

Our experiments illustrate how the approach exemplified by Nellie provides grounded and logical explanations, performing comparably or better than approaches that do not satisfy these properties. We evaluate models on two multiple-choice QA datasets constructed so that correct answers are supported by facts in the WorldTree corpus:

EntailmentBank Dalvi et al. (2021) is a dataset of entailment trees for declarativized answers to the AI2 Reasoning Challenge (ARC) dataset Clark et al. (2018), showing how the hypothesis can be derived via compositional entailment hops from WorldTree facts. We recast the test set, initially designed to test tree reconstruction, into QA by retrieving the corresponding multiple-choice ARC questions from which the hypotheses were constructed.

WorldTree Xie et al. (2020) is a subset of the ARC dataset annotated with undirected explanation graphs whose nodes are facts from the WorldTree tablestore. We note that WorldTree explanations do not show how facts should combine. There is no guarantee that fully grounded trees exist for these questions using the WorldTree corpus alone. The difficulty of this task is akin to that of a course exam: the teacher (us) provides the student (the model) with a very large study guide of facts, but expects the student to use these facts by composing them to reason coherently about a problem.

Our task metric is accuracy: whether a generated proof of the correct option outscores any other.⁷⁷7If it produces no proofs, it gives no answer and is wrong. Nellie searches for up to $p$ =10 proofs of max depth $d$ =5 with a timeout of $t$ =180 seconds per option.

Baselines

We evaluate Nellie against Entailer Tafjord et al. (2022), another system that produces entailment tree proofs via backward chaining. Entailer stops recurring not when it finds entailing facts from a corpus, but rather when the model believes that a subquery is true with high confidence. Its trees are thus not grounded in verified facts. We reimplemented their algorithm using their T5-11B-based model, reporting their configuration of a max tree depth (D) of 3 and minimum of 1 (i.e. $\geq 1$ decomposition). We also evaluate their ablated setting which recurs exactly once (D=1). This is a baseline that is neither grounded nor particularly interpretable, generating just a pair of statements. To isolate the impact of model size, we also evaluate an Entailer-3B model based on the same T5-3B model as Nellie’s DRG.⁸⁸8We obtained the training data from Tafjord et al. (2022) and trained our model in consultation with the authors. We also compare against grounded xQA methods without logical structure (see Fig 2): PathNet Kundu et al. (2019), which constructs 2-hop chains by linking entities between facts, and three approaches that build graphs from facts using linear programming: TupleILP Khot et al. (2017), ExplanationLP Thayaparan et al. (2021), and Diff-Explainer Thayaparan et al. (2022).⁹⁹9We show results from [Thayaparan et al. (2021) & 2022].

	Explanations		QA Accuracy (%)
	Grounded	Logical	Ovr	Easy	Chal
EntailmentBank QA
Nellie (3B)	Yes	Yes	71.4	76.4	60.4
Entailer-3B
(D $=$ 3)	No	Yes	48.7	52.8	39.6
(D $=$ 1)	No	No	64.9	71.2	50.9
Entailer-11B
(D $=$ 3)	No	Yes	73.2	77.3	64.2
(D $=$ 1)	No	No	71.1	76.4	59.4
WorldTree QA
Nellie (3B)	Yes	Yes	71.4	75.7	60.9
Entailer-3B
(D $=$ 3)	No	Yes	45.2	50.1	33.3
(D $=$ 1)	No	No	47.7	51.6	38.5
Entailer-11B
(D $=$ 3)	No	Yes	73.2	76.7	64.6
(D $=$ 1)	No	No	74.1	78.7	63.0
PathNet	Yes	No	43.4
TupleILP	Yes	No	49.8
ExplanationLP	Yes	No	62.6
Diff-Explainer	Yes	No	71.5

Table 1: Nellie performance vs. comparable XQA systems.

5.1 Results

Table 1 shows QA performance. Nellie’s overall (Ovr) accuracy of over 70% matches that of the best-performing grounded baseline, Diff-Explainer, on WorldTree, and is within 2 points of the best logically directed baseline, Entailer-11B. This is notable given Entailer-11B is a much larger model and has no requirement to provide grounded proofs. Nellie outperforms the same-sized Entailer-3B baseline by a margin of 22% on EntailmentBank and 26% on WorldTree under its default max D = 3 configuration, and even outperforms the less explainable D = 1 variant.

Figure 6 shows the results of ablating Nellie’s two conditional generation modules and replacing them with vanilla generation. Removing both template- and retrieval-conditioned generation lowers Nellie’s performance in all circumstances, highlighting the empirical benefit of structured guidance. Ablating TCG (( $-$ TCG), and the drop from ( $-$ RCG) to ( $-$ Both)) reduces performance by 1-1.5 points. Ablating RCG (Nellie vs ( $-$ RCG)) drops it by 3-4.

5.2 Domain Generalization and Knowledge Scaling

While Nellie was trained on datasets centered around WorldTree, we show that it can perform in another domain by altering the knowledge over which it reasons. We consider OpenBookQA Mihaylov et al. (2018), a dataset that requires reasoning over facts not included in WorldTree; each question is associated with one WorldTree science fact (“metals conduct electricity”), but also one fact from a separate pool of common knowledge (“a suit of armor is made of metal”).

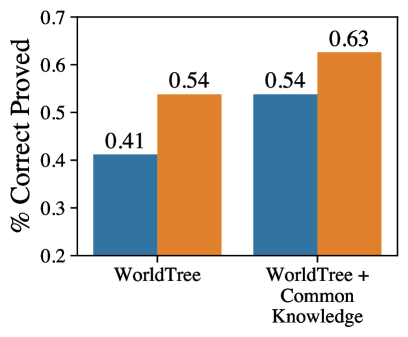
As with a classical expert system, we have designed Nellie to be “improvable merely by making statements to it” McCarthy (1959). This suggests that as we increase the provided knowledge store, we should expect Nellie to reason more effectively. Because WorldTree does not cover all the knowledge required to answer OBQA questions, we test whether Nellie performs better on them when we add the common knowledge to its retrieval index. As the common knowledge annotations are one fact per question and are not designed specifically for entailment, it is unlikely a priori that a fully grounded entailment tree can be created using the available knowledge alone, making this a challenging task.

Figure 7 shows Nellie’s accuracy with and without RCG. We do not use TCG, as the targeted common knowledge is free-form. We find that QA accuracy increases 11-12% with the common knowledge added. The percent of correct statement proved also increases 9-12%. These results also highlight the importance of RCG, as it provides a 5% QA boost and 13% on correct proof rate. These results show that Nellie can be applied out-of-the-box to a dataset requiring reasoning over a different source of free-form NL knowledge.

5.3 Tree Error Analysis

We find that Nellie can produce high quality proofs of correct hypotheses; examples are shown in Figure 8 (left) and §F. However, the system can also generate proofs for incorrect answers that bypass its entailment filters. We can diagnose (and perhaps annotate) error patterns to address in future work. We list a few categories, depicted in Figure 8 (right). A common pattern of error is Hypernym Property Inheritance Errors (also known as the “fallacy of the undistributed middle”), in which the model assumes that a member of a taxonomic class has a property of their hypernym, but the property is not universal. A colloquial example is inferring penguins can fly from penguins are birds & birds can fly. We also observe an amount of Errors from Semantic Drift Khashabi et al. (2019) between inference hops, culminating in RTE model false positives. E.g., in block $2$ of Fig 8 (right), which object loses temperature during heat transfer changes between hops. Figure 9 shows the distribution of these errors on a set of 136 incorrect answers from EntailmentBank. The predominant error case is a failure to find any proof of the correct option.

Correct Answer Tree Analysis

To investigate whether Nellie reaches a right solution with right vs wrong reasoning, we manually inspected for reasoning errors in 50 correct answer trees produced by NELLIE. We found that 39/50 (78%) of trees were perfectly acceptable. Most of the 11 unacceptable trees were due to incompleteness at one decomposition step.

6 Conclusion

We propose a reimagined version of a classical expert system that relies on the inferential power of LLMs rather than handcrafted rules. Nellie has the skeleton of a symbolic theorem prover, but the provided rules invoke neural predicates that allow for systematic reasoning over NL statements. To dynamically generate inferences, we introduce two mechanisms for knowledge-guided generation: conditioning decompositions on retrieval or model-selected inference templates. Our search algorithm undergirds Nellie, an explainable reasoning system that performs end-to-end QA by searching for grounded entailment trees. We find that Nellie equals or exceeds the performance of comparable XQA systems, while providing explanations with the simultaneous guarantees of logical directionality and groundedness in human-provided text. This work thus suggests a new way to jointly reap the benefits of both modern neural methods and traditional reasoning.

Acknowledgements

Thanks to Nils Holzenberger, Kyle Richardson, Elias Stengel-Eskin, Marc Marone, Kate Sanders, Rachel Wicks, and Andrew Blair-Stanek for comments on earlier drafts. Thank you to Abbey Coogan for feedback on figure design.

References

Akiba et al. [2019] Takuya Akiba, Shotaro Sano, Toshihiko Yanase, Takeru Ohta, and Masanori Koyama. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of SIGKDD, 2019.
Andreas et al. [2016] Jacob Andreas, Marcus Rohrbach, Trevor Darrell, and Dan Klein. Neural module networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2016.
Arabshahi et al. [2021a] Forough Arabshahi, Jennifer Lee, Antoine Bosselut, Yejin Choi, and Tom Mitchell. Conversational multi-hop reasoning with neural commonsense knowledge and symbolic logic rules. In Proceedings of EMNLP, 2021.
Arabshahi et al. [2021b] Forough Arabshahi, Jennifer Lee, Mikayla Gawarecki, Kathryn Mazaitis, Amos Azaria, and Tom Mitchell. Conversational neuro-symbolic commonsense reasoning. In Proceedings of AAAI, 2021.
Bos and Markert [2005] Johan Bos and Katja Markert. Recognising textual entailment with logical inference. In Proceedings of HLT and EMNLP, 2005.
Bosselut et al. [2021] Antoine Bosselut, Ronan Le Bras, and Yejin Choi. Dynamic neuro-symbolic knowledge graph construction for zero-shot commonsense question answering. AAAI, 2021.
Bostrom et al. [2022] Kaj Bostrom, Zayne Sprague, Swarat Chaudhuri, and Greg Durrett. Natural language deduction through search over statement compositions. In Findings of ACL: EMNLP 2022, 2022.
Clark et al. [2018] Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. Think you have solved question answering? try arc, the ai2 reasoning challenge. arXiv:1803.05457, 2018.
Clark et al. [2021] Peter Clark, Oyvind Tafjord, and Kyle Richardson. Transformers as soft reasoners over language. In Proceedings of IJCAI, 2021.
Creswell and Shanahan [2022] Antonia Creswell and Murray Shanahan. Faithful reasoning using large language models. arXiv preprint arXiv:2208.14271, 2022.
Dalvi et al. [2021] Bhavana Dalvi, Peter Jansen, Oyvind Tafjord, Zhengnan Xie, Hannah Smith, Leighanna Pipatanangkura, and Peter Clark. Explaining answers with entailment trees. In Proceedings of EMNLP, 2021.
Dalvi Mishra et al. [2022] Bhavana Dalvi Mishra, Oyvind Tafjord, and Peter Clark. Towards teachable reasoning systems: Using a dynamic memory of user feedback for continual system improvement. In Proceedings of EMNLP, 2022.
Das et al. [2021] Rajarshi Das, Manzil Zaheer, Dung Thai, Ameya Godbole, Ethan Perez, Jay Yoon Lee, Lizhen Tan, Lazaros Polymenakos, and Andrew McCallum. Case-based reasoning for natural language queries over knowledge bases. In Proceedings of EMNLP, 2021.
Demszky et al. [2018] Dorottya Demszky, Kelvin Guu, and Percy Liang. Transforming question answering datasets into natural language inference datasets. arXiv:1809.02922, 2018.
Green et al. [1961] Bert F. Green, Alice K. Wolf, Carol Chomsky, and Kenneth Laughery. Baseball: An automatic question-answerer. 1961.
Gupta et al. [2020] Nitish Gupta, Kevin Lin, Dan Roth, Sameer Singh, and Matt Gardner. Neural module networks for reasoning over text. In International Conference on Learning Representations, 2020.
He et al. [2022] Hangfeng He, Hongming Zhang, and Dan Roth. Rethinking with retrieval: Faithful large language model inference. arXiv preprint arXiv:2301.00303, 2022.
Holtzman et al. [2019] Ari Holtzman, Jan Buys, Li Du, Maxwell Forbes, and Yejin Choi. The curious case of neural text degeneration. In ICLR, 2019.
Hong et al. [2022] Ruixin Hong, Hongming Zhang, Xintong Yu, and Changshui Zhang. METGEN: A module-based entailment tree generation framework for answer explanation. In Findings of ACL: NAACL 2022, 2022.
Jackson [1986] P Jackson. Introduction to expert systems. 1986.
Jansen and Ustalov [2019] Peter Jansen and Dmitry Ustalov. TextGraphs 2019 shared task on multi-hop inference for explanation regeneration. In Proceedings of the Thirteenth Workshop on Graph-Based Methods for Natural Language Processing (TextGraphs-13), 2019.
Jhamtani and Clark [2020] Harsh Jhamtani and Peter Clark. Learning to explain: Datasets and models for identifying valid reasoning chains in multihop question-answering. In Proceedings of EMNLP (EMNLP), 2020.
Ji et al. [2022] Ziwei Ji, Nayeon Lee, Rita Frieske, Tiezheng Yu, Dan Su, Yan Xu, Etsuko Ishii, Yejin Bang, Andrea Madotto, and Pascale Fung. Survey of hallucination in natural language generation. ACM Computing Surveys, 2022.
Johnson et al. [2019] Jeff Johnson, Matthijs Douze, and Hervé Jégou. Billion-scale similarity search with GPUs. IEEE Transactions on Big Data, 2019.
Jones et al. [2000] Karen Sparck Jones, Steve Walker, and Stephen E. Robertson. A probabilistic model of information retrieval: development and comparative experiments - part 1. Inf. Process. Manag., 2000.
Jung et al. [2022] Jaehun Jung, Lianhui Qin, Sean Welleck, Faeze Brahman, Chandra Bhagavatula, Ronan Le Bras, and Yejin Choi. Maieutic prompting: Logically consistent reasoning with recursive explanations. In Proceedings of EMNLP, 2022.
Kalyanpur et al. [2021] Aditya Kalyanpur, Tom Breloff, David Ferrucci, Adam Lally, and John Jantos. Braid: Weaving symbolic and neural knowledge into coherent logical explanations. AAAI, 2021.
Kautz and Selman [1999] Henry Kautz and Bart Selman. Unifying sat-based and graph-based planning. In IJCAI, 1999.
Kautz et al. [1992] Henry A Kautz, Bart Selman, et al. Planning as satisfiability. In ECAI, 1992.
Kazemi et al. [2023] Mehran Kazemi, Najoung Kim, Deepti Bhatia, Xin Xu, and Deepak Ramachandran. LAMBADA: Backward chaining for automated reasoning in natural language. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), 2023.
Khashabi et al. [2019] Daniel Khashabi, Erfan Sadeqi Azer, Tushar Khot, Ashish Sabharwal, and Dan Roth. On the possibilities and limitations of multi-hop reasoning under linguistic imperfections. arXiv:1901.02522, 2019.
Khot et al. [2017] Tushar Khot, Ashish Sabharwal, and Peter Clark. Answering complex questions using open information extraction. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), 2017.
Khot et al. [2018] Tushar Khot, Ashish Sabharwal, and Peter Clark. Scitail: A textual entailment dataset from science question answering. In AAAI, 2018.
Khot et al. [2020] Tushar Khot, Peter Clark, Michal Guerquin, Peter Jansen, and Ashish Sabharwal. Qasc: A dataset for question answering via sentence composition. In Proceedings of AAAI, 2020.
Khot et al. [2021] Tushar Khot, Daniel Khashabi, Kyle Richardson, Peter Clark, and Ashish Sabharwal. Text modular networks: Learning to decompose tasks in the language of existing models. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2021.
Khot et al. [2022] Tushar Khot, Harsh Trivedi, Matthew Finlayson, Yao Fu, Kyle Richardson, Peter Clark, and Ashish Sabharwal. Decomposed prompting: A modular approach for solving complex tasks. In The Eleventh International Conference on Learning Representations, 2022.
Kojima et al. [2022] Takeshi Kojima, Shixiang Shane Gu, Machel Reid, Yutaka Matsuo, and Yusuke Iwasawa. Large language models are zero-shot reasoners. arXiv:2205.11916, 2022.
Kundu et al. [2019] Souvik Kundu, Tushar Khot, Ashish Sabharwal, and Peter Clark. Exploiting explicit paths for multi-hop reading comprehension. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 2019.
Lewis et al. [2019] Mike Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, and Luke Zettlemoyer. Bart: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. arXiv:1910.13461, 2019.
Lyu et al. [2023] Qing Lyu, Shreya Havaldar, Adam Stein, Li Zhang, Delip Rao, Eric Wong, Marianna Apidianaki, and Chris Callison-Burch. Faithful chain-of-thought reasoning. In ACL. Association for Computational Linguistics, 2023.
Lyu et al. [2024] Qing Lyu, Marianna Apidianaki, and Chris Callison-Burch. Towards Faithful Model Explanation in NLP: A Survey. Computational Linguistics, 2024.
Madaan et al. [2021] Aman Madaan, Niket Tandon, Dheeraj Rajagopal, Peter Clark, Yiming Yang, and Eduard Hovy. Think about it! improving defeasible reasoning by first modeling the question scenario. In Proceedings of EMNLP, 2021.
Manhaeve et al. [2018] Robin Manhaeve, Sebastijan Dumancic, Angelika Kimmig, Thomas Demeester, and Luc De Raedt. Deepproblog: Neural probabilistic logic programming. NIPS, 2018.
McCarthy [1959] John McCarthy. Programs with common sense, 1959.
Metaxiotis et al. [2002] Kostas S Metaxiotis, Dimitris Askounis, and John Psarras. Expert systems in production planning and scheduling: A state-of-the-art survey. Journal of Intelligent Manufacturing, 2002.
Mihaylov et al. [2018] Todor Mihaylov, Peter Clark, Tushar Khot, and Ashish Sabharwal. Can a suit of armor conduct electricity? a new dataset for open book question answering. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, 2018.
Musen and Van der Lei [1988] Mark A Musen and Johan Van der Lei. Of brittleness and bottlenecks: Challenges in the creation of pattern-recognition and expert-system models. In Machine Intelligence and Pattern Recognition. 1988.
Nguyen et al. [2016] Tri Nguyen, Mir Rosenberg, Xia Song, Jianfeng Gao, Saurabh Tiwary, Rangan Majumder, and Li Deng. Ms marco: A human generated machine reading comprehension dataset. In CoCo@ NIPs, 2016.
Olausson et al. [2023] Theo Olausson, Alex Gu, Ben Lipkin, Cedegao Zhang, Armando Solar-Lezama, Joshua Tenenbaum, and Roger Levy. LINC: A neurosymbolic approach for logical reasoning by combining language models with first-order logic provers. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, 2023.
Pan et al. [2019] Zhufeng Pan, Kun Bai, Yan Wang, Lianqiang Zhou, and Xiaojiang Liu. Improving open-domain dialogue systems via multi-turn incomplete utterance restoration. In Proceedings of EMNLP-IJCNLP, 2019.
Pan et al. [2023] Liangming Pan, Alon Albalak, Xinyi Wang, and William Wang. Logic-LM: Empowering large language models with symbolic solvers for faithful logical reasoning. In Findings of ACL: EMNLP 2023, 2023.
Picco et al. [2021] Gabriele Picco, Thanh Lam Hoang, Marco Luca Sbodio, and Vanessa Lopez. Neural unification for logic reasoning over natural language. In Findings of ACL: EMNLP 2021, 2021.
Polu and Sutskever [2020] Stanislas Polu and Ilya Sutskever. Generative language modeling for automated theorem proving. ArXiv, 2020.
Raffel et al. [2020] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J Liu. Exploring the limits of transfer learning with a unified text-to-text transformer. JMLR, 2020.
Reimers and Gurevych [2019] Nils Reimers and Iryna Gurevych. Sentence-BERT: Sentence embeddings using Siamese BERT-networks. In Proceedings of EMNLP-IJCNLP, 2019.
Riazanov and Voronkov [2002] Alexandre Riazanov and Andrei Voronkov. The design and implementation of vampire. AI communications, 2002.
Ribeiro et al. [2022] Danilo Neves Ribeiro, Shen Wang, Xiaofei Ma, Rui Dong, Xiaokai Wei, Henry Zhu, Xinchi Chen, Zhiheng Huang, Peng Xu, Andrew O. Arnold, and Dan Roth. Entailment tree explanations via iterative retrieval-generation reasoner. In NAACL-HLT, 2022.
Rocktäschel and Riedel [2017] Tim Rocktäschel and Sebastian Riedel. End-to-end differentiable proving. Advances in neural information processing systems, 2017.
Russell and Norvig [2010] Stuart Russell and Peter Norvig. Artificial intelligence: a modern approach. 2010.
Saha et al. [2023a] Swarnadeep Saha, Omer Levy, Asli Celikyilmaz, Mohit Bansal, Jason Weston, and Xian Li. Branch-solve-merge improves large language model evaluation and generation, 2023.
Saha et al. [2023b] Swarnadeep Saha, Xinyan Yu, Mohit Bansal, Ramakanth Pasunuru, and Asli Celikyilmaz. MURMUR: Modular multi-step reasoning for semi-structured data-to-text generation. In Findings of ACL: ACL 2023, 2023.
Schank [1983] Roger C Schank. Dynamic memory: A theory of reminding and learning in computers and people. 1983.
Schubert [2015] Lenhart Schubert. Semantic representation. Proceedings of AAAI, 29(1), Mar. 2015.
Sessa [2002] Maria I Sessa. Approximate reasoning by similarity-based sld resolution. Theoretical computer science, 2002.
Sprague et al. [2022] Zayne Sprague, Kaj Bostrom, Swarat Chaudhuri, and Greg Durrett. Natural language deduction with incomplete information. In Proceedings of EMNLP, 2022.
Stern et al. [2010] Roni Stern, Tamar Kulberis, Ariel Felner, and Robert Holte. Using lookaheads with optimal best-first search. In Proceedings of AAAI, 2010.
Tafjord et al. [2021] Oyvind Tafjord, Bhavana Dalvi, and Peter Clark. ProofWriter: Generating implications, proofs, and abductive statements over natural language. In Findings of ACL: ACL-IJCNLP 2021, 2021.
Tafjord et al. [2022] Oyvind Tafjord, Bhavana Dalvi Mishra, and Peter Clark. Entailer: Answering questions with faithful and truthful chains of reasoning. In Proceedings of EMNLP, 2022.
Thayaparan et al. [2021] Mokanarangan Thayaparan, Marco Valentino, and André Freitas. Explainable inference over grounding-abstract chains for science questions. In Findings of ACL: ACL-IJCNLP 2021, 2021.
Thayaparan et al. [2022] Mokanarangan Thayaparan, Marco Valentino, Deborah Ferreira, Julia Rozanova, and André Freitas. Diff-explainer: Differentiable convex optimization for explainable multi-hop inference. TACL, 2022.
Valentino et al. [2022] Marco Valentino, Mokanarangan Thayaparan, and André Freitas. Case-based abductive natural language inference. In Proceedings of the 29th International Conference on Computational Linguistics, 2022.
Wang and Komatsuzaki [2021] Ben Wang and Aran Komatsuzaki. GPT-J-6B: A 6 Billion Parameter Autoregressive Language Model, 2021.
Weber et al. [2019] Leon Weber, Pasquale Minervini, Jannes Münchmeyer, Ulf Leser, and Tim Rocktäschel. NLProlog: Reasoning with weak unification for question answering in natural language. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 2019.
Wei et al. [2022] Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Ed Chi, Quoc Le, and Denny Zhou. Chain of thought prompting elicits reasoning in large language models. arXiv:2201.11903, 2022.
Welleck et al. [2022] Sean Welleck, Jiacheng Liu, Ximing Lu, Hannaneh Hajishirzi, and Yejin Choi. Naturalprover: Grounded mathematical proof generation with language models. arXiv:2205.12910, 2022.
Wong et al. [2023] Lionel Wong, Gabriel Grand, Alexander K. Lew, Noah D. Goodman, Vikash K. Mansinghka, Jacob Andreas, and Joshua B. Tenenbaum. From word models to world models: Translating from natural language to the probabilistic language of thought, 2023.
Xia et al. [2024] Yu Xia, Rui Wang, Xu Liu, Mingyan Li, Tong Yu, Xiang Chen, Julian McAuley, and Shuai Li. Beyond chain-of-thought: A survey of chain-of-x paradigms for llms, 2024.
Xie et al. [2020] Zhengnan Xie, Sebastian Thiem, Jaycie Martin, Elizabeth Wainwright, Steven Marmorstein, and Peter Jansen. WorldTree v2: A corpus of science-domain structured explanations and inference patterns supporting multi-hop inference. In Proceedings of the Twelfth Language Resources and Evaluation Conference, 2020.
Yadav et al. [2019] Vikas Yadav, Steven Bethard, and Mihai Surdeanu. Quick and (not so) dirty: Unsupervised selection of justification sentences for multi-hop question answering. In Proceedings of EMNLP-IJCNLP, 2019.
Yang et al. [2022] Kaiyu Yang, Jia Deng, and Danqi Chen. Generating natural language proofs with verifier-guided search. In Proceedings of EMNLP, 2022.
Ye et al. [2023] Xi Ye, Qiaochu Chen, Isil Dillig, and Greg Durrett. SatLM: Satisfiability-aided language models using declarative prompting. In Thirty-seventh Conference on Neural Information Processing Systems, 2023.
Zelle and Mooney [1996] John M. Zelle and Raymond J. Mooney. Learning to parse database queries using inductive logic programming. In Proceedings of AAAI, 1996.

Appendix A Model Details and Training

We train the components of Nellie to be able to answer questions in the Science QA domain. The different neural modules are trained on reformulations of existing datasets for scientific reasoning. We use the following sources: WorldTree Explanations Xie et al. [2020] and EntailmentBank Dalvi et al. [2021] are used as described in the paper. eQASC Jhamtani and Clark [2020] and SciTaiL Khot et al. [2018] are datasets of two- and one-premise entailment questions.

QA2D Our QA2D model is a T5-11B Raffel et al. [2020] fine-tuned by Tafjord et al. [2022] on the original QA2D dataset Demszky et al. [2018].

Retrieval Module

The dense retrieval model is a SentenceTransformers Siamese BERT-Network encoder Reimers and Gurevych [2019] pretrained on the MS MARCO IR corpus Nguyen et al. [2016], which we fine-tune via ranking loss to maximize the cosine similarity between a hypothesis and its support facts. We gather $h,f_{1}$ from the WorldTree, EntailmentBank, and eQASC training sets, then sample random negatives during training.

Dynamic Rule Generator

The DRG is a T5-3B model Raffel et al. [2020] fine-tuned on $h\rightarrow[f_{1},f_{2}]$ pairs drawn from eQASC, which are numerous (26K) but noisy, and the binary composition steps from the EntailmentBank training set, which are few (3.8K) but ultimately rooted in facts from WorldTree. To make the DRG able to condition on templates, we adopt the span masking strategy from Raffel et al. [2020] to create a randomly masked version $\hat{f}_{1}$ of each $f_{1}$ and then train the model on $h,\hat{f}_{1}\rightarrow f_{1},f_{2}$ pairs. For each original triplet, we create one training example with a template, and one in which $\hat{f}_{1}$ is an empty <mask>, giving the model the dual capacity for non-template-generation.

Entailment Filters

We find that a mixture of strategies helps prioritize precision over recall when filtering candidates. For 1-premise filtering for unification and 2-premise filtering for rule generation, we fine-tune a separate pair of models consisting of a SentenceTransformer cross-encoder classifier and a T5 seq2seq. The former is trained via classification loss, the latter via sequence cross entropy loss. The 1-premise filters are trained on the SciTail dataset, the 2-premise filters on eQASC and EntailmentBank. For 2-premise entailment, we additionally add a “self-ask” filter, which following Tafjord et al. [2022] is a T5 model fine-tuned to produce its 0-to-1 confidence that a statement is true. If the confidence is below 0.5 for either $f_{1}$ or $f_{2}$ , we filter the pair. As in Tafjord et al. [2022], we train our DRG seq2seq in a multitask fashion so that it serves as both the rule generator as well as the “self-ask” filter and (half of) the 2-premise entailment filter.

A.1 Training

We use the default training parameters from the SentenceTransformers library¹⁰¹⁰10https://tinyurl.com/mvhbmfcc in order to train CrossEncoder-based classifier and Bi-encoder retriever models for 3 epochs. We correspondingly use the default fine-tuning parameters from the HuggingFace library in order to train our T5-based generation and classification models.

Appendix B Hyperparameters

The DRG produces $40$ (pre-filter) candidates divided evenly amongst the set of templates drawn via case-based retrieval from the top-( $k$ =10) most similar questions to a given query hypothesis. It also generates $40$ free-generated candidates, and $40$ retrieval-conditioned ones ( $4$ each for the $10$ top-scoring retrieved $f_{1}$ ’s). It therefore considers $120$ candidate decompositions at each recursion step. All sampling is done via nucleus sampling ( $p=.95$ ). RTE models filter all candidates for which the classification softmax likelihood of entailment is less than $0.7$ . We remove duplicates before filtering.

We used Optuna Akiba et al. [2019] to find the number of facts for retrieval-conditioned generation, the $p$ value for nucleus sampling, the entailment threshold, and the number of candidates generated at each recursion step. We used as our objective the overall QA accuracy on the EntailmentBank dev set. We ran it for about 300 trials, and found that the most important parameters were the entailment threshold (too low = too many bad proofs, too high = no proofs) and the nucleus $p$ (less than 0.8 reduced QA performance by 10-15. Experiments were run on 24GB Quadro RTX 6000s.

WorldTree Relation	Template
INSTANCES	<mask>is <mask>
ACTION	<mask>to <mask>
KINDOF	<mask>is a kind of <mask>
PROP-THINGS	<mask>are <mask>
ACTION	<mask>for <mask>
AFFORDANCES	<mask>can <mask>
IFTHEN	if <mask>then <mask>
PROP-THINGS	<mask>has <mask>
CAUSE	<mask>causes <mask>
MADEOF	<mask>made of <mask>
PROP-THINGS	<mask>have <mask>
REQUIRES	<mask>requires <mask>
ACTION	<mask>is when <mask>
USEDFOR	<mask>used to <mask>
PARTOF	<mask>a part of <mask>
CHANGE	<mask>changes <mask>
USEDFOR	<mask>used for <mask>
ATTRIBUTE-VALUE-RANGE	<mask>means <mask>
AFFECT	<mask>has <mask>impact on <mask>
PROP-ANIMAL-ATTRIB	<mask>is a <mask>animal
SOURCEOF	<mask>is a source of <mask>
CONTAINS	<mask>contains <mask>
COUPLEDRELATIONSHIP	as <mask>will <mask>
CHANGE-VEC	<mask>decreases <mask>
COMPARISON	<mask>than <mask>
ACTION	<mask>is when <mask>to <mask>
CAUSE	<mask>can cause <mask>
LOCATIONS	<mask>found <mask>
COMPARISON	<mask>more <mask>
PROP-INHERITEDLEARNED	<mask>is <mask>characteristic
DURING	<mask>during <mask>
CHANGE-VEC	<mask>increases <mask>
AFFORDANCES	<mask>can <mask>by <mask>
EXAMPLES	an example of <mask>is <mask>
SOURCEOF	<mask>produces <mask>
CONTAINS	<mask>contain <mask>
CHANGE	<mask>converts <mask>
COMPARISON	<mask>is <mask>than <mask>
FORMEDBY	<mask>formed by <mask>
CONSUMERS-EATING	<mask>eat <mask>
SOURCEOF	<mask>provides <mask>
PROP-RESOURCES-RENEWABLE	<mask>is <mask>resource
ATTRIBUTE-VALUE-RANGE	<mask>means <mask>of <mask>
COMPARISON	<mask>less <mask>
COUPLEDRELATIONSHIP	as <mask>decreases <mask>will <mask>
PROP-CONDUCTIVITY	<mask>is <mask>conductor
PROP-GENERIC	<mask>is a property of <mask>
HABITAT	<mask>live in <mask>
MEASUREMENTS	<mask>is a measure of <mask>
COUPLEDRELATIONSHIP	as <mask>increases <mask>will <mask>

Figure 10: Partial list of WorldTree templates used for guided generation, sorted by frequency of occurrence in EntailmentBank trees (full list omitted for space).

Appendix C QA2D Conversion

The following is an example conversion by our QA2D model of a multiple-choice question into a set of candidate hypotheses to prove.

Q: Ethanol is an alternative fuel made from corn. What is one of the unfavorable effects of using ethanol as a fuel?

(A)

decreased cost of fuel production
(B)

decrease in farm land available for food production
(C)

increase in the consumption of fossil fuels
(D)

increased carbon footprint from driving automobiles

Converted to the following hypotheses:

(A)

Using ethanol has an unfavorable effect on the cost of fuel.
(B)

Using ethanol as fuel decreases farm land available for food production.
(C)

Using ethanol as fuel increases in the consumption of fossil fuels.
(D)

The use of ethanol as an alternative fuel can lead to increased carbon footprints.

Appendix D WorldTree Templates

Table 10 depicts the infilling templates gathered from WorldTree and used for template-guided rule generation. We manually annotated this list. The full set of templates is of size $150$ .

Appendix E Search Algorithm

Algorithm 1 depicts Nellie’s search algorithm, the logic of which is implemented in a meta-interpreter coded in DeepProbLog Manhaeve et al. [2018].

Appendix F Example Proofs

Figure 11 illustrates more proofs generated by Nellie for questions from EntailmentBank and WorldTree.

Appendix G Impact of Design Choices

Nellie is comprised of numerous modules that are very difficult to evaluate in isolation given a lack of in-domain test sets for tasks like QA2D, decomposition generation ( $H\rightarrow F1,F2$ ) compositional RTE ( $H\Leftarrow F1,F2$ ), single-premise RTE ( $H\Leftarrow F1$ ), and fact retrieval. Below, we enumerate some modeling choices, alternatives we tried, and the extent to which we observed them impact the system.

•

QA2D:
Nellie uses: Tafjord et al. [2022]’s T5-11B model.
We also tried: using GPT-J Wang and Komatsuzaki [2021] with in-context-learning exemplars drawn from EntailmentBank. This results in 10+ point drop in QA, mainly because (A) EntailmentBank hypotheses are designed to be generics instead of question-conditioned statements and (B) GPT-J tended to generate true statements even for wrong answer options.
•

Decomposition generation ( $H\rightarrow F1,F2$ ):
Nellie uses: A T5-3B model trained in a multi-angle fashion similar to Tafjord et al. [2022], using additional data for compositional entailment and decomposition generation.
We also tried: Using a T5-Large model trained only on the decomposition data. This allowed us to generate far more decomposition candidates per hypothesis, but rate of obtaining a good decomposition was far lower. This led to 5+ point drop in QA.
•

Compositional RTE ( $H\Leftarrow F1,F2$ ):
Nellie uses: A sequence of (1) The same T5-3B model as for generation and (2) a cross-encoder trained on eQASC and EntailmentBank.
We also tried: (A) using a bi-encoder trained via contrastive loss (this was not as effective at ruling out bad decompositions), (B) not training the bi-encoder to condition on the question, and (C) only training on EntailmentBank (as Tafjord et al. [2022] do). All three variants reduce QA by 3-7%.
•

Single-premise RTE ( $H\Leftarrow F1$ ):
Nellie uses: (1) A cross-encoder trained on Sci-Tail
We also tried: an off-the-shelf RTE model¹¹¹¹11https://huggingface.co/cross-encoder/nli-deberta-v3-base, which had too high a false positive rate to be effective.
•

Fact Retrieval:
Nellie uses: a Sentence-Transformers bi-encoder pretrained on MS MARCO and fine-tuned on $(H,F1)$ pairs drawn from WorldTree, EntailmentBank, and eQASC.
We also tried: the same bi-encoder off-the-shelf without finetuning. This only dropped performance by 3-4 points.

1:procedure Prove(

H

m

d

)

\rightarrow

proofs

tree^{(1)}(H),\dots tree^{(m)}(H)

& scores

s^{(1)}(H),\dots s^{(m^{\prime})}{(H)}

2: i. check weak unification against

K

3: entailing premises

P={\color[rgb]{0,0,1}\textsc{PremiseLookup}}(H)

4: if

P

nonempty

5: then return proofs

=[(p\vdash{}H)\text{ for }p\in P]

, scores

=[{\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p\vdash{}H)\text{ for }p\in P]

6: elif

d=d_{\text{max}}

7: then Fail

8: ii. generate candidate decompositions: // If

H

does not unify against

K

, decompose it

9: decompositions

D={\color[rgb]{0,0,1}\textsc{RuleGen}}(H)

10: iii. check whether any decompositions pairs both unify: // this step amortizes premise lookups

11: proofs = []; scores = []

12: forall

(p_{1},p_{2})\in D

13: if

p_{1}\in K

and

\exists p_{2}^{\prime}\in{\color[rgb]{0,0,1}\textsc{PremiseLookup}}(p_{2})

// if

p_{1}

already grounded, its subtree is leaf

14: then proofs +=

(\{p_{1},(p_{2}^{\prime}\vdash{}p_{2})\}\vdash{}H)

15: scores +=

\min({\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{2}^{\prime}\vdash{}p_{2}),{\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{1}\land p_{2}\vdash{}H))

// tree score is min of scores used to construct it

16: elif

\exists p_{1}^{\prime}\in{\color[rgb]{0,0,1}\textsc{PremiseLookup}}(p_{1})

and

\exists p_{2}^{\prime}\in{\color[rgb]{0,0,1}\textsc{PremiseLookup}}(p_{2})

17: then proofs +=

(\{(p_{1}^{\prime}\vdash{}p_{1}),(p_{2}^{\prime}\vdash{}p_{2})\}\vdash{}H)

18: scores +=

\min({\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{1}^{\prime}\vdash{}p_{1}),{\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{2}^{\prime}\vdash{}p_{2}),{\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{1}\land p_{2}\vdash{}H))

19: if proofs not empty

20: then return proofs, scores

21: iv. recur on generated premises: // if still no proof, need to recur

22: proofs = []; scores = []

23: forall

(p_{1},p_{2})\in D

24: if

{\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{1}\land p_{2}\vdash{}H)>\max(\text{scores})

and

\text{len}(\text{proofs})<m

// only recur if chance of better score

25: then

(\text{proof}_{p_{1}},S_{p_{1}})={\color[rgb]{0,0,1}\textsc{Prove}}(p_{1},1,d+1)

26:

(\text{proof}_{p_{2}},S_{p_{2}})={\color[rgb]{0,0,1}\textsc{Prove}}(p_{2},1,d+1)

27: recursive score

S_{r}=\min(S_{p_{1}},S_{p_{2}},{\color[rgb]{1,.5,0}\textsc{Score}_{e}}(p_{1}\land p_{2}\vdash{}H))

28: if

S_{r}>\max(\text{scores})

29: then proofs +=

(\{\text{proof}_{p_{1}},\text{proof}_{p_{2}}\}\vdash{}H)

30: scores +=

S_{r}

31: return proofs, scores

32:

33:procedure PremiseLookup(H)

\rightarrow

premises

P

s.t.

\forall p\in P,p\vdash{}H

// try to ground H in K via weak entailment

34: candidate premises

P={\color[rgb]{1,.5,0}\textsc{Retrieve}_{K}}(H,n_{f})

// retrieve candidate premises s.t.

p\vdash{}H

35: forall

f\in{\color[rgb]{1,.5,0}\textsc{OnePremiseFilters}}

36:

P=f(P,H)

// only keep premises that pass all filters

37: return

P

38:

39:procedure RuleGen(

H

)

\rightarrow

decompositions

D=(p_{1}^{1},p_{2}^{1}),\dots(p_{1}^{c},p_{2}^{c})

// find candidate pairs s.t.

p_{1}\land p_{2}\vdash{}H

40:

D

= []

41:

D

{\color[rgb]{1,.5,0}\textsc{Generate}}(H,n=n_{v})

42: WTTemplates = CaseBasedRetrieveTemplate(H)

43: outputs per template

o_{t}=n_{t}/\text{len}({\color[rgb]{0.51953125,0.69921875,0.421875}\textsc{WTTemplates}})

44: forall

t\in{\color[rgb]{0.51953125,0.69921875,0.421875}\textsc{WTTemplates}}

do // generate candidates for each of 50 templates in WTTemplates

45:

D

{\color[rgb]{1,.5,0}\textsc{Generate}}([H\ t],n=o_{t})

// T5 model accepts optional

t

appended to

H

46: retrieved first premises

P_{1}={\color[rgb]{1,.5,0}\textsc{Retrieve}_{K}}(H,n_{f})

47: outputs per premise

o_{r}=n_{r}/\text{len}(P_{1})

48: forall

p_{K}\in P_{1}

do // generate candidates with retrieved support facts as first premise

49:

D

{\color[rgb]{1,.5,0}\textsc{Generate}}(H,\text{prefix}=p_{K},n=o_{r})

// Force decode

p_{K}

then generate a

p_{2}

50: forall

f\in{\color[rgb]{1,.5,0}\textsc{TwoPremiseFilters}}

do // includes entailment, regex, self-asking filters

51:

D=f(D,H)

// only keep premise pairs that pass all filters

52: return

D

Algorithm 1 Nellie’s backchaining algorithm, coded in Prolog, for searching for proof list

tree^{(1)}(H),\dots tree^{(m^{\prime})}(H)

with scores

s^{(1)}(H),\dots s^{(m^{\prime})}(H);m^{\prime}\leq m

for a hypothesis

H

against factbase

K

. The rule generator produces

n_{v}

candidates via vanilla nucleus sampling,

n_{t}

candidates via sampling from templates, and

n_{r}

candidates whose first fact is retrieved from K. The search is capped at max depth

d_{\text{max}}

. All Generate, Retrieve, and entailment scorer

\textsc{Score}_{e}

calls in forall loops are batched. All module outputs are cached. OnePremiseFilters and TwoPremiseFilters are ordered lists of neural entailment models.

\vdash{}

denotes weak entailment.

Question	Nellie Proof
In what way can forest fires affect the lithosphere? (A) increasing soil erosion (B) causing air pollution (C) increasing seismic activity (D) causing violent dust storms
The snowshoe hare sheds its fur twice a year. In the summer, the fur of the hare is brown. In the winter, the fur is white. Which of these statements best explains the advantage of shedding fur? (A) Shedding fur keeps the hare clean. (B) Shedding fur helps the hare move quickly. (C) Shedding fur keeps the hare’s home warm. (D) Shedding fur helps the hare blend into its habitat.
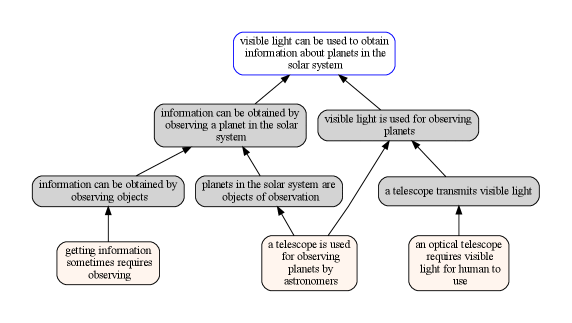
Scientists use large optical telescopes to obtain information about the planets in the solar system. What wavelengths of electromagnetic radiation provide this information? (A) gamma radiation (B) infrared radiation (C) radio waves (D) visible light

Nellie: A Neuro-Symbolic Inference Engine for Grounded, Compositional, and Explainable Reasoning