Negativity volume of the generalized Wigner function in gravitating hybrid system
Abstract
We evaluate the gravity-induced negativity volume of the generalized Wigner function in a hybrid system consisting of a particle in a two-localized superposition state and an oscillator. The generalized Wigner function can capture the nonclassicality of the system. The increase in the negativity volume of the generalized Wigner function can be an indicator of the entanglement generation, which is demonstrated in the hybrid system generating the gravity-induced entanglement in various initial states. Moreover, by comparing the behaviors of the negativity volume with the entanglement fidelity, we show that the nonclassical feature of entanglement is properly identified by the criterion based on the negativity volume of the generalized Wigner function when the oscillator is initially in a thermal state.
I INTRODUCTION
Wigner function describes a distribution function in the phase space, which appears in various fields of sciences (e.g., [1]). It is known that the Wigner function defined for a particle in classical mechanics always takes positive values. In contrast to classical mechanics, the Wigner function defined for a continuous variable system in quantum mechanics may have negative values, which is used as an indicator of the nonclassicality of the system [2]. Such a property of the Wigner function can be measured in experiments, which is commonly used in quantum optics as a quantum signature [3, 4, 5, 6].
The Wigner function for qubit systems has been extensively proposed [7, 8, 9, 10, 11, 12], which is defined on the Bloch sphere using the Euler angles. This Wigner function enables us to analyze the discrete systems in the continuous phase space parameterized by the angles. However, unlike the usual Wigner function for continuous variable systems, the Wigner function for qubit systems has negative regions on the Bloch sphere even for the arbitrary pure state of qubits. Hence, the negative region of the Wigner function does not simply characterize the nonclassicality of the discrete system. Thus, the Wigner function as an indicator of quantumness including qubit systems is not trivial. Under such circumstances, Ref. [10] introduced the negativity volume of the generalized Wigner function as an indicator of the nonclassical feature for a hybrid system.
The hybrid system, consisting of the discrete and continuous variable subsystems, is one of the central research in quantum information science; quantum information processing [13], quantum teleportation [14, 15], and quantum entanglement [16, 17]. The generalized Wigner function in the hybrid system is obtained in Ref. [7], but it is demonstrated that the negative values do not necessarily characterize the nonclassicality because of the property of the Wigner function in qubit systems. However, Ref. [10] showed that there is a critical value for the negativity volume of the Wigner function for the separable hybrid system; if the negativity volume is larger than the critical value, nonclassicality appears. We note that this criterion is a sufficient condition, not a necessary condition.
In the present study, we consider the generalized Wigner function of the hybrid system consisting of a particle in a two-state superposition and an oscillator, which are gravitationally interacting. Refs. [18, 20, 21, 19] discussed the quantum entanglement through the gravitational interaction in this hybrid system. Recently, the experimental proposal of the gravity-induced entanglement between two particles has attracted interest [22, 23]. The quantum entanglement is known as a nonlocal quantum correlation, which is not newly generated by classical processes (e.g. [24]). Refs. [22, 23] showed that two particles in a superposition state are entangled if Newtonian gravity obeys quantum mechanics, which was shown as a feasible experimental proposal in the future. This two-particle model has been the subject of several advanced studies [25, 26, 27, 28, 29]. In addition, gravitational entanglement between mechanical oscillators in optomechanical systems has also been investigated [30, 31, 32, 33, 34, 35]; experiments [36, 37, 38] and theories [39, 40, 41, 42, 43] have been developed towards the realization of macroscopic quantum states to verify the quantum nature of gravity. Furthermore, quantum entanglement generation by Newtonian gravity has been discussed from the viewpoint of quantum field theory and gravitons [44, 45, 46, 47, 48, 49, 50, 51, 52, 53].
For the hybrid system considered in the present paper, we evaluate the gravity-induced negativity volume of the generalized Wigner function as a quantity to characterize the quantumness of gravity and discuss its correspondence with the condition for the quantum entanglement based on the generalized Wigner function [10]. We discuss the applicability of the quantum entanglement criterion with the generalized Wigner function in comparison with the entanglement fidelity criterion proposed in Ref. [54, 55, 56]. In particular, we show that the condition based on the generalized Wigner function correctly captures the entanglement even when the oscillator is initially in a thermal state.
The present paper is organized as follows: In Sec. II, we briefly review the entanglement criterion with the generalized Wigner function for a hybrid system, which was proposed in Ref. [10]. In Sec. III, after briefly reviewing the hybrid system to detect the gravity-induced entanglement considered in Refs. [18, 19], we evaluate the evolution of the negativity volume in the hybrid system for three different initial states to determine the entanglement generation. In Sec. IV, we evaluate the entanglement fidelity for the three states introduced in Sec. III, to verify that the criterion with the negativity volume works properly. Sec. V is devoted to summary and conclusions. In Appendix A, we introduce the generalized Wigner function and explain the negativity volume for a hybrid system following Ref. [10].
II WIGNER FUNCTION FOR HYBRID SYSTEM
In this section, we introduce the generalized Wigner function for the hybrid system described by a continuous variable and a discrete variable. We first consider the Wigner function for the continuous variable system defined by
| (1) |
where is the density matrix, is the displacement operator, and is the parity operator, and and are the creation and annihilation operators. It is well known that this Wigner function characterizes the nonclassical nature of continuous variable systems and that it has negative values in quantum states such as a Shrödinger-cat state.
On the other hand, the Wigner function for the discrete system is defined to satisfy the Stratonovich-Weyl conditions as follows [7, 8, 9, 10, 11, 12]:
| (2) |
where is the unitary operator of SU(2) and is the parity operator. are the Euler angles and are the Pauli operators. The negative value of the Wigner function of the discrete system does not simply characterize the quantum nature of the system. For the general pure qubit state,
| (3) |
we derive the Wigner function as
| (4) |
Considering the state for , the Wigner function reduces to
| (5) |
which has the negative values on the Bloch sphere. Hence, the Wigner function of the discrete system has negative values even for a pure state.
To characterize the nonclassicality of the hybrid system, the authors of Ref. [10] introduced the negativity volume of the generalized Wigner function as
| (6) |
where is the generalized Wigner function defined by
| (7) |
The Wigner function and the negativity volume for the reduced density matrix for the continuous variable system and for the qubit are respectively defined as
| (8) | ||||
| (9) |
where and . The authors of Ref. [10] showed that the negativity volume of the arbitrary pure qubit state (3) is the same value
| (10) |
and suggested that this negativity volume is the upper bound for any qubit state. They also expected that the entanglement criterion for the hybrid system is expressed as follows; the state is entangled if the inequality
| (11) |
is violated. Here, the critical value corresponds to the maximum value for the separable hybrid system written as . Hence, this criterion indicates that when the negativity volume is larger than the critical value, additional nonclassicality appears, namely entanglement.
On the other hand, there is no upper limit on the negativity volume for the reduced continuous variable system . There is the possibility in which a basis transformation can result in different values of the reduced negativity volume, even for the same state. For example, we consider the state , where and are the states of a qubit, and is the coherent state of a continuous variable. Tracing over the qubit system, the reduced state is mixed state and the reduced negativity volumes and are zero. However, we consider the transformation of the basis as and , and the reduced state is written in the mixed state . Then, the reduced negativity volumes and are non-zero. Thus, the treatment of negativity volume for the reduced system of a continuous variable system coupled to a qubit is non-trivial. Despite such a problem, in the present paper, we demonstrate that the criterion based on the negativity volume of the generalized Wigner function is efficient by comparing the fidelity-based condition for various initial states such as superposed qubit-coherent, -thermal, and -cat state. We omit the subscript and for simplicity.
III negativity volume AND ENTANGLEMENT INDUCED BY GRAVITY IN HYBRID SYSTEM
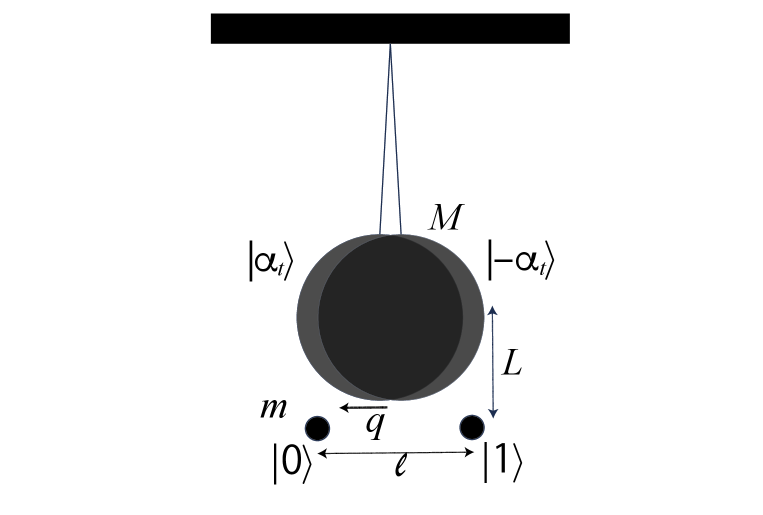
In this section, we consider the hybrid system consisting of a spin particle with mass and an oscillator with mass considered in Refs. [18, 19]. Figure 1 shows a schematic plot of the system. The spin particle is prepared as the superposition state of the two spatially localized states separated by distance by using the Stern-Gerlach scheme. Then, the oscillator also becomes the superposition state due to gravitational interaction with the spatially-localized superposed particle. The Hamiltonian of the hybrid system is
| (12) |
where are the creation and annihilation operators and is the frequency of the oscillator. Here, we ignore the Larmor precession for simplicity. Hamiltonian describes the gravitational interaction given by
| (13) |
where is the position operator of the oscillator, is the distance between the spin particle and the oscillator, is the distance between the positions of the superposed particle and is the gravitational constant. Here, we define the dimensionless position operator and introduce the gravitational coupling as
| (14) |
Hamiltonian is rewritten as and the unitary evolution is
| (15) |
where we defined
| (16) |
III.1 INITIAL QUBIT-COHENRENT STATE
We assume that the particle and the oscillator are initially in a superposed state and a coherent state, respectively. The state of the total system is
| (17) |
which evolves by the Hamiltonian (12) as
| (18) |
where and we ignore the global phase. The generalized Wigner function of the state is given by
| (19) |
Here, the reduced density matrix of the oscillator is
| (20) | ||||
| (21) |
and the corresponding Wigner functions are
| (22) |
Because this state is the mixed state of two Gaussian states, the negativity volume of the reduced oscillator’s state is zero. Hence, if the inequality
| (23) |
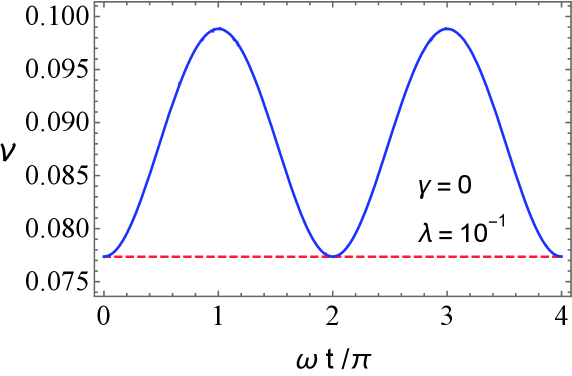
is violated, the state is expected to be entangled. Fig. 2 shows the behavior of the negativity volume for . We here use to easily understand the behavior of the negativity volume of the Wigner function, although is much smaller in realistic situations. The red dashed line represents the critical value in the right-hand side of the inequality (23). The negativity volume at the initial time in the separable state is the same as the critical value. The result is consistent with the criterion that the state is entangled when the negativity volume is larger than the critical value in this case.
III.2 INITIAL QUBIT-THERMAL STATE
We next consider the thermal state as the initial state of the oscillator. In a realistic situation assuming an experiment, the thermal effect should be taken into account, and the generation of the gravity-induced entanglement is non-trivial. The entanglement in the hybrid system under the thermal effect has not been explicitly estimated [18, 19]. We perform the estimation through the negativity volume of the generalized Wigner function of the hybrid system.
The initial density matrix of the total system is
| (24) |
where with the temperature is thermal phonon occupancy number. The evolution of the density matrix by the Hamiltonian (12) is
| (25) |
and the generalized Wigner function is
| (26) |
Then, the reduced density matrix of the oscillator is
and the Wigner function is obtained by
| (27) |
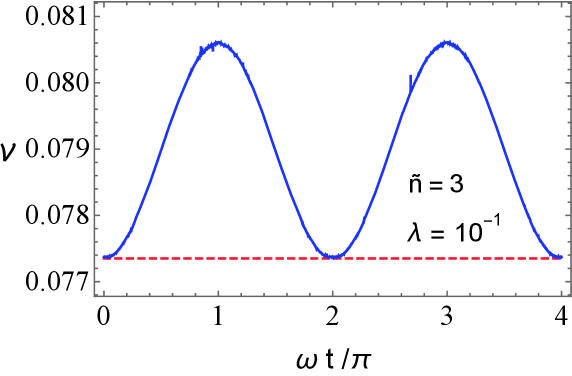
These Wigner functions of the reduced state are always non-negative and the negativity volume is zero, . Then, the inequality (11) reduces to the inequality (23). Hence, the violation of the inequality (23) is the criterion for the entanglement generation due to gravity. Figure 3 shows the behavior of the negativity volume and critical value for . The entanglement behavior for the initial qubit-thermal state is similar to that for the initial qubit-coherent state, but the maximum value of the negativity volume is smaller due to the thermal effects. However, the criterion based on the negativity volume of the generalized Wigner function detects the entanglement even for the mixed state in the hybrid system.
III.3 INITIAL QUBIT-CAT STATE
The results in the previous subsections are the case that the Wigner function of the reduced state of the oscillator is non-negative. We here consider the cat state of the oscillator, where its Wigner function has negative values and the negativity volume of the Wigner function is non-zero. We investigate this model to verify that the inequality (11) can be used as an entanglement criterion of a hybrid system.
The initial density matrix of the total system is
| (28) |
where . The evolved state by unitary operator (15) is given by
| (29) |
and the generalized Wigner function is
| (30) |
Tracing over the qubit system, the reduced density matrix of the oscillator is derived by
| (31) | ||||
| (32) | ||||
| (33) |
and the Wigner function is
| (34) | ||||
| (35) |
Here, the Wigner function of each reduced state has negative regions because the reduced state is the non-Gaussian state. Hence, the inequality for testing the entanglement is
| (36) |
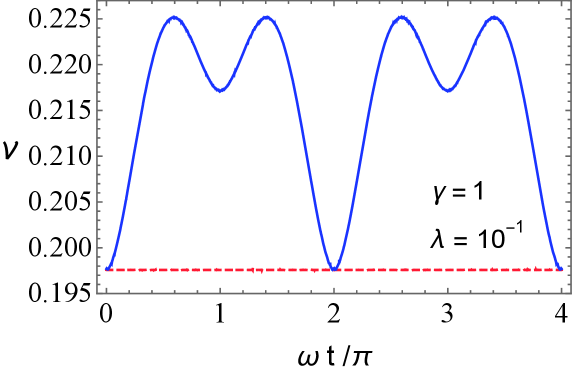
Figure 4 shows the negativity volume (blue curve) and critical value (red dashed curve) for and . The critical value (red dashed curve) is a function of time, but it is almost constant for the parameters. The negativity volume is larger than the critical value except for . Because the total system is in a pure state, the entanglement should be generated. The result indicates that the entanglement generation due to the gravitational interaction is captured by the negativity volume of the generalized Wigner function.
IV ENTANGLEMENT FIDELITY
In this section, we discuss how the evaluation of the entanglement by the Wigner function is consistent with that by the fidelity proposed in Ref. [54, 55, 56]. We here rewrite the Hamiltonian (12) as
| (37) |
According to the entanglement criterion Ref. [54, 55, 56], the state is separable if and only if the equality
| (38) |
is satisfied, where the operator is given by
| (39) |
and we define the initial state as . This criterion is applicable to a initial product state of the pure qubit system and any other system, and is applicable to all the systems analyzed in the previous section. Eq. (38) is rewritten as
| (40) |
and this equation holds when the following operators and are equal:
| (41) | ||||
| (42) |
To evaluate the identification of the operators and , we introduce the fidelity as
| (43) |
and the state is entangled if and only if Eq. (40) is not satisfied, namely, .
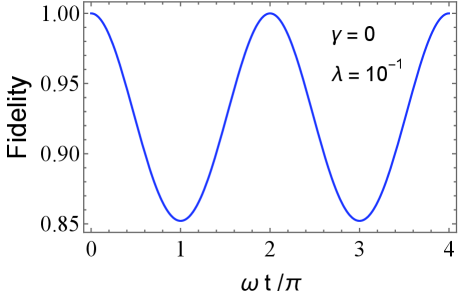
For the initial qubit-coherent state (17) in Sec. III-A, we derive the fidelity as
| (44) |
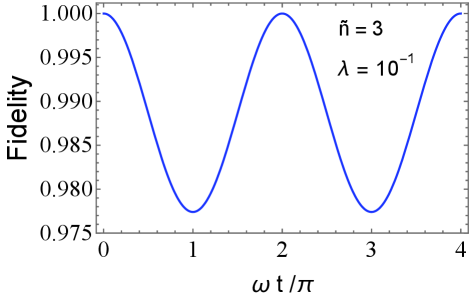
which is not dependent on . Similarly, the fidelity for the initial qubit-thermal state (24) is obtained [57] as
| (45) |
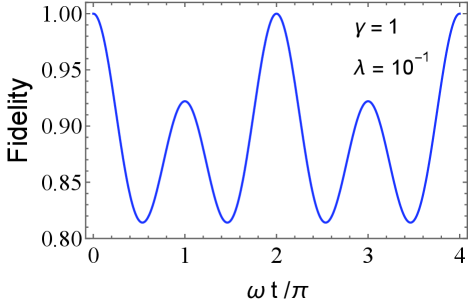
and the fidelity for the initial qubit-cat state is
| (46) |
where .
Each panel of Fig. 5 plots the behavior of the fidelity (44), (45), and (46), as a function of time . We find that the region where is the same as the region where the negativity volume is larger than the critical value in Figs. 2, 3, 4. Moreover, the fidelity for the qubit-thermal state is closer to than that of the qubit-coherent state, which corresponds to the fact that the negativity volume of the qubit-thermal state is smaller than that of the initial qubit-coherent state. Thus the comparison of the conditions for quantum entanglement demonstrated the consistency between the method with the negativity volume of the generalized Wigner function and the method with fidelity, both of which properly detect the quantum entanglement in the hybrid system. In all these models, the signature of entanglement is completely captured by the negativity volume of the generalized Wigner function.
V SUMMARY AND CONCLUSION
We examined the quantum nature of gravity in terms of the generalized Wigner function in a hybrid system consisting of a two-level particle and an oscillator. The two-level particle means a spatially localized superposed state at two different points and the total system evolves into nonclassical entangled states through gravitational interaction. We discussed the entanglement due to gravity by using the quantum entanglement criterion, which states that an increase in the negativity volume of the generalized Wigner function corresponds to quantum entanglement, as proposed in Ref. [10]. Although this criterion is not a necessary condition, we demonstrated that the entanglement is adequately captured by comparing it with the condition using the fidelity. Our results suggest that the criterion with the generalized Wigner function is valid for detecting the gravity-induced entanglement, though the increase in the negativity volume is small in a realistic situation because gravity is weak.
Acknowledgements.
D. Miki thanks Prof. Kae Nemoto for her hospitality during his stay at OIST and for useful discussions on the topic of the present paper. D. M. is supported by JSPS KAKENHI, Grant No. 22J21267, K.Y. is supported by JSPS KAKENHI, Grant No. JP22H05263 and No. JP23H01175.Appendix A ENTANGLEMENT CRITERION BASED ON THE GENERALIZED WIGNER FUNCTION
We explain the entanglement criterion proposed in Ref. [10]. Here, we consider the separable state of a hybrid system , where is positive values satisfying . The generalized Wigner function of the separable system is
| (47) |
and the negativity volume is
| (48) |
Since the negativity volume of the Wigner function for the qubit system is upper bounded by the pure state, , then the negativity volume of the separable state of the hybrid system satisfies the following inequality:
| (49) |
Hence, if the inequality is violated, it means the nonclassicality of the hybrid system. We note that this criterion is the only sufficient criterion for the entanglement generation and there are cases where the inequality (49) is satisfied even though the state is quantum entangled, as shown in Ref. [10]. Also, there is no restriction of the negativity volume for the reduced continuous variable system .
References
- [1] E. A Calzetta and B-L. B. Hu, Nonequilibrium quantum field theory, (Cambridge University Press, New York, 2008)
- [2] A. Kenfact and K. Życzkowski, Negativity of the Wigner function as an indicator of non-classicality, J. Opt. B: Quantum Semiclass. Opt. 6 (2004) 396-404
- [3] K. Banaszek, C. Radzewicz, K. Wódkiewicz, and J. S. Krasiński Direct measurement of the Wigner function by photon counting Phys. Rev. A , 674 (1999)
- [4] A. I. Lvovsky, H. Hansen, T. Aichele, O. Benson, J. Mlynek, and S. Schiller Quantum State Reconstruction of the Single-Photon Fock State Phys. Rev. Lett. , 050402 (2001)
- [5] Alessandro Zavatta, Silvia Viciani, and Marco Bellini, Tomographic reconstruction of the single-photon Fock state by high-frequency homodyne detection, Phys. Rev. A , 053821 (2004)
- [6] A. I. Lvovsky and M. G. Raymer, Continuous-variable optical quantum-state tomography, Rev. Mod. Phys. , 299 (2009)
- [7] T. Tilma, M. J. Everitt, J. H. Samson, W. J. Munro, and K. Nemoto, Wigner functions for arbitrary quantum system, Phys. Rev. Lett. 117, 180401 (2016)
- [8] R. P. Rundle, P. W. Mills, T. Tilma, J. H. Samson, and M. J. Everitt, Simple procedure for phase-space measurement and entanglement validation, Phys. Rev. A 96, 022117 (2017)
- [9] Y. Tian, Z. Wang, P. Zhang, G. Li, J. Li, and T. Zhang, Measurement of complete and continuous Wigner functions for discrete atomic systems, Phys. Rev. A 97, 013840 (2018)
- [10] I. I. Arkhipov, A. Barasiński, and J. Svozilik, Negativity volume of the generalized Wigner function as an entanglement witness for hybrid bipartite states, Sci. Rep. 8, 16955 (2018)
- [11] R. P. Rundle, T. Tilma, J. H. Samson, V. M. Dwyer, R. F. Bishop, and M. J. Everitt, General approach to quantum mechanics as a statistical theory, Phys. Rev. A 99, 012115 (2019)
- [12] B. I. Davies, R. P. Rundle, V. M. Dwyer, J. H. Samson, T. Tilma, and M. J. Everitt, Visualizing spin degrees of freedom in atoms and molecules, Phys. Rev. A 100, 042102 (2019)
- [13] U. L. Andersen, J. S. Neergaard-Nielsen, P. van Loock, and A. Furusawa, Hybrid discrete- and continuous-variable quantum information, Nature Phys. , 713 (2015)
- [14] N. Gisin and R. Thew, Quantum communication, Nature Photon. , 165 (2007)
- [15] A. E. Ulanov, D. Sychev, A. A. Pushkina, I. A. Fedorov, and A. I. Lvovsky, Quantum teleportation between discrete and continuous encodings of an optical qubit, Phys. Rev. Lett. , 160501 (2017)
- [16] K. Kreis and P. van Loock, Classifying, quantifying, and witnessing qudit-qumode hybrid entanglement, Phys. Rev. A , 032307 (2012)
- [17] H. Jeong, A. Zavatta, M. Kang, Seung-Woo Lee, L. S. Costanzo, S. Grandi, T. C. Ralph, and M. Bellini, Generation of hybrid entanglement of light, Nature Photon. , 564 (2014)
- [18] D. Carney, H. Müller, and J. M. Taylor, Using an Atom Interferometer to Infer Gravitational Entanglement Generation, PRX Quantum 2, 030330 (2021)
- [19] A. Matsumura and K. Yamamoto, Leggett-Garg inequality for testing quantumness of gravity, Phys. Rev. A 106, 012214 (2022)
- [20] K. Strltsov, J. S. Pedernales, and M. B. Plenio, On the Significance of Interferometric Revivals for the Fundamental Description of Gravity, Universe 2022, 8(2) 58
- [21] Yue Ma, Thomas Guff, Gavin Morley, Igor Pikovski, and M. S. Kim, Limits on inference of gravitational entanglement, Phys. Rev. Research 4, 013024 (2022)
- [22] S. Bose, A. Mazumdar, G. W. Morley, H. Ulbricht, M. Toroš, M. Paternostro, A. A. Geraci, P. F. Barker, M. S. Kim, and G. Milburn, Spin Entanglement Witness for Quantum Gravity, Phys. Rev. Lett. , 240401 (2017)
- [23] C. Marletto and V. Vedral, Gravitationally Induced Entanglement between two Massive Particles is Sufficient Evidence of Quantum Effects in Gravity, Phys. Rev. Lett. , 240402 (2017)
- [24] R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki, Quantum Entanglement, Rev, Mod. Phys. 81, 865 (2009)
- [25] H. Chau Nguyen and F. Bernards, Entanglement dynamics of two mesoscopic objects with gravitational interaction, Eur. Phys. J. D 74, 69 (2020)
- [26] D. Miki, A. Matsumura, and K. Yamamoto, Entanglement and decoherence of massive particles due to gravity, Phys. Rev. D 103, 026017 (2021)
- [27] A. Matsumura, Field-induced entanglement in spatially superposed objects, Phys. Rev. D 104, 046001 (2021)
- [28] Y. Sugiyama, A. Matsumura, and K. Yamamoto, Effects of photon field on entanglement generation in charged particles, Phys. Rev. D 104, 046001 (2021)
- [29] T. Feng and V. Vedral, Amplification of gravitationally induced entanglement, Phys. Rev. D 106, 066013 (2022)
- [30] H. Miao, D. Martynov, H. Yang, and A. Datta, Quantum correlations of light mediated by gravity, Phys. Rev. A , 063804 (2020)
- [31] T. Krisnanda, G. Y. Tham, M. Paternostro, and T. Paterek, Observable quantum entanglement due to gravity, Quantum Inf. , 12 (2020)
- [32] A. Matsumura and K. Yamamoto, Gravity-induced entanglement in optomechanical systems, Phys. Rev. D , 106021 (2020)
- [33] A. Datta and H. Miao, Signatures of the quantum nature of gravity in the differential motion of two masses, Quantum Sci. Technol. , 045014 (2021)
- [34] D. Miki, A. Matsumura and K. Yamamoto, Non-Gaussian entanglement in gravitating masses: The role of cumulants, Phys. Rev. D , 026011 (2022)
- [35] A. D. K. Plato, D. Rätzel, and C. Wan, Enhanced Gravitational Entanglement via Modulated Optomechanics, Quantum 7, 1177 (2023)
- [36] N. Matsumoto, S. B. Cataño-Lopez, M. Sugawara, S. Suzuki, N. Abe, K. Komori, Y. Michimura, Y. Aso, and K. Edamatsu, Demonstration of Displacement Sensing of a mg-Scale Pendulum for mm- and mg-Scale Gravity Measurements, Phys. Rev. Lett. 122, 071101 (2019)
- [37] S. B. Cataño-Lopez, J. G. Santiago-Condori, K. Edamatsu, and N. Matsumoto, High-Q Milligram-Scale Monolithic Pendulum for Quantum-Limited Gravity Measurements, Phys. Rev. Lett. 124, 221102 (2020)
- [38] N. Matsumoto and N. Yamamoto, Preparing mechanical squeezing of a macroscopic pendulum near quantum regimes, arXiv:2008.10848
- [39] Y. Chen, Macroscopic Quantum Mechanics: Theory and Experimental Concepts of Optomechanics, J. Phys. B: At. Mol. Opt. Phys. 46, 104001 (2013)
- [40] W. P. Bowen, G. J. Bilburn, Quantum Optomechanics, (CRC Press, 2015)
- [41] H. Rudolph, U. Delić, M. Aspelmeyer, K. Hornberger, ans B. A. Stickler, Force-Gradient Sensing and Entanglement via Feedback Cooling of Interacting Nanoparticles, Phys. Rev. Lett. 129, 193602 (2022)
- [42] D. Miki, N. Matsumoto, A. Matsumura, T. Shichijo, Y. Sugiyama, K. Yamamoto, and N. Yamamoto, Generating quantum entanglement between macroscopic objects with continuous measurement and feedback control, Phys. Rev. A 107, 032410 (2023)
- [43] D. Miki, A. Matsumura and K. Yamamoto, Quantum signature of gravity in optomechanical systems with conditional measurement, arXiv:2311.00563
- [44] A. Belenchia, R. M. Wald, F. Giacomini, E. Castro-Ruiz, C. Brukner, and M. Aspelmeyer, Quantum superposition of massive objects and the quantization of gravity, Phys. Rev. D 98, 126009 (2018)
- [45] R.J. Marshman, A. Mazumdar, and S. Bose, Locality and entanglement in table-top testing of the quantum nature of linearized gravity, Phys. Rev. A 101, 052110 (2020)
- [46] D. Carney, Newton, entanglement, and the graviton, Phys. Rev. D 105, 024029 (2022)
- [47] D. L. Danielson, G. Satishchandran, and R. M. Wald, Gravitationally Mediated Entanglement: Newtonian Field vs. Gravitons, Phys. Rev. D 105, 086001 (2022)
- [48] S. Bose, A. Mazumdar, M. Schut, and M. Toroš, Mechanism for the quantum natured gravitons to entangle masses, Phys. Rev. D 105, 106028 (2022)
- [49] Y. Hidaka, S. Iso, and K. Shimada, Complementarity and causal propagation of decoherence by measurement in relativistic quantum field theories, Phys. Rev. D 106, 076018 (2022)
- [50] Y. Sugiyama, A. Matsumura, and K. Yamamoto, Consistency between causality and complementarity guaranteed by Robertson inequality in quantum field theory, Phys. Rev. D 106, 125002 (2022)
- [51] D. Biswas, S. Bose, A. Mazumdar, and M. Toroš, Gravitational Optomechanics: Photon-Matter Entanglement via Graviton Exchange, Phys. Rev. D 108, 064023 (2023)
- [52] Y. Hidaka, S. Iso, and K. Shimada, Entanglement Generation and Decoherence in a Two-Qubit System Mediated by Relativistic Quantum Field, Phys. Rev. D 107, 085003 (2023)
- [53] Y. Sugiyama, A. Matsumura, and K. Yamamoto, Quantum uncertainty of gravitational field and entanglement in superposed massive particles, arXiv:2308.03093
- [54] K. Roszak and Ł. Cywiński, Characterization and measurement of qubit-environment-entanglement generation during pure dephasing, Phys. Rev. A 92, 032310 (2015)
- [55] K. Roszak, Criteria for system-environment entanglement generation for systems of any size in pure-dephasing evolutions, Phys. Rev. A 98, 052344 (2018)
- [56] M. Strzałka, D. Kwiatkowski, Ł. Cywiński, and K. Roszak, Qubit-environment negativity versus fidelity of conditional environmental states for a nitrogen-vacancy-center spin qubit interacting with a nuclear environment, Phys. Rev. A 102, 042602 (2020)
- [57] P. Marian, optimal purifications and fidelity for displaced thermal states, Phys. Rev. A 76, 054307 (2007)