Nano-mechanics driven by Andreev tunneling

Introduction. Modern nanomechanical resonators fundamentals characterized by low damping and fine-tuning of the resonant frequency are widely used nowadays as supersensitive quantum detectors sensing -huttelnano and as the mechanical component for various nanoelectromechanical systems (NEMS) NEMS ,blencowe . The latter represent a promising platform for studying the fundamental phenomena generated by the quantum-mechanical interplay between nanomechanical resonator and electronic subsystem ekinci ,cleland .

Large amount of fascinating physical phenomena have been predicted and observed in various NEMS, e.g. energy level quantization of a nanomechanical oscillator quantlevelsSQ , a strong resonant coupling of nanomechanical oscillator to superconducting qubits laserCoolSQ , mechanical cooling coolingexp ; nqds ; gorelikcooling , a single-atom lasing effect atomlasing ; laserCoolSQ , mechanical transportation of Cooper pairs shuttlenature and the generation of self-driven mechanical oscillations by a DC charge flow shuttle ; blanter ; huttel1 ; huttel2 ; huttel3 ; self , just to name a few.

Significant part of these effects are based on the resonant excitation of low damped mechanical modes by coherent quantum dynamics occurring in the electronic subsystem. A straightforward method to establish coherent quantum dynamics in mesoscopic devices, e.g., the quantum beats, the microwave induced Rabi oscillations etc., is to use the macroscopic phase coherence of superconducting (SC) elements incorporated into NEMS, see, for example, the review parafiloreview . In particular, in superconducting hybrid junctions flensberg -baransky the coherent electronic transport is determined by the presence of Andreev bound states andreevlevel ,andreevlevel2 . The applied DC or AC currents induce the transitions between Andreev bound states, and the coherent high-frequency oscillations in an electronic subsystem occur gorelikcooling . These coherent charge oscillations can excite the mechanical modes in the resonant limit only, when the frequency of mechanical mode matches Andreev energy level difference.

On other hand, an incoherent quantum dynamics occurring in the electronic subsystem can induce the mechanical instability and subsequent formation of the self-driven mechanical oscillations in hybrid junctions. Incoherent quantum fluctuations of electric charge can be easily mediated by tunneling of a single electron. The self-driven oscillations generated by a DC electronic flow have been predicted in shuttle ; blanter , later observed in a carbon nanotube (CNT) based transistor huttel1 , and studied in detail huttel2 ,huttel3 , see, e.g., self for recent experiment.

A nontrivial interplay between coherent and incoherent electric charge variation and its influence on the performance of NEMS can be achieved in a nanomechanical Andreev device, where normal and SC metals are bridged by a mechanically active mediator.

In this Letter, we present a particular NEMS setup where the mechanical oscillations are strongly affected by a weak coupling to the electronic part of a system. We demonstrate that in the adiabatic limit as the frequency of mechanical oscillations is much smaller than the typical frequencies of electron dynamics, simultaneous presence of coherent Andreev tunneling and incoherent single electron tunneling can induce mechanical instability of the resonator and result in the appearance of the self-sustained mechanical oscillations.

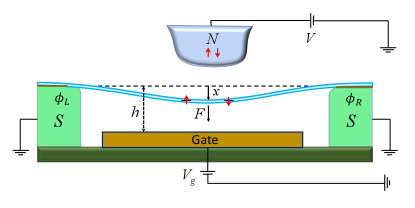
Model. We consider a metallic single-wall carbon nanotube suspended between two grounded SC electrodes and coupled to a scanning tunneling microscope (STM) tip via electron tunneling. The two SC electrodes are characterized by the same modulus $\Delta$ and different phases $\phi_{L,R}$ of SC order parameter, and corresponding Josephson phase difference, $\phi=\phi_{R}-\phi_{L}$. We study the case where the CNT mean-level spacing is greater than temperature $k_{B}T$ and the bias-voltage $eV$ applied between STM tip and CNT. It allows us to treat the CNT as a movable single-level quantum dot (QD). The capacitive coupling between the CNT and a gate is controlled by a gate voltage $V_{g}$. We aslo assume the dynamics of the CNT bending is reduced to the dynamics of the fundamental flexural mode. The scheme of the described model is presented in Fig.1.

The Hamiltonian of the model reads as follows

$\displaystyle H=H_{N}+H_{S}+H_{CNT}+H_{tun}.$

(1)

The first two terms in Eq.(1) are the Hamiltonians of an STM tip (normal lead) and two SC leads, accordingly:

	$\displaystyle H_{N}=\sum_{k\sigma}(\varepsilon_{k}-eV)c^{{\dagger}}_{k\sigma}c_{k\sigma},$		(2)
	$\displaystyle H_{S}=\sum_{kj\sigma}\left\{\xi_{kj}a^{{\dagger}}_{kj\sigma}a_{kj\sigma}-\Delta e^{i\phi_{j}}(a^{{\dagger}}_{kj\uparrow}a^{{\dagger}}_{-kj\downarrow}+H.c.)\right\}.$		(3)

Here, $c_{k\sigma}$ ($c_{k\sigma}^{{\dagger}}$) and $a_{kj\sigma}$ ($a_{kj\sigma}^{{\dagger}}$) are annihilation (creation) operators of electrons in the normal and $j$-th SC leads ($j=L,R$) with energies $\varepsilon_{k}$ and $\xi_{kj}$, correspondingly. The index $\sigma=\uparrow,\downarrow$ indicates the spin of electrons in the leads.

The Hamiltonian of the single-level vibrating CNT-QD reads as follows

$\displaystyle H_{CNT}=\sum_{\sigma}$

$\displaystyle\varepsilon_{0}d^{{\dagger}}_{\sigma}d_{\sigma}+\frac{\hbar\omega_{0}}{2}(\hat{p}^{2}+\hat{x}^{2})-F\hat{x}\sum_{\sigma}n_{\sigma}.$

(4)

The quantum dynamics of the electronic degree of freedom is described by the first term in Eq. (4), where $\varepsilon_{0}$ is the QD electron energy level, and $d_{\sigma}$, $d_{\sigma}^{{\dagger}}$ are annihilation and creation operators of the electrons in the QD, $n_{\sigma}=d^{{\dagger}}_{\sigma}d_{\sigma}$ footnote .

The second term in Eq. (4) characterizes the CNT vibrations with the frequency $\omega_{0}$, and the dimensionless operators $\hat{x}=\hat{X}/x_{0}$, $\hat{p}=x_{0}\hat{P}/\hbar$ are canonically conjugated displacement and momentum of the CNT-QD. Here, $x_{0}=\sqrt{\hbar/m\omega_{0}}$ is the amplitude of the zero-point oscillations of the CNT, and $m$ is the mass of the CNT. Electromechanical interaction determined by the third term in Eq. (4), is achieved through the electrostatic interaction of the charged CNT-QD with the gate electrode. The interaction strength is $F\propto(ex_{0}/h)V_{g}\beta$ blanter ,blanterbook , where $h$ is the distance between the CNT and gate electrode, and $\beta\sim 0.1$ is a geometrical factor associated with the capacitances in the system.

The last term in Eq. (1),

	$\displaystyle H_{tun}=\sum_{k\sigma}e^{-\hat{x}/\lambda}\left(t_{k}^{n}c^{{\dagger}}_{k\sigma}d_{\sigma}+(t_{k}^{n})^{\ast}d^{{\dagger}}_{\sigma}c_{k\sigma}\right)$
	$\displaystyle+\sum_{kj\sigma}\left(t_{k}^{s}a^{{\dagger}}_{kj\sigma}d_{\sigma}+(t_{k}^{s})^{\ast}d^{{\dagger}}_{\sigma}a_{kj\sigma}\right),$		(5)

describes the tunneling processes between the CNT and i) the STM tip with deflection dependent hopping amplitude, i.e. $t_{k}^{n}\exp(-\hat{x}/\lambda)$, where $\lambda=l/x_{0}$ and $l$ is the tunneling length of the barrier; ii) SC leads with the hopping amplitude $t_{k}^{s}$.

Mechanical instability. In order to rigorously demonstrate the phenomenon of mechanical instability in the SC hybrid junction, we analyze the dynamics of the CNT’s flexural mode by using the reduced density matrix technique. By treating the tunneling Hamiltonian (Nano-mechanics driven by Andreev tunneling) as a perturbation and tracing out the electronic degrees of freedom in the normal and SC leads, one can get a quantum master equation for the reduced density matrix operator (in $\hbar=1$ units):

$\displaystyle\dot{\rho}=$

$\displaystyle-i[H_{CNT},\rho]+i\Gamma_{S}(\phi)[d^{{\dagger}}_{\uparrow}d^{{\dagger}}_{\downarrow}+d_{\downarrow}d_{\uparrow},\rho]-\sum_{\sigma}\mathcal{L}[\rho].$

(6)

Here, $\Gamma_{S}(\phi)=2\pi\nu_{0}|t_{k}^{s}|^{2}\cos(\phi/2)$ is the Josephson phase dependent strength of the intra-QD electron pairing induced by the coherent Andreev tunneling, $\nu_{0}$ is the electron density of states in the leads, and $\mathcal{L}[\rho]$ is a Lindbladian operator in the high-voltage regime $eV\gg\varepsilon_{0},\omega_{0}$ novotny ,fedorets :

$\displaystyle\mathcal{L}[\rho]=\frac{\Gamma}{2}\left\{\begin{array}[]{c}\{e^{-\frac{2\hat{x}}{\lambda}}d_{\sigma}d^{{\dagger}}_{\sigma},\rho\}-2e^{-\frac{\hat{x}}{\lambda}}d^{{\dagger}}_{\sigma}\rho d_{\sigma}e^{-\frac{\hat{x}}{\lambda}},V>0,\\ \{e^{-\frac{2\hat{x}}{\lambda}}d_{\sigma}^{{\dagger}}d_{\sigma},\rho\}-2e^{-\frac{\hat{x}}{\lambda}}d_{\sigma}\rho d_{\sigma}^{{\dagger}}e^{-\frac{\hat{x}}{\lambda}},V<0,\end{array}\right.$

(9)

where $\Gamma=2\pi\nu_{0}|t_{k}^{n}|^{2}$ is the QD energy level width produced by a single electron tunneling. The quantum master equation (6) is justified in the deep sub-gap regime under the following assumptions: all relevant energies are smaller than the SC gap, $eV,k_{B}T,\varepsilon_{0}\ll\Delta$.

Density matrix $\rho$ acts in the finite Fock space of the two-fold degenerate single-electron level in the QD. The four possible electronic states are $|0\rangle$, $|\sigma\rangle=d^{{\dagger}}_{\sigma}|0\rangle$ ($\sigma=\uparrow,\downarrow$), and $|2\rangle=d^{{\dagger}}_{\uparrow}d^{{\dagger}}_{\downarrow}|0\rangle$. In this representation the reduced density matrix $\rho$ contains five nonzero elements: $\rho_{00}$, $\rho_{\uparrow\uparrow}$$=$$\rho_{\downarrow\downarrow}$$\equiv$$\rho_{1}$, $\rho_{22}$, $\rho_{02}$, and $\rho_{20}$. Using the normalization condition $\rho_{00}+2\rho_{1}+\rho_{22}=1$ one can eliminate the $\rho_{1}$ component of the density matrix from further consideration. Therefore, the joint dynamics of the electronic and mechanical subsystems is determined by the matrix

$\displaystyle\hat{\varrho}=\frac{1}{2}\left(\begin{array}[]{cc}\rho_{22}-\rho_{00}&2\rho_{20}\\ 2\rho_{02}&\rho_{00}-\rho_{22}\end{array}\right).\,$

(12)

If the amplitude of the CNT displacement is larger than the amplitude of zero-point oscillation, one can treat the dynamics of the CNT bending as a classical with time-evolution governed by Newton’s equation. Introducing the dimensionless time units as $\omega_{0}t\rightarrow t$ we obtain a closed system of the relevant equations for the CNT displacement $x$ and matrix $\hat{\varrho}$ Eq. (12) in the following form:

	$\displaystyle\ddot{x}+Q^{-1}\dot{x}+x=\alpha+\alpha\textrm{Tr}\{\sigma_{3}\hat{\varrho}\},$		(13)
	$\displaystyle{\omega_{0}}\dot{\hat{\varrho}}=-i[\varepsilon(x)\sigma_{3}-\Gamma_{S}(\phi)\sigma_{1},\hat{\varrho}]-\Gamma(x)\left(\hat{\varrho}-\frac{\kappa}{2}\sigma_{3}\right),$		(14)

where dimensionless parameter $\alpha=F/\omega_{0}$, $\sigma_{i}$ ($i=1,2,3$) are the Pauli matrices, $\varepsilon(x)=\varepsilon_{0}-\alpha x$, $\Gamma(x)=\Gamma\exp(-2x/\lambda)$, and $\kappa=\textrm{sgn}(V)$. An environment induced damping of the mechanical subsystem is determined by the term $\propto Q^{-1}$, where $Q\sim 10^{6}$ huttel1 is the quality factor. In the adiabatic limit, $\omega_{0}/\Gamma\ll 1$, we obtain $\hat{\varrho}(t)$ from Eq. (14), and the non-linear part of Eq. (13) is presented in the following form:

$\displaystyle\textrm{Tr}\{\sigma_{3}\hat{\varrho}(t)\}=\kappa\left(1-\frac{4\Gamma_{S}^{2}(\phi)}{D(x(t),\phi)}\right)+\dot{x}(t)\eta(x(t)),$

(15)

where $D(x,\phi)$$=$$\xi^{2}(x)+\Gamma^{2}(x)$, $\xi(x)=2\sqrt{\varepsilon^{2}(x)+\Gamma_{S}^{2}(\phi)}$ is the energy difference between two Andreev levels of the QD-SC subsystem, and a mechanical friction coefficient $\eta(x)$, induced by interaction with the electronic degree of freedom, reads as

$\displaystyle\eta(x)=\alpha\mathcal{I}(x)\left(\lambda^{-1}C_{1}(x)+\alpha\frac{\varepsilon(x)}{\Gamma^{2}(x)}C_{2}(x)\right).$

(16)

Here, $\mathcal{I}(x)=\kappa 4\Gamma(x)\Gamma_{S}^{2}(\phi)/D(x,\phi)$ is the DC flow of electrons between the STM tip and SC leads, and

$\displaystyle C_{1}(x)=\frac{6\Gamma^{2}(x)-2\xi^{2}(x)}{D^{2}(x,\phi)},C_{2}(x)=\frac{20\Gamma^{2}(x)+4\xi^{2}(x)}{D^{2}(x,\phi)}.$

(17)

The frequency of a typical CNT-based resonator is $\omega_{0}\sim 1~{}\textrm{GHz}$, while the amplitude of zero-point fluctuations is $x_{0}\approx 2~{}\textrm{pm}$. Assuming $V_{g}\sim 100~{}\textrm{mV}$, $h\sim 10^{-7}\textrm{m}$, and the tunneling length $l\simeq 10^{-10}\textrm{m}$ we estimate dimensionless coupling constants to be $\alpha\sim 0.1$ and $\lambda^{-1}\sim 10^{-2}$.

After substituting Eq.(15) in Eq.(13), we found non-linear equation for the CNT deformation local in time. In the limit $\alpha,\lambda^{-1}\ll 1$ a small shift of the equilibrium position (static solution) is obtained as

$\displaystyle x_{c}=\alpha+\kappa\alpha\frac{4\varepsilon^{2}(0)+\Gamma^{2}}{D(0,\phi)}+O(\alpha^{2},\alpha\lambda^{-1}).$

(18)

The stability of the static solution is studied by linearizing Eq. (15). In the limit $\Gamma\gg\omega_{0}$, the time evolution of the small CNT deviation from its equilibrium position $\delta x(t)=x(t)-x_{c}$ is given by footnote2

$\displaystyle\delta\ddot{x}+\left(Q^{-1}-\eta(0)\right)\delta\dot{x}+\delta x=0.$

(19)

The static solution $x_{c}$ of the system at $\eta(0)>Q^{-1}$ becomes unstable with respect to the generation of mechanical oscillation with amplitude exponentially increasing in time. Development of instability results in the appearance of self-sustained mechanical oscillations, governed by the nonlinearity of r.h.s. Eq. (13).

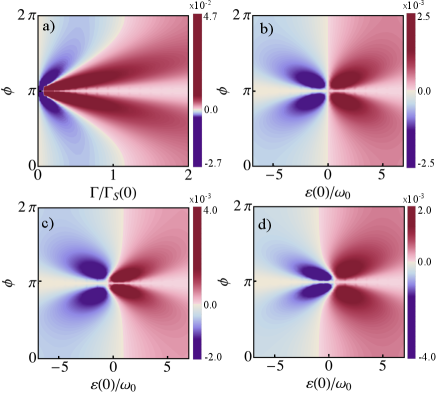
Next, we analyze the influence of various parameters on the coefficient $\eta(0)$ which we call a pumping coefficient in what follows. First, we note that $\eta(0)$ linearly increases with the electromechanical coupling $\alpha$ and the DC flow $\propto\mathcal{I}(0)$. Moreover, the pumping coefficient $\eta(0)$ changes a sign depending on the direction of the electronic flow, i.e. the sign of $eV$. At $|eV|\gg 2\varepsilon_{0}$, bias voltage affects the phenomenon under consideration solely by this means. Below we analyze the case of $eV>0$ only.

The various dependencies of the pumping coefficient $\eta(0)$ on the parameters $\phi$, $\Gamma/\Gamma_{S}(0)$ and $\varepsilon(0)$ obtained from Eqs. (16) and (17) are shown in Fig. 2 (red color scheme indicates $\eta(0)>0$, while blue scheme – $\eta(0)<0$). In the case $\varepsilon(0)$$=$$\varepsilon_{0}$$=$$0$, the pumping coefficient $\eta(0)\propto\kappa\alpha/\lambda$ is determined by the ratio between $\Gamma$ and $\Gamma_{S}(\phi)$, since only the first term in Eq. (16) contributes. The pumping coefficient changes its sign when $\Gamma=\sqrt{4/3}\Gamma_{S}(\phi)$, see Fig. 2(a). If the dependence of the electron hopping on the amplitude of the CNT oscillations is negligible, i.e. $\lambda^{-1}=0$, the pumping coefficient $\eta(0)\propto\kappa\alpha^{2}\varepsilon(0)$ is determined by the sign of $\varepsilon(0)$. Such behavior is illustrated in Fig. 2(b). General case, when both terms in Eq. (17) contribute into the pumping coefficient Eq. (16), is shown in Fig. 2(c) and (d) for positive ($\alpha>0$) and negative ($\alpha<0$) electrostatic interaction, respectively.

The origin of the pumping processes, and corresponding mechanical instability can be qualitatively explained as follows: since two electronic states $|0\rangle$ and $|2\rangle$ in the QD are not the eigenstates of the QD-SC subsystem, the quantum Rabi oscillations emerge with a frequency proportional to the energy difference between Andreev levels $\xi(x,\phi)$. These Rabi oscillations occur in the form of periodic in time single-Cooper pair transfer between SC leads and the QD. However, an incoherent single electron tunneling from the STM tip to the QD can interrupt the coherent oscillations as well as resume them.

As this takes place, the averaged charge in the QD is governed by the interplay between two processes: i) a coherent Rabi oscillations and ii) an incoherent single electron tunneling. Both processes and their main characteristics, $\Gamma(x)$ and $\xi(x)$, are controlled by the CNT displacement and vary in time if $\delta\dot{x}(t)\neq 0$. Such variations give rise to a correction of the average charge in the QD, that is proportional to the velocity of the QD, thereby generating effective friction force. We note that the amplitude of the effective friction force is determined by two terms (see Eq. (16)), where the first term is induced by the time variation of the hopping amplitude of single electron tunneling $\dot{\Gamma}(x(t))\propto\lambda^{-1}\dot{x}$, while the second term is generated by the time variation of the Rabi frequency $\dot{\xi}(x(t))\propto\alpha\varepsilon(0)\dot{x}$.

DC electric current. The self-sustained oscillations affect the DC current flow between the STM tip and SC leads. This phenomenon allows one to verify the mechanical instability through the electric current measurement.

The expression for the DC current is given by

$\displaystyle I_{N}(x(t))=e\Gamma\left(x(t)\right)\left(\kappa-\textrm{Tr}\{\sigma_{3}\hat{\varrho}(t)\}\right).$

(20)

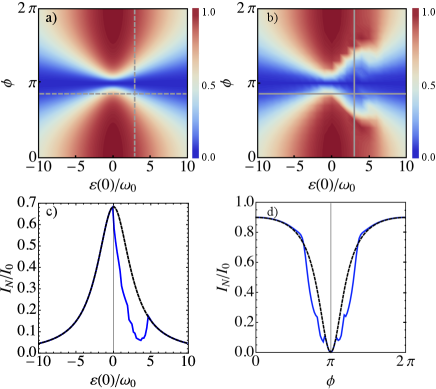
If the pumping coefficient $\eta(0)<Q^{-1}$, the mechanical oscillations of the CNT are damped, and the DC electric current is expressed as $I_{N}(0)=e\mathcal{I}(0)$. This expression coinsides with the DC current obtained in the absence of electromechanical interaction. Such dependence is shown in Fig. 3(a). The DC current strongly depends on the Josephson phase difference $\phi$ and the QD energy level $\varepsilon(0)$. The current reaches its maximum at $\varepsilon(0)=0$ and vanishes at $\phi=\pi$. Besides, $I_{N}(0)$ is proportional to $\propto\Gamma\Gamma_{S}^{2}$, revealing Andreev tunneling andreevtunneling since only two electrons (the Cooper pair) can tunnel from the QD to the SC leads.

In the regime of mechanical instability $\eta(0)>Q^{-1}$, the static solution becomes unstable and CNT vibrations develop into pronounced self-sustained oscillations of finite amplitude. As a result, the current exhibits periodic oscillations with the frequency $\omega_{0}$. The averaged over the period of mechanical oscillations DC current is obtained numerically and the result is presented in Fig. 3(b). The projections of $I_{N}$ at fixed $\phi$ and $\varepsilon(0)$ are presented in Fig. 3 (c) and (d). As one can see in Fig. 3, pronounced self-sustained oscillations of the CNT-QD suppress the charge current in the region of parameters obeyed $\eta(0)>Q^{-1}$ condition. The strength of this current suppression depends on the amplitude of the CNT self-oscillations and correspondingly on the pumping strength $\eta(0)$.

Conclusions. We predict the phenomenon of mechanical instability and corresponding self-sustained oscillations in a hybrid nanoelectromechanical device consisting of a carbon nanotube suspended between two SC leads and placed near a voltage-biased normal STM tip. Such effect is based on a peculiar interplay of the coherent quantum-mechanical Rabi oscillations induced by the Andreev tunneling between the CNT and SC leads, and an incoherent single electron tunneling between the STM tip and CNT. We obtain that the observed mechanical instability and self-sustained oscillations of finite amplitude are determined by two parameters: the relative position of the single-electron energy level, and the Josephson phase difference between the SC leads. Numerical analysis demonstrates that the predicted mechanical instability develops into pronounced self-sustained bending oscillations of the CNT resonator which, in its turn, result in a suppression of the DC electric current flowing between the STM tip and SC leads. This effect allows one to detect the predicted mechanical instability through the DC current measurement. A SQUID sensitivity to an external magnetic field can be achieved by using proposed nanomechanical Andreev device through the control of the Josephson phase difference by a magnetic flux.

Acknowledgement. This work was supported by the Institute for Basic Science in Korea (IBS-R024-D1). LYG and RIS thank the IBS Center for Theoretical Physics of Complex Systems for their hospitality. M.V.F. acknowledges the partial financial support of the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST ”MISIS” $K2-2020-001$.