Corresponding author: ][email protected]

Present address: ]Okinawa Institute of Science and Technology Graduate University, Onna, Okinawa 904-0495, Japan Corresponding author: ][email protected]

The observation of electromagnetic (EM) radiation in the terahertz frequency range emitted from a stack (mesa) of intrinsic Josephson junctions (IJJs) Kleiner et al. (1992) in Bi₂Sr₂CaCu₂O_8+δ (Bi-2212) highlights the potential of such materials in monolithically fabricated solid-state terahertz sources Ozyuzer et al. (2007); Welp et al. (2013); Kakeya and Wang (2016); Kashiwagi et al. (2017). The mutual synchronization of IJJ mesas has been demonstrated to produce output powers of up to 0.6 mW Benseman et al. (2013a), where the maximum output power exceeds the sum of the individual emission powers. Although numerical study suggests a possible coupling between the mesas through the Bi-2212 substrate Lin and Koshelev (2013), there is no direct experimental evidence showing the mutual synchronization. So far, to investigate these phenomena with multi-degree-of-freedom, the frequency and intensity of the emitted EM wave have been considered good measures. Besides these characteristics, the polarization includes rich information for characterizing the Josephson plasma wave (JPW) polarized along the $c$-axis inside a mesa Elarabi et al. (2017, 2018). Since a JPW is converted to a polarized photon according to the mesa geometry Koyama et al. (2009); Hu and Lin (2009); Savel’ev et al. (2010); Klemm and Kadowaki (2010), perfect polarization is the hallmark of coherent excitation of the JPW.

In this study, we demonstrate synchronization of macroscopic Josephson oscillations in two simultaneously biased mesas coupled via a superconducting base crystal by measuring complete Stokes parameters. Our focus is on the polarization of photons emitted from individual mesas and arrays of mesas. Most importantly, we observed a drastic change in the axial ratio for the simultaneous emission. This suggests the possibility of active control of the synchronization in mesa arrays, which is the most promising way to increase the integrated output power.

Mesas 100$\times$400 µm² in size with two silver strip electrodes were milled from a Bi-2212 crystal by photolithography and argon milling methods. Figure 1(a) shows an optical microscopy image of the Bi-2212 mesa array. We refer to the two mesas as A1 and A2. Profile measurements using atomic force microscopy (Keyence Corp., Model VN-8000) demonstrate that the mesas vary marginally in size. Widths of A1 and A2 were measured as 94 µm and 91 µm, respectively, with thicknesses of 1.4 µm corresponding to 910 IJJs.

The current-voltage characteristics (IVCs) for A1 and A2 show the large hysteresis typical of underdamped Josephson junctions SM . Simultaneous emission occurs when A1 and A2 are biased in parallel. Hereinafter, we refer to the parallel connection as A1$\parallel$A2. The maximum intensity is obtained at 16.8 mA, which is higher than the sum of the bias currents for the maximum emission powers of A1 and A2 individually. Also, the maximum intensity for A1$\parallel$A2 was almost half of that for A2. This can be explained by considering the local temperature increase Wang et al. (2009, 2010); Gross et al. (2012); Benseman et al. (2013b); Minami et al. (2014); Tsujimoto et al. (2014); Benseman et al. (2015). Benseman et al. demonstrated that the self-heating effect limits the power output and in fact may prevent synchronization among multiple mesas Benseman et al. (2013a). A variety of studies on the cavity resonance effect have demonstrated that spontaneous synchronization among stacked IJJs is accompanied by the formation of standing EM waves inside the Bi-2212 mesa Ozyuzer et al. (2007); Tsujimoto et al. (2010); Kashiwagi et al. (2011); Tsujimoto et al. (2016); Kashiwagi et al. (2018); Zhang et al. (2019). For a thin rectangular mesa of width $w$ and length $\ell$, the cavity frequency for a transverse magnetic $(mp)$ mode is given by $f_{mp}^{r}=(c_{0}/2n)\sqrt{(m/w)^{2}+(p/\ell)^{2}}$, where the two indices $m$ and $p$ correspond to the numbers of electric field nodes in the width and length directions, respectively, and $n=4.2$ is the experimentally obtained refractive index Tsujimoto et al. (2016); Kadowaki et al. (2010). Here, the radiation frequencies measured using Fourier transform interferometry ranged continuously from 0.56 to 0.66 THz depending on the bias point SM . These values are in good agreement with the calculated $f_{1p}^{r}$ with $0<p<6$. If we assume $m\geq 2$, the calculated $f_{mp}^{r}$ values fail to coincide with the observed values for any $p$. Hence, only one EM node is present along the mesa width, and a non-zero $p$ value is expected to produce an elliptical polarization.

Here, we present the measurements of the Stokes parameters, which allow for the quantitative analysis of polarized photons emitted from individual mesas and from synchronized arrays SM . Figure 1(b) shows a schematic view of the synchronized array. Measurement was performed by allowing the polarized radiation to propagate sequentially through two polarizing elements, a quarter-wave plate (QWP), and a linear wire grid polarizer (WGP). The QWP consists of a stack of parallel metal-plate waveguides Nagai et al. (2015). We used terahertz time-domain spectroscopy Madeo et al. (2010); Maussang et al. (2016) to verify that the QWP works correctly in the emission frequency range around 0.6 THz SM . Figure 1(c) shows the measurement configuration. The QWP can be rotated through an angle $\theta$ and is followed by a fixed WGP whose transmission axis is fixed in the width direction ($\theta=0$ deg).

Figures 2(a) and 2(b) show polar plots of the bolometer output for A1 and A1$\parallel$A2, respectively, as a function of $\theta$ at the bias conditions that result in the maximum output powers. The error bars in the radial direction correspond to fluctuations in the bolometer output signal, mostly owing to background noise. The four independent Stokes parameters, $S_{0}$, $S_{1}$, $S_{2}$, and $S_{3}$, which are summarized in Table SI SM , are obtained from this data. The solid lines shown in Figs. 2(a) and 2(b) represent the calculated results using the four Stokes parameters. The experimental data are slightly asymmetric with respect to both the major and minor axes. This is due to the imperfect alignment of the parallel metal-plate waveguides in the QWP. Nevertheless, the calculation results fit the experimental data within the error bars.

The E-field vector at the detection plane is given by $\bm{B}(t)=E_{0x}e^{i(\omega t+\delta_{x})}\bm{i}+E_{0y}e^{i(\omega t+\delta_{y})}\bm{j}$, where the $x$- and $y$-axes are parallel to the mesa width and length, respectively, $t$ represents time, $E_{0x}$ and $E_{0y}$ are the respective amplitudes, and $\delta_{x}$ and $\delta_{y}$ are the respective phase constants. Figures 2(c) and 2(d) are the corresponding polarization ellipses for A1 (red), A2 (blue), and A1$\parallel$A2 (green). The fourth Stokes parameter $S_{3}$ determines the helicity of the photons: a positive (negative) $S_{3}$ indicates left (right)-handed helicity with respect to the direction of propagation. Note that the $E$-field rotates forward (counter-)clockwise for left (right)-handed helicity from the viewpoint of the detector. The arrows on the ellipses indicate the direction of the $E$-field rotation. For both mesas, the major axis of the polarization ellipse is oriented along the $x$ axis, i.e., $-\pi/4<\psi<\pi/4$, which is consistent with excitation of $(1p)$ cavity modes.

In the pioneering study of EM-wave emission from an IJJ mesa, it is demonstrated that the emission from rectangular mesas is linearly polarized along the mesa width Ozyuzer et al. (2007). The present results suggest, however, that the emitted waves are elliptically polarized with a finite axial ratio at an arbitrary orientation angle. We stress that these polarization parameters contain information essential for understanding the electromagnetism inside the emitting mesa. For example, the orientation angle $\psi$ is derived from the phase difference $\delta_{xy}=\delta_{x}-\delta_{y}$, namely, $\delta_{yx}=\pm\pi/2$ gives $\psi=0$ and $\delta_{yx}=0$ gives $\psi=30$ deg for $E_{0x}^{2}/E_{0y}^{2}\sim 3$. We also found that the actual polarization parameters are, in fact, dependent on the bias condition and $T_{b}$. Nevertheless, the observed $E_{0x}$ was greater than $E_{0y}$ in all cases, directly suggesting the predominance of the $(1p)$ cavity mode for elongated rectangular mesas.

When two mesas are biased to emit simultaneously, the far-field waves should be described in terms of the superposition of the $E$-fields generated from each mesa. Thus, the total $E$-field depends on the phase difference between the macroscopic Josephson oscillations. The observed pattern for A1$\parallel$A2 shown in Fig. 2(b) exhibits four-fold symmetry with respect to $\theta$, suggesting that the two mesas generate photons synchronously. It is likely that $\psi$ and the helicity for A1$\parallel$A2 are dominated by the photon from A2, which emits more intensively than A1 (Fig. 2(c)). Most importantly, we found that the axial ratio increases significantly from 2 for the individual emissions to 24 for the simultaneous emission. We propose that this pronounced effect on the axial ratio is an indication of the phase synchronization between the two mesas as a result of EM coupling.

We observed the same behavior from other mesas shown in Fig. 1(a) and another supplemental sample, where each mesa showed slightly different polarization depending on the geometrical configuration SM . The amplitude ratio $E_{0x}\textfractionsolidus E_{0y}$ explains the predominance of cavity resonances in the width direction over those in the length direction. Since we injected the DC bias current into A1 and A2 using a left strip electrode as shown in Fig. 1(a), the resonance in the width direction may be degraded by a non-uniform current distribution in the mesa Kakeya et al. (2012); Tsujimoto et al. (2014). This explanation is supported by the observation $E_{0x}/E_{0y}=1.4$ for A1 and, in contrast, 2.0 for supplemental mesas with a symmetrical electrode configuration SM . This technique allows for dynamic control of polarization by adjusting the current distribution in the mesa.

In Fig. 3(a), we plot the polarization ellipses obtained by calculating the locus of $\bm{E}(t)$. According to antenna theory for a transverse magnetic cavity, $E_{0x}$ (or $E_{0y}$) is proportional to the magnitude of the magnetic currents parallel to the $y$-axis (or $x$-axis). Hence, in order to calculate $\bm{E}(t)$, we assume that the anisotropy is equal to the inverse mesa aspect, i.e., $E_{0x}/E_{0y}=\ell/w$. This geometrical effect coincides with the numerical simulation for a locally heated square IJJ mesa Asai and Kawabata (2017). By comparing Fig. 3(a) with Fig. 2(c), we can estimate $\delta_{yx}$ to be $3\pi/4$ (135 deg) for A1 and $-\pi/4$ ($-45$ deg) for A2.

Let us describe our results in terms of quantum mechanics. The quantum-superposition state of the photon emitted from the parallel-biased mesa array of A1$\parallel$A2 is described as

where $\bm{S}_{i}$ ($i=\textrm{A1, A2, or A1$\parallel$A2}$) represents the Stokes vector as a quantum number. Two complex numbers $\alpha$ and $\beta$ represent the probability amplitudes (i.e., $|\alpha|^{2}+|\beta|^{2}=1$) and phases of the unperturbed states $\ket{\omega_{\textrm{A1}},\bm{S}_{\textrm{A1}}}$ and $\ket{\omega_{\textrm{A2}},\bm{S}_{\textrm{A2}}}$, respectively. According to the dispesrsion relation of the transverse JPW Kadowaki et al. (1997), angular frequencies $\omega_{\textrm{A1}}$ and $\omega_{\textrm{A2}}$ are determined by the wavenumbers $\bm{k}_{\textrm{A1}}$ and $\bm{k}_{\textrm{A2}}$ of the Josephson plasmons (quantized JPW) independently of the polarization. Our concern is finding the 4$\times$4 perturbation matrix $V_{m}$ that satisfies $\begin{pmatrix}\ket{\omega_{\textrm{A1}}^{\prime},\bm{k}_{\textrm{A1}^{\prime}}}\\ \ket{\omega_{\textrm{A2}}^{\prime},\bm{k}_{\textrm{A2}^{\prime}}}\end{pmatrix}=V_{m}\begin{pmatrix}\ket{\omega_{\textrm{A1}},\bm{k}_{\textrm{A1}}}\\ \ket{\omega_{\textrm{A2}},\bm{k}_{\textrm{A2}}}\end{pmatrix}.$ Here, inter-mesa coupling $V_{m}$ causes perturbation and may include non-diagonal elements, which involve a general question in non-linear physics regarding the symmetry of the matrix.

Figure 3(b) shows polarization $\bm{S}_{\textrm{A1$\parallel$A2}}$ calculated by taking the superposition into consideration. We used the actual intensity ratio obtained by measurement. The orientation angle in the range of $0<\psi<\pi/2$ is in good agreement with Fig. 2(d). It is noteworthy that the modulus $|\beta/\alpha|$ represents the degree of interaction between the two mesas and $|\beta/\alpha|=0.9$ coincides with our results. Meanwhile, the argument of $\beta/\alpha$ corresponds to the phase difference between A1 and A2.

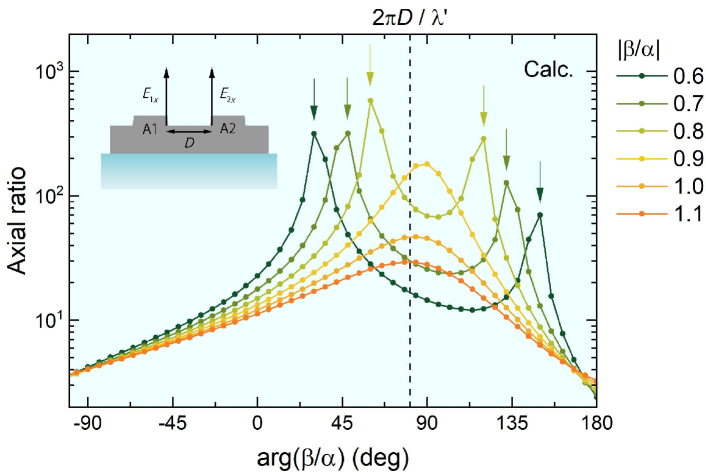
Figure 4 shows the variation of axial ratio as a function of $\arg(\beta/\alpha)$. As indicated by arrows, two singular states exhibiting perfect polarization are emitted when $|\beta/\alpha|<0.9$. For example, two singular states with very large axial ratio can be observed at $\arg(\beta/\alpha)=45$ deg and at 135 deg when $|\beta/\alpha|=0.7$. We suggest that such perfect polarization is attributed to coherent excitation of the Josephson plasmon. See Supplemental Material for $|\beta/\alpha|$-dependence of $\bm{S}_{\textrm{A1$\parallel$A2}}$ SM .

The origin of inter-mesa coupling $V_{m}$ arises from the propagation of JPWs through the Bi-2212 base crystal. The inset of Fig. 4 shows a schematic cross-sectional view of the mesa array. The dashed line in Fig. 4 represents the phase delay $2\pi D/\lambda^{\prime}$ due to the finite propagation time, where $D=58$ µm is the interspace between the two mesas and $\lambda^{\prime}=\lambda/n$ is the effective wavelength. We assume that JPWs can propagate from one mesa to another mesa through the base crystal and diffract at the mesa edge. This situation strongly supports the view that the base crystal can mediate the EM interaction Benseman et al. (2013a); Lin and Koshelev (2013), the mechanism of which has been unclear in previous works. Furthermore, we found that the total intensity of simultaneous emission $S_{0}$ reaches a maximal value as $2\pi D/\lambda^{\prime}$ coincides with a multiple of $\arg(\beta/\alpha)$ SM .

In conclusion, we demonstrated the synchronization of macroscopic Josephson oscillations in two simultaneously biased Bi-2212 IJJ mesas coupled via a base crystal by measuring the complete Stokes parameters. We used an achromatic QWP and a linear WGP to analyze the orthogonal components of the emitted $E$-fields. We proved that the coherent radiation is elliptically polarized with the major axis oriented in the width direction. Most importantly, we observed a significant increase in the axial ratio for simultaneous emission, suggesting that Josephson plasma in the Bi-2212 base crystal can mediate an interaction between two individual mesas. This finding represents a possible means of manipulating the synchronization of IJJ arrays, and is the most promising way to increase the integrated radiation power.