Multisections with divides and Weinstein 4-manifolds
1. Introduction
There are various methods to diagrammatically encode a -dimensional manifold, each of which is based on a decomposition theorem which breaks up the manifold into simple pieces such that the diagram encodes the way these pieces glue together (e.g. handle decompositions, Lefschetz pencils/fibrations). The most recent such method is the development of trisections by Gay and Kirby [GayKir16], generalized to multisections in [IslNay20]. Symplectic structures have played a key role in 4-dimensional topology, due to connections with gauge theory. Compatibility between symplectic topology with handle decompositions arose from Weinstein’s construction [Wei91] and in the -dimensional case was diagrammatically encoded by a Legendrian surgery diagram by Gompf [Gompf98]. Similarly compatibility between symplectic manifolds and Lefschetz pencils and fibrations was established [Don99, GompfStipsicz, LoiPie01], so a symplectic manifold can be encoded by the fiber and base surfaces, pencil points, and ordered vanishing cycles. A notion of compatibility between trisections and symplectic manifolds was proposed in [LamMei18] and shown to exist in [LamMeiSta20], but this compatibility did not yield a simple diagrammatic way to encode a symplectic structure (rather it was motivated by attempts to obtain genus bounds).
In this article we define a stronger compatibility between a multisection and a symplectic structure, which can be diagrammatically encoded by collections of curves on a surface. In addition to the diagrammatic data of the smooth multisection, we keep track of another multi-curve representing the dividing set of convex surfaces in contact manifolds. Thus, we call our decomposition of a symplectic manifold a multisection with divides. Our main result is that every -dimensional Weinstein domain admits a multisection with divides.
Definition 1.1.
A multisection with divides of a symplectic filling with contact boundary is a decomposition , such that
-
•
.
-
•
for .
-
•
for all
-
•
Each is a symplectic filling of .
-
•
is a contact Heegaard splitting of
-
•
is a contact Heegaard splitting of
A bisection with divides is a multisection with divides with .
The advantage of using contact Heegaard splittings is that the handlebodies each carry a standard positive and a standard negative contact structure, which are contactomorphic. This is one of the key ideas which we use to make multisections compatible with symplectic and contact geometry.
Remark 1.2.
In the fourth bullet point of Definition 1.1, we ask for to be a symplectic filling. Note that in our setting weak, strong, Liouville, and Weinstein fillability are all equivalent, because there is a unique weak symplectic filling of up to symplectic deformation, and this filling is actually Weinstein (thus strong and Liouville) [NW].

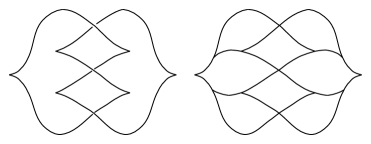
An essential feature of these multisections with divides is that they can be encoded as a sequence of cut systems together with a fixed dividing set on a closed surface. An example of such a diagrammatic representation together with a schematic of what this encodes can be seen in Figure 1.
We are able to encode symplectic geometric data diagrammatically because our multisection with divides decompositions are geometrically restrictive by asking each Heegaard splitting to be a contact Heegaard splitting (see section 2.1 for the definition). A typical multisection of a symplectic manifold would be unlikely to satisfy this condition, even if it were a “Weinstein multisection” as in [LamMei18, LamMeiSta20]. Therefore, it is surprising that these geometrically restrictive multisection decompositions actually exist quite generally. Our main theorem is the following.
Theorem.
Every compact 4-dimensional Weinstein domain admits a multisection with divides.
We give two proofs of this theorem each with distinct advantages. Both proofs also yield algorithmic methods to produce a diagram for the multisection with divides. The first proof takes as input a Kirby-Weinstein diagram, and produces a bisection with divides. The disadvantage of this algorithm is that the core surface will generally have very high genus, which is typically highly inefficient. On the other hand, the output only has two sectors, instead of arbitrarily many.
The second proof takes as input a positive allowable Lefschetz fibration (PALF) and produces a multisection with divides. In this case, the genus is more controlled, being determined by the topology of the fiber of the PALF, however there may be many sectors (potentially one for each Lefschetz singularity). More specifically we prove the following.
Theorem.
Let be a PALF whose regular fiber is a genus surface with boundary components and singular fibers. Then admits a genus -section with divides.
One can compare these results and Definition 1.1 to the definition of Weinstein trisection for closed symplectic manifolds in [LamMei18, LamMeiSta20]. The main difference is that those prior definitions do not require any compatibility between the contact structure induced on the boundary of each sector and the Heegaard splitting of the boundary induced by the trisection. As a consequence, there is not easy diagrammatic data that encodes the contact and symplectic topology in these prior definitions. (The most likely candidate for such diagrammatic data is a weighted foliation for each handlebody, but the data of a weighted foliation is not discrete.) By contrast, in our more restrictive notion of multisection with divides, the symplectic and contact geometry can be diagrammatically encoded by a single dividing set on the core surface.
Remark 1.3.
Smooth multisections are compatible with both closed manifolds and manifolds with boundary. In this article, we have given the definition of a multisection for divides in the case that our symplectic manifold has contact boundary. The definition naturally extends to closed manifolds. Although in this article we establish the existence of our decompositions for Weinstein domains rather than closed symplectic manifolds, this is a key step towards establishing existence of the analogous multisections with divides for all closed symplectic manifolds via results of Donaldson [Don96] and Giroux [Gir02, Gir17].
The monodromy of a Lefschetz fibration is a product of right handed Dehn twists. In general, there can be multiple ways to write the same mapping class element as a product of right handed Dehn twists. Swapping out one of these with another is called a monodromy substitution. A number of important symplectic cut and paste operations like rational blow-down can be seen as a monodromy substitution operation on a Lefschetz fibration [EndGur10] [EMV11]. By tracking the change induced by a monodromy substitution on a PALF through our algorithm, we are able to realize these cut and paste operations on multisections with divides. In Figure 15, we demonstrate this explicitly for the monodromy substitution coming from the lantern relation, which induces a -rational blowdown.
We conclude the paper with a classification of genus-1 multisections with divides. The smooth genus-1 multisections with boundary were previously classified in [IKLM] to exist if and only if the manifold is a linear plumbings of 2-spheres. Our requirement that the multisections be compatible with genus-1 contact Heegaard splittings restricts this significantly more, as in the following theorem.
Theorem.
Genus-1 -sections with divides correspond to plumbings of disk bundles over 2-spheres, each of Euler number .
The organization of this paper is as follows. Section 2 discusses the way we will ask contact structures to be compatible with Heegaard splittings and -dimensional handlebodies. Section 3 gives our first proof of our main theorem, showing how to turn a Kirby-Weinstein handlebody diagram into a multisection with divides. Section 4 gives the second proof of our main theorem, showing how to turn a PALF into a multisection with divides. Section 5 classifies genus-1 multisections with divides and shows how multisection diagrams with divides can be stabilized to increase the genus of the surface. Finally, in Section 6 we discuss some questions for future research.
2. Contact geometry and Heegaard splittings
In this section, we explain the compatibility condition between contact structures and Heegaard splittings which we will require on the boundary of each sector. We also give a diagrammatic formulation of this compatibility. We begin with some background on surfaces in contact manifolds.
A surface embedded in a contact 3-manifold is said to be convex if there exists a contact vector field for such that is transverse to . Convex surfaces are generic, meaning every smoothly embedded surface has a -small isotopy to a convex surface [Gir91, Hon00]. Given a contact vector field transverse to we obtain a multicurve called the dividing set, denoted . This multicurve is defined by and the isotopy class of this curve is an invariant of the embedding of up to isotopy through convex surfaces.
The dividing set captures all of the contact geometric information of in a neighbourhood obtained by flowing by the contact vector field. More precisely we have the Giroux flexibility theorem.
Theorem 2.1.
([Gir91]) Let be a closed orientable surface, and and be convex embeddings of . Suppose is a contact vector field transverse to . If the oriented multicurves and are isotopic, then there exists an isotopy for such that .
Given a handlebody, , a spine for is a graph, , such that retracts onto . If additionally carries a contact structure, then a spine, , is said to be a Legendrian spine if each edge is a Legendrian arc or knot. By combining Darboux’s theorem with the standard neighborhood for Legendrians [Geiges, Theorem 2.5.8], we see that Legendrian spines have a standard tight contact neighborhood, determined by the ribbon neighborhood of the spine tangent to the contact planes.
2.1. Contact Heegaard splittings
Definition 2.2.
A contact Heegaard splitting of a contact manifold is a Heegaard splitting such that and are contactomorphic to standard neighborhoods of Legendrian spines and .
We will call the handlebodies which are standard neighborhoods of Legendrian graphs standard contact handlebodies. Note that a smooth handlebody of a given genus typically has multiple different “standard” contact structures, which are differentiated by the number of components of the dividing set on the boundary. The different options come from the fact that there are generally multiple different surfaces with boundary whose doubles are a genus surface (determined by the number of boundary components).
This notion of contact Heegaard splittings originated with Giroux [Giroux] and was also developed by Torisu [Tor00], and can be equivalently formulated as follows.
Lemma 2.3 ([Giroux, Tor00]).
Let be a Heegaard splitting of with a convex surface. The following are equivalent
-
(1)
and are standard neighborhoods of Legendrian graphs
-
(2)
and are two halves of an open book decomposition supporting
-
(3)
For each handlebody , there exists a set of compression disks cutting into a ball, such that the boundary of each compression disk intersects the dividing set on in exactly two points.
Though these equivalences are known, we review how to pass between them. If we start with and as standard neighborhoods of Legendrian graphs, we can see the page of the corresponding open book decomposition as a contact framed ribbon of the Legendrian. The contact planes are tangent to along the Legendrian, so in a standard neighborhood, is a positive area form when restricted to this page. Moreover, in the standard model, we can identify (where for ), such that is positive on each . In this way, we see that the first characterization gives rise to the second characterization. Conversely, given a supporting open book decomposition, we can Legendrian realize a spine on two pages. Restricting the contact structure defined on an abstract open book to half of the pages, we see that this is a standard neighborhood of this Legendrian spine. The dividing set on the boundary of a standard neighborhood of a Legendrian graph is precisely the intersection of the contact framed ribbon with . The meridian of each edge of the graph thus intersects the dividing set in exactly two points. Similarly, if and are two halves of an open book decomposition, the dividing set on is the binding of the open book . A collection of compressing disks for is given by where is a collection of arcs on which cut into a disk. Each intersects the binding in exactly two points (the endpoints of in ). If we have a Heegaard splitting with compression disks for each handlebody which each intersect the dividing set in two points, we can cut along these compressing disks to get a ball with the unique tight contact structure. Reversing the cuts amounts to attaching standard contact -handles which gives a standard neighborhood of a Legendrian graph.
There is a fundamental challenge in obtaining compatibility between a multisection and a symplectic structure. Each interior -dimensional handlebody in a multisection appears in the boundary of two -dimensional sectors, but the boundary orientations are opposite to each other. Viewing a sector as a symplectic filling of its boundary induces a contact structure on the boundary which is a positive contact structure with respect to the boundary orientation. The sign of a contact structure (with respect to a fixed orientation) is an inherent property of the contact planes which measures the direction/handedness of the twisting of the contact planes. Note, this is not the same as the co-orientation of the contact structure which depends only on the contact form, not the contact structure. Therefore, we cannot have identical contact structures on a fixed manifold realize both positive and negative contact structures with respect to a fixed orientation. In general this suggests that we would need two different contact structures on each interior of a multisection. However, as we show in the following lemma, there are both positive and negative standard contact handlebodies which are orientation reversing contactomorphic to each other. Both the positive and negative contact structures are supported by the same half open book.
Lemma 2.4.
Let be a surface with boundary. Let be a -form on which evaluates positively on the oriented boundary of such that is an area form on . Consider where whenever . Using as the coordinate parametrizing the direction, let
Then (respectively ) is a positive (respectively negative) contact structure on supported by the trivial half open book on (with pages ).
Proof.
is a contact structure because
is a volume form on . Note that is independent of so the form is well-defined on the quotient .
To check that it is supported by the open book, we need to verify that evaluates positively on the binding and is a positive area form on the pages. Indeed if is a vector positively tangent to , , and is a positive area form on by assumption. ∎
Remark 2.5.
Note, it is always possible to find such a -form on a surface with non-empty boundary. Also, observe the orientation reversing diffeomorphism which sends to takes to .
2.2. Contact Heegaard diagrams
Motivated by the third characterization in Lemma 2.3, we define a diagrammatic version of contact Heegaard splittings.
Definition 2.6.
A contact Heegaard diagram is a quadruple such that:
-
•
is a closed oriented surface.
-
•
is a multicurve which separates into two homeomorphic surfaces with boundary.
-
•
is a cut system for such that each curve intersects twice.
Given a contact Heegaard diagram, we can reconstruct a contact manifold together with a contact Heegaard splitting. In particular, if is one of the halves of , then we endow each of the handlebodies the standard contact structures coming from . This induces an open book with page and binding , which in turn induces a contact structure. Conversely, every contact Heegaard splitting has a contact Heegaard diagram by characterization (3) of Lemma 2.3.
This correspondence allows us to give a classification of genus-1 contact Heegaard splittings of as we will see in Section 5.1. In particular, by Euler characteristic considerations, genus-1 contact Heegaard splittings correspond to open book decompositions of with an annular page. The monodromy then consists or a left-handed or right handed Dehn twist about the core of this annulus. The right handed Dehn twist gives the tight contact structure on whereas the left handed Dehn twist gives an overtwisted structure. These lead to the Heegaard diagrams shown in Figure 2.

2.3. Dividing sets on standard neighborhoods from Legendrian front projections
In Section 3, we will be looking at Heegaard splittings of , or more generally where one handlebody is a standard neighborhood of a Legendrian graph described via a front projection, and the other handlebody is the complement. In order to verify that the complement is a standard contact handlebody, it will be useful to know exactly how to draw the dividing set on the boundary of the standard neighborhood of an explicitly embedded Legendrian graph in terms of the front projection.
We will mainly focus on trivalent Legendrian graphs. Higher valence vertices can be split into trivalent vertices by growing additional Legendrian edges via a Legendrian deformation which preserves the standard neighborhood and thus, the dividing set on its boundary. Given a front projection representing a Legendrian embedding in , we can draw the corresponding dividing set on the boundary of a standard neighborhood. Recall that the dividing set on the boundary of a standard contact handlebody is the boundary of the page of the compatible open book decomposition. A page of the open book is given by the contact framed ribbon of the Legendrian knot. Considering how the contact framing wraps around at left and right cusps and at left and right trivalent vertices, we obtain the local models for the dividing set as shown in Figure 3. The first five models cover the generic front projections of a trivalent Legendrian graph. The last model includes a Legendrian arc which degenerately projects to a single point, whose two end points are trivalent vertices. We can isotope this model to a generic front projection as in Figure 4, and thus derive its local model from the previous models. We include this last “compound” model for convenience as we will use it extensively in implementing our algorithm of Section 3.1.

3. Kirby-Weinstein handlebody diagrams and multisections with divides
In this section we will show how to use a Kirby-Weinstein handlebody diagram to produce a bisection with divides. A consequence of our proof is an algorithm to obtain a multisection diagram with divides (defined in Section 3.2) from a Kirby-Weinstein diagram.
3.1. Existence of bisections with divides from Kirby-Weinstein handlebody diagrams
Theorem 3.1.
Every compact -dimensional Weinstein domain admits a bisection with divides.
Proof.
By definition, a Weinstein -manifold has a Weinstein handle structure. By [Gompf98], this handle structure can be represented in a standard form by a Legendrian front projection with -handles (which we will call a Kirby-Weinstein diagram). We will give an algorithm to convert a Kirby-Weinstein diagram in Gompf standard form into a multisection diagram with divides. If we ignore the symplectic and contact structure, the smooth part of this algorithm essentially follows those in [GayKir16] and [MeiSchZup16] used for converting a Kirby diagram into a trisection.
The union of the - and -handles will be . This is diffeomorphic to and with the Weinstein structure of restricted to , it is a Weinstein filling of its boundary .
We will construct a contact Heegaard splitting of such that the Legendrian attaching spheres for the -handles of are a subset of the Legendrian core of . Then we will define to be a collar of together with the -handles of . Because the attaching spheres of the -handles are a subset of the Legendrian core of , we will see that will be diffeomorphic to . There is a naturally induced Heegaard splitting of given by where is obtained from by doing Legendrian surgery on the attaching spheres of the -handles. We will then show that this is also a contact Heegaard splitting, and that is a symplectic filling of this contact manifold.
Let be the Legendrian attaching link for the -handles of in . To construct the appropriate contact Heegaard splitting of , we will add Legendrian tunnels to , yielding a Legendrian graph containing . A standard contact neighborhood of will be and its complement will be . The first purpose of the tunnels is to ensure that the complement of the neighborhood of is a handlebody. Additional tunnels will be added to ensure this handlebody has the standard contact structure.
The construction of is as follows.
-
(1)
Start with in Gompf standard form.
-
(2)
If there is any -handle of whose belt sphere is disjoint from , add a Legendrian circle which passes through that -handle once.
-
(3)
For each -handle add Legendrian arcs to connect all the strands that pass through that -handle on the left and right as shown in Figure 6.
-
(4)
At each crossing in the diagram, add a Legendrian arc which projects to the crossing point connecting the over- and under-strands. See Figure 4 for generic front projections for a Legendrian isotopic graph.
-
(5)
Add Legendrian arcs to connect disconnected components until the graph is connected.
-
(6)
The resulting front projection divides up the plane into regions, such that the boundary of each region is a Legendrian unknot. Add further Legendrian arcs to cut up each region as in Figure 5 so that at the end, each region is bounded by a Legendrian unknot with . Namely, every region in the front projection should have a unique “right cusp” and a unique “left cusp” where a vertex is a right (resp. left) cusp of a region if the two edges on the boundary of the region which meet in the vertex both approach the vertex from the left (resp. right). Note that here we can treat each crossing as a single vertex by shrinking the Legendrian arc connecting the two strands by a Legendrian deformation.



Now if is a standard contact neighborhood of , and is the complement, we want to show that is a contact Heegaard splitting. If there are no -handles in the Kirby-Weinstein diagram, is a smooth handlebody because we put tunnels at each crossing, so is diffeomorphic to a -ball with one handle attached for each bounded planar region in the diagram of . When there are -handles in the Kirby-Weinstein diagram, there is an additional compressing disk for each -handle as seen in Figure 7.

Using the models from Figure 3, we can draw the dividing set on the boundary of in terms of the front projection. To see that has the standard contact structure, we show that there is a set of compressing curves for on such that each curve intersects the dividing set in two points.
Let be the bounded regions of the complement of the front projection of , and let . If there are no -handles in the handle diagram for , then form a collection of compressing disks for , which cut into a ball. If there are -handles, there is also a compressing disk as in Figure 7 for each -handle. After performing handleslides over the regions that pass through the -handle, we can realize this compressing curve as in Figure 6 so that it intersects the dividing set in exactly two points. To see that that boundary of each intersects the dividing set in two points, we use the property from the last step of the construction of , that each region is bounded by a Legendrian unknot with , meaning there is a unique left cusp (which may be a vertex) and a unique right cusp (which may be a vertex). Any other vertices along the boundary of the region have the two edges on the boundary of this region entering the vertex from different sides. Examining all of the ways that our local models in Figure 3 may appear as the boundary of a region, we see that each cusp (either a standard cusp or a vertex cusp) contributes one intersection point between the dividing set , and the remaining edges and vertices in the boundary of the region do not contribute any intersections between the dividing set and . Thus we see that is a standard contact handlebody.
Next, we look at the second sector . We need to show that , that there is a contact structure on with a contact Heegaard splitting such that is a symplectic filling of . Recall that is obtained from by attaching -handles along the Legendrian link with framing where is the framing induced by the contact planes. Since is embedded in (the core of ) is smoothly diffeomorphic to . A natural Heegaard splitting of is given by where ( surgery of along ). There is a well-defined contact structure obtained by Legendrian surgery, which agrees with the contact structure on near (since the surgery is performed on the interior). Therefore the dividing set on can be viewed as the same as the dividing set on , but the compressing curves for change based on the surgery. Namely, for each component of , the compressing curve changes from a meridian of to a -framed copy of on . Since the dividing set is parallel to the framing of , the framing of intersects the dividing set exactly twice. Therefore, is a standard contact handlebody with the contact structure induced by Legendrian surgery on .. Note that is also a standard contact handlebody, using the negative contact structure on from Lemma 2.4. Putting these together, we get a contact Heegaard splitting of .
It suffices to show that is a Weinstein filling of where the contact structure on is given by the contact Heegaard splitting . For this, notice that is a -handlebody, and if we restrict to this subset of , up to shrinking , the symplectic structure must be a standard neighborhood of the isotropic spine of . In other words, with the symplectic structure is symplectomorphic to a Weinstein -handlebody. Moreover, the induced unique tight contact structure on is supported by the open book (viewing ). This open book with trivial monodromy gives rise exactly to the contact Heegaard splitting (where we collapse along ). Since , (with the contact Heegaard splitting ) is obtained from the Weinstein -handlebody (with the contact Heegaard splitting ) by attaching Weinstein -handles along Legendrian knots in , we have that is a Weinstein filling of the contact Heegaard splitting .
∎
3.2. Multisection diagrams with divides
A fundamental feature of multisections with divides is that they can be completely encoded on a surface. In this section we define these diagrams and show how the previous proof gives an algorithm for obtaining a bisection diagram with divides from a Kirby-Weinstein handlebody diagram.
Definition 3.2.
A multisection diagram with divides is a closed orientable surface, together with a set of dividing curves and cut systems such that for all
-
•
Each curve in intersects in two points.
-
•
is a contact Heegaard splitting of the tight contact structure on for some .
Remark 3.3.
The condition that each curve in each cut system intersects the dividing set in two points is easily checked. However, it is potentially difficult to check whether the union of two consecutive contact handlebodies forms the tight contact structure on .
The proof of Theorem 3.1 gives an algorithmic method to obtain a multisection diagram with divides as follows.
Starting from a Kirby-Weinstein handlebody diagram, construct the Legendrian graph as in the proof. Use the models from Figure 3 to draw the dividing set on as the boundary of the neighborhood of () in terms of the front projection.
We can describe cut systems for the handlebodies , , and as follows. The cut system is given by taking the regions of the planar diagram together with a curve tracing through the vertical tunnels added between the 2-handles passing through each 1-handle, as in Figure 6–note the curve in this figure intersects the dividing set in two points. As the regions are diagrams of unknots, each of the curves given by the boundary of a region intersects the dividing set twice. This ensures that the pair is a diagram of a standard contact handlebody.
The cut system is given by taking a meridian of each tunnel together with a meridian of each knot in the Kirby-Weinstein diagram. Using the local model at the top of Figure 3 and Figure 8 we see that these curves intersect the dividing set twice so that is also a standard contact handlebody. Because represents a Heegaard splitting of the boundary of the - and -handles of the Kirby-Weinstein handlebody diagram, it is symplectically fillable and thus must support the tight contact structure on a connected sum of copies of .

To obtain , we start by taking a Legendrian push off of each knot component in the diagram. Each such component intersects its chosen meridian in once and does not intersect the dividing set at all. Adding a left handed twist about the meridian to each component gives a curve whose surface framing is the contact framing and which intersects the dividing set twice. Then replacing each meridian in with the corresponding gives a diagram representing a contact Heegaard splitting of a connected sum of copies of . Therefore is a bisection diagram with divides of the given manifold.
This algorithm is carried out in Figures 9 and 10 for the result of attaching a Weinstein handle to the max right handed trefoil and in Figures 11 and 12 for the Weinstein domain , which is a disk bundle over .



Note that the cut systems and which are output from our algorithm have a very particular form. More specifically, each component of either agrees with or is dual to a component of . In the latter case, there exists a curve in which is disjoint from the dividing set, dual to the component with respect to , such that where is a right-handed Dehn twist about with respect to the orientation on induced as the boundary of . Let’s call two cut systems related in this way standard Weinstein cobordant. By isotoping each into the Legendrian core of the handlebody , we find a Legendrian link in such that the framing for this link is represented by the corresponding curves in , ( represents the contact framing, and is a meridian of the surgery torus so represents the contact framing ). Thus we see that if two cut systems with a dividing set are standard Weinstein cobordant, the corresponding sector can be endowed with the structure of a Weinstein cobordism from to obtained by attaching Weinstein -handles to . We can always endow the first sector with the structure of a Weinstein -handlebody (since by definition is a contact Heegaard splitting of with the tight (fillable) contact structure). Therefore, we have an (overly strong) condition that ensures a multisection diagram with divides corresponds to a Weinstein -manifold.
Proposition 3.4.
Let be a multisection diagram with divides such that are standard Weinstein cobordant for . Then corresponds to a Weinstein -manifold.
In Section 4, we will see another condition that ensures a multisection diagram with divides corresponds to a Weinstein -manifold. It is an interesting question to ask whether there is a general characterization of all multisection diagrams with divides which correspond to Weinstein -manifolds. In general, we only expect a multisection diagram with divides to correspond to a symplectic -manifold, which may not admit any global Weinstein structure.
4. PALFs, monodromy substitution and multisections with divides
4.1. PALFS and monodromy factorizations
Fibration structures on symplectic manifolds have a long history of study, dating to Donaldson’s work in [Don99] where it was shown that every closed symplectic 4-manifold admits a Lefschetz pencil. Conversely, Gompf proved that every 4-manifold with a Lefschetz pencil admits a symplectic structure [GompfStipsicz]. The corresponding objects in the Weinstein category are positive allowable Lefschetz fibrations.
Definition 4.1.
A Lefschetz fibration on is a map to a surface such that near each critical point of , there are local orientation preserving coordinates such that is modeled on . A positive allowable Lefschetz fibration (PALF) is a Lefschetz fibration whose base is and whose regular fiber is a compact surface with boundary such that every vanishing cycle is homologically essential (allowable).
Following Loi and Piergallini [LoiPie01], every Weinstein domain admits a PALF. Conversely, every PALF supports a Weinstein structure [GompfStipsicz].
In this section, we will show how to use the PALF structure to obtain a decomposition of a Weinstein domain as a multisection with divides. As in Figure 13, we cut the disk into closed subdisks, , such that
-
•
Each contains a unique critical value of ,
-
•
is diffeomorphic to an interval for ,
-
•
, and
-
•
.
Then let , , for , . Then and (after quotienting by the factor along points in which is a Weinstein homotopic domain).
Theorem 4.2.
The decomposition is a multisection with divides for .
Proof.
Each is a -dimensional handlebody since it is diffeomorphic to . Thus to check this is a multisection with divides it suffices to check that (1) each is symplectomorphic to a -dimensional Weinstein -handlebody and (2) that is a contact Heegaard splitting of .
First we look at each . We will use as the regular fiber. The vanishing cycles are curves in which collapse to the critical point under parallel transport from to the critical value. The model for Lefschetz singularities shows that is diffeomorphic to the manifold obtained from by attaching a -handle along with framing given by one less than the page framing. is certainly a -handlebody, so the result will still be a -dimensional -handlebody if this -handle cancels with one of the -handles of . Thus to see that is diffeomorphic to a -handlebody it suffices to check that there is a meridional disk in which intersects exactly once.
As is a PALF, is homologically essential. Thus, by Poincare-Lefschetz duality, there exists an arc such that . Parallel transport defines diffeomorphisms which identify with . Then is a meridional disk of which intersects at a single point. Thus is a -dimensional -handlebody.
Since and is a disk, has the structure of a Weinstein manifold induced by the (restricted) PALF. This agrees with the symplectic structure on since both are compatible with the Lefschetz fibration.
To see that gives a contact Heegaard splitting of with the contact structure induced by the Weinstein structure on , we use the open book construction of contact Heegaard splittings. Restricting to gives an open book decomposition of which supports the contact structure induced by the Weinstein structure on since the Weinstein structure comes from the Lefschetz fibration structure. and are precisely the two halves of the open book which give a contact Heegaard splitting. ∎
4.2. Multisection diagrams with divides from a PALF
A PALF can be encoded combinatorially through the fiber surface and the ordered set of vanishing cycles . In this section we show how to use the combinatorial data of a PALF to obtain the combinatorial data of the multisection diagram with divides corresponding to the decomposition from Theorem 4.2.
The monodromy about a Lefschetz critical value with vanishing cycle is a right handed Dehn twist about , which we denote by . Thus a PALF can equivalently be encoded by an ordered sequence of right handed Dehn twists about the vanishing cycles called a monodromy factorization.
The core surface of the multisection is diffeomorphic to the union of two copies of glued together along their boundary. The dividing set on is given by the boundary of . More precisely, if is the diffeomorphism defined by parallel transport, (note we are suppressing the quotient of the direction at points in ).
To understand a multisection diagram with divides, we want to fix an identification of , and then draw cut systems for each handlebody . We will use to identify as . Then the restriction of to gives a diffeomorphism from to .
Let be a complete arc system for i.e. a collection of properly embedded arcs which cut into a disk. Then gives a cut system of disks for . We want to see the boundaries of these disks on our fixed identification of . Namely, we want to describe the curves in . Each is the identity on , and defines parallel transport along the arc from to over which lies. Since the define parallel transport, and we are using to identify with , we see that in is the image of under the monodromy around the curve which goes from to along the curve and then goes from to along the curve. This monodromy is . Thus, the cut system for is obtained from the cut system for by applying the right handed Dehn twist where . Any choice of complete arc system defines a cut system for by gluing together the same arcs on and .
To summarize, given a PALF with fiber and ordered vanishing cycles , the corresponding multisection with divides is given by
-
•
where and are copies of ( is oppositely oriented).
-
•
The dividing set is .
-
•
The cut system for is where is a complete arc system for .
-
•
For , the cut system for is obtained from the cut system for by applying a right handed Dehn twist about .
Note that each cut curve intersects the dividing set in exactly two points (the end points of the arc ). (This is clearly true for , and it remains true for each because the Dehn twists are applied in the interior of which is disjoint from the dividing set.)

Remark 4.4.
Note that the output of a PALF yields a slightly more general condition which ensures that a multisection with divides corresponds to a Weinstein manifold. In this case, every consecutive pair of cut systems differs by a right handed Dehn twist about a curve which lies entirely in the side of the dividing set. Let’s call such generalized standard Weinstein cobordant (gsWc). (This generalizes the notion of standard Weinstein cobordant from Proposition 3.4.) If consecutive cut systems and are gsWc where the curve defining the Dehn twist relating them is dual to one of the components of , they define a smooth multisection by Lemma 4.5. Furthermore, whenever we have gsWc cut systems representing handlebodies and forming the Heegaard splitting on the boundary of a sector , we can again interpret as a Weinstein cobordism from to . This is because we can use the Lefschetz fibration interpretation of and then view the Lefschetz critical point as an attachment of a Weinstein -handle to . Since can either be interpreted as a filling or a Weinstein cobordism, the sector also supports a Weinstein structure making it a filling of its boundary, and a Weinstein structure making it a cobordism from to . This shows that Proposition 3.4 holds under the more general assumption that consecutive pairs of cut systems are gsWc, and the curve defining the Dehn twist for a pair of cut systems is dual to one of the curves from the first cut system.
The previous construction suggests that multisection can also be encoded by a monodromy factorization, and here, we show that this is indeed the case. Through some care, one can determine a particular monodromy factorization from a multisection, however for the present paper it will be sufficient to have a family of possible factorizations.
Fixing a surface , a system of cut curves defines a handlebody with boundary . Given a handlebody, we can choose any system of cut curves which bound disks in the handlebody to encode it. If we specify a diffeomorphism of , we can apply that diffeomorphism to a cut curve system, to produce a new cut curve system. If the original cut curve system defines a handlebody , we let denote the handlebody defined by the image of a cut-system for under the map . Note this is independent of the choice of cut-system for , because two different cut systems and for will be related by some sequence of handle slides, and thus will be related to by a sequence of handle slides as well. We begin with a lemma which yields a sufficient condition for and to form a Heegaard splitting of when is a Dehn twist.
Lemma 4.5.
Let be a closed genus surface, be a simple closed curve on , and be a (right or left handed) Dehn twist about . Let be a handlebody with boundary . Suppose there exists a properly embedded disk whose boundary, , is non-separating on such that . Then is a Heegaard splitting of .
Proof.
We will produce a Heegaard diagram of which consists of parallel curves and two curves intersecting once, which proves the lemma. Extend to a cut system, , for . Now each point of can be eliminated by the following process: start at the point and follow until we meet the first point of call the resulting arc and the curve in at this intersection . Sliding over along eliminates this intersection and does not introduce any new intersections between and . Repeating this process, using narrower and narrower sliding bands, we may eliminate all intersections of and except for the point .
We may then obtain a Heegaard diagram for by taking the Dehn twist of the cut system resulting from these slides on about . As is disjoint from all of the curves other than there are curves which are unchanged by the twisting and are therefore parallel. On the other hand and intersect once, providing the desired Heegaard diagram. ∎
Using the above lemma, we obtain a sufficient criteria for Dehn twists on cut systems to yield two sequential handlebodies in a multisection. Conversely, the following proposition shows that the sequential handlebodies in all multisections can be obtained in the fashion.
Proposition 4.6.
Let be a genus- multisection with multisection surface , and with . Let be the 3-dimensional handlebodies lying at the boundaries of the . Then there exist curves such that .
Proof.
For each handlebody, , we will show how to produce the curves . Recall that the handlebodies and meet at the multisection surface to form a a Heegaard splitting of . Consider a Heegaard diagram of . By Waldhausen’s theorem [Wald68], after a sequence of handle slides there is a cut system of curves … for and for such that for and for for .
For we let . Then, . Moreover, since does not intersect any of the other for , for . Then the product takes a cut system for to a cut system for . ∎
We call the product a monodromy factorization for . By following through our construction in Theorem 4.2, we can track the monodromy of a PALF onto the monodromy of a multisection which immediately yields the following.
Corollary 4.7.
Suppose that is a Weinstein manifold which admits a PALF with fiber surface and monodromy factorization . Then admits an n-section with divides with multisection surface , dividing set , and monodromy factorization obtained by applying the Dehn twists of to .
4.3. Monodromy Substitution
In this section we will demonstrate how a monodromy substitution affects a multisection with divides. We begin with the analogous construction for PALFs.
Definition 4.8.
Let be a PALF with fiber surface and monodromy factorization . Suppose that for some and curves we have that, as mapping classes, . Then we may obtain a new Lefschetz fibration with monodromy factorization given by
We say that the new Lefschetz fibration is obtained by a monodromy substitution on .
Monodromy substitution has been used extensively to produce new symplectic manifolds from existing ones. In particular, in [EndGur10], the authors show that the lantern relation, pictured in Figure 14, can be used to perform a rational blowdown on the configuration (see [GomSti99] Section 8.5 for an exposition on these operations). This was later generalized in [EMV11] to realize an infinite family of rational blowdowns as monodromy substitutions using daisy relations. In general, any monodromy substitution can be thought of as some symplectic cut-and-paste operation.

There is an analogous process of monodromy substitution on a multisection.
Definition 4.9.
Let be a multisection (not necessarily with boundary) starting at the handlebody with monodromy factorization given by . Let be the handlebody and suppose that is a sequence of curves such that for all we have that is dual to some disk in (this will guaranteed that the assumptions of Lemma 4.5 hold). Suppose further that . Then we may obtain a new multisection starting at the handlebody and specified by the monodromy factorization . We call a monodromy substitution of .
It follows immediately from Corollary 4.7 that we can find monodromy substitutions by doubling a PALF and a monodromy substitution of that PALF. Carrying this out for the lantern relation gives us a monodromy substitution on a multisection with divides yielding the operation outlined in Figure 15.

5. Genus-1 multisections and stabilizations
5.1. Classification of genus 1 multisections with divides
In this subsection we will provide a characterization of genus-1 multisections with divides. For examples of the diagrams for the unique 2- and 3-sections with divides, see Figure 16. Smooth genus-1 multisections are well characterized by their diagrams, which consist of sequences with In [IKLM], the authors show that smooth genus-1 -sections with boundary correspond to linear plumbings of disk bundles over the sphere. Moreover, given the oriented sequence of cut curves defining a genus-1 multisection diagram, the Euler number of the disk bundle is given by the algebraic intersection .
Proposition 5.1.
There is a unique genus-1 n-section with divides for each . These correspond to the linear plumbing of disk bundles of Euler number over the sphere (’s).
Proof.
First we observe that the linear plumbing of disk bundles of Euler number supports a PALF structure whose fiber is an annulus with vanishing cycles all parallel to the core circle of the annulus. By the algorithm in Theorem 4.2, these Weinstein domains have genus multisections.
Now we show that these are the only genus multisections with divides.
For a contact Heegaard splitting of , the dividing set consists of two parallel curves. Fixing coordinates for , we may assume, after an orientation preserving homeomorphism that and . The dividing set will be two parallel curves of slope . Note that intersects the dividing set twice if and only if . Therefore . Since corresponds to a contact Heegaard splitting for an overtwisted contact structure on , we must have .
We first treat the case , and then proceed inductively. In this case, we seek to find the possible slopes for . As , all curves which intersect once are given by Dehn twists of about . In addition the requirement that means that is a single Dehn twist of about . If this Dehn twist is left handed, then the quadruple gives a diagram for the overtwisted , so the Dehn twist must be right handed. Therefore and by the classification of smooth genus 1 multisections gives a bisection with divides of the disk bundle of Euler number over the sphere.
In general suppose that is a sequence of curves defining a -section with divides. Then, as in the base case, is a right handed Dehn twist of about and is a right handed Dehn twist of about . Therefore, so that we have indeed plumbed an additional -sphere. ∎

5.2. Stabilization
Here, we will introduce an operation on multisections with divides which takes a genus- -section and produces a genus- -section. An explicit example of this process applied to the genus-1 bisection of can be seen in Figure 18.
This stabilization operation can be seen from both the perspective of a handle decomposition, as in Section 3.1 or from the perspective of a PALF. We will focus on the second perspective, and we recall the definition of a stabilization of a PALF.
Definition 5.2.
Let be a PALF with fiber surface monodromy factorization Then a stabilization of is a PALF with fiber surface and monodromy factorization where is obtained by attaching a 2-dimensional 1-handle to and is a curve on intersecting the belt sphere of the attached 1-handle geometrically once.

By doubling the 1-handle used in a stabilization of a PALF, we obtain the diagram in Figure 17. When glued to a multisection with divides appropriately we obtain a new multisection with divides, whose construction is outlined in the following definition.
Definition 5.3.
Let be a multisection with divides with a diagram given by . Suppose is made up of the curves . Let and be two points on and be an arc between and which is contained in . Let be the surface obtained by removing neighbourhoods of and and gluing in the surface shown in Figure 17 to the resulting boundary where the gluing is performed so that the arc meets the arc to form a curve . By slight abuse of notation, we will keep the notation for the simple closed curve on after performing surgery. We then obtain a new multisection with diagram given by where, for i , and .
We can easily see that is still a multisection diagram with divides. The condition that each curve in each cut system intersects the dividing set in two points is ensured by looking at the model in Figure 17 and the fact that the curve we Dehn twist about is disjoint from the dividing set. That still represents a multisection smoothly follows from Lemma 4.5. That represents a contact Heegaard splitting of the tight contact structure on follows from the fact that we can obtain this contact Heegaard splitting as the boundary of a PALF sector as in the proof of Theorem 4.2.
Observe that the manifold represented by is related to the manifold represented by by attaching a single -handle. Thus if represents a Weinstein domain, then also represents a Weinstein domain obtained by attaching a single Weinstein -handle. (Note that there is no constraint on the attaching data for a -handle attachment to be Weinstein.) By Remark 4.4, the new sector amounts to attaching a Weinstein cobordism to . Therefore, the stabilized diagram also represents a Weinstein domain. Furthermore, the Weinstein cobordism from the sector attaches a Weinstein -handle which cancels with the added -handle (the attaching sphere of the -handle intersects the belt sphere of the -handle in one point). Therefore, in total, we have added a trivial Weinstein cobordism (one which is Weinstein homotopic to a trivial cobordism). Namely, if before stabilization, the multisection diagram with divides represented a Weinstein domain, then after stabilization, the multisection diagram with divides represents the same Weinstein domain up to Weinstein homotopy. We summarize in the following proposition.
Proposition 5.4.
Let be a multisection with divides which admits a multisection diagram with divides given by . Let be a stabilization of with a multisection diagram for given by . Then, is a multisection diagram with divides, and the Weinstein manifolds encoded by and are Weinstein homotopic.

6. Questions
Donaldson [Don96] and Giroux [Gir02, Gir17] proved that every symplectic manifold admits a symplectic divisor such that the complement of a standard neighborhood of the divisor is a Weinstein domain. In search of a diagrammatic theory for closed symplectic manifolds, one strategy would be to find a suitable structure on the neighborhood of the divisor,and glue as in [IslNay20] to a multisection with divides for the Weinstein complement. This leads us to the following questions.
Question 6.1.
Can we construct analogous multisections with divides for symplectic -manifolds with concave boundary? In particular, concave neighborhoods of symplectic divisors. Do we need different diagrammatic information to encode concave boundary? How do we specify in a multisection diagram how to symplectically glue convex pieces to concave pieces?
The results of Section 4 primarily consisted of using PALFs to obtain information about multisections with divides, but in favorable conditions (see Remark 4.4), this construction can be reversed to obtain a PALF from a multisection with divides. It is an open question as to whether two PALFs corresponding to the same Weinstein 4-manifold are related by stabilization, Hurwitz equivalence, and an overall conjugation. We have translated the stabilization move in Section 5.2, and using a similar approach, the other two moves can readily be translated into moves on multisections with divides. Here, techniques used in the stable equivalence of trisections in [GayKir16] could prove fruitful in addressing the following question.